Numerical simulation of secondary breakup of shear-thinning droplets
Abstract
The breakup of non-Newtonian droplets is ubiquitous in numerous applications. Although the non-Newtonian property can significantly change the droplet breakup process, most previous studies consider Newtonian droplets, and the effects of the non-Newtonian properties on the breakup process are still unclear. This study focuses on the secondary breakup of shear-thinning droplets by numerical simulation. The volume of fluid method is used to capture interface dynamics on adaptive grids. To compare shear-thinning droplets and Newtonian droplets, a new definition of the Ohnesorge number is proposed by considering the characteristic shear rate in the droplet induced by the airflow. The results show that compared with the Newtonian fluid, the shear-thinning properties can change the effective viscosity distribution inside the droplet, alter the local deformation, change the droplet morphology, and affect the transition in the droplet breakup regime.
I Introduction
The breakup of droplets is a ubiquitous process in nature and many industrial applications, such as raindrop formation, fuel injection, spray cooling, and powder production. Compared with Newtonian fluids, the characteristics of non-Newtonian fluids have significant effects on the deformation and breakup of droplets. As a common type of non-Newtonian fluids, shear-thinning fluids are widely used in many applications, for example, the atomization of gel fuel in engines. Gel fuel is a type of fuel that can be obtained by gelling traditional fuels. It generally exhibits a shear-thinning property Natan and Rahimi (2002); Padwal, Natan, and Mishra (2021) and has great potential for rocket propulsion. However, the shear-thinning property of gel fuel makes the atomization process complex. To utilize gel fuel effectively, more efforts are needed to understand its atomization process. During the atomization, secondary breakup is a process that droplets further deform and break up into smaller droplets under aerodynamic force. The droplet breakup directly affects the final droplet size of a spray, which further affects the ignition delay and the combustion efficiency in fuel combustion processes. In addition, the shear-thinning property is common in polymer solutions, complex fluids, and suspensions. The breakup of shear-thinning droplets is also involved in many other applications, such as spray coating of thin-film catalyst layers and spray drying in material synthesis. Therefore, it is important to study the breakup of shear-thinning droplets for the relevant applications.
To understand droplet dynamics in the secondary breakup, many researchers have carried out experimental studies using Newtonian fluids Cao et al. (2007); Dai and Faeth (2001); Joseph, Beavers, and Funada (2002); Kulkarni and Sojka (2014); Opfer et al. (2014); Xu, Wang, and Che (2020); Zhao et al. (2010, 2013, 2016). Numerical simulations also play an important role in the study of secondary breakup Dorschner et al. (2020); Feng (2010); Jain et al. (2015, 2019); Jiao et al. (2019); Ling, Zhong, and Peng (2021); Marcotte and Zaleski (2019); Meng and Colonius (2017); Obenauf and Sojka (2021); Rimbert et al. (2020); Stefanitsis et al. (2019); Yang et al. (2017, 2016); Zhu et al. (2021). It can provide detailed information about the breakup process, which is difficult to measure directly in experiments. It is also helpful to understand droplet breakup in different conditions such as high-density ratio Jain et al. (2019), pulsating airflow Ling, Zhong, and Peng (2021), and airflow pressure Zhu et al. (2021). For example, numerical simulations have shown that the liquid-gas density ratio significantly affects the transition state of the critical Weber number and the breakup mode Marcotte and Zaleski (2019); Yang et al. (2017, 2016). The change in the Reynolds number causes significant changes in droplet acceleration, deformation, and breakup dynamics Jain et al. (2019).
For non-Newtonian fluids, the mechanism of secondary droplet breakup has been studied via experiments Gao et al. (2014); Qian et al. (2021); Snyder, Arockiam, and Sojka (2010); Wang et al. (2021); Zhao et al. (2011) and numerical simulations Cao et al. (2022); Chu et al. (2020); Fu et al. (2019); Kant and Banerjee (2022); Markovich et al. (2019); Minakov et al. (2019); Tavangar, Hashemabadi, and Saberimoghadam (2015); Verhulst et al. (2009); Wong et al. (2019). These studies typically focused on the power-law rheological model Cao et al. (2022); Kant and Banerjee (2022); Qian et al. (2021); Wang et al. (2021), Bingham rheological model Markovich et al. (2019); Minakov et al. (2019); Tavangar, Hashemabadi, and Saberimoghadam (2015); Zhao et al. (2011), Herschel-Bulkley rheological model Chu et al. (2020), and Oldroyd-B rheological model Snyder, Arockiam, and Sojka (2010); Verhulst et al. (2009). The results showed that the non-Newtonian characteristics are an important factor affecting the droplet breakup process. For the shear-thickening property, it can induce a hardening deformation mode when the droplet enters the airflow field Wang et al. (2021). For the shear-thinning property, it can make the liquid ring and liquid segments generated by the droplet unable to be completely fragmented under aerodynamic force Qian et al. (2021), and there is a significant change in the deformation rate near the critical Weber number Cao et al. (2022). For polymer solution, Herschel-Bulkley constitutive equations can be used to describe the shear-thinning behavior, and the liquid bag will form an obvious reticular structure which is very different from the breakup of Newtonian fluids Chu et al. (2020). Coal water slurry can be treated as Bingham liquid approximately. Based on the morphology, deformation, and breakup regimes, the breakup of coal water slurry droplets can be categorized into hole breakup and tensile breakup modes Markovich et al. (2019); Minakov et al. (2019). For viscoelastic droplets, apparent persistent ligaments are formed during the bag breakup, rather than being broken directly into smaller droplets for Newtonian droplets Snyder, Arockiam, and Sojka (2010). Although it is widely accepted that the non-Newtonian property can significantly change the droplet breakup process, the above studies mainly focus on the morphology and the difficulty of droplet deformation and breakup, but the mechanism of difference is still not clear, for example, the reason of the unique deformation characteristics of the non-Newtonian droplets.
In this study of the breakup of droplets, we focus on the influence of the shear-thinning property on the breakup process. We find that the shear-thinning property can significantly affect the droplet breakup process by inducing unique viscosity distribution within the droplet. The volume of fluid (VOF) method and adaptive mesh refinement (AMR) technique are used to capture the gas-liquid interface. To compare shear-thinning droplets and Newtonian droplets, a new definition of the Ohnesorge number is proposed by considering the characteristic shear rate in the droplet induced by the airflow. The numerical results are compared with the experimental results to verify the numerical model. The results of shear-thinning droplets are compared with that of Newtonian droplets. Finally, the effects of rheological parameters on the droplet deformation and the breakup mode are analyzed by considering the distribution of the effective viscosity in the droplet.
II Models and methods
II.1 Problem description
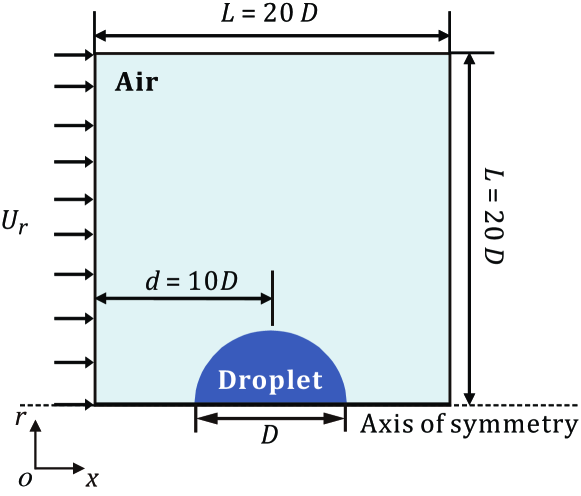
A schematic diagram of the simulation is shown in Fig. 1. An axisymmetric domain is adopted to reduce the computation cost, similar to many previous studies Cao et al. (2022); Feng (2010); Jain et al. (2019); Marcotte and Zaleski (2019). The axisymmetric setting can allow us to consider the initial spherical shape of the droplet and the axisymmetric deformation. However, once the droplet breaks up, the process is three-dimensional, and 2D axisymmetric simulation cannot fully capture the process. Therefore, with the axisymmetric setting, we mainly consider the deformation of the droplet before the breakup. Even though three-dimensional (3D) simulation is possible and adopted by some studies Yang et al. (2017, 2016); Chu et al. (2020); Tavangar, Hashemabadi, and Saberimoghadam (2015), 2D simulation allows us to use a very fine mesh to capture the details of the flow and droplet deformation, which is important for us to unveil the effects of the shear-thinning rheology of the droplet.
The left boundary of the domain is set as uniform velocity inflow . The right and the top boundaries are set free outflow, i.e., a Neumann condition for velocity and a Dirichlet condition for pressure . The droplet has an initial diameter of mm, and it is initially located on the axis 10 away from the left boundary (see the Supplementary Material for the effect of the distance from the left boundary). At the beginning of the simulation, the velocity in the whole domain is set to zero. Then the droplet gradually deforms in the air stream. To quantify the droplet deformation, we use the cross-stream diameter (i.e., the droplet diameter in the cross direction). This parameter is normalized by the initial droplet diameter as .
II.2 Mathematical model
The system contains a droplet of a shear-thinning fluid exposed to the airflow. The droplet and air are considered as incompressible fluids with constant densities. Similar to many previous studies Cao et al. (2022); Meng and Colonius (2017), mass transfer, heat transfer, and gravity are neglected in the simulation because it is very weak in most applications of droplet deformation and breakup processes. With the VOF method, the flow field can be modeled by a single continuum Hirt and Nichols (1981). The continuity equation, the momentum equation, and the transport equation of the volume fraction Berberovic (2010) are solved
| (1) |
| (2) |
| (3) |
where is the velocity vector; is the dynamic viscosity; is the deformation rate tensor given by , and is the surface tension coefficient. In the last item of Eq. (2), represents the surface tension force of the gas-liquid interface. In Eq. (3), is the volume fraction of the liquid in the control volume. It is = 1 if the control volume is full of liquid, and = 0 if full of gas. indicates the existence of an interface in the control volume.
The density and the viscosity of the fluid are expressed as:
| (4) |
| (5) |
where the subscripts and denote the gas (air) and the liquid (shear-thinning or Newtonian droplet) phases, respectively.
The power-law fluid model is adopted to describe the rheology of the shear-thinning fluid Arnold et al. (2010):
| (6) |
where is the effective viscosity, is the shear rate, is the consistency index, and is the flow index of the power-law fluid. When , Eq. (6) describes a Newtonian fluid. When the fluid is shear-thinning, and when the fluid is shear-thickening. In this study, the flow index and the consistency index are varied in the range of and , respectively. The other properties of shear-thinning fluids, Newtonian fluids, and air used in the simulation are listed in Table 1, except otherwise explicitly specified. The density and the surface tension of the droplet are set according to the properties of water. The viscosity of the Newtonian fluid is calculated according to the Ohnesorge number defined in Eq. (12). The governing equations are solved by the open-source multiphase flow solver Basilisk Popinet . Quadtree space discretization is adopted for adaptive mesh refinement (AMR) Lagrée, Staron, and Popinet (2011); Popinet (2003, 2009), which dynamically changes the grid structure according to the local interface shape and the velocity field. Hence, it can increase the simulation resolution without significantly increasing the computational demand.
To quantify the influence of shear-thinning rheological properties on the deformation and breakup process, several dimensionless numbers are used, including the Ohnesorge number, the Weber number, and the dimensionless time. The Ohnesorge number and the Weber number We can be obtained by nondimensionalize the momentum equation (2). By introducing the following variables, , , , , , , , , the momentum equation can be nondimensionalized,
| (7) | ||||
It should be noted that in the definition of the Ohnesorge number, the viscosity of the fluid is involved, which is not a constant for the shear-thinning droplet and depends on the shear rate. Hence, the Ohnesorge number in Eq. (7) is defined in Eq. (12), which can consider the characteristic effective viscosity at the characteristic shear rate in the shear thinning droplet, and the detail will be discussed in Sec. III.1. The Weber number We in Eq. (7) represents the ratio of inertia to surface tension force,
| (8) |
The Weber number in the simulations is varied by changing the initial relative velocity between gas and liquid phases (). Instead of using directly, the dimensionless time is defined following Nicholls and Ranger Nicholls and Ranger (1969):
| (9) |
Hence, .
| Fluids | Viscosity, (Pas) | Density, (kg/m3) | Surface tension, (N/m) |
| Shear-thinning fluid | Eq. (6) | 1000 | 0.07 |
| Newtonian fluid | 1000 | 0.07 | |
| Air | 1.2 | - |
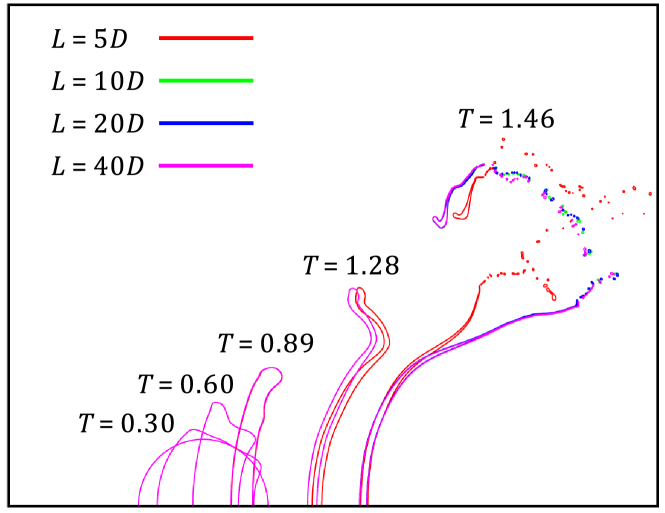
In the simulation, the size of the computational domain needs to be large enough that the selection of the boundary does not affect the simulation results. To select the proper size of the computational domain, four sizes were tested and the results are shown in Fig. 2. The comparison shows that the difference in the early stage of droplet deformation is indistinguishable. As the droplet deforms, the differences gradually become noticeable (). The droplet morphology after the breakup () shows that the domain size of is sufficient to capture the whole process of droplet deformation and breakup, therefore, is selected as the default domain size for further simulations.
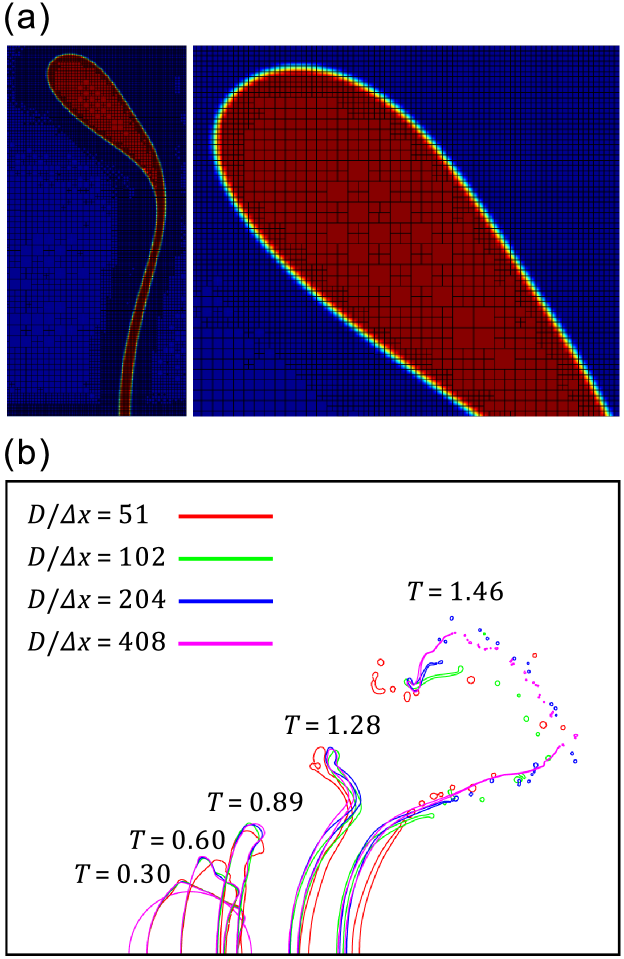
The mesh size in the simulation determines the accuracy and numerical stability, which is crucial for capturing the liquid-gas interface during the droplet deformation and breakup. The adaptive mesh refinement is performed as shown in Fig. 3(a). Compared with static global mesh refinement, the computation time and storage cost of adaptive mesh refinement can be greatly reduced. We progressively increase the maximum level of refinement and compare the results. Fig. 3(b) shows the contours of droplets at four mesh resolutions of = 51, 102, 204, and 408, where is the minimum mesh size. The results show that when is greater than 204, the droplet deformation and breakup are almost independent of the mesh size. Therefore, is used in the following simulations to study the deformation and breakup of droplets.
II.3 Experimental validation
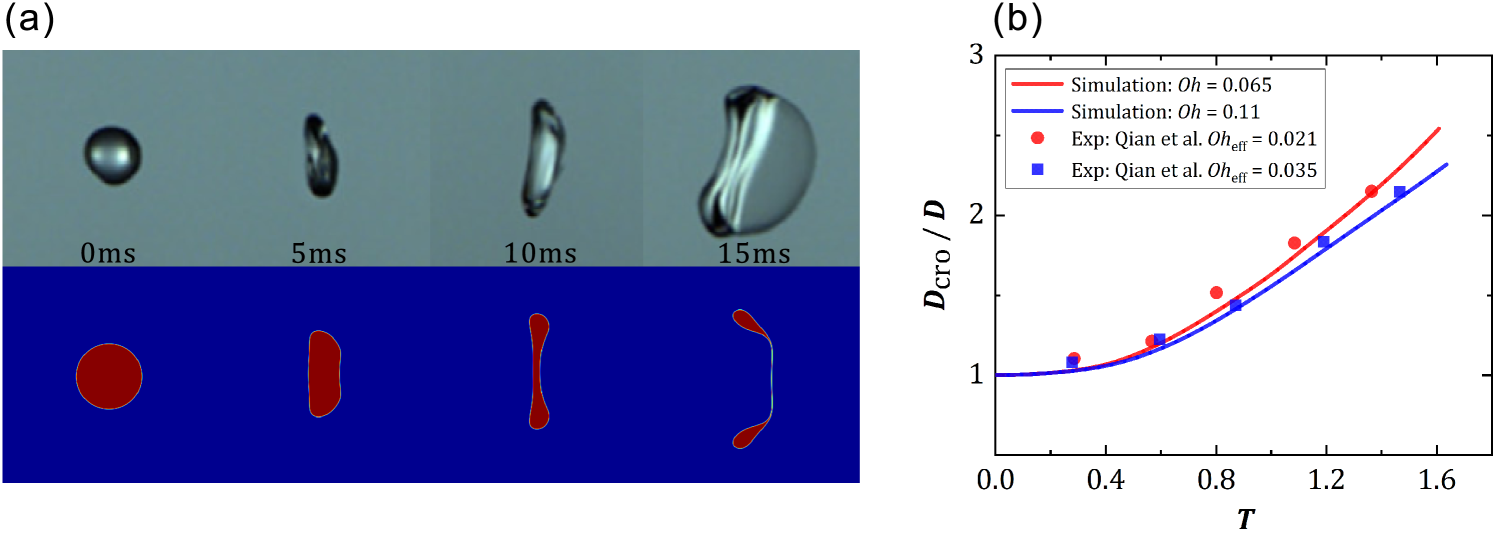
The numerical results are validated against experimental data in Ref. 27, as shown in Fig. 4. The droplet used in Ref. 27 is a 0.2% CMC solution, which is a shear-thinning fluid. The deformation and breakup process of a droplet with from the experiment and simulation is compared in Fig. 4(a). The numerical result is consistent with the experimental result and can reproduce the bag breakup process. In addition, for the multimode breakup, the evolution of the cross-stream diameter of two droplets ( and 0.11) at We = 33 from the experiment and simulations is shown in Fig. 4(b). It can be seen that this numerical model can capture the morphological changes of the droplets reasonably well.
III Results and discussions
III.1 Comparison between Newtonian and shear-thinning droplets
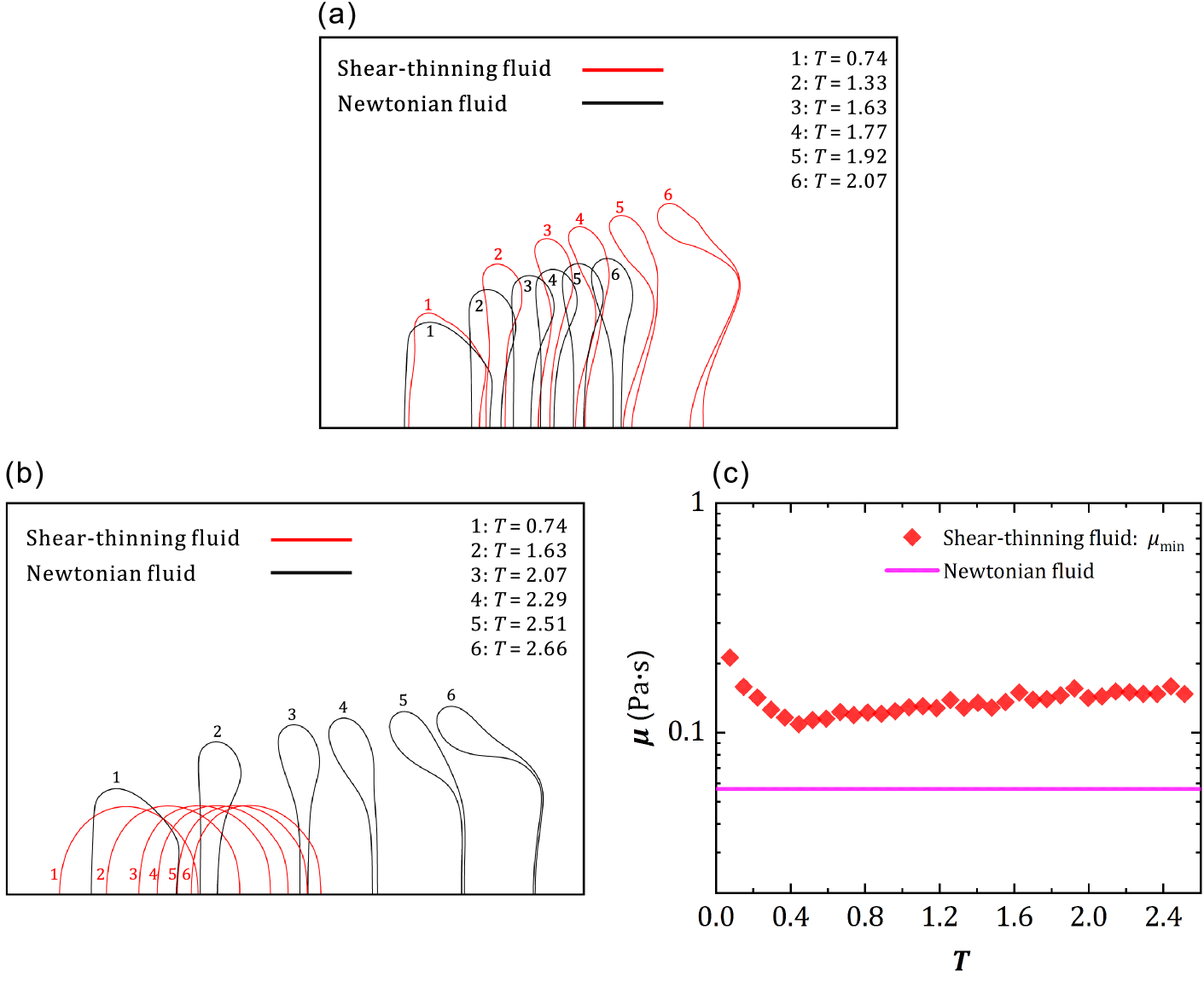
To compare the breakup between Newtonian and shear-thinning droplets, two approaches are widely used. One is to simply change the flow index . If the fluid is Newtonian, and if the fluid is shear-thinning. This approach has been widely used in many studies Cao et al. (2022); Kant and Banerjee (2022); Qian et al. (2021). The breakup process of two droplets using this approach is compared in Fig. 5(a). We can see that as the fluid changes from the Newtonian to shear-thinning (), there is a significant change in the droplet breakup process. The two breakup processes are in different modes at the same We, i.e., the Newtonian droplet is in the bag breakup regime while the shear-thinning droplet is in the multimode breakup regime. This is because in this approach, the magnitudes of viscosities of the two droplets are significantly different. When comparing Newtonian and shear-thinning fluids, it is important to have the same characteristic viscosity. To keep the relative importance of the viscosity the same, a second approach is widely used. Because of the shear-thinning property, the effective viscosity in the droplet is different everywhere. Therefore, a characteristic viscosity should be selected, corresponding to a characteristic shear rate. Many studies used as the characteristic shear rate Chu et al. (2020); Kant and Banerjee (2022). By using this, we can maintain the same effective viscosity by adjusting when we change . The comparison between a Newtonian droplet and a shear-thinning droplet by this approach is shown in Fig. 5(b). We can see that the two breakup processes are also in different modes, i.e., the Newtonian droplet is in the bag breakup regime while the shear-thinning droplet is in the vibrational regime. Moreover, the minimum effective viscosity of the shear-thinning droplet is actually always larger than that of the Newtonian droplet as shown in Fig. 5(c). This indicates that the shear-thinning droplet is too more viscous than the Newtonian droplet, and it is not reasonable to compare these two cases by this approach.
To make a reasonable comparison between Newtonian and shear-thinning droplets, we consider this process by examining the characteristic shear rate. For droplet breakup, the characteristic velocity that determines the characteristic shear rate should be the characteristic velocity in the droplet , not the characteristic velocity in the air . Therefore, the characteristic shear rate () should be . Since the flow velocity in the droplet is induced by the external airflow, we can estimate the characteristic internal velocity of the droplet by considering the inertia of the air and the droplet fluid. Compared with other forces (such as the viscous force), the kinetic energy of the air is the main contribution to the deformation and the breakup of the droplet. Therefore, the inertia of the air should be at the same scale as the inertia of the droplet fluid, , where and are the characteristic velocities in the air and the liquid. As the airflow velocity can be characterized by the relative airflow velocity , we can then have . Therefore, the characteristic shear rate can be estimated as
| (10) |
Then, the characteristic effective viscosity of the droplets in the deformation and breakup process can be written as
| (11) |
Hence, the Ohnesorge number can be expressed as:
| (12) |
For Newtonian fluids (i.e., and ), the Ohnesorge number recovers the original definition. Since both and affect the Ohnesorge number, in some simulations, to maintain the same while changing or , we change accordingly.
Based on the above selection of the characteristic shear rate and the definition of the Ohnesorge number, the deformation and breakup processes of Newtonian droplets and shear-thinning droplets are considered under the same We number and same number, i.e., the same characteristic shear rate and the same effective viscosity. Two typical cases are considered first, one in the bag breakup regime (, , Fig. 6), and the other in multimode breakup regime (, , Fig. 8). The comparison can show that, using this proposed approach, the processes for Newtonian and shear-thinning droplets are comparable. Therefore, the current selection of the characteristic shear rate and the definition of the Ohnesorge number is better than the previous approaches.
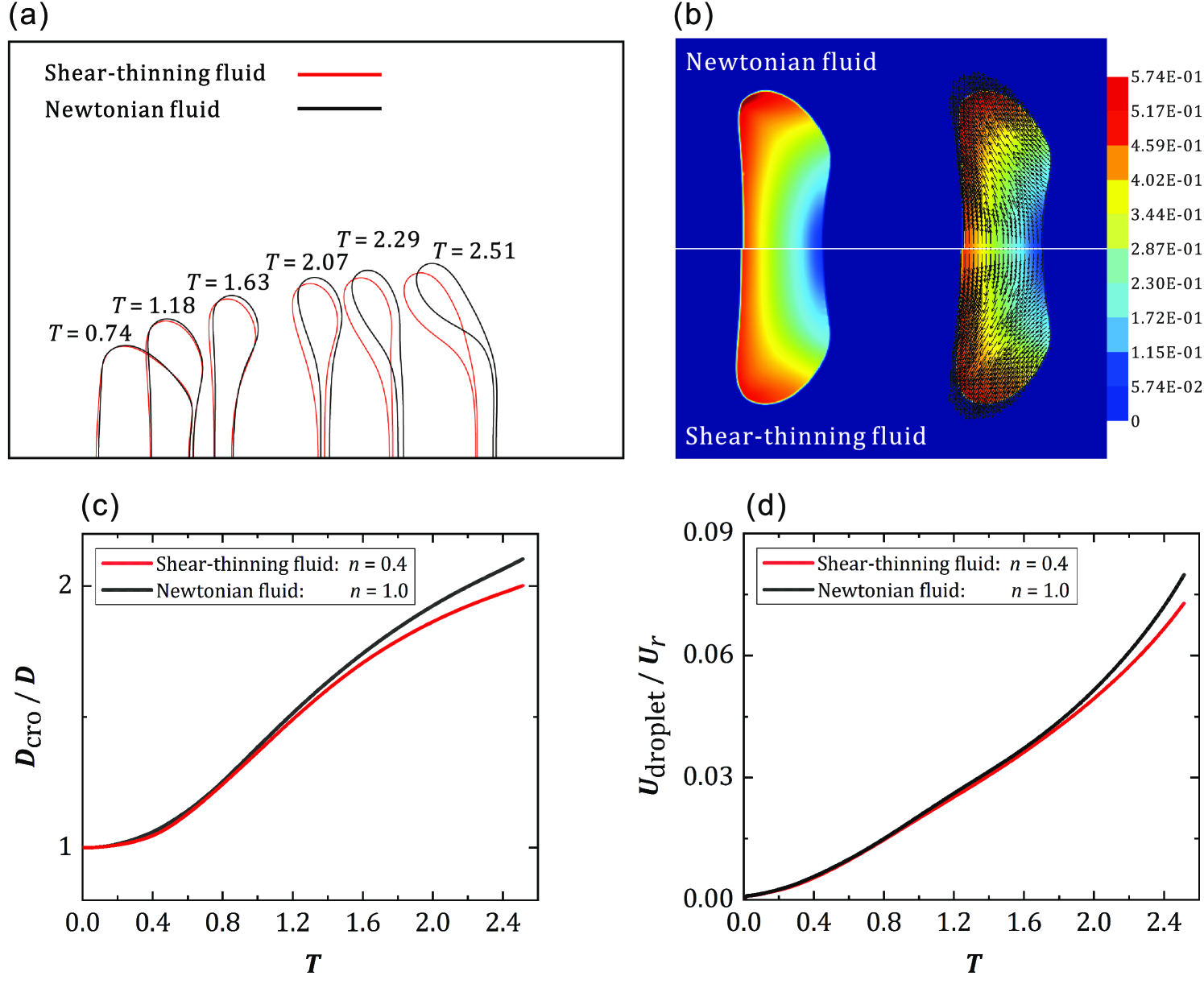
For the bag breakup (, ), in the early stage, the difference in the deformation between the two droplets is small as shown in Fig. 6(a) (Multimedia view). Comparing the velocity fields between the two droplets, we can see that the Newtonian droplet has a high-velocity region on the windward side near the rim, and the internal velocity field is more uniform for the shear-thinning droplets as shown in Fig. 6(b). This will lead to differences in the later deformation of the droplet. In addition, the change rates of , and in these two droplets are almost the same as shown in Fig. 6. While in the later stage, compared with Newtonian fluids, the deformation of the shear-thinning droplet near the center increases, and the center of droplets becomes thinner. The change rate of the cross-stream diameter and the centroid velocity of the shear-thinning droplet is also slower than that of the Newtonian droplet, as shown in Figs. 6(c) and 6(d).
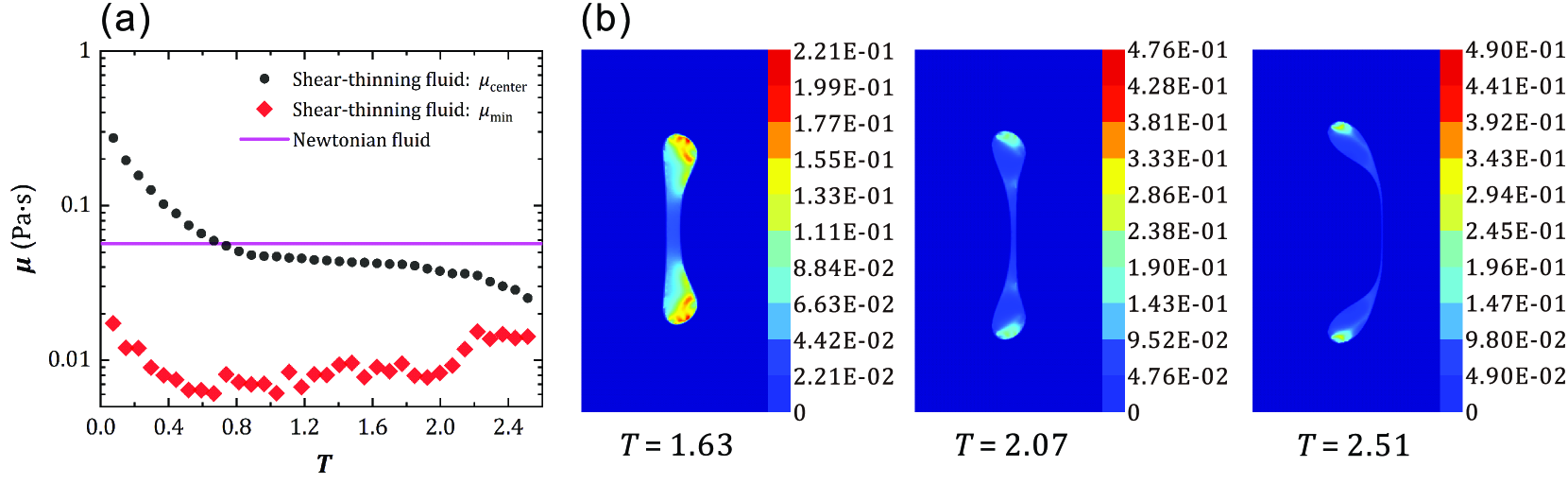
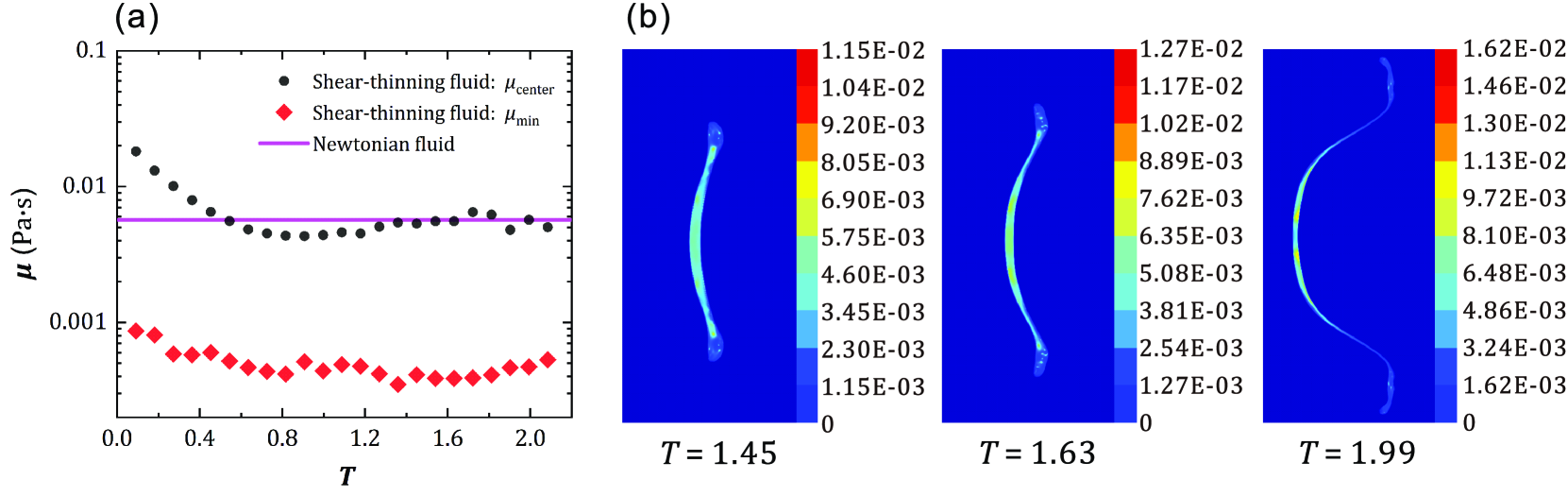
To analyze the origin of the difference between the Newtonian droplet and the shear-thinning droplet in the bag breakup process, the effective viscosity at the droplet center (i.e., the center point on the axis) and the minimum effective viscosity of the shear-thinning droplet are shown in Fig. 7(a). In the later stage, due to the shear-thinning property, and are much smaller than the viscosity of the Newtonian droplet. The distribution of the effective viscosity in the shear-thinning droplet is shown in Fig. 7(b). Even though the characteristic viscosity of the shear-thinning droplet (the effective viscosity at the characteristic shear rate in Eq. (10)) is the same as that of the Newtonian droplet, the effective viscosity is varied within the shear-thinning droplet, which affects the deformation of the droplet. There is a low-viscosity region near the center of the shear-thinning droplet, which enhances the deformation of the droplet center. The position of the minimum effective viscosity is mainly near the center of droplets as shown in Fig. 7(b). Compared with the Newtonian droplet, the effective viscosity around the center of the shear-thinning droplet decreases, and the deformation of the droplet increases.
For the multimode breakup (, ), the difference in the droplet shape between the Newtonian droplet and the shear-thinning droplet in the early stage is also small, as shown in Fig. 8(a) (Multimedia view). By comparing the velocity fields of the two droplets, we can see that the high-speed region is distributed near the rim of the shear-thinning droplet, while it is mainly on the windward side of the rim of the Newtonian fluid, as shown in Fig. 8(b). Such difference will lead to different extent of deformation near the rim of the droplets. In addition, this can also be shown quantitatively by , and in Figs. 8(c) and 8(d). In the later deformation stage, the radial stretching of the shear-thinning droplet near the rim is stronger than that of the Newtonian droplet, while the Newtonian droplet shows stronger forward stretching near the rim and higher overall acceleration. Hence, the change rates of and of the Newtonian droplet are larger than that of the shear-thinning droplet.
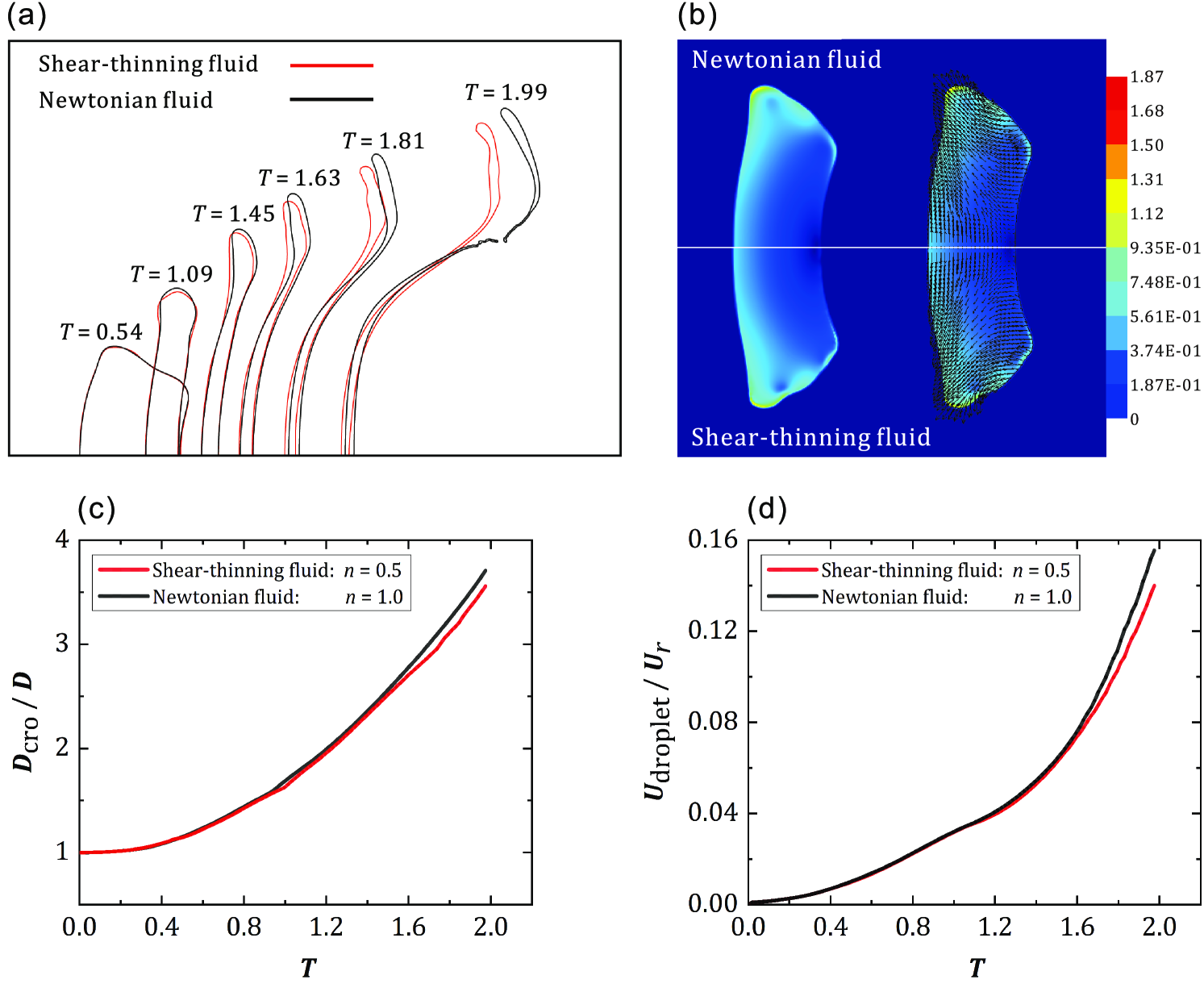
To explain the differences between the two fluids in the multimode breakup process, the effective viscosity at the droplet center and the minimum effective viscosity of the shear-thinning droplet are shown in Fig. 9(a). The minimum effective viscosity inside the shear-thinning droplet is much smaller than that of the Newtonian fluid and is close to the viscosity of the Newtonian droplet. In addition, the distribution of the local viscosity within the shear-thinning droplet is shown in Fig. 9(b), which shows that the viscosity distribution in the shear-thinning droplet is very different from the Newtonian droplet. In the later stage, due to the shear-thinning property, the local viscosity in the outer region is much smaller than that in the inner region, as shown in Fig. 9(b). Compared with the bag breakup case, the effective viscosity is smaller and the aerodynamic effect is stronger in this case. There is also a low-viscosity region in this case but it has transferred from the center to the rim of the shear-thinning droplet, as shown in Fig. 9(b). The low-viscosity region near the rim of the shear-thinning droplet enhances the deformation of the droplet rim. Therefore, the shear-thinning droplet has a strong radial stretching around the rim than the Newtonian droplet.
III.2 Effect of flow index
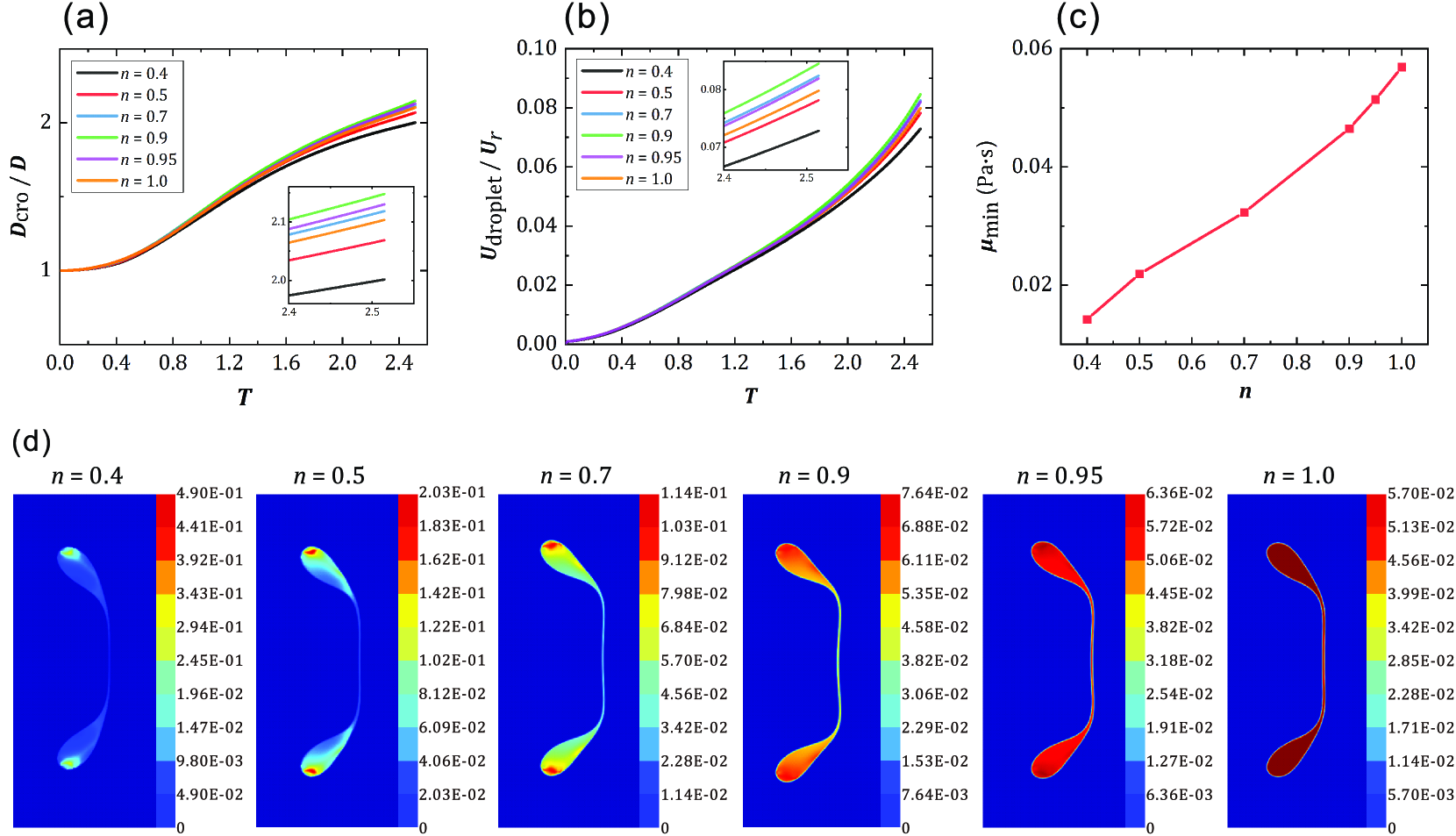
The influence of the rheological parameters on the deformation and breakup mode in the process of droplet breakup is analyzed by changing . The value of is fixed to ensure that the effective viscosity in the simulation is comparable. The effect of on the droplet deformation in the bag breakup mode is analyzed by decreasing from 1 to 0.4, while keeping and . As the value of decreases, the change rates of and first increase slightly and then decrease, and the maximum change rates of these two parameters are at as shown in Figs. 10(a) and 10(b).
This effect can be explained by the shear-thinning property of the droplet. The smaller the value of is, the stronger the shear-thinning effect is. Hence, as decreases, the local effective viscosity inside droplets has a significant change, and the minimum effective viscosity decreases as shown in Fig. 10(c). In addition, the difference in the viscosity within the droplet is more obvious as shown in Fig. 10(d). Because the low-viscosity region is mainly located near the droplet center, the deformation near the droplet center is gradually enhanced. In contrast, the high viscosity around the rim of the droplet hinders the deformation of the droplet. In addition, when approaches 1, the viscosity distribution is almost uniform, and there is no easy-to-deform region. Hence, without strong local deformation, the deformation of the droplet is also relatively slow when approaches 1. Therefore, the shear-thinning property causes the transition of the change rates of and .
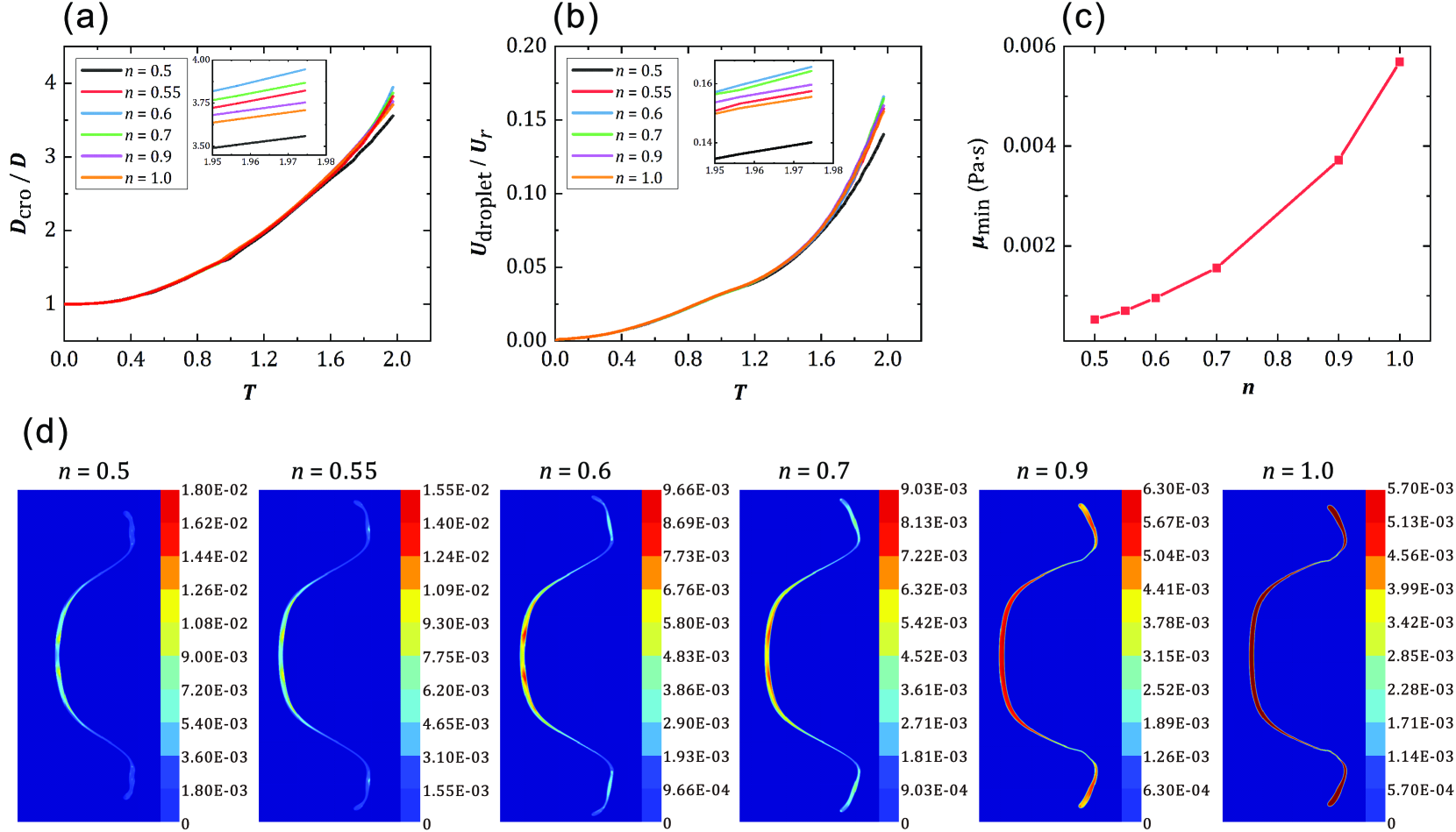
The effect of on the multimode breakup process (We = 30, = 0.010746) is also analyzed. As increases, the change rates of and also first increase and then decrease, and the maximum change rates of these two parameters are at as shown in Figs. 11(a) and 11(b). For this case, as decreases, the shear-thinning effect increases, and the minimum effective viscosity also decreases as shown in Fig. 11(c). In addition, the low-viscosity region is mainly located near the droplet rim and the differences between high-viscosity and low-viscosity regions are significant as shown in Fig. 11(d). As decreases, the radial stretching of the droplet at the rim is gradually enhanced. While the high viscosity region near the center of droplets also hinders the deformation. In addition, when approaches 1, the deformation is also hindered because the viscosity distribution is almost uniform and there is no easy-to-deform region. Therefore, as decreases, there is a change for the rim, i.e., from the forward stretching to the radial stretching. This effect can also be explained by the shear-thinning property. When decreases, the local effective viscosity decreases due to high local velocity and high local shear rate. Therefore, with the decrease of the local effective viscosity, the rim of the droplet is more likely to be accelerated and make stronger radial stretching at a smaller value.
III.3 Effect of Weber number
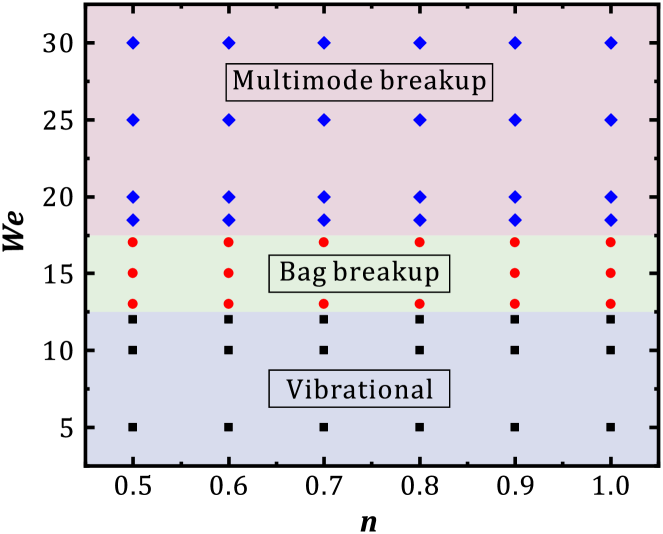
The effect of the Weber number We on the deformation and breakup mode of shear-thinning droplets is analyzed in this section. To consider the effect of We, we fixed other parameters ( and ) and changed the airflow velocity from 8.54 to 22.59 m/s (that is, We from 5 to 35) to explore its influence. Meanwhile, to maintain the constant as changes, we change accordingly. Then, we change the Weber number We and the power-law index , and produce a regime map for the breakup mode in the We– space, as shown in Fig. 12. We can see that the increase of We alters the breakup mode: as the We increases, the droplet changes from the vibrational to the bag breakup, and finally to the multimode breakup. This could be attributed to the higher inertia at large We, which accelerates the droplet deformation remarkably. In addition, the results show that does not influence the breakup mode. This is mainly because we have considered the effect of on the viscosity by using a modified definition of the Ohnesorge number by Eq. (12). Hence, when we change , the overall effect of the viscosity does not change because is fixed at a low value and the effect of is mainly on the local viscosity distribution and the local deformation of the droplet. We will see that the change of does affect the breakup mode when the number is large in Section III.4.
To further see the effect of the Weber number on the droplet deformation and breakup quantitatively, we vary the droplet Weber number and analyze the cross-stream diameter and the centroid velocity of the droplet, as shown in Fig. 13. The change rates of and increase significantly as We increases, as shown in Figs. 13(a) and 13(b). This is because of the stronger effect of the inertia, the differences between high-viscosity and low-viscosity regions are significant and decreases with the increase of We, as shown in Fig. 13(c), which accelerates the droplet deformation. The distribution of the effective viscosity is shown in Fig. 13(d). We can see that, as the Weber number increases, the low-viscosity region gradually transits from the center region to the rim region of the droplet. As the low-viscosity region moves, the deformation of the droplet is also affected.
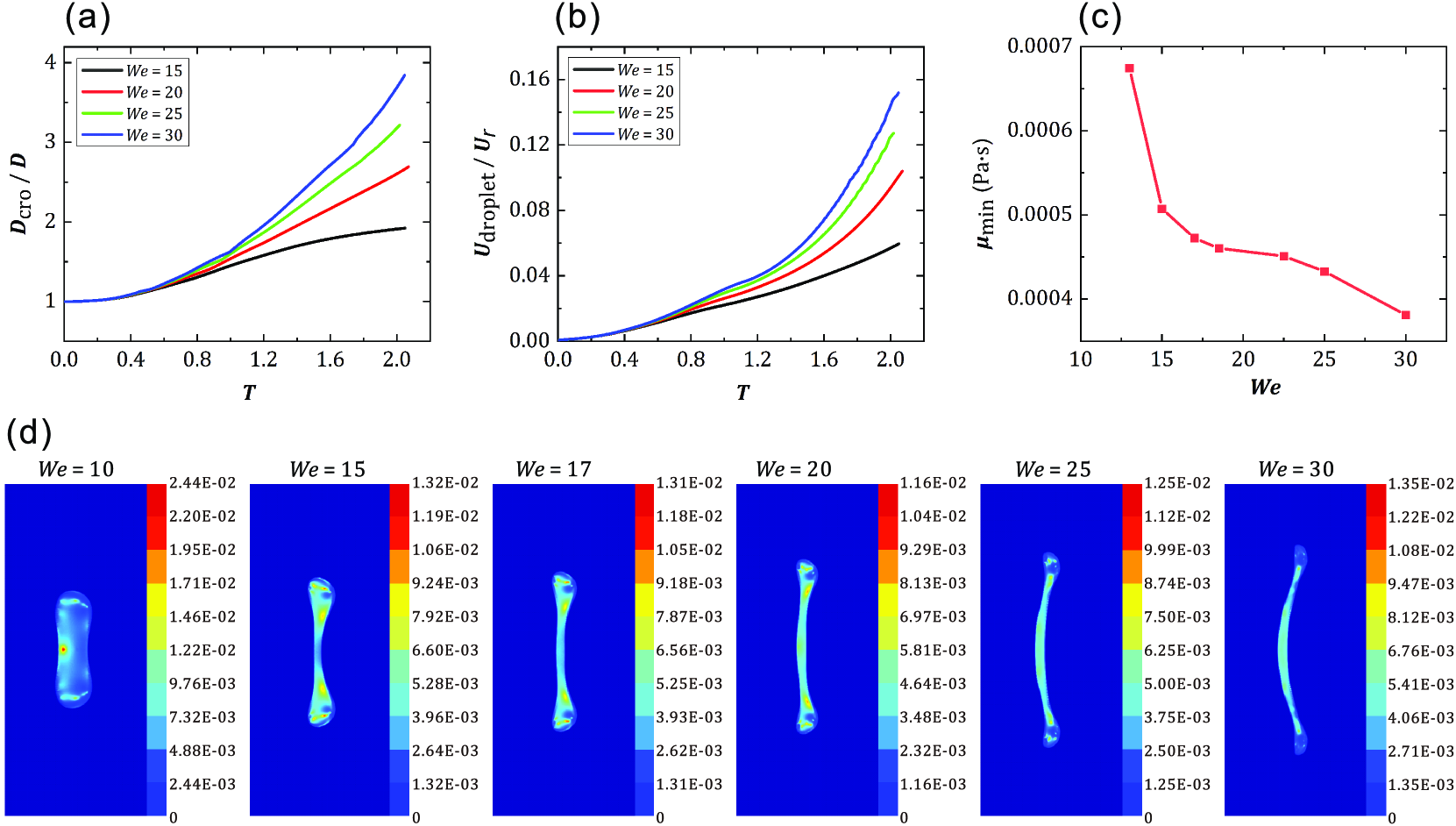
III.4 Effect of Ohnesorge number
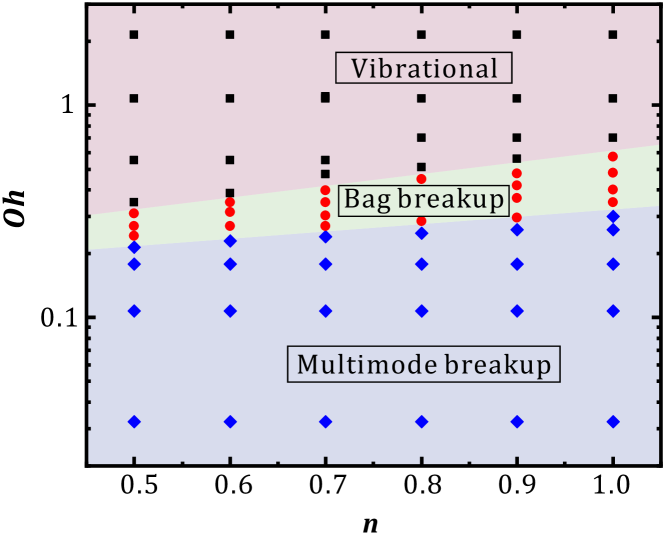
The effects of the Ohnesorge number on the deformation process and breakup mode of shear-thinning droplets are analyzed in this section. To consider the effect of , we fix other parameters (We and ) and change the consistency index to explore its influence. Then, we vary and to produce a regime map in the – space, as shown in Fig. 14. Three modes occur as and vary, namely multimode breakup, bag breakup, and vibrational mode. When is small and is large, the breakup is a multimode breakup, which is mainly because the effective viscosity is small and the droplet deforms easily. As increases, the low-viscosity region transfers from the rim to the center of the droplet, and the breakup is in the bag breakup mode. When is large and is small, the effective viscosity is very large. Hence, the droplet only vibrates instead of breakup. From Fig. 14, we can also see that as increases, the transitional for the change in the breakup mode increases. This is mainly because when is large, the value of needs to be increased to reach the same breakup mode, then the number increases accordingly.
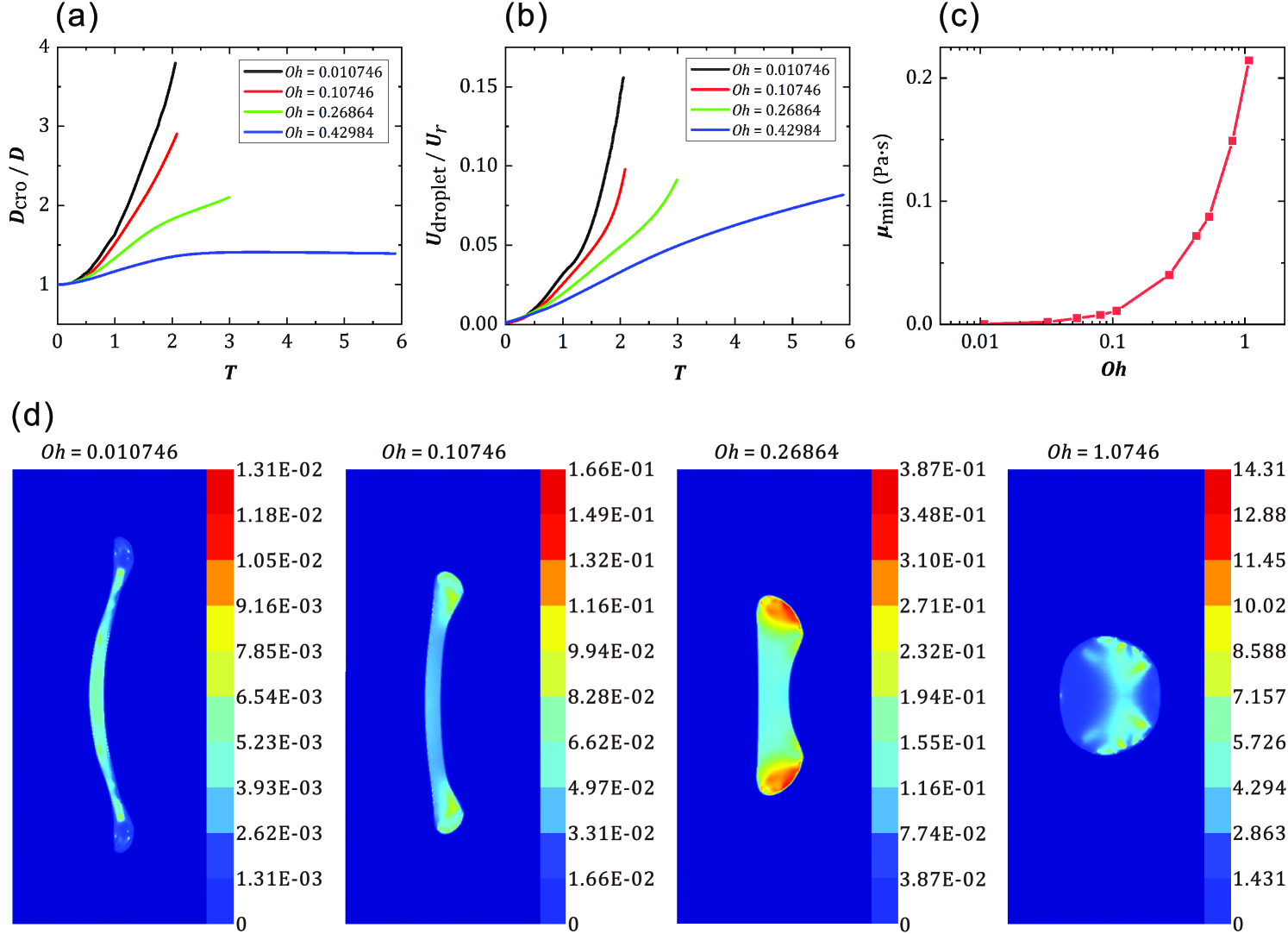
To study the effect of the Ohnesorge number on droplet deformation and breakup quantitatively, we vary the Ohnesorge number and analyze the cross-stream diameter and the centroid velocity of the droplet. As increases, the change rates of and of droplets decrease significantly, as shown in Figs. 15(a) and 15(b). This is because of the higher viscous stress within the droplet at large , which inhibits the droplet deformation remarkably. To confirm this, the minimum effective viscosity for different at = 1.97 is given in Fig. 15(c). When is small and as it increases, the aerodynamic force dominates the deformation of the droplet and the minimum effective viscosity has a small increase. With the further increase of , significantly increases as shown in Fig. 15(c). In addition, the distribution of the effective viscosity within the shear-thinning droplets is plotted in Fig. 15(d). With the increases of , the effective viscosity of the droplet increases, and the low-viscosity region inside the droplet transits from the rim of the droplet to the center. Hence, a high-viscosity region appears on the leeward side of the droplet and prohibits the deformation of the droplet. Therefore, the deformation and breakup mode of droplets are also affected.
IV Conclusion
In this study, we consider the secondary breakup of shear-thinning droplets by numerical simulation. To compare between shear-thinning droplets and Newtonian droplets, a new definition of the Ohnesorge number is proposed by considering the characteristic shear rate in the droplet induced by the airflow. The cross-stream diameter and the centroid velocity of the droplet are used to quantify the deformation process of the droplet. The results show that the shear-thinning property can affect the droplet deformation both in the bag breakup and multimode breakup regimes by influencing the local effective viscosity within the droplet. During the bag breakup, as the power-law index decreases there has small local effective viscosity near the center of the droplets, which accelerates the droplet deformation near the center remarkably. During the multimode breakup, as decreases, the low viscosity region transits from the center to the rim of droplets and the radial stretching deformation of the droplet is significantly enhanced. Under the same effective viscosity, as the Weber number increases, the minimum effective viscosity decreases, and the breakup transits from the vibrational to the bag breakup, and then to the multimode breakup. As the Ohnesorge number increases, the effective viscosity increases and the deformation degree of the droplets is significantly inhibited. This study mainly considers the deformation and breakup of shear-thinning droplets. Other types of non-Newtonian fluids can affect the process, such as shear-thickening fluids, Bingham fluids, and viscoelastic fluids. The method used in this study can also be extended to consider the non-Newtonian rheology of other fluids, which requires further studies. The results of this study are not only useful for unveiling the influence mechanism of shear-thinning properties in the process of the secondary breakup, but also are helpful to relevant applications such as fuel atomization, spray painting, and powder production.
Supplementary Material
See supplementary material for the effect of the initial distance of the droplet from the left boundary.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant nos. 51676137 and 51921004).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
- Natan and Rahimi (2002) B. Natan and S. Rahimi, “The status of gel propellants in year 2000,” International Journal of Energetic Materials and Chemical Propulsion 5, 172–194 (2002).
- Padwal, Natan, and Mishra (2021) M. B. Padwal, B. Natan, and D. P. Mishra, “Gel propellants,” Prog. Energ. Combust. 83, 100885 (2021).
- Cao et al. (2007) X. K. Cao, Z. G. Sun, W. F. Li, H. F. Liu, and Z. H. Yu, “A new breakup regime of liquid drops identified in a continuous and uniform air jet flow,” Phys. Fluids 19, 057103 (2007).
- Dai and Faeth (2001) Z. Dai and G. Faeth, “Temporal properties of secondary drop breakup in the multimode breakup regime,” Int. J. Multiphase Flow 27, 217–236 (2001).
- Joseph, Beavers, and Funada (2002) D. D. Joseph, G. S. Beavers, and T. Funada, “Rayleigh-Taylor instability of viscoelastic drops at high Weber numbers,” J. Fluid. Mech. 453, 109–132 (2002).
- Kulkarni and Sojka (2014) V. Kulkarni and P. E. Sojka, “Bag breakup of low viscosity drops in the presence of a continuous air jet,” Phys. Fluids 26, 072103 (2014).
- Opfer et al. (2014) L. Opfer, I. V. Roisman, J. Venzmer, M. Klostermann, and C. Tropea, “Droplet-air collision dynamics: evolution of the film thickness,” Phys. Rev. E. 89, 013023 (2014).
- Xu, Wang, and Che (2020) Z. Xu, T. Wang, and Z. Che, “Droplet deformation and breakup in shear flow of air,” Phys. Fluids 32, 052109 (2020).
- Zhao et al. (2010) H. Zhao, H. Liu, W. Li, and J. Xu, “Morphological classification of low viscosity drop bag breakup in a continuous air jet stream,” Phys. Fluids 22, 114103 (2010).
- Zhao et al. (2013) H. Zhao, H. Liu, J. Xu, W. Li, and K. Lin, “Temporal properties of secondary drop breakup in the bag-stamen breakup regime,” Phys. Fluids 25, 054102 (2013).
- Zhao et al. (2016) H. Zhao, W. Zhang, J. Xu, W. Li, and H. Liu, “Influence of surfactant on the drop bag breakup in a continuous air jet stream,” Phys. Fluids 28, 054102 (2016).
- Dorschner et al. (2020) B. Dorschner, L. Biasiori-Poulanges, K. Schmidmayer, H. El-Rabii, and T. Colonius, “On the formation and recurrent shedding of ligaments in droplet aerobreakup,” J. Fluid. Mech. 904, A20 (2020).
- Feng (2010) J. Q. Feng, “A deformable liquid drop falling through a quiescent gas at terminal velocity,” J. Fluid. Mech. 658, 438–462 (2010).
- Jain et al. (2015) M. Jain, R. S. Prakash, G. Tomar, and R. V. Ravikrishna, “Secondary breakup of a drop at moderate Weber numbers,” Proc. R. Soc. A. 471, 20140930 (2015).
- Jain et al. (2019) S. S. Jain, N. Tyagi, R. S. Prakash, R. V. Ravikrishna, and G. Tomar, “Secondary breakup of drops at moderate Weber numbers: effect of density ratio and Reynolds number,” Int. J. Multiphase Flow 117, 25–41 (2019).
- Jiao et al. (2019) D. Jiao, K. Jiao, F. Zhang, and Q. Du, “Direct numerical simulation of droplet deformation in turbulent flows with different velocity profiles,” Fuel 247, 302–314 (2019).
- Ling, Zhong, and Peng (2021) C. Ling, Y. Zhong, and L. Peng, “Three-dimensional numerical research on the effects of lateral pulsating airflow on droplet breakup,” Phys. Fluids 33, 033303 (2021).
- Marcotte and Zaleski (2019) F. Marcotte and S. Zaleski, “Density contrast matters for drop fragmentation thresholds at low Ohnesorge number,” Phys. Rev. Fluids 4, 103604 (2019).
- Meng and Colonius (2017) J. C. Meng and T. Colonius, “Numerical simulation of the aerobreakup of a water droplet,” J. Fluid. Mech. 835, 1108–1135 (2017).
- Obenauf and Sojka (2021) D. G. Obenauf and P. E. Sojka, “Theoretical deformation modeling and drop size prediction in the multimode breakup regime,” Phys. Fluids 33, 092113 (2021).
- Rimbert et al. (2020) N. Rimbert, S. Castrillon Escobar, R. Meignen, M. Hadj-Achour, and M. Gradeck, “Spheroidal droplet deformation, oscillation and breakup in uniform outer flow,” J. Fluid. Mech. 904, A15 (2020).
- Stefanitsis et al. (2019) D. Stefanitsis, I. Malgarinos, G. Strotos, N. Nikolopoulos, E. Kakaras, and M. Gavaises, “Numerical investigation of the aerodynamic breakup of droplets in tandem,” Int. J. Multiphase Flow 113, 289–303 (2019).
- Yang et al. (2017) W. Yang, M. Jia, Z. Che, K. Sun, and T. Wang, “Transitions of deformation to bag breakup and bag to bag-stamen breakup for droplets subjected to a continuous gas flow,” Int. J. Heat Mass Tran. 111, 884–894 (2017).
- Yang et al. (2016) W. Yang, M. Jia, K. Sun, and T. Wang, “Influence of density ratio on the secondary atomization of liquid droplets under highly unstable conditions,” Fuel 174, 25–35 (2016).
- Zhu et al. (2021) W. Zhu, N. Zhao, X. Jia, X. Chen, and H. Zheng, “Effect of airflow pressure on the droplet breakup in the shear breakup regime,” Phys. Fluids 33, 053309 (2021).
- Gao et al. (2014) J. Gao, N. S. Rodrigues, P. E. Sojka, and J. Chen, “Measurement of aerodynamic breakup of non-Newtonian drops by digital in-line holography,” in Fluids Engineering Division Summer Meeting (2014) p. V002T11A009.
- Qian et al. (2021) L. Qian, X. Zhong, C. Zhu, and J. Lin, “An experimental investigation on the secondary breakup of carboxymethyl cellulose droplets,” Int. J. Multiphase Flow 136, 103526 (2021).
- Snyder, Arockiam, and Sojka (2010) S. Snyder, N. Arockiam, and P. Sojka, “Secondary atomization of elastic non-Newtonian liquid drops,” in 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (2010) p. 6822.
- Wang et al. (2021) Z. Y. Wang, H. Zhao, W. F. Li, J. L. Xu, and H. F. Liu, “Secondary breakup of shear thickening suspension drop,” Phys. Fluids 33, 093103 (2021).
- Zhao et al. (2011) H. Zhao, H. Liu, J. Xu, and W. Li, “Secondary breakup of coal water slurry drops,” Phys. Fluids 23, 113101 (2011).
- Cao et al. (2022) Q. Cao, W. Liao, B. Natan, F. Feng, and W. Wu, “Secondary atomization of non-Newtonian kerosene gel at low Weber numbers: A numerical study,” Aerosp. Sci. Technol. 120, 107280 (2022).
- Chu et al. (2020) G. Chu, L. Qian, X. Zhong, C. Zhu, and Z. Chen, “A numerical investigation on droplet bag breakup behavior of polymer solution,” Polymers 12, 2172 (2020).
- Fu et al. (2019) P. Fu, L. Hou, Z. Ren, Z. Zhang, X. Mao, and Y. Yu, “A droplet/wall impact model and simulation of a bipropellant rocket engine,” Aerosp. Sci. Technol. 88, 32–39 (2019).
- Kant and Banerjee (2022) K. Kant and R. Banerjee, “Study of the secondary droplet breakup mechanism and regime map of Newtonian and power law fluids at high liquid-gas density ratio,” Phys. Fluids 34, 043108 (2022).
- Markovich et al. (2019) D. M. Markovich, A. Shebeleva, A. Minakov, A. Lobasov, A. Shebelev, P. A. Kuibin, and M. A. Vorobyev, “Numerical modelling of destruction of a drop of non-Newtonian fluid in a gas flow,” EPJ Web. Conf. 196, 00042 (2019).
- Minakov et al. (2019) A. V. Minakov, A. A. Shebeleva, P. A. Strizhak, M. Y. Chernetskiy, and R. S. Volkov, “Study of the Weber number impact on secondary breakup of droplets of coal water slurries containing petrochemicals,” Fuel 254, 115606 (2019).
- Tavangar, Hashemabadi, and Saberimoghadam (2015) S. Tavangar, S. H. Hashemabadi, and A. Saberimoghadam, “CFD simulation for secondary breakup of coal-water slurry drops using OpenFOAM,” Fuel Process Technol. 132, 153–163 (2015).
- Verhulst et al. (2009) K. Verhulst, R. Cardinaels, P. Moldenaers, Y. Renardy, and S. Afkhami, “Influence of viscoelasticity on drop deformation and orientation in shear flow,” J. Non-Newton. Fluid Mech. 156, 29–43 (2009).
- Wong et al. (2019) V. L. Wong, K. Loizou, P. L. Lau, R. S. Graham, and B. N. Hewakandamby, “Characterizing droplet breakup rates of shear-thinning dispersed phase in microreactors,” Chem. Eng. Res. Des. 144, 370–385 (2019).
- Hirt and Nichols (1981) C. W. Hirt and B. D. Nichols, “Volume of fluid (VOF) method for the dynamics of free boundaries,” J. Comput. Phys. 39, 201–225 (1981).
- Berberovic (2010) E. Berberovic, Investigation of free-surface flow associated with drop impact: numerical simulations and theoretical modeling, Thesis, Technische Universität (2010).
- Arnold et al. (2010) R. Arnold, W. Anderson, P. Santos, M. deRidder, and O. Campanella, “Comparison of monomethylhydrazine/hydroxypropylcellulose and hydrocarbon/silica gels,” in 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition (2010) p. 422.
- (43) S. Popinet, “Basilisk, a free-software program for the solution of partial differential equations on adaptive cartesian meshes,” http://basilisk.fr .
- Lagrée, Staron, and Popinet (2011) P.-Y. Lagrée, L. Staron, and S. Popinet, “The granular column collapse as a continuum: validity of a two-dimensional Navier-Stokes model with a (I)-rheology,” J. Fluid. Mech. 686, 378–408 (2011).
- Popinet (2003) S. Popinet, “Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries,” J. Comput. Phys. 190, 572–600 (2003).
- Popinet (2009) S. Popinet, “An accurate adaptive solver for surface-tension-driven interfacial flows,” J. Comput. Phys. 228, 5838–5866 (2009).
- Nicholls and Ranger (1969) J. A. Nicholls and A. A. Ranger, “Aerodynamic shattering of liquid drops,” AIAA J. 7, 285–290 (1969).