Observability and State Estimation for a Class of Nonlinear Systems
Abstract
We derive sufficient conditions for the solvability of the state estimation problem for a class of nonlinear control time-varying systems which includes those, whose dynamics have triangular structure. The state estimation is exhibited by means of a sequence of functionals approximating the unknown state of the system on a given bounded time interval. More assumptions guarantee solvability of the state estimation problem by means of a hybrid observer.
Index Terms:
nonlinear systems, observability, state estimation, hybrid observers.I Introduction
Many important approaches have been presented in the literature concerning the state estimation problem for a given nonlinear control system (see for instance [1] - [19], [21] - [25], [27], [28] and relative references therein). Most of them are based on the existence of an observer system exhibiting state estimation. The corresponding hypotheses include observability assumptions and persistence of excitation. In [8], [9] and [10] Luenberger type observers and switching estimators are proposed for a general class of triangular systems under weaker assumptions than those adopted in the existing literature. In [16] and [24] the state estimation is exhibited for a class of systems by means of a hybrid observer.
The present note is inspired by the approach adopted in [16], where a ”hybrid dead-beat observer” is used, as well as by the methodologies applied in [20], [26] and [29], where, fixed point theorems are used for the establishment of sufficient conditions for observability and asymptotic controllability. Our main purpose is to establish that, under certain hypotheses, including persistence of excitation, the State Estimation Design Problem (SEDP) around a given fixed value of initial time is solvable for a class of nonlinear systems by means of a sequence of mappings , exclusively dependent on the dynamics of the original system, the input and the corresponding output , and further each is independent of the time-derivatives of and . An algorithm for explicit construction of these mappings is provided.
We consider time-varying finite dimensional nonlinear control systems of the form:
| (1.1a) | |||
| with output | |||
| (1.1b) | |||
where is the input of (1.1). Our main results establish sufficient conditions for the approximate solvability of the SEDP for (1.1). The paper is organized as follows. Section II contains definitions, assumptions, as well as statement and proof of our main result (Proposition 2.1) concerning the state estimation problem for the general case (1.1). We apply in Section III the main result of Section II for the derivation of sufficient conditions for the solvability of the same problem for certain subclasses of systems (1.1), whose dynamics have triangular structure (Proposition 3.1). According to our knowledge, the sufficient conditions proposed in Sections II, III are weaker than those imposed in the existing literature for the solvability of the observer design problem for the same class of systems. More extensions are discussed in Section IV of present work, concerning the solvability of the SEDP by means of a hybrid observer under certain additional assumptions (Proposition 4.1).
Notations: For given , denotes its usual Euclidean norm. For a given constant matrix , denotes its transpose and is its induced norm. For any nonempty set and map we adopt the notation .
II Hypotheses and Main Result
In this section we provide sufficient conditions for observability of (1.1) and solvability of the SEDP. We assume that for each the mappings , and are continuous and further is (locally) Lipschitz continuous with respect to , i.e., for every bounded and there exists a constant such that
| (2.1) |
Also, assume that for any the mappings , and are measurable and locally essentially bounded in . Let and let be a nonempty set of inputs of (1.1) (without any loss of generality it is assumed that is independent of the initial state). Define by the set of outputs of (1.1) defined on the interval corresponding to some input :
| (2.2) |
provided that where is the maximum time of existence of the solution of (1.1) with initial .
Definition II.1
Let be a nonempty subset of . We say that (1.1) is observable over , if for all , almost all near , input and output , there exists a unique such that
| (2.3) |
According to Definition 2.1, observability is equivalent to the existence of a (probably noncausal) functional , such that, for every for which (2.3) holds for certain and , we have:
| (2.4) |
and is exclusively dependent on the input and the output of (1.1) and is in general noncausal. Knowledge of satisfying the previous properties guarantees knowledge of the initial state value, thus knowledge of the future values of the solution of (1.1), provided that the system is complete.
Definition II.2
Let be a nonempty subset of . We say that the SEDP is solvable for (1.1) over , if there exists a functional , , near , being in general noncausal, such that (2.4) is fulfilled for every for which (2.3) holds for certain and further is exclusively depended on and and the dynamics of (1.1) and it does not include any differentiation of their arguments. It turns out that is independent of the time-derivatives of and , whenever they exist.
It is worthwhile to remark here that the approach proposed in [16] for the construction of a hybrid dead-beat observer for a subclass of systems (1.1) is based on an explicit construction of a (noncausal) map satisfying (2.4). However, for general nonlinear systems, the precise and direct determination of the functional is a difficult task. The difficulty comes from our requirements for the candidate to be exclusively dependent on and and the dynamics of system and, for practical reasons, it should be independent of the time-derivatives of and . We next provide a weaker sequential type of definition of the solvability of SEDP, which is adopted in the present work, in order to achieve the state determination for general case (1.1) by employing an explicit approximate strategy.
Definition II.3
We say that the approximate SEDP is solvable for system (1.1) over , if there exist functionals (being in general noncausal), such that, if we denote:
| (2.5) |
then
(I) the mappings are exclusively dependent on the input and the corresponding output , the dynamics of system (1.1) and further their domains do not include any differentiation of their arguments. It turns out that each should be independent of the time-derivatives of and (whenever they exist);
(II) the following hold:
| (2.6a) | |||
| (2.6b) |
It should be emphasised that uniqueness requirement in (2.6b) is not essential. We may replace (2.6b) by the assumption that there exists satisfying both (2.3) and (2.6a). Then uniqueness of such a vector is a consequence of (2.6a), definition (2.5) and the fact that each functional exclusively depends on and .
Obviously, according to the definitions above, the following implications hold:
Solvability of SEDP Solvability of approximate SEDP Observability (over ).
For completeness, we note that the first implication follows by setting in (2.4). The second implication is a direct consequence of both assumptions (2.6a,b), definition (2.5) and the exclusive dependence of each from and . The converse claims are not in general valid; particularly, observability does not in general imply solvability of the (approximate) SEDP, due to the additional requirements of Definitions 2.2 and 2.3 concerning the independence , , respectively, from the time-derivatives of and .
From (2.6a) we deduce that, if the approximate SEDP is solvable for (1.1) over , then for any for which it holds:
| (2.7) |
Remark II.1
(i) Condition (2.7) guarantees that for any given interval with , the unknown solution of (1.1) is uniformly approximated by a sequence of trajectories of the system
with as given in Definition 2.2.
(ii) If the system (1.1) is complete, then (2.7) implies solvability of the approximate SEDP, thus, observability for (1.1) over . Indeed, let and without loss of generality consider arbitrary . It follows by invoking the forward completeness assumption and (2.7) that , where and simultaneously (2.3) and (2.6a) hold with and , instead of and , respectively. Moreover, due to the backward completeness, is the unique vector for which .
In order to state and establish our main result, we first require the following notations and additional assumptions for the dynamics of (1.1). Consider , , , and . We denote by the fundamental matrix solution of
| (2.8a) | |||
| (2.8b) |
and define the mappings:
| (2.9) |
| (2.10) |
We are in a position to provide our main assumptions together with the statement and proof of our main result.
A1. For system (1.1) we assume that there exists a nonempty subset of in such a way that for all , close to and for each and it holds:
| (2.11) |
where the map is given by (2.9);
A2. In addition, we assume that for every , close to , , , and constants there exists a constant such that
| (2.12) |
Assumption A1 is a type of persistence of excitation and A2 is a type of contraction condition. Assumptions A1 and A2 are in general difficult to be checked, however, they are both fulfilled for a class of nonlinear triangular systems, under weak assumptions that are exclusively expressed in terms of system’s dynamics (see (3.1) in the next section). We are in a position to state and prove our main result. Our approach leads to an explicit algorithm for the state estimation.
Proposition II.1
Assume that A1 and A2 are fulfilled. Then the approximate SEDP is solvable for (1.1) over the set ; consequently (1.1) is observable over .
Proof:
Let , , , with as given in A1 and A2, and let be a solution of (1.1) corresponding to and satisfying (2.3). Consider the trajectory of the auxiliary system:
| (2.13a) | |||
| (2.13b) | |||
for certain initial . The map is written:
| (2.14) |
By multiplying by and integrating we find:
The latter in conjunction with (2.9) - (2.11) yields:
| (2.15) |
By considering the solution of (1.1) corresponding to same with and with same initial , it follows from (2.13) that the mappings and coincide, therefore, from (2.14) we get:
| (2.16) |
Let and define:
| (2.17) |
Then, by (2.15) and (2.16) we have:
| (2.18) |
Next, consider a strictly increasing sequence defined as:
| (2.19) |
Since, due to continuity of , the set is bounded, there exists an integer such that
| (2.20) |
Let
| (2.21) |
By virtue of (2.1), (2.12) and (2.16) it follows that for the above there exists a decreasing continuous function with and such that
| (2.22) |
Finally, define:
| (2.23a) | |||
| (2.23b) | |||
with arbitrary
| (2.24) |
Then by (2.19) and (2.21)-(2.23) we get
| (2.25) |
According to (2.22b) let . Then, from (2.17), (2.21)-(2.24) and the fact that the sequence is decreasing, we have:
| (2.26) |
therefore, by invoking (2.18), (2.19), (2.20), (2.23) and (2.25) it follows:
| (2.27) |
Quite similarly, by induction we get:
| (2.28) |
which implies
| (2.29) |
where the values above are exclusively dependent on the values of the input and the output and the dynamics of system and they are independent of any time-derivatives of and , thus both (2.6a) and (2.6b) are fulfilled. We conclude that the approximate SEDP is solvable for (1.1) over , therefore, system (1.1) is observable over . ∎
The existence result of Proposition 2.1 does not in general determine explicitly the desired sequence of mappings exhibiting (2.27). The reason is that, although existence of the constant satisfying (2.19) is guaranteed from boundedness of , its precise determination requires knowledge of a bound of the previous set, which, in general, is not available. The rest part of this section is devoted for the establishment of a constructive algorithm, exhibiting the state determination. The corresponding procedure is based on the approach given in proof of Proposition 2.1 plus some appropriate modifications.
Algorithm
To simplify the procedure, we distinguish two cases:
Case I: First, we assume that a bounded region of the state space is a priori known, where the unknown initial state of (1.1) belongs. Particularly, assume that for all , almost all near and input , an open ball of radius centered at zero is known, such that the corresponding set of outputs of (1.1) is modified as follows:
| (2.30) |
For the case above we adopt a slight modification of the approach used for the proof of Proposition 2.1. Our proposed algorithm contains two steps:
Step 1: Define
| (2.31) |
where the latter is involved in (2.28). Notice that, due to the additional assumption (2.28), it follows that (2.19) holds with and for close to . Next, consider a strictly increasing sequence satisfying the first equality of (2.18), namely,
| (2.32) |
and with as above. We set and find a decreasing sequence with and in such a way that
| (2.33) |
Step 2: Consider the sequence with arbitrary initial satisfying (2.23) with and set
| (2.34) |
It then follows that (2.27) holds with unique satisfying (2.3). Particularly, we have:
| (2.35) |
therefore, the sequence of mappings , as defined by (2.32), exhibits the state determination. above satisfies the desired (2.5) and (2.6).
Case II (General Case): We now provide an algorithm, which exhibits the state determination for the general case, without any additional assumption. The algorithm contains two steps:
Step 1: Repeat the same procedure followed in Case I, with and construct a sequences of mappings
| (2.36a) | |||
| associated with appropriate decreasing sequences , with , by pretending that and in such a way that, if we define , we have: | |||
| (2.36b) | |||
Step 2: Define
| (2.37) |
Notice that, since the set is bounded, there exists an integer such that . The latter in conjunction with (2.33) yields:
| (2.38) |
which, due to selection , implies . We conclude that for the general case the sequence of mappings , as defined by (2.34), exhibits the state determination. Finally, it should be noted that, according to the methodology above, contrary to the approach adopted in the proof of Proposition 2.1, the specific knowledge of satisfying (2.35) is not required.
III Application
In this section we apply the results of Section II to triangular systems (1.1) of the form:
| (3.1a) | |||
| with output | |||
| (3.1b) | |||
where we make the following assumptions:
H1 (Regularity Assumptions). It is assumed that for each the mappings , , and are measurable and locally essentially bounded and for each fixed and the mappings and are (locally) Lipschitz.
Obviously, (3.1) has the form of (1.1) with
| (3.2a) | |||
| (3.2b) | |||
| (3.2c) | |||
We also make the following observability assumption:
H2. There exists a measurable set with nonempty interior such that for all , close to and for each and it holds:
| (3.3) |
Proposition III.1
For the system (3.1) assume that H1 and H2 hold with for certain close to . Then there exists a set with such that the approximate SEDP is solvable over for the system (3.1) by employing the methodology of Proposition 2.1; consequently, (3.1) is observable over .
Remark III.1
A stronger version of assumption (3.3), is required in [8], [9], [25], [27], [28], for the construction of Luenberger type observers for a more general class of triangular systems. Particularly, in all previously mentioned works it is further imposed that the mappings are . We note that the second conclusion of Proposition 3.1 concerning observability can alternatively be obtained under H1 and H2 as follows: By exploiting (3.3) and applying successive differentiation with respect to time, we can determine a map satisfying (2.4) with the information of the time-derivatives of and output (details are left to the reader). But this map is not acceptable for the solvability of SEDP for (3.1), due to the additional requirements of Definition 2.2 that the candidate should be independent of the time-derivatives of and .
Proof:
We establish that the assumptions H1 and H2 guarantee that conditions A1 and A2 of previous section are fulfilled for (3.1), therefore by invoking Proposition 2.1 we get the desired statement. We first evaluate the fundamental solution of (2.8) with as given by (3.2a) for certain . We find:
| (3.4) |
where each function satisfies
| (3.5a) | |||
| for certain constants and functions with | |||
| (3.5b) | |||
Particularly, due to (3.3), we have:
| (3.6) |
for certain nonzero constants . Notice, that the above representation is feasible for almost all due to our regularity assumptions concerning . For simplicity, we may assume next that (3.4) - (3.6) hold for every . We now calculate by taking into account (3.2c) and (3.4):
| (3.7) |
Notice that , as defined by (2.9), satisfies (2.11) since otherwise, there would exist sequences and a nonzero vector with and in such a way that . Then by using (3.7) we get , which by virtue of (3.5) and (3.6) implies that , a contradiction. We conclude that relation (2.11) of A1 holds with . In order to establish A2, we calculate, according to definition (2.9) and by using (3.7):
| (3.8) |
where and the functions above satisfy (3.5). Define , and let and
| (3.9) |
By (3.1a), (3.2c), (3.4) and (3.9) we find:
| (3.10) |
near , , where the functions have the form:
| (3.11) |
for certain , and in such a way that, due to (3.9) and Lipschitz continuity property of , the following holds for every :
| (3.12) |
for certain constant . Also, we evaluate from (3.8):
| (3.13) |
where and above satisfy (3.5a). From (2.10), (3.7) and (3.10) - (3.12) we also find:
| (3.14) |
for near , where and each above satisfy again (3.11) and (3.12). The latter in conjunction with (3.9), (3.13) and (3.14) implies A2. To be precise, the following holds: For every , close to , , and constants and , a constant can be found satisfying (2.12). We conclude that both A1 and A2 are fulfilled for the case (3.1), hence, according to Proposition 2.1, the approximate SEDP is solvable for (3.1) over a set with . ∎
Example III.1
We illustrate the nature of our methodology by considering the elementary case of the planar single-input triangular system with output that has the form (3.1) with
We may assume that each admissible input is any nonzero measurable and essentially locally bounded function and for simplicity, let for near zero. Obviously, the system above satisfies H1 and H2. Let us choose as initial condition and calculate the corresponding output trajectory (see Figure 1 below).
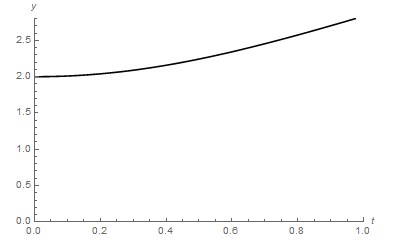
We next apply the methodology suggested in the previous section, in order to confirm that our proposed algorithm converges to above. For simplicity, let us assume that is a priori known that the “unknown” initial state is contained into the ball of radius centered at zero. We take and as in the proposed algorithm (Case I). By taking into account the known values of , we find a decreasing sequence satisfying (2.31) converging to ; particularly, take . Then, choose an arbitrary constant initial map, say ; with and , for and successively apply (2.22b), in order to evaluate the desired sequence . Figures 2 and 3 present the corresponding values of errors and confirms that the evaluated pair of terms converges to the pair .
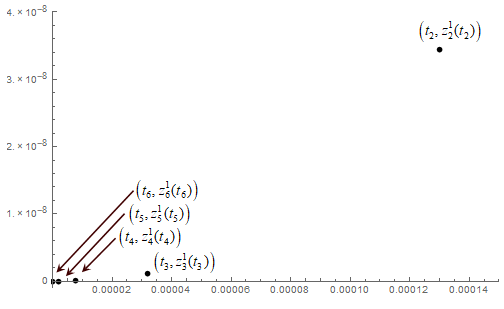
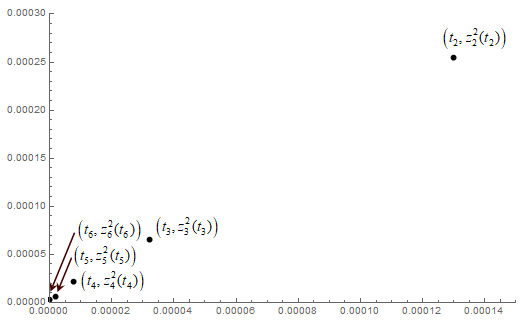
Finally, we remark that, since the system is forward complete, then for any the sequence of mappings with uniformly approximates the unknown solution on the interval .
IV Additional Hypotheses and Hybrid Observer
In this section we briefly present a hybrid-observer technique for the state estimation for (1.1). The proof of the following proposition is based on a modification of the approach employed in Section II.
Proposition IV.1
For the system (1.1) we make the same assumptions with those imposed in statement of Proposition 2.1. Also, assume that for any and input there exists a constant such that
| (4.1) |
Then, there exists a sequence such that, if for any arbitrary constant we define:
| (4.2a) | |||
| (4.2b) | |||
where , then the system below exhibits the global state estimation of (1.1):
| (4.3a) | |||
| (4.3b) |
particularly, it holds:
| (4.4) |
Proof:
Let be a solution of (1.1) corresponding to . Let and consider the sequence , with as defined in (4.1), and let be a decreasing sequence with
| (4.5) |
We next proceed by using a generalization of the procedure employed for the proof of Proposition 2.1. First, we find a decreasing sequence , with such that
| (4.6) |
with and as defined by (2.18) and (2.19), respectively. Then, consider the sequence of mappings , as precisely defined in (2.22) and again define:
| (4.7) |
Then, as in proof of Propostion 2.1 we can show, by exploiting (4.6), that
| (4.8) |
We are now in a position to show (4.4). We take into account (4.1)-(4.3), (4.5), (4.8), definition of and consider the difference between the integral representation of the solutions of (1.1a) and (4.3a). Then, by successively applying the Gronwall - Bellman inequality, we can estimate:
| (4.9) |
and the above, in conjunction with (4.5), asserts that
The latter implies the desired (4.4). Details are left to the reader. ∎
V Conclusion
Sufficient conditions for observability and solvability of the state estimation for a class of nonlinear control time - varying systems are derived. The state estimation is exhibited by means of a sequence of functionals approximating the unknown state of the system on a given bounded time interval. Each functional is exclusively dependent on the dynamics of system, the input and the corresponding output . The possibility of solvability of the state estimation problem by means of hybrid observers is briefly examined.
References
- [1] T. Ahmed-Ali and F. Lamnabhi-Lagarrigue, “Sliding observer-controller design for uncertain triangular nonlinear systems,” IEEE Transactions on Automatic Control, vol. 44, no. 6, pp. 1244–1249, 1999.
- [2] J. H. Ahrens and H. K. Khalil, “High-gain observers in the presence of measurement noise,” Automatica, vol. 45, no. 4, pp. 936–943, 2009.
- [3] M. Alamir, “Optimization based non-linear observers revisited,” International Journal of Control, vol. 72, no. 13, pp. 1204–1217, 1999.
- [4] A. Alessandri and A. Rossi, “Increasing-gain observers for nonlinear systems: Stability and design,” Automatica, vol. 57, pp. 180–188, 2015.
- [5] V. Andrieu, L. Praly, and A. Astolfi, “High gain observers with updated gain and homogeneous correction terms,” Automatica, vol. 45, no. 2, pp. 422–428, 2009.
- [6] A. Astolfi and L. Praly, “Global complete observability and output-to-state stability imply the existence of a globally convergent observer,” Mathematics of Control, Signals, and Systems, vol. 18, no. 1, pp. 32–65, 2006.
- [7] G. Besançon and A. Ticlea, “An immersion-based observer design for rank-observable nonlinear systems,” IEEE Transactions on Automatic Control, vol. 52, no. 1, pp. 83–88, 2007.
- [8] D. Boskos and J. Tsinias, “Sufficient conditions on the existence of switching observers for nonlinear time-varying systems,” Eur. J. Control, vol. 19, pp. 87–103, 2013.
- [9] ——, “Observer Design for Nonlinear Triangular Systems with Unobservable Linearization,” International Journal of Control, vol. 86, pp. 721–739, 2013.
- [10] ——, “Observer Design for a General Class of Triangular Systems,” Proc. 21st Symp. Math. Theory Netw. Syst. (MTSN), 2014.
- [11] H. Du, C. Qian, S. Yang, and S. Li, “Recursive design of finite-time convergent observers for a class of time-varying nonlinear systems,” Automatica, vol. 49, no. 2, pp. 601–609, 2013.
- [12] P. Dufour, S. Flila, and H. Hammouri, “Observer design for MIMO non-uniformly observable systems,” IEEE Transactions on Automatic Control, vol. 57, no. 2, pp. 511–516, 2012.
- [13] J. P. Gauthier, H. Hammouri, and S. Othman, “A Simple Observer for Nonlinear Systems Applications to Bioreactors,” IEEE Transactions on Automatic Control, vol. 37, no. 6, pp. 875–880, 1992.
- [14] J.-P. Gauthier and I. Kupka, Deterministic Observation Theory and Applications. Cambridge: Cambridge University Press, 2001.
- [15] T. Hoàng, W. Pasillas-Lépine, and W. Respondek, “A switching observer for systems with linearizable error dynamics via singular time-scaling,” Proc. 21st Symp. Math. Theory Netw. Syst. (MTNS), 2014.
- [16] I. Karafyllis and Z. P. Jiang, “Hybrid dead-beat observers for a class of nonlinear systems,” Systems and Control Letters, vol. 60, no. 8, pp. 608–617, 2011.
- [17] I. Karafyllis and C. Kravaris, “Global exponential observers for two classes of nonlinear systems,” Systems and Control Letters, vol. 61, no. 7, pp. 797–806, 2012.
- [18] D. Karagiannis, M. Sassano, and A. Astolfi, “Dynamic scaling and observer design with application to adaptive control,” Automatica, vol. 45, no. 12, pp. 2883–2889, 2009.
- [19] N. Kazantzis and C. Kravaris, “Nonlinear observer design using Lyapunov’s auxiliary theorem,” Proceedings of the 36th IEEE Conference on Decision and Control, vol. 5, no. June 1997, pp. 241–247, 1997.
- [20] J. Klamka, “On the global controllability of perturbed nonlinear systems,” IEEE Trans. Automat. Control 20 (1), pp. 170–172, 1975.
- [21] A. J. Krener and M. Xiao, “Observers for linearly unobservable nonlinear systems,” Systems and Control Letters, vol. 46, no. 4, pp. 281–288, 2002.
- [22] P. Krishnamurthy and F. Khorrami, “Dynamic High-Gain Scaling: State and Output Feedback With Application to Systems With ISS Appended Dynamics Driven by All States,” IEEE Trans. Autom. Control, vol. 49, no. 12, pp. 2219–2239, 2004.
- [23] T. Ménard, E. Moulay, and W. Perruquetti, “Global finite-time observers for non linear systems,” in Proceedings of the IEEE Conference on Decision and Control, 2009, pp. 6526–6531.
- [24] H. Ríos and A. R. Teel, “A hybrid observer for fixed-time state estimation of linear systems,” in 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, 2016, pp. 5408–5413.
- [25] D. Theodosis, D. Boskos, and J. Tsinias, “Observer design for triangular systems under weak observability assumptions,” IEEE Transactions on Automatic Control, 2018.
- [26] J. Tsinias, “Links between asymptotic controllability and persistence of excitation for a class of time-varying systems,” Systems and Control Letters, vol. 54, no. 11, pp. 1051–1062, 2005.
- [27] ——, “Time-varying observers for a class of nonlinear systems,” Syst. Control Lett., vol. 57, no. 12, pp. 1037–1047, 2008.
- [28] J. Tsinias and D. Theodosis, “Luenberger-type observers for a class of nonlinear triangular control systems,” IEEE Trans. Autom. Control, vol. 61, no. 12, pp. 3797–3812, 2016.
- [29] Y. Yamamoto and I. Sugiura, “Some sufficient conditions for the observability of nonlinear systems,” J. Optim. Theory Appl., vol. 13, no. 6, pp. 660–669, 1974.