Observation of the Quantum Boomerang Effect
Abstract
A particle in an Anderson-localized system, if launched in any direction, should on average return to its starting point and stay there. Despite the central role played by Anderson localization in the modern understanding of condensed matter, this “quantum boomerang” effect, an essential feature of the localized state, was only recently theoretically predicted. We report the experimental observation of the quantum boomerang effect. Using a degenerate gas and a phase-shifted pair of optical lattices, we not only confirm the predicted dependence of the boomerang effect on Floquet gauge, but also elucidate the crucial role of initial state symmetries. Highlighting the key role of localization, we observe that as stochastic kicking destroys dynamical localization, the quantum boomerang effect also disappears. Measured dynamics are in agreement with numerical models and with predictions of an analytical theory we present which clarifies the connection between time-reversal symmetry and boomerang dynamics. These results showcase a unique experimental probe of the underlying quantum nature of Anderson localized matter.
Anderson localization is a quintessential effect of disorder in a variety of physical systems [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. Disordered lattice models enjoy a robust theoretical proof of localization and remain a hotbed for discovery even today. While transport in disordered media has been studied for more than 50 years, a fundamental dynamical feature of Anderson-localized matter known as the “quantum boomerang” effect was only recently theoretically predicted [13, 14, 15]. The central prediction of the quantum boomerang is that, for an appropriate average over disorder realizations, a wavepacket launched with any nonzero momentum will return to and localize at its initial position [13]. This surprising phenomenon can be understood as a consequence of both Anderson localization and time-reversal symmetry: the long-time density distribution for a wavepacket with an initial momentum (i) is time-independent because of localization and (ii) does not depend on the sign of because of time-reversal symmetry. Together, these features imply that at long times the wavepacket must settle at its initial position. The quantum boomerang effect is predicted to occur in a broad class of disordered or pseudo-disordered tight-binding models [15] including the quantum kicked rotor (QKR), a momentum-space realization of a disordered quasi-1D wire [16, 17] which provides an ideal platform for the study of the interplay between localization, chaos, interactions, and transport [18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]. In any context, the quantum boomerang effect contravenes classical predictions and serves as a sensitive diagnostic of the quantum nature of localization, with the potential, for example, to map mobility edges [13, 31].
We report the experimental observation and characterization of the quantum boomerang effect. Using a degenerate gas and a pair of phase-shifted optical lattices to create a kicked rotor with tunable initial conditions (Fig. 1), we observe the boomerang’s distinctive return dynamics. We experimentally characterize the dependence of the dynamics on symmetry properties, Floquet gauge, and initial state, and confirm that results agree with an analytical theory we develop in the appendices. Finally, we measure the controlled destruction of the boomerang effect by stochastic kicking. The atom-optics kicked-rotor realization of the quantum boomerang offers three key advantages: (i) finite-width quasimomentum distributions naturally achieve single-shot disorder averaging, (ii) working in momentum space rather than position space enables simple observation of boomerang dynamics with single-site resolution, and (iii) symmetry properties can be straightforwardly tuned by adjusting properties of the quench [32, 33, 34].
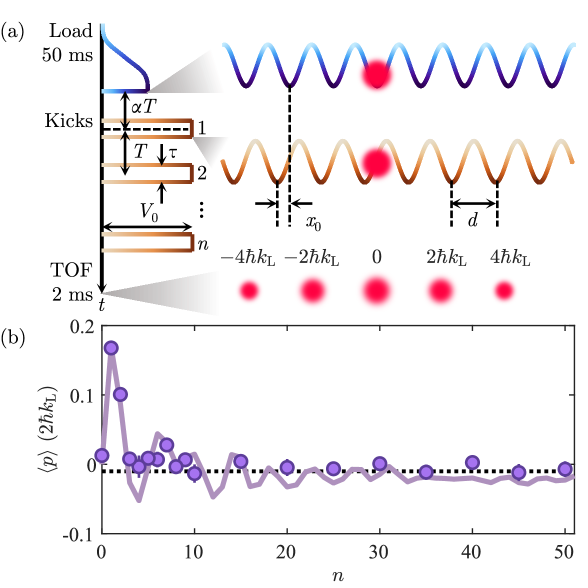
We begin each experiment by preparing a Bose-Einstein condensate (BEC) of 7Li atoms and then tuning interatomic interactions to zero with a Feshbach resonance. A typical experimental sequence from this point on is depicted in Fig. 1a. The atoms are exposed in turn to two coaxial optical lattices with lattice constant , wave vector , recoil energy , and tunable relative offset . is the atomic mass. To prepare an initial wavefunction which is well-localized in position space within each lattice site, we adiabatically load the BEC into the first optical lattice over , reaching a final depth of . At , we suddenly turn off the first lattice and quench into a Hamiltonian created by repeated kicking with the second, spatially-shifted lattice:
| (1) |
As described by Eq. 1, the second, phase-shifted lattice is pulsed times to depth with pulse shape , effective pulse width , and period ; the first pulse peaks a delay time after the quench. Having measured the finite time of this quench to be approximately , we define halfway through the quench and recognize a systematic uncertainty in the reported values of . Because of the adiabatic loading into the first lattice and the relative phase shift, the atomic ensemble starts out centered at a nonzero position given by . This is analogous to the situation in a position-space quantum boomerang, where the initial state is centered at nonzero momentum.
To make concrete the connection to the kicked rotor we introduce dimensionless variables , , and as well as dimensionless parameters , an effective Planck’s constant, and , encoding kicking strength. Substituting these into Eq. 1, rescaling the Hamiltonian , and taking the -function limit of , we recover the canonical QKR Hamiltonian . This gives rise to a single-particle 1-cycle Floquet operator .
Figure 1b illustrates the main result of this work: we experimentally observe the departure from and return to zero average momentum which is the key signature of the quantum boomerang effect [13]. Here , s, , and , which correspond to , . While the first kick imparts momentum asymmetry due to the lattice phase offset, the system returns to zero average momentum at long times. The experimental result agrees well with fit-parameter-free time-dependent Schrödinger equation (TDSE) simulations of the finite-pulse width Hamiltonian (1) using a split-step method described in appendix D.
This demonstration of the quantum boomerang effect enables an in-depth experimental characterization of the circumstances under which it can occur. Our measurements reveal a rich interplay among symmetries and quench dynamics which is well described by the analytic theory we present in the appendices. Specifically, it is the relation between the symmetry properties of the initial state and the Floquet gauge defined by the quench which dictates the presence or absence of the quantum boomerang effect in the quantum kicked rotor. This interplay offers a contrast to static disordered systems, in which initial state symmetries are also important but which lack a Floquet gauge degree of freedom. We note for clarity that the QKR Hamiltonian itself is of course time-reversal and parity symmetric independent of Floquet gauge and spatial phase choices, so long as one references appropriate symmetry axes. For the remainder of the paper, we will solely refer to time-reversal and parity symmetry with respect to inversions about and unless otherwise stated. is then clearly parity symmetric, and only when does the evolution also become time-reversal invariant. As we show in Appendix A, the initial Bloch state ensemble we experimentally prepare satisfies the exact properties necessary to observe a boomerang effect under these conditions: it is (i) parity asymmetric to allow for nontrivial early-time momentum dynamics and (ii) time-reversal symmetric () to ensure a complete return to 0 average momentum at late-times. This interplay of symmetries arising from the QKR quench protocol enables the quantum boomerang effect to be switched on or off by adjusting the Floquet gauge.
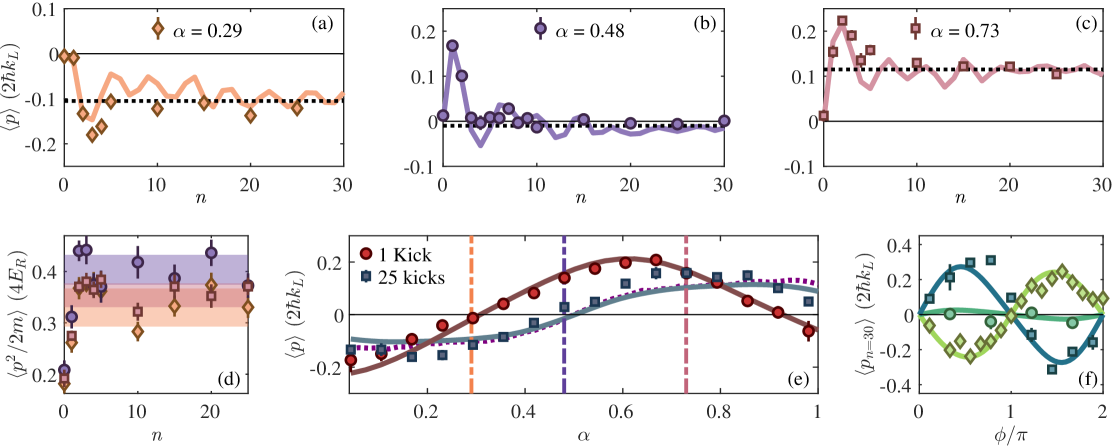
Fig. 2 demonstrates this dependence on Floquet gauge with a detailed characterization of the average momentum evolution for various . Measurements at values of 0.29, 0.48, and 0.73 (Fig. 2a-c) exhibit fundamental differences in the dynamical behavior. As discussed above, only near do we observe the quantum boomerang effect: a sharp initial increase in followed by a decline back to the initial value of 0. Resolution of the precise boomerang condition is limited experimentally by timing noise on the location of the first pulse and the finite quench time of the acousto-optic modulators. In contrast, evolution under the other two Floquet gauges converges to nonzero momentum values at long times, indicating the absence of the full quantum boomerang effect. Each data set agrees well with fit-parameter-free numerical predictions, and all late-time momenta match the analytical predictions of the Floquet diagonal ensemble (Eq. 6).
Fig. 2d shows that the observed energy evolution is qualitatively consistent for all three values of , with each ensemble exhibiting dynamical localization as expected for a non-interacting quantum kicked rotor [35, 18, 24]. We note that the energy for appears to saturate at a slightly higher value than the other gauges, a result consistent with the predictions of Ref. [15].
A key feature of quantum boomerang dynamics which can be probed with a kicked rotor is the contrast between short- and long-time evolution. Fig. 2e maps out the Floquet gauge dependence of momentum in these two regimes. Since the energy saturates after only five kicks, we take 25 kicks as a reasonable proxy for the infinite-time limit predicted by relaxation to the Floquet diagonal ensemble (see Eq. 6). The initial momentum asymmetry imparted to the rotor after one kick arises purely from the Talbot effect, a periodic re-imaging of the wavefunction in time under free-evolution as a result of the spatially periodic lattice exciting only quantized momentum modes; this Talbot effect is intimately related to the extensively explored quantum resonance phenomena in the QKR [36, 37, 38, 39]. The Talbot oscillation for a Bloch state is illustrated in Fig. 3d, where for our experiment, s.
In contrast, the long-time behavior is governed by localization physics and symmetries surrounding the quench. One feature of both experimental and theoretical results in Fig. 2e is that the long-time momentum should be an odd function about , a result we prove in appendix C. This result is connected to the resemblance between forward time-evolution in the gauge (propagation with ) and backward time-evolution in the gauge (propagation with ). The anti-symmetry about is dictated by the time-reversal invariance of the initial Bloch state ensemble. We note that because this property arises due to similarities between forward evolution in one gauge and backward evolution in the other, it only manifests as an (anti-)symmetry in the forward evolution of both gauges in the long-time limit (see Eq. 7); at short times, no symmetry is generically expected, as evidenced by the 1-kick data.
The odd parity of the late-time momentum about is further reflected in Fig. 2f, which shows the late-time momentum as a function of initial wavepacket position for three different values of . Here a shift in the relative lattice phase is exactly analogous to variation in the initial launch velocity of a position space boomerang. We observe that regardless of initial position, values near 0 and 1 result in opposite-sign, non-zero late-time momenta. The only exception occurs when the initial state recovers parity symmetry at or and the average momentum dynamics become trivial. Near , the entire curve collapses toward 0. This indicates that, as mentioned above, it is time-reversal symmetry which plays the fundamental role in determining the return of the boomerang. The initial position which controls the degree of parity asymmetry is instead more closely related to the amplitude of the early-time boomerang dynamics.
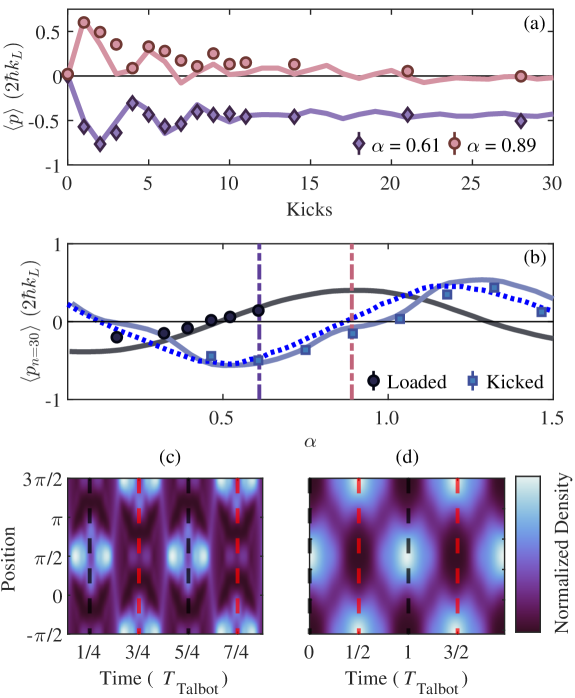
The demonstrated control of symmetry properties by varying opens up the possibility of realizing quantum boomerang dynamics starting from more exotic initial states. Fig. 3 explores the quench dynamics of an initial state with an essentially homogeneous distribution in position space, achieved by replacing the adiabatic lattice load with a single kick. The initial wavefunction, approximately with the effective kick impulse, is neither time-reversal symmetric nor well-localized in position. Intuitively one would not expect such a state to demonstrate quantum boomerang dynamics, as our understanding of the position-space quantum boomerang effect is based on a well-defined initial velocity. Despite these expectations, the data in Fig. 3a reveal a clear quantum boomerang effect, though at a Floquet gauge , very different from the value of 0.5 expected for a time-reversal symmetric state. This can be understood by observing that free evolution maps this initial state into a time-reversal but not parity invariant wavefunction after a time , as illustrated numerically in Fig. 3c and proven analytically in Appendix B. Thus, one expects to observe the boomerang effect at for the kicked initial state, in good agreement with numerical and experimental results in Fig. 3. This finding demonstrates that even for quenched states completely unlike traditional boomerang starting points, the Floquet gauge freedom can restore the boomerang effect in certain cases where the Talbot effect defines a new time-inversion symmetric point.
We note that while the kicked state is not initially time-reversal symmetric, it is invariant under simultaneous parity-time inversion (). As we show in Appendix C, this different symmetry condition manifests in the late-time momentum exhibiting even rather than odd symmetry about . These different Floquet gauge properties for the two initial state symmetries we consider are demonstrated and contrasted in Fig. 3b, which clearly distinguishes the different parity about (see also data for the adiabatically loaded initial condition plotted for a broader range of in Fig. 2e). We note that the data are not perfectly symmetric on the appropriate intervals, as demonstrated by comparison to the Floquet diagonal ensemble predictions. We attribute this to the fact that the symmetry is only established in the infinite-time limit, with deviations present at any finite time. Nevertheless, such deviations from the long-time limit are small, and our finite-time observations clearly reflect the idealized theoretical predictions. For the kicked state data shown, the symmetry is most apparent when extending to cases where is slightly greater than 1 111 The experimental delay-time definition and Floquet gauge definition of is only consistent on . For data and simulations shown, we define solely by the delay-time definition. To make the Floquet gauge definition consistent with this, one should redefine the quenched initial state as , with the original quenched state for cases, denoting the integer part of , and taking the Floquet gauge to be . .
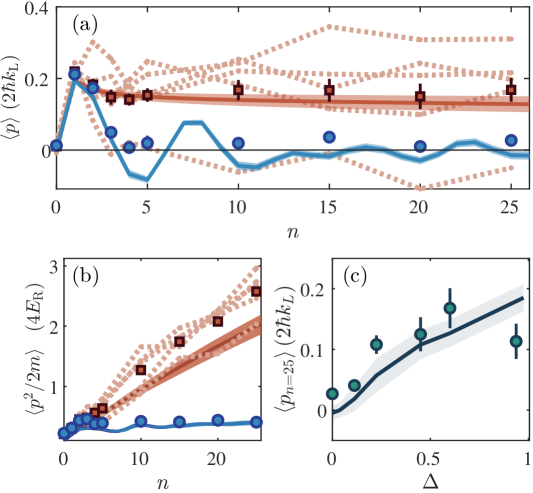
The final set of results we describe (Fig. 4) probes the question: what happens to quantum boomerang dynamics as localization is destroyed? In the QKR context, dynamical localization can be tunably disrupted by introducing temporal stochasticity into the kicking sequence [41, 24]. To implement this, we add a deviation to the delay time after the kick, where is randomly selected from a uniform distribution in the range . The parameter quantifies the degree of randomness and can range from 0 to 1. Fig. 4a shows the time evolution of average momentum for (no randomness) and , with the first kick fixed so that , and with the same experimental parameters as in Fig. 2b. In contrast to the characteristic boomerang-like evolution when , each of the five experimental realizations of randomness for exhibits a different behavior. The mean momentum over these disorder realizations demonstrates the destruction of the quantum boomerang effect, with a long-time average momentum significantly different from zero, and agrees reasonably well with the result of disorder-averaged simulations. Fig. 4b shows the evolution of the average energy for the same experiments: the destruction of dynamical localization by random kicking and the approach to classical linear-time energy growth are clearly visible in both experiment and theory, and are associated with the destruction of the quantum boomerang effect in Fig. 4a. To directly probe the dependence of the quantum boomerang on the disorder strength, we plot in Fig. 4c the disorder-averaged mean momentum after 25 kicks as a function of . Measured long-time increases monotonically up to and agrees reasonably well with disorder-averaged numerical predictions. An interesting topic for further study is the relationship between the degree of destruction of the boomerang effect (measured, for example, by long-time average momentum) and the exponent characterizing energy growth [42, 43, 44].
In this work we have presented the first experimental evidence for the quantum boomerang effect in an Anderson-localized system. The measurements confirm theoretical predictions [13, 15] and demonstrate that boomerang dynamics can occur from a variety of initial conditions including even a homogeneous density distribution. These experimental results, along with the analytical theory we present in the appendices, elucidate the crucial role of parity and time-reversal symmetry in determining the presence or absence of the quantum boomerang effect. We have probed the dependence of boomerang dynamics upon Anderson localization itself by measuring the effect of tunably random kicking sequences: results confirm that classical diffusion induced by stochasticity destroys both dynamical localization and the quantum boomerang effect. These experiments validate a new, powerful probe of the uniquely quantum-mechanical nature of localization applicable to a general class of disordered systems and suggest a variety of intriguing topics for future exploration. These include boomerang phenomena in higher-dimensional systems, different symmetry classes [45], more exotic initial states, and the presence or absence of many-body boomerang effects in interacting systems [14] or even many-body localized states. Applications of our demonstration — that adjusting the Floquet gauge can switch on or off the boomerang effect — are an intriguing possibility. Beyond the context of the quantum kicked rotor, the investigation of boomerang-like phenomena in condensed matter systems and implications of these results for ultrafast electron dynamics in disordered solids represent unexplored frontiers.
Acknowledgments
We thank Toshihiko Shimasaki, Esat Kondakci, and Yifei Bai for helpful conversations. D.W. acknowledges support from the Air Force Office of Scientific Research (FA9550-20-1-0240), the Army Research Office (W911NF-20-1-0294), the National Science Foundation (CAREER 1555313), and the Eddleman Center for Quantum Innovation, and from the NSF QLCI program through grant number OMA-2016245. T.M. acknowledges CNPq (grant no. 311079/2015-6). T.M. and F.S. are supported by the Serrapilheira Institute (grant number Serra-1812-27802). R.S. and E.N.-M. acknowledge support from the UCSB NSF Quantum Foundry through the Q-AMASEi program (Grant No. DMR-1906325). A.C. acknowledges support from the NSF Graduate Research Fellowship Program (grant DGE2040434).
Author Contributions
R.S., J.T., H.M., E.N.-M. and E.S. performed the measurements. R.S., J.T., and H.M. analyzed the data. R.S., H.M., J.T., E.S., F.S., and A.C. performed numerical modeling. A.C., T.M., and F.S. performed the theoretical symmetry analysis with assistance from P.V. R.S., J.T., H.M., A.C., and D.W. drafted the manuscript with input from all authors. D.W. supervised the experiments. All authors contributed insights in discussions on the project.
Appendix A Deriving Conditions for the QKR Boomerang Effect
Here we show that the symmetry conditions on the initial state and Floquet gauge described in the main text indeed enable the boomerang effect in the QKR model. Explicitly, we consider the canonical QKR Hamiltonian considered in the main text (reproduced here and reverting to standard variable notations for clarity)
| (2) |
To be explicit, here we define on the interval , taking the cases and 1 to be distinct from each other and consistent with the definition in the Floquet operator
| (3) |
That is, for the kicks occur just after (before) . Here we continue to refer to symmetry operations only about fixed axes. is evidently parity inversion (, ) symmetric at all times
| (4) |
The operator obeys . Only for does the system also become time-reversal (, ) symmetric. The complex conjugation operation associated with time-reversal acts on the position space wave-function as . For the case, is additionally parity-time inversion (, ) symmetric.
We use the following intuitive definition for the QKR boomerang effect in momentum space. (i) The boomerang should exhibit non-trivial average momentum dynamics at short times, in particular a departure from followed by a relaxation toward the initial value. (ii) At late times, a true boomerang should have an average momentum equivalent to the initial momentum. Explicitly, we will show that (i) is only compatible with parity asymmetric states. Restricting ourselves to the case of 0 initial momentum, we then show that time-reversal symmetry of the quenched initial state and Floquet gauge guarantees (ii).
We consider solutions to the time-dependent Schrodinger equation , where is the initial state quenched into the Hamiltonian. Our analysis will concern the behavior of . First we consider the evolution of an arbitrary state and its parity inverted counterpart . Let and correspond to the time-evolved states and respectively. From parity symmetry (4), we have , and from this can conclude
| (5) |
This holds for any initial state and , as well as at all times . From this, it immediately follows that a necessary condition for observing (i), and thus the boomerang, is that ; otherwise , guaranteeing that (ii) is satisfied but in a trivial way. Since all of the remaining analysis is also concerned with , we hereafter assume that parity asymmetry is satisfied to derive non-trivial results.
Now we begin to investigate the behavior concerning (ii). Considering the Floquet spectral decomposition of the initial state with , the long-time average momentum given by the Floquet diagonal ensemble is
| (6) |
One can also consider the opposite limit by decomposing in the basis of . Since the eigenstates of a unitary operator and its Hermitian-conjugate are identical (both are eigenstates of the same self-adjoint, time-independent Floquet Hamiltonian), the prediction of the Floquet diagonal ensemble is the same. This leads to the conclusion that
| (7) |
This also holds for any initial state and .
Now finally we consider time-reversal symmetric states . Under parity-time inversion, we then have the relation
| (8) |
Now consider the full solution and . For , the parity-time inversion symmetry of the Hamiltonian implies that is another solution with a corresponding momentum evolution . From (8), it is straightforward to see that this solution corresponds to the evolution of the parity-inverted initial state, i.e. ; note that while a parity-time inverted state about a different time-axis can be defined for arbitrary , such a state will not coincide with and will consequently prevent the following conclusions. Defining in the same way as before, this result implies . Combining this with (5), we thus have
| (9) |
One can deduce this relation intuitively by noting that backward propagation under for a time-reversal symmetric initial state simply corresponds to receiving kicks of the opposite sign. Finally, the combination of (7) and (9) yields the final result
| (10) |
We conclude this appendix by discussing the important role of quasi-momentum averaging and the applicability of this argument to the experiment. First, we point out that the experimentally relevant quasi-momentum averages are explicitly consistent with the presented argument for boomerang dynamics. In the primary experimental results presented, the initial state is an ensemble of ground-band Bloch states , where denotes quasi-momentum, and we reference the functional form with respect to a cosine external potential. Generically, the entire Bloch ensemble will be parity asymmetric () due to the non-zero shift of the peak density away from , and thus condition (i) remains trivially satisfied. However, time-reversal symmetry demands a real spatial wave-function (), and this is only true for . The solution is to observe that the superposition is real for arbitrary , and thus the averaging can be performed so long as the quasi-momentum distribution is symmetric. Even though this argument is based on the coherent superposition of states, the conclusion holds for thermal quasi-momentum distributions as the QKR dynamics are quasi-momentum conserving and the momentum operator does not mix quasi-momentum sectors. We note that a similar disorder symmetrization can also be applied to the Anderson model, where an explicit average over parity-conjugated disorder potential pairs and ensures the validity of the above argument at the level of individual disorder realizations (switching for as well as the role of time and parity-time reversal). It is important to keep in mind, however, that such an explicit symmetrization of the disorder averaging is not required for observing the boomerang effect in the Anderson model; whether a boomerang effect exists for asymmetric quasi-momentum distributions in the QKR is an open question for future exploration.
Despite the fact that the argument presented in this section holds for individual pairs of quasi-momentum, we stress that quasi-momentum disorder averaging remains critical for practically observing boomerang dynamics. Our proof of (ii) is based on the assumption that the momentum expectation value relaxes in the long-time limit to the static diagonal ensemble prediction. However, individual quasi-momentum states will exhibit large momentum oscillations at all times and only relax in the sense of the time-averaged momentum. This is in contrast to our experimental results where the system has a finite-width quasi-momentum distribution (due more to finite size than to finite temperature), and subsequently the instantaneous momentum relaxes to 0, only exhibiting small fluctuations about this value for large times. We interpret the latter situation as more representative of a true boomerang effect.
Appendix B Time-Reversal Symmetry for Kicked State under Talbot Dynamics
Here we explicitly prove that the kicked initial state preparation indeed leads to a time-reversal symmetric state after free-evolution by . For this analysis, we consider 0 quasi-momentum. Using the Jacobi-Anger expansion for the initial wavefunction described in the main text, we can decompose the initial kicked state in a discrete momentum basis indexed by integers as
| (11) |
where is the Bessel function of the first kind. The quarter-Talbot period free evolution is described by with and . Noting that we have
| (12) |
The condition on the momentum coefficients for a time-reversal symmetric or real position-space wavefunction is , where . Using , we straightforwardly confirm this condition
| (13) |
Taken with the proof in appendix A, this supports the claim that the kicked state should exhibit a boomerang effect for . We note that this argument is only exact for 0 quasi-momentum, and the experimental kicked initial state data relies on a narrow quasi-momentum distribution about 0 for clear observation of the boomerang effect; however in considering corrections to this argument, one should keep in mind that the initial state (11) considered in this analysis is already only an approximate description of the experimental reality.
Appendix C Floquet Gauge Symmetry Properties of Late-Time Momentum
Here we prove that the infinite-time momentum is either an even or odd function of about 1/2 for states with the given symmetry properties explored in the experiment. First we consider initial states with time-reversal symmetry such that
| (14) |
We note the relation
| (15) |
For compactness, we will henceforth denote the state after kicks in the gauge as () and use similar notation for expectation values. The momentum evolution in the gauge is then given by
| (16) |
Using (14), (15) and , we find
| (17) | ||||
| (18) |
That is, forward quench dynamics in the gauge possess an opposite momentum evolution to backward evolution under the gauge . Note that this is essentially a generalization of equation (9) to arbitrary ; evaluating this property at in conjuction with (7) serves as an alternative proof that the late-time zero momentum feature of the boomerang effect only depends on simultaneous time-reversal symmetry of the Floquet gauge and quenched state. Leaving arbitrary, taking the limit , and applying (7), we derive the odd function result for time-reversal symmetric states
| (19) |
Next we consider a state with the symmetry
| (20) |
Replacing in (17), making use of the parity symmetry of the evolution (4), and noting that , we instead find
| (21) |
Taking the infinite-time limit in the same way as before, we arrive at the desired even function result
| (22) |
Here we suggest an intuitive understanding for the difference between the two cases. Whereas the backward evolution in for a time-reversal symmetric state only differs from the forward evolution in by the sign of the kicks, which leads to opposite sign momentum impulses and subsequently (19), the backward free-evolution in of the parity-time reversal symmetric state produces an additional parity inversion with respect to the forward free-evolution in (for instance, see Fig. 3c), cancelling the kick inversion to yield (22).
Appendix D TDSE and Diagonal Ensemble Numerics
In all TDSE calculations discussed in this work we compute the dynamics of individual Bloch states and average over a Gaussian quasimomentum distribution of standard deviation , which both models our finite-width BEC and realizes the disorder average in standard Anderson model calculations. 222According to the adiabatic theorem, the BEC wavefunction after the lattice load state-preparation is a superposition of Bloch states , where denotes quasimomentum, weighted by the initial Gaussian momentum wavefunction ( before the load becomes ) and with a -dependent phase. Due to the periodicity of , it can be shown that the -dependent phase does not affect the time-evolution of and .. The simulation mesh contains points and the kicks are modeled as Gaussian pulses with of , calculated by fitting the pulses experimentally measured on an oscilloscope. During the free expansion stages of the experiment we numerically evolve the wavefunction in the momentum basis, while during the kicks we utilize a split-step method. We evolve the wavefunction with the kinetic energy operator in the momentum basis for half a time step, Fourier transform the wavefunction into the position basis and evolve with the kick operator (which is diagonal in the position basis) for a full time step, then finally Fourier transform back into the momentum basis and apply the kinetic energy operator for another half time step. This is repeated for all time steps over the duration of the pulse. We average over a uniform distribution of kicking lattice depths with a 10% width to account for the atoms radially sampling the measured Gaussian cross section of the lattice, as well as drift in the kicking laser power. We suspect that a portion of the remaining discrepancy between theory and experiment results from slight differences in initial conditions arising from imperfect lattice loading, along with potential undersampling of data points.
In Figs. 2e and 3b, we compute the Floquet diagonal ensemble predictions by diagonalizing the ideal QKR Floquet operator 3. The diagonal ensemble momentum 6 is computed for ideal states which should exhibit the Floquet gauge symmetries discussed in appendix C. For comparison with the load-preparation data, we use a Gaussian Bloch state ensemble, while for comparison with the kick-preparation data, we use with the effective preparation kick impulse. Quasimomentum averaging is accomplished via the same method used in the TDSE numerics.
References
- Anderson [1958] P. W. Anderson, Absence of Diffusion in Certain Random Lattices, Phys. Rev. 109, 1492 (1958).
- Fishman et al. [1982] S. Fishman, D. R. Grempel, and R. E. Prange, Chaos, Quantum Recurrences, and Anderson Localization, Phys. Rev. Lett. 49, 509 (1982).
- Grempel et al. [1984] D. R. Grempel, R. E. Prange, and S. Fishman, Quantum dynamics of a nonintegrable system, Phys. Rev. A 29, 1639 (1984).
- Haake [2010] F. Haake, Quantum Signatures of Chaos, Springer, Berlin, Heidelberg (2010).
- Casati et al. [1979] G. Casati, B. V. Chirikov, F. M. Izraelev, and J. Ford, Stochastic behavior of a quantum pendulum under a periodic perturbation, in Stochastic Behavior in Classical and Quantum Hamiltonian Systems, Lecture Notes in Physics, Vol. 93, edited by G. Casati and J. Ford (Springer, Berlin/Heidelberg, 1979) pp. 57–75.
- Wiersma et al. [1997] D. S. Wiersma, P. Bartolini, A. Lagendijk, and R. Righini, Localization of light in a disordered medium, Nature 390, 671 (1997).
- Hu et al. [2008] H. Hu, A. Strybulevych, J. H. Page, S. E. Skipetrov, and B. A. van Tiggelen, Localization of ultrasound in a three-dimensional elastic network, Nature Physics 4, 945 (2008).
- Billy et al. [2008] J. Billy, V. Josse, Z. Zuo, A. Bernard, B. Hambrecht, P. Lugan, D. Clément, L. Sanchez-Palencia, P. Bouyer, and A. Aspect, Direct observation of Anderson localization of matter waves in a controlled disorder, Nature 453, 891 (2008).
- Roati et al. [2008] G. Roati, C. D’Errico, L. Fallani, M. Fattori, C. Fort, M. Zaccanti, G. Modugno, M. Modugno, and M. Inguscio, Anderson localization of a non-interacting Bose–Einstein condensate, Nature 453, 895 (2008).
- Chabé et al. [2008] J. Chabé, G. Lemarié, B. Grémaud, D. Delande, P. Szriftgiser, and J.-C. Garreau, Experimental Observation of the Anderson Metal-Insulator Transition with Atomic Matter Waves, Phys. Rev. Lett. 101, 255702 (2008).
- Manai et al. [2015] I. Manai, J.-F. Clément, R. Chicireanu, C. Hainaut, J. C. Garreau, P. Szriftgiser, and D. Delande, Experimental Observation of Two-Dimensional Anderson Localization with the Atomic Kicked Rotor, Phys. Rev. Lett. 115, 240603 (2015).
- Ying et al. [2016] T. Ying, Y. Gu, X. Chen, X. Wang, S. Jin, L. Zhao, W. Zhang, and X. Chen, Anderson localization of electrons in single crystals: LiXFe7Se8, Science Advances 2, e1501283 (2016).
- Prat et al. [2019] T. Prat, D. Delande, and N. Cherroret, Quantum boomeranglike effect of wave packets in random media, Physical Review A 99, 023629 (2019).
- Janarek et al. [2020] J. Janarek, D. Delande, N. Cherroret, and J. Zakrzewski, Quantum boomerang effect for interacting particles, Physical Review A 102, 013303 (2020).
- Tessieri et al. [2021] L. Tessieri, Z. Akdeniz, N. Cherroret, D. Delande, and P. Vignolo, Quantum boomerang effect: Beyond the standard Anderson model, Physical Review A 103, 063316 (2021).
- Garreau [2017] J.-C. Garreau, Quantum simulation of disordered systems with cold atoms, C. R. Physique 18, 31 (2017).
- Altland and Zirnbauer [1996] A. Altland and M. R. Zirnbauer, Field Theory of the Quantum Kicked Rotor, Phys. Rev. Lett. 77, 4536 (1996).
- Moore et al. [1995] F. L. Moore, J. C. Robinson, C. F. Bharucha, B. Sundaram, and M. G. Raizen, Atom Optics Realization of the Quantum -Kicked Rotor, Phys. Rev. Lett. 75, 4598 (1995).
- Hainaut et al. [2019] C. Hainaut, A. Rançon, J.-F. Clément, I. Manai, P. Szriftgiser, D. Delande, J.-C. Garreau, and R. Chicireanu, Experimental realization of an ideal Floquet disordered system, New Journal of Physics 21, 035008 (2019).
- Hainaut et al. [2017] C. Hainaut, I. Manai, R. Chicireanu, J.-F. Clément, S. Zemmouri, J.-C. Garreau, P. Szriftgiser, G. Lemarié, N. Cherroret, and D. Delande, Return to the Origin as a Probe of Atomic Phase Coherence, Phys. Rev. Lett. 118, 184101 (2017).
- Hainaut et al. [2018a] C. Hainaut, A. Rançon, J.-F. Clément, J.-C. Garreau, P. Szriftgiser, R. Chicireanu, and D. Delande, Ratchet effect in the quantum kicked rotor and its destruction by dynamical localization, Phys. Rev. A 97, 061601(R) (2018a).
- Hainaut et al. [2018b] C. Hainaut, I. Manai, J.-F. Clément, J.-C. Garreau, P. Szriftgiser, G. Lemarié, N. Cherroret, D. Delande, and R. Chicireanu, Controlling symmetry and localization with an artificial gauge field in a disordered quantum system, Nature Communications 9, 1382 (2018b).
- White et al. [2013] D. H. White, S. K. Ruddell, and M. D. Hoogerland, Experimental realization of a quantum ratchet through phase modulation, Phys. Rev. A 88, 063603 (2013).
- Cao et al. [2021] A. Cao, R. Sajjad, H. Mas, E. Q. Simmons, J. L. Tanlimco, E. Nolasco-Martinez, T. Shimasaki, H. E. Kondakci, V. Galitski, and D. M. Weld, Interaction-driven breakdown of dynamical localization in a kicked quantum gas (2021), arXiv:2106.09698 [cond-mat.quant-gas] .
- Toh et al. [2021] J. H. S. Toh, K. C. McCormick, X. Tang, Y. Su, X.-W. Luo, C. Zhang, and S. Gupta, Observation of Many-body Dynamical Delocalization in a Kicked Ultracold Gas (2021), arXiv:2106.13773 [cond-mat.quant-gas] .
- Shrestha et al. [2012] R. K. Shrestha, J. Ni, W. K. Lam, S. Wimberger, and G. S. Summy, Controlling the momentum current of an off-resonant ratchet, Phys. Rev. A 86, 043617 (2012).
- Lemarié et al. [2017] G. Lemarié, C. A. Müller, D. Guéry-Odelin, and C. Miniatura, Coherent backscattering and forward-scattering peaks in the quantum kicked rotor, Phys. Rev. A 95, 043626 (2017).
- Lopez et al. [2012] M. Lopez, J.-F. Clément, P. Szriftgiser, J. C. Garreau, and D. Delande, Experimental Test of Universality of the Anderson Transition, Phys. Rev. Lett. 108, 095701 (2012).
- Rylands et al. [2020] C. Rylands, E. B. Rozenbaum, V. Galitski, and R. Konik, Many-Body Dynamical Localization in a Kicked Lieb-Liniger Gas, Phys. Rev. Lett. 124, 155302 (2020).
- Rajak et al. [2019] A. Rajak, I. Dana, and E. G. Dalla Torre, Characterizations of prethermal states in periodically driven many-body systems with unbounded chaotic diffusion, Phys. Rev. B 100, 100302(R) (2019).
- Pasek et al. [2017] M. Pasek, G. Orso, and D. Delande, Anderson Localization of Ultracold Atoms: Where is the Mobility Edge?, Phys. Rev. Lett. 118, 170403 (2017).
- Sadgrove et al. [2007] M. Sadgrove, M. Horikoshi, T. Sekimura, and K. Nakagawa, Rectified Momentum Transport for a Kicked Bose-Einstein Condensate, Phys. Rev. Lett. 99, 043002 (2007).
- Dana et al. [2008] I. Dana, V. Ramareddy, I. Talukdar, and G. S. Summy, Experimental Realization of Quantum-Resonance Ratchets at Arbitrary Quasimomenta, Phys. Rev. Lett. 100, 024103 (2008).
- Delvecchio et al. [2020] M. Delvecchio, F. Petiziol, and S. Wimberger, Resonant Quantum Kicked Rotor as A Continuous-Time Quantum Walk, Condens. Matter 5, 4 (2020).
- Shepelyansky [1986] D. L. Shepelyansky, Localization of quasienergy eigenfunctions in action space, Phys. Rev. Lett. 56, 677 (1986).
- Lepers et al. [2008] M. Lepers, V. Zehnlé, and J.-C. Garreau, Kicked-rotor quantum resonances in position space, Phys. Rev. A 77, 043628 (2008).
- Deng et al. [1999] L. Deng, E. W. Hagley, J. Denschlag, J. E. Simsarian, M. Edwards, C. W. Clark, K. Helmerson, S. L. Rolston, and W. D. Phillips, Temporal, Matter-Wave-Dispersion Talbot Effect, Phys. Rev. Lett. 83, 5407 (1999).
- Duffy et al. [2004] G. J. Duffy, S. Parkins, T. Müller, M. Sadgrove, R. Leonhardt, and A. C. Wilson, Experimental investigation of early-time diffusion in the quantum kicked rotor using a Bose-Einstein condensate, Phys. Rev. E 70, 056206 (2004).
- d’Arcy et al. [2001] M. B. d’Arcy, R. M. Godun, M. K. Oberthaler, D. Cassettari, and G. S. Summy, Quantum Enhancement of Momentum Diffusion in the Delta-Kicked Rotor, Phys. Rev. Lett. 87, 074102 (2001).
- Note [1] The experimental delay-time definition and Floquet gauge definition of is only consistent on . For data and simulations shown, we define solely by the delay-time definition. To make the Floquet gauge definition consistent with this, one should redefine the quenched initial state as , with the original quenched state for cases, denoting the integer part of , and taking the Floquet gauge to be .
- Oskay et al. [2003] W. H. Oskay, D. A. Steck, and M. G. Raizen, Timing noise effects on dynamical localization, Chaos, Solitons & Fractals 16, 409 (2003).
- Ringot et al. [2000] J. Ringot, P. Szriftgiser, J. C. Garreau, and D. Delande, Experimental evidence of dynamical localization and delocalization in a quasiperiodic driven system, Phys. Rev. Lett. 85, 2741 (2000).
- White et al. [2014] D. H. White, S. K. Ruddell, and M. D. Hoogerland, Phase noise in the delta kicked rotor: from quantum to classical, New Journal of Physics 16, 113039 (2014).
- Klappauf et al. [1998] B. G. Klappauf, W. H. Oskay, D. A. Steck, and M. G. Raizen, Observation of Noise and Dissipation Effects on Dynamical Localization, Phys. Rev. Lett. 81, 1203 (1998).
- Blümel and Smilansky [1992] R. Blümel and U. Smilansky, Symmetry breaking and localization in quantum chaotic systems, Phys. Rev. Lett. 69, 217 (1992).
- Note [2] According to the adiabatic theorem, the BEC wavefunction after the lattice load state-preparation is a superposition of Bloch states , where denotes quasimomentum, weighted by the initial Gaussian momentum wavefunction ( before the load becomes ) and with a -dependent phase. Due to the periodicity of , it can be shown that the -dependent phase does not affect the time-evolution of and .