2022
[1,2]\fnmTulasi N \surParashar
[1]\orgdivSchool of Chemical and Physical Sciences, \orgnameVictoria University of Wellington, \orgaddress\streetGate 7, Kelburn Parade, Kelburn, \cityWellington, \postcode6012, \countryNew Zealand
2]\orgdivDepartment of Physics and Astronomy, \orgnameUniversity of Delaware, \orgaddress\streetSharp Laboratory, \cityNewark, \stateDelaware, \postcode19711, \countryUSA
Observations of Cross Scale Energy Transfer in the Inner Heliosphere by Parker Solar Probe
Abstract
The solar wind, a continuous flow of plasma from the sun, not only shapes the near Earth space environment but also serves as a natural laboratory to study plasma turbulence in conditions that are not achievable in the lab. Starting with the Mariners, for more than five decades, multiple space missions have enabled in-depth studies of solar wind turbulence. Parker Solar Probe (PSP) was launched to explore the origins and evolution of the solar wind. With its state-of-the-art instrumentation and unprecedented close approaches to the sun, PSP is starting a new era of inner heliospheric exploration. In this review we discuss observations of turbulent energy flow across scales in the inner heliosphere as observed by PSP. After providing a quick theoretical overview and a quick recap of turbulence before PSP, we discuss in detail the observations of energy at various scales on its journey from the largest scales to the internal degrees of freedom of the plasma. We conclude with some open ended questions, many of which we hope that PSP will help answer.
keywords:
keyword1, Keyword2, Keyword3, Keyword41 Introduction
Since the advent of the space race, the importance of space weather and space environment in general has increased in our lives. The solar wind that shapes this space environment has been a subject of intensive study ever since its prediction and first measurements ParkerApJ58a ; NeugebauerJGR66 . Million degree hot corona is responsible for the acceleration of the solar wind and its eventual escape from the sun into the interplanetary medium. The solar wind, like most naturally occuring as well as man made plasmas, is turbulent in nature krommes2002fundamental ; tsytovich2016introduction ; yamada2008anatomy ; ColemanApJ68 ; MatthaeusJGR82 ; BrunoLRSP13 . The solar wind, being easily accessible through many space missions, serves as a natural laboratory for studying plasma turbulence in situ. These measurements have allowed testing and refinement of plasma turbulence theories, which are relevant for many other astrophysical systems such as the interstellar medium cordes1985small ; falceta2014turbulence ; armstrong1995electron , accretion disks balbus1998instability ; abramowicz2013foundations , and the intracluster medium SchueckerAA04 ; churazov2012x ; mohapatra2020turbulence .
Turbulence is believed to be an important player in heating the solar corona hendrix1996magnetohydrodynamic ; MattEA99-ch ; cranmer2007self . The subsonic coronal plasma accelerates to become supersonic at a few solar radii and eventually super Alfvénic at around . Beyond this Alfvén critical region, the strong coronal magnetic field loses control of the plasma. The shears introduce Kelvin Helmholtz like dynamics, creating large scale roll ups in the solar wind DeforestApJ16 ; TelloniApJ22 . These roll-ups push the solar wind towards isotropization at the largest scales introducing an important step in its turbulent evolution RuffoloApJ20 . As the solar wind evolves, the turbulence is believed to keep the wind hotter than what is expected from a simple adiabatic expansion RichardsonEA95 . The outer scale of turbulence, the Alfvénicity, and the amplitude of turbulent fluctuations all play an important role in the evolution of the solar wind. Accurate understanding of turbulent processes and their evolution is also critical for improving our global heliospheric models UsmanovApJ11 ; GamayunovApJ12 ; SokolovApJ13 ; oran2014coronal ; ChhiberApJS17 ; vanderHolstApJ22 .
Iconic missions such as Mariner, Voyager, Helios, and Ulysses ushered an era of exploration of macroscopic as well as turbulent properties of the solar wind. We refer the reader to excellent reviews by Tu & Marsch TuSSR95 , Bruno & Carbone BrunoLRSP13 , and Verscharen et. al. VerscharenLRSP19 for a comprehensive view of solar wind turbulence in the heliosphere before PSP. The basic macroscopic properties of the solar wind are well described in the seminal book by Hundhausen Hundhausen . Parker Solar Probe FoxSSR16 , with its state-of-the-art instrumentation and unprecedented close approaches to the sun is enabling hitherto impossible studies of plasma turbulence close to the sun. In this review paper we discuss how PSP has enhanced our understanding of the turbulent transfer of energy across scales in the inner heliosphere.
We start by describing a phenomenology of scale to scale spectral transfer from energy containing to kinetic scales in section 2. In section 3 we discuss the findings from prior missions such as Voyager, Helios, and Ulysses on the evolution of turbulence in the heliosphere. In section 4 we discuss the new findings enabled by the Parker Solar Probe mission before concluding with a summary of the findings and potential future directions in section 5.
2 Turbulent scale-to-scale transfer of energy
Fully developed turbulence is ideally characterized BatchelorTHT by an input of energy at some large scales, which is then conservatively transferred to progressively smaller scales in the inertial range. The cascaded energy is eventually converted to internal energy at the dissipative scales TennekesLumley . The large scale dynamics of plasmas are well described by magnetohydrodynamic description down to fairly small scales WuPRL13 ; KarimabadiPP13 ; WanPP16 . However, in kinetic plasmas, the hydrodynamic notion of a single dissipative scale is replaced by a multitude of smaller scales including the inertial lengths and gyro-radii of protons and electrons, the Debye length and other hybrid scales. The nature of the cascade modifies at some of these scales, rendering the hydrodynamic cascade picture to be relatively simpler in comparison. More sophisticated theories of turbulence are needed to describe the nature of turbulence at kinetic scales SchekochihinApJS09 ; BoldyrevApJ13 ; EyinkPRX18 . Even with the lack of a well accepted kinetic plasma turbulence theory, we can study the transfer of energy across scales in a quantitative way, down to kinetic scales and smaller with appropriate methods. We now describe a phenomenology of such a transfer from the largest scales to kinetic scales and into the internal degrees of freedom.
Energy at large scales: The energy at the largest scales is input by direct sources of energy or by large scale instabilities and is subsequently cascaded down to smaller scales BiskampBook03 . In hydrodynamics the turbulent cascade adjusts in such a way as to balance the energy input at the largest scales by dissipation at the small scales KarmanPRSLA38 . This von Kármán Howarth description of the decay when generalized to MHD can be written as HossainPFL95 ; WanJFM12 ; BandyopadhyayPRX18
| (1) |
where is the decay rate for with the Elsässer variables defined as with , , and being the fluctuating velocity, magnetic field, and density, and the energy containing scales. The proportionality constant can depend on a lot of conditions such as the Reynolds number , cross helicity , and the ratio of thermal to magnetic pressures MccombPRE15 ; MatthaeusApJL16 ; BandyopadhyayPRX18 .
The von Kármán Howarth similarity, although a simplified large scale description, describes the balance of large scale energy input and dissipation really well not only in hydrodynamics but also in kinetic plasmas down to very small scales (of the order of a few ion inertial scales ) WuPRL13 ; ParasharApJ15 . In the solar wind the von Kármán Howarth similarity has been recently shown to be applicable to the magnetic field fluctuations RoyApJL21 . As discussed in the section 4, PSP has allowed an examination of the balance between energy input and heating rate.
Energy in the inertial range: Assuming isotropy, homogeneity, constancy of scale-to-scale energy transfer rate , and locality of transfer in the scale space, Kolmogorov Kolmogorov41a identified the power spectrum of hydrodynamic turbulence to be (K41), where is the energy density in wavenumber and is assumed to be constant across scales and uniform in space. The K41 phenomenology when extended to MHD predicts spectral slopes varying between and KraichnanPFL65 ; GoldreichApJ95 ; VermaPP99 ; ZhouRMP04 . This scaling has been observed in hydrodynamic turbulence behind a grid ChampagneJFM78 , Earth’s magnetosheath ParasharPRL18 , solar wind KiyaniPTRSA15 , interstellar medium FraternaleApJ19 , and the intracluster medium SchueckerAA04 . If one considers non-uniform dissipation, intermittency emerges while minimally affecting the isotropic form of the spectral law KolmogorovJFM62 ; PolitanoPRE95 ; VermaPR04 .
The cascade of energy from large to small scales in the inertial range is quantitatively described, under the assumptions of homogeneity, time stationarity, and isotropy, by the so called third order law. For the conservative part of the cascade, in hydrodynamics, the third order structure function is related to decay rate by , where is the lag and is the magnitude of a velocity increment computed at lag PopeBook . This third order law was generalized to incompressible MHD by Politano and Pouquet in 1998 PolitanoPRE98 .
| (2) |
where is the lag at which the increment is computed, and denote appropriate averaging. The incompressible third order law can further be generalized to include more physics in the form of anisotropy PodestaJFM08 , compressibility AndresPRE17 , shears WanPP09 , Hall physics GaltierPRE08 , some combination of such effects FerrandJPP21 , or be generalized to electron MHD GaltierJGR08 . This von Kármán Howarth Yaglom Politano Pouquet (KHYPP) law or Politano-Pouquet (PP) law and many of its extensions to Hall/compressible MHD have been used to measure and test the cascade rates in simulations, solar wind, and Earth’s magnetosheath Sorisso-ValvoPRL07 ; MarinoApJL08 ; OsmanEA11-3rd ; VerdiniApJ15 ; HellingerApJL18 ; BandyopadhyayPRL20-PP . The cascade rates have also been compared to the expected rates of plasma heating in the solar wind to test if turbulence can account for heating of the solar wind (see discussion in sections 3 and 4).
The cascade of energy is actually even more complicated in models as simple as compressible MHD where a compressive cascade proceeds in parallel to a magnetic cascade AluiePRL11 . There exists a small scale ‘decoupled range’ where the magnetic energy and kinetic energy cascades proceed conservatively with the same cascade rate BianPRL19 . In this picture the exchange between kinetic and magnetic fluctuations happens at relatively large scales in the inertial range. There are also suggestions that magnetic reconnection, and in some situations large scale instabilities, could potentially bypass the cascade and transfer energy directly into the kinetic range and into internal degrees of freedom SquirePRL17 ; FranciApJL17 ; KunzJPP20 .
The third order law approach becomes cumbersome with the addition of more physics. Moreover the accuracy of this approach depends on the terms retained in the fluid model. An alternative approach to studying scale-to-scale transfer of energy in the fully kinetic limit is to apply scale filtering techniques to the Vlasov equation YangPP17 ; EyinkPRX18 ; CamporealePRL18 ; CerriPP20 . Starting with the Vlasov equation, applying scale filtering techniques, one arrives at YangPP17 ; YangApJ22
| (3) |
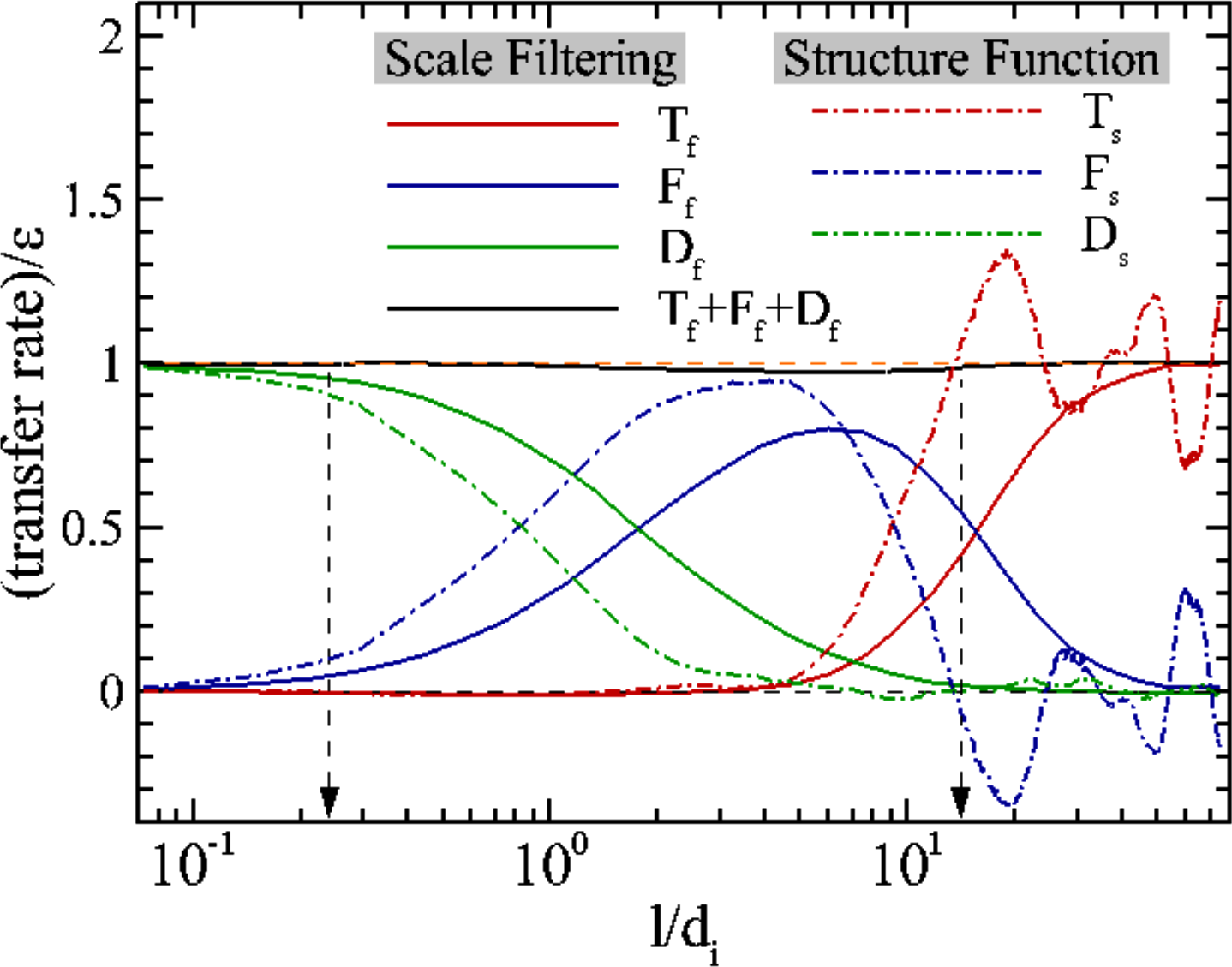
where represents a scale filtered quantity and represents a density weighted filtered quantity. is the filtered fluid flow energy, is the filtered electromagnetic energy, and are spatial transport terms, , and are the subgrid scale fluxes, is the rate of flow energy conversion to internal energy through pressure strain interactions (see the discussion of energy at kinetic scales below), and is the rate of energy conversion from electromagnetic fluctuations into fluid flow through filtered . For details of these equations see YangApJ22 .
The equations 3 can be combined to write:
| (4) |
with , , and representing the decay of energy, the inertial range fluxes, and “dissipation” respectively. These quantities can be directly compared to the generalized von Kármán Howarth equations as shown in Fig. 1. The solid lines represent scale filtered quantities, and the dashed lines correspond to equivalent terms in the von Kármán Howarth equations. The structure function approach seems to achieve a range reminiscent of an inertial range where the inertial range flux is comparble to the decay rate , while the scale filtered flux remains short of even at its peak. However, the scale filtered equations show energy conservation, within numerical error, across scales, giving a quantitative handle on flow of energy across scales in an accurate manner. The von Kármán Howarth equations contain varied limits of physics based on the model for which they are written HellingerApJL18 and hence energy conservation has been imposed to estimate the surrogate dissipation (shown as a green dot-dashed line). The situation is even more dramatic when the bandwidth available for the cascade is small (e.g. in 3D fully kinetic simulations or the Earth’s magnetosheath). See Yang et. al. YangApJ22 for more detailed discussion of these issues. In a recent preprint Hellinger et. al. HellingerArXiv22 have included pressure strain interactions to modify the von Kármán equations. This modification extends the range of validity of these equations down to sub-proton scales implying the important role played by pressure-strain interactions in the kinetic range energy transfer; see also YangApJ22 .
Energy transfer at kinetic scales: At the ion kinetic scales, some of the energy is removed into heating the ions, and the rest of it cascades down to smaller scales, eventually dissipating at electron scales. Heating of plasma111We use the terms ‘dissipation’ and ‘heating’ in a relaxed way to mean a transfer of turbulent fluctuation energy into the internal degrees of freedom of the plasma regardless of the (ir)reversible nature of the processes involved. can potentially happen in many ways including wave-particle interactions such as Landau damping HollwegPRL71 ; ChenNature19 , cyclotron resonances HollwegJGR02 ; KasperPRL13 , magnetic pumping DawsonNF65 ; LichkoApJL17 , and stochastic heating ChandranApJ10-1 ; XiaApJ13 ; MalletJPP19 ; CerriApJ21 ; MartinovicApJ21 . In the stochastic heating picture, particles experiencing large electric fluctuation changes at their gyro scales can get stochastic kicks perpendicular to the mean magnetic field changing their magnetic moment. This effect, that depends on turbulent fluctuation amplitude at the proton gyro scale gets enhanced near intermittent structures such as current sheets ChandranApJ10-1 ; XiaApJ13 ; MalletJPP19 . Moreover, landau damping has also been shown to occur in or near current sheets TenbargeApJ13 .
Many factors such as plasma , turbulence amplitude, proton-electron temperature ratio, Alfvénicity etc. can potentially regulate the fraction of energy going into heating the ions WuPRL13 ; HughesGRL14 ; MatthaeusApJL16 . A simplified view MatthaeusApJL16 proposes that the ratio of the local nonlinear time at the ion scales to the cyclotron time is an important factor in deciding the partitioning of energy between ions and electrons. If the kinetic scale nonlinear time is comparable to or smaller than the proton cyclotron time, significant nonlinear evolution of turbulent magnetic fluctuations happens within a gyroperiod and hence the protons can get significant stochastic kicks, leaving a smaller amount of energy to cascade down to electron scales and eventually heat them. Such dependence of relative proton-electron heating has been shown to hold in simulations as well as recently in MMS data MatthaeusApJL16 ; RoyApJL22 .
Although the exact processes responsible for heating the ions can vary from one scenario to the other, the mathematical terms responsible for the transfer are fairly straightforward to understand. The transfer of energy from electromangnetic fields and bulk flow energy into internal degrees of freedom happens via a collisionless generalization of viscosity. The equations for time evolution of electromagnetic energy , fluid flow kinetic energy , and internal energy can be written in a straightforward manner from the Vlasov Maxwelll set of equations as YangPRE17
| (5) |
where the subscript represents the species, is the pressure tensor, is the heat flux vector, is the total electric current density, and is the electric current density of species . The divergence terms simply transport energy in its current form and are not responsible for conversion from one form into another. The term is responsible for transfer of energy from electromagnetic fields into bulk flow and the term (called PS for short) is responsible for transferring energy from bulk fluid motions into internal degrees of freedom DelSartoPRE16 ; YangPRE17 .
The pressure tensor can be separated into a trace and a traceless part by defining where and, . The stress tensor can be similarly decomposed where , , and . With these decompositioins, the pressure stress interaction separates as . The first part is typically abbreviated as and the second part as Pi-D. is the familiar heating/cooling due to compressions rarefactions term. The pressure tensor is symmetric and hence only the symmetric stresses of bulk velocity interact with the traceless part of the pressure tensor to achieve the conversion into internal energy. In the highly collisional limit, the Pi-D term reduces to the familiar viscous heating term HuangBook .
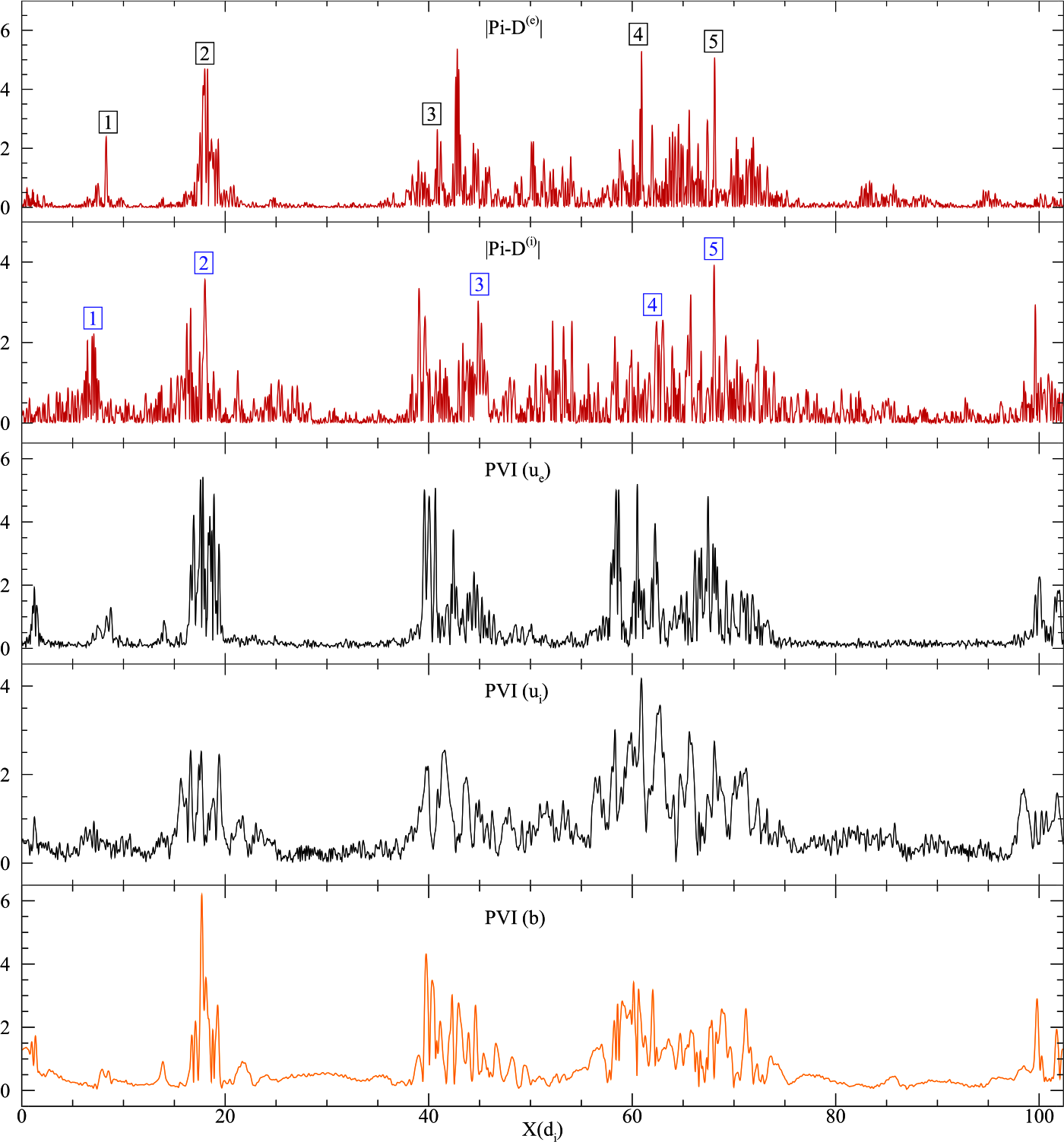
Kinetic activity, including the heating of the ions via the Pi-D channels takes place intermittently near strong current sheets ServidioPRL12 ; ServidioApJL14 ; FranciAIP15 ; DelSartoPRE16 ; ParasharApJ16b . Sheared magnetic fields produce strong current sheets, which in turn develop vortex quadrupoles near them MatthaeusGRL82 ; ParasharApJ16b . Although the vorticity is the antisymmetric part of the velocity strain tensor, the vortices are stretched into sheet like structures in the large Reynolds number limit, creating symmetric parts of the velocity strain tensor. This symmetric part contracts with the traceless pressure tensor to transfer energy from bulk turbulent motions into internal degrees of freedom DelSartoPRE16 ; YangPRE17 . The pressure strain interaction has been shown to be an effective description of plasma heating in simulations as well as in magnetosheath data YangPP17 ; SitnovGRL18 ; MatthaeusApJ20 ; BandyopadhyayPRL20 .
The intermittent sites near which the dissipation occurs can be identified using partial variance of increments (PVI), defined as where GrecoSSR18 , or via the unaveraged kernel of the third order law (Eqn. 2), also called Local Energy Transfer rate (LET) Sorisso-ValvoSP18 . Fig 2 shows cuts of Pi-D for ions and electrons from a 2.5D fully kinetic simulation along with PVI computed from velocities of ions and electrons and magnetic field YangPP17 . The locations of enhanced dissipation, identified by spikes in Pi-D, are clustered near large PVI values. Large PVI values have been shown to be strongly correlated with hotter ions in the solar wind OsmanApJL11 , and with higher fluxes of energetic particles TesseinApJL13 . More on this below.
An imbalanced cascade, with different powers in the and fluctuations and relevant for example for inner heliospheric conditions, could modify the cascade at ion kinetic scales affecting the ion heating rates and resulting cascade to smaller scales. The ‘helicity barrier’ inhibits the cascade of energy to scales smaller than proton kinetic scales, resulting in a build-up of energy at the proton scales. This build-up of proton scale kinetic energy can result in generation of cyclotron waves, which can heat the protons perpendicularly SquireNatureAstron22 . This enhanced energy dissipation at ion kinetic scales can result in very steep spectra just below ion kinetic scales (approaching ), eventually returning to the more familiar close to electron scales.
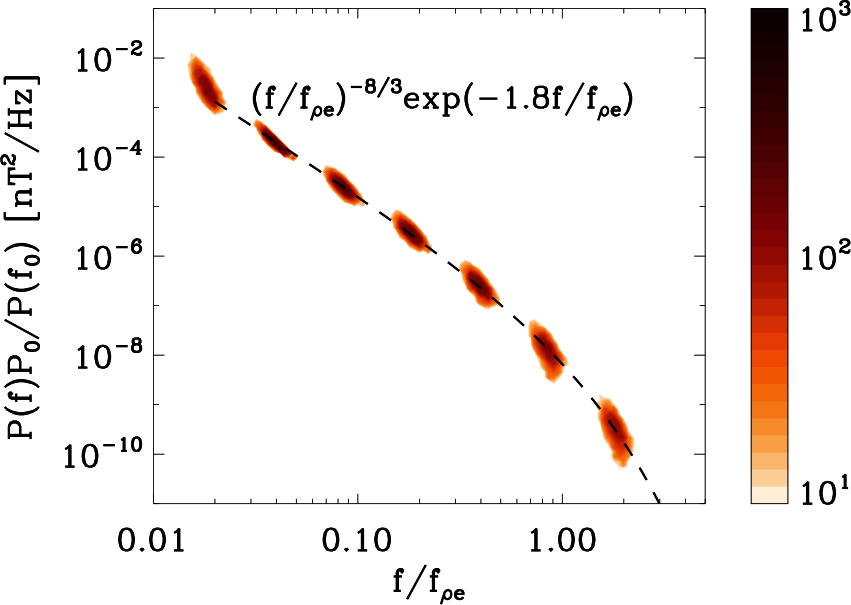
Close to electron scales, the magnetic energy spectra are exponentially damped. Fig. 3 shows magnetic energy spectra computed using magnetic field measurements from the search coil magnetometer (SCM) on Helios. The 3344 individual spectra have been rescaled by their amplitude at roughly 20 electron gyroperiods. The colours represent 2D histograms with darker colours representing more points. The spectra show a power-law behaviour with superposed with exponential decay at electron scales indicating strong damping of magnetic fluctuations AlexandrovaApJ12 ; TenbargeApJ13 ; ArroArXiv21 .
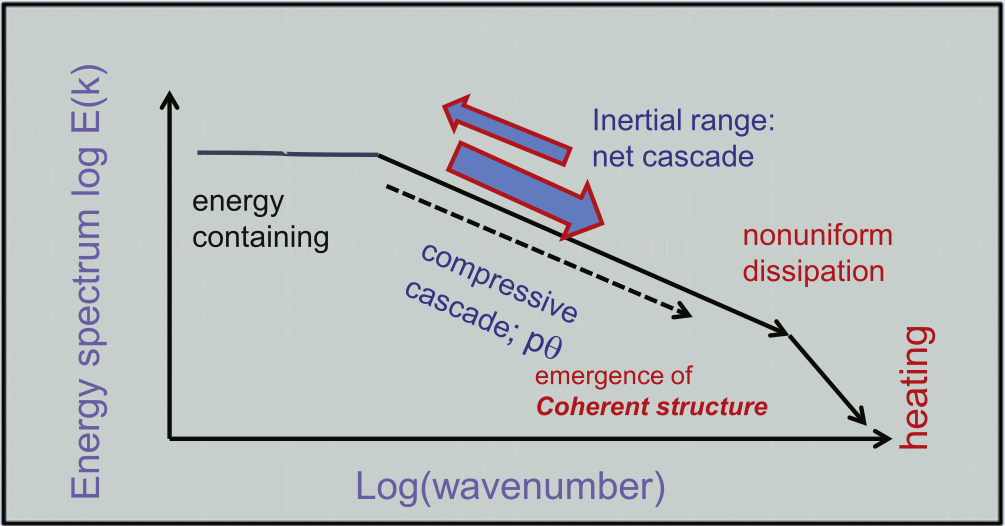
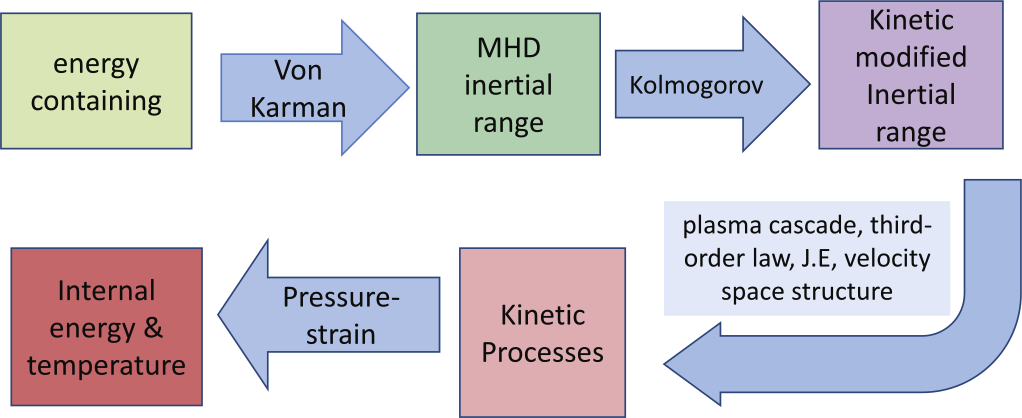
Based on the above considerations, an overall view of the cascade of energy from large to small scales emerges to be as follows (see Fig. 4 and MatthaeusApJ20 for an in-depth discussion): The energy containing scales input energy at the von Kármán rate into the inertial range. In the inertial range a cascade of energy to smaller scales via incompressible as well as compressive cascades transfers energy conservatively to smaller scales. The cascade also generates intermittent structures where pressure strain interactions transfer energy into internal degrees of freedom. The remaining part of the energy is transferred down to smaller scales where kinetic effects become dominant and dissipation ends the cascade.
3 Turbulence in the heliosphere before PSP
The dynamics of turbulence and its effects on the evolution of the solar wind have been studied in-depth since the late 60s. The observations from Mariners, Voyagers, Helios, and Ulysses revealed how the turbulent power, Alfvénicity, power spectra, spectral anisotropy, turbulent cascade, and intermittency evolve with heliocentric distance. For comprehensive view of solar wind turbulence we refer the reader to Tu & Marsch, Bruno & Carbone, and Verscharen et. al. TuSSR95 ; BrunoLRSP13 ; VerscharenLRSP19 .
Among the pioneering and landmark early studies of turbulence in the interplanetary medium, an important example is the work of Coleman ColemanApJ68 . This study synthesized analysis of Mariner 2 data, taking in to account earlier observations (HolzerJGR66, ; Coleman66, ) as well as the important suggestion (SturrockPRL66, ) that energy in waves or turbulence may be responsible for heating the corona. Coleman ColemanApJ68 developed this idea by postulating that the physical processes leading this heating would be governed approximately by ideas from classical hydrodynamic turbulence theory Chandra49-apj adapted to plasma in the approach of Kraichnan KraichnanPFL65 . This lead to a heating rate due to the cascade that was found to be reasonably in accord with observed temperatures at 1au. Several decades of research have elaborated on these ideas.

As the solar wind expands, the turbulent power decreases with heliocentric distance BelcherJGR74 . From earlier inner heliospheric observations (RobertsEA90, ), one may argue that this decrease is consistent with WKB theory VermaRoberts93 . However it is also consistent with a driven, dissipative expanding MHD system ZankJGR96 which gives very similar radial profiles for appropriate parameter choices. Interestingly the solutions are not consistent with an undriven dissipative turbulence system, which would provide power at 1 au that is less than what is observed. The observed decreasing total power reflects as well in the reduced spectral densities with increasing heliocentric distance BavassanoJGR82 ; HorburyJGR01 ; BrunoEMP09 . Describing this evolution of the spectrum and understanding the somewhat subtle physical effects that enter this description has been the subject of intensive study, even until the time of this writing.
Fig. 5 shows power spectra for magnetic field computed from Helios and Ulysses data BrunoEMP09 . The left panel shows trace magnetic power spectra for fast wind intervals and the right panel shows the same for slow wind intervals at various heliocentric distances. Two important features are clearly identified. The fast wind spectra show a break at large scales and transition from to at some large scale. The location of this spectral break shifts to lower frequencies or larger scales as the solar wind expands in the heliosphere. The break frequency follows a power law decrease of with heliocentric distance. There is some variability in the powerlaw values of this variation. This will be discussed below as well as in section 4. Secondly, the slow wind spectra do not show a transition to an regime, potentially owing to the more advanced state of evolution of the observed slow wind.
The first theoretical studies to attempt description of the radial evolution of heating Hollweg86 ; HollwegJohnson88 and the radial evolution of the spectral shapes TuJGR84 ; TuJGR88 made major steps towards merging the ideas of turbulence theory with spatial transport modeling of radial evolution of solar wind properties, a theory classically exemplified by WKB theory Hollweg74 . It was soon recognized that refinements of these approaches were required for greater veracity, including the crucial development of non-WKB transport theory MarschTu89 ; ZhouMatt89 and transport theory to describe the turbulence fluctuations at energy containing scales MatthaeusJGR94 that feed energy into the inertial range
The energy containing scale, identified by the correlation length , increases with increasing heliocentric distance SmithJGR01 ; RuizSP14 . Measurements from Voyager and Ulysses show the increase to follow , in contrast to the expectation of break frequency variation of . Along with the highly nonadiabatic behavior of the proton temperature RichardsonEA95 ; SmithJGR01 , the observed variation of correlation scale is a strong indication of the macroscopic influence of active turbulence evolution in the interplanetary medium.
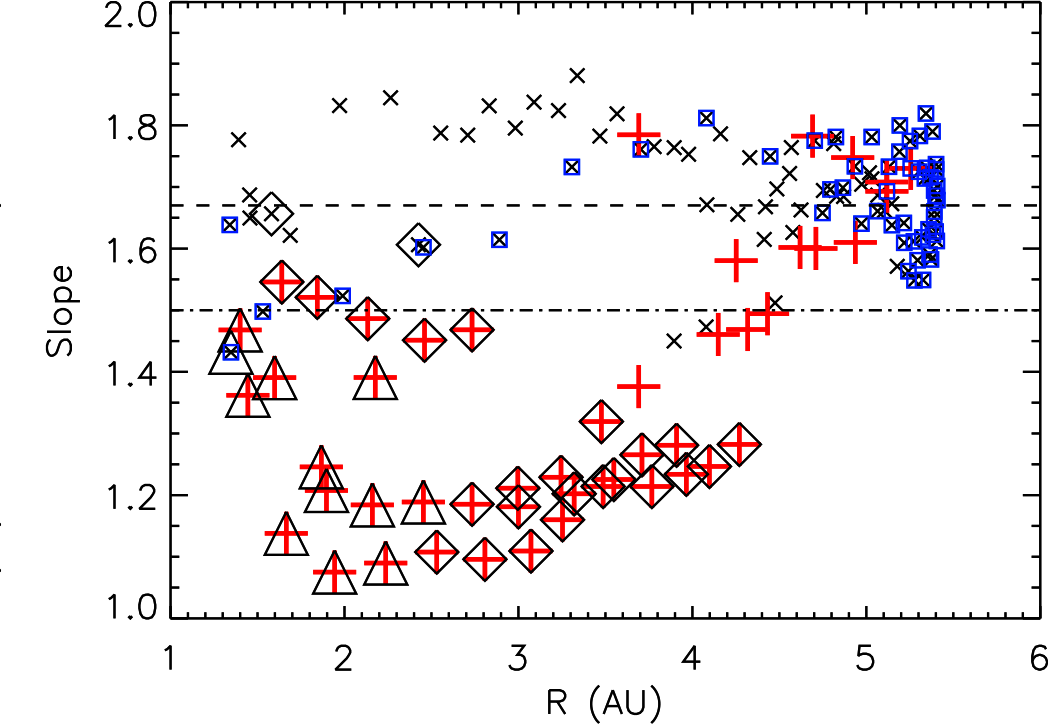
The characteristics of the plasma velocity fluctuations are also indicative of turbulence and of turbulence evolution as the solar wind ages. The velocity spectra evolve with heliocentric distance towards a state that is closer to a Kolmogorov-like spectral index. Fig. 6 shows slopes of velocity wavenumber spectra from Ulysses data as a function of heliocentric distance RobertsJGR10 . The slopes were computed using power law fits to the velocity spectra in the Hz to Hz range. Red pluses represent very fast wind with speed km/s and black crosses represent rest of the intervals. These intervals show a significant scatter in spectral slopes between 1-2AU but show a gradual rise of the slope from to in the outer heliosphere. A reason behind this could potentially be that the Hz fitting range might be in the energy containing range in the inner heliosphere and in the inertial range as the wind expands and the break point moves to lower frequencies (see for example Fig 5). The points enclosed in blue squares are within 20∘ of the ecliptic and hence directly comparable with results from other missions such as Helios and PSP. The slopes near the ecliptic vary from to as heliocentric distance increases. As interesting as this may be, one must recall that the standard Kolmogorov theory applied to MHD does not make a specific universal prediction about the velocity spectrum itself, but rather, in the usual sense, for the total incompressive energy spectrum.
The turbulence is in an “imbalanced” high cross helicity state in the inner heliosphere. It is highly Alfvénic with the outward propagating Elsässer field () dominating the energy budget. This is usually argued to be a consequence of the launching of outward-propagating waves in the lower corona and photosphere, along with the potential filtering effect that may occur at the Alfvén critical surface (Only outward waves propagate away.) However it is well known that an admixture of inward-type cross helicity is required to drive an incompressive MHD cascade KraichnanPFL65 . A widely accepted explanation for how the cascade is enabled is that interactions with Alfvén speed gradients, i.e., “reflections,” MattEA99-ch or, equally well, interaction with shears MattEA99-swh that tap velocity field energy and produced both senses of Elasässer propagation, can produce the required flux of inward fluctuations.
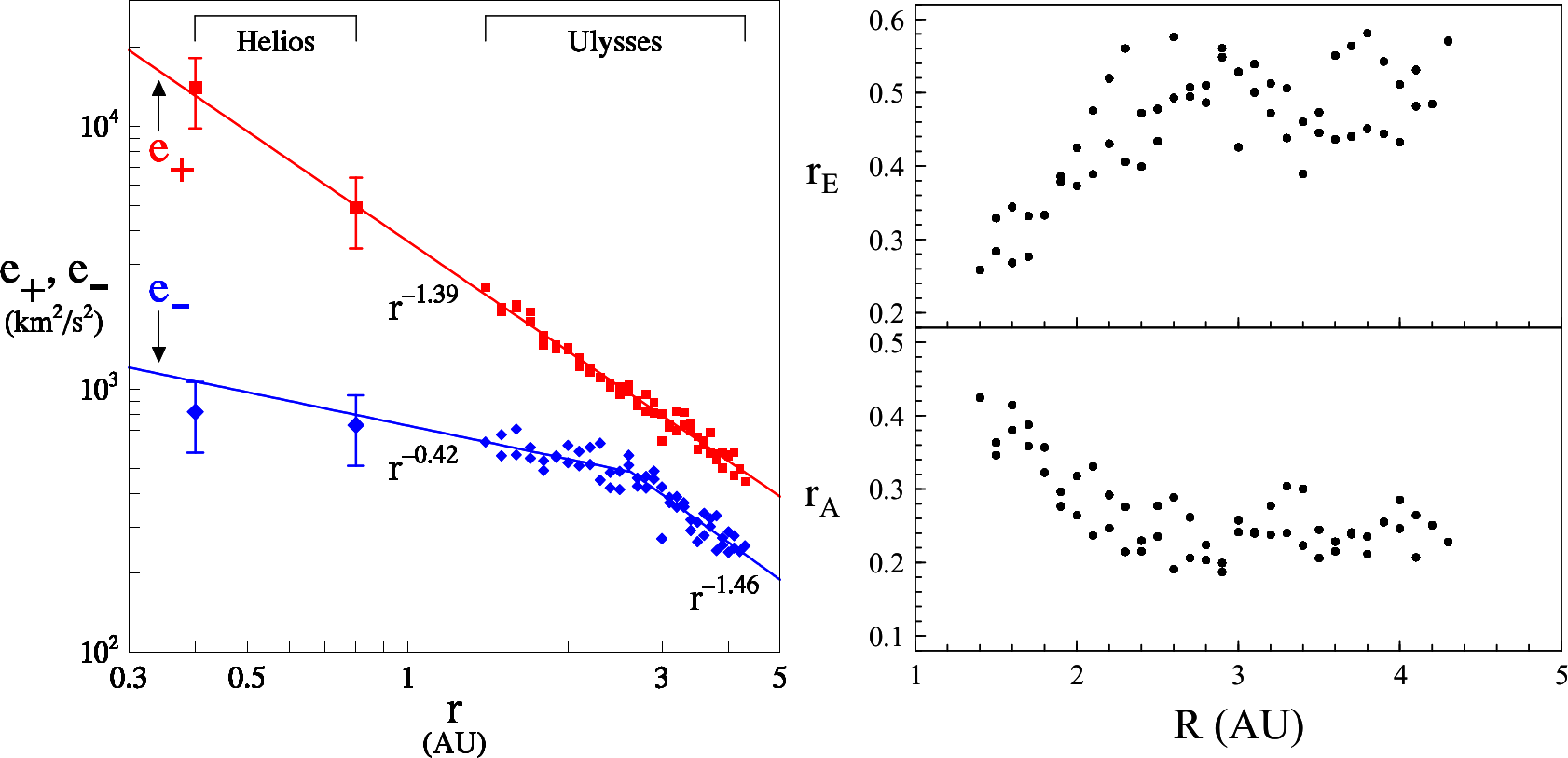
High latitude solar wind turbulence shows a smaller inertial range than what is observed in the ecliptic because of the lack of shears GoldsteinGRL95 , or perhaps weaker shears BreechEA08 . As the solar wind expands, the cross helicity and the Alfvénicity of the solar wind fluctuations decrease RobertsJGR87 ; GoldsteinGRL95 ; MatthaeusGRL04 ; BavassanoJGR00 . Fig. 7 shows the radial evolution of Elsässer variances (left panel), the ratio of energies contained in the Elsässer variables, called Elsässer ratio in the top right panel, and the Alfvén ratio in the bottom right panel. The outward Elsässer energy decreases significantly faster than the inward Elsässer energy out to roughly 2.5AU beyond which both decrease in a similar fashion. The ratio of the two Elsässer energies increases gradually as the turbulence becomes less Alfvénic; this ratio fluctuates around 0.5 beyond 2.5AU.
Apart from the variation of cross helicity, there is also systematic radial evolution of the Alfvén ratio. This quantity is defined as the ratio of energy density in the velocity fluctuations to energy density in magnetic fluctuations, i.e., . In the inner heliosphere, the inertial range decreases and stabilizes at values around . Like cross helicity, is influenced by both expansion and shear. An equivalent quantity is the residual energy defined as , a quantity that is not related to ideal invariants and so is not associated with a conserved spectral flux. Even if it cannot “cascade” in the usual sense, exhibits distinctive properties, such as attaining moderately negative values in the inertial range of MHD turbulence and in the solar wind over a fairly wide range of parameters. (For observations, see, e.g., MatthaeusJGR82 .) There have been numerous phenomenological theories developed to describe the behavior of residual energy, e.g., StriblingMatt91 ; MullerGrappin04 ; BoldyrevEA11 ; GrappinEA16 .
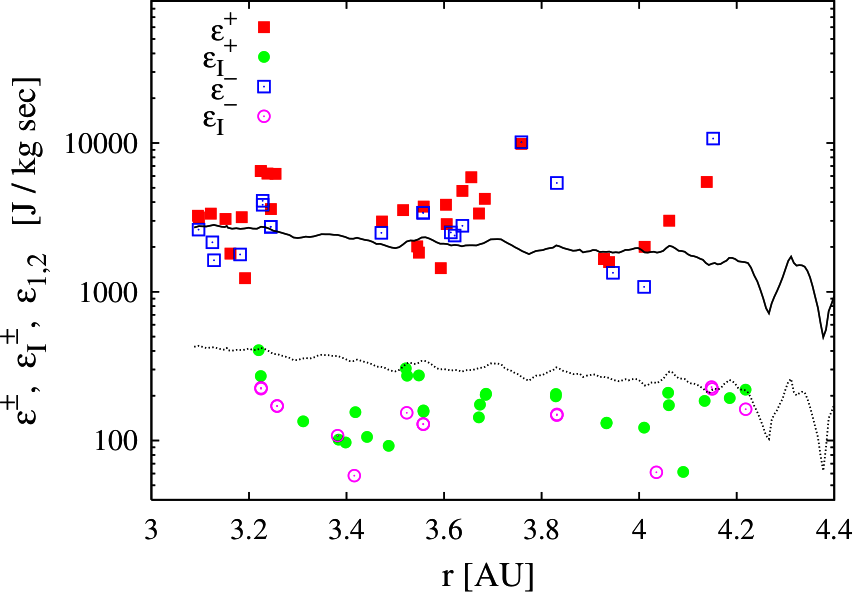
The temperature of the solar wind drops slower than expected as it expands until the pickup ions introduce a new significant source of energy in its evolution MarschJGR82 ; WangJGR01 ; MatteiniGRL07 ; HellingerJGR13 . The heating rate computed from large scale properties in the solar wind at 1AU is sufficiently larger than the required heating rate VasquezJGR07 . The nonlinear cascade of energy to smaller scales, measured by the third order law (Eqn. 1), has also been established in the solar wind Sorisso-ValvoPRL07 ; MacBrideEA08 ; CarbonePRL09 ; MacBrideEA-sw11 ; MarinoApJ12 . The incompressible cascade rate, studied in the polar wind using Ulysses data, can provide a significant fraction of energy required to heat the solar wind MarinoApJL08 . When generalized phenomenologically to include compressibility effects via density weighted Elsässer fields, the cascade rate increases significantly. Fig. 8 shows cascade rates computed for both incompressible Elsässer variables as well as density weighted Elsässer variables. The compressive estimates are about an order of magnitude higher and for both estimates follow the heating rate required for heating the solar wind protons VermaJGR95 ; VasquezJGR07 ; MarinoApJL08 .
Near kinetic scales the cascaded energy is transferred partially into proton internal energy and partially cascaded down to electron scales. Data from Helios missions have been used to compute the expected stochastic heating rates in the inner heliosphere BourouaineApJ13 ; MartinovicApJ19 . The stochastic heating rate appears to be sufficient to heat the solar wind. However, the radial dependence of the SH rate is very steep () and it decreases more rapidly than the expected heating rate. This disparity is larger for the fast solar wind streams. The stochastic heating process is enhanced in the presence of the intermittent structures ChandranApJ10-1 ; XiaApJ13 ; MalletJPP19 .
In simulations, and in observations at 1au, the heating of plasmas has been shown to happen intermittently ParasharPP11 ; OsmanApJL11 ; OsmanPRL12a ; TenbargeApJ13 ; YangPP17 . Until recently there have not been many studies that investigated intermittent heating behaviour in the inner heliosphere; this is discussed more in a later section below. However, the radial evolution of intermittency has been studied in some detail BrunoJGR03 ; ParasharApJL19 ; CuestaApJS22 . The kurtosis at a given time-scale seems to increase with increasing heliocentric distance BrunoJGR03 . When plotted as a function of plasma scales (e.g. multiples of proton inertial length ), the kurtosis drops with increasing heliocentric distance ParasharApJL19 ; CuestaApJS22 . The proton inertial length increases faster than the outer scale of the turbulence in expanding wind. This reduces the bandwidth available for the inertial range cascade, and hence the level of intermittency as identified by scale dependent kurtosis at a given plasma scale.
4 Parker Solar Probe Observations
Parker Solar Probe was launched in 2018 to study the origins and evolution of the solar wind FoxSSR16 . The science objectives of the probe are to “trace the flow of energy that heats the corona and accelerates the solar wind”, to “determine the structure and dynamics of the magnetic fields at the sources of solar wind”, and to “explore the mechanisms that accelerate and transport energetic particles” FoxSSR16 . The mission carries four instruments: Electromagnetic Fields Investigation (FIELDS) BaleSSR16 , Integrated Science Investigation of the Sun (ISIS ) McComasSSR16 , Solar Wind Electrons Alphas and Protons (SWEAP) KasperSSR16 , and Wide-field Imager for Solar Probe (WISPR) VourlidasSSR16 . The data from FIELDS, SWEAP, and ISIS have extensively been used to study the origins and evolution of solar wind turbulence and its role in energetic particle dynamics. In this section we discuss PSP’s contributions to our understanding of how the turbulent energy flows from large to small scales in the inner heliosphere. After a brief overview of the turbulence properties (see RaouafiEA22SSR for an in-depth review), we provide an in-depth discussion of the turbulent transfer of energy from large scales to small scales.
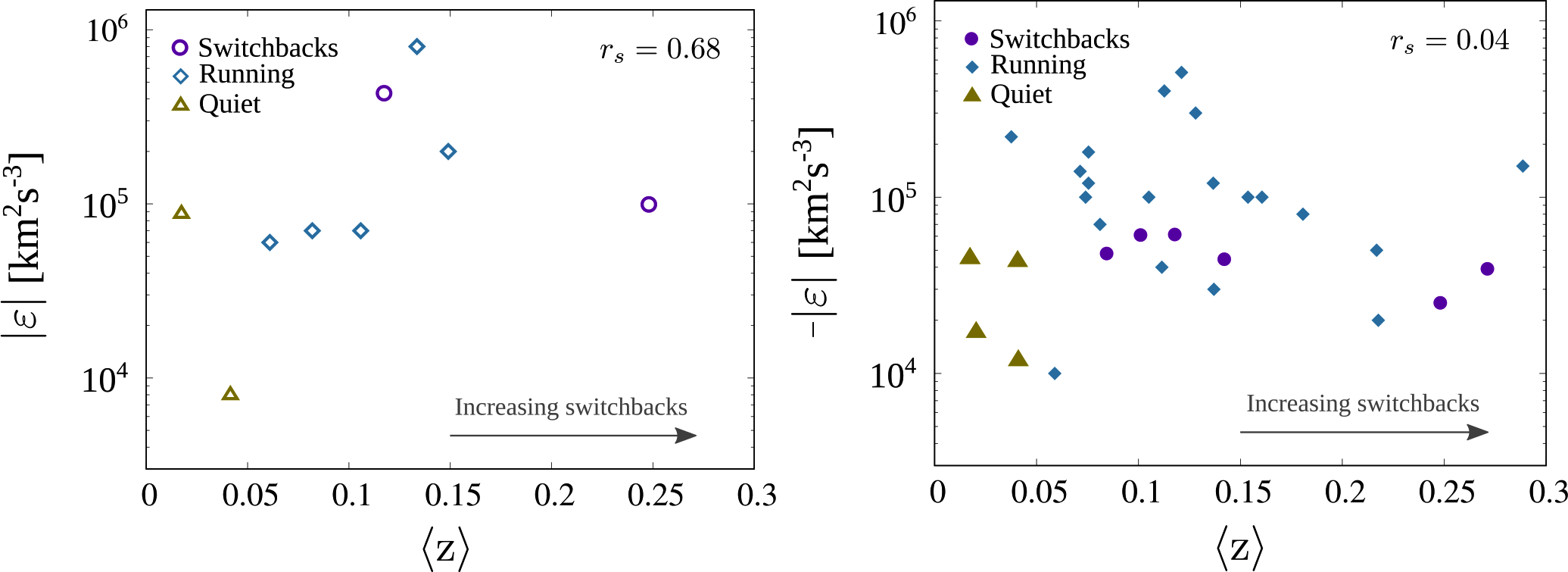
As one approaches closer to the sun, the turbulence becomes more structured. Intermittent patches of reversals in radial magnetic field are enbedded in ‘smoother and less turbulent flow with near radial magnetic field’ BaleNature19 . These routinely observed feature of the solar wind, also called ‘magnetic switchbacks’ typically show a sharp reversal in the sign of the radial component of the magnetic field BaloghGRL99 ; MatteiniGRL14 ; BorovskyJGR16 ; deWitApJS20 . The origins of switchbacks are debated. Proposed mechanisms involve interchange reconnection, in-situ generation by expanding turbulence, and velocity shears FiskApJL20 ; SquireApJL20 ; RuffoloApJ20 . In the shear driven picture, large velocity shears across magnetic flux tubes are dominated by the strong magnetic field in the corona. After the Alfvén critical zone, the magnetic field is not strong and velocity shears can produce “flocculated” roll ups and switchbacks in-situ DeforestApJ16 ; ChhiberApJL18 ; RuffoloApJ20 . A consequence of such shear driven in-situ generation of switchbacks is that their number should drop in the sub-Alfvénic wind inside magnetically dominated corona. Early hints of that are already being observed in the PSP data BandyopadhyayApJL22 ; KasperPRL21 . A significant amount of literature stemming from PSP observations has focused on comparing and contrasting the nature of turbulence in and outside switchbacks (see e.g. deWitApJS20 ; BourouaineApJL20 ; MartinovicApJS20 ; TeneraniApJS20 ; McManusApJS20 ; MartinovicApJ21 ; BandyopadhyayApJL22 and references therein for a sampling of topics studied in the context of switchbacks by PSP).
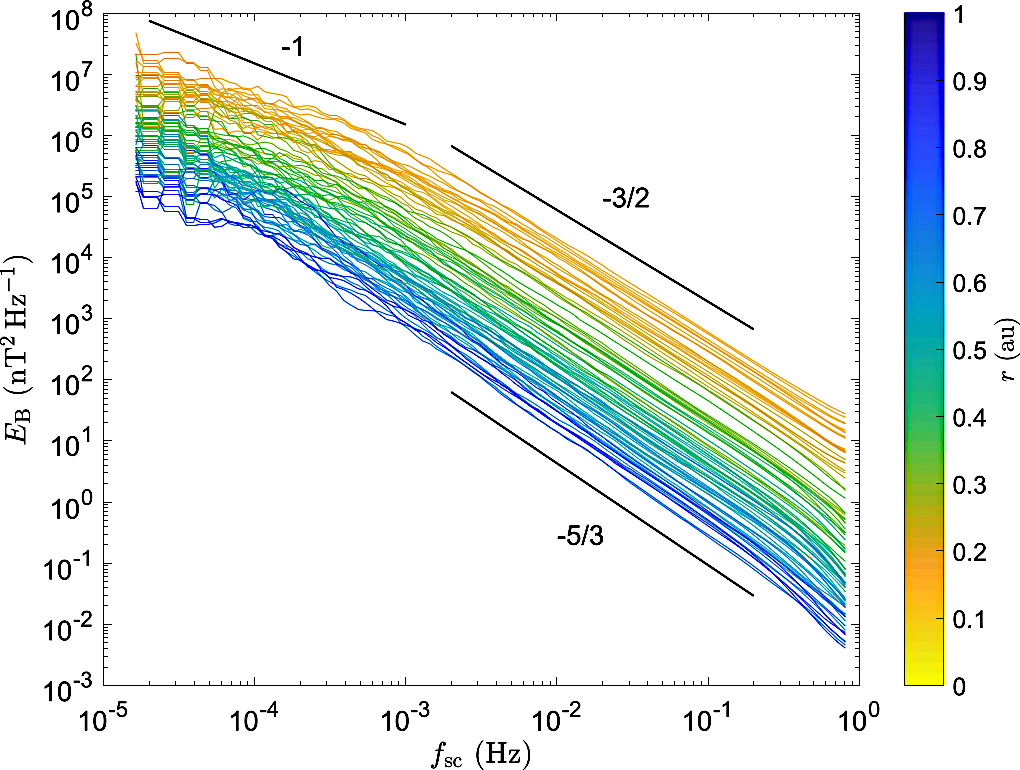
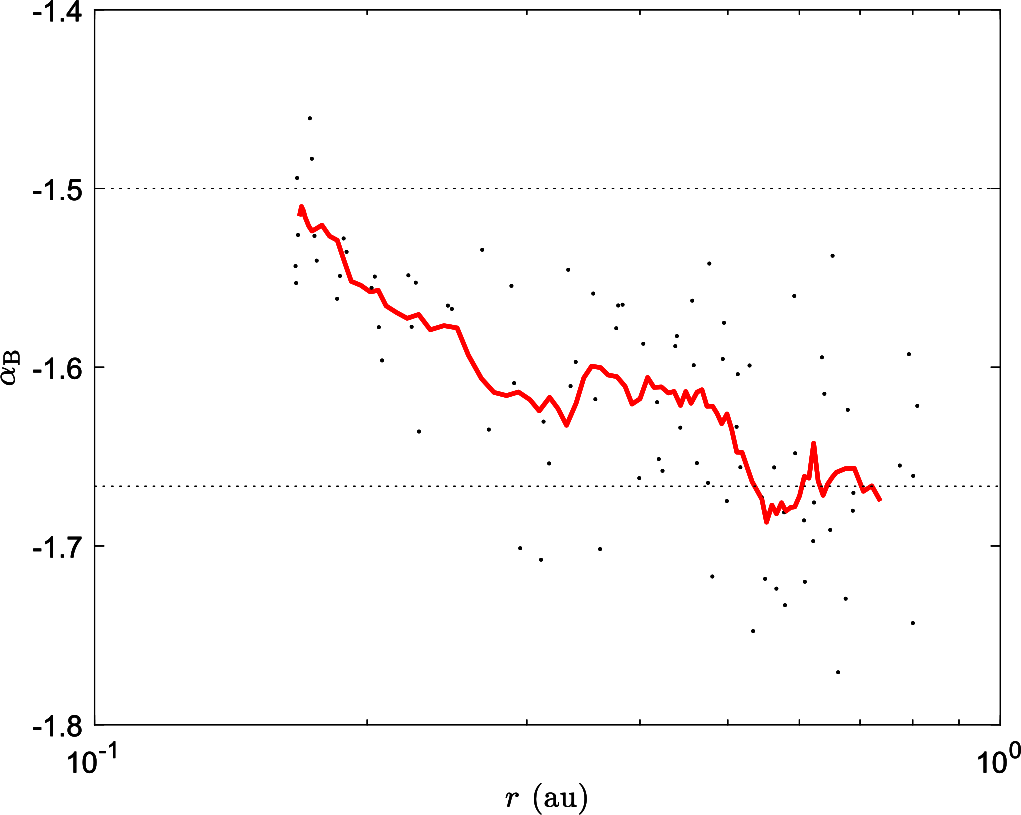
The turbulent power, at the energy containing and inertial range scales, increases sunwards, consistent with earlier findings BelcherJGR74 ; BavassanoJGR82 ; HorburyJGR01 ; BrunoEMP09 ; ChenApJS20 .The inertial range slopes of the magnetic field power spectra gradually shift from Kolmogorov-like Kolmogorov41a to Irochnikov-Kraichnan like KraichnanPFL65 with decreasing radial distance ChenApJS20 . Fig. 9 shows magnetic field spectra from the first two orbits of PSP in the left panel and the computed slopes in the right panel. Net power in the magnetic fluctuations is seen to rise sunwards. Most of the spectra show a range at the largest scales and the inertial range slopes transition from in the inner heliosphere to at 1au. Another analysis, using Hilbert Huang Transform (HHT), computed multifractal scalings for magnetic field fluctuations observed by PSP AlbertiApJ20 . The spectral slopes are confirmed to transition from IK like -3/2 to Kolmogorov like -5/3 at 0.4au. The turbulence also shows a transition at this radial distance from monofractal to multi-fractal nature.
The outer scale of the turbulence, as characterized by the correlation time, changes from at around 0.17AU to a couple of hours at around 1AU ParasharApJS20 ; ChenApJS20 . The spectral break in Fig. 9 between and regimes is seen to shift to lower frequencies with increasing heliocentric distance, consistent with earlier studies BavassanoJGR82 ; BrunoEMP09 ; BrunoApJL14 . The large-scale break frequency has been shown to follow a power-law variation with heliocentric distance BrunoLRSP13 ; ChenApJS20 ; WuApJL20 . The power-law exponent was found to be by ChenApJS20 . Although WuApJL20 did not perform a fit to their data, the qualitative behaviour shown by them is similar to that shown by BrunoLRSP13 with an exponent of . Interestingly, these variations are seen in previous studies as well HorburyAA96 ; KleinSW92 ; BrunoLRSP13 ; RuizSP14 . The slope found by ChenApJS20 is shallower than what was found by BrunoLRSP13 and steeper than those found by RuizSP14 . Recently, Cuesta et. al. CuestaApJS22 studied the heliocentric variation of the outer scale using data from Helios, Voyager, and three intervals from PSP. The Voyager values are consistent with RuizSP14 , Helios data show a slightly steeper rise, and the three PSP intervals are placed to indicate a very steel slope in the inner heliosphere. The turbulence evolution models ZankJGR96 ; MatthaeusJPP96 predict slopes shallower than -1 and are consistent with RuizSP14 . A comprehensive study is needed to understand the origins of such differences. At the kinetic scales, the break frequency between the inertial range and sub-proton range also shifts to lower frequencies as DuanApJS20 . The kinetic scale break frequency is observed to be closely correlated with the cyclotron frequency along with other parameters such as plasma .
Consistent with earlier observations, the Alfvénicity of the fluctuations decreases with heliocentric distance. The cross helicity as well as the energy budget of sunward and outward Elsässer variables, decreases as the wind expands ShiAA21 . The dominant outward Elsässer variable decays faster than the sunward Elsässer variable (see Fig 7, reproduced from BavassanoJGR00 ; BrunoLRSP13 , and equivalent figures in ChenApJS20 ). Some intervals in the inner heliosphere show a decrease in cross helicity across scales, indicating a possibility of strong velocity shears destroying the cross helicity in the inertial range ParasharApJS20 . MHD simulations with shears as well as analysis of Helios intervals with shear show a similar reduction in cross helicity at shear sites RobertsJGR92 .
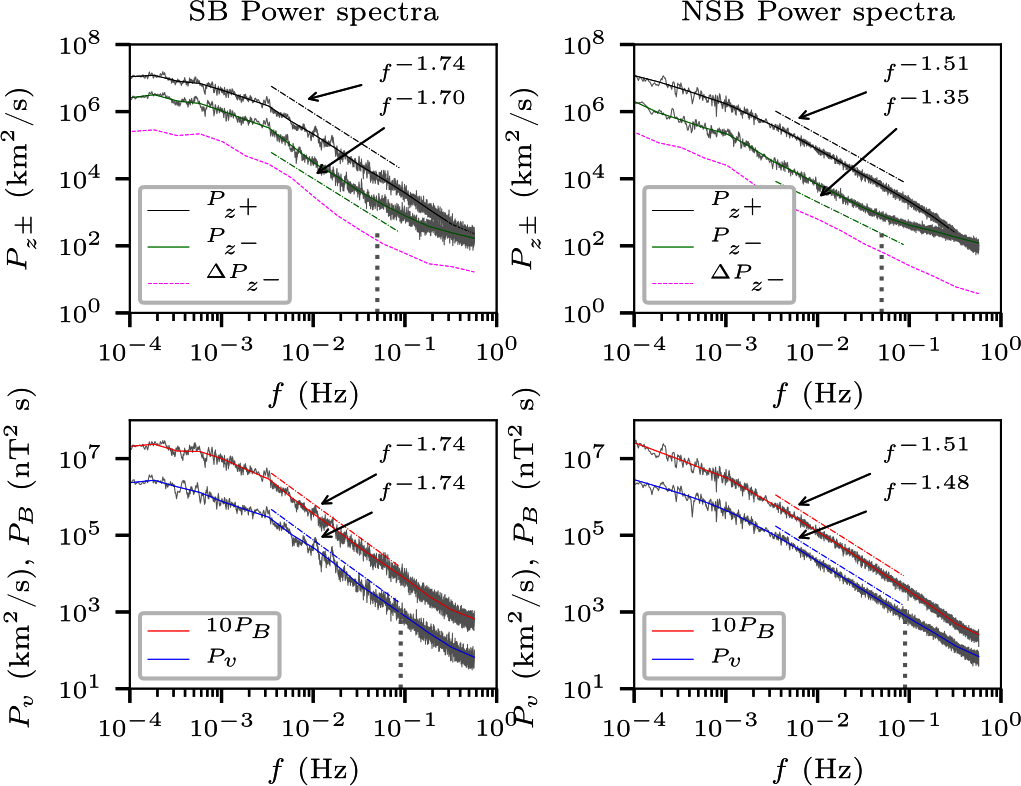
While many quantities important for turbulence, e.g. the magnitudes of wind speed, temperature, magnetic field and density, remain comparable between SBs and nearby ‘quiet’ regions, some properties of turbulence such as spectral signatures, decay rates, and intermittency properties vary significantly between switchbacks and non-switchback intervals BourouaineApJL20 ; MartinovicApJ21 . Fig. 10 shows power spectra in the spacecraft reference frame for intervals with and without switchbacks from PSP’s first encounter in November 2018. Left panels show Elsässer, velocity, and magnetic field spectra for the switchback interval and the right panels show the same spectra for non-switchback intervals. The spectra for all variables in the SB intervals show Kolmogorov like spectra, while the NSB intervals show IK like spectra. A potential reason behind this could be intense driving of turbulence by velocity shears that are likely responsible for switchbacks RuffoloApJ20 . The more evolved turbulence in the SB regions produces larger PVI events with higher probability MartinovicApJ21 .
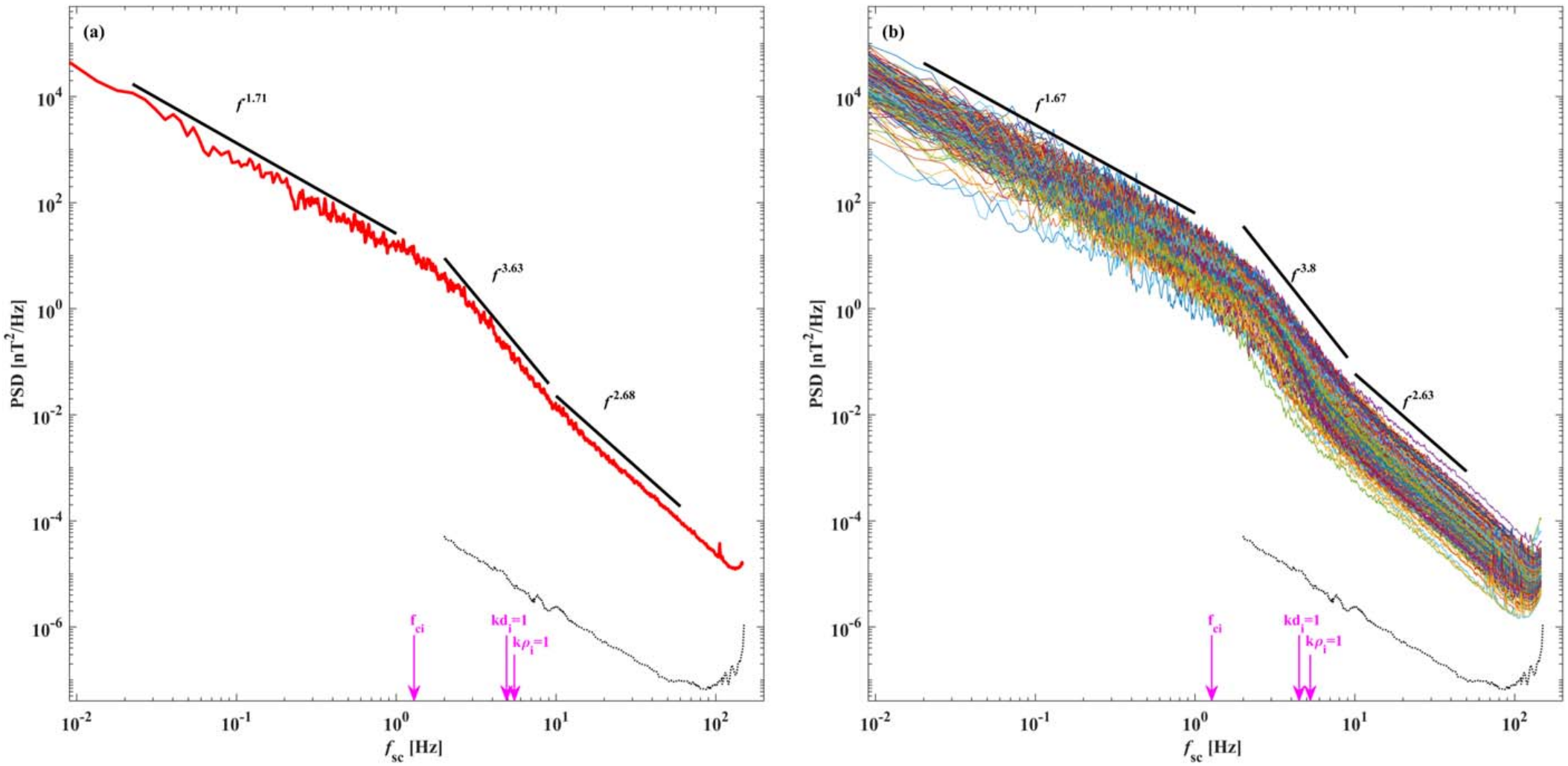
Another commonly observed feature of turbulence in the inner heliosphere is the enhanced steepening of magnetic field power spectra near the ion kinetic scales. Fig 11 shows magnetic field spectra computed using the merged Fluxgate magnetometer (FGM) and Search Coil Magnetometer (SCM) data BowenJGR20 ; HuangApJL21 . The spectra shown are from encounter 1 of PSP, specifically from November 4-7, 2018. A transition range near proton kinetic scales is seen with a slope of . This sharp transition indicates a modified cascade or enhanced dissipation at kinetic scales or a combination thereof. The spectra return to approaching electron kinetic scales. Such transition range has also been observed at 1AU in Wind observations DenskatJGR84 ; LeamonJGR99 . One of the possible explanations proposed for this transition is the “helicity barrier”, which emerges in imbalanced turbulence and reduces electron dissipation of kinetic Alfvén waves (KAWs) MeyrandJPP21 ; SquireNatureAstron22 .
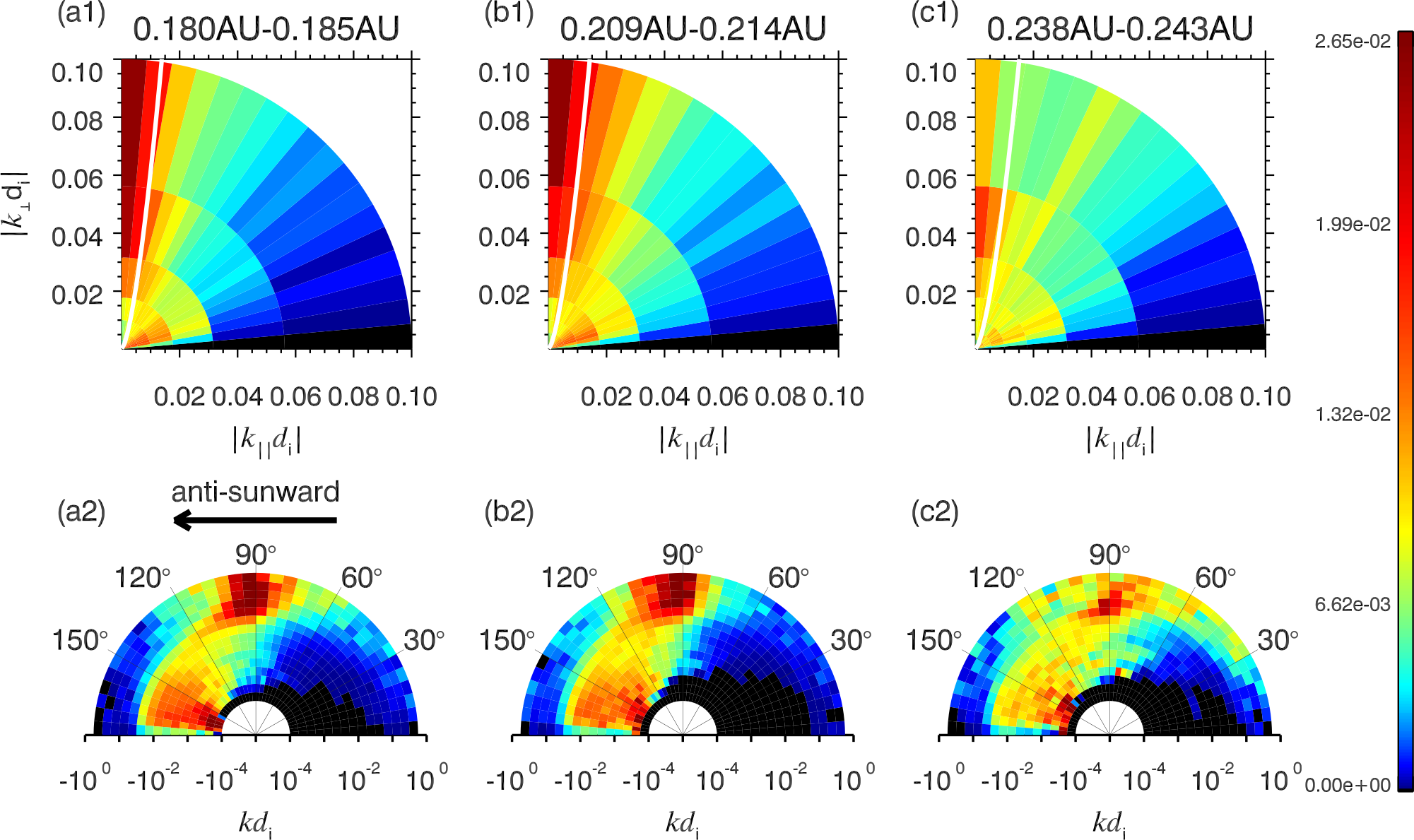
As expected for MHD turbulence, the fluctuations are highly anisotropic in nature. Fig 12 shows an example from the first encounter of PSP ZhuApJL20 . The top row shows probability distribution functions (PDFs) of identified wave vectors in the plane, and the bottom row shows the PDFs in plane. The wavenumbers studied were in the MHD regime. In the inertial range, for the fluctuations are predominantly parallel. Towards the tail of the inertial range, for , the fluctuations are predominantly perpendicular. Also the outward component of the Alfvénic fluctuations dominates. The fluctuations are still highly anisotropic in the transition and kinetic ranges, with power in perpendicular fluctuations being roughly an order of magnitude higher than the parallel fluctuations DuanApJL21 ; ZhangApJL22 .
In summary, the turbulence observed by PSP shows a lot of structure with interspersed switchbacks and “quiet” Alfvénic intervals. The SBs generally have more evolved turbulence compared to NSB intervals. The power is distributed highly anisotropically in the wavenumber space. The Alfvénicity of the wind decreases with increasing heliocentric distance, and the imbalance of turbulence is likely responsible for a steep transition range near proton kinetic scales. We now discuss the PSP observations of energy transfer across scales.
4.1 Energy at large scales
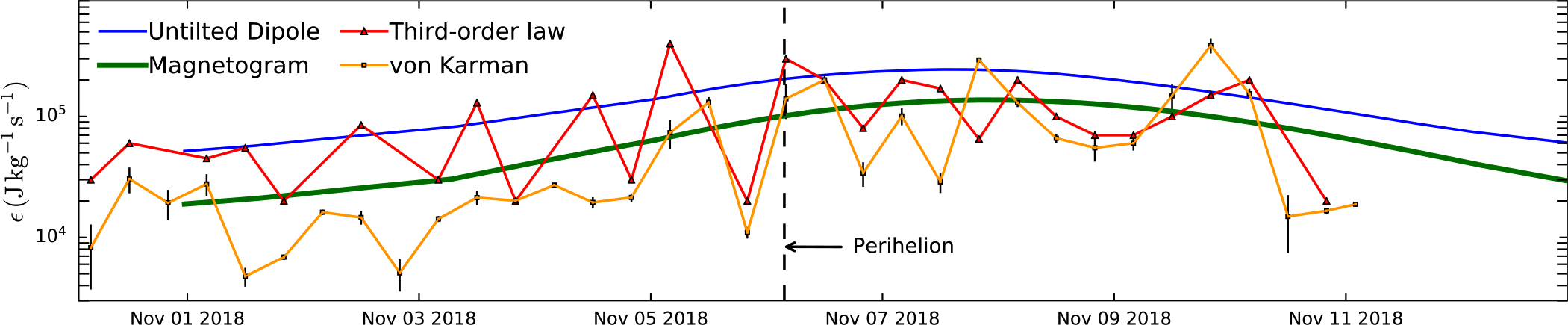
The plasma driven at large scales by various solar inputs, in-situ velocity shears, and instabilities receives energy at a rate quantified by the von Kármán decay rate. Fig 13 shows the decay rates computed from encounter 1 of PSP BandyopadhyayApJS20b . The squares with orange line show the von Kármán decay rate based on large scale parameters and the triangles with red line show the energy transfer rates estimated by fitting the third order structure functions following the Politano Pouquet law (see next subsection for more details). The two smooth solid lines show two decay rates computed from two global simulations ChhiberApJS19 . The thin blue line is a simulation with sun’s magnetic field represented as an untilted dipole, and the green line is a simulation with the magnetogram from the time of encounter 1. The decay rates increase with decreasing heliocentric distance, changing by more than an order of magnitude within a few solar radii in which the encounter data were collected. The overall decay rates obtained near the perihelion are a couple of orders of magnitude larger than J Kg-1s-1 decay rate that is observed at 1au CoburnPTRSA15 . The von Kármán decay rates and the third order law estimates match better in the outgoing part of E1, presumably because that was highly Alfvénic slow wind, which might have a higher density of intermittent structures. The global simulations estimate the decay rates reasonably well with the magnetogram simulation overlapping really well with the two estimates from PSP.
The heating rates in the inner heliosphere have also recently been computed from angular broadening studies of Crab nebula RajaApJ21 . The angular broadening observations were used to estimate the average density perturbations, which were then converted to velocity fluctuations assumig kinetic Alfvén wave like properties. The decay rates computed from these velocity fluctuation levels are in the same ballpark as the numbers quoted in BandyopadhyayApJS20b .
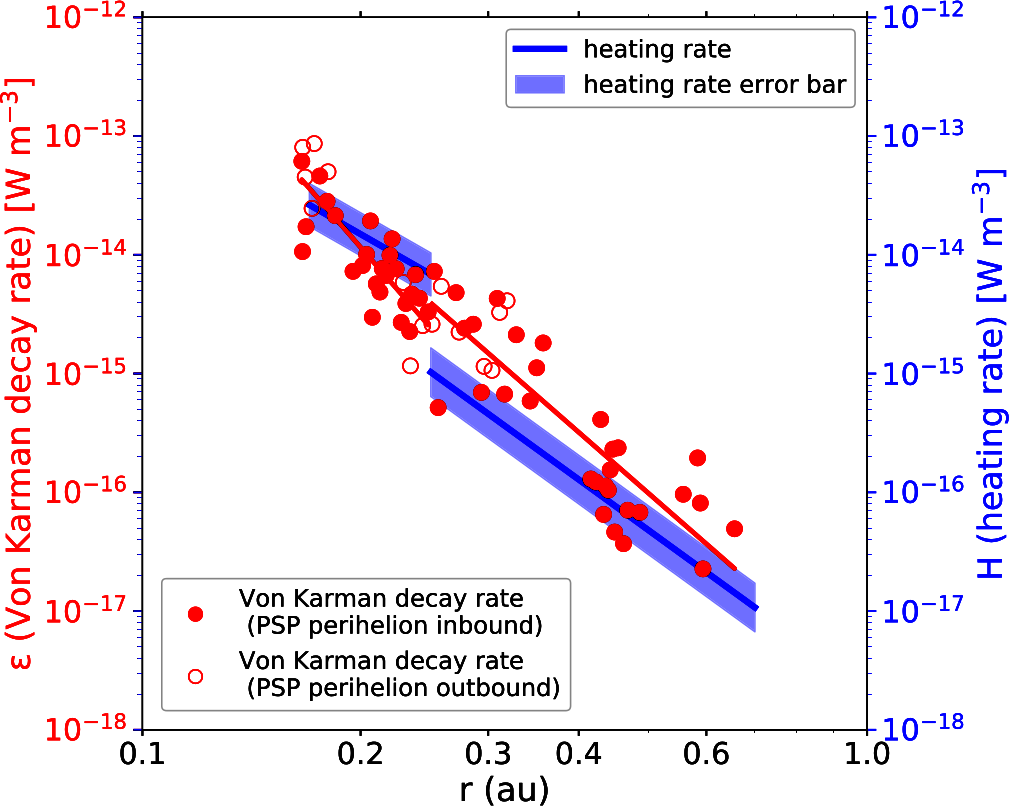
As seen in simulations WuPRL13 ; ParasharApJ15 ; MatthaeusApJL16 ; ShayPP18 and in previous observations VasquezJGR07 ; StawarzApJ09 ; CoburnPTRSA15 , the von Kármán decay rate determines the rate of dissipation even in kinetic plasmas. PSP has already been used to test this balance in the inner heliosphere. Fig 14 shows the von Kármán decay rates and proton heating rates esitmated using first three encounters worth of data WuApJ22a . The red dots represent the von Kármán decay rate and the lines+shaded regions represent estimates of solar wind heating rates of protons TuSSR95 ; WuApJL20 ; MartinovicApJS20 . The von Kármán decay rate is not only consistent with the energy supply rate estimated from the evolution of the large scale break frequency (see fig. 3 of WuApJ22a ) but is also consistent with proton heating rate. This balance between the energy input rate and dissipation implies that the energy cascades in the inertial range down to kinetic scales in a conservative fashion.
4.2 Energy in the inertial range
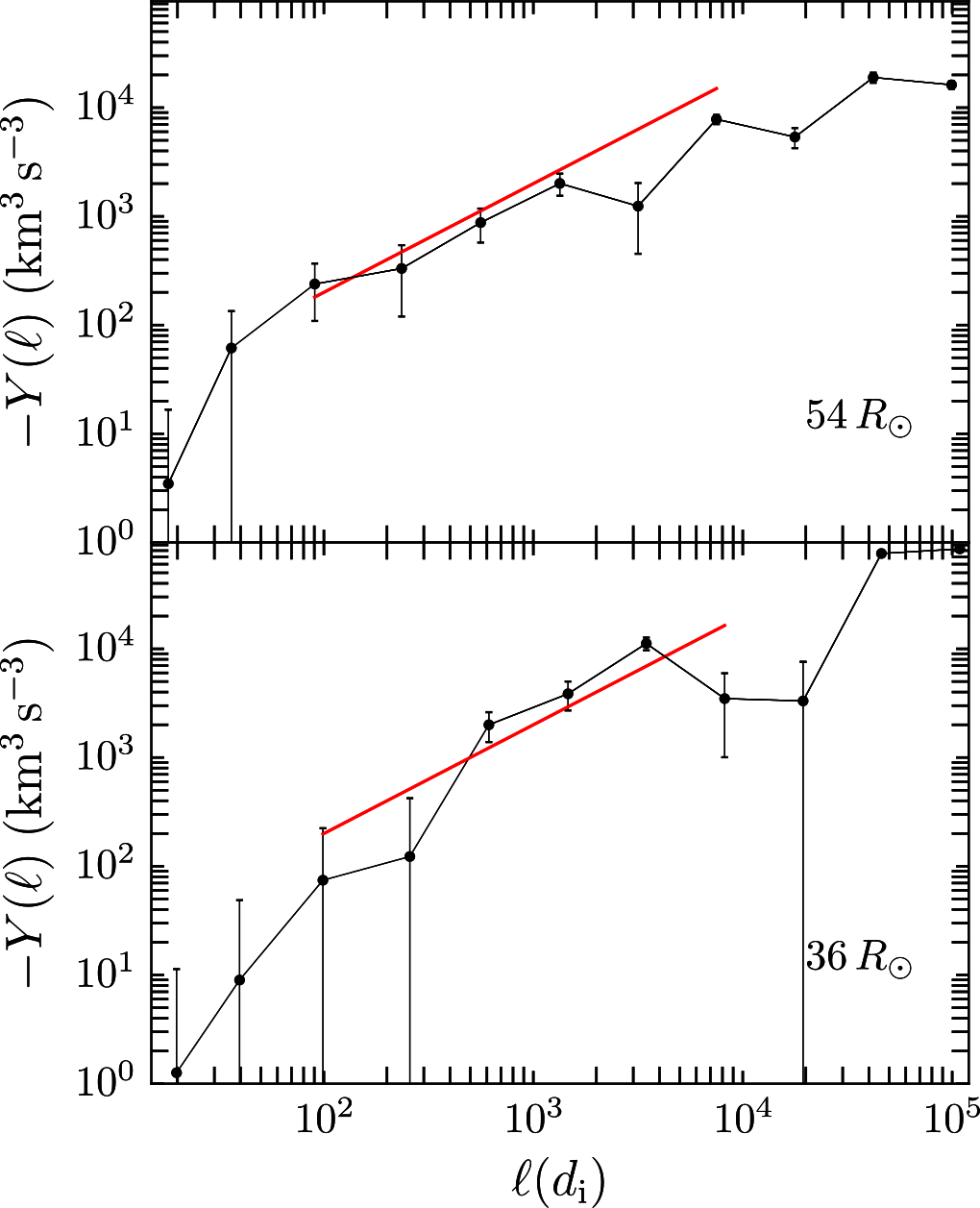
The energy input at the large scales cascades down to kinetic scales through the inertial range. This cascade rate can be quantified using the Politano Pouquet MHD generalization of Yaglom’s 3rd order law (see e.g. Eqn. 2). Fig 15 shows two examples of the third order fluxes computed at two different radial distances using the incompressible version of the PP law. The red lines show linear scaling laws. These linear scalings, when identified, can be used to estimate the cascade rate in the inertial range BandyopadhyayApJS20b . The cascade rates identified this way are compared with the von Kármán decay rates in Fig 13 as squares with an orange line. The third order law decay rates are comparable to the von Kármán decay rates and are also comparable to simulation findings. A recent study compared the cascade rates in sub-Alfvénic wind with super-Alfvénic wind ZhaoApJL22 . The cascade rate was computed to be higher in the sub-Alfvénic interval compared to the super-Alfvénic interval although longer sub-Alfvénic intervals would be needed to get statistically significant results. The cascade rates were also dominated by compressive terms compared to incompressive terms.
It is possible to estimate the decay rates from the isotropic and anisotropic versions of the PP law. Both isotropic and anisotropic cascade rates increase with decreasing heliocentric distance. This increase correlates well with the well established increase in fluctuation amplitude, Alfvénicity, and temperature with decreasing heliocentric distance AndresArXiv21 . The compressible cascade rates computed from PSP’s first encounter have been compared to compressible cascade rates at 1AU (THEMIS data) and 1.6AU (near Mars using MAVEN data). The compressible cascade rates show a drop by five orders of magnitude AndresApJ21 between 0.2au (PSP) and 1.6au (MAVEN). The density fluctuations are larger in the inner heliosphere. As the wind expands, it approaches a nearly incompresible state MatthaeusJGR90 ; AdhikariApJ17 . This change in the nature of solar wind turbulence could be related to the decrease in compressible decay rates.
The presence of switchbacks can affect the cascade rates as well. Fig. 16 shows the cascade rates computed in switchbacks identified during the first encounter of PSP HernandezApJL21 . Some switchback intervals show positive decay rate and some show negative decay rates. Although the interpretation of a negative cascade rate is unclear, it could imply a local transfer of energy to larger scales. The intervals that show a net positive cascade rate in the inertial rage show a visibly identifiable correlation with the switchback parameter HernandezApJL21 (see deWitApJS20, , for the definition of and detailed analysis of switchback properties). No such correlation is observed in cases when a negative cascade rate is identified in an interval HernandezApJL21 . The finding that the cascade rate is enhanced by the presence of switchbacks is consistent with the notion of more evolved turbulence in switchbacks (see e.g. Fig. 10). A local weak formulation of PP98 law gives a local in space and time dissipation function DavidApJ22 . This local dissipation function also shows different behavior in and outside the switchbacks. It is predicted to follow scaling in the inertial range, in the viscous/dissipative range, and at the discontinuities where is the scale at which the local dissipation measure is computed. The dissipation measure , when averaged over the interval, shows behaviour similar to the third order law but locally it shows an unexplained scaling of at the locations of switchbacks.
4.3 Energy at kinetic scales
The cascaded energy is partially dissipated at the proton kinetic scales and part of it is cascaded down to electron scales. Various dissipative mechanisms and pathways have been proposed to explain dissipation in kinetic plasmas. These include wave-particle interactions such as cyclotron resonance HollwegJGR02 and Landau damping TenbargeApJ13 , stochastic heating ChandranApJ10-1 ; MartinovicApJ21 , and heating at intermittent locations ParasharPP11 ; TenbargeApJ13 ; WanPP16 . Heating at intermittent locations can happen because of processes such as reconnection ShayPP18 , and possibly because of Landau damping as well TenbargeApJ13 . A mechanism agnostic approach focuses on the action of pressure strain interaction term, which also happens intermittently YangPP17 (see section 2 for a detailed discussion).
PSP’s state-of-the-art very high time cadence measurements in the inner heliosphere have enabled identification of various wave modes including circularly polarized waves and electrostatic waves BowenApJS20 ; BowenApJ20 ; VernieroApJS20 ; MalaspinaApJS20 ; VechAA21 ; ZhaoApJ21 ; CattellApJL21 . The waves are found to last anywhere from a few seconds BowenApJS20 to “wave storms” a few hours long VernieroApJ22 . Coincident with the ion scale waves is a broadening of the beam of proton velocity distribution function (VDF) that is being termed as “hammerhead” of the proton VDF. It was also shown by VernieroApJ22 that these features are consistent with the expectations of quasilinear diffusion in velocity space in the presence of waves. A recent paper studies proton VDFs in the presence of cyclotron waves BowenArXiv21 . The VDFs show signatures consistent with qualisilinear diffusion in the velocity space, indicating a possibility of cyclotron heating. This quasilinear diffusion is accompanied by steepening of magnetic power spectra to near proton scales. A potential explanation for such a combination of observations was recently proposed SquireNatureAstron22 . It is suggested that a helicity barrier inhibits a cascade of energy to smaller scales MeyrandJPP21 . This results in a proton scale build up of energy and a steep transition range just below proton scales. This proton scale build up of energy in-turn generates ion-cyclotron waves, which can participate in preferential resonant heating of ions SquireNatureAstron22 . This steepening of magnetic spectra at proton scales has also been used to estimate a dissipative removal of energy at proton scales. It was estimated that the power removed from the magnetic fluctuations at proton scales is sufficient to heat the solar wind BowenPRL20 .
Another pathway to dissipation is stochastic heating ChandranApJ10-1 ; CerriApJ21 where particles experience stochastic kicks by the changing electric potential during their orbit (see section 2 for a discussion). The stochastic heating rate increases with decreasing heliocentric distance as MartinovicApJ21 . It is larger in the fast wind compared to slow wind. Moreover, stochastic heating is enhanced inside the switchback regions. As mentioned before, stochastic heating enhances in the presence of intermittent structures. SBs show enhanced probability of finding large PVI values, and hence the turbulence in SBs is likely more intermittent. This could potentially enhance the stochastic heating rate. There is ample evidence for intermittent heating at 1au as well as in the inner heliosphere.
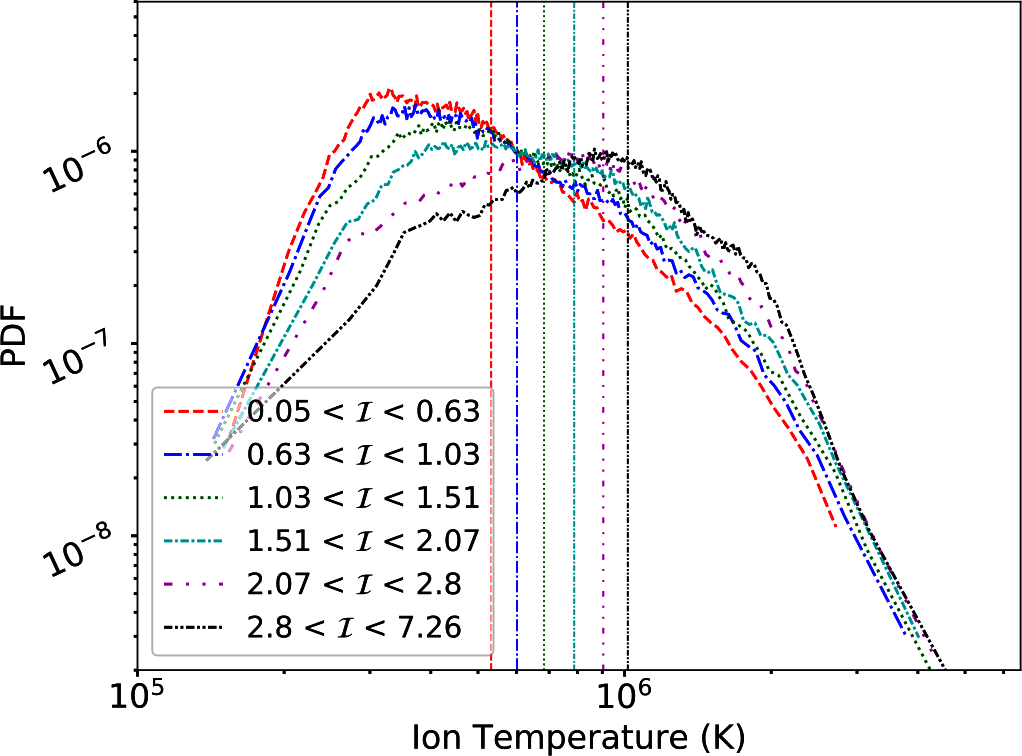
At 1AU, the protons are observed to be hotter near strong PVI sites OsmanApJL11 . Similar analysis in the inner heliosphere using PSP yields no new surprises. Fig 17 shows the probability distribution functions of temperature conditioned on PVI values. The probability of finding a higher temperature, say greater than K, is higher for data conditioned on higher PVI values and the opposite is true for lower temperatures, say a few K. This is also quantified by the increasing median value of temperature with increasing PVI value. Vertical lines in Fig 17 show this systematic trend in the median temperature rise, indicating hotter populations for larger PVI values.
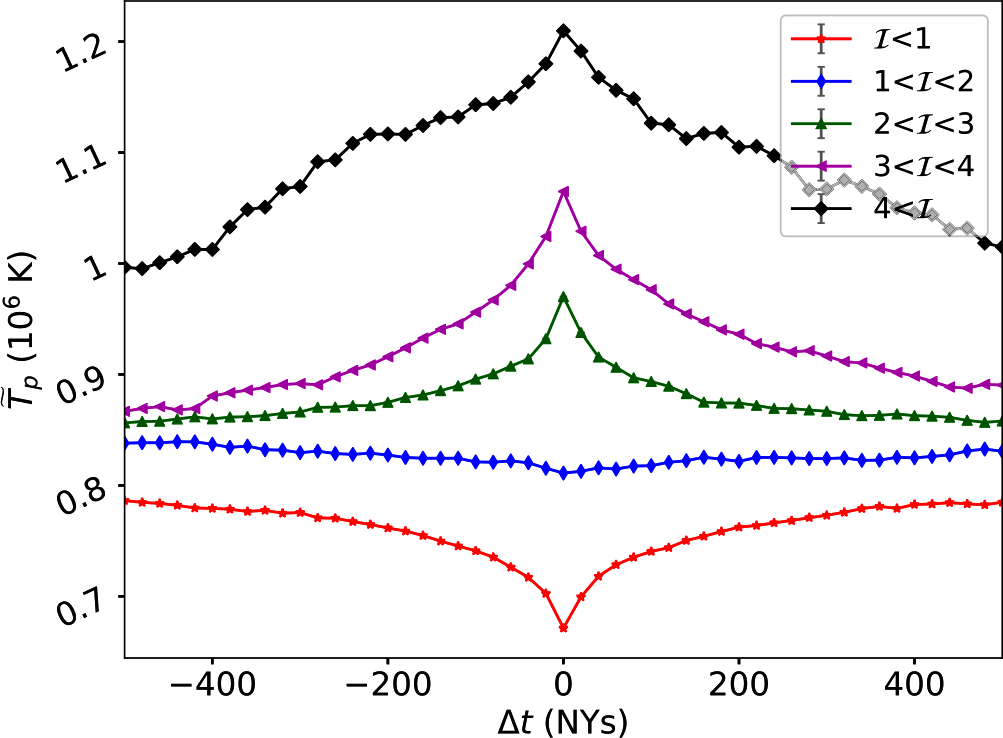
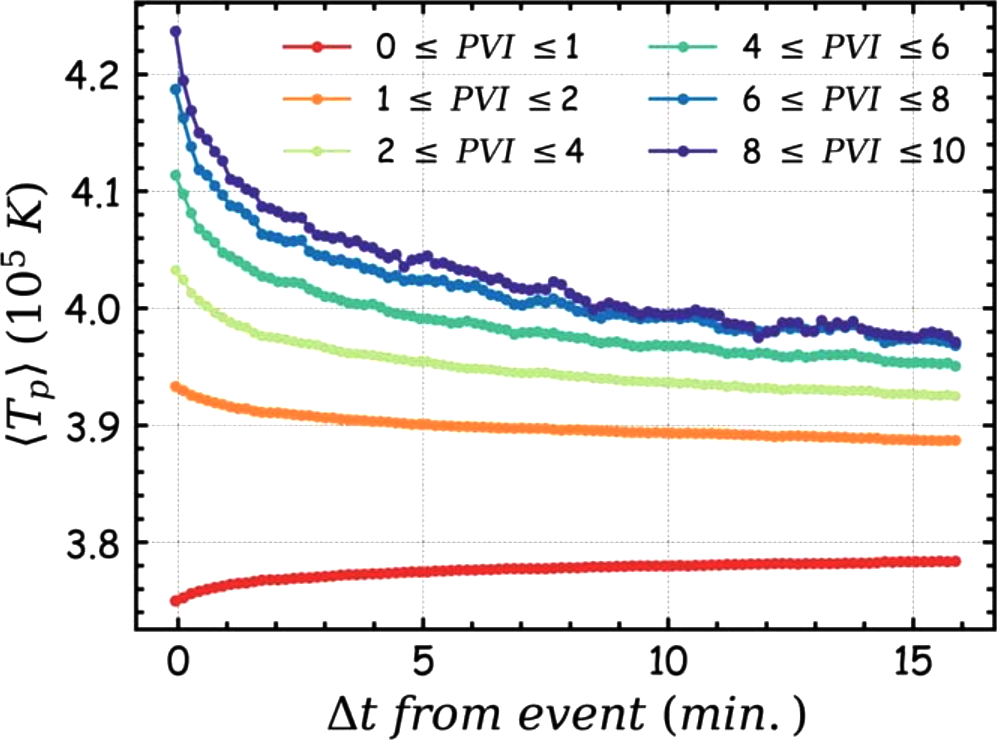
The proximity of dissipation and intermittent structures can also be quantified by computing the average temperature in the vicinity of PVI structures. This technique has been used to not only identify heating at intermittent structures OsmanPRL12a , but also to show enhanced energetic particle fluxes near such intermittent structures TesseinApJL13 . The average is computed as where is the conditional average temperature for all events, is the lag relative to the PVI position, is the location of PVI event, and and are the thresholds for seleccting particular PVI values. Fig 18 shows conditional average temperatures for various PVI thresholds from the second half of PSP’s encounter 1 in the left panel and from the first six encounters in the right panel. Evidently, the temperature in the vicinity of larger PVI values is larger, even out to about a correlation length away, when compared to smaller PVI values. The fact that PVI values appear to be clustered in the inner heliosphere ChhiberApJS20 could be one of the potential reasons behind consistently higher temperatures this far away from the intermittent PVI events.
.
Another possibility to study intermittent dissipation is to use LET, the local kernel of the third order law (Eqn. 2). Although LET varies significantly from one point to the other, its average at a given scale quantifies the net flow of energy into/out of that scale SorrisoJPP18 . In a similar analysis to Fig. 18 using Helios data, the LET was shown to correlate better than PVI with the mean temperature even though there was shown to be a strong correlation between LET and PVI Sorisso-ValvoSP18 . A potential reason behind the apparent lack of correlation between PVI and temperature in Helios data could be an artefact of the coarse resolution of Helios data which would not allow resolution of large small scale increments and hence the most intense PVI structures. PSP, with its fast measurements, allows resolution of PVIs at much finer scales and recovers the behaviour shown in Fig. 18.
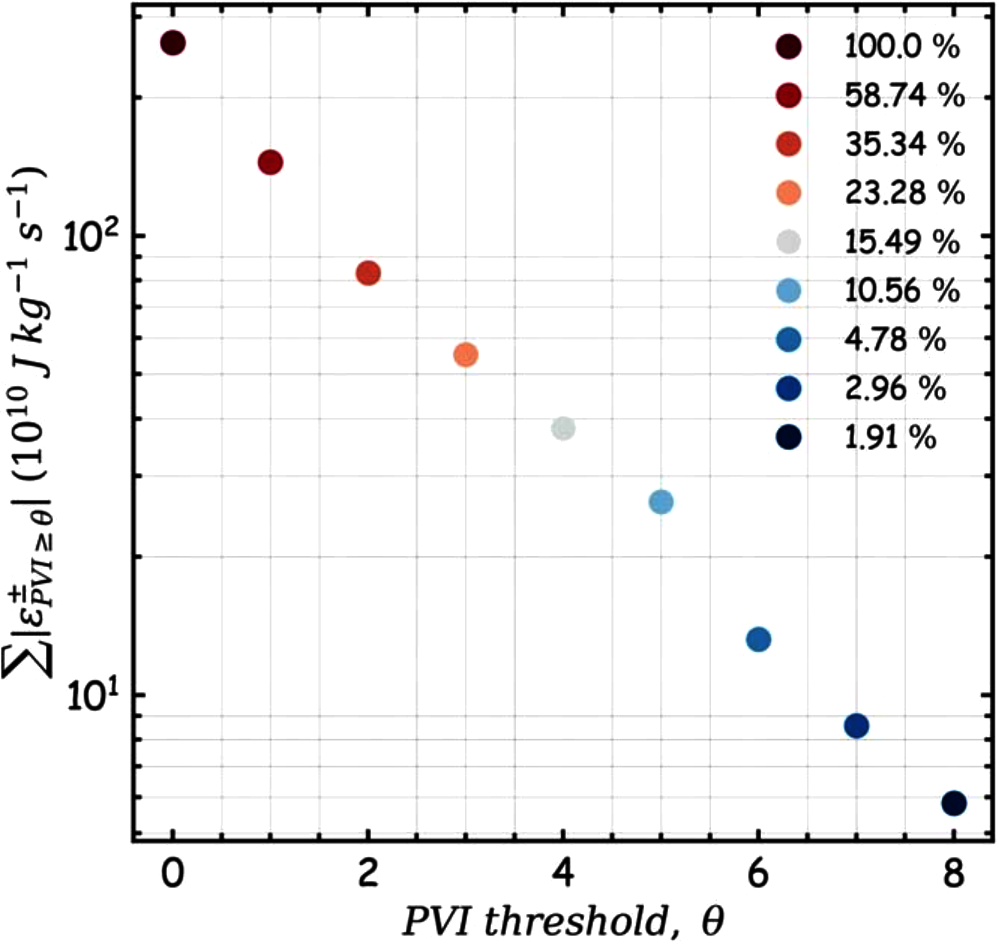
Larger PVI events occupy smaller fraction of the total volume but contribute significantly more to the budget of internal energy , where is the specific heat capacity, is the Boltzmann constant, the density, and the temperature. At 1AU, using ACE data, it has been shown that PVI occupy only 19% of the volume but contribute 50% to the internal energy budget, while PVI occupy only 2% of the volume but contribute to the internal energy budget OsmanPRL12a . Fig. 19 shows the total absolute value of LET conditioned on PVI threshold from first six encounters of PSP Sioulas_2022 . There are some similarities and differences in these findings when compared to Osman et. al. OsmanPRL12a . Here PVI contribute to the absolute LET measure, significantly less than what was estimated by OsmanPRL12a . On the other hand, PVI contribute which is consistent with the findings of OsmanPRL12a . Evidently LET is a very different measure of dissipation compared to internal energy. The differences in the inferences of Sioulas_2022 and OsmanPRL12a could potentially stem from the different nature of these measures, or from other considerations such as enhanced possibility of wave damping BowenArXiv21 ; SquireNatureAstron22 , or from yet largely unexplored clustering properties of the PVI events ChhiberApJS20 or the transition of turbulence to monofractal behaviour at sub-proton scales potentially owing to scale invariance of current sheets in the kinetic range ChhiberApJL21 . Moreover, LET and PVI are scale dependent quantities. Similar studies with varied LET computation scale are required to explore such connections further.
5 Summary and Conclusions
The origins and evolution of the solar wind have been a mystery ever since its prediction and discovery ParkerApJ58a ; NeugebauerJGR66 ; TuSSR95 ; MarschLRSP06 ; BrunoLRSP13 ; VerscharenLRSP19 . Many iconic missions have enhanced our understanding of the processes that contribute to origins and evolution of the solar wind. However, the solar coronal dynamics were largely studied using remote observations until very recently. Parker Solar Probe is allowing the exploration of hitherto unexplored regions approaching and inside the Alfvén critical surface. Recently PSP entered the magnetically dominated solar corona between 19.7 and 18.4 solar radii KasperPRL21 . As PSP approaches closer to the sun, eventually reaching 9.8 , it will allow exploration of various processes active in the solar corona, including the turbulence that potentially plays an important role in the heating of the Solar Corona.
In this paper we have focused primarily on the transfer of energy across scales in the inner heliosphere as observed by the Parker Solar Probe in the last four years. Rather than adopting a more detailed and mathematical scale to scale transfer approach Verma2019 that may not be amenable to spacecraft analysis, we adopt a more empirical approach based on the taxonomy of energy-containing scales, inertial range scales and kinetic scales. Based on such an approach, a significant amount of work has been done in the last four years on various aspects of solar wind properties and the turbulence. We refer the reader to Raouafi et al RaouafiEA22SSR for a detailed discussion of many other aspects that were not covered here.
As the solar wind expands from inner heliosphere to the outer heliosphere, its turbulent nature changes dramatically DeforestApJ16 ; ChenApJS20 . Expanding from the solar corona, the wind becomes supersonic in the Alfvén critical region. Beyond the Alfvén critical region, the magnetic field loses control and velocity shears at flux tube boundaries can create flocculation, isotropizing the wind at the largest scales, and advancing the wind’s turbulent evolution DeforestApJ16 ; ChhiberApJL18 ; RuffoloApJ20 .
The amplitudes of turbulent fluctuations decrease radially outwards while the outer scale gets larger. The outer scales increases as a power-law with increasing heliocentric distance. The power-laws exponents found for outer scale vary between whereas theoretical models predict the exponent to be generally less than 1 KleinSW92 ; HorburyAA96 ; RuizSP14 ; BrunoApJL14 ; ChenApJS20 ; WuApJL20 . Intermittency increases from inner heliosphere up to 1au. A clear transition is seen at roughly 0.4au AlbertiApJ20 ; CuestaApJL22 . Although it might appear that the bandwidth available for the turbulent cascade might keep increasing with increasing outer scale even beyond 1au, the inner scale (for example ) expands faster than the outer scale. This results in a reduced Reynolds number with increasing heliocentric distance. The reduction in the Reynolds number in-turn implies reduced intermittency, as quantified by radially decreasing small scale kurtosis and PVI values ParasharApJL19 ; CuestaApJS22 .
The fluctuations are highly Alfvénic and imbalanced in the inner heliosphere with outward propagating fluctuations dominating the energy budget BavassanoJGR00 . The Alfvénicity drops as the wind expands with the dominant species () decaying significantly faster than the minor species () GoldsteinGRL95 ; BreechEA08 ; RobertsJGR87 ; MatthaeusGRL04 ; StriblingMatt91 . This is reflected in the decreasing cross helicity with increasing heliocentric distance as well.
Going sunwards, the enhanced fluctuation levels of velocity, magnetic field, as well as density imply that the energy input rate at the largest scales increases WuApJ22a . The von Kármán Howarth decay rate increases by two orders of magnitude going from 1au to 0.2au BandyopadhyayApJS20b . This enhanced decay rate balances estimated heating rates for the solar wind. In the inertial range, the incompressive decay rates compare favourably with the von Kármán Howarth decay rate and increase by a couple of orders of magnitude approaching the sun. The compressive component of the cascade rate could be significant in the inner heliosphere owing to the increased density fluctuations as well. It can decrease by as much as five orders of magnitude from 0.2au to 2au AndresApJ21 , likely a consequence of the solar wind’s evolution towards a nearly incompressible state.
At the kinetic scale, the cascade is modified by kinetic physics as well as dissipation BowenArXiv21 . The spectral slopes in the imbalanced inner heliospheric turbulence routinely show a steep transition range with powerlaw just below proton kinetic scales DenskatJGR84 ; LeamonJGR99 ; HuangApJL21 . This potentially happens because of enhanced heating of protons and an inhibition of the cascade to smaller scales MeyrandJPP21 ; SquireNatureAstron22 .
The transfer of energy into internal degrees of freedom has been shown to happen via wave-particle interactions, stochastic heating as well as in intermittent locations VechAA21 ; MartinovicApJ19 ; MartinovicApJS20 ; QudsiApJS20 . Distribution functions in the presence of waves show signatures expected of quasilinear diffusion in the velocity space BowenArXiv21 ; VernieroApJ22 . Larger PVI values have been shown to associate favourably with hotter plasma, consistent with simulations as well as 1au observations QudsiApJ20 . Local measures of dissipation have also been shown to relate with enhanced intermittent heating DavidApJ22 ; Sioulas_2022 .
Many of the properties discussed above modify significantly in the presence of switchbacks. The turbulence appears to be more evolved inside switchbacks. The power spectra become Kolmogorov like inside SBs even when nearby NSB intervals show IK-like behaviour BourouaineApJL20 . The stochastic heating rate, the incompressive cascade rate, and PVI values etc. are enhanced in the presence of SBs MartinovicApJS20 .
Although PSP is already enabling a significant progress in studying turbulent transfer of energy across scales in the heliosphere, many open questions remain.
-
•
How do we get true estimates of heating rates from single spacecraft measurements?
-
•
Do such estimates modify the balance between the von Kármán Howarth decay rate and true heating rates?
-
•
How do local dissipation measures (e.g. LET Sioulas_2022 , DavidApJ22 , field particle correlation VernieroJGR21 ) match with the large scale decay rates?
-
•
What are the relative contributions of various cascade terms (incompressible, compressible, hall, etc.) to the inertial range estimates of decay rates?,
-
•
How does this cascaded energy partition between ions and electrons? How much energy is taken away from the cascade by ion heating and how much is left to cascade down to electron scales?
-
•
How does the cascade proceed closer to the electron scales?,
-
•
Is there an identifiable relationship between intermittent dissipation and wave-particle interactions?
-
•
How do the conclusions to above mentioned questions vary with ambient conditions?
Building upon the approximately six decades of research, PSP is allowing an in-depth exploration of turbulent regimes that were not accessible up to now, both in (time/length) scales and in proximity to the sun. With the abundance of switchbacks, identification of waves in turbulence, new proton VDF features, modified turbulence properties, and observations of turbulence in the sub-Alfvénic solar corona, PSP is only getting started. Over the next few decades, PSP will allow greater discoveries related to the origins of the solar wind, its evolution and the consequent turbulent properties.
6 Acknowledgements
The authors would like to dedicate this paper to late Dr. Eugene Parker, the pioneer of this field. Dr. Parker’s seminal works on plasma astrophysics not only inspired generations of plasma astrophysicists but also paved the way for modern space physics. Inspired by his seminal findings, the Parker Solar Probe is taking our understanding and view of the Solar Wind to the next level. We would like to thank the PSP instrument teams for creating state-of-the-art instruments that are enabling cutting edge science in the inner heliosphere. We also thank our collaborators who made possible much of the science discussed in this paper. TNP would like to thank the AAPPS-DPP committee for the invitation to deliver a talk on the subject and to write this review paper. This research is supported in part by the NASA Parker Solar Probe Mission under a GI grant 80NSSC21K1765 and the ISOIS team (Princeton SUB0000165), by the IMAP project (Princeton SUB0000317), by the MMS mission under a Theory and Modeling grant 80NSSC19K0565, and by HSR grants 80NSSC18K1648 and 80NSSC19K0284.
References
- \bibcommenthead
- (1) Parker, E.N.: Dynamics of the interplanetary gas and magnetic fields. The Astrophysical Journal 128, 664 (1958)
- (2) Neugebauer, M., Snyder, C.W.: Mariner 2 observations of the solar wind: 1. average properties. Journal of Geophysical Research 71(19), 4469–4484 (1966)
- (3) Krommes, J.A.: Fundamental statistical descriptions of plasma turbulence in magnetic fields. Physics Reports 360(1-4), 1–352 (2002)
- (4) Tsytovich, V.N.: An Introduction to the Theory of Plasma Turbulence: International Series of Monographs in Natural Philosophy vol. 44. Elsevier, ??? (2016)
- (5) Yamada, T., Itoh, S.-I., Maruta, T., Kasuya, N., Nagashima, Y., Shinohara, S., Terasaka, K., Yagi, M., Inagaki, S., Kawai, Y., et al.: Anatomy of plasma turbulence. Nature physics 4(9), 721–725 (2008)
- (6) Coleman Jr, P J: Turbulence, Viscosity, and Dissipation in the Solar-Wind Plasma. The Astrophysical Journal 153, 371 (1968). https://doi.org/10.1086/149674
- (7) Matthaeus, W.H., Goldstein, M.L.: Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. Journal of Geophysical Research 87(A8), 6011–6028 (1982)
- (8) Bruno, R., Carbone, V.: The solar wind as a turbulence laboratory. Living Reviews in Solar Physics 10(2) (2013). https://doi.org/10.12942/lrsp-2013-2
- (9) Cordes, J., Weisberg, J., Boriakoff, V.: Small-scale electron density turbulence in the interstellar medium. The Astrophysical Journal 288, 221–247 (1985)
- (10) Falceta-Gonçalves, D., Kowal, G., Falgarone, E., Chian, A.-L.: Turbulence in the interstellar medium. Nonlinear Processes in Geophysics 21(3), 587–604 (2014)
- (11) Armstrong, J., Rickett, B., Spangler, S.: Electron density power spectrum in the local interstellar medium. The Astrophysical Journal 443, 209–221 (1995)
- (12) Balbus, S.A., Hawley, J.F.: Instability, turbulence, and enhanced transport in accretion disks. Reviews of modern physics 70(1), 1 (1998)
- (13) Abramowicz, M.A., Fragile, P.C.: Foundations of black hole accretion disk theory. Living Reviews in Relativity 16(1), 1–88 (2013)
- (14) Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., Briel, U.: Probing turbulence in the coma galaxy cluster. Astronomy & Astrophysics 426(2), 387–397 (2004)
- (15) Churazov, E., Vikhlinin, A., Zhuravleva, I., Schekochihin, A., Parrish, I., Sunyaev, R., Forman, W., Böhringer, H., Randall, S.: X-ray surface brightness and gas density fluctuations in the coma cluster. Monthly Notices of the Royal Astronomical Society 421(2), 1123–1135 (2012)
- (16) Mohapatra, R., Federrath, C., Sharma, P.: Turbulence in stratified atmospheres: implications for the intracluster medium. Monthly Notices of the Royal Astronomical Society 493(4), 5838–5853 (2020)
- (17) Hendrix, D., Van Hoven, G.: Magnetohydrodynamic turbulence and implications for solar coronal heating. The Astrophysical Journal 467, 887 (1996)
- (18) Matthaeus, W.H., Zank, G.P., Oughton, S., Mullan, D., Dmitruk, P.: Coronal heating by magnetohydrodynamic turbulence driven by reflected low-frequency waves. The Astrophysical Journal 523(1), 93 (1999)
- (19) Cranmer, S.R., Van Ballegooijen, A.A., Edgar, R.J.: Self-consistent coronal heating and solar wind acceleration from anisotropic magnetohydrodynamic turbulence. The Astrophysical Journal Supplement Series 171(2), 520 (2007)
- (20) DeForest, C., Matthaeus, W., Viall, N., Cranmer, S.: Fading coronal structure and the onset of turbulence in the young solar wind. The Astrophysical Journal 828(2), 66 (2016)
- (21) Telloni, D., Adhikari, L., Zank, G.P., Zhao, L., Sorriso-Valvo, L., Antonucci, E., Giordano, S., Mancuso, S.: Possible evidence for shear-driven kelvin–helmholtz instability along the boundary of fast and slow solar wind in the corona. The Astrophysical Journal 929(1), 98 (2022)
- (22) Ruffolo, D., Matthaeus, W.H., Chhiber, R., Usmanov, A.V., Yang, Y., Bandyopadhyay, R., Parashar, T., Goldstein, M.L., DeForest, C., Wan, M., et al.: Shear-driven transition to isotropically turbulent solar wind outside the alfvén critical zone. The Astrophysical Journal 902(2), 94 (2020)
- (23) Richardson, J.D., Paularena, K.I., Lazarus, A.J., Belcher, J.W.: Radial evolution of the solar wind from IMP 8 to Voyager 2. Geophysical Research Letters 22, 325 (1995)
- (24) Usmanov, A.V., Matthaeus, W.H., Breech, B.A., Goldstein, M.L.: Solar wind modeling with turbulence transport and heating. The Astrophysical Journal 727(2), 84 (2011)
- (25) Gamayunov, K.V., Zhang, M., Pogorelov, N.V., HEERIkHUISEN, J., Rassoul, H.K.: Self-consistent model of the interstellar pickup protons, alfvénic turbulence, and core solar wind in the outer heliosphere. The Astrophysical Journal 757(1), 74 (2012)
- (26) Sokolov, I.V., Van der Holst, B., Oran, R., Downs, C., Roussev, I.I., Jin, M., Manchester, W.B., Evans, R.M., Gombosi, T.I.: Magnetohydrodynamic waves and coronal heating: Unifying empirical and mhd turbulence models. The Astrophysical Journal 764(1), 23 (2013)
- (27) Oran, R.: Coronal heating and solar wind acceleration by alfvén wave turbulence: a global computational model and observations. PhD thesis, The University of Michigan (2014)
- (28) Chhiber, R., Subedi, P., Usmanov, A.V., Matthaeus, W.H., Ruffolo, D., Goldstein, M.L., Parashar, T.N.: Cosmic-ray diffusion coefficients throughout the inner heliosphere from a global solar wind simulation. The Astrophysical Journal Supplement Series 230(2), 21 (2017)
- (29) van der Holst, B., Huang, J., Sachdeva, N., Kasper, J., Manchester IV, W., Borovikov, D., Chandran, B., Case, A., Korreck, K., Larson, D., et al.: Improving the alfvén wave solar atmosphere model based on parker solar probe data. The Astrophysical Journal 925(2), 146 (2022)
- (30) Tu, C.Y., Marsch, E.: MHD structures, waves and turbulence in the solar wind: Observations and theories. Space Science Reviews 73(1), 1–210 (1995)
- (31) Verscharen, D., Klein, K.G., Maruca, B.A.: The multi-scale nature of the solar wind. Living Reviews in Solar Physics 16(1), 5 (2019)
- (32) Hundhausen, A.J.: Coronal Expansion and the Solar Wind. Springer, New York (1972)
- (33) Fox, N., Velli, M., Bale, S., Decker, R., Driesman, A., Howard, R., Kasper, J.C., Kinnison, J., Kusterer, M., Lario, D., et al.: The solar probe plus mission: Humanity’s first visit to our star. Space Science Reviews 204(1-4), 7–48 (2016)
- (34) Batchelor, G.K.: The Theory of Homogeneous Turbulence. Cambridge University Press, Cambridge, UK (1970)
- (35) Tennekes, H., Lumley, J.L.: A First Course in Turbulence. The MIT press, ??? (1972)
- (36) Wu, P., Wan, M., Matthaeus, W., Shay, M., Swisdak, M.: von kármán energy decay and heating of protons and electrons in a kinetic turbulent plasma. Physical review letters 111(12), 121105 (2013)
- (37) Karimabadi, H., Roytershteyn, V., Wan, M., Matthaeus, W.H., Daughton, W., Wu, P., Shay, M., Loring, B., Borovsky, J., Leonardis, E., Chapman, S.C., Nakamura, T.K.M.: Coherent structures, intermittent turbulence, and dissipation in high-temperature plasmas. Physics of Plasmas 20(1), (2013). https://doi.org/10.1063/1.4773205
- (38) Wan, M., Matthaeus, W., Roytershteyn, V., Parashar, T., Wu, P., Karimabadi, H.: Intermittency, coherent structures and dissipation in plasma turbulence. Physics of Plasmas (1994-present) 23(4), 042307 (2016)
- (39) Schekochihin, A., Cowley, S., Dorland, W., Hammett, G., Howes, G.G., Quataert, E., Tatsuno, T.: Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. The Astrophysical Journal Supplement Series 182(1), 310 (2009)
- (40) Boldyrev, S., Horaites, K., Xia, Q., Perez, J.C.: Toward a theory of astrophysical plasma turbulence at subproton scales. The Astrophysical Journal 777(1), 41 (2013)
- (41) Eyink, G.L.: Cascades and dissipative anomalies in nearly collisionless plasma turbulence. Physical Review X 8(4), 041020 (2018)
- (42) Biskamp, D.: Magnetohydrodynamic Turbulence. Cambridge University Press, ??? (2003)
- (43) De Karman, T., Howarth, L.: On the statistical theory of isotropic turbulence. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, vol. 164, pp. 192–215 (1938). The Royal Society
- (44) Hossain, M., Gray, P.C., Pontius, D.H., Matthaeus, W.H., Oughton, S.: Phenomenology for the decay of energy containing eddies in homogeneous mhd turbulence. Physics of Fluids (1994-present) 7(11), 2886–2904 (1995). https://doi.org/10.1063/1.868665
- (45) Wan, M., Oughton, S., Servidio, S., Matthaeus, W.H.: von kármán self-preservation hypothesis for magnetohydrodynamic turbulence and its consequences for universality. Journal of Fluid Mechanics 697, 296–315 (2012)
- (46) Bandyopadhyay, R., Oughton, S., Wan, M., Matthaeus, W.H., Chhiber, R., Parashar, T.N.: Finite dissipation in anisotropic magnetohydrodynamic turbulence. Phys. Rev. X 8, 041052 (2018). https://doi.org/10.1103/PhysRevX.8.041052
- (47) McComb, W., Berera, A., Yoffe, S., Linkmann, M.: Energy transfer and dissipation in forced isotropic turbulence. Physical Review E 91(4), 043013 (2015)
- (48) Matthaeus, W.H., Parashar, T.N., Wan, M., Wu, P.: Turbulence and proton–electron heating in kinetic plasma. The Astrophysical Journal Letters 827(1), 7 (2016)
- (49) Parashar, T.N., Matthaeus, W.H., Shay, M.A., Wan, M.: Transition from kinetic to mhd behavior in a collisionless plasma. The Astrophysical Journal 811(2), 112 (2015)
- (50) Roy, S., Chhiber, R., Dasso, S., Ruiz, M., Matthaeus, W.: von karman correlation similarity of the turbulent interplanetary magnetic field. The Astrophysical Journal Letters 919(2), 27 (2021)
- (51) Kolmogorov, A.: The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Akademiia Nauk SSSR Doklady 30, 301–305 (1941)
- (52) Kraichnan, R.H.: Inertial-range spectrum of hydromagnetic turbulence. Physics of Fluids (1958-1988) 8(7), 1385–1387 (1965)
- (53) Goldreich, P., Sridhar, S.: Toward a theory of interstellar turbulence. 2: Strong alfvenic turbulence. The Astrophysical Journal 438, 763–775 (1995). https://doi.org/10.1086/175121
- (54) Verma, M.K.: Mean magnetic field renormalization and kolmogorov’s energy spectrum in magnetohydrodynamic turbulence. Physics of Plasmas 6(5), 1455–1460 (1999)
- (55) Zhou, Y., Matthaeus, W.H., Dmitruk, P.: Colloquium: Magnetohydrodynamic turbulence and time scales in astrophysical and space plasmas. Rev. Mod. Phys. 76(4), 1015–1035 (2004). https://doi.org/10.1103/RevModPhys.76.1015
- (56) Champagne, F.: The fine-scale structure of the turbulent velocity field. Journal of Fluid Mechanics 86(1), 67–108 (1978)
- (57) Parashar, T.N., Chasapis, A., Bandyopadhyay, R., Chhiber, R., Matthaeus, W.H., Maruca, B., Shay, M.A., Burch, J.L., Moore, T.E., Giles, B.L., Gershman, D.J., Pollock, C.J., Torbert, R.B., Russell, C.T., Strangeway, R.J., Roytershteyn, V.: Kinetic range spectral features of cross helicity using the magnetospheric multiscale spacecraft. Phys. Rev. Lett. 121, 265101 (2018). https://doi.org/10.1103/PhysRevLett.121.265101
- (58) Kiyani, K.H., Osman, K.T., Chapman, S.C.: Dissipation and heating in solar wind turbulence: from the macro to the micro and back again. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 373(2041), 20140155 (2015) https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2014.0155. https://doi.org/10.1098/rsta.2014.0155
- (59) Fraternale, F., Pogorelov, N.V., Richardson, J.D., Tordella, D.: Magnetic turbulence spectra and intermittency in the heliosheath and in the local interstellar medium. The Astrophysical Journal 872(1), 40 (2019)
- (60) Kolmogorov, A.N.: A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high reynolds number. Journal of Fluid Mechanics 13(1), 82–85 (1962)
- (61) Politano, H., Pouquet, A.: Model of intermittency in magnetohydrodynamic turbulence. Physical Review E 52(1), 636 (1995)
- (62) Verma, M.K.: Statistical theory of magnetohydrodynamic turbulence: recent results. Physics Reports 401(5-6), 229–380 (2004)
- (63) Pope, S.B.: Turbulent Flows. Cambridge university press, ??? (2000)
- (64) Politano, H., Pouquet, A.: von kármán–howarth equation for magnetohydrodynamics and its consequences on third-order longitudinal structure and correlation functions. Physical Review E 57(1), 21 (1998)
- (65) Podesta, J.: Laws for third-order moments in homogeneous anisotropic incompressible magnetohydrodynamic turbulence. Journal of Fluid Mechanics 609, 171–194 (2008)
- (66) Andrés, N., Sahraoui, F.: Alternative derivation of exact law for compressible and isothermal magnetohydrodynamics turbulence. Physical Review E 96(5), 053205 (2017)
- (67) Wan, M., Servidio, S., Oughton, S., Matthaeus, W.H.: The third-order law for increments in magnetohydrodynamic turbulence with constant shear. Physics of plasmas 16(9), 090703 (2009)
- (68) Galtier, S.: von kármán–howarth equations for hall magnetohydrodynamic flows. Physical Review E 77(1), 015302 (2008)
- (69) Ferrand, R., Galtier, S., Sahraoui, F.: A compact exact law for compressible isothermal hall magnetohydrodynamic turbulence. Journal of Plasma Physics 87(2) (2021)
- (70) Galtier, S.: Exact scaling laws for 3d electron mhd turbulence. Journal of Geophysical Research: Space Physics 113(A1) (2008)
- (71) Sorriso-Valvo, L., Marino, R., Carbone, V., Noullez, A., Lepreti, F., Veltri, P., Bruno, R., Bavassano, B., Pietropaolo, E.: Observation of inertial energy cascade in interplanetary space plasma. Physical review letters 99(11), 115001 (2007)
- (72) Marino, R., Sorriso-Valvo, L., Carbone, V., Noullez, A., Bruno, R., Bavassano, B.: Heating the solar wind by a magnetohydrodynamic turbulent energy cascade. The Astrophysical Journal 677(1), 71 (2008)
- (73) Osman, K.T., Wan, M., Matthaeus, W.H., Weygand, J.M., Dasso, S.: Anisotropic third-moment estimates of the energy cascade in solar wind turbulence using multispacecraft data. Physical Review Letters 107, 165001 (2011). https://doi.org/10.1103/PhysRevLett.107.165001
- (74) Verdini, A., Grappin, R., Hellinger, P., Landi, S., Müller, W.C.: Anisotropy of third-order structure functions in mhd turbulence. The Astrophysical Journal 804(2), 119 (2015)
- (75) Hellinger, P., Verdini, A., Landi, S., Franci, L., Matteini, L.: von kármán–howarth equation for hall magnetohydrodynamics: Hybrid simulations. The Astrophysical Journal 857(2), 19 (2018). https://doi.org/10.3847/2041-8213/aabc06
- (76) Bandyopadhyay, R., Sorriso-Valvo, L., Chasapis, A., Hellinger, P., Matthaeus, W.H., Verdini, A., Landi, S., Franci, L., Matteini, L., Giles, B.L., et al.: In situ observation of hall magnetohydrodynamic cascade in space plasma. Physical Review Letters 124(22), 225101 (2020)
- (77) Aluie, H.: Compressible turbulence: the cascade and its locality. Physical review letters 106(17), 174502 (2011)
- (78) Bian, X., Aluie, H.: Decoupled cascades of kinetic and magnetic energy in magnetohydrodynamic turbulence. Physical review letters 122(13), 135101 (2019)
- (79) Squire, J., Kunz, M.W., Quataert, E., Schekochihin, A.: Kinetic simulations of the interruption of large-amplitude shear-alfvén waves in a high- plasma. Physical review letters 119(15), 155101 (2017)
- (80) Franci, L., Cerri, S.S., Califano, F., Landi, S., Papini, E., Verdini, A., Matteini, L., Jenko, F., Hellinger, P.: Magnetic reconnection as a driver for a sub-ion-scale cascade in plasma turbulence. The Astrophysical Journal Letters 850(1), 16 (2017)
- (81) Kunz, M., Squire, J., Schekochihin, A., Quataert, E.: Self-sustaining sound in collisionless, high- plasma. Journal of Plasma Physics 86(6) (2020)
- (82) Yang, Y., Matthaeus, W.H., Parashar, T.N., Haggerty, C.C., Roytershteyn, V., Daughton, W., Wan, M., Shi, Y., Chen, S.: Energy transfer, pressure tensor, and heating of kinetic plasma. Physics of Plasmas 24(7), 072306 (2017) http://dx.doi.org/10.1063/1.4990421. https://doi.org/10.1063/1.4990421
- (83) Camporeale, E., Sorriso-Valvo, L., Califano, F., Retinò, A.: Coherent structures and spectral energy transfer in turbulent plasma: a space-filter approach. Physical review letters 120(12), 125101 (2018)
- (84) Cerri, S., Camporeale, E.: Space-filter techniques for quasi-neutral hybrid-kinetic models. Physics of Plasmas 27(8), 082102 (2020)
- (85) Yang, Y., Matthaeus, W.H., Roy, S., Roytershteyn, V., Parashar, T., Bandyopadhyay, R., Wan, M.: Pressure-strain interaction as the energy dissipation estimate in collisionless plasma. Astrophys. J. 929, 142 (2022). https://doi.org/10.3847/1538-4357/ac5d3e
- (86) Hellinger, P., Montagud-Camps, V., Franci, L., Matteini, L., Papini, E., Verdini, A., Landi, S.: Ion-scale transition of plasma turbulence: Pressure-strain effect. arXiv preprint arXiv:2203.12322 (2022)
- (87) Hollweg, J.V.: Nonlinear landau damping of alfvén waves. Physical Review Letters 27(20), 1349 (1971)
- (88) Chen, C., Klein, K., Howes, G.G.: Evidence for electron landau damping in space plasma turbulence. Nature communications 10(1), 1–8 (2019)
- (89) Hollweg, J.V., Isenberg, P.A.: Generation of the fast solar wind: A review with emphasis on the resonant cyclotron interaction. Journal of Geophysical Research: Space Physics 107(A7), 12 (2002)
- (90) Kasper, J.C., Maruca, B.A., Stevens, M.L., Zaslavsky, A.: Sensitive test for ion-cyclotron resonant heating in the solar wind. Physical review letters 110(9), 091102 (2013)
- (91) Dawson, J.M., Uman, M.F.: Heating a plasma by means of magnetic pumping. Nuclear Fusion 5(3), 242 (1965)
- (92) Lichko, E., Egedal, J., Daughton, W., Kasper, J.: Magnetic pumping as a source of particle heating and power-law distributions in the solar wind. The Astrophysical Journal Letters 850(2), 28 (2017)
- (93) Chandran, B.D.G., Li, B., Rogers, B.N., Quataert, E., Germaschewski, K.: Perpendicular ion heating by low-frequency alfvén-wave turbulence in the solar wind. The Astrophysical Journal 720(1), 503 (2010)
- (94) Xia, Q., Perez, J.C., Chandran, B.D., Quataert, E.: Perpendicular ion heating by reduced magnetohydrodynamic turbulence. The Astrophysical Journal 776(2), 90 (2013)
- (95) Mallet, A., Klein, K.G., Chandran, B.D., Grošelj, D., Hoppock, I.W., Bowen, T.A., Salem, C.S., Bale, S.D.: Interplay between intermittency and dissipation in collisionless plasma turbulence. Journal of Plasma Physics 85(3) (2019)
- (96) Cerri, S.S., Arzamasskiy, L., Kunz, M.W.: On stochastic heating and its phase-space signatures in low-beta kinetic turbulence. The Astrophysical Journal 916(2), 120 (2021)
- (97) Martinović, M.M., Klein, K.G., Huang, J., Chandran, B.D., Kasper, J.C., Lichko, E., Bowen, T., Chen, C.H., Matteini, L., Stevens, M., et al.: Multiscale solar wind turbulence properties inside and near switchbacks measured by the parker solar probe. The Astrophysical Journal 912(1), 28 (2021)
- (98) TenBarge, J., Howes, G., Dorland, W.: Collisionless damping at electron scales in solar wind turbulence. The Astrophysical Journal 774(2), 139 (2013)
- (99) Hughes, R.S., Gary, S.P., Wang, J.: Electron and ion heating by whistler turbulence: Three-dimensional particle-in-cell simulations. Geophysical Research Letters 41(24), 8681–8687 (2014)
- (100) Roy, S., Bandyopadhyay, R., Yang, Y., Matthaeus, W.H., Adhikari, S., Parashar, T.N., Chasapis, A., Li, H., Gershman, D.J., Giles, B.L., Burch, J.L.: Turbulent energy transfer and proton-electron heating in collisionless plasmas. Physical Review X (Under Review)
- (101) Yang, Y., Matthaeus, W.H., Parashar, T.N., Wu, P., Wan, M., Shi, Y., Chen, S., Roytershteyn, V., Daughton, W.: Energy transfer channels and turbulence cascade in vlasov-maxwell turbulence. Phys. Rev. E 95, 061201 (2017). https://doi.org/10.1103/PhysRevE.95.061201
- (102) Del Sarto, D., Pegoraro, F., Califano, F.: Pressure anisotropy and small spatial scales induced by velocity shear. Physical Review E 93(5), 053203 (2016)
- (103) Huang, K.: Statistical Mechanics. John Wiley & Sons, ??? (2008)
- (104) Servidio, S., Valentini, F., Califano, F., Veltri, P.: Local kinetic effects in two-dimensional plasma turbulence. Physical review letters 108(4), 045001 (2012)
- (105) Servidio, S., Osman, K., Valentini, F., Perrone, D., Califano, F., Chapman, S., Matthaeus, W., Veltri, P.: Proton kinetic effects in vlasov and solar wind turbulence. The Astrophysical Journal Letters 781(2), 27 (2014)
- (106) Franci, L., Hellinger, P., Matteini, L., Verdini, A., Landi, S.: Two-dimensional hybrid simulations of kinetic plasma turbulence: Current and vorticity vs proton temperature. In: AIP Conference Proceedings, vol. 1720, p. 040003 (2016). AIP Publishing LLC
- (107) Parashar, T.N., Matthaeus, W.H.: Propinquity of current and vortex structures: Effects on collisionless plasma heating. The Astrophysical Journal 832(1), 57 (2016)
- (108) Matthaeus, W.H.: Reconnection in two dimensions: Localization of vorticity and current near magnetic x-points. Geophysical Research Letters 9(6), 660–663 (1982)
- (109) Sitnov, M., Merkin, V., Roytershteyn, V., Swisdak, M.: Kinetic dissipation around a dipolarization front. Geophysical Research Letters 45(10), 4639–4647 (2018)
- (110) Matthaeus, W.H., Yang, Y., Wan, M., Parashar, T.N., Bandyopadhyay, R., Chasapis, A., Pezzi, O., Valentini, F.: Pathways to dissipation in weakly collisional plasmas. The Astrophysical Journal 891(1), 101 (2020). https://doi.org/10.3847/1538-4357/ab6d6a
- (111) Bandyopadhyay, R., Matthaeus, W.H., Parashar, T.N., Yang, Y., Chasapis, A., Giles, B.L., Gershman, D.J., Pollock, C.J., Russell, C.T., Strangeway, R.J., et al.: Statistics of kinetic dissipation in the earth’s magnetosheath: Mms observations. Physical Review Letters 124(25), 255101 (2020)
- (112) Greco, A., Matthaeus, W., Perri, S., Osman, K., Servidio, S., Wan, M., Dmitruk, P.: Partial variance of increments method in solar wind observations and plasma simulations. Space Science Reviews 214(1), 1 (2018)
- (113) Sorriso-Valvo, L., Carbone, F., Perri, S., Greco, A., Marino, R., Bruno, R.: On the statistical properties of turbulent energy transfer rate in the inner heliosphere. Solar Physics 293(1), 1–16 (2018)
- (114) Osman, K.T., Matthaeus, W.H., Greco, A., Servidio, S.: Evidence for inhomogeneous heating in the solar wind. The Astrophysical Journal Letters 727(1), 11 (2011)
- (115) Tessein, J., Matthaeus, W., Wan, M., Osman, K., Ruffolo, D., Giacalone, J.: Association of suprathermal particles with coherent structures and shocks. The Astrophysical Journal Letters 776(1), 8 (2013)
- (116) Squire, J., Meyrand, R., Kunz, M.W., Arzamasskiy, L., Schekochihin, A.A., Quataert, E.: High-frequency heating of the solar wind triggered by low-frequency turbulence. Nature Astronomy, 1–9 (2022)
- (117) Alexandrova, O., Jagarlamudi, V.K., Hellinger, P., Maksimovic, M., Shprits, Y., Mangeney, A.: Spectrum of kinetic plasma turbulence at 0.3–0.9 astronomical units from the sun. Physical Review E 103(6), 063202 (2021)
- (118) Alexandrova, O., Lacombe, C., Mangeney, A., Grappin, R., Maksimovic, M.: Solar wind turbulent spectrum at plasma kinetic scales. The Astrophysical Journal 760(2), 121 (2012)
- (119) Arrò, G., Califano, F., Lapenta, G.: Spectral properties and energy cascade at kinetic scales in collisionless plasma turbulence. arXiv preprint arXiv:2112.12753 (2021)
- (120) Holzer, R.E., McLeod, M.G., Smith, E.J.: Preliminary results from the ogo 1 search coil magnetometer: Boundary positions and magnetic noise spectra. Journal of Geophysical Research 71(5), 1481–1486 (1966)
- (121) Coleman, P.J.: Hydromagnetic waves in the interplanetary plasma. Phys. Rev. Lett. 17, 207–211 (1966)
- (122) Sturrock, P., Hartle, R.: Two-fluid model of the solar wind. Physical Review Letters 16(14), 628 (1966)
- (123) Chandrasekhar, S.: Turbulence—A physical theory of astrophysical interest. Astrophys. J. 110, 329–339 (1949)
- (124) Belcher, J.W., Burchsted, R.: Energy densities of alfvén waves between 0.7 and 1.6 au. Journal of Geophysical Research 79(31), 4765–4768 (1974)
- (125) Roberts, D.A., Goldstein, M.L., Klein, L.W.: The amplitudes of interplanetary fluctuations: Stream structure, heliocentric distance, and frequency dependence. J. Geophys. Res. 95, 4203–4216 (1990)
- (126) Verma, M.K., Roberts, D.A.: The radial evolution of the amplitudes of “dissipationless” turbulent solar wind fluctuations. J. Geophys. Res. 98, 5625 (1993)
- (127) Zank, G., Matthaeus, W., Smith, C.: Evolution of turbulent magnetic fluctuation power with heliospheric distance. Journal of Geophysical Research: Space Physics 101(A8), 17093–17107 (1996)
- (128) Bavassano, B., Dobrowolny, M., Mariani, F., Ness, N.: Radial evolution of power spectra of interplanetary alfvénic turbulence. Journal of Geophysical Research: Space Physics 87(A5), 3617–3622 (1982)
- (129) Horbury, T., Balogh, A.: Evolution of magnetic field fluctuations in high-speed solar wind streams: Ulysses and helios observations. Journal of Geophysical Research: Space Physics 106(A8), 15929–15940 (2001)
- (130) Bruno, R., Carbone, V., Vörös, Z., D’Amicis, R., Bavassano, B., Cattaneo, M., Mura, A., Milillo, A., Orsini, S., Veltri, P., et al.: Coordinated study on solar wind turbulence during the venus-express, ace and ulysses alignment of august 2007. Earth, Moon, and Planets 104(1), 101–104 (2009)
- (131) Hollweg, J.V.: Transition region, corona, and solar wind in coronal holes. J. Geophys. Res. 91, 4111 (1986)
- (132) Hollweg, J.V., Johnson, W.: Transition region, corona, and solar wind in coronal holes: Some two fluid models. J. Geophys. Res. 93, 9547 (1988)
- (133) Tu, C.-Y., Pu, Z.-Y., Wei, F.-S.: The power spectrum of interplanetary alfvénic fluctuations: Derivation of the governing equation and its solution. Journal of Geophysical Research: Space Physics 89(A11), 9695–9702 (1984)
- (134) Tu, C.-y.: The damping of interplanetary alfvénic fluctuations and the heating of the solar wind. Journal of Geophysical Research: Space Physics 93(A1), 7–20 (1988)
- (135) Hollweg, J.V.: Transverse alfvén waves in the solar wind: Arbitrary and . J. Geophys. Res. 79, 1539 (1974)
- (136) Marsch, E., Tu, C.-Y.: Dynamics of correlation functions with Elsässer variables for inhomogeneous mhd turbulence. Journal of Plasma Physics 41, 479–491 (1989)
- (137) Zhou, Y., Matthaeus, W.H.: Non-WKB evolution of solar wind fluctuations: A turbulence modeling approach. Geophysical Research Letters 16, 755 (1989)
- (138) Matthaeus, W.H., Oughton, S., Pontius Jr, D.H., Zhou, Y.: Evolution of energy-containing turbulent eddies in the solar wind. Journal of Geophysical Research: Space Physics 99(A10), 19267–19287 (1994)
- (139) Smith, C.W., Matthaeus, W.H., Zank, G.P., Ness, N.F., Oughton, S., Richardson, J.D.: Heating of the low-latitude solar wind by dissipation of turbulent magnetic fluctuations. Journal of Geophysical Research: Space Physics 106(A5), 8253–8272 (2001)
- (140) Ruiz, M.E., Dasso, S., Matthaeus, W., Weygand, J.: Characterization of the turbulent magnetic integral length in the solar wind: from 0.3 to 5 astronomical units. Solar Physics 289(10), 3917–3933 (2014)
- (141) Roberts, D.A.: Evolution of the spectrum of solar wind velocity fluctuations from 0.3 to 5 au. Journal of Geophysical Research: Space Physics 115(A12) (2010)
- (142) Matthaeus, W.H., Zank, G.P., Smith, C.W., Oughton, S.: Turbulence, spatial transport, and heating of the solar wind. Physical Review Letters 82, 3444–3447 (1999). https://doi.org/10.1103/PhysRevLett.82.3444
- (143) Goldstein, B., Smith, E., Balogh, A., Horbury, T., Goldstein, M., Roberts, D.: Properties of magnetohydrodynamic turbulence in the solar wind as observed by ulysses at high heliographic latitudes. Geophysical Research Letters 22(23), 3393–3396 (1995)
- (144) Breech, B., Matthaeus, W.H., Minnie, J., Bieber, J.W., Oughton, S., Smith, C.W., Isenberg, P.A.: Turbulence transport throughout the heliosphere. Journal of Geophysical Research 113 (2008). https://doi.org/10.1029/2007JA012711
- (145) Roberts, D., Klein, L., Goldstein, M., Matthaeus, W.: The nature and evolution of magnetohydrodynamic fluctuations in the solar wind: Voyager observations. Journal of Geophysical Research: Space Physics 92(A10), 11021–11040 (1987)
- (146) Matthaeus, W.H., Minnie, J., Breech, B., Parhi, S., Bieber, J., Oughton, S.: Transport of cross helicity and radial evolution of alfvénicity in the solar wind. Geophysical research letters 31(12) (2004)
- (147) Bavassano, B., Pietropaolo, E., Bruno, R.: On the evolution of outward and inward alfvénic fluctuations in the polar wind. Journal of Geophysical Research: Space Physics 105(A7), 15959–15964 (2000)
- (148) Stribling, T., Matthaeus, W.H.: Relaxation processes in a low order three-dimensional magnetohydrodynamics model. Physics of Fluids B boldVol3, 1848 (1991)
- (149) Müller, W.-C., Grappin, R.: The residual energy in freely decaying magnetohydrodynamic turbulence. Plasma Physics and Controlled Fusion 46(12B), 91–96 (2004). https://doi.org/10.1088/0741-3335/46/12b/008
- (150) Boldyrev, S., Perez, J.C., Borovsky, J.E., Podesta, J.J.: Spectral scaling laws in magnetohydrodynamic turbulence simulations and in the solar wind. The Astrophysical Journal 741, 19 (2011). https://doi.org/10.1088/2041-8205/741/1/L19
- (151) Grappin, R., Müller, W.-C., Verdini, A.: Alfvén-dynamo balance and magnetic excess in magnetohydrodynamic turbulence. Astron. Astrophys. 589, 131 (2016) arXiv:1603.03559 [astro-ph.SR]. https://doi.org/10.1051/0004-6361/201628097
- (152) Carbone, V., Marino, R., Sorriso-Valvo, L., Noullez, A., Bruno, R.: Scaling laws of turbulence and heating of fast solar wind: the role of density fluctuations. Physical review letters 103(6), 061102 (2009)
- (153) Marsch, E., Mühlhäuser, K.-H., Schwenn, R., Rosenbauer, H., Pilipp, W., Neubauer, F.: Solar wind protons: Three-dimensional velocity distributions and derived plasma parameters measured between 0.3 and 1 au. Journal of Geophysical Research: Space Physics 87(A1), 52–72 (1982)
- (154) Wang, C., Richardson, J.: Energy partition between solar wind protons and pickup ions in the distant heliosphere: A three-fluid approach. Journal of Geophysical Research 106, 29401–29408 (2001)
- (155) Matteini, L., Landi, S., Hellinger, P., Pantellini, F., Maksimovic, M., Velli, M., Goldstein, B.E., Marsch, E.: Evolution of the solar wind proton temperature anisotropy from 0.3 to 2.5 au. Geophysical Research Letters 34(20) (2007)
- (156) Hellinger, P., Trávníček, P.M., Štverák, Š., Matteini, L., Velli, M.: Proton thermal energetics in the solar wind: Helios reloaded. Journal of Geophysical Research: Space Physics (2013)
- (157) Vasquez, B.J., Smith, C.W., Hamilton, K., MacBride, B.T., Leamon, R.J.: Evaluation of the turbulent energy cascade rates from the upper inertial range in the solar wind at 1 au. Journal of Geophysical Research: Space Physics 112(A7) (2007)
- (158) MacBride, B.T., Smith, C.W., Forman, M.A.: The turbulent cascade at 1 AU: Energy transfer and the third-order scaling for MHD. The Astrophysical Journal 679, 1644–1660 (2008). https://doi.org/10.1086/529575
- (159) MacBride, B.T., Forman, M.A., Smith, C.W.: Turbulence and third moment of fluctuations: Kolmogorov’s law and its mhd analogues in the solar wind. In: Fleck, B., Zurbuchen, T.H., Lacoste, H. (eds.) Proc. Solar Wind 11 – Soho 16 “Connecting Sun and Heliosphere”, vol. SP-592, pp. 613–616. ESA, Noordwijk, The Netherlands (2005)
- (160) Marino, R., Sorriso-Valvo, L., D’Amicis, R., Carbone, V., Bruno, R., Veltri, P.: On the occurrence of the third-order scaling in high latitude solar wind. The Astrophysical Journal 750(1), 41 (2012)
- (161) Verma, M., Roberts, D., Goldstein, M.: Turbulent heating and temperature evolution in the solar wind plasma. Journal of Geophysical Research: Space Physics 100(A10), 19839–19850 (1995)
- (162) Bourouaine, S., Chandran, B.D.: Observational test of stochastic heating in low- fast-solar-wind streams. The Astrophysical Journal 774(2), 96 (2013)
- (163) Martinović, M.M., Klein, K.G., Bourouaine, S.: Radial evolution of stochastic heating in low- solar wind. The Astrophysical Journal 879(1), 43 (2019)
- (164) Parashar, T.N., Servidio, S., Breech, B., Shay, M.A., Matthaeus, W.H.: Effect of driving frequency on excitation of turbulence in a kinetic plasma. Physics of Plasmas 18(9), 092302 (2011)
- (165) Osman, K., Matthaeus, W., Wan, M., Rappazzo, A.: Intermittency and local heating in the solar wind. Physical review letters 108(26), 261102 (2012)
- (166) Bruno, R., Carbone, V., Sorriso-Valvo, L., Bavassano, B.: Radial evolution of solar wind intermittency in the inner heliosphere. Journal of Geophysical Research: Space Physics 108(A3) (2003)
- (167) Parashar, T.N., Cuesta, M., Matthaeus, W.H.: Reynolds number and intermittency in the expanding solar wind: Predictions based on voyager observations. The Astrophysical Journal Letters 884(2), 57 (2019). https://doi.org/10.3847/2041-8213/ab4a82
- (168) Cuesta, M.E., Parashar, T.N., Chhiber, R., Matthaeus, W.H.: Intermittency in the expanding solar wind: Observations from parker solar probe (0.16 au), helios 1 (0.3–1 au), and voyager 1 (1–10 au). The Astrophysical Journal Supplement Series 259(1), 23 (2022)
- (169) Bale, S., Goetz, K., Harvey, P., Turin, P., Bonnell, J., Dudok de Wit, T., Ergun, R., MacDowall, R., Pulupa, M., André, M., et al.: The fields instrument suite for solar probe plus. Space science reviews 204(1), 49–82 (2016)
- (170) McComas, D., Alexander, N., Angold, N., Bale, S., Beebe, C., Birdwell, B., Boyle, M., Burgum, J., Burnham, J., Christian, E., et al.: Integrated science investigation of the sun (isis): Design of the energetic particle investigation. Space Science Reviews 204(1), 187–256 (2016)
- (171) Kasper, J.C., Abiad, R., Austin, G., Balat-Pichelin, M., Bale, S.D., Belcher, J.W., Berg, P., Bergner, H., Berthomier, M., Bookbinder, J., et al.: Solar wind electrons alphas and protons (sweap) investigation: Design of the solar wind and coronal plasma instrument suite for solar probe plus. Space Science Reviews 204(1), 131–186 (2016)
- (172) Vourlidas, A., Howard, R.A., Plunkett, S.P., Korendyke, C.M., Thernisien, A.F., Wang, D., Rich, N., Carter, M.T., Chua, D.H., Socker, D.G., et al.: The wide-field imager for solar probe plus (wispr). Space Science Reviews 204(1), 83–130 (2016)
- (173) et al., N.R.: Parker solar probe: Three years of solar cycle minimum discoveries. Space Science Rev. (2022)
- (174) Bale, S., Badman, S., Bonnell, J., Bowen, T., Burgess, D., Case, A., Cattell, C., Chandran, B., Chaston, C., Chen, C., et al.: Highly structured slow solar wind emerging from an equatorial coronal hole. Nature 576(7786), 237–242 (2019)
- (175) Balogh, A., Forsyth, R., Lucek, E., Horbury, T., Smith, E.: Heliospheric magnetic field polarity inversions at high heliographic latitudes. Geophysical research letters 26(6), 631–634 (1999)
- (176) Matteini, L., Horbury, T.S., Neugebauer, M., Goldstein, B.E.: Dependence of solar wind speed on the local magnetic field orientation: Role of alfvénic fluctuations. Geophysical Research Letters 41(2), 259–265 (2014)
- (177) Borovsky, J.E.: The plasma structure of coronal hole solar wind: Origins and evolution. Journal of Geophysical Research: Space Physics 121(6), 5055–5087 (2016)
- (178) de Wit, T.D., Krasnoselskikh, V.V., Bale, S.D., Bonnell, J.W., Bowen, T.A., Chen, C.H., Froment, C., Goetz, K., Harvey, P.R., Jagarlamudi, V.K., et al.: Switchbacks in the near-sun magnetic field: long memory and impact on the turbulence cascade. The Astrophysical Journal Supplement Series 246(2), 39 (2020)
- (179) Fisk, L., Kasper, J.: Global circulation of the open magnetic flux of the sun. The Astrophysical Journal Letters 894(1), 4 (2020)
- (180) Squire, J., Chandran, B.D., Meyrand, R.: In-situ switchback formation in the expanding solar wind. The Astrophysical Journal Letters 891(1), 2 (2020)
- (181) Chhiber, R., Usmanov, A.V., DeForest, C.E., Matthaeus, W.H., Parashar, T.N., Goldstein, M.L.: Weakened magnetization and onset of large-scale turbulence in the young solar wind—comparisons of remote sensing observations with simulation. The Astrophysical Journal Letters 856(2), 39 (2018)
- (182) Bandyopadhyay, R., Matthaeus, W., McComas, D., Chhiber, R., Usmanov, A., Huang, J., Livi, R., Larson, D., Kasper, J., Case, A., et al.: Sub-alfvénic solar wind observed by the parker solar probe: Characterization of turbulence, anisotropy, intermittency, and switchback. The Astrophysical Journal Letters 926(1), 1 (2022)
- (183) Kasper, J., Klein, K., Lichko, E., Huang, J., Chen, C., Badman, S., Bonnell, J., Whittlesey, P., Livi, R., Larson, D., et al.: Parker solar probe enters the magnetically dominated solar corona. Physical review letters 127(25), 255101 (2021)
- (184) Bourouaine, S., Perez, J.C., Klein, K.G., Chen, C.H., Martinović, M., Bale, S.D., Kasper, J.C., Raouafi, N.E.: Turbulence characteristics of switchback and nonswitchback intervals observed by parker solar probe. The Astrophysical Journal Letters 904(2), 30 (2020)
- (185) Martinović, M.M., Klein, K.G., Kasper, J.C., Case, A.W., Korreck, K.E., Larson, D., Livi, R., Stevens, M., Whittlesey, P., Chandran, B.D., et al.: The enhancement of proton stochastic heating in the near-sun solar wind. The Astrophysical Journal Supplement Series 246(2), 30 (2020)
- (186) Tenerani, A., Velli, M., Matteini, L., Réville, V., Shi, C., Bale, S.D., Kasper, J.C., Bonnell, J.W., Case, A.W., De Wit, T.D., et al.: Magnetic field kinks and folds in the solar wind. The Astrophysical Journal Supplement Series 246(2), 32 (2020)
- (187) McManus, M.D., Bowen, T.A., Mallet, A., Chen, C.H., Chandran, B.D., Bale, S.D., Larson, D.E., de Wit, T.D., Kasper, J.C., Stevens, M., et al.: Cross helicity reversals in magnetic switchbacks. The Astrophysical Journal Supplement Series 246(2), 67 (2020)
- (188) Chen, C., Bale, S., Bonnell, J., Borovikov, D., Bowen, T., Burgess, D., Case, A., Chandran, B., De Wit, T.D., Goetz, K., et al.: The evolution and role of solar wind turbulence in the inner heliosphere. The Astrophysical Journal Supplement Series 246(2), 53 (2020)
- (189) Alberti, T., Laurenza, M., Consolini, G., Milillo, A., Marcucci, M.F., Carbone, V., Bale, S.D.: On the scaling properties of magnetic-field fluctuations through the inner heliosphere. The Astrophysical Journal 902(1), 84 (2020)
- (190) Parashar, T.N., Goldstein, M.L., Maruca, B.A., Matthaeus, W.H., Ruffolo, D., Bandyopadhyay, R., Chhiber, R., Chasapis, A., Qudsi, R., Vech, D., Roberts, D.A., Bale, S.D., Bonnell, J.W., de Wit, T.D., Goetz, K., Harvey, P.R., MacDowall, R.J., Malaspina, D., Pulupa, M., Kasper, J.C., Korreck, K.E., Case, A.W., Stevens, M., Whittlesey, P., Larson, D., Livi, R., Velli, M., Raouafi, N.: Measures of scale-dependent alfvénicity in the first PSP solar encounter. The Astrophysical Journal Supplement Series 246(2), 58 (2020). https://doi.org/10.3847/1538-4365/ab64e6
- (191) Bruno, R., Trenchi, L.: Radial dependence of the frequency break between fluid and kinetic scales in the solar wind fluctuations. The Astrophysical Journal Letters 787(2), 24 (2014)
- (192) Wu, H., Tu, C., Wang, X., He, J., Yang, L.: Energy supply for heating the slow solar wind observed by parker solar probe between 0.17 and 0.7 au. The Astrophysical Journal Letters 904(1), 8 (2020)
- (193) Horbury, T., Balogh, A., Forsyth, R., Smith, E.: The rate of turbulent evolution over the sun’s poles. Astronomy and Astrophysics 316, 333–341 (1996)
- (194) Klein, L., Matthaeus, W., Roberts, D., Goldstein, M.: Evolution of spatial and temporal correlations in the solar wind: Observations and interpretation. In: Solar Wind Seven, pp. 197–200. Elsevier, ??? (1992)
- (195) Matthaeus, W.H., Zank, G.P., Oughton, S.: Phenomenology of hydromagnetic turbulence in a uniformly expanding medium. Journal of plasma physics 56(3), 659–675 (1996)
- (196) Duan, D., Bowen, T.A., Chen, C.H., Mallet, A., He, J., Bale, S.D., Vech, D., Kasper, J., Pulupa, M., Bonnell, J.W., et al.: The radial dependence of proton-scale magnetic spectral break in slow solar wind during psp encounter 2. The Astrophysical Journal Supplement Series 246(2), 55 (2020)
- (197) Shi, C., Velli, M., Panasenco, O., Tenerani, A., Réville, V., Bale, S.D., Kasper, J., Korreck, K., Bonnell, J., de Wit, T.D., et al.: Alfvénic versus non-alfvénic turbulence in the inner heliosphere as observed by parker solar probe. Astronomy & Astrophysics 650, 21 (2021)
- (198) Roberts, D.A., Goldstein, M.L., Matthaeus, W.H., Ghosh, S.: Velocity shear generation of solar wind turbulence. Journal of Geophysical Research: Space Physics 97(A11), 17115–17130 (1992)
- (199) Huang, S., Sahraoui, F., Andrés, N., Hadid, L., Yuan, Z., He, J., Zhao, J., Galtier, S., Zhang, J., Deng, X., et al.: The ion transition range of solar wind turbulence in the inner heliosphere: Parker solar probe observations. The Astrophysical journal letters 909(1), 7 (2021)
- (200) Bowen, T.A., Bale, S.D., Bonnell, J.W., Dudok de Wit, T., Goetz, K., Goodrich, K., Gruesbeck, J., Harvey, P.R., Jannet, G., Koval, A., et al.: A merged search-coil and fluxgate magnetometer data product for parker solar probe fields. Journal of Geophysical Research: Space Physics 125(5), 2020–027813 (2020)
- (201) Denskat, K., Beinroth, H., Neubauer, F., et al.: Interplanetary magnetic field power spectra with frequencies from 2.4 x 10^-5 hz to 470 hz from helios-observations during solar minimum conditions. Journal of geophysics 54(1), 60–67 (1984)
- (202) Leamon, R.J., Smith, C.W., Ness, N.F., Wong, H.K.: Dissipation range dynamics: Kinetic Alfvén waves and the importance of e. Journal of Geophysical Research 104(A10), 22331 (1999)
- (203) Meyrand, R., Squire, J., Schekochihin, A.A., Dorland, W.: On the violation of the zeroth law of turbulence in space plasmas. Journal of Plasma Physics 87(3) (2021)
- (204) Zhu, X., He, J., Verscharen, D., Duan, D., Bale, S.D.: Wave composition, propagation, and polarization of magnetohydrodynamic turbulence within 0.3 au as observed by parker solar probe. The Astrophysical Journal Letters 901(1), 3 (2020)
- (205) Duan, D., He, J., Bowen, T.A., Woodham, L.D., Wang, T., Chen, C.H., Mallet, A., Bale, S.D.: Anisotropy of solar wind turbulence in the inner heliosphere at kinetic scales: Psp observations. The Astrophysical Journal Letters 915(1), 8 (2021)
- (206) Zhang, J., Huang, S., He, J., Wang, T., Yuan, Z., Deng, X., Jiang, K., Wei, Y., Xu, S., Xiong, Q., et al.: Three-dimensional anisotropy and scaling properties of solar wind turbulence at kinetic scales in the inner heliosphere: Parker solar probe observations. The Astrophysical Journal Letters 924(2), 21 (2022)
- (207) Bandyopadhyay, R., Goldstein, M.L., Maruca, B.A., Matthaeus, W.H., Parashar, T.N., Ruffolo, D., Chhiber, R., Usmanov, A., Chasapis, A., Qudsi, R., Bale, S.D., Bonnell, J.W., de Wit, T.D., Goetz, K., Harvey, P.R., MacDowall, R.J., Malaspina, D.M., Pulupa, M., Kasper, J.C., Korreck, K.E., Case, A.W., Stevens, M., Whittlesey, P., Larson, D., Livi, R., Klein, K.G., Velli, M., Raouafi, N.: Enhanced energy transfer rate in solar wind turbulence observed near the sun from parker solar probe. The Astrophysical Journal Supplement Series 246(2), 48 (2020). https://doi.org/10.3847/1538-4365/ab5dae
- (208) Chhiber, R., Usmanov, A.V., Matthaeus, W.H., Parashar, T.N., Goldstein, M.L.: Contextual predictions for parker solar probe. II. turbulence properties and taylor hypothesis. The Astrophysical Journal Supplement Series 242(1), 12 (2019). https://doi.org/10.3847/1538-4365/ab16d7
- (209) Coburn, J.T., Forman, M.A., Smith, C.W., Vasquez, B.J., Stawarz, J.E.: Third-moment descriptions of the interplanetary turbulent cascade, intermittency and back transfer. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 373(2041), 20140150 (2015)
- (210) Raja, K.S., Subramanian, P., Ingale, M., Ramesh, R., Maksimovic, M.: Turbulent proton heating rate in the solar wind from 5–45 r. The Astrophysical Journal 914(2), 137 (2021)
- (211) Wu, H., Tu, C., He, J., Wang, X., Yang, L.: Consistency of von karman decay rate with the energy supply rate and heating rate observed by parker solar probe. The Astrophysical Journal 926(2), 116 (2022)
- (212) Shay, M., Haggerty, C., Matthaeus, W., Parashar, T., Wan, M., Wu, P.: Turbulent heating due to magnetic reconnection. Physics of Plasmas 25(1), 012304 (2018)
- (213) Stawarz, J.E., Smith, C.W., Vasquez, B.J., Forman, M.A., MacBride, B.T.: The turbulent cascade and proton heating in the solar wind at 1 au. The Astrophysical Journal 697(2), 1119 (2009)
- (214) Zhao, L.-L., Zank, G., Telloni, D., Stevens, M., Kasper, J., Bale, S.: The turbulent properties of the sub-alfvénic solar wind measured by the parker solar probe. The Astrophysical Journal Letters 928(2), 15 (2022)
- (215) Andrés, N., Sahraoui, F., Hadid, L., Galtier, S., et al.: About the incompressible energy cascade rate in anisotropic solar wind turbulence. arXiv preprint arXiv:2112.13748 (2021)
- (216) Andrés, N., Sahraoui, F., Hadid, L., Huang, S., Romanelli, N., Galtier, S., Dibraccio, G., Halekas, J.: The evolution of compressible solar wind turbulence in the inner heliosphere: Psp, themis, and maven observations. The Astrophysical Journal 919(1), 19 (2021)
- (217) Matthaeus, W.H., Goldstein, M.L., Roberts, D.A.: Evidence for the presence of quasi-two-dimensional nearly incompressible fluctuations in the solar wind. Journal of Geophysical Research: Space Physics 95(A12), 20673–20683 (1990)
- (218) Adhikari, L., Zank, G., Hunana, P., Shiota, D., Bruno, R., Hu, Q., Telloni, D.: Ii. transport of nearly incompressible magnetohydrodynamic turbulence from 1 to 75 au. The Astrophysical Journal 841(2), 85 (2017)
- (219) Hernández, C.S., Sorriso-Valvo, L., Bandyopadhyay, R., Chasapis, A., Vásconez, C.L., Marino, R., Pezzi, O.: Impact of switchbacks on turbulent cascade and energy transfer rate in the inner heliosphere. The Astrophysical Journal Letters 922(1), 11 (2021)
- (220) David, V., Galtier, S., Sahraoui, F., Hadid, L.: Energy transfer, discontinuities, and heating in the inner heliosphere measured with a weak and local formulation of the politano–pouquet law. The Astrophysical Journal 927(2), 200 (2022)
- (221) Bowen, T.A., Mallet, A., Huang, J., Klein, K.G., Malaspina, D.M., Stevens, M., Bale, S.D., Bonnell, J.W., Case, A.W., Chandran, B.D., et al.: Ion-scale electromagnetic waves in the inner heliosphere. The Astrophysical Journal Supplement Series 246(2), 66 (2020)
- (222) Bowen, T.A., Bale, S.D., Bonnell, J., Larson, D., Mallet, A., McManus, M.D., Mozer, F.S., Pulupa, M., Vasko, I.Y., Verniero, J., et al.: The electromagnetic signature of outward propagating ion-scale waves. The Astrophysical Journal 899(1), 74 (2020)
- (223) Verniero, J., Larson, D., Livi, R., Rahmati, A., McManus, M., Pyakurel, P.S., Klein, K., Bowen, T., Bonnell, J., Alterman, B., et al.: Parker solar probe observations of proton beams simultaneous with ion-scale waves. The Astrophysical Journal Supplement Series 248(1), 5 (2020)
- (224) Malaspina, D.M., Halekas, J., Berčič, L., Larson, D., Whittlesey, P., Bale, S.D., Bonnell, J.W., de Wit, T.D., Ergun, R.E., Howes, G., et al.: Plasma waves near the electron cyclotron frequency in the near-sun solar wind. The Astrophysical Journal Supplement Series 246(2), 21 (2020)
- (225) Vech, D., Martinović, M., Klein, K.G., Malaspina, D.M., Bowen, T.A., Verniero, J.L., Paulson, K., De Wit, T.D., Kasper, J.C., Huang, J., et al.: Wave-particle energy transfer directly observed in an ion cyclotron wave. Astronomy & Astrophysics 650, 10 (2021)
- (226) Zhao, L.-L., Zank, G., He, J., Telloni, D., Adhikari, L., Nakanotani, M., Kasper, J., Bale, S.: Mhd and ion kinetic waves in field-aligned flows observed by parker solar probe. The Astrophysical Journal 922(2), 188 (2021)
- (227) Cattell, C., Breneman, A., Dombeck, J., Short, B., Wygant, J., Halekas, J., Case, T., Kasper, J., Larson, D., Stevens, M., et al.: Parker solar probe evidence for scattering of electrons in the young solar wind by narrowband whistler-mode waves. The Astrophysical journal letters 911(2), 29 (2021)
- (228) Verniero, J., Chandran, B., Larson, D., Paulson, K., Alterman, B., Badman, S., Bale, S., Bonnell, J., Bowen, T., de Wit, T.D., et al.: Strong perpendicular velocity-space diffusion in proton beams observed by parker solar probe. The Astrophysical Journal 924(2), 112 (2022)
- (229) Bowen, T.A., Squire, J., Bale, S.D., Chandran, B., Duan, D., Klein, K.G., Larson, D., Mallet, A., McManus, M.D., Meyrand, R., et al.: The in situ signature of cyclotron resonant heating. arXiv preprint arXiv:2111.05400 (2021)
- (230) Bowen, T.A., Mallet, A., Bale, S.D., Bonnell, J., Case, A.W., Chandran, B.D., Chasapis, A., Chen, C.H., Duan, D., de Wit, T.D., et al.: Constraining ion-scale heating and spectral energy transfer in observations of plasma turbulence. Physical Review Letters 125(2), 025102 (2020)
- (231) Qudsi, R.A., Bandyopadhyay, R., Maruca, B.A., Parashar, T.N., Matthaeus, W.H., Chasapis, A., Gary, S.P., Giles, B.L., Gershman, D.J., Pollock, C.J., Strangeway, R.J., Torbert, R.B., Moore, T.E., Burch, J.L.: Intermittency and ion temperature–anisotropy instabilities: Simulation and magnetosheath observation. The Astrophysical Journal 895(2), 83 (2020). https://doi.org/10.3847/1538-4357/ab89ad
- (232) Chhiber, R., Goldstein, M.L., Maruca, B.A., Chasapis, A., Matthaeus, W.H., Ruffolo, D., Bandyopadhyay, R., Parashar, T.N., Qudsi, R., de Wit, T.D., Bale, S.D., Bonnell, J.W., Goetz, K., Harvey, P.R., MacDowall, R.J., Malaspina, D., Pulupa, M., Kasper, J.C., Korreck, K.E., Case, A.W., Stevens, M., Whittlesey, P., Larson, D., Livi, R., Velli, M., Raouafi, N.: Clustering of intermittent magnetic and flow structures near parker solar probe’s first perihelion—a partial-variance-of-increments analysis. The Astrophysical Journal Supplement Series 246(2), 31 (2020). https://doi.org/10.3847/1538-4365/ab53d2
- (233) Qudsi, R.A., Maruca, B.A., Matthaeus, W.H., Parashar, T.N., Bandyopadhyay, R., Chhiber, R., Chasapis, A., Goldstein, M.L., Bale, S.D., Bonnell, J.W., de Wit, T.D., Goetz, K., Harvey, P.R., MacDowall, R.J., Malaspina, D., Pulupa, M., Kasper, J.C., Korreck, K.E., Case, A.W., Stevens, M., Whittlesey, P., Larson, D., Livi, R., Velli, M., Raouafi, N.: Observations of heating along intermittent structures in the inner heliosphere from PSP data. The Astrophysical Journal Supplement Series 246(2), 46 (2020). https://doi.org/10.3847/1538-4365/ab5c19
- (234) Sioulas, N., Velli, M., Chhiber, R., Vlahos, L., Matthaeus, W.H., Bandyopadhyay, R., Cuesta, M.E., Shi, C., Bowen, T.A., Qudsi, R.A., Stevens, M.L., Bale, S.D.: Statistical analysis of intermittency and its association with proton heating in the near-sun environment. The Astrophysical Journal 927(2), 140 (2022). https://doi.org/10.3847/1538-4357/ac4fc1
- (235) Sorriso-Valvo, L., Perrone, D., Pezzi, O., Valentini, F., Servidio, S., Zouganelis, I., Veltri, P.: Local energy transfer rate and kinetic processes: the fate of turbulent energy in two-dimensional hybrid vlasov–maxwell numerical simulations. Journal of Plasma Physics 84(2) (2018)
- (236) Chhiber, R., Matthaeus, W.H., Bowen, T.A., Bale, S.D.: Subproton-scale intermittency in near-sun solar wind turbulence observed by the parker solar probe. The Astrophysical Journal Letters 911(1), 7 (2021)
- (237) Marsch, E.: Kinetic physics of the solar corona and solar wind. Living Reviews in Solar Physics 3(1) (2006)
- (238) Verma, M.K.: Energy Transfers in Fluid Flows: Multiscale and Spectral Perspectives. Cambridge University Press, ??? (2019)
- (239) Cuesta, M.E., Chhiber, R., Roy, S., Goodwill, J., Pecora, F., Jarosik, J., Matthaeus, W.H., Parashar, T.N., Bandyopadhyay, R.: Isotropization and evolution of energy-containing eddies in solar wind turbulence: Parker solar probe, helios 1, ace, wind, and voyager 1. The Astrophysical Journal Letter (2022)
- (240) Verniero, J., Howes, G., Stewart, D., Klein, K.: Determining threshold instrumental resolutions for resolving the velocity-space signature of ion landau damping. Journal of Geophysical Research: Space Physics 126(5), 2020–028361 (2021)