Observing Strategies for the Detection of Jupiter Analogs
Abstract
To understand the frequency, and thus the formation and evolution, of planetary systems like our own solar system, it is critical to detect Jupiter-like planets in Jupiter-like orbits. For long-term radial-velocity monitoring, it is useful to estimate the observational effort required to reliably detect such objects, particularly in light of severe competition for limited telescope time. We perform detailed simulations of observational campaigns, maximizing the realism of the sampling of a set of simulated observations. We then compute the detection limits for each campaign to quantify the effect of increasing the number of observational epochs and varying their time coverage. We show that once there is sufficient time baseline to detect a given orbital period, it becomes less effective to add further time coverage – rather, the detectability of a planet scales roughly as the square root of the number of observations, independently of the number of orbital cycles included in the data string. We also show that no noise floor is reached, with a continuing improvement in detectability at the maximum number of observations tested here.
1 Introduction
As planet search efforts mature, techniques improve, and ever-larger data sets are obtained, the detection of planets like our own Jupiter is becoming more tractable. These “Jupiter analogs” are critically important for understanding the frequency of planetary systems with architectures similar to our own solar system (e.g. Cumming et al., 2008; Gould et al., 2010; Wittenmyer et al., 2011). Jupiter analogs are interesting and important for a number of reasons. Firstly, most exoplanetary systems found to date are markedly different from our own Solar system, featuring Jupiter-mass planets on short-period orbits more reminiscent of the terrestrial planets. While such systems are fascinating in their own right, it is clearly important to search for systems that more closely resemble our own. This is particularly true looking forward, when we consider the ongoing efforts of planet-search programs to find Earth-like planets that could potentially host life.
Over the years, the presence of Jupiter-analogs has been invoked as a key factor in determining the habitability of Earth-like planets (Ward & Brownlee, 2000; Greaves et al., 2004). Although the idea that Jupiter-analogs are required to shield terrestrial planets from impacts has been conclusively dismantled (e.g. Horner & Jones, 2008; Horner et al., 2010; Horner & Jones, 2012), the presence of such planets could still prove to be an important mechanism that drives the delivery of water to planets that might otherwise have formed as dry, lifeless husks. For an in-depth discussion of this idea, we direct the interested reader to p.285-6 of Horner & Jones (2010), and references therein.
Regardless of their role in ensuring (or threatening) the habitability of telluric worlds, the search for Jupiter-analogs will provide a key datum for models of planetary formation and evolution - attempting to answer the question “how common are planetary systems like our own.” To date, the most prolific means of detecting Jupiter-analog planets has been the radial-velocity method. While direct imaging and microlensing have contributed to the pool of known Jupiter analogs (e.g. Chauvin et al., 2004; Marois et al., 2010; Gaudi et al., 2008; Dong et al., 2009), those planets detected by radial velocity remain the most amenable for detailed orbital characterisation. The radial-velocity technique is well-established, having been in use by several planet-search teams for nearly 20 years. A key disadvantage of searching for Jupiter analogs in this way is that one must observe for at least a full orbital cycle to properly constrain the period and amplitude of a planet candidate.
For this sort of work, there is no substitute for time. The Anglo-Australian Planet Search (AAPS) has been in operation for nearly 14 years, and has discovered some 40 planets (e.g. Tinney et al., 2001; Butler et al., 2001; Jones et al., 2006, 2010; Tinney et al., 2011). A key strength of this program is that the AAPS has used the same instrumental setup throughout its lifetime: the UCLES spectrograph on the 3.9m Anglo-Australian Telescope. AAT+UCLES has enabled the AAPS to amass a database of velocities with precisions of 2-3 m s-1 for most of its target stars. This is exactly the type of data set required to robustly detect the signals of Jupiter-like planets in Jupiter-like orbits. The long-term velocity stability achieved by the AAPS has enabled the discovery of six such planets to date: HD 30177b (Butler et al. 2006: yr, M sin =9.7MJup) HD 160691c (McCarthy et al. 2004: yr, M sin =1.9MJup), GJ 832b (Bailey et al. 2009: yr, M sin =0.6MJup), HD 134987c (Jones et al. 2010: yr, M sin =0.8MJup), HD 142c (Wittenmyer et al. 2012: yr, M sin =5.3MJup), and HD 4732c (Sato et al. 2013: yr, M sin =2.4MJup).
Given the significant and ever-tightening constraints on large-telescope time, it is prudent to optimise the observing strategy used to detect particular classes of planets (Ford, 2008; Bottom et al., 2013). The AAPS, in recognition of its primary strength in detecting Jupiter-like planets, has recently adjusted its target list and observing strategy to be able to make meaningful, quantitative statements on the frequency of these types of planets (Wittenmyer et al., 2011). In this paper, we examine the impact of various observing strategies on the detectability of Jupiter analogs. Specifically, we ask what number and duration of observations would most efficiently enable the detection of planets with velocity amplitudes similar to that of Jupiter ( m s-1). We construct simulated data sets which build on the extant AAPS data (Section 2), and we use these results (Section 3) to draw general conclusions (Section 4) on the optimal approach for detecting Jupiter analogs in the face of extremely limited telescope time.
2 Numerical Methods
2.1 Constructing the simulated data sets
From the main AAPS sample of 250 stars, we wish to define a subsample of stars which have both low intrinsic stellar activity and a sufficient observational baseline to be useful for the detection of Jupiter analogs. Following our previous work on this subject (Wittenmyer et al., 2011), we chose those stars which have, at present, at least 30 epochs over a time baseline of at least 3000 days. We then excluded those stars which did not satisfy the criterion , an empirical relation derived from the AAPS data examined in Wittenmyer et al. (2011) which can be used as a simple estimate of whether the 12 m s-1 velocity amplitude of Jupiter would be detectable at 99% confidence. After this cut, 103 stars remained, and all further analysis was done using those data.
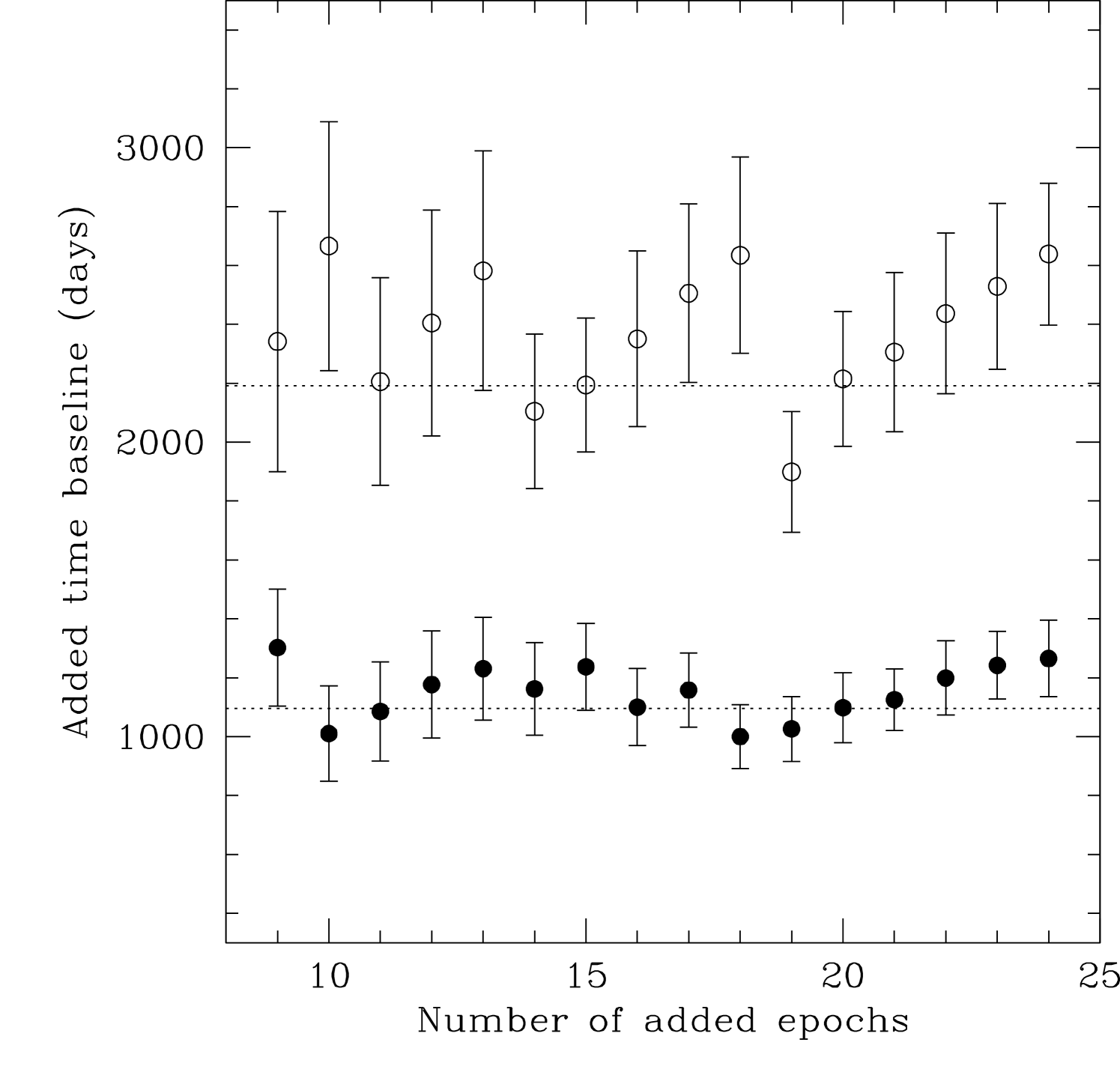
The epochs of real observational data are never purely random: stars can only be observed at night, and most targets are unobservable for a portion of the year. When combined with the exigencies of telescope scheduling (planet-search programs are usually assigned time during bright lunations) real data can contain significant gaps. To better simulate the sampling characteristics of real data, we made the following assumptions: (1) one observation in a 10-night block every 30 days (bright-time scheduling), (2) the target is unobservable for four consecutive months every year, and (3) poor weather randomly prevents the observation 33% of the time. These conditions were selected for the following reasons: (1) planet-search programs are usually allocated time in bright lunations owing to the brightness of the targets, (2) for a mid-latitude site such as the Anglo-Australian Telescope (AAT), with planet-survey targets distributed randomly in right ascension, the average target is unobservable for four months in a year111Here we define “unobservable” to mean that the target spends less than one hour at an airmass less than 2., and (3) the long-term weather conditions at the AAT yield a 33% loss rate (this “weather allowance” is accounted for in the proposal process). Using this procedure, we added simulated observations to the current AAPS data (as of 2012 July) until reaching a desired number of added data points (chosen to lie between 9 and 24222These values were chosen to reflect the minimum (1.5 epochs/yr in 6 years) and maximum (8 epochs/yr for 3 years) practical cadences for a typical shared large telescope). In the interest of informing strategic plans for planet-search programs, we investigated the effect of adding observations over two timescales: three and six years. The frequency of observations (e.g. monthly or alternate months) was adjusted so that the resulting total time baseline of new data remained approximately constant at three and six years. Figure 1 shows the time baseline added using this approach, averaged over the 103 stars. In total, 32 artificial data sets were created for each target considered here: points added over 3 and 6 year periods. The radial velocity of the simulated data point is drawn from a Gaussian distribution with a FWHM equal to the RMS of the existing data for that star. The uncertainty on the simulated radial velocity is drawn at random (with replacement) from the uncertainties of the existing real data. The result is a simulated future data set with the same properties as the original data.
2.2 Assessing Detectabilities
Throughout this work, we assessed the detectability of radial-velocity signals using the algorithm described extensively in our previous work (Wittenmyer et al., 2006, 2011). Here we only consider circular orbits (after e.g. Cumming et al. 2008), as previous work has shown that circular-orbit detection limits are a good approximation to the result that would be obtained for planets with 0.5 (Cumming & Dragomir, 2010; Wittenmyer et al., 2010, 2011). In brief, for each of 100 trial periods, a Keplerian signal is added to the data, then a Lomb-Scargle periodogram (Lomb, 1976; Scargle, 1982) is used to search for the injected signal. The radial velocity semi-amplitude of the artificial planet is increased until 100% of the signals are recovered with at least 99.9% significance at the correct period. That value of is then the detection limit for that trial period. As we are concerned with long-period planets, we only consider periods from 1000-5000 days, evenly distributed in log space. Throughout this work, the figure of merit used to assess the impact of added data is the mean detection limit averaged over 100 trial periods in the range 1000-5000 days.
3 Results
3.1 Duration of Observations
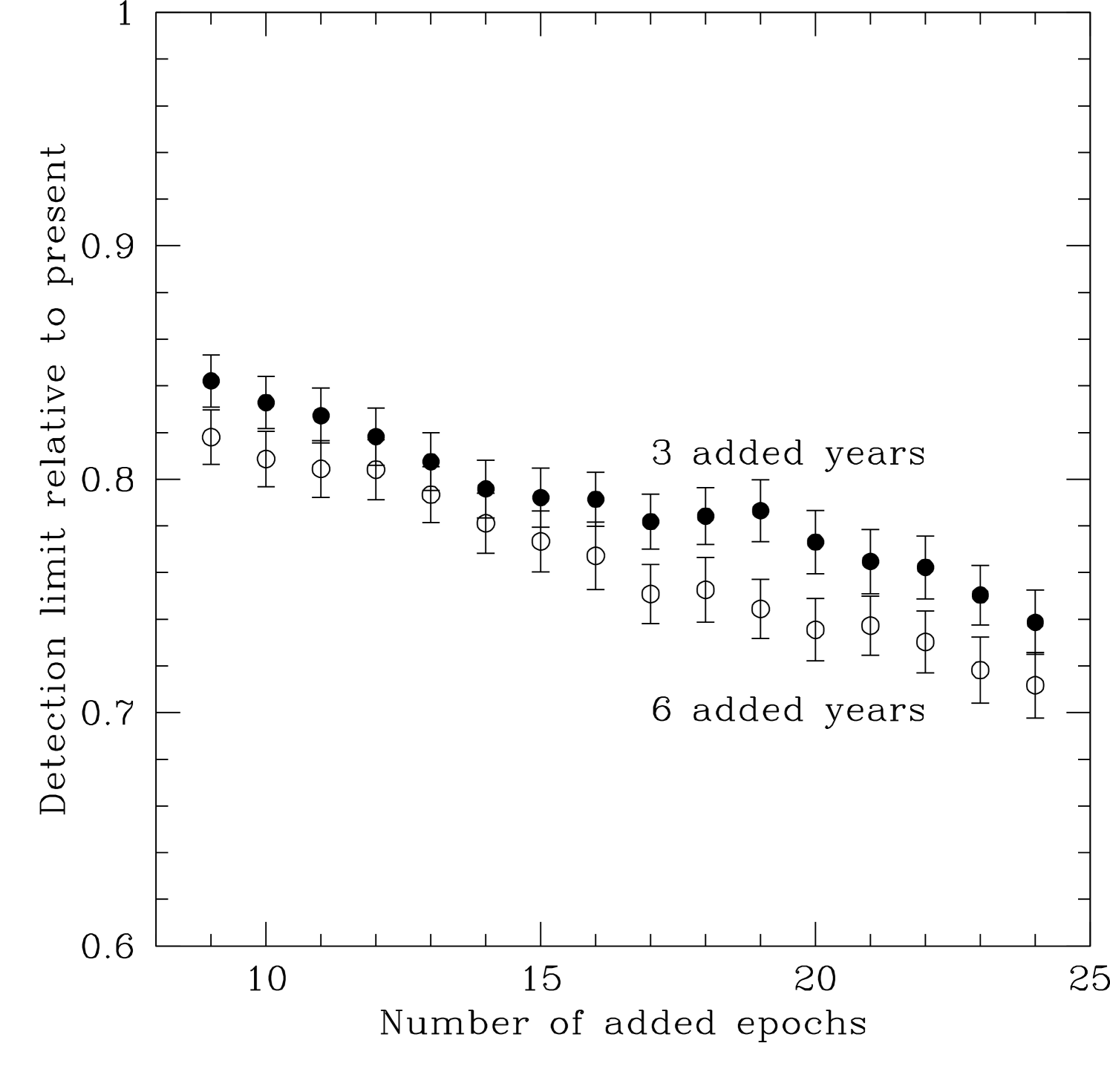
The most obvious question here is: “How does the number of added epochs affect the detectability of Jupiter analogs?” A related issue is whether there is a point of diminishing return, where adding more data or more frequent observations does not make meaningful improvements in the overall detectability. To determine the improvement to be had by various levels of observational effort, we also computed the detection limits for the 103-star sample exactly as above, but using only the existing AAPS data. This gives a “benchmark” detectability for each star, against which we can then compare the results from the simulated observations on a star-by-star basis. For each star, we divide the mean limit (averaged over periods from 1000-5000 days) by that obtained for the “benchmark” or present data set. The grand means of these ratios (averaged over the 103 stars) are plotted in Figure 2. From this figure, we can answer two questions: (1) What is the effect of adding epochs (within a fixed time), and (2) What is the impact of the observational baseline for a given number of epochs? Our results show that, for the range of added epochs simulated here, there remains a linear relationship between the number of epochs and the achievable detection limit. That is, the points shown in Figure 2 do not level off, up to 24 added epochs. On the second question, we see that there is no statistically significant difference between epochs added over 3 years and epochs added over 6 years, though this applies only for planets with days (14 years) as this is the maximum period considered in the detection-limit calculation.
3.2 Number of Observations
The results of this experiment, in which we added simulated observations to real AAPS data, show that the amount of added time coverage is less important than the number of added observations. It is worth noting here that the selected stars all had at least 3000 days (8 years) of time coverage before adding new data. Adding about 1000 or 2000 days (3 or 6 years) of new data thus has little effect on the detectability of Jupiter-like planets in the 1000-5000 day period range. We also note that the total number of epochs for each star varies greatly, with some stars at present having 35 epochs, and others having well over 100.
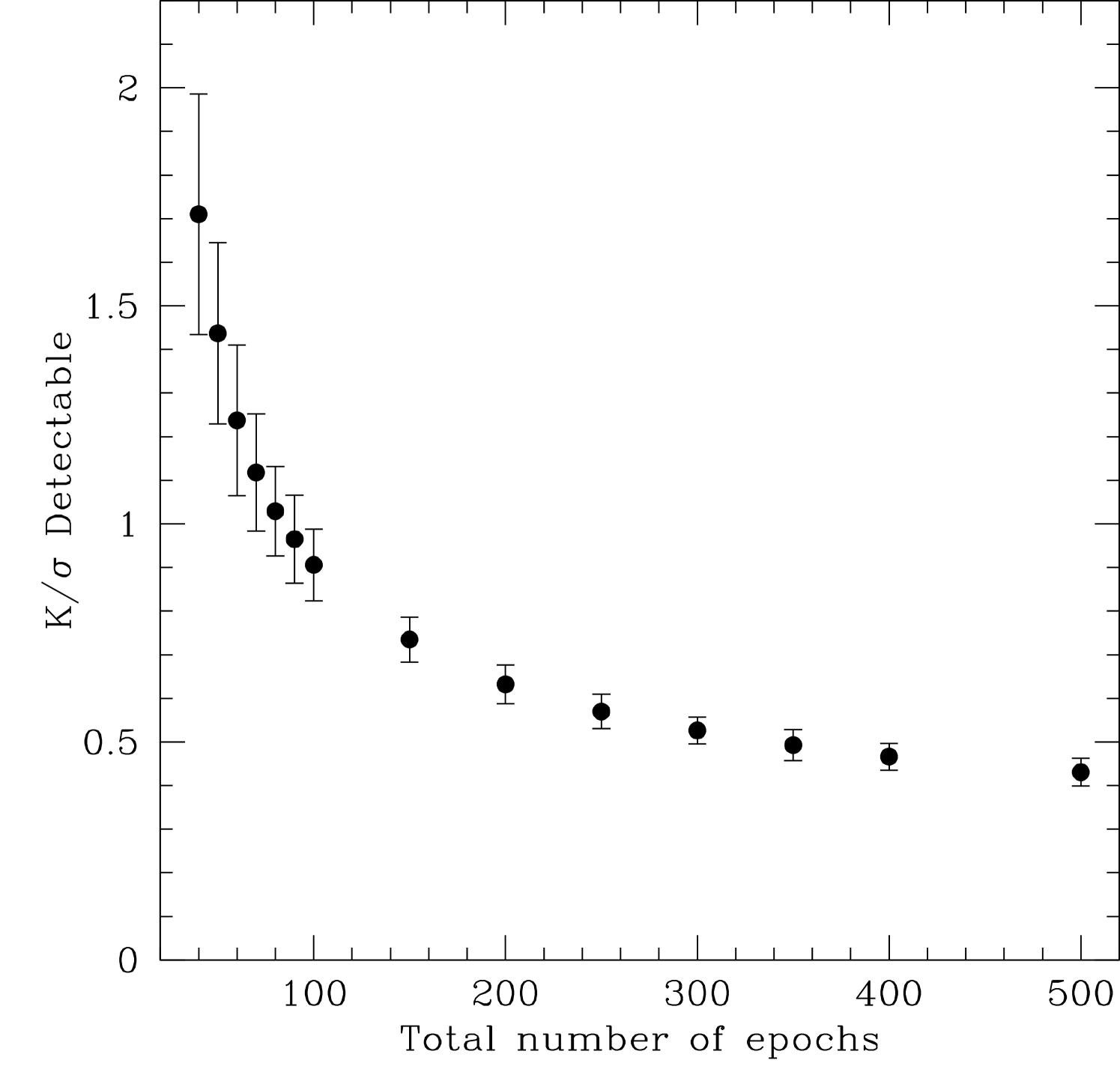
Since this could have biased the results shown in the Figure 2, we ran a second suite of simulations with slightly different initial conditions – less “realistic” but more controlled. We created wholly artificial data sets with a fixed number of observations , ranging from 40 to 500 epochs. The time sampling was done exactly as described above, with the natural result that data sets with more observations had a longer timespan. The average time coverage of the simulated data sets ranged from 7.2 years () to 92 years (). We have chosen the minimum as 40 epochs, which yields a time baseline of 7.20.7 years, consistent with the initial selection of AAPS stars used in the first suite of simulations. Also, in recognition of the fact that radial-velocity noise is almost certainly not Gaussian in nature (O’Toole et al., 2009a, b; Tuomi et al., 2013), we chose instead to draw the value of the simulated data point (and its uncertainty) from a “master” set of 531 observations from a selection of known stable stars in the AAPS catalog. Those velocities have an RMS of 3.0 m s-1, which is typical of the long-term accuracy and precision achieved by AAT/UCLES over the lifetime of the AAPS. In this way, we assure that the simulated data are purely noise, with the characteristics of velocity noise from actual observed stars. The result is 100 simulated data sets each with epochs, for between 40 and 500. We computed the detection limits as described above, and calculated the mean velocity amplitude averaged over 100 trial periods for each data set, again averaging over periods from 1000-5000 days. Trial periods for which all simulated planets were not detected were ignored. Table 1 and Figure 3 show the results, where we have averaged the mean from each data set over all 100 sets at each value of .
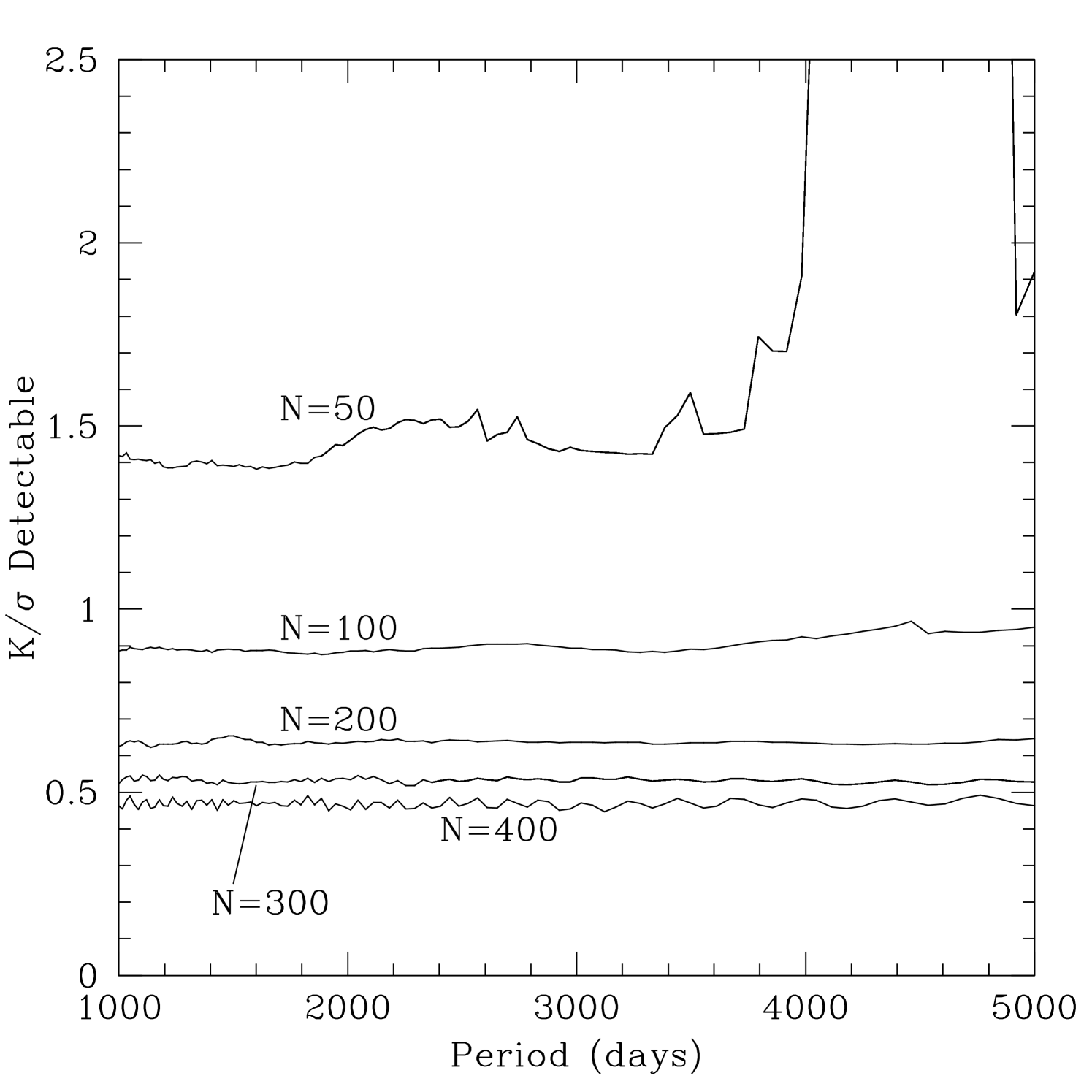
We see from Table 1 and Figure 3 that the detection limit scales approximately as , with the greatest marginal improvement occurring when the total duration extends beyond 4000 days (i.e. for ). This is the expected result for data consisting of Gaussian (white) noise (e.g. Cochran & Hatzes 1996); for the purposes of long-period planet detection, the radial-velocity noise distribution may be closer to Gaussian than is commonly expected. Up to the limit of our tests, , no noise floor is reached - the detectabilities continue to improve as . We emphasize that this result applies for planets in the period range we have tested here: between 1000 and 5000 days. Obviously, continuing to observe a given star indefinitely would permit the detection of arbitrarily long periods shorter than the total duration of observations. The period dependence of our results is shown in Figure 4. Obviously, for the case, where the total time coverage is only about 9 years (3300 days), periods substantially longer than this baseline are virtually undetectable. This artifact disappears once the time coverage exceeds the 5000-day maximum trial period, and we see no significant period dependence for the larger- trials.
The mean detection limit drops below the 3.0 m s-1 scatter of the input data after about 80 points (Figure 3, and reaches 0.5 when 300-350 epochs are obtained. Our result is applicable to other data sets with different noise properties – the detection limit would then simply scale with the overall noise. This can be seen from recent HARPS results, where the lowest-amplitude planetary signals are indeed at levels consistent with our results in Figure 3. For example, HD 10180b has 0.62 with measurements (Lovis et al., 2011). Similarly, Pepe et al. (2011) report HD 20794c with 0.68 and measurements. Because most radial-velocity planet search programs on shared large telescopes have similar sampling constraints, our results can thus be applied to other data sets by scaling the noise accordingly.
4 Conclusions
Taken together, the tests we have performed can inform the strategies used by long-running radial-velocity planet search programmes such as the AAPS, in order to make best use of limited telescope time to efficiently detect (or rule out) Jupiter-like planets. We have shown that, once there is sufficient observational baseline to detect long-period Jupiter analogs, there is not much added benefit to extending that time base (except to detect ever-longer periods, e.g. Saturn analogs with 30-year periods). That is, for a Keplerian velocity signal with a given orbital period and amplitude , including more orbital cycles in the observed data does not have a significant effect on the detectability of that signal.
We have also performed detailed simulations of radial-velocity observations, sampled according to a realistic schedule and with noise characteristics identical to actual data from the Anglo-Australian Planet Search. Those simulations showed that the Keplerian velocity amplitude detectable from a data set scales approximately as , to the maximum tested. That is, the radial-velocity noise may be closer to white than one might have expected.
We note, however, that for extremely low-amplitude signals such as those detected for Alpha Centauri B (Dumusque et al., 2012) and Tau Ceti (Tuomi et al., 2013), stellar noise at the m s-1 level has a critical impact on the detectability of such small signals. The red noise introduced by star spots, differential rotation, and convective blueshift is of an amplitude too small to be especially relevant to this work. In this work, we have concentrated on the detectability of Jupiter-like planets with relatively large amplitudes of order 10 m s-1.
We conclude that it remains worthwhile to continue radial-velocity observations of suitably stable stars to robustly detect or exclude long-period giant planets. However, the targets must be chosen carefully to ensure that the 10-15 m s-1 signals of Jupiter-like planets are reliably detectable. For ever-longer orbital periods, approaching Saturn-like orbits (30 yr), opportunities are now emerging to combine the complementary strengths of legacy radial-velocity data with rapidly improving direct-imaging technology from new instruments such as the Gemini Planet Imager. The powerful combination of these two approaches will soon yield direct measurements of the occurrence rate of Jupiter analogs, and the first detailed characterisation of such objects orbiting nearby Sun-like stars.
References
- Bailey et al. (2009) Bailey, J., Butler, R. P., Tinney, C. G., et al. 2009, ApJ, 690, 743
- Bottom et al. (2013) Bottom, M., Muirhead, P. S., Johnson, J. A., & Blake, C. H. 2013, arXiv:1302.3910
- Butler et al. (2001) Butler, R. P., Tinney, C. G., Marcy, G. W., et al. 2001, ApJ, 555, 410
- Butler et al. (2006) Butler, R. P., Wright, J. T., Marcy, G. W., et al. 2006, ApJ, 646, 505
- Chauvin et al. (2004) Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29
- Cochran & Hatzes (1996) Cochran, W. D., & Hatzes, A. P. 1996, Ap&SS, 241, 43
- Cumming & Dragomir (2010) Cumming, A., & Dragomir, D. 2010, MNRAS, 401, 1029
- Cumming et al. (2008) Cumming, A., Butler, R. P., Marcy, G. W., Vogt, S. S., Wright, J. T., & Fischer, D. A. 2008, PASP, 120, 531
- Dong et al. (2009) Dong, S., Bond, I. A., Gould, A., et al. 2009, ApJ, 698, 1826
- Dumusque et al. (2012) Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207
- Ford (2008) Ford, E. B. 2008, AJ, 135, 1008
- Gaudi et al. (2008) Gaudi, B. S., Bennett, D. P., Udalski, A., et al. 2008, Science, 319, 927
- Gould et al. (2010) Gould, A., Dong, S., Gaudi, B. S., et al. 2010, ApJ, 720, 1073
- Greaves et al. (2004) Greaves, J. S., Wyatt, M. C., Holland, W. S., & Dent, W. R. F. 2004, MNRAS, 351, L54
- Horner & Jones (2008) Horner, J., & Jones, B. W. 2008, International Journal of Astrobiology, 7, 251
- Horner & Jones (2010) Horner, J., & Jones, B. W. 2010, International Journal of Astrobiology, 9, 273
- Horner et al. (2010) Horner, J., Jones, B. W., & Chambers, J. 2010, International Journal of Astrobiology, 9, 1
- Horner & Jones (2012) Horner, J., & Jones, B. W. 2012, International Journal of Astrobiology, 11, 147
- Jones et al. (2010) Jones, H. R. A., et al. 2010, MNRAS, 403, 1703
- Jones et al. (2006) Jones, H. R. A., Butler, R. P., Tinney, C. G., et al. 2006, MNRAS, 369, 249
- Lomb (1976) Lomb, N. R. 1976, Ap&SS, 39, 447
- Lovis et al. (2011) Lovis, C., Ségransan, D., Mayor, M., et al. 2011, A&A, 528, A112
- Marois et al. (2010) Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080
- McCarthy et al. (2004) McCarthy, C., Butler, R. P., Tinney, C. G., et al. 2004, ApJ, 617, 575
- O’Toole et al. (2009a) O’Toole, S. J., Tinney, C. G., Jones, H. R. A., et al. 2009a, MNRAS, 392, 641
- O’Toole et al. (2009b) O’Toole, S. J., Jones, H. R. A., Tinney, C. G., et al. 2009b, ApJ, 701, 1732
- Pepe et al. (2011) Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58
- Sato et al. (2013) Sato, B., Omiya, M., Wittenmyer, R. A., et al. 2013, ApJ, 762, 9
- Scargle (1982) Scargle, J. D. 1982, ApJ, 263, 835
- Tinney et al. (2001) Tinney, C. G., Butler, R. P., Marcy, G. W., et al. 2001, ApJ, 551, 507
- Tinney et al. (2011) Tinney, C. G., Butler, R. P., Jones, H. R. A., Wittenmyer, R. A., O’Toole, S., Bailey, J., & Carter, B. D. 2011, ApJ, 727, 103
- Tuomi et al. (2013) Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, in press. arXiv:1212.4277
- Ward & Brownlee (2000) Ward, P., & Brownlee, D. 2000, Rare earth : why complex life is uncommon in the universe / Peter Ward, Donald Brownlee. New York : Copernicus, c2000.
- Wittenmyer et al. (2006) Wittenmyer, R. A., Endl, M., Cochran, W. D., Hatzes, A. P., Walker, G. A. H., Yang, S. L. S., & Paulson, D. B. 2006, AJ, 132, 177
- Wittenmyer et al. (2010) Wittenmyer, R. A., O’Toole, S. J., Jones, H. R. A., Tinney, C. G., Butler, R. P., Carter, B. D., & Bailey, J. 2010, ApJ, 722, 1854
- Wittenmyer et al. (2011) Wittenmyer, R. A., Tinney, C. G., O’Toole, S. J., Jones, H. R. A., Butler, R. P., Carter, B. D., & Bailey, J. 2011, ApJ, 727, 102
- Wittenmyer et al. (2012) Wittenmyer, R. A., Horner, J., Tuomi, M., et al. 2012, ApJ, 753, 169
- Wright et al. (2011) Wright, J. T., Fakhouri, O., Marcy, G. W., et al. 2011, PASP, 123, 412
| Mean (m s-1) | |||
|---|---|---|---|
| 40 | 5.110.82 | ||
| 50 | 4.330.63 | 0.85 | 0.89 |
| 60 | 3.660.51 | 0.84 | 0.91 |
| 70 | 3.310.40 | 0.91 | 0.93 |
| 80 | 3.080.31 | 0.93 | 0.94 |
| 90 | 2.860.30 | 0.93 | 0.94 |
| 100 | 2.670.24 | 0.94 | 0.95 |
| 150 | 2.210.16 | 0.83 | 0.82 |
| 200 | 2.010.14 | 0.86 | 0.87 |
| 250 | 1.690.12 | 0.89 | 0.89 |
| 300 | 1.580.09 | 0.94 | 0.91 |
| 350 | 1.460.11 | 0.92 | 0.93 |
| 400 | 1.400.09 | 0.95 | 0.94 |
| 500 | 1.280.10 | 0.91 | 0.89 |