Occupancy distributions of homogeneous queueing systems under opportunistic scheduling^††thanks: An earlier version of this manuscript appeared at the Information Theory and Applications Workshop, UCSD, 2008.

We analyze a queueing system that arises under opportunistic scheduling of packet transmissions from a collection of queues with time-varying service rates. The system of interest is motivated by cellular data communications in which a single transceiver serves multiple mobile stations through distinct channels. Transmission scheduling has been well-studied in this context under the guiding principle of opportunism, which broadly refers to exploiting channel variations to maximize transmission capacity in the long term. In this we paper consider two generic opportunistic scheduling policies and obtain asymptotically exact descriptions of the resulting queue length distributions in symmetric systems of statistically identical queues.

Explicit analysis of queue lengths under opportunistic scheduling is generally difficult due to model complexities and lack of closed-form expressions. In related work Tassiulas and Ephremides [10] considered a queueing system under an on/off channel model in which each queue is independently either connected, and in turn it is eligible for service at a standard rate, or disconnected and it cannot be serviced. It is shown that transmitting from a longest connected queue stabilizes queue lengths if that is at all feasible, and that it minimizes occupancy of symmetric systems in which queues have identical load and channel statistics. This policy is coined LCQ. Explicit description of queue length distributions under LCQ is not available, but several bounds for mean packet delay are obtained in [3, 6] for LCQ and some of its variants. In more general models that admit multiple transmission rates and simultaneous transmissions, max-weight scheduling policies and their variations are shown in [9, 7] to asymptotically minimize a range of occupancy measures along a certain heavy-traffic limit. In the special case when one queue can transmit at a time, max-weight transmits from a queue that maximizes the product of instantaneous queue length and transmission rate. Tails of queue length distributions under such policies are studied in [8, 12] via large deviations analysis.

Here we consider a system of $n$ queues under an on/off channel model in which each queue is connected independently with probability $q\in(0,1]$. A continuous-time Markovian model is adopted where packet transmission rate is $n$ and packet arrival rate is $\lambda<1$ per queue. It can be seen that $\lambda$ is also the load factor of the system; hence the condition $\lambda<1$ is necessary to have positive-recurrent queue lengths. We analyze this system for large values of the system size $n$, under the LCQ scheduling policy and under its low-complexity variant, namely $LCQ(d)$, that transmits from a longest queue within $d\geq 1$ randomly selected connected queues. It is apparent that LCQ($d$) is not particularly suitable for non-symmetric systems, yet our goal here is to obtain a generic evaluation of its underlying principle, which may be tailored to specific circumstances.

We establish that as the system size $n$ increases equilibrium distribution of queue occupancies under the LCQ policy converges to the deterministic distribution centered at 0. Hence asymptotically almost all queues are empty in equilibrium. The number of queues with one packet is $\Theta(1)$ and the number of queues with more than one packet is $o(1)$ as $n\rightarrow\infty$. In particular maximum queue size tends to one. The total number of packets in the system is therefore given by the number of nonempty queues, and this number is shown to have the same equilibrium distribution as the positive-recurrent birth-death process with birth rate $\lambda$ and death rate $1-(1-q)^{j}$ at state $j\in\mathbb{Z}_{+}$. Note that the latter rate is equal to the probability of having at least one connected queue within a given set of $j$ queues, and that the nature of the total system occupancy may be anticipated once maximum queue size is determined to be one. The obtained description leads to asymptotic mean packet delay via Little’s law as the rate of packet arrivals to the system is readily seen to be $n\lambda$.

The analysis technique applied to LCQ can be extended, although with excessive tediousness, to symmetric max-weight policies in cases when each queue can be serviced independently at rate $nR$ for some random variable $R$. Above conclusions about LCQ offer substantial insight about queue occupancies in that more general setting. Namely if $R$ exceeds $\lambda$ with positive probability (note that this condition is necessary for positive recurrence of queue lengths), then stochastic coupling with a related LCQ system yields that the maximum queue length in equilibrium tends to 1 as $n\rightarrow\infty$. In turn, equilibrium distribution of total system occupancy should be expected to resemble that of a birth-death process with birth rate $\lambda$ and death rate $E[\max\{R_{1},R_{2},\cdots,R_{j}\}]$ at state $j$, where $R_{1},R_{2},\cdots,R_{j}$ are independent copies of $R$.

We obtain the equilibrium distribution $\{p_{k}\}_{k=0}^{\infty}$ of individual queue occupancy under the LCQ($d$) policy in the limit as $n\rightarrow\infty$. Specifically $p_{k}=v^{*}_{k}-v^{*}_{k+1}$ where $v^{*}_{0}=1$ and

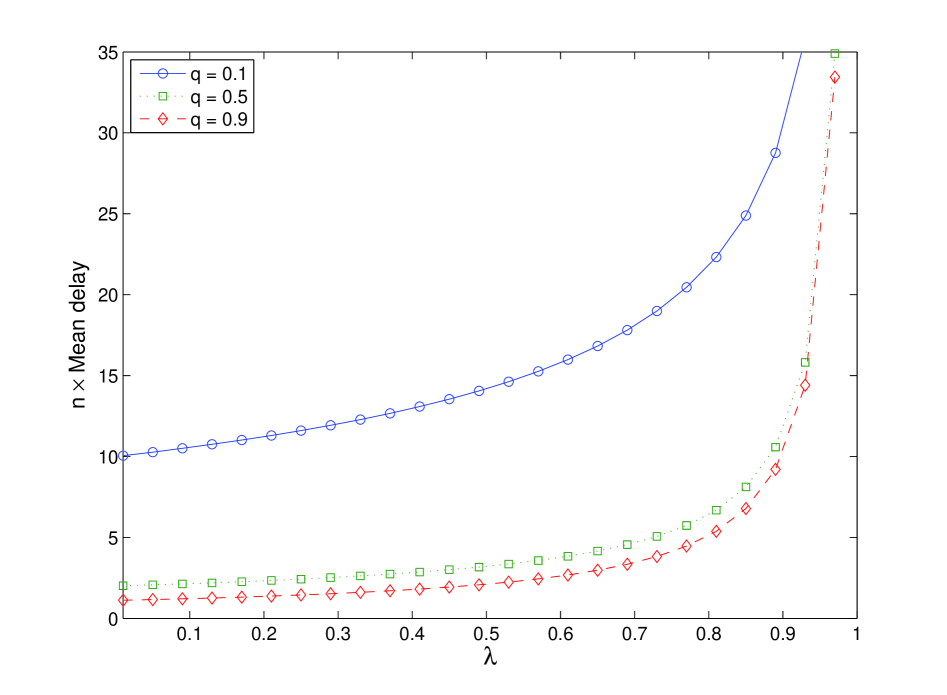
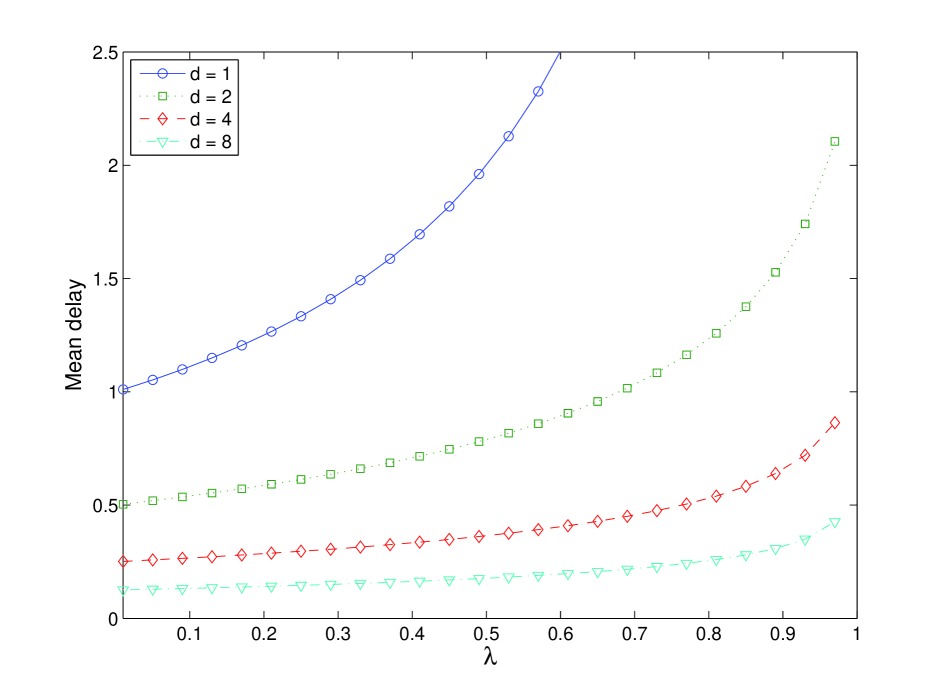
This distribution is shown to have tails that decay as $\Theta((\lambda/d)^{k})$ as queue size $k\rightarrow\infty$. Hence, in terms of tail occupancy probabilities, the choice parameter $d$ has the equivalent effect of reducing the system load by the same factor. Yet, for any fixed $d$, system occupancy under LCQ($d$) is larger than that of LCQ by a factor of order $n$. Numerical values of asymptotic mean packet delay under LCQ and LCQ($d$) are illustrated in Figure 1. We also conclude that if $d$ is allowed to depend on $n$ so that $d\rightarrow\infty$ but $d/n\rightarrow 0$ then order of the alluded disparity reduces to $n/d$. This suggests that for moderate values of $d$ and $n$ LCQ($d$) and LCQ may be expected to have comparable packet delay.

The present analysis is based on approximating system dynamics via asymptotically exact differential representations that amount to functional laws of large numbers. Hence besides the mentioned equilibrium properties the paper also describes transient behavior of queue occupancies. The present analysis of LCQ($d$) is inspired by the work of Vvedenskaya et al. [11] which concerns an analogue of this policy that arises in routing and load balancing. It should perhaps be noted that the choice parameter $d$ appears to have a substantially more pronounced effect in the routing context. Our conclusions about the LCQ policy require a more elaborate technical approach. Here we apply a technique due to Kurtz [5] to obtain a suitable asymptotic description of the system. Related applications of this technique can be found in [1, 4, 13].

The rest of this paper is organized as follows. We continue in Section 2 with formal description of the model and the notation adopted in the paper. The policies LCQ$(d)$ and LCQ are analyzed respectively in Sections 3 and 4. The paper concludes with final remarks in Section 5.

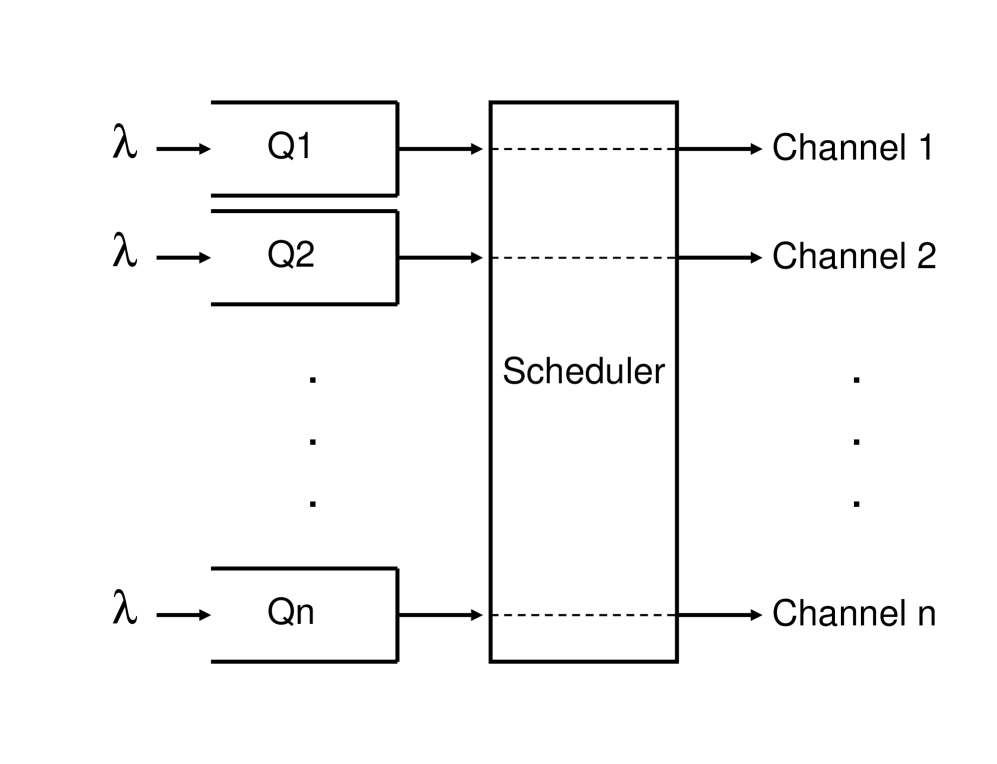
Consider $n$ queues each serving a dedicated stream of packet arrivals as illustrated in Figure 2. Arrivals of each stream occur according to an independent Poisson process with rate $\lambda<1$ packets per unit time and transmission time of each packet is exponentially distributed with mean $n^{-1}$, chosen independently of the prior history of the system. Each queue is serviced by a designated channel but at most one channel can transmit at a time. Channel states fluctuate randomly and each channel is eligible for transmission with probability $q\in(0,1]$ independently of other channels. Queues with eligible channels are called connected. We assume that channel states remain constant during packet transmission and that they are determined anew, independently of each other and of the current queue lengths, just before the next transmission decision.

Let $m_{k}(t)$ denote the number of queues with $k$ or more packets at time $t$, and let

be the fraction of such queues in the system. In particular

the sequence $\{1-u_{k}(t)\}_{k=0}^{\infty}$ is the empirical cumulative distribution function of queue occupancies, and $\sum_{k\geq 1}u_{k}(t)$ is the empirical average queue occupancy in the system at time $t$. We denote by $P_{n}$ and $E_{n}$ respectively probabilities and expectations associated with system size $n$. In particular if $q_{i}(t)$ denotes the occupancy of the $i$-th queue at time $t$ then by the symmetry of the model

Let $U$ denote the collection of sequences $\mathbf{u}=\{u_{k}\}_{k=0}^{\infty}$ that satisfy relation (1), and endow $U$ with metric $\rho$ that is defined by

Note that convergence in $U$ is equivalent to coordinate-wise convergence, and that $U$ is compact as each coordinate lies in a compact interval.

For each time $t$ let $\mathbf{u}(t)$ denote the sequence $\{u_{k}(t)\}_{k=0}^{\infty}$. We represent the trajectory $(\mathbf{u}(t):t\geq 0)$ by the symbol $\mathbf{u}(\cdot)$, and say that $\mathbf{u}(\cdot)$ converges to a given trajectory $\mathbf{v}(\cdot)$ uniformly on compact time-sets (uoc) if for all $t>0$

We focus on LCQ($d$) which randomly and independently selects $d$ connected queues and transmits from a longest queue within this collection. For convenience of analysis we assume that repetitions are allowed in the selection procedure, and that if all selected queues are empty or no connected queue exists at a scheduling instant then the scheduler makes a new selection after idling for the transmission time of a hypothetical packet. This latter assumption can be seen to imply that scheduling instances form a Poisson process of rate $n$.

For $k=1,2,3,\cdots$ let $\mathbf{e}_{k}=\{e_{k}(i)\}_{i=0}^{\infty}$ where

Here and in the rest of the paper $1\{\cdot\}$ denotes 1 if its argument is true and 0 otherwise. Jumps of the process $\mathbf{u}(\cdot)$ are of the form $\pm n^{-1}\mathbf{e}_{k}$ for some $k$. Namely $\mathbf{u}(\cdot)$ changes by $+n^{-1}\mathbf{e}_{k}$ whenever some queue with exactly $k-1$ packets has a new arrival, and by $-n^{-1}\mathbf{e}_{k}$ whenever a packet transmission is scheduled from a queue with exactly $k$ packets. The number of queues with $k-1$ packets at time $t$ is given by $n(u_{k-1}(t)-u_{k}(t))$; hence the former event occurs at instantaneous rate $n\lambda(u_{k-1}(t)-u_{k}(t))$. The latter event occurs if and only if, upon completion of a packet transmission, $(i)$ there exists a connected queue and $(ii)$ the scheduler inspects at least one connected queue with $k$ packets but none with more than $k$ packets. To determine the instantaneous rate of this event let $\tau$ be a scheduling instant and let

Namely $\alpha_{n}$ is the probability that there exists a connected queue at time $\tau$. Since channel states are assigned independently of queue lengths at time $\tau$, a connected queue at this time has strictly less than $k$ packets with probability $1-u_{k}(\tau)$. Therefore, given that a connected queue exists, the maximum queue length inspected by the scheduler is equal to $k$ with (conditional) probability $(1-u_{k+1}(\tau))^{d}-(1-u_{k}(\tau))^{d}$. Since scheduling instants occur at constant rate $n$, instantaneous rate of transmissions from a queue of size $k$ is $n\alpha_{n}((1-u_{k+1}(t))^{d}-(1-u_{k}(t))^{d})$. In particular $\mathbf{u}(\cdot)$ is a time-homogeneous Markov process whose generator can be sketched as

It offers some convenience in the subsequent discussion to represent the process $\mathbf{u}(\cdot)$ via the “random time change” construction of [2, Chapter 6]. Namely

where $A_{k-1}(\cdot),~D_{k}(\cdot)$, $k=1,2,\cdots$, are mutually independent Poisson processes each with unit rate. In informal terms, the processes $A_{k}(\cdot)$ and $D_{k}(\cdot)$ clock respectively arrivals to and departures from some queue with length $k$, and the construction (3) is based on suitably expediting these processes to match the instantaneous transition rates given in (2). Martingale decomposition of the Poisson processes used in (3) yields

where $\mbox{\boldmath$\varepsilon$}(t)=\{\varepsilon_{k}(t)\}_{k=0}^{\infty}$ is such that each coordinate process $\varepsilon_{k}(\cdot)$ is a real-valued martingale adapted to the filtration generated by $\mathbf{u}(\cdot)$.

Let $U_{o}$ denote the set of system states in which average queue occupancy is finite. That is,

Let $\mathbf{v}^{*}=\{v^{*}_{k}\}_{k=0}^{\infty}\in U$ be defined by setting $v^{*}_{0}=1$ and

Since $1-\sqrt[d]{1-\lambda v^{*}_{k-1}}\leq\lambda v^{*}_{k-1}$ it follows that $v^{*}_{k}\leq\lambda^{k}$; in particular $\mathbf{v}^{*}\in U_{o}$. It can be readily verified by substitution that $\mathbf{v}^{*}$ is an equilibrium point for the differential system (5). The following lemma establishes that $\mathbf{v}^{*}$ is the unique stable equilibrium for trajectories that start in $U_{o}$.

We provide a proof based on the following auxiliary result:

Theorem 5, which establishes convergence over finite time intervals, is complemented next by showing that equilibrium distribution of $\mathbf{u}(\cdot)$ converges as $n\rightarrow\infty$ to the deterministic measure concentrated at $\mathbf{v}^{*}$.

Suppose that (11) is false so that for some infinite subsequence $\{n^{\prime}\}$ of $\{n\}$ and some $\delta>0$

Due to Lemma 7 and compactness of $U_{o,\lambda}$ one can choose $t(\varepsilon)$ such that if $\mathbf{v}(0)\in U_{o,\lambda}$ then $\rho(\mathbf{v}(t),\mathbf{v}^{*})<\varepsilon/2$ for $t\geq t(\varepsilon)$. Let $\mathbf{u}(0)$ have the same distribution as $\mathbf{u}^{*}$ and let $\mathbf{v}(0)=\mathbf{u}(0)$. By Theorem 5 there is a further subsequence $\{n^{\prime\prime}\}$ of $\{n^{\prime}\}$ such that $P_{n^{\prime\prime}}(\rho(\mathbf{u}(t(\varepsilon)),\mathbf{v}(t(\varepsilon)))>\varepsilon/2)<\delta$ whenever $n^{\prime\prime}$ is large enough. Since $P_{n^{\prime\prime}}(\mathbf{u}^{*}\in U_{o,\lambda})=1$, the choice of $t(\varepsilon)$ implies that $P_{n^{\prime\prime}}(\rho(\mathbf{u}(t(\varepsilon)),\mathbf{v}^{*})>\varepsilon)<\delta$ for those values of $n^{\prime\prime}$. However $\mathbf{u}(t(\varepsilon))$ and $\mathbf{u}^{*}$ have identical distributions as the latter is in equilibrium; leading to a contradiction with (12). Hence no sequence $\{n^{\prime}\}$ and constant $\delta>0$ satisfy (12); so (11) holds. By definition of $\rho$ equality (11) implies that each entry $u^{*}_{k}$ of $\mathbf{u}^{*}$ converges in probability to the constant $v^{*}_{k}$; since $0\leq u^{*}_{k}\leq 1$, so does $E_{n}[u_{k}^{*}]$. $\bf\Box$

We conclude the discussion of LCQ($d$) with a relationship between $d$ and the tail probabilities of equilibrium queue occupancy:

Given $\mathbf{m}(\tau)$ at a scheduling instant $\tau$, the maximum occupancy over all connected queues at time $\tau$ is equal to $k=1,2,\cdots$ with probability $(1-q)^{m_{k+1}(\tau)}-(1-q)^{m_{k}(\tau)}$; hence under the LCQ policy $\mathbf{u}(\cdot)$ is a time-homogenous Markov process with jump rates

This process can be constructed as in Section 3, so that

where $\varepsilon_{k}(\cdot)$ is a martingale that vanishes as $n\rightarrow\infty$. The sequence of processes $\mathbf{u}(\cdot):n=1,2,\cdots$ converges in distribution along subsequences of $\{n\}$, but identifying a limit is relatively more involved than for the LCQ$(d)$ policy since the process $\mathbf{m}(\cdot)$ fluctuates persistently for all values of $n$ and the integrand in (20) does not converge. Rather than this integrand, here we study the behavior of the integral in (20) via an averaging technique due to Kurtz [5]. In reading this section the reader may find it helpful to consult related applications of this technique in [1, 4, 13].

Let $\Omega$ denote the set of sequences $\mbox{\boldmath$\omega$}=\{\omega_{k}\}_{k=0}^{\infty}$ such that $\omega_{k}\in\mathbb{Z}_{+}\cup\{\infty\}$, $\omega_{0}=\infty$, and $\omega_{k}\geq\omega_{k+1}$. Define the mapping $h:\Omega\mapsto[0,1]^{\infty}$ by setting

with the understanding that $1+\infty=\infty$ and $1/\infty=0$. Let $\Omega$ be endowed with metric $\rho_{o}$ defined by

In particular $\Omega$ is compact with respect to the induced topology. We denote by $\mathcal{L}$ the collection of measures $\mu$ on the product space $[0,\infty)\times\Omega$ such that $\mu([0,t)\times\Omega)=t$ for each $t>0$. Let $\mathcal{L}$ be endowed with the topology corresponding to weak convergence of measures restricted to $[0,t)\times\Omega$ for each $t$. Since $\Omega$ is compact, so is $\mathcal{L}$ due to Prohorov’s Theorem.

Let $\xi$ be a random member of $\mathcal{L}$ defined by

Here $\mathcal{B}(\Omega)$ denotes Borel sets of $\Omega$. Note that equality (20) can be expressed in terms of $\xi$ as

where

Compactness of $\mathcal{L}$ implies that each subsequence of $\{n\}$ has a further subsequence along which $\xi$ converges in distribution. This property is also possessed by $\mathbf{u}(\cdot)$, and therefore by the pair $(\mathbf{u}(\cdot),\xi)$.

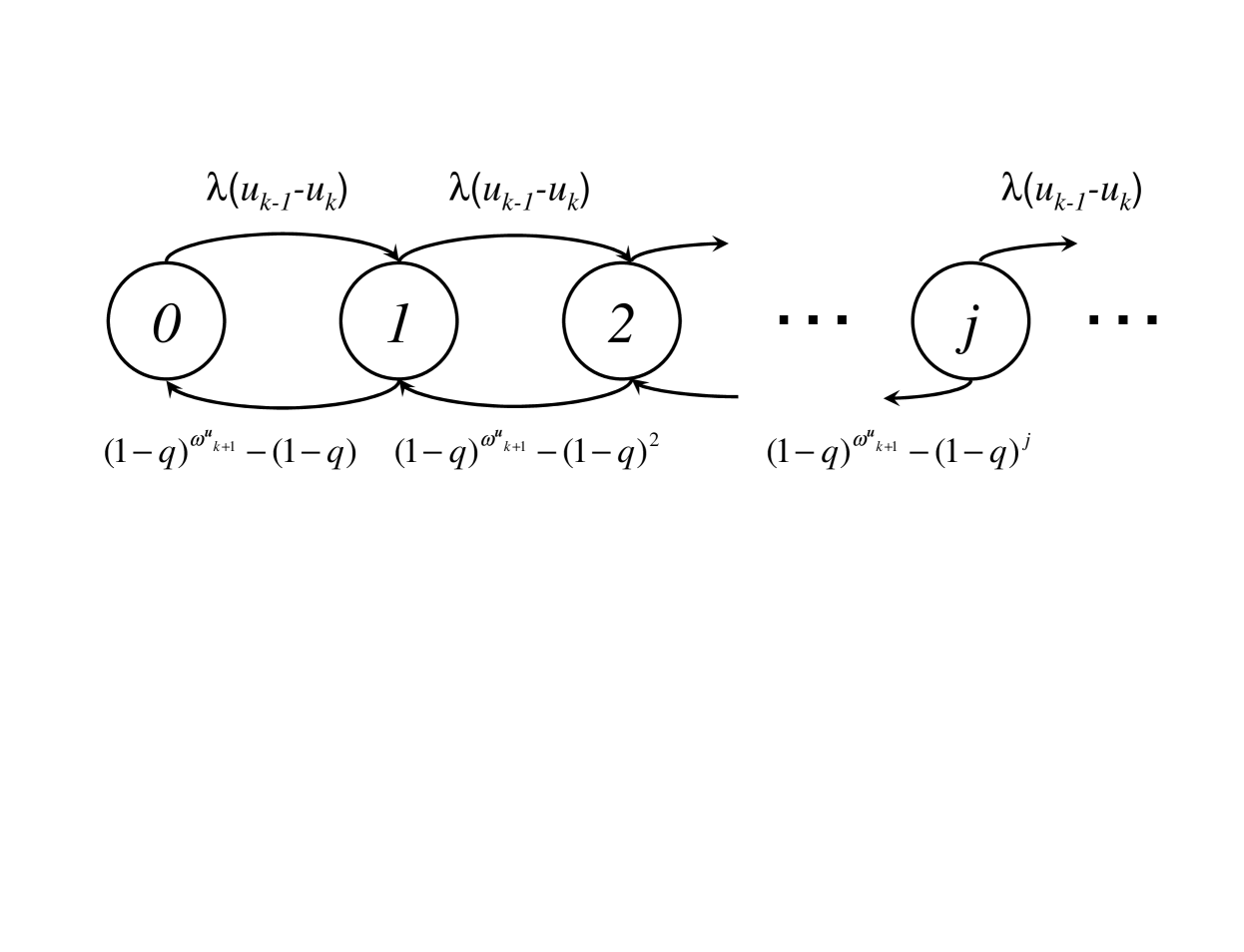
The following definition is useful in characterizing possible limits of $(\mathbf{u}(\cdot),\xi)$: For fixed $\mathbf{u}\in U$ let $\omega^{\mathbf{u}}(\cdot)$ denote the Markov process with states in $\Omega$ and with the following transition rates:

See Figure 3 for a partial illustration of this process. The process $\omega^{\mathbf{u}}(\cdot)$ bears a certain resemblance to $\mathbf{m}(\cdot)=n\mathbf{u}(\cdot)$, which can be observed by inspecting the generators (19) and (21), though it should be noted that in (21) $\mathbf{u}=\{u_{k}\}_{k=0}^{\infty}$ is a constant and has no binding to instantaneous values of $\omega^{\mathbf{u}}(\cdot)$. We also point out that $\omega^{\mathbf{u}}(\cdot)$ evolves on a compactified state space and it is reducible due to the states that involve $\infty$; hence it has multiple equilibrium distributions in general.

Let $\mathcal{F}$ denote the collection of bounded continuous functions $f:\Omega\mapsto\mathbb{R}$ such that $f(\mbox{\boldmath$\omega$})$ depends on a finite number of entries in the sequence $\mbox{\boldmath$\omega$}=\{\omega_{k}\}_{k=0}^{\infty}\in\Omega$. Given $f\in\mathcal{F}$ define the function $G^{f}:\Omega\times U\mapsto\mathbb{R}$ by setting