On computing sets of integers with maximum number of pairs summing to powers of 2

In April 2021, Dan Ullman and Stan Wagon in the “Problem of the Week 1321” [3] defined a function $f(A)$ of a finite set $A$ of integers as the number of $2$-element subsets of $A$ that sum to a power of $2$. They gave an example $f\big{(}\{-1,3,5\}\big{)}=3$ and further defined a function $g(n)$ as the maximum of $f(A)$ over all $n$-element sets $A$. The problem asked for a proof that $g(10)\geq 14$, which was quickly improved to $g(10)\geq 15$ by the readers.

It was noted that the problem has a natural interpretation as finding a maximal graph of order $n$, where the vertices are labeled with pairwise distinct integers and the sum of the endpoint labels for each edge is a power of $2$. In March 2022, M. S. Smith proved that such a graph cannot contain a cycle $C_{4}$, limiting the candidate graphs to well-studied squarefree graphs [2]. Smith’s result made it easy to establish the values of $g(n)$ for all $n\leq 9$, and led to creation of the sequence A352178 to the Online Encyclopedia of Integer Sequences (OEIS) [8]. It further provided a nontrivial upper bound for $g(n)$, namely the number of squarefree graphs of order $n$ (given by sequence A006855 in the OEIS).

The problem has received further attention after Neil Sloane presented it at the popular Numberphile Youtube channel in September 2022 [1]. This was followed by a few improvements, including the values $g(10)=15$ and $g(11)=17$ from Matthew Bolan [5] and Firas Melaih [4], respectively. These results were obtained via graph-theoretical treatment of the problem by manually analyzing a few candidate graphs.

At the same time, two methods were proposed for obtaining lower bounds for $g(n)$, giving those at least for all $n\leq 100$, which are listed in sequences A347301 and A357574 in the OEIS.

In the present paper, we propose an algorithm for testing admissibility of a given graph, i.e., whether its vertices can be labeled with pairwise distinct integers such that the sum of the endpoint labels for each edge is a power of $2$. We use our algorithm to bound $g(n)$ from above, and together with the known lower bounds to establish the values of $g(n)$ for $n$ in the interval $[12,18]$. Also, interpreting Smith’s result as saying that the cycle $C_{4}$ is a minimal forbidden subgraph (MFS), we find larger MFSs and show that there are none on $5$, $6$, $8$, or $9$ vertices, while there are $2$ MFSs on $7$ vertices, $15$ MFSs on $10$ vertices, and $77$ MFSs on $11$ vertices. We have also enumerated all maximal admissible graphs of orders $14$, $15$, $16$ and established that there are $4$, $28$, and $2$ of them, respectively.

A given graph $G$ on $n$ vertices with $m$ edges is admissible if and only if the following matrix equation is admissible:

where

• •

  $M$ is the $m\times n$ incidence matrix of $G$ with rows and columns indexed by the edges and vertices of $G$, and so $M$ is a $\{0,1\}$-matrix with each row containing exactly two $1$’s;

• •

  $L=(l_{1},l_{2},\dots,l_{n})^{T}$ is a column vector of pairwise distinct integer vertex labels;

• •

  $X=(x_{1},x_{2},\dots,x_{m})^{T}$ is a column vector formed by powers of $2$ representing the sums of edges’ endpoint labels.¹¹1The elements of $X$ are not required to be distinct.

Both $L$ and $X$ in this equation are unknown and have to be determined.

We start with solving (1) for $L$ in terms of $X$, that is we compute a (partial) solution of the form $l_{i}=p_{i}(x_{1},\dots,x_{m})$, where $p_{i}$ are linear polynomials with rational coefficients ($i\in\{1,2,\dots,n\}$). Such a solution exists if and only if $K_{l}\cdot X=0$, where $K_{l}$ is the a matrix with rows forming a basis of the left kernel of $M$. For better efficiency, we will assume that $K_{l}$ has integer elements and is LLL-reduced. Let $E$ be the set of elements of $K_{l}X$, which are linear homogeneous polynomials with integer coefficients representing linear equations in $x_{1},\dots,x_{m}$.

Let $K_{r}$ be a matrix with columns form a basis of the right kernel of $M$. For a connected graph $G$, it is known that $K_{r}$ has size $n\times t$, where $t=1$ or $t=0$ depending on whether $G$ is bipartite [9]. We find it convenient to view an $n\times 0$ matrix as composed of $n$ empty rows (and so all rows are equal). Adding a linear combination of the columns of $K_{r}$ to a solution $L$ to equation (1) turns it into another solution $L^{\prime}$ (with the same $X$), and furthermore all solutions can be obtained this way. The following theorem implies that for any set of pairwise distinct rows of $K_{r}$, we can find a linear combination of the of the columns of $K_{r}$ such that the corresponding elements of $L^{\prime}$ will also be pairwise distinct.

Theorem 1 implies that we need to take care only of the pairs of elements of $L$ corresponding to the equal rows of $K_{r}$. For any equal rows of $K_{r}$ with indices $i<j$, we compute $q(x_{1},\dots,x_{m}):=(p_{i}(x_{1},\dots,x_{m})-p_{j}(x_{1},\dots,x_{m}))c$, where $c$ is a positive integer factor making all coefficients of $q$ integer. If $q$ is zero polynomial, then the condition $l_{i}\neq l_{j}$ is unattainable, and thus the graph $G$ is inadmissible. On the other hand, if $q$ consists of just a single term with a nonzero coefficient, then the condition $l_{i}\neq l_{j}$ always holds, and we ignore such $q$. In the remaining case, when $q$ contains two or more terms with nonzero coefficient, we add $q$ to the set $N$.

Our next goal is to solve the system of equations $E$ and inequations²²2We deliberately use the term inequation to denote relationship $p\neq 0$ and to avoid confusion with inequalities traditionally denoting relationships $\geq$, $\leq$, $>$, or $<$. $N$ in powers of $2$, which we describe in the next section. For each solution $X=X_{0}$, we substitute it in the system (1) turning it into a standard matrix equation, which we solve for $L$ composed of pairwise distinct integers $l_{i}$ (such a solution is guaranteed to exist). We outline the above description in Algorithm 1.

For given finite sets $E$ and $N$ of nonzero linear polynomials in $x_{1},x_{2},\dots,x_{m}$, our goal is to find all $n$-tuples of nonnegative integers $(y_{1},y_{2},\dots,y_{m})$ such that

As simple as it sounds, the following theorem provides a foundation for our algorithms.

Applying Theorem 2 to an equation $c_{1}x_{1}+\dots+c_{m}x_{m}\in E$, we conclude that if only one of the coefficients $c_{1},c_{2},\dots,c_{m}$ is nonzero, then the system $(E,N)$ is inadmissible. Otherwise, if there are two or more nonzero coefficients among $c_{1},c_{2},\dots,c_{m}$, then there exists a pair of indices $i<j$ such that $c_{i}\neq 0$, $c_{j}\neq 0$, and $\nu_{2}(c_{i}x_{i})=\nu_{2}(c_{j}x_{j})$, implying that we can make a substitution $x_{i}=2^{\nu_{2}(c_{j})-\nu_{2}(c_{i})}x_{j}$ or $x_{j}=2^{\nu_{2}(c_{i})-\nu_{2}(c_{j})}x_{i}$ (we pick one with integer coefficients). Then we proceed with making this substitution in $E$ and $N$ reducing the number of indeterminates, and if it does not make any elements of $N$ evaluate to zero, we proceed with solving the reduced system recursively. After the pair $(i,j)$ is explored, we add a new inequation $2^{\nu_{2}(c_{i})}x_{i}-2^{\nu_{2}(c_{j})}x_{j}$ to $N$ (to prevent obtaining the same solutions again in future), and proceed to a next pair of indices.

We outline the above description in Algorithm 2. For given sets $E$ and $N$ of linear equations and inequations in $x_{1},\dots,x_{m}$, function SolveInPowers$(E,\ N)$ computes the set of their solutions in powers of $2$. Each solution is given in the form of a map $s$ from the set of variables $Y:=\{y_{1},y_{2},\dots,y_{m}\}$ to linear polynomials in these variables, representing the exponents in the powers of $2$. Namely, $s$ sends every variable from $Y$ either to itself (when it’s a free variable), or to a linear polynomial of the free varaibles. For example, the map $\{y_{1}\to y_{2}+1,\ y_{2}\to y_{2},\ y_{3}\to y_{2}+y_{4}+3,y_{4}\to y_{4}\}$ corresponds to the solution $(x_{1},x_{2},x_{3},x_{4})=(2^{y_{2}+1},2^{y_{2}},2^{y_{2}+y_{4}+3},2^{y_{4}})$, where $y_{2}$ and $y_{4}$ are free variables taking nonnegative integer values.

We used the results of the previous sections to find minimal forbidden subgraphs (MFS) of small order, i.e., inadmissible graphs in which every proper subgraphs is admissible. It is easy to see that each MFS must be connected. It is further almost trivial task to verify that $C_{4}$ is the smallest MFS and the only one on $4$ vertices. Therefore, for $n>4$ we can restrict our attention to connected squarefree graphs as candidates, which we generate in SageMath [7] with the function nauty_geng() based on nauty tool [6] supporting both connected (option -c) and squarefree (option -f) graphs. This significantly speeds up the algorithm and eliminates the need to test the presence of MFS $C_{4}$ as a subgraph.

We look for MFSs, other than $C_{4}$ iteratively increasing their order, accumulating found MFSs in a set $S$ (initially empty). For each candidate graph $G$, we check if $G$ contains any graphs from $S$ as a subgraph using the SageMath function is_subgraph(). If $G$ contains any of the graphs from $S$, we go to the next candidate graph $G$. Otherwise, we test admissibility of $G$ by calling $\textsc{GraphSolve}(G)$. If $G$ is inadmissible, then it represents an MFS and we add it to $S$. The described algorithm is outlined in Algorithm 3.

We confirmed that the smallest MFS is the cycle $C_{4}$ as it was originally proved by Smith, and the next two have order $7$ (Fig. 1). It happens that one of these graphs was previously proved to be inadmissible by Bolan while showing that $g(10)=15$ [5].

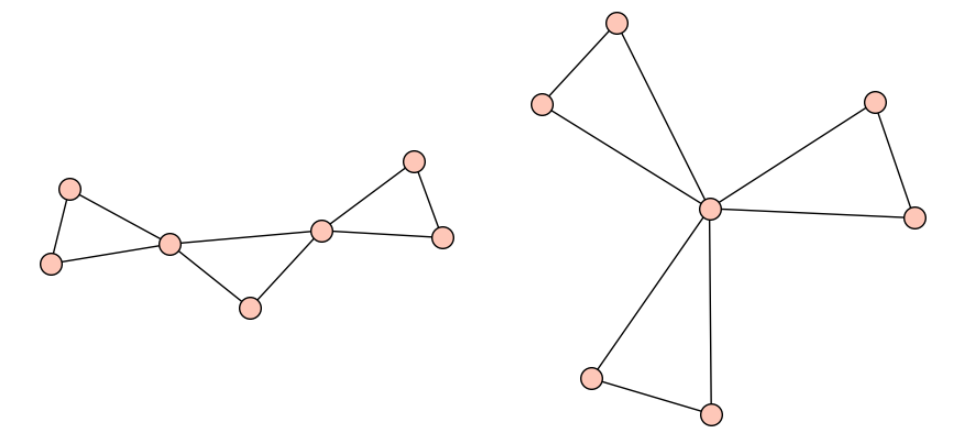
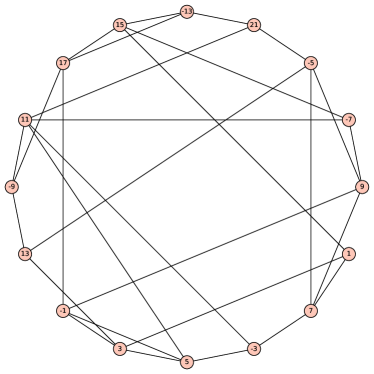
There are no MFSs of order $8$ or $9$, but there are $15$ of them of order $10$ (Fig. 2), and there are $77$ MFSs of order $11$. We use MFSs of order $\leq 10$ for quick filtering some inadmissible graphs.

We also used the proposed algorithms for computing values of $g(n)$ (sequence A352178 in the OEIS) for $n$ in $[12,18]$ using the known lower and upper bounds:

In all these cases, the value of $g(n)$ happens to coincide with the lower bound, and thus the problem can be posed as verifying that larger values (up to the upper bound) are not possible. For values $n\leq 13$ this can be done directly by generating all larger connected squarefree graphs and testing them for admissibility. For example, there are only $957$ such graphs of order $13$ with $22$ or more edges.

We find the following statements helpful:

From $g(13)=21$, Theorem 3 implies that $g(14)\leq 24$, which matches the lower bound. Hence, we obtain $g(14)=24$ without any computation.

For $n=15$, Theorem 3 implies that $g(15)\leq 27$. If an admissible graph with $27$ edges exists, the minimum degree should be at least $3$. This can be enforced with the option -d3 of nauty_geng(), which generates $8280$ such candidate graphs, but our check shows that neither of them is admissible. Hence, $g(15)=26$.

For $n=16$, Theorem 3 implies that $g(16)\leq 29$ and thus $g(16)=29$.

For $n=17$, Theorem 3 implies that $g(17)\leq 32$. If an admissible graph with $32$ edges exists, the minimum degree should be at least $3$. There are $1023100$ such candidate graphs, which is possible to check directly although it would be quite time consuming. Instead, we approached this problem from another side—by constructing candidate graphs from the maximal admissible graphs of order $16$ as explained below. This way we established that there are no admissible graph of order $17$ with $32$ edges, thus proving that $g(17)=31$.

For $n=18$, Theorem 3 implies that $g(18)\leq 34$ and thus $g(18)=34$.

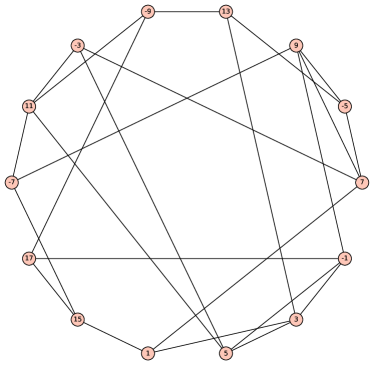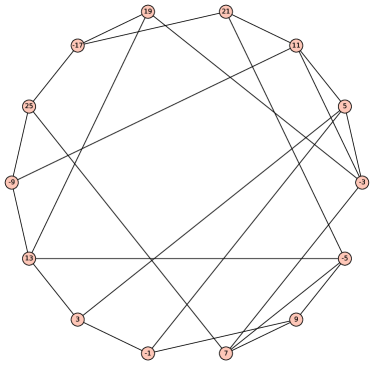
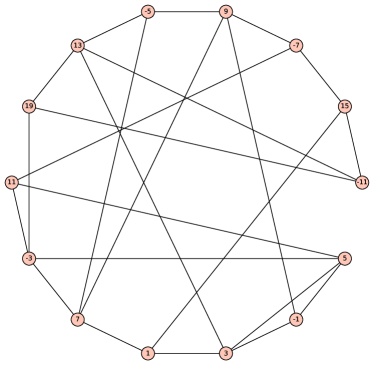
The maximal admissible graphs of each order $n\leq 14$ can be obtained directly from the candidate graphs generated by nauty_geng(). In particular, for $n=14$ we can restrict our attention to the $2184$ connected squarefree graphs with minimum degree $3$, among which we identified only $4$ admissible graphs (Fig. 3).

To construct maximal admissible graphs of order $15$, we noticed that either they contain a vertex of degree $2$ whose removal results in a maximal admissible graph of order $14$, or their minimal degree is at least $3$. We obtained $20$ maximal admissible graphs of the first type (by adding a vertex of degree $2$ to the maximal admissible graphs of order $14$ in all possible ways, and testing admissibility of the resulting graphs), and $8$ maximal admissible graphs of the second type by testing $33608$ candidate graphs generated by nauty_geng().

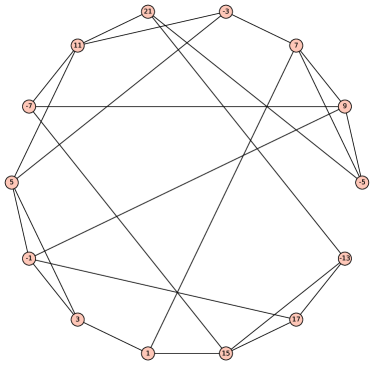
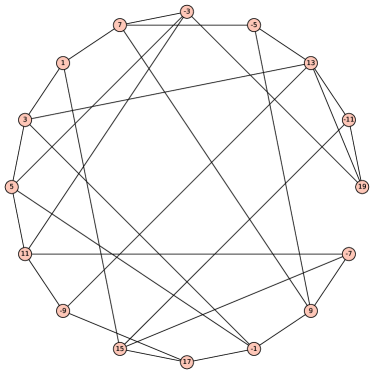
Similarly, we further extended maximal admissible graphs of order $15$ to those of order $16$ by adding a vertex of degree $3$, which resulted in just two maximal admissible graphs of order $16$ (Fig. 4). However, extending them to graphs of order $17$ with $32$ edges by adding a vertex of degree $3$ produced no admissible graphs, thus proving that $g(17)=31$.

The author thanks Neil Sloane for his nice introduction to the problem [1] and proofreading of the earlier version of this paper.