On Definite Iterated Belief Revision with Belief Algebras††thanks: This is an extended version of the corresponding IJCAI 2025 paper with the same title.
Abstract
Traditional logic-based belief revision research focuses on designing rules to constrain the behavior of revision operators. Frameworks have been proposed to characterize iterated revision rules, but they are often too loose, leading to multiple revision operators that all satisfy the rules under the same belief condition. In many practical applications, such as safety critical ones, it is important to specify a definite revision operator to enable agents to iteratively revise their beliefs in a deterministic way. In this paper, we propose a novel framework for iterated belief revision by characterizing belief information through preference relations. Semantically, both beliefs and new evidence are represented as belief algebras, which provide a rich and expressive foundation for belief revision. Building on traditional revision rules, we introduce additional postulates for revision with belief algebra, including an upper-bound constraint on the outcomes of revision. We prove that the revision result is uniquely determined given the current belief state and new evidence. Furthermore, to make the framework more useful in practice, we develop a particular algorithm for performing the proposed revision process. We argue that this approach may offer a more predictable and principled method for belief revision, making it suitable for real-world applications.
1 Introduction
Updating or revising the beliefs of an agent in light of new evidence is a fundamental process in both everyday life and scientific activities. For instance, Newton’s laws of motion were widely accepted for centuries until discoveries at very small scales or very high speeds revealed their limitations. Similarly, our knowledge is continuously updated and enriched through learning and communication. To formalize this process, researchers in artificial intelligence have developed the subfield of belief change (see, e.g., Doyle (1979); Harper (1976)). Among the most influential contributions to this field is the AGM framework Alchourron et al. (1985), which has inspired numerous extensions and applications in areas such as game theory and argumentation Williams (1996); van Harmelen et al. (2008); Fermé and Hansson (2011); Diller et al. (2015); Zhang (2010).
Motivation
The AGM framework addresses various forms of belief change, including belief revision, which is of particular interest in this paper. The AGM framework, along with its various subsequent developments, aims to update a current belief state to a new one when new evidence is acquired. This process can be formally described syntactically as revising a set of logical formulas (belief set) with a single logical formula (new evidence) Alchourron et al. (1985). Alternatively, it can be characterized semantically using preferences over possible worlds (total preorder) Katsuno and Mendelzon (1991), where the revision process involves updating these preferences based on new evidence. Furthermore, belief revision based on partial preorders and iterated belief revision have been extensively studied Lehmann (1995); Boutilier (1996); Darwiche and Pearl (1997); Nayak et al. (2003); Booth and Chandler (2016); Aravanis et al. (2019); Kern-Isberner et al. (2024). Researchers have primarily focused on how to constrain belief revision behaviors through postulates or how to characterize revision with new semantics, leading to the proposal of various rule systems Liberatore (2024); Bonanno (2025). These rule systems are evaluated from different perspectives to build a comprehensive framework. However, these rule systems are often too loose, resulting in multiple revision operators that all satisfy the same set of rules, which might not be desirable in practice. For example, in scenarios where multiple intelligent agents collaborate in urban traffic management, their initial beliefs are aligned. Upon acquiring new traffic condition information, these agents must update their traffic control strategies deterministically so that they maintain aligned beliefs, otherwise the transportation system might descend into chaos.
Contributions
The goal and main contribution of this paper is not to establish a new rule system for belief revision, but to explore a simple and effective way to represent belief information in more depth, and to propose a definite revision operator suitable for applications requiring deterministic revision. To this end, we use belief algebra (introduced in Meng et al. (2015)) as the foundational tool for representing belief information. Unlike preorders over worlds, a belief algebra represents belief information as a preference relation over subsets of worlds. In our framework, both the current belief state and the new evidence are represented as belief algebras. Specifically, the iterated belief revision process is modeled as revising a belief algebra with another belief algebra to produce a new belief algebra . By analyzing the structural properties of a belief algebra, we propose a set of revision postulates, including an upper bound constraint on the outcomes of revision, and prove that these postulates inherently induce a unique revision operator. Additionally, we discuss the algorithmic implementation of this iterated belief revision framework, providing practical support for designing agents with belief revision capabilities in applications.
Organization
The rest of the paper is organized as follows: Section 2 discusses related work and Section 3 introduces basic knowledge. Section 4 explores properties of belief algebras, and Section 5 considers a special case of revision with a belief algebra. Section 6 extends the discussion to general cases and Section 7 describes the practical algorithm. Finally, Section 8 concludes the paper.
2 Related Work
Various research efforts have focused on representing belief information in iterated revision. Spohn Spohn (1988) introduced the concept of ordinal conditional function (OCF) to encode preference information over worlds and developed a process called conditionalization to revise OCFs. Williams Williams (1994) proposed a formula-based counterpart to OCF, mapping formulas to ordinals based on their resistance to change. Darwiche and Pearl Darwiche and Pearl (1997) advanced the field by representing belief information as total preorders on worlds and extending the AGM framework with four postulates to characterize iterated revision.
Several researchers have improved the DP (Darwiche and Pearl) framework’s settings. Benferhat et al. Benferhat et al. (2005) used partial preorders, while Peppas and Williams Peppas and Williams (2014) employed semiorders. Ma et al. Ma et al. (2015) revised epistemic states with partial epistemic states. Andrikopoulou et al. Andrikopoulou et al. (2025) discussed belief revision under filters that are subsets of partially ordered sets. Benferhat et al. Benferhat et al. (2000) enhanced the representation of new evidence by using an epistemic state, proposing postulates for minimal-model preserving operators and proving the uniqueness of the revision result given a total preorder and a new total preorder as evidence. This aligns with our discussion in Section 5, as their operator satisfies (RE1)–(RE3). Meanwhile, new frameworks and semantic structures continue to be proposed Liberatore (2024); Bonanno (2025).
Many works aim to define the most “reasonable” revision rules, yet achieving consensus on rationality remains challenging. These debates often resemble philosophical discussions, focusing on abstract principles rather than practical implementations. The rationality of the basic AGM rules has been questioned Aravanis (2023). Sauerwald and Thimm Sauerwald and Thimm (2024) considered the realizability of AGM revision and contraction operators in Epistemic Spaces. Some researchers, such as Booth and Meyer (2006); Jin and Thielscher (2007); Nayak et al. (2003), have observed that the DP framework can produce counter-intuitive revision results. To address that issue, they proposed modifications or additions to the DP postulates. For instance, Nayak, Pagnucco, and Peppas Nayak et al. (2003) introduced conjunction postulates, treating consistent evidences as order-independent, while Jin and Thielscher Jin and Thielscher (2007) proposed a weaker independence postulate. Notably, these works primarily focus on rule construction, with limited attention to operator selection.
While the exploration of revision rules continues, the potential and application prospects of belief revision have also received significant attention Hunter and Boyarinov (2022); Baroni et al. (2022). This shift reflects a growing interest in leveraging belief revision for practical, real-world problems. In applications such as constrained differential privacy Liu et al. (2023) and text generation by large language models Wilie et al. (2024), the focus has shifted towards applications of revision. In industrial agent design, selecting a specific update algorithm is crucial to enable agents to iteratively refine their beliefs. To address this, our work focuses on representing belief information through belief algebra building on Meng et al. (2015), and proposes a unique revision operator by strengthening revision rules in a natural way, aiming to provide a deterministic and practical solution for real-world applications.
3 Preliminaries
We recall some necessary knowledge for what will follow.
3.1 Belief as A Total Preorder
In this paper, we restrict our discussion to belief revision in a finite propositional language . We denote by the set of all (possible) worlds (i.e., interpretations).
For each propositional formula , we denote by the set of all worlds of , i.e., . We will also use a consequence operator to obtain the set of formulas implied by .
A (partial) preorder on is a binary relation on that is reflexive and transitive. A preorder is called total if any two elements in are comparable under . We write if and , and if but . The strict part of a preorder is the set .
A belief set is a set of formulas in that is deductively closed, i.e., . Generally, belief revision is the process of changing a current belief state with a new piece of evidence, where the current belief state and the new evidence can be represented in different ways. For example, in the AGM framework, the current belief state is represented as a belief set and the new evidence is represented as a formula.
When belief revision needs to be done sequentially, known as iterated belief revision, the representation mechanism of the AGM framework is not suitable anymore. A more sophisticated structure known as epistemic state is then used to represent belief information. In their original paper, Darwiche and Pearl Darwiche and Pearl (1997) captured the concept of an epistemic state in terms of a revision operator. Particularly, an epistemic state is a set of beliefs and conditional beliefs satisfying several postulates. A conditional belief has the form , where are formulas in . An agent has a conditional belief if she will believe whenever she believes . Within the DP framework, an epistemic state can be characterized semantically as a total preorder on worlds as follows.
Lemma 1 ( Darwiche and Pearl (1997)).
Suppose consists of a belief set and several conditional beliefs, then is an epistemic state iff there is a total preorder on worlds such that:
-
(ES1) iff there is a world in such that for all .
-
(ES2) iff there is a world in such that for all .
3.2 Belief as A Belief Algebra
To provide a unified representation of belief information, the concept of belief algebra was introduced in Meng et al. (2015). It is a class of ordering structures on , the power set of possible worlds, which can intuitively capture the belief preference of an agent, and is actually more general than total preorder (see Section 5).
Definition 1 (Meng et al. (2015)).
Suppose is a binary relation on , and write . Then is called a belief algebra (BA) if it satisfies the following rules ():
-
(A0) .
-
(A1) iff .
-
(A2) If , then .
-
(A3) If and , then .
-
(A4) If and , , then .
Roughly speaking, directly describes the belief preference of agents in a semantic way. For instance, means that is more believable than , and if and are incomparable in , then the agent has no idea which one is more believable. (A0) shows that we only need to compare disjoint subsets of . (A1) shows that each nonempty set has a higher preference level than the empty set. (A2) shows that is a strict ordering. (A3) shows that satisfies certain transitivity. (A4) considers the case where if is more believable than and is more believable than , then is more believable than .
Traditionally, the semantic characterization of an epistemic state is often represented as a total preorder on , where is the set of all possible worlds. In contrast, a belief algebra is defined as an ordering relation on , the power set of . Interestingly, a total preorder on can be naturally extended to a belief algebra on . This relationship can be formalized in the following theorem:
Theorem 1 (Meng et al. (2015)).
Let be a total preorder on . Define a binary relation on as follows: if and only if and such that Then is a belief algebra.
This theorem demonstrates that the structure of a total preorder on can be lifted to a belief algebra on , preserving the agent’s belief preferences in a more expressive and generalized framework. The relation captures the intuition that a subset is preferred over if there exists at least one world in that is strictly preferred to all worlds in . This extension provides a natural bridge between traditional epistemic states and the more general belief algebra framework.
Definition 2 (Complete Belief Algebra (CBA)).
A belief algebra is called a complete belief algebra (CBA) if it can be generated from a total preorder on in the manner described in Theorem 1.
Complete belief algebras provide a natural connection between total preorders on , and the more expressive framework of belief algebras. They capture the intuition that belief preferences over subsets of worlds can be fully determined by a total preorder on individual worlds.
Example 1.
Suppose is a total preorder and thus an epistemic state. Let and . For the sake of brevity we use for representing , for , and so on. Then this total preorder is equivalent to a complete belief algebra as follows:
4 Exploring Belief Algebra in More Depth
Given two belief algebras and on , we denote by iff . Also, we will not distinguish between and , and and , whenever it is self-explanatory based on context. For each belief algebra , is always contained in by . It is not difficult to verify that is a belief algebra. Then for each belief algebra on , we always have .
A subset of (defined in Definition 1) can generate a belief algebra.
Definition 3.
Given , we denote by the smallest subset of that contains and is closed under the rules (A1), (A3) and (A4) used for expansion.
Example 2.
Suppose and . Then for each belief algebra , if we have . Again, for the sake of brevity we use for representing , for , and so on. With respect to (A3) we have that are all in , and by (A4) . Then it can be verified that is the smallest belief algebra which contains .
If also satisfies (A2), then is a belief algebra by definition, and we will also use to denote this belief algebra. Here we always assume that the agent is rational and is always a belief algebra when represents some belief information. Given , can be obtained by closing under (A1), (A3), and (A4).
With the operator , one can see that each CBA is entirely determined by preferences on the sets consisting of a single world.
There is a 1-1 correspondence between CBAs and total preorders, which is given as follows.
Lemma 4 (Meng et al. (2015)).
There is a 1-1 correspondence between CBAs and total preorders:
-
•
Suppose is a total preorder on . Let iff s.t. , . Then is a CBA.
-
•
Suppose is a CBA. Let iff , and iff and . Then is a total preorder on .
Each CBA is totally decided by preferences on the sets consisting of a single world, which is implied straightforwardly by Lemma 4.
Corollary 1.
Suppose and are CBAs, then:
-
•
, where .
-
•
If and have the same preferences on single world sets, i.e., for any , iff , then .
The following proposition shows how to construct new belief algebras from existing belief algebras.
Proposition 1.
Suppose and are belief algebras. Then is a belief algebra.
Proof.
We only need to show that satisfies (A0)-(A4). We take (A3) as an example, as the rest can be proven in similar and/or simpler fashion. If , and , then and since satisfy (A3). Hence . This means that satisfies (A3). ∎
Corollary 2.
Suppose is a belief algebra and , and is the set of all the belief algebras that contains . Then is a belief algebra, and .
Proof.
By Definition 3 and , we have . Then satisfies (A2), and is the smallest belief algebra containing . Thus, and . On the other hand, by Proposition 1, we know that any finite intersection of belief algebras is also a belief algebra, and contains only finite number of belief algebras because is a finite set, so is a belief algebra containing . Then and we have . ∎
The following result unveils the structure of , which consists of levels of subsets of worlds.
Lemma 5 (Meng et al. (2015)).
Suppose is a belief algebra. Then there is a unique chain, called backbone, , such that:
-
(Ch1) is a partition of , i.e., consists of pairwise disjoint nonempty subsets of and .
-
(Ch2) For each , if are two disjoint nonempty subsets of , then and are incomparable in , i.e., and .
The above lemma shows that the backbone is the core structure of a belief algebra. (Ch2) shows that for each in a backbone, any subsets of can not be compared with one another. In terms of belief preferences, this means that an agent has no preference on subsets of . Another important concept is the support of a subset of w.r.t. some backbone.
Definition 4.
Let be the backbone of a belief algebra. The support of a nonempty set w.r.t. is defined as , where and , if . That is, is the largest under in the backbone such that .
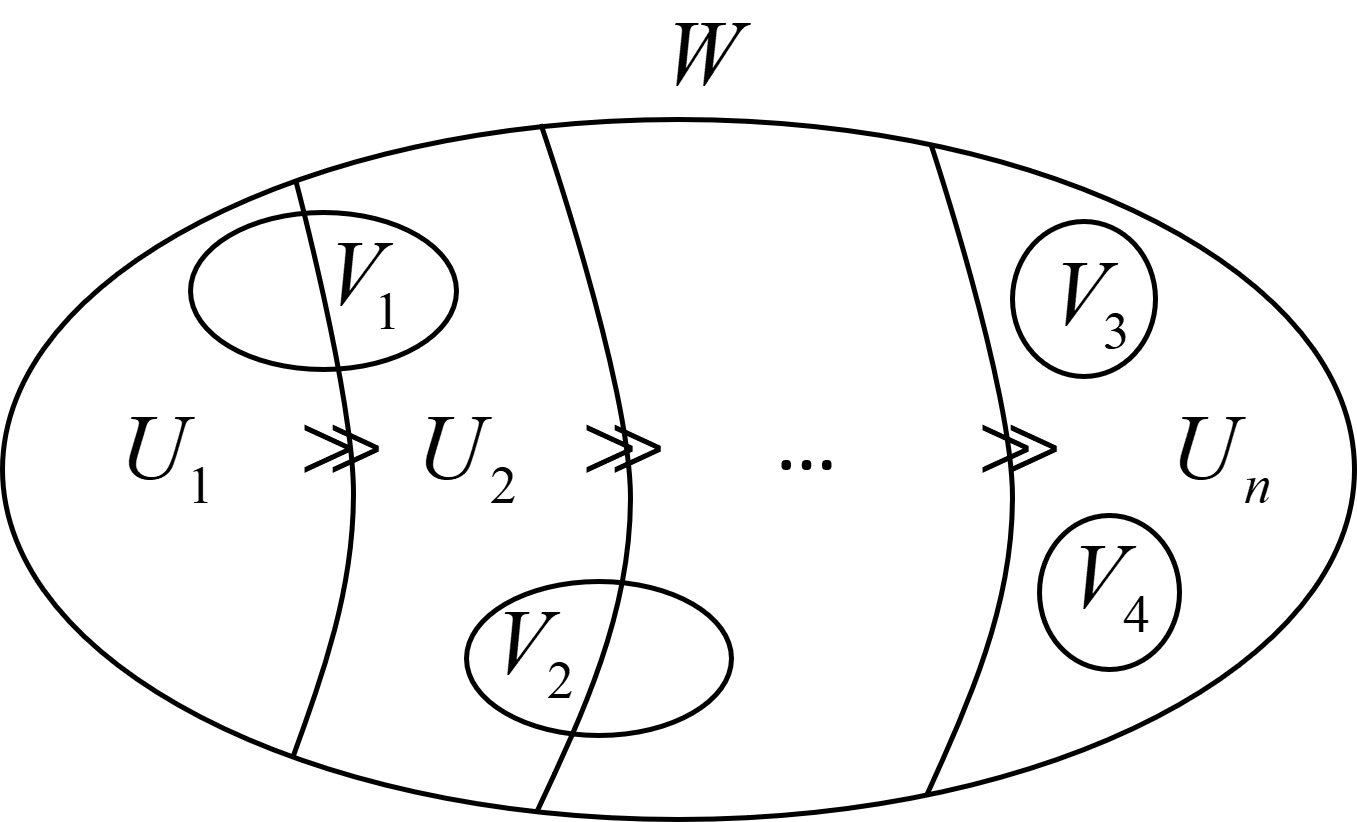
Figure 1 gives an illustration of the above definitions. Moreover, the preferences of an agent are “consistent” with the backbone in the sense of property (1) in Lemma 6 that follows.
Lemma 6 (Meng et al. (2015)).
The relations between belief algebras and their backbones are as follows:
-
(1)
Suppose is a belief algebra, then only if .
-
(2)
Suppose is a complete belief algebra, then if and only if .
-
(3)
Suppose is a belief algebra, and is its backbone. Then there is a unique complete belief algebra containing and having the same backbone with . Moreover, .
The above lemma shows that there are different belief algebras that have the same backbone , and there is a unique complete belief algebra with as its backbone, viz., the largest one containing all the pairs s.t. . Roughly speaking, the backbone of a belief algebra is the “core” belief information that reflects the main preferences of the agent. Taking Figure 1 as an example, a belief algebra with as its backbone may or may not contain , but if it is CBA, then it must contain , and it should never contain because .
Definition 5.
Suppose is a belief algebra. Then we denote by the complete belief algebra that contains and has the same backbone as . Suppose and are both belief algebras. Then we write if these two belief algebras have the same backbone and .
Example 3.
Let be a propositional language with two variables and . Suppose Bob’s current belief state is represented as a total preorder , and the new evidence is a formula such that the worlds that entail are represented as . In this situation, Bob holds a new preference that . These belief preferences can be represented using belief algebra. Following the notation in Example 2, Bob’s current belief information can be represented as: Similarly, the new evidence can be represented as . Note that is a complete belief algebra (CBA), while is not a CBA. The backbone of the former is , while the backbone of the latter is . Moreover, .
Note that is different from . It actually means that and contain the same “core” belief information, but is “less informational” than , in the sense that any revision result of should be contained in that of , as we will see later in the postulate (RA5). Let be the set of belief algebras over the worlds of . It is easy to check that as defined above is a partial order on . We also use to denote the partial order set .
Theorem 2.
Let be a backbone and denote by is the backbone of the set of belief algebras having as backbone. Suppose . Then:
-
(1)
.
-
(2)
is a belief algebra, and .
Remark 1.
Theorem 2 shows that is a lattice that contains the smallest element and the largest element . Here, a lattice is a set equipped with a partial order such that every two elements have a unique supremum (also called the least upper bound) and a unique infimum (also called the greatest lower bound). Furthermore, is divided into disjoint parts by the backbone, and each part is a lattice under (see Figure 2).
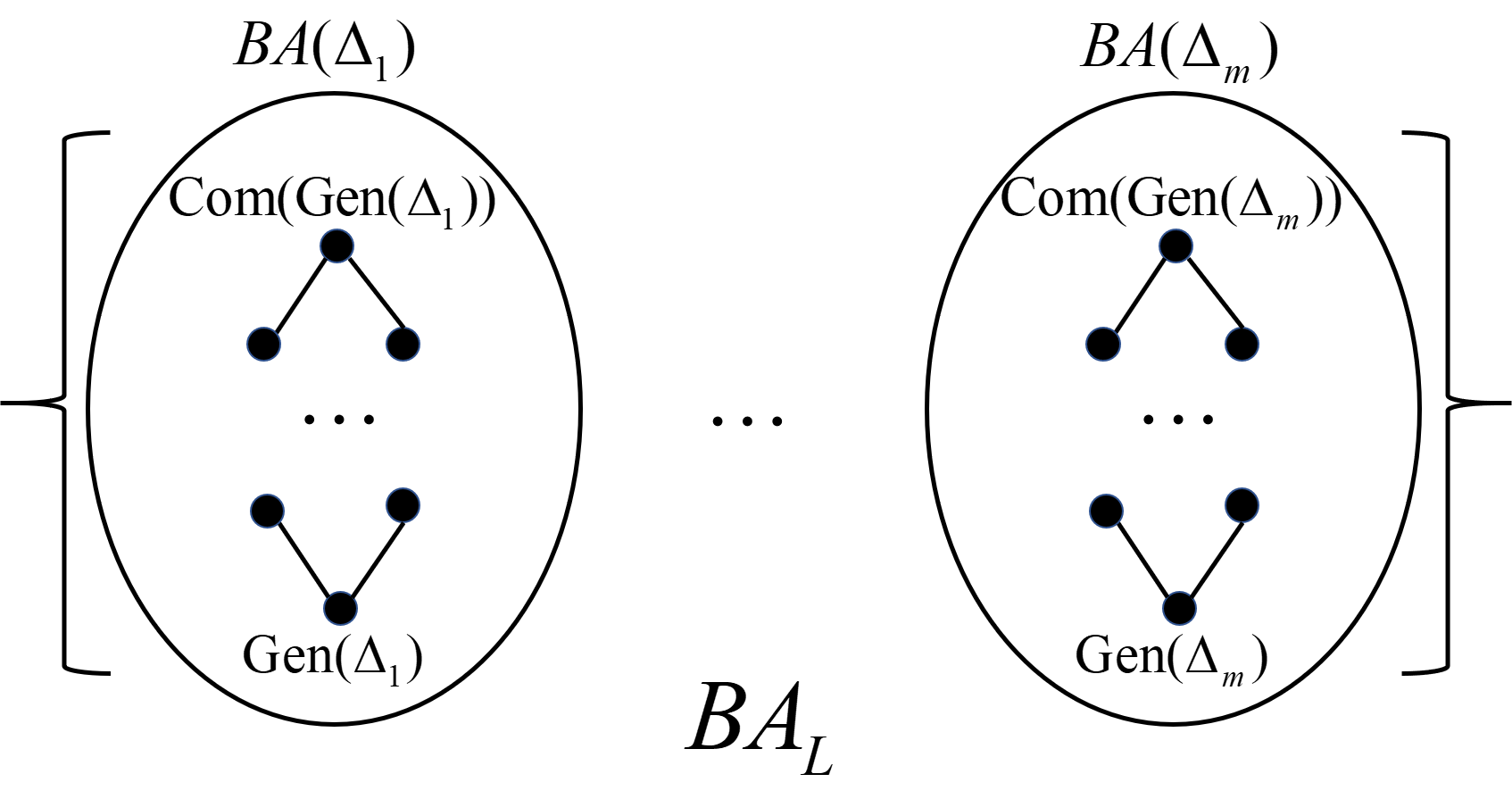
Example 4.
Suppose . Let , , , . Then are all belief algebras, and they all have the same backbone . is a complete belief algebra, and , , but can not be compared by . Furthermore, is the smallest element in , and is the biggest one.
5 Special Case: Revising CBA with CBA
Before discussing the general case of revision with belief algebras, we first consider a simplified scenario where the agent’s current belief, the new evidence, and the revision result are all represented as complete belief algebras (CBAs; see Definition 2). This process is equivalent to revising an existing total preorder by a new total preorder to obtain a revised total preorder .
Inspired by existing research (e.g., Alchourron et al. (1985); Darwiche and Pearl (1997); Ma et al. (2015)), we propose the following revision rules for this setting. The revision of a total preorder by another total preorder, denoted as , has been studied in Benferhat et al. (2000) and is known as a minimal-model preserving operator. This operator can be equivalently characterized by the following postulates:
-
(RE1) is a total preorder.
-
(RE2) , where .
-
(RE3) If , then: if and only if .
The postulate (RE1) is natural by underlying setting. The postulate (RE2) requires that the new belief information (corresponding to the strict part of the new total preorder) must be fully incorporated into the revision result. Finally, (RE3) ensures that for worlds with equal (non)preference under , the preference relation from is preserved in . This allows the revision process to retain more of the original belief information while incorporating the new evidence.
Example 5.
Following Example 3, Bob’s current belief is which has as its strict part. Now, instead of considering revision by a formula, we consider revision by another total preorder . Then has an empty strict part, which means that cannot lead to any new preference. In this sense, all the strict orderings of can be kept into the revision result. It is natural that . Suppose instead . Then, in , all worlds are ordered by . In this sense, no information in is useful and . On the other hand, if . Then, and ( and respectively) can not be distinguished in , but and are in . Following the information in , Bob should hold and in . Then .
Interestingly, it can be shown that revision results satisfying the above postulates are unique.
Theorem 3.
Suppose and are total preorders. Then there is a unique revision operator satisfying (RE1)-(RE3).
Proof.
For any , we define a binary relation on as follows.
-
•
iff , or and .
-
•
iff and .
It is not difficult to check that is a total preorder. Next we only need to show that if an operator satisfies (RE1)-(RE3) then the revision result of is exactly . Let . By (RE1), is a total preorder. Since is a total preorder, for any , exactly one of , , and will happen. If (, respectively) then (, respectively) by (RE2). If then we have iff by (RE3). That is equivalent to say, if and , then , and if and , then . In the end, we have iff , and iff . Therefore, . ∎
Remark 2.
However, the above revision framework has the great limitation of not being able to deal with more general cases such as the new evidence or even the current belief state is not a total preorder, which is common in real-world applications, e.g., the agent only holds incomplete belief information. Therefore, it is necessary to consider other solutions without such limitation.
6 Revision with Belief Algebras
In this section, we extend our discussion to a more general framework of iterated belief revision based on a belief algebra, rather than restricting ourselves to CBAs. This framework allows for a richer representation of belief states and supports more flexible revision processes. For simplicity, we assume that the agent is rational (i.e. both her belief and the new evidence do not contain “conflicting information”). If not specified otherwise, we always suppose that the agent’s current belief state is a belief algebra , the new evidence is a belief algebra , and the revision result is also a belief algebra denoted by , where is a revision operator from to .
To give postulates to characterize rational revisions, following literature, e.g., Alchourron et al. (1985); Darwiche and Pearl (1997); Jin and Thielscher (2007), we first assume that new evidence has a higher preference, that is, belief information of is more believable than . Then should be kept in , and we have:
-
(RA1)
Since and collectively cover all the agent’s belief information, we assume that is entirely determined by and and is generated by some subset of . This leads to the following postulate:
-
(RA2) There is an s.t. .
(RA2) requires that the revision result cannot be generated with information outside , and if and have conflicting information, one should choose a consistent subset in order to generate a belief algebra.
Notice that a complete belief algebra is equivalent to a total preorder on worlds. Revising a complete belief algebra by another complete belief algebra is equivalent to revising a total preorder by another total preorder. The following postulates (RA3) and (RA4) are thus inspired by (RE1) and (RE3) for revising total preorders in Section 5, respectively.
-
(RA3) Suppose and are complete belief algebras. Then is also a complete belief algebra.
-
(RA4) Suppose and are complete belief algebras, and in . Then iff .
Theorem 4.
Suppose satisfies (RA1)–(RA4), and and are complete belief algebras. . Then , and the result of revising by is unique.
Proof.
Suppose the corresponding total preorders of are respectively. Let , where is the operator which satisfies (RE1)-(RE3). Then is a total preorder, and iff , or and . Since are CBAs, we have iff , iff , and iff . We denote by the corresponding CBA of . Then iff . That is to say, iff , or and . In summary, for any , iff . The “if” part here shows and , because is a CBA and each CBA is totally decided by the preferences on single world sets according to Corollary 1. Then . The “only if ” part here shows that if , then we have , which means since is also a CBA. Therefore, we have .
To show that the result is unique, suppose that is an operator on which satisfies (RA1)–(RA4). Then we only need to show that if then . By (RA3), is a CBA because and are CBAs. Let . Then , one of the following two cases is true.
-
(Case 1) If or then we have or , respectively, by (RA1).
-
(Case 2) If and then is holding in by Proposition 4. Therefore, iff by (RA4).
Therefore, we have iff or . That is to say, iff . Recall that and are both CBAs. Then we have by Corollary 1. ∎
This above theorem generalizes Theorem 3 and shows that, under the postulates (RA1)-(RA4), the revision operator is deterministic when applied to complete belief algebras. Specifically, the revision result is uniquely determined by combining the preference relations from and in a principled way. The set captures the preferences from that are consistent with the structure of , ensuring that the revision process preserves as much of the original belief information as possible while fully incorporating the new evidence. The following corollary establishes a direct correspondence between the revision operator for complete belief algebras and the revision operator for their equivalent total preorders.
Corollary 3.
Suppose, and are complete belief algebras, and and are their equivalent total preorders on worlds, respectively. If satisfies (RA1)-(RA4), and satisfies (RE1)-(RE3), then the corresponding total preorder of is exactly .
Proof.
This conclusion follows intuitively, and we only provide a proof sketch.
Let and . Note that by the proof of Theorem 4, the revision operator under (RA1)-(RA4) ensures that in iff either (from ), or and (preserved from ).
On the other hand, by the proof of Theorem 3 the revision operator defined by (RE1)-(RE3) ensures that iff either (from ) or and (preserved from ).
This structural correspondence guarantees that is exactly the CBA corresponding to by Lemma 4. ∎
Example 6.
Suppose, and are backbones, then and are complete belief algebras. In this sense, , and , where is the backbone of .
For the case where and are possibly incomplete belief algebras, we include the following postulate:
-
(RA5) If , then .
Recall that means that and and have the same backbone. (RA5) means that if and contain less information than and , respectively, and they have the same core belief information (i.e., same backbones), then also contains less belief information than . From (RA5), the following proposition is easy to verify.
Proposition 2.
If satisfies (RA5), then .
The above proposition shows that is an upper bound of (under ).
Furthermore, we suppose a rational agent will keep maximal information from to under (RA1)–(RA5), which is a “minimal change” rule. Hence, we assume that is maximum in , i.e., there is no belief algebra such that , where . Then we have the following postulate.
-
(RA6) If and , , then .
We arrive to one of the major results in this work:
Theorem 5.
Suppose satisfies (RA1)-(RA6), and are belief algebras. Then the revision result of is unique, and .
Proof.
is a defined complete belief algebra by Theorem 4 and satisfies (RA1)-(RA6) . Since is a subset of , is a belief algebra by Corollary 2. By (RA2), there is a such that . By (RA5), we have . Then, . Furthermore, we have . As a result, we can conclude that , where is a belief algebra. By (RA6), we have . ∎
The above theorem shows that there is only one operator that satisfies (RA1)–(RA6). The postulate (RA5) provides an upper bound for the revision result. On the other hand, (RA6) imposes a conditional maximality requirement on the revision result, which, together with (RA5), leads to the uniqueness of the revision operator . In the next section, we will discuss how to algorithmically compute the revision result of this operator, providing a practical method for performing iterated belief revision in the belief algebra framework.
7 A Practical Algorithm and Discussion
In this section, we provide a practical algorithm for computing the revision result based on the postulates (RA1)–(RA6).
7.1 Algorithm
We begin with a direct characterization of the revision result.
Proposition 3.
Suppose and are belief algebras, satisfies –, and . Then , and and .
Proof.
Therefore, we can use Algorithm 1 to get .
In the first step of the algorithm, we need to compute and . Given a belief algebra , to calculate , we need to obtain the backbone of first. Let , and . Then . It can be verified that is indeed the backbone of , and more details can be found in Meng et al. (2015). With the backbone of , can be constructed by defining as , if . Then can be computed by Theorem 4, and thus can be obtained accordingly. Note that one can get for some by calculating the closure of under (A1), (A3), and (A4).
Example 7.
In Example 3, as Bob’s current belief corresponds to a total preorder , it can be characterized as a CBA , where
Here for simplicity, we use a sequence of numbers to represent the set of worlds (). For example, represents and represents . The new evidence with worlds can be characterized as , where
Note that the backbone of is . Then
By Theorem 4, we know , and
Then the backbone of is , and is
Then
The backbone of is . It is not difficult to verify that . Furthermore, is also equal to . In other words, is generated by . In Example 3, these orderings are exactly the part that must be maintained under the DP framework. On the other hand, if the new evidence is , where instead, then the revision result under the proposed framework will be , because will induce the preference information .
Now we return to the traditional belief revision setting, where the current belief is represented as a total preorder on possible worlds, and the new evidence is a formula . This revision setting can be viewed as revising a complete belief algebra by a new belief algebra generated by the formula . Suppose that is the revision operator on satisfying (RA1)–(RA6). Then the revision process proceeds as follows:
-
•
(Step 1) Represent and by belief algebras. Let be the corresponding complete belief algebra of i.e., iff . Similarly, can be equivalently represented by .
-
•
(Step 2) Calculate . Note that is equivalent to a total preorder s.t. iff and . Moreover, is also equivalent to a total preorder . Following (RE1)-(RE3) (by Corollary 3, (RA1)-(RA4) equivalently), we can conclude that the strict part of is as follows.
-
–
If then iff .
-
–
If then iff .
-
–
If and then .
-
–
-
•
(Step 3) Calculate . From the result of last step, we can see that
-
–
If , then iff .
-
–
If , then iff .
-
–
If , and , then .
It should be noted that, the preferences on single worlds in and remain unchanged after revision, and in is also maintained if and .
-
–
-
•
(Step 4) Calculate . Then we get the revision result .
Remark 3.
It is evident that the above revision process attempts to preserve as much information from as possible, particularly those preferences consistent with . This strategy aligns with the principles of the AGM and DP frameworks. However, unlike these frameworks, the specific preference relations to be preserved are determined by the upper bound . Only those preferences consistent with are included in the final result, and they must be included. This is the reason why the revision operator produces a unique result.
7.2 Discussion
Our iterative framework builds upon Meng et al. (2015). The belief algebra framework naturally extends to scenarios where the agent’s beliefs are partial or incomplete. Unlike total preorders, which require a complete ranking of all worlds, belief algebras allow for the representation of preferences over subsets of worlds, even when some preferences are unspecified. This flexibility is particularly useful in real-world applications where the agent may have limited or uncertain information.
A key distinction with Meng et al. (2015) is that we provide a deeper analysis of the structure of belief algebra and introduce two core revision rules, (RA5) and (RA6). (RA5) imposes a macro-level constraint on belief revision, ensuring that the revision result does not exceed the outcome under complete information when belief information is insufficient. (RA6), on the other hand, requires preserving as much of the original belief information as possible under these constraints. Interestingly, these rules induce a unique revision result. Under our framework, agents with the same belief algebra and evidence will produce identical revision outcomes. While traditional views attribute different revision results to varying operators, we argue that rational agents share highly similar revision operators, and differences arise from their distinct belief algebras.
8 Conclusion
In this paper, we proposed an iterated belief revision framework based on belief algebra where the current belief state, new evidence, and revision results are all represented as belief algebras. Through a deep analysis of the structure of belief algebra and inspired by existing principles of belief revision, we devised natural postulates for rational revision behaviors, including (RA5), which imposes an upper-bound constraint on revision results, ensuring that no revision exceeds the outcome under complete information, and (RA6), which requires preserving as much of the original belief information as possible while satisfying the upper-bound constraint. Interestingly, these postulates induce a unique revision operator, providing a deterministic and principled approach to belief revision. This uniqueness offers a clear guideline for selecting specific revision operators in practical applications.
Moreover, we developed a practical revision algorithm under the new framework, demonstrating its feasibility for real-world use. In future work, we aim to explore efficient methods for representing original belief information (e.g., logical statements or preferences) as belief algebra. Additionally, we will focus on improving the efficiency of our algorithm, reducing its complexity (currently, it is exponential to the number of worlds), and testing its application in specific domains, such as knowledge or rule revision in large language models.
Acknowledgments
We would like to thank the anonymous reviewers for their invaluable help to improve the paper. This work was supported by the National Natural Science Foundation of China under Grant numbers 61806170 and 62276218; the Fundamental Research Funds for the Central Universities under Grant numbers 2682022ZTPY082 and 2682023ZTPY027; the French National Research Agency under Grant number SA21PD01; and University of Montpellier under Grant number PP21PD01-RM06.
References
- Alchourron et al. [1985] Carlos E. Alchourron, Peter Gärdenfors, and David Makinson. On the logic of theory change: Partial meet contraction and revision functions. The Journal of Symbolic Logic, 50(2):510–530, 1985.
- Andrikopoulou et al. [2025] Maria Andrikopoulou, Theofanis Aravanis, James P. Delgrande, Panagis Karazeris, and Pavlos Peppas. Filters-based revision. Annals of Mathematics and Artificial Intelligence, 2025.
- Aravanis et al. [2019] Theofanis I. Aravanis, Pavlos Peppas, and Mary-Anne Williams. Observations on darwiche and pearl’s approach for iterated belief revision. In IJCAI, pages 1509–1515, 2019.
- Aravanis [2023] Theofanis I. Aravanis. Collective belief revision. Journal of Artificial Intelligence Research, 78:1221–1247, 2023.
- Baroni et al. [2022] Pietro Baroni, Eduardo Fermé, Massimiliano Giacomin, and Guillermo Ricardo Simari. Belief revision and computational argumentation: A critical comparison. Journal of Logic, Language and Information, 31(4):555–589, 2022.
- Benferhat et al. [2000] Salem Benferhat, Sébastien Konieczny, Odile Papini, and Ramón Pino Pérez. Iterated revision by epistemic states: axioms, semantics and syntax. In ECAI, pages 13–17, 2000.
- Benferhat et al. [2005] Salem Benferhat, Sylvain Lagrue, and Odile Papini. Revision of partially ordered information: Axiomatization, semantics and iteration. In IJCAI, pages 376–381, 2005.
- Bonanno [2025] Giacomo Bonanno. A kripke-lewis semantics for belief update and belief revision. Artificial Intelligence, 339:104259, 2025.
- Booth and Chandler [2016] Richard Booth and Jake Chandler. Extending the harper identity to iterated belief change. In IJCAI, pages 987–993, 2016.
- Booth and Meyer [2006] Richard Booth and Thomas Andreas Meyer. Admissible and restrained revision. Journal of Artificial Intelligence Research, 26:127–151, 2006.
- Boutilier [1996] Craig Boutilier. Iterated revision and minimal change of conditional beliefs. Journal of Philosophical Logic, 25(3):263–305, 1996.
- Darwiche and Pearl [1997] Adnan Darwiche and Judea Pearl. On the logic of iterated belief revision. Artificial Intelligence, 89(1):1–29, 1997.
- Diller et al. [2015] Martin Diller, Adrian Haret, Thomas Linsbichler, Stefan Rümmele, and Stefan Woltran. An extension-based approach to belief revision in abstract argumentation. In IJCAI, pages 2926–2932, 2015.
- Doyle [1979] Jon Doyle. A truth maintenance system. Artificial Intelligence, 12(3):231–272, 1979.
- Fermé and Hansson [2011] Eduardo L. Fermé and Sven Ove Hansson. AGM 25 years: Twenty-five years of research in belief change. Journal of Philosophical Logic, 40(2):295–331, 2011.
- Harper [1976] W. L. Harper. Rational conceptual change. PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association, 1976:462–494, 1976.
- Hunter and Boyarinov [2022] Aaron Hunter and Konstantin Boyarinov. BRL: A toolkit for learning how an agent performs belief revision. In Ana Paula Rocha, Luc Steels, and H. Jaap van den Herik, editors, ICAART, pages 753–756. SCITEPRESS, 2022.
- Jin and Thielscher [2007] Yi Jin and Michael Thielscher. Iterated belief revision, revised. Artificial Intelligence, 171(1):1–18, 2007.
- Katsuno and Mendelzon [1991] Hirofumi Katsuno and Alberto O Mendelzon. Propositional knowledge base revision and minimal change. Artificial Intelligence, 52(3):263–294, 1991.
- Kern-Isberner et al. [2024] Gabriele Kern-Isberner, Alexander Hahn, Jonas Haldimann, and Christoph Beierle. Total preorders vs ranking functions under belief revision - the dynamics of empty layers. In KR, 2024.
- Lehmann [1995] Daniel Lehmann. Belief revision, revised. In IJCAI, pages 1534–1540, 1995.
- Liberatore [2024] Paolo Liberatore. Representing states in iterated belief revision. Artificial Intelligence, 336:104200, 2024.
- Liu et al. [2023] Likang Liu, Keke Sun, Chunlai Zhou, and Yuan Feng. Two views of constrained differential privacy: Belief revision and update. In Brian Williams, Yiling Chen, and Jennifer Neville, editors, AAAI, pages 6450–6457, 2023.
- Ma et al. [2015] Jianbing Ma, Weiru Liu, and Salem Benferhat. A belief revision framework for revising epistemic states with partial epistemic states. International Journal of Approximate Reasoning, 59:20–40, 2015.
- Meng et al. [2015] Hua Meng, Hui Kou, and Sanjiang Li. Belief revision with general epistemic states. In AAAI, pages 1553–1559, 2015.
- Nayak et al. [2003] Abhaya C Nayak, Maurice Pagnucco, and Pavlos Peppas. Dynamic belief revision operators. Artificial Intelligence, 146(2):193–228, 2003.
- Peppas and Williams [2014] Pavlos Peppas and Mary-Anne Williams. Belief change and semiorders. In KR, 2014.
- Sauerwald and Thimm [2024] Kai Sauerwald and Matthias Thimm. The realizability of revision and contraction operators in epistemic spaces. pages 665–670, 2024.
- Spohn [1988] Wolfgang Spohn. Ordinal conditional functions: A dynamic theory of epistemic states. In W. Spohn, editor, Causation, Coherence, and Concepts, pages 19–41. Springer, 1988.
- van Harmelen et al. [2008] Frank van Harmelen, Vladimir Lifschitz, and Bruce Porter. Handbook of Knowledge Representation. Elsevier, 2008.
- Wilie et al. [2024] Bryan Wilie, Samuel Cahyawijaya, Etsuko Ishii, Junxian He, and Pascale Fung. Belief revision: The adaptability of large language models reasoning. In EMNLP, pages 10480–10496, 2024.
- Williams [1994] Mary-Anne Williams. Transmutations of knowledge systems. In KR, pages 619–629, 1994.
- Williams [1996] Mary-Anne Williams. Applications of belief revision. In Transactions and Change in Logic Databases, 1996.
- Zhang [2010] Dongmo Zhang. A logic-based axiomatic model of bargaining. Artificial Intelligence, 174(16-17):1307–1322, 2010.