On Einstein-non linear-Maxwell-Yukawa de-Sitter black hole thermodynamics

Black holes which are the solutions of Einstein’s equation are the most important and intriguing objects in physics with many fascinating physical properties. A special attention is devoted to their thermodynamics proprieties which have been studied over years in several different contexts since the seminal works of Hawking, Page, Bardeen and Bekenstein [1, 2, 3, 4, 5, 6]. In particular the study of phases transitions of the black holes in AdS space [7, 8, 9] and the analogy between the critical van der Waals gas behavior and the charged AdS black hole one [10, 11, 12, 13, 14, 15, 16] leading to so-called extended phase space. In this context the negative cosmological constant $\Lambda$ can be the thermodynamic pressure defined as $P=-\frac{\Lambda}{8\pi}$. However, when a positive cosmological constant (de Sitter spacetime), the situation is quite different.

The current cosmological observations indicate that the universe is expanding with an accelerated rate, and may tend to de Sitter space asymptotically then in order to construct the whole history of the evolution of our universe, we need to understand the classical and quantum nature of the de Sitter spacetime. This comprehension triggered a deep investigation of the thermodynamic properties of de Sitter background [17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31], knowing that black holes in such spacetime generally possess an event horizon and a cosmological one, which radiate thermally [17, 18]. Consequently, there are different thermodynamics quantities corresponding to each of the two horizons that satisfy the first law of thermodynamics while the corresponding entropies verify the area formula [32, 21].

Born and Infeld have first introduced the nonlinear electrodynamics in order to remove the central singularity of the point-like charges and obtained finite energy solutions for particles by extending Maxwell’s theory [33]. Hereafter, Plebanski and al. have extended the model and presented other kinds of nonlinear electrodynamics Lagrangians [34]. Lately, a variety of nonlinear electrodynamics models have been studied extensively, one of the main reason of this intensive investigation is that such theories appear as effective theories at low energy limits of heterotic string theory [35]. In addition, the nonlinear electrodynamics has also been used to get solutions describing baryon configurations which are consistent with confinement in the AdS/CFT conjecture context [36]. In other contexts, the ability on nonlinear electrodynamics to remove curvature singularities showed a very promising results. As an example, in cosmology, one can call upon nonlinear electrodynamics to explain the inflationary epoch and the late-time accelerated expansion of the universe [37, 38]. Different black hole solutions in general relativity coupled to nonlinear electrodynamics have appeared in black hole field theory literature, where the nonlinear electrodynamics is a source of field equations satisfying the weak energy condition, hence recovering the Maxwell theory in the weak field limit [39, 40, 41, 42, 43, 44, 45].

In addition to Born-Infeld model, other classes of nonlinear electrodynamics have been proposed, ranging from power Maxwell invariant (PMI)[46, 47], $\arcsin$ [48], logarithmic [49] and exponential [50, 51] to models inspired from string theory with very complex form [52, 53, 54, 55]. In [56], the authors consider gravity coupled with a Yukawa-like electric potential, described by the scalar potential, $\phi(r)=\frac{q}{r}e^{-\alpha r}$, where $q$ stands the electric charge and $\alpha$ is a positive constant. By using this ansatz, the theory becomes highly nonlinear and involves two degrees of freedom, namely the charge $q$ and Yukawa charge $\alpha$. The consideration of Yukawa-like electric potential is lent from the nuclear physics[57, 58] and some studies of gravitational potential in the framework of $f(R)$ modified theory of gravity [59, 60, 61, 62]. In our framework, the parameter $\alpha$ is employed to confine the electromagnetic force to a shorter range. In light of all these motivations, we perform in the present work a natural generalization of the paper [56] to de-Sitter spacetime and present a comprehensive analysis of the thermodynamic properties of such black hole from various points of view.

The organization of the paper is as follow: First, we extended the static and spherically symmetric Maxwell-Yukawa solution found in [56] to de-Sitter spacetime, and also discuss its horizons and extremal case. Then we perform a thermodynamics analysis to probe the thermal phase picture via the continuity of heat capacity, its sign and the swallowtail structure of the Gibbs free energy. In section $4$, we use a local approach, which means that each horizon is treated independently. Whereas in section $5$ the event, cosmological and inner horizons are treated simultaneously. This treatment is dubbed the thermodynamics from a global point of view. After that, we recall the notion of effective thermodynamics of the black hole, which has been emerged recently years to investigate the de Sitter black hole thermodynamics. In section $7$, we discuss the Strong-Weak electric interaction transitions and explain how it can be related to the phase transitions. Then we extend the formalism of the effective thermodynamics from two to three horizons. The last section is devoted to our conclusion.

Here, we start by a concise review of the static spherical symmetry black hole solution in Einstein-Yukawa-Maxwell gravity and our extension to de-Sitter spacetime. Yukawa potential in the spherical coordinate system is given by

$$\phi(r)=\dfrac{q}{r}e^{-\alpha r},$$

(1)

in which $q$ denotes the electric charge located at the origin and $\alpha$ is a positive constant. We consider the electric potential and Maxwell’s field as,

$$\text{A}=\phi(r)dt,\quad\text{F}=Edt\wedge dr,$$

(2)

The electromagnetic field and the Maxwell invariant stand for,

$$E=-\phi^{\prime}(r)=\dfrac{q\left(1+\alpha r\right)}{r^{2}}e^{-\alpha r},\quad\mathcal{F}=F_{\mu\nu}F^{\mu\nu}=-2E^{2}.$$

(3)

Then, we introduce the static and spherically symmetric line element ansatz,

$$ds^{2}=-f(r)dt^{2}+\dfrac{dr^{2}}{f(r)}+r^{2}d\Omega^{2},$$

(4)

We examine the Einstein-Hilbert action within the nonlinear electrodynamics Lagrangian $\mathcal{L}=\mathcal{L}(\mathcal{F})$ associated with the Maxwell-Yukawa potential in de-Sitter spacetime

$$S=\dfrac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left[\left(R-\dfrac{\Lambda}{2}\right)+\mathcal{L}(\mathcal{F})\right]$$

(5)

in which $R$ is the Ricci scalar and $\Lambda>0$ is the cosmological constant that characterizes the de Sitter space. The Lagrangian $\mathcal{L}$ is given by [56]

$$\mathcal{L}=\dfrac{4C_{0}q}{r^{4}}\left[\left(\alpha^{3}r^{3}-1-\left(1+\alpha r\right)^{2}\right)e^{-\alpha r}-\alpha^{4}r^{4}\mathcal{E}_{1}(\alpha r)\right]+C_{1}$$

(6)

where $C_{0}$ and $C_{1}$ are integration constants, $\mathcal{E}_{1}(x)$ is the exponential integral defined by the formula [63]

$$\mathcal{E}_{1}(x)=\int_{1}^{\infty}\dfrac{e^{-xt}}{t}dt.$$

(7)

It is worth to notice that the $C_{1}$ may be interpreted as an effective cosmological constant which we will neglect in the rest of this study since we are already considering a dS space. Thus, one obtains the metric function,

$$f(r)=1-\dfrac{2m}{r}+\dfrac{qC_{0}\left(\alpha^{3}r^{3}-\alpha^{2}r^{2}+2\alpha r-6\right)e^{-\alpha r}}{6r^{2}}-\left(\dfrac{\Lambda}{3}+\dfrac{\alpha^{4}qC_{0}}{6}\mathcal{E}_{1}(\alpha r)\right)r^{2}.$$

(8)

The parameter $m$ is an integration constant regarded as mass. To determine $C_{0}$, we consider the limit of vanishing $\alpha$ $(\alpha\to 0)$ for the metric function

$$f(r)=1-\dfrac{2m}{r}-\dfrac{qC_{0}}{r^{2}}-\dfrac{\Lambda}{3}r^{2}.$$

(9)

hence recovering the Reissner-Nordstrom dS black hole solution. This implies $C_{0}=-q$. Consequently, Eq. (8) becomes,

$$f(r)=1-\dfrac{2m}{r}-\dfrac{q^{2}\left(\alpha^{3}r^{3}-\alpha^{2}r^{2}+2\alpha r-6\right)e^{-\alpha r}}{6r^{2}}-\left(\dfrac{\Lambda}{3}-\dfrac{\alpha^{4}q^{2}}{6}\mathcal{E}_{1}(\alpha r)\right)r^{2};$$

(10)

which is the final form of the ENLMY-dS black hole solution. By rescaling the variables : $\rho=\alpha r$, $M=\alpha m$, $Q=\alpha q$ and $\lambda=\Lambda/\alpha$; the metric function reads

$$f(\rho)=1-\dfrac{2M}{\rho}-\dfrac{Q^{2}\left(\rho^{3}-\rho^{2}+2\rho-6\right)e^{-\rho}}{6\rho^{2}}-\left(\dfrac{\lambda}{3}-\dfrac{Q^{2}}{6}\mathcal{E}_{1}(\rho)\right)\rho^{2},$$

(11)

Eq. (11) shows that $f(\rho)$ is not explicitly dependent on $\alpha$ which acts as a scale factor, so it can be chosen as $\alpha=1$. Hence, irrespective of the value of $\alpha$, one can study the global properties of the resulting solution. Nevertheless, we should keep in mind that $\alpha$ is a ”charge” that corresponds to a potential which play a part in black hole thermodynamics. Having obtained the essential of the ENLMY-dS black hole solution, we will investigate its phase structure within different thermodynamics points of view.

Before probing the phase picture, an overview of the black hole horizon and their extremal cases is necessary. The relation between the black hole mass $M$ and its horizon radius is naturally established from the equation of horizons $f(\rho)=0$,

$$M=\dfrac{\rho}{2}-\dfrac{Q^{2}\left(\rho^{3}-\rho^{2}+2\rho-6\right)e^{-\rho}}{12\rho}-\left(\dfrac{\lambda}{6}-\dfrac{Q^{2}}{12}\mathcal{E}_{1}(\rho)\right)\rho^{3}.$$

(12)

We depict in Fig. 1 the behavior of the black hole mass $M$ as function of the radius $\rho$ for different values of cosmological constant $\lambda$.

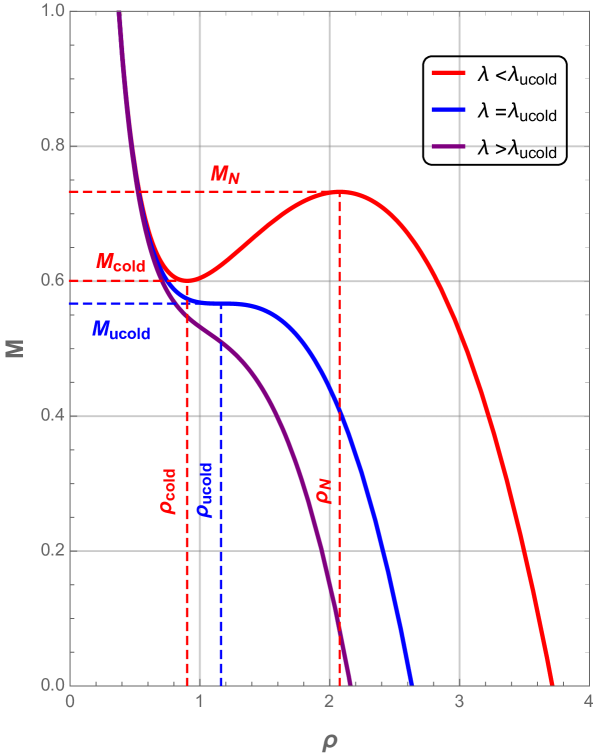
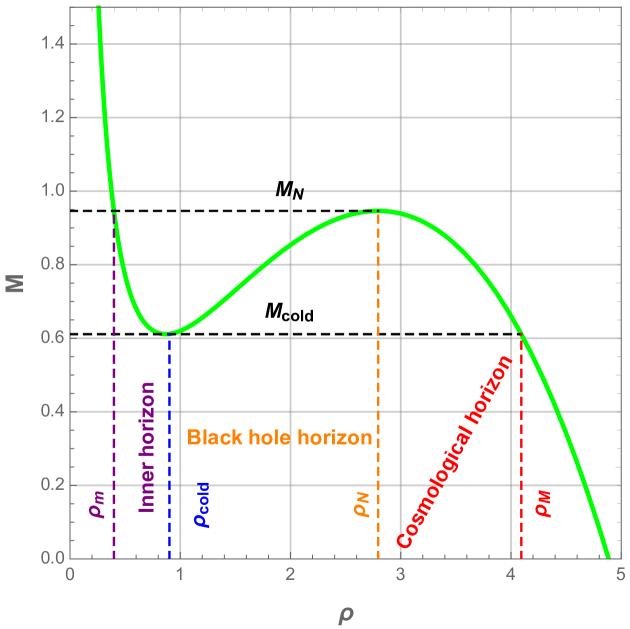
For the appropriate values of the electric charge $Q$ and the cosmological constant $\lambda<\lambda_{ucold}$, the black hole mass plot presents a local minimum followed by a local maximum that are both located above the horizontal axis. These local extrema imply that the black hole has three horizons: the inner horizon $\rho_{-}$, the event horizon $\rho_{+}(>\rho_{-})$ and the cosmological horizon $\rho_{c}(>\rho_{+})$. When the cosmological constant reaches the critical value $\lambda=\lambda_{ucold}$, the mass curve shows an inflection point where the three horizons coincide. In this case, the black hole is dubbed ultra-cold black hole. From Fig. 2, we can see that ultra-cold black hole with larger electric charge has larger horizon radius and larger mass, whereas the critical value for the cosmological constant is smaller one.

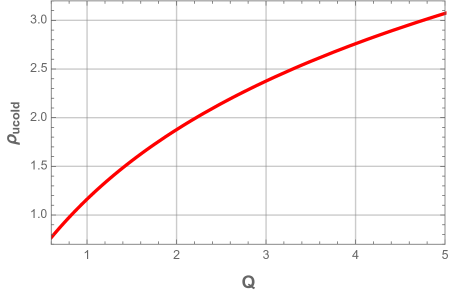
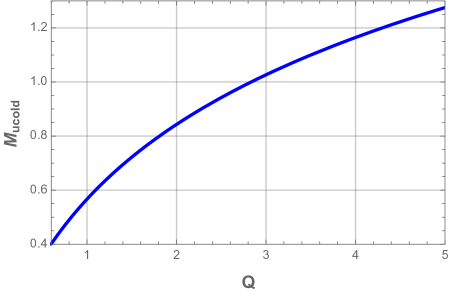
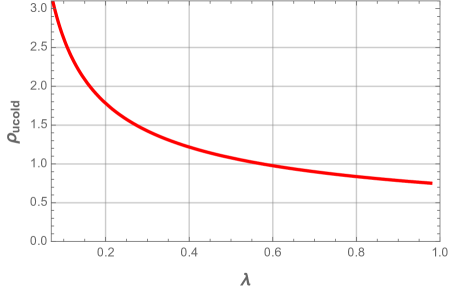
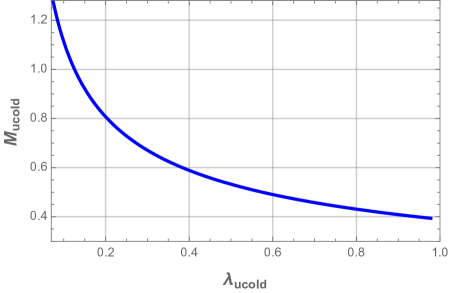
In the case where $\lambda>\lambda_{ucold}$, no black hole exists whatever its mass phase. The critical value of the cosmological constant for the existence of the ENLMY charged dS black hole is larger than that for the usual charged dS black hole. This can be explained by the electric repulsion which is much more weaker in the nonlinear Maxwell-Yukawa electrodynamics than in the usual electrodynamics.

For the case $\lambda<\lambda_{ucold}$, the situation is quite different, on can note that the black hole phase exists only for a range of mass values, $M\in[M_{cold},M_{N}]$, where $M_{cold}$ and $M_{N}$ are functions of the charges and cosmological constant. When $M=M_{N}$, the event horizon $\rho_{+}$ and the cosmological one $\rho_{c}$ coincide, this give rise to a new phase called Nariai black hole with an event horizon radius noted $\rho_{N}$. The latter and its associated mass are depicted in Fig. 3 as a function of the charge and cosmological constant.

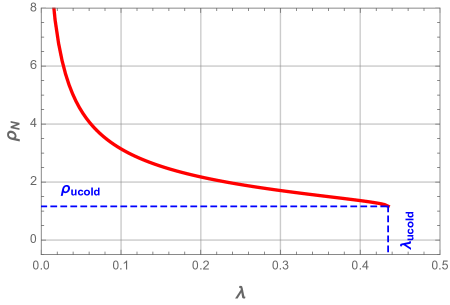
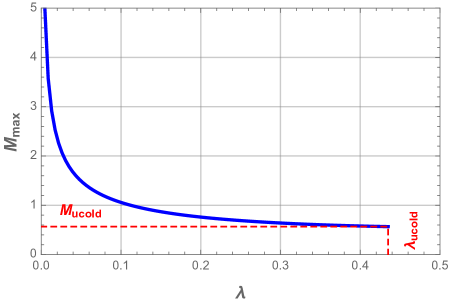
From Fig. 3 we notice that both the event horizon radius and mass of the Nariai black hole should decrease as the cosmological constant increases till the value $\lambda=\lambda_{ucold}$.

When $M=M_{cold}$, the inner horizon $\rho_{-}$ and the event horizon $\rho_{+}$ coincide, this phase is dubbed cold black hole. Fig. 4 illustrates the plots of its event horizon radius $\rho_{cold}$ and corresponding mass as a function of the charge and cosmological constant.

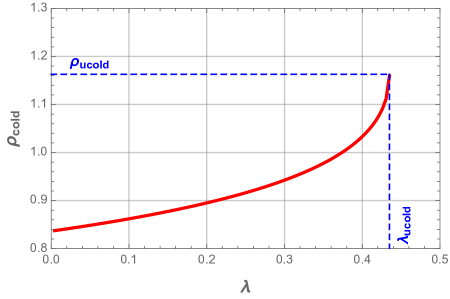
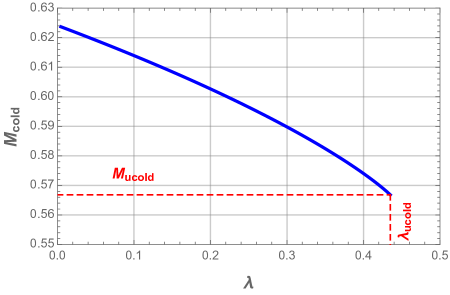
We clearly see that the event horizon radius of the cold black hole increases, but its mass decreases as the cosmological constant get larger till the value $\lambda=\lambda_{ucold}$.

After discussing various black hole possible solutions and their extremal case, the next section will be dedicated to the investigation of the thermodynamics from the local point of view.

In the extended phase space, the entropy $S$, the electric charge $Q$, Yukawa charge $\alpha$, and the thermodynamic pressure $P$ are interpreted as a complete set of the extensive thermodynamics variables. Their associated conjugate quantities are the temperature $T$, the pseudo-electrical potential $\Phi_{q}$, the pseudo-Yukawa potential $\Phi_{\alpha}$, and the thermodynamic volume $V$ respectively. Under these considerations, one can establish the first law of thermodynamics for each horizon: the event horizon, the cosmological and the inner one as follow,

$$\begin{split}&dM=T_{+}dS_{+}+V_{+}dP+\Phi_{q_{+}}dQ+\Phi_{\alpha_{+}}d\alpha,\\ &dM=-T_{c}dS_{c}+V_{c}dP+\Phi_{q_{c}}dQ+\Phi_{\alpha_{c}}d\alpha,\\ &dM=-T_{-}dS_{-}+V_{-}dP+\Phi_{q_{-}}dQ+\Phi_{\alpha_{-}}d\alpha.\end{split}$$

(13)

Note that the minus signs in front of $T_{c}$ and $T_{i}$ are introduced to ensure an increasing entropy: As the cosmological and inner horizon radius $r_{c,-}$ increase, the mass $M$ should decrease. Then, on can write the black hole mass, Eq. (12), in terms of the event, inner and cosmological horizons, respectively as

$$\begin{split}&M(\rho_{\pm,c},P,Q)=\dfrac{\rho_{\pm,c}}{2}-\dfrac{Q^{2}\left(\rho_{\pm,c}^{3}-\rho_{\pm,c}^{2}+2\rho_{\pm,c}-6\right)e^{-\rho_{\pm,c}}}{12\rho_{\pm,c}}-\left(\dfrac{\lambda}{6}-\dfrac{Q^{2}}{12}\mathcal{E}_{1}(\rho_{\pm,c})\right)\rho_{\pm,c}^{3},\\ \end{split}$$

(14)

Note that the Yukawa charge $\alpha$ is implicitly included in all variables by the re-scaling performed previously, thus we should take it into account when necessary. In what follows, to perform the thermodynamic analysis and phase transition for each horizon independently, we assume that the horizons are located far away from each other to avoid their overlapping.

The scaled Hawking temperature corresponding to each horizon is given by [64, 65],

$$\begin{split}T_{\pm,c}&=\dfrac{1}{4\pi}\left.\dfrac{\partial f(\rho)}{\partial\rho}\right|_{\rho=\rho_{+}}\\ =&\dfrac{1}{8\pi\rho_{+}^{3}}\left[\rho_{+}^{2}\left(2+16P\rho_{+}^{2}+Q^{2}\rho_{+}^{2}\mathcal{E}(\rho_{+})\right)\right.\left.-Q^{2}\left(2+\rho_{+}\left(2+\rho_{+}\left(\rho_{+}-1\right)\right)\right)e^{-\rho_{+}}\right]\\ T_{-,c}=&-\dfrac{1}{4\pi}\left.\dfrac{\partial f(\rho)}{\partial\rho}\right|_{\rho=\rho_{-,c}}\\ =&-\dfrac{1}{8\pi\rho_{-,c}^{3}}\left[\rho_{-,c}^{2}\left(2+16P\rho_{-,c}^{2}+Q^{2}\rho_{-,c}^{2}\mathcal{E}(\rho_{-,c})\right)\right.\left.-Q^{2}\left(2+\rho_{-,c}\left(2+\rho_{-,c}\left(\rho_{-,c}-1\right)\right)\right)e^{-\rho_{-,c}}\right]\\ \end{split}$$

(15)

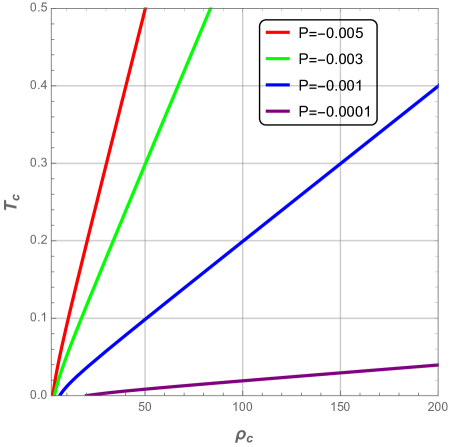
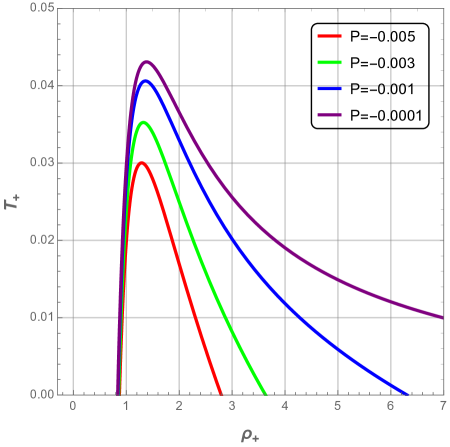
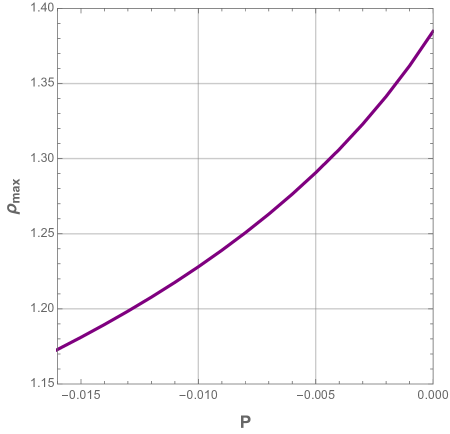
where, we have defined the pressure to be $P=-\lambda/8\pi<0$. In Fig. 5, we plot the variation of the scaled temperatures as a function of each reduced horizons. One can notice from Fig. 5 that the temperatures $T_{-,c}$ are monotonous in terms of the inner and cosmological radius $\rho_{-,c}$, whereas the event horizon temperature $T_{+}$ presents a maximum $T_{max}$ value listed in Table 1 with its corresponding radius, then decreases as the event horizon radius $\rho_{+}$ increases.

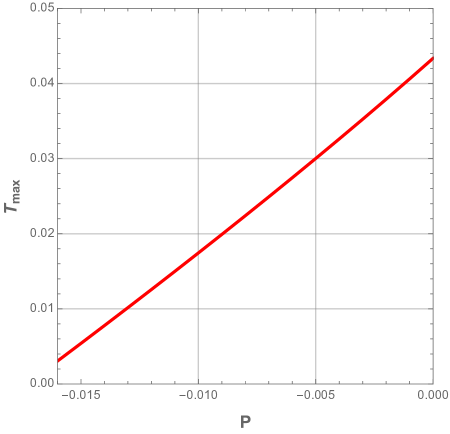
The maximum temperature $T_{max}$ and its corresponding event horizon radius $\rho_{max}$ are illustrated in Fig. 5 where we see that both quantities are increasingly monotonous functions of pressure $P$.

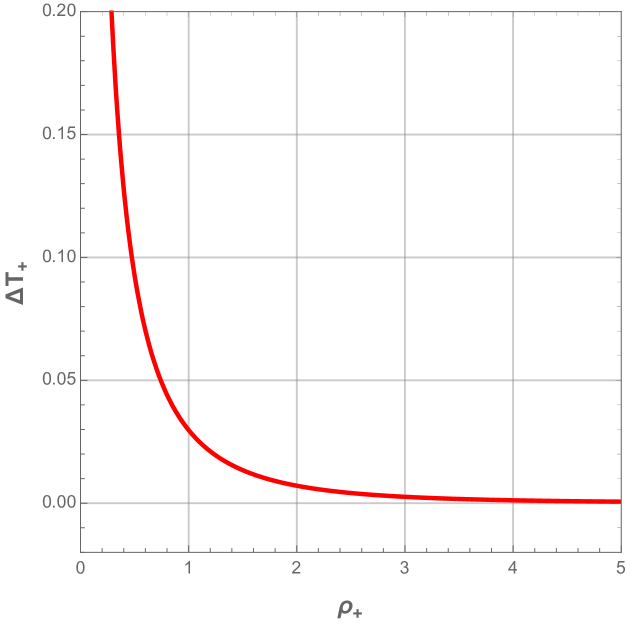
Now, a comparison between the ENLMY and usual charged dS black holes with the same size, charge and the pressure is needed. For that, we depict in Fig. 7 the difference of temperature as a function of horizon radius $\rho_{+}$. One can easily see that the ENLMY charged dS black hole is exponentially hotter than the usual charged black hole when $\rho\to 0$.

From the expression of the first law Eq. (13), the formulas of mass Eq. (14) and temperature Eq. (15), we can evaluate the entropy corresponding to each horizon,

$$S_{+}=\int\dfrac{1}{T_{+}}\dfrac{\partial M}{\partial\rho_{+}}d\rho_{+}=\pi\rho^{2}_{+},$$

(16)

$$S_{-,c}=-\int\dfrac{1}{T_{-,c}}\dfrac{\partial M}{\partial\rho_{-,c}}d\rho_{-,c}=\pi\rho^{2}_{-,c}.$$

(17)

Having obtained the black hole temperature and entropy associated with each horizon, we proceed further and evaluate other relevant thermodynamics variables composing the first law. The electric potential associated with the charge $q$ is :

$$\Phi_{q_{\pm,c}}=\left.\dfrac{\partial M}{\partial Q}\right)_{S_{\pm,c},P,\alpha}=\dfrac{Q}{6\rho_{\pm,c}}\left[\rho_{\pm,c}^{4}\mathcal{E}(\rho_{\pm,c})+\left(6+\rho_{\pm,c}\left(\rho_{\pm,c}\left(\rho_{\pm,c}-1\right)-2\right)\right)e^{-\rho_{\pm,c}}\right]$$

(18)

while the potentials corresponding to Yukawa charge are given by,

$$\Phi_{\alpha_{\pm,c}}=\left.\dfrac{\partial M}{\partial\alpha}\right)_{S_{\pm,c},P,Q}=\dfrac{Q}{3}\left[\rho_{\pm,c}^{3}\mathcal{E}(\rho_{\pm,c})+\left(\rho_{\pm,c}\left(\rho_{\pm,c}-1\right)-2\right)e^{-\rho_{\pm,c}}\right],$$

(19)

and the thermodynamic volumes read as,

$$V_{\pm,c}=\left.\dfrac{\partial M}{\partial P}\right)_{S_{\pm,c},Q,\alpha}=\dfrac{4}{3}\pi r_{\pm,c}^{3}$$

(20)

All above thermodynamics variables on the event and inner/cosmological horizons satisfy the Smarr and Smarr-like formulas which, by a scaling argument, can be expressed as,

$$\begin{split}M&=2\left(T_{+}S_{+}-V_{+}P\right)+Q\Phi_{q_{+}}-\alpha\Phi_{\alpha_{+}},\\ M&=-2\left(T_{-,c}S_{-,c}+V_{-,c}P\right)+Q\Phi_{q_{+}}-\alpha\Phi_{\alpha_{-,c}},\\ \end{split}$$

(21)

Note that the Yakawa potential energy is simply given by the formula:

$$E_{Y}=q\Phi_{q}-\dfrac{\alpha}{2}\Phi_{\alpha}=\dfrac{q^{2}}{r}e^{-\alpha r}=q\phi(r).$$

(22)

Hence, we can express the heat capacity at constant pressure on the event, inner and cosmological horizons respectively as,

$$C_{P+}=\left.\dfrac{\partial M}{\partial T_{+}}\right)_{P},\hskip 14.22636ptC_{P-,c}=-\left.\dfrac{\partial M}{\partial T_{-},c}\right)_{P},\hskip 14.22636pt$$

(23)

Next we display in Fig. 8 and Fig. 9 the heat capacity $C_{P+}$ as a function of the reduced horizon $\rho$ and temperature respectively, for different values of the pressure $P$.

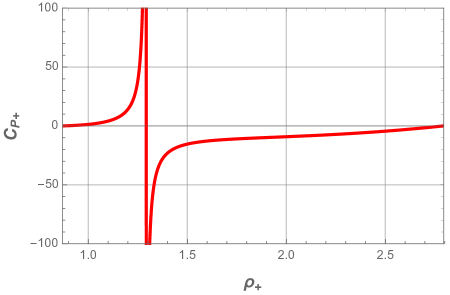
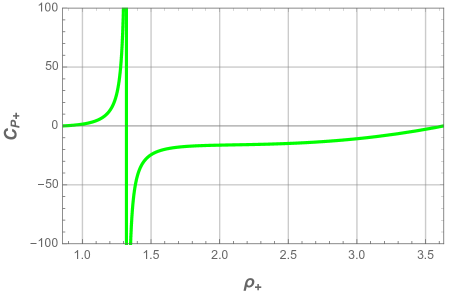
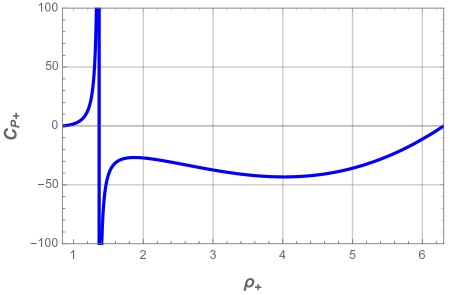
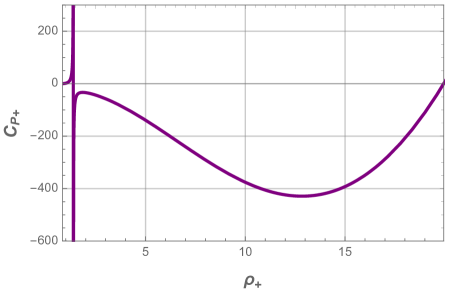
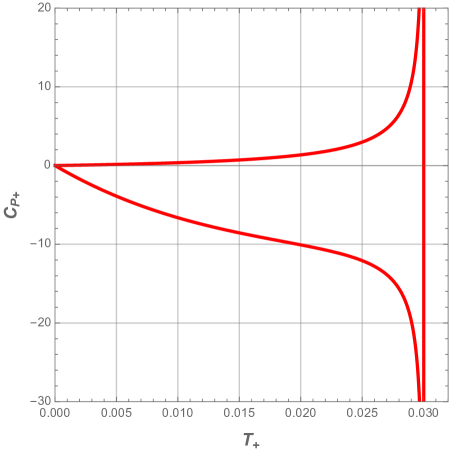
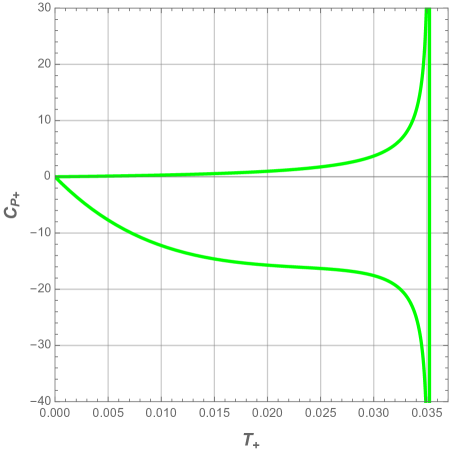
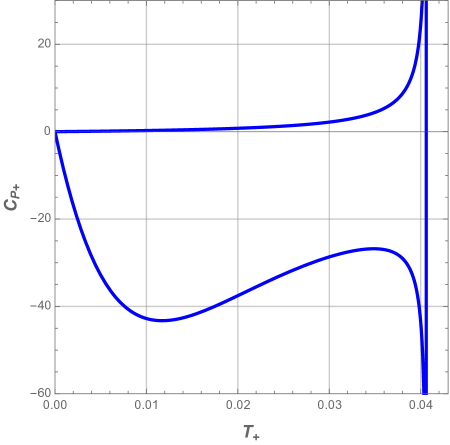
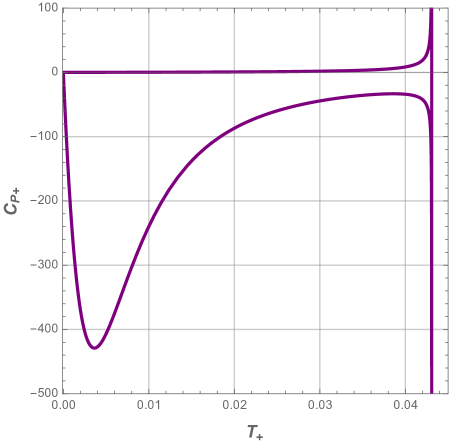
In all panels of the above figures, we easily deduce that the heat capacity $C_{P+}$ presents a discontinuity at the local maximum $T_{max}$. This singularity involves a thermal phase transition between a stable small black hole and unstable large black one at this critical point. We also note that the system is dominated by the unstable phase when the pressure $P$ decreases.

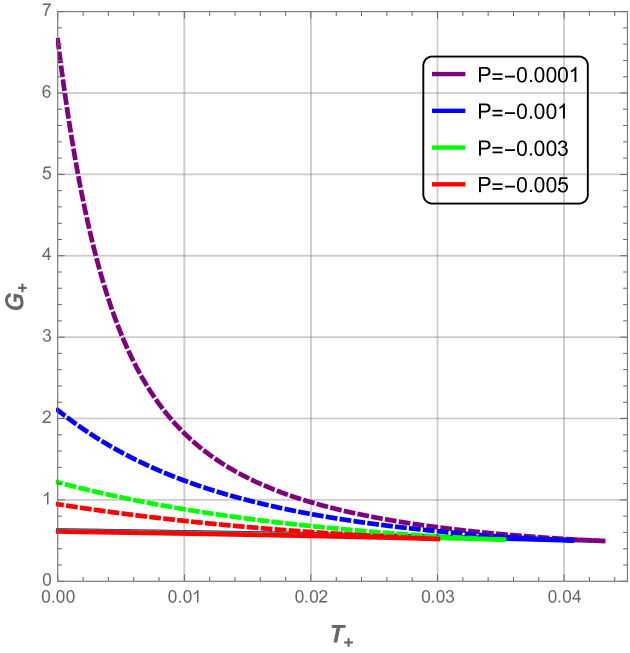
In Fig. 10, the characteristic swallowtail behavior of the Gibbs free energy $G_{+}=M-T_{+}S_{+}$ shows that first-order phase transition occurs between large and small black holes. It is worth to notice that both branches meet at the cusp: The lower branch corresponds to small black hole stable phase, while the upper one to the large black hole unstable phase.

With respect to the cosmological horizon, the heat capacity $C_{Pc}$ is always negative and thus the cosmological horizon becomes larger. Next step, we focus on the study of the equation of state. To this end, we illustrate in Fig. 11 the variation of the pressure $P$ as a function of the horizon radius $\rho$ for fixed charge $Q$.

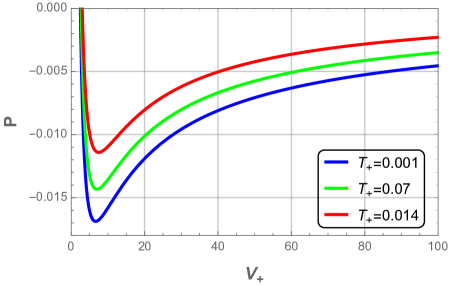
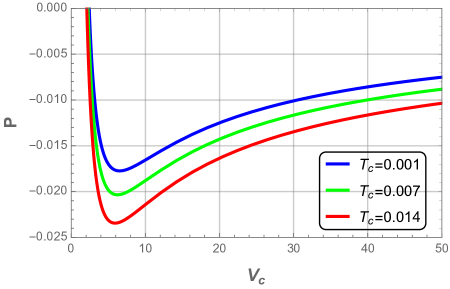
From the $P-\rho$ diagram we see that the event and cosmological horizons have the same shape. However, by comparison to the event horizon, the larger temperatures cosmological horizon correspond to smaller pressures.

After presenting the local thermodynamics context, where each horizon is treated separately, we will focus in the next section on the global thermodynamics view where the horizons are simultaneously analyzed.

To study all the horizons simultaneously, we note that

	$\displaystyle G_{c}\left(\rho_{c},P,Q\right)$	$\displaystyle=-G\left(\rho_{+}\to\rho_{c},P,Q\right),$		(24)
	$\displaystyle G_{-}\left(\rho_{-},P,Q\right)$	$\displaystyle=-G\left(\rho_{+}\to\rho_{-},P,Q\right),$		(25)

This means that the information about the thermodynamics of all horizons is in fact encoded in $G_{+}$, provided we extend its validity to “all admissible radii” $\rho_{+}$, and hence to negative temperatures $T_{+}$. The latter correspond to positive temperature of the cosmological and inner horizons. Therefore, in these regions, the thermodynamic equilibrium occurs for the global maximum (rather than minimum) of $G_{+}$.

Now, for a fixed pressure $P$ and charge $Q$, we introduce the radius of cold black hole $\rho_{cold}$ and the radius associated with Nariai black hole $\rho_{N}$. We also denote by $\rho_{m}$ the minimal radius of the inner horizon, which occurs for the Nariai limit, and $\rho_{M}$ the maximal radius of the cosmological horizon, happening at the extremal black hole . This is illustrated by Fig. 12 where the black hole mass variation is plotted as a function of the horizon radius.

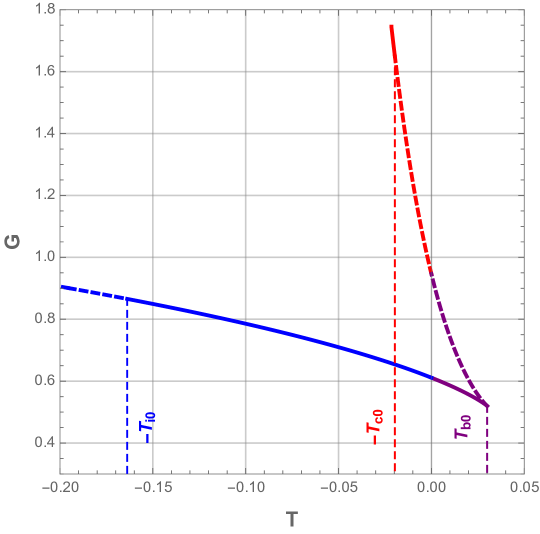
In Fig. 13, we plot the Gibbs free energy function $G=G(T)$ for the range $\rho\in[\rho_{m},\rho_{M}]$, with an interpretation of each thermodynamic quantities for different ranges of $\rho$.

• •

  In the range of radius $\rho\in[r_{m},\rho_{cold}]$, the $G=-G_{-}$ and $T=-T_{-}$ are the inner horizon quantities and the global maximum of $G$ corresponds to a thermodynamic preferred state.

• •

  The domain $\rho\in[\rho_{cold},\rho_{N}]$, the $G=G_{+}$ and $T=T_{+}$ denote black hole horizon quantities while $G$ is minimized by the thermodynamic preferred state.

• •

  Finally, the interval $\rho\in[\rho_{N},\rho_{M}]$,the $G=-G_{c}$ and $T=-T_{c}$ are seen as cosmological horizon quantities and the preferred state again corresponds to the maximum of $G$. As is illustrated in Fig. 13.

Having defined the Gibbs free energy $G$ that describes the thermodynamic behavior of each involved horizons, we will focus on the stability and the phase structure of such a black hole. In Fig. 14, we illustrate the temperatures of all horizons in terms of the ratio $x=\rho_{+}/\rho_{c}$ taking into account that only admissible values of $x$ which range between extremal and Nariai’ bounds, $x\in[x_{m}=\frac{\rho_{cold}}{\rho_{N}},1]$.

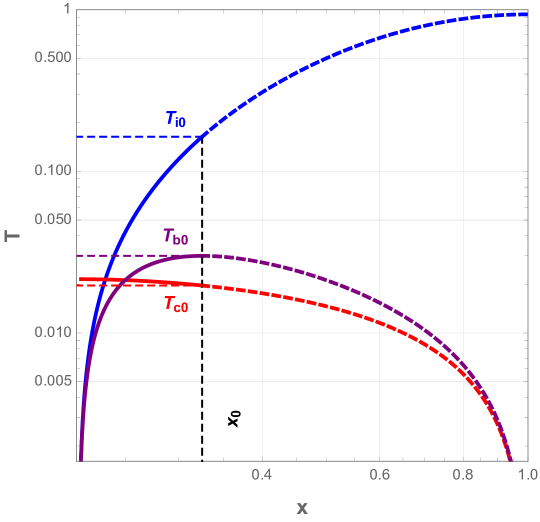
From the previous plots, we directly observe how the temperatures behave when $\rho_{+}$ $(x)$ increases. We also see from Fig. 13 that for small variations of $T$ (till the cusp), the black hole keeps moving along a lower branch with low Gibbs free energy, and hence is in a preferred thermal phase. However, by crossing the cusp, the black hole migrates to the upper black hole branch which is unstable. Therefore, we conclude that the instability regions exist not only for the black hole horizon but also for the cosmological and inner horizon branches.

This explains how the thermodynamics of each horizon interplay towards the understanding of the thermodynamic behavior of the whole system.

The effective black hole thermodynamics of dS black hole has attracted increasing interest in literature [19, 66, 23, 24, 67, 68, 69, 70, 71], thus, it is justified to investigate such a black hole where the main ingredient for such a formalism is to focus on an observer located between the black hole horizon and the cosmological one, and attribute to the system an “effective temperature”.

If the event and cosmological horizons are not located far away, one cannot analyze the thermodynamics and thermal phase transition in an independent way. Since the temperatures on the event and cosmological horizons are different, the black hole generally cannot be in thermodynamic equilibrium, except for the degenerate case $\rho_{+}=\rho_{c}$

In the effective thermodynamics framework, the thermodynamic first law and Smarr-like formula [71] read as:

$$dM=T_{eff}dS_{eff}+V_{eff}dP+\Phi_{q_{eff}}dQ+\Phi_{\alpha_{eff}}d\alpha,$$

(26)

$$M=-2(T_{eff}S_{eff}+V_{eff}P)+\Phi_{q_{eff}}Q-\Phi_{\alpha_{eff}}\alpha.$$

(27)

then, by using Eq. (13) and Eq. (21), they can be written as,

$$\begin{split}dM=&-\dfrac{T_{+}T_{c}}{T_{+}+T_{c}}d(S_{c}-S_{+})+\dfrac{V_{+}T_{c}+V_{c}T_{+}}{T_{+}+T_{c}}dP+\dfrac{\Phi_{q_{+}}T_{c}+\Phi_{q_{c}}T_{+}}{T_{+}+T_{c}}dQ+\dfrac{\Phi_{\alpha_{+}}T_{c}+\Phi_{\alpha_{c}}T_{+}}{T_{+}+T_{c}}d\alpha,\end{split}$$

(28)

$$\begin{split}M=&-2\left(\dfrac{T_{+}T_{c}}{T_{+}+T_{c}}(S_{c}-S_{+})+\dfrac{V_{+}T_{c}+V_{c}T_{+}}{T_{+}+T_{c}}P\right)+\dfrac{\Phi_{q_{+}}T_{c}+\Phi_{q_{c}}T_{+}}{T_{+}+T_{c}}Q-\dfrac{\Phi_{\alpha_{+}}T_{c}+\Phi_{\alpha_{c}}T_{+}}{T_{+}+T_{c}}\alpha.\end{split}$$

(29)

The effective thermodynamic variables are given by,

$$\begin{split}&T_{eff}=\dfrac{T_{+}T_{c}}{T_{+}+T_{c}},\hskip 14.22636ptV_{eff}=\dfrac{V_{+}T_{c}+V_{c}T_{+}}{T_{+}+T_{c}},\\ &\Phi_{q_{eff}}=\dfrac{\Phi_{q_{+}}T_{c}+\Phi_{q_{c}}T_{+}}{T_{+}+T_{c}},\hskip 14.22636pt\Phi_{\alpha_{eff}}=\dfrac{\Phi_{\alpha_{+}}T_{c}+\Phi_{\alpha_{c}}T_{+}}{T_{+}+T_{c}}\end{split}$$

(30)

while the effective entropy is defined as in [70, 71],

$$S_{eff}=S_{c}-S_{+}$$

(31)

From Fig. (21) it is worth to notice that the pressure can be expressed in terms of the horizon radii, especially if one considers black hole thermodynamics with a fixed cosmological horizon. This scenario will be examined thereafter.

In Fig. 15, we plot the behavior of the effective temperature $T_{eff}$ as a function of the horizon radius $\rho_{+}$ for different values of electric charge $Q$.

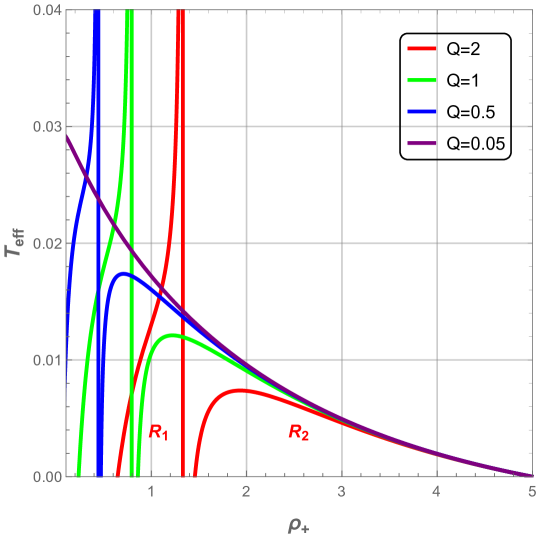
For large $Q$, there exist two regions, $R_{1}$ and $R_{2}$ which are separated by negative temperatures forbidden region $\rho_{+}\in\left[\rho_{div},\rho_{0}\right]$ , where $\rho_{div}$ and $\rho_{0}$ denote a divergent point and a zero-temperature point of $T_{eff}$ respectively. In the region $R_{1}$, $T_{eff}$ is an increasingly monotonous function of $\rho_{+}$ with an inflection point, while in the second region $R_{2}$, $T_{eff}$ first increases until a maximum value, then decreases when $\rho_{+}$ becomes large. Due to the existence of forbidden region, the black hole freezes in one of these two regions without possible transition to the other one.

In the next step in our analysis, we evaluate the effective heat capacity at constant pressure, $C_{P_{eff}}$, and reveal its singularities with the aim to probe its thermal phase structure. The effective heat capacity $C_{P_{eff}}$ can be defined as:

$$C_{P_{eff}}=\left.\dfrac{\partial M}{\partial T_{eff}}\right)_{P}=\left(\dfrac{\partial M}{\partial\rho_{+}}-\dfrac{\partial M}{\partial\rho_{c}}\dfrac{\frac{\partial P}{\partial\rho_{+}}}{\frac{\partial P}{\partial\rho_{c}}}\right)\left(\dfrac{\partial T_{eff}}{\partial\rho_{+}}-\dfrac{\partial T_{eff}}{\partial\rho_{c}}\dfrac{\frac{\partial P}{\partial\rho_{+}}}{\frac{\partial P}{\partial\rho_{c}}}\right)^{-1}.$$

(32)

In Fig. 16, we plot the heat capacity as a function of the horizon radius $\rho_{+}$ with different values of the electric charge $Q$.

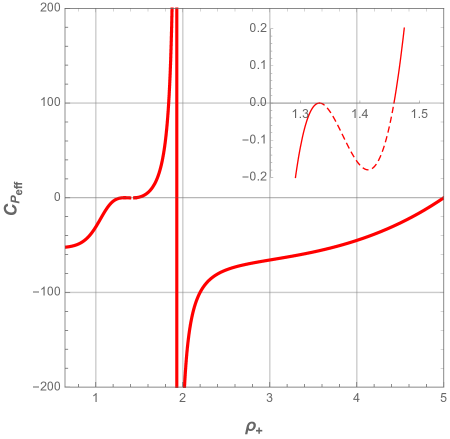
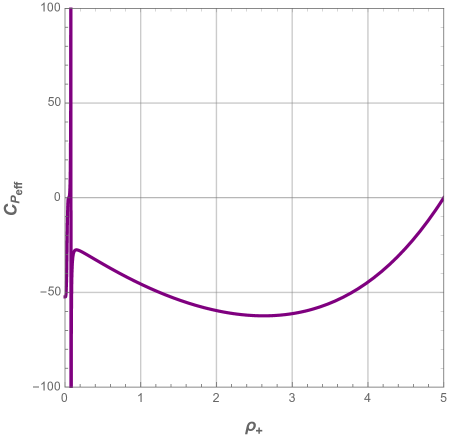
From this figure, one can easily deduce the thermodynamic stability of such a system and derive its thermal phase transition. For large electric charge $Q$, if the black hole resides in the first region $R_{1}$, the heat capacity $C_{P_{eff}}$ is negative, hence the black hole is unstable and no thermal phase transition occurs. Alternatively, if the black hole subsists in the region $R_{2}$, the heat capacity $C_{P_{eff}}$ presents a singularity that can be interpreted as a thermal phase transition between an unstable large black hole ($C_{P_{eff}}<0$ ) and a stable small black hole ($C_{P_{eff}}>0$ ).

However, for the small electric charge scenario, the first region $R_{1}$ should disappear, thus the black hole remains in the second region $R_{2}$. This means that the black hole undergoes a thermal phase transition between an unstable and stable phases. In this regime, when $Q$ decreases below a certain small value, the black hole is again unstable with no possible thermal phase transition, a situation similar to that where the black hole resides in $R_{1}$.

The previous suggested phase transitions can also be recovered through analysis of the Gibbs free energy $G_{eff}$ given by,

$$G_{eff}=M-T_{eff}S_{eff},$$

(33)

and plotted in Fig. 17.

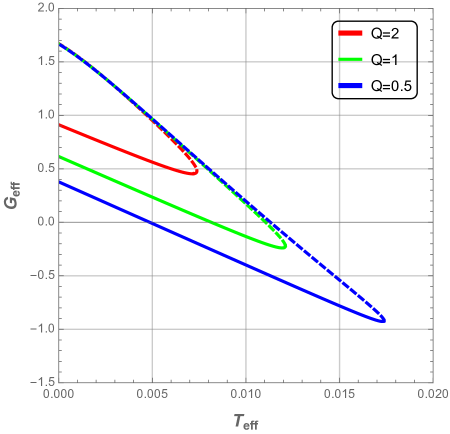
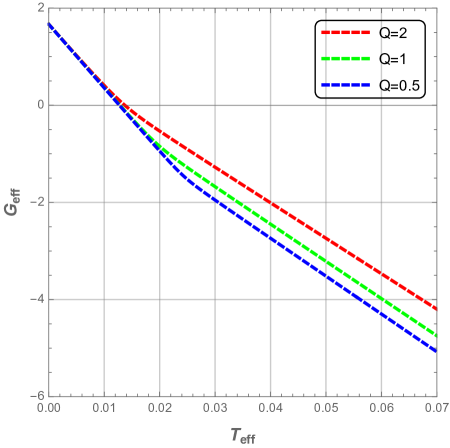
From Fig. 17, one can clearly see that for the black hole residing in the region $R_{1}$, the effective free Gibbs energy $G_{eff}$ is a decreasingly monotonous linear function of the effective temperature $T_{eff}$ with the presence of a point where $G_{eff}$ changes the slope. This change of slope can suggest a thermal phase transition at this point (See next section). Otherwise, for the black hole staying in the region $R_{2}$, $G_{eff}$ is a multi-valued function as indicated by the presence of the swallowtail figure. Thus a thermal phase transition between an unstable phase (large black hole i.e dashed line) and stable phase (small black hole i.e solid line) should occur. Here, the black hole with a larger electric charge has a smaller critical effective temperature.

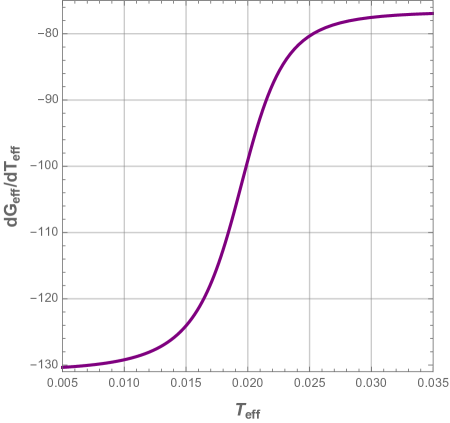
In the previous section, we have seen that the effective free Gibbs energy in the first region $R_{1}$ changes its slope at a certain temperature which means that the derivative of $G_{eff}$ may probably show a discontinuity at this point. In order to look at this, we study first the effective heat capacity $C_{P_{eff}}$ and its first partial derivative which we plot in Fig. 18.

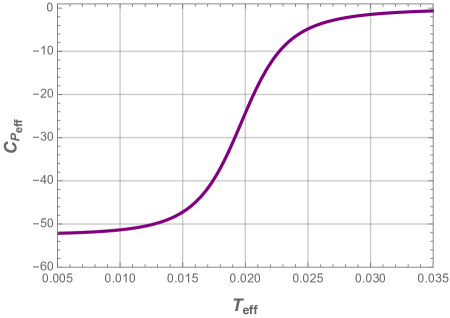
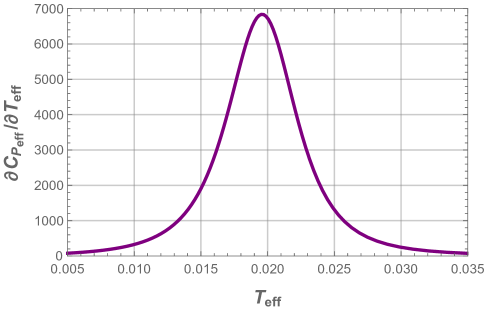
We see that the effective heat capacity suffers form a discontinuity which correspond to a divergent point in its partial derivative. If we look further at the first and second derivatives of the effective Gibbs free energy $G_{eff}$, we notice from Fig. 19, that $\frac{dG_{eff}}{dT_{eff}}$ (panel a) has a discontinuity, as the effective heat capacity, whereas $\frac{d^{2}G_{eff}}{dT_{eff}^{2}}$ (panel b) diverges at this point²²2Here we assume that very large values are assimilated to infinity..

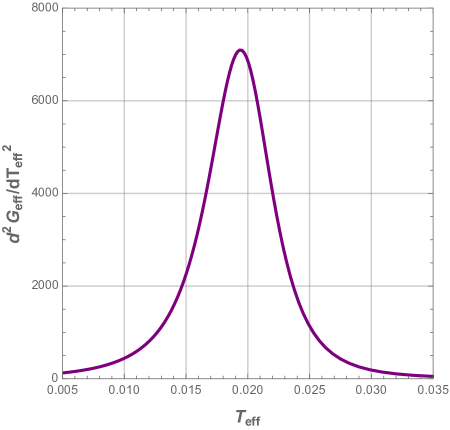
Finally, probably for the first time in black hole thermodynamics, we introduce the logarithmic effective heat capacity $C_{P_{eff}}$ by analogy with the $\beta$-function introduced in [72] to study the metal-insulator transition in condensed matter physics ³³3$\beta$-function is defined by $\beta(G)=\frac{dLog(G)}{dLog(L)}$, where $G$ is the conductance and $L$ is the system size. $\beta(G)$ is positive in the metallic phase and negative in the insulator phase. This function changes its monotony due to the interactions as it was demonstrated in [73]. We accordingly define the logarithmic effective heat capacity $C_{P_{eff}}$ as,

$$\begin{split}CL_{P_{eff}}&=\left.\dfrac{\partial\log(M)}{\partial\log(T_{eff})}\right)_{P}\\ &=\left(\dfrac{\partial\log(M)}{\partial\rho_{+}}-\dfrac{\partial\log(M)}{\partial\rho_{c}}\dfrac{\frac{\partial P}{\partial\rho_{+}}}{\frac{\partial P}{\partial\rho_{c}}}\right)\left(\dfrac{\partial\log(T_{eff})}{\partial\rho_{+}}-\dfrac{\partial\log(T_{eff})}{\partial\rho_{c}}\dfrac{\frac{\partial P}{\partial\rho_{+}}}{\frac{\partial P}{\partial\rho_{c}}}\right)^{-1},\end{split}$$

(34)

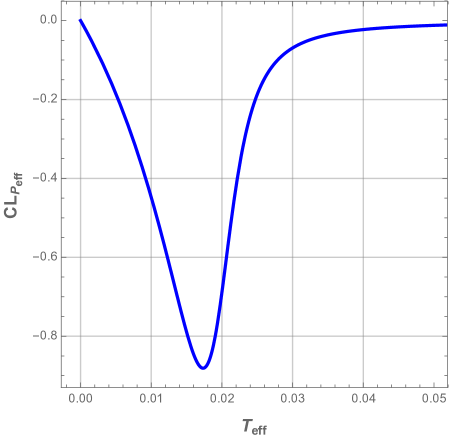
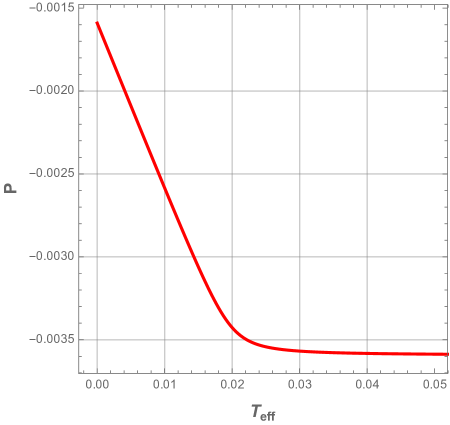
that we illustrate in Fig. 20 (panel a) as a function of the effective temperature. We also show in the panel b, the behavior of pressure as a function of the effective temperature.

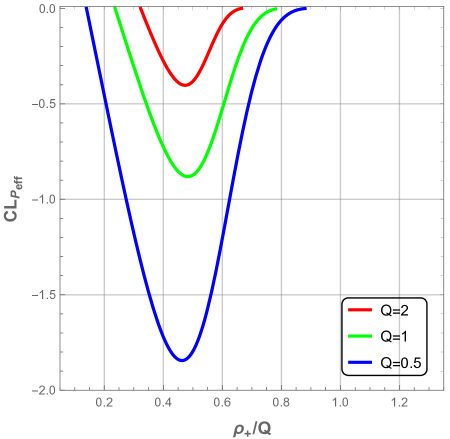
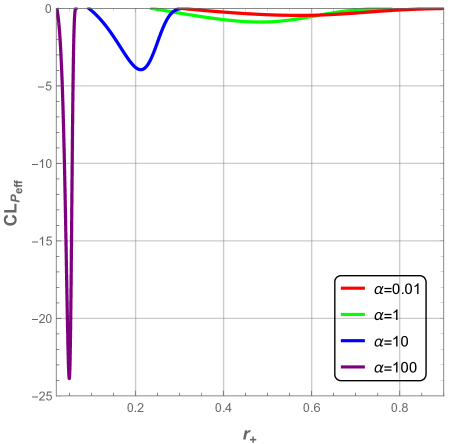
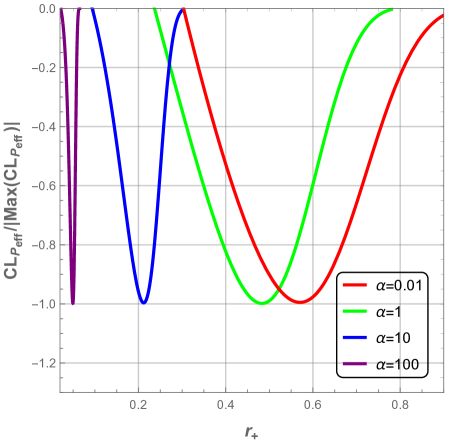
We clearly see that we have a thermal transition between the strong interacting phase and the weak interacting phase. These two phases are unstable. The critical radius $\rho_{+s}$ of this transition is proportional to electric charge as it is shown in Fig. 21, where we have plotted the logarithmic effective heat capacity $CL_{P_{eff}}$ as a function of the radius $\rho_{+}$ (left panel), and as a function of the ratio $\rho_{+}/Q$ in the right panel.

We also note that the electric interaction is weaker in ENLMY dS black hole than the usual charged black hole due to the exponential decreasing of Yukawa potential. Besides; when $\rho_{+}\to 0$, the interactions become stronger and thus the black hole is strongly unstable. Hence, when the Yukawa charge is quite large the critical non-rescaled event horizon radius is almost vanishing as illustrated by Fig. 22.

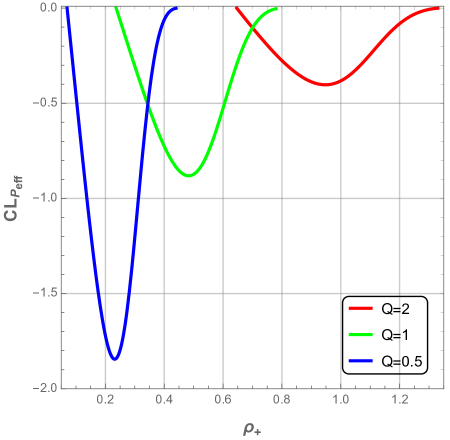
Besides, the effect of the Yukawa charge $\alpha$ on the critical radius $r_{+s}$ is plotted in Fig. 23.

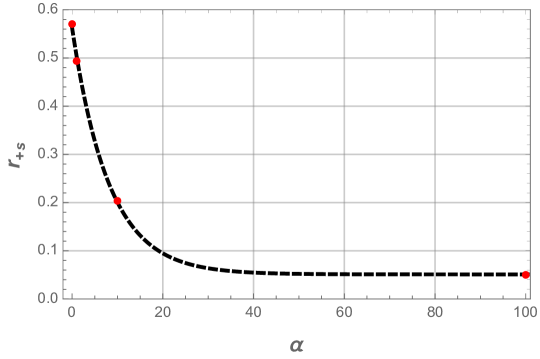
The critical radius $r_{+s}$ of strong-weak electric transition decreases exponentially when Yukawa charge $\alpha$ increases as it is displayed in Fig. 23. By fitting our result, we can describe the behavior of $r_{+s}$ quantity by a nice formula given by:

$$r_{+s}=0.05+0.51e^{-0.12\alpha}.$$

(35)

In this last section, we extend the results obtained in section 6 related to effective thermodynamics with two horizons to the three horizons. First we define the effective entropy of the three horizons as,

$$S_{eff}=S_{c}+S_{-}-S_{+}$$

(36)

then, from Eq. (13) and Eq. (21), we assume that the effective first thermodynamics law and the effective Smarr-like formula of three horizons can read as:

$$\begin{split}dM=&-\dfrac{T_{+}T_{c}T_{-}}{T_{+}T_{c}+T_{+}T_{-}+T_{-}T_{c}}d(S_{c}+S_{-}-S_{+})+\dfrac{V_{+}T_{c}T_{-}+V_{c}T_{+}T_{-}+V_{-}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}dP\\ &+\dfrac{\Phi_{q_{+}}T_{c}T_{-}+\Phi_{q_{c}}T_{+}T_{-}+\Phi_{q_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}dQ+\dfrac{\Phi_{\alpha_{+}}T_{c}T_{-}+\Phi_{\alpha_{c}}T_{+}T_{-}+\Phi_{\alpha_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}d\alpha.\end{split}$$

(37)

$$\begin{split}M=&-2\dfrac{T_{+}T_{c}T_{-}}{T_{+}T_{c}+T_{+}T_{i}+T_{-}T_{c}}(S_{c}+S_{-}-S_{+})-2\dfrac{V_{+}T_{c}T_{-}+V_{c}T_{+}T_{i}+V_{-}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}P\\ &+\dfrac{\Phi_{q_{+}}T_{c}T_{-}+\Phi_{q_{c}}T_{+}T_{-}+\Phi_{q_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}Q-\dfrac{\Phi_{\alpha_{+}}T_{c}T_{-}+\Phi_{\alpha_{c}}T_{+}T_{-}+\Phi_{\alpha_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}\alpha.\end{split}$$

(38)

Hence, the effective thermodynamic variables are given by,

$$\begin{split}&T_{eff}=\dfrac{T_{+}T_{c}T_{-}}{T_{+}T_{c}+T_{+}T_{-}+T_{-}T_{c}},\\ &V_{eff}=\dfrac{V_{+}T_{c}T_{-}+V_{c}T_{+}T_{-}+V_{-}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}},\\ &\Phi_{q_{eff}}=\dfrac{\Phi_{q_{+}}T_{c}T_{-}+\Phi_{q_{c}}T_{+}T_{-}+\Phi_{q_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}},\\ &\Phi_{\alpha_{eff}}=\dfrac{\Phi_{\alpha_{+}}T_{c}T_{-}+\Phi_{\alpha_{c}}T_{+}T_{-}+\Phi_{\alpha_{-}}T_{+}T_{c}}{T_{+}+T_{c}+T_{-}}.\end{split}$$

(39)

We note that from Eq. (21) the pressure and electric charge could be expressed as a function of horizon radii, particularly if we consider black hole thermodynamics with fixed cosmological and inner horizons (treated below).

First we define the characteristic ratio $a_{\rho}=\frac{\rho_{c}}{\rho_{-}}$, that varies from $1$ to $+\infty$, and plot the effective temperature as a function of the event horizon radius.

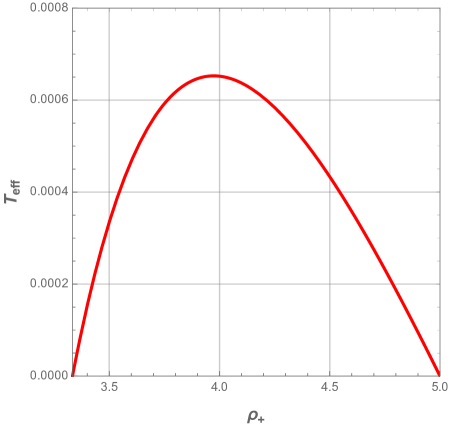
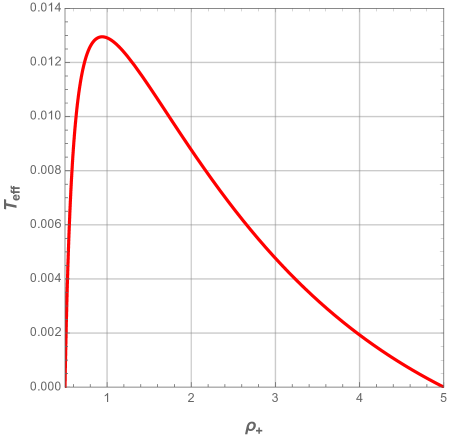
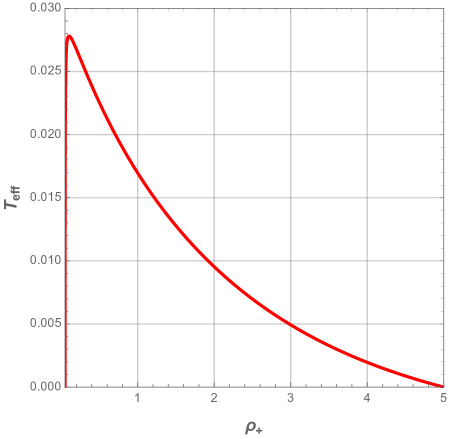
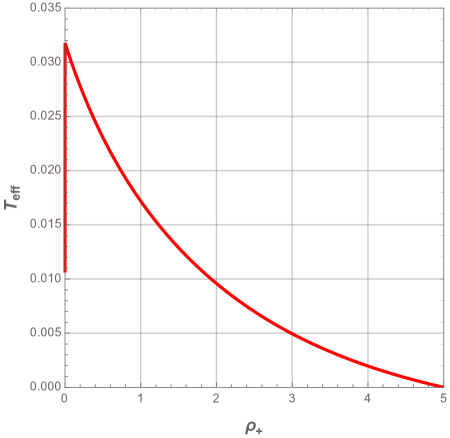
From Fig. 24, it can be seen that we have just the second region $R_{2}$ determined previously in Section 6, while the first region $R_{1}$ has vanished. Since the behavior of the effective temperature $T_{eff}$ depends on the ratio $a_{\rho}$, for small $a_{\rho}$, $T_{eff}$ should first increase until a maximum, then decreases when $\rho_{+}$ gets large. For large $a_{\rho}$, with the increasing part of $T_{eff}$ almost disappearing, the effective temperature behaves as decreasing monotonous function of $\rho_{+}$.

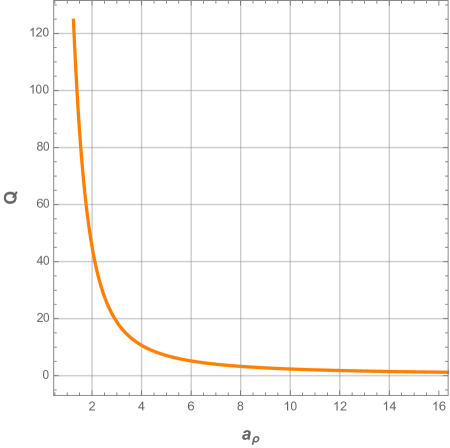
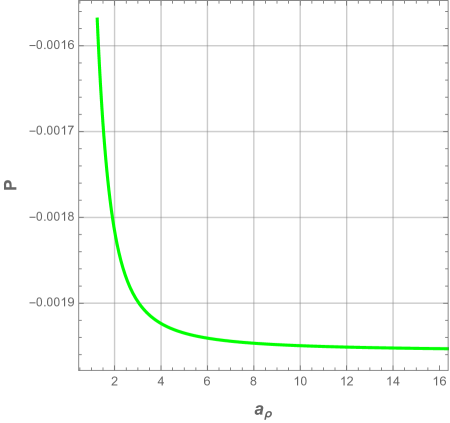
We plot in Fig. 25 the electric charge $Q$ and thermodynamic pressure $P$ as a function of the characteristic ratio $a_{\rho}$. Their behaviors show that the black hole can undergo a thermodynamic phase transition only if the electric charge $Q$ and cosmological constant are quite large. When $Q\to 0$ and $P\to 0$ the black hole phase is in unstable phase.

After that, we define the effective free Gibbs energy as $G_{eff}=M-T_{eff}S_{eff}$ and plot its variation as a function of the effective temperature in Fig. 26.

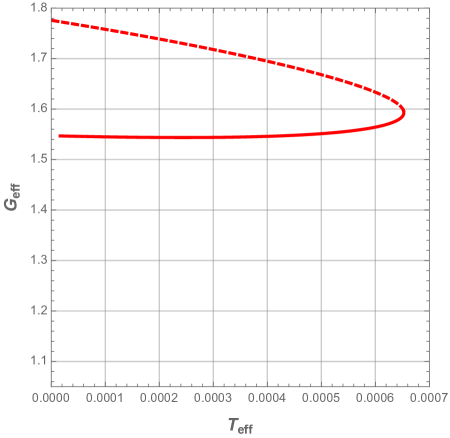
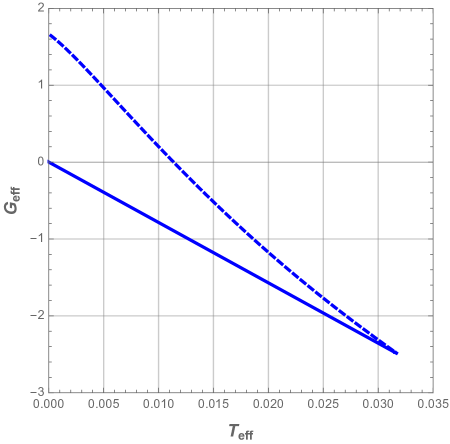
For small values of the characteristic ratio $a_{\rho}$, the black hole undergoes a phase transition between a stable and unstable phases. Whereas, for large values of $a_{\rho}$, the black hole is only stable near the extreme case where $\rho_{+}\to\rho_{-}$, dubbed ”cold black hole” ⁴⁴4 For example, if $a_{\rho}=10^{3}$, the black hole is stable when $\frac{\rho_{+}}{\rho_{-}}<1.04$. Hence, this phase can well be omitted for $a_{\rho}\to\infty$, since in this scenario, the unstable phase dominates.

The thermodynamics of asymptotically de Sitter black hole is considered as one of the main keys to our comprehension of Gravity. However, compared to anti-de sitter thermodynamics, it remains relatively unexplored. The present work considered such a topic: we have first extended the black hole solution of Einstein gravity coupled to a non-linear electromagnetic field and Yukawa potential initially treated in [56] to the dS spacetime with a static and spherical symmetric ansatz. Then we have shown that such a solution presents three distinct horizons, namely the event, cosmological and inner horizons. We have employed several approaches to disclose the phase structure of Einstein nonlinear Maxwell Yukawa dS black hole in the extended phase space.

By following the strategy employed by Kubiznak et al. [31] to derive several thermodynamic first laws (one for each horizon) and explore their thermodynamics as if they were independent thermodynamic systems, we were able to uncover the rich phase structure of de Einstein non-linear Maxwell Yukawa dS black hole solution. In addition to that, we have also proposed an analysis with a simultaneous treatment of all horizons. Afterward, by assuming that the event and cosmological horizons are not located far away, we have used an approach based on the effective thermodynamics of the black hole. We studied the internal correlation of these systems (cosmological and inner horizons), which enabled us to evaluate a single Gibbs free energy-like quantity $G$ that captures their individual thermodynamic behavior and contains information about possible phase transitions of the whole de Sitter system. In the end, we have extended the formalism of effective thermodynamics initially based on the correlation between two horizons to the correlation of three black hole horizons.

Last, from a close look at Eq. (30) and Eq. (39), we determined that the effective temperatures behave like an association of ohmic resistances in an electrical circuit. This remarkable finding may open a new window on a possible analogy between both systems and constitute an interesting field of future investigations.