cuhk1]Department of Mechanical and Automation Engineering, The Chinese University of Hong Kong, HKSAR, China cuhk2]Department of Mechanical and Automation Engineering, The Chinese University of Hong Kong, HKSAR, China
On Estimating the Probabilistic Region of Attraction for Partially Unknown Nonlinear Systems: An Sum-of-Squares Approach
Abstract
Estimating the region of attraction for partially unknown nonlinear systems is a challenging issue. In this paper, we propose a tractable method to generate an estimated region of attraction with probability bounds, by searching an optimal polynomial barrier function. Techniques of Chebyshev interpolants, Gaussian processes and sum-of-squares programmings are used in this paper. To approximate the unknown non-polynomial dynamics, a polynomial mean function of Gaussian processes model is computed to represent the exact dynamics based on the Chebyshev interpolants. Furthermore, probabilistic conditions are given such that all the estimates are located in certain probability bounds. Numerical examples are provided to demonstrate the effectiveness of the proposed method.
keywords:
Region of attraction, Sum-of-squares programming, Chebyshev interpolants, Gaussian processes.1 Introduction
Tracking the performance of uncertain nonlinear systems is an essential problem of significant research interests. In engineering practices, the concepts of safety and stability are central to these uncertain nonlinear systems in most scenarios, e.g., flight dynamics, bipedal robotics and power systems [1, 2, 3, 4]. Consequently, scientists across multiple disciplines have summarized this type of problem into the analysis of region of attraction (ROA, also called domain of attraction). Estimating the ROA can directly obtain the safety or the stability margin in many practical implementations [5].
Fruitful results have been obtained to estimate the ROA of fixed nonlinear systems. Exploiting the sublevel set of Lyapunov functions is one of the useful methods [6]. Barrier functions are another powerful tool to guarantee safety such that states avoid entering a specified unsafe region [7], [8]. To meet the safety and the stability conditions simultaneously, the quadratic programs have been investigated to find qualified Lyapunov barrier functions [9]. Meanwhile, sum-of-squares programmings (SOSPs) are proposed to find more permissive results in polynomial systems [10, 11, 12, 13]. However, in many engineering practices, there exist model inaccuracies and unknown disturbances that might influence the system dynamics or even result in operation failures in the worst case.
To handle with the above issue, effective methods have been proposed regarding partially unknown systems. First, Lyapunov-based methods are developed and extended to uncertain systems, where a Lyapunov certified ROA (LCROA) estimation is conducted for uncertain, polynomial systems [14], [15]. Furthermore, learning-based methods have been studied in the literature. Among these, the use of Gaussian processes (GP) is shown to be a promising approach to quantify the uncertainty in the stochastic process [16, 17]. The idea of unifying SOSP and GP naturally arises to compute the LCROA [18, 19, 20].
Inspired by the work in [21] that firstly uses GP to compute the barrier certified ROA (BCROA), based on our previous work in [13, 22], this paper combines SOSPs and GP to estimate the optimal BCROA of partially unknown nonlinear systems. Different from the learned polynomial systems in [20], we use Chebyshev interpolants and polynomial mean functions of GP models to find the optimal BCROA rather than LCROA with relaxed assumptions. The polynomial mean function is proven to be more flexible to match other nonlinear kernels instead of polynomial kernel. To the best of our knowledge, this paper is the first to compute barrier functions via SOSPs in partially unknown nonlinear systems.
The main contributions of this paper are threefold. First, a learned polynomial system is built with probability bounds. Second, a positive but safe sample policy is developed to prepare appropriate prior information for higher accuracy of the GP model. Third, a tractable method based on SOSP is proposed to compute the probabilistic optimal BCROA.
2 Preliminary
Consider an autonomous system as follows,
| (1) |
where denotes the state, denote the polynomial and the non-polynomial term respectively, and denotes the unknown term. All the terms in (1) are Lipschitz continuous.
Without losing generality, systems with a single equilibrium are considered, and this equilibrium could be transformed to the origin via variables substitution [23].
Assumption 1.
The origin () is a single stable equilibrium of (1), that is .
To model the system dynamics in a Bayesian framework as developed in [24], we define a prior distribution of noise over measurements .
Assumption 2.
The noise over the system measurements of (1) is uniformly bound by , i.e., .
The known dynamics can be computed directly. Thus, can be obtained by subtracting from . In this work, we restrict our attention to the system (1) with bounded :
Assumption 3.
The unknown term in (1) exists a bounded norm in the reproducing kernel Hilbert space (RKHS), i.e., , where is a constant.
As [21] introduced, the RKHS is a Hilbert space of square integrable functions that contains functions of the form , where denotes coefficient and denotes a symmetric positive definite kernel function of states . For more details about the RKHS norm, we kindly refer interested readers to [25].
2.1 Barrier Functions
To introduce the barrier function, let us first consider a simple autonomous system as follows,
| (2) |
where is locally Lipschitz continuous with a single stable equilibrium point at the origin. As we mentioned, the safety and stability of (2) can be guaranteed by ROA.
State trajectories starting inside the barrier function certified ROA (BCROA) will never enter into the unsafe region as defined,
| (3) | ||||||
Meanwhile, the Lyapunov function certified ROA (LCROA) denotes a sublevel set of . The state trajectories inside will always converge to the origin. The following lemma demonstrates a relationship between and .
Lemma 1.
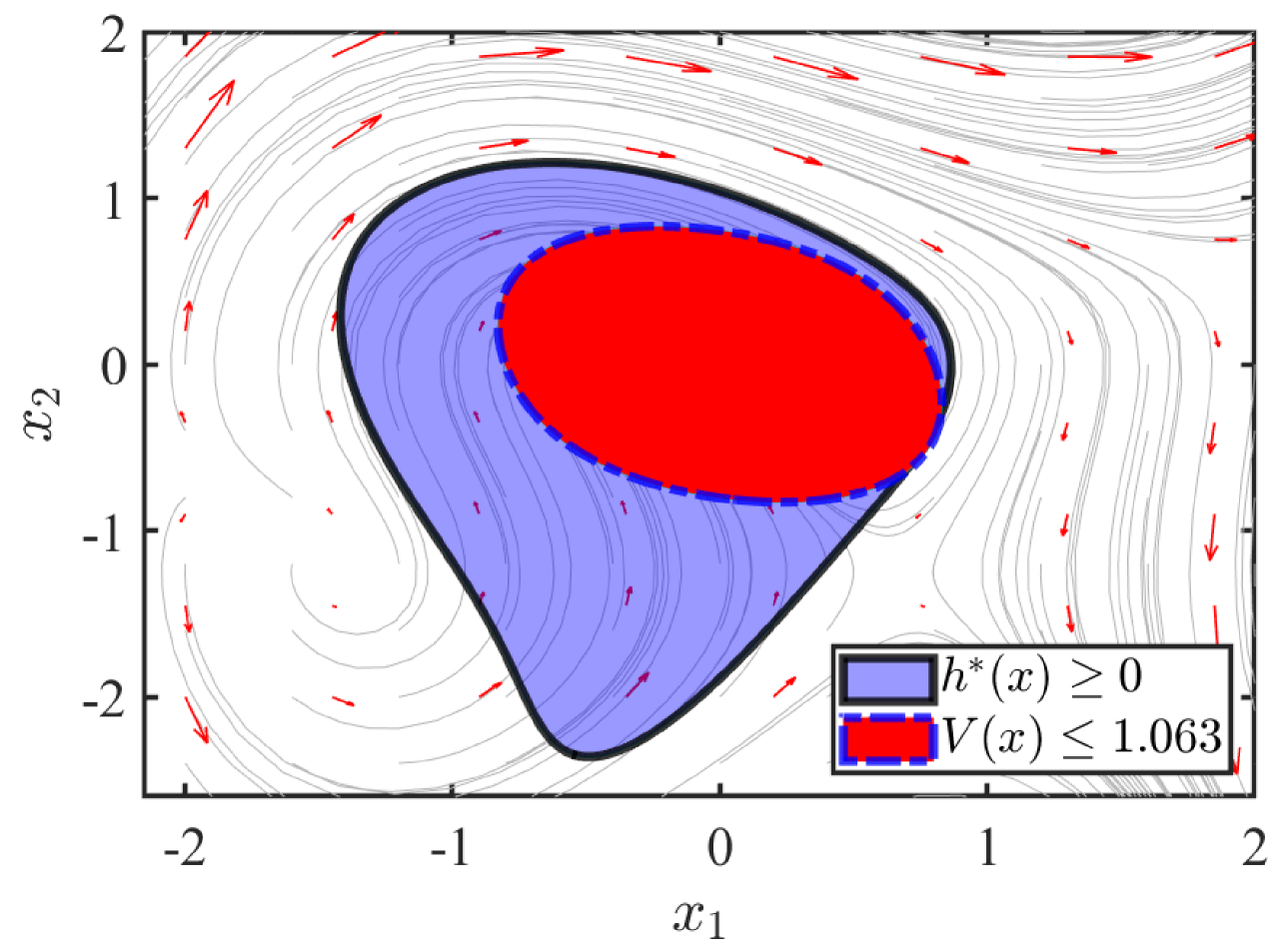
The details about how to obtain a Lyapunov maximum sublevel and an optimal barrier function are introduced [13]. In Example 1, we will illustrate the comparison of LCROA and BCROA.
Example : Consider an autonomous system
| (4) |
Let denote the LCROA and denote the BCROA. In (4), is established by a degree polynomial , and is obtained by another degree polynomial barrier function based on .
2.2 Gaussian Processes
Gaussian processes (GP) provide a non-parametric regression method to capture the unknown dynamics in Bayesian framework. In the GP model, every variable is associated with a normal distribution, where the prior and the posterior GP model of these variables obey a joint Gaussian distribution [24]. A GP model is characterized by the mean function and the covariance function , where computes the similarity between any two states . In most cases, the covariance function is also called a kernel. The measurements of in (1) can be used to construct a GP model with polynomial mean functions as follows.
Proposition 1.
Suppose there exist measurements of in (1) that satisfy Assumption 2, 3. Then, the following GP model of can be established with polynomial mean function and covariance function as,
| (5) | ||||
where is a query state, is a monomial vector, is a coefficient vector, is a kernel Gramian matrix and .
Proof.
See Appendix. ∎
3 Learning the Partially Unknown System
To illustrate our work about learning the partially unknown dynamics (1) in polynomial form, we propose the approximated probabilistic model in (12), which combines Chebyshev interpolants and a GP model as shown in the first two subsections. We also introduce a covariance oriented safe sample policy based on GP to learn the dynamics consistently in the third subsection.
3.1 Chebyshev Interpolants
Chebyshev interpolants provide a useful way to approximate a class of nonlinear functions with a bounded remainder [26]. The term in (1) can be approximated by the Chebyshev interpolants of degree in as,
| (6) |
where denotes the subscript of the coefficients vector and the Chebyshev polynomials vector that satisfies,
| (7) | ||||
Note that, Chebyshev interpolants are applicable to any arbitrary interval by the following transformation,
| (8) |
We define the remainder based on (6). The following inequality from [26] declares that the remainder of Chebyshev interpolants is bounded over the domain.
Lemma 2.
(Theorem 8.2 of [26]) Let an analytic function in be analytically containable to the open Bernstein ellipse , where it satisfies for some . Then, its Chebyshev interpolants satisfies
The Bernstein ellipse has foci and major radius for all . For more details about the Bernstein ellipses, we kindly refer to the book by Trefethe [26].
where the unknown term satisfies Assumption 2, 3,
| (10) |
The approximation accuracy of Chebyshev interpolants is linearly dependent on the degree. We will illustrate a comparison in the following example.
Example : Consider a nonlinear function approximated by the Chebyshev interpolants of degree and in , the higher degree approximation is more accurate with less bounded remainder in Figure 2.
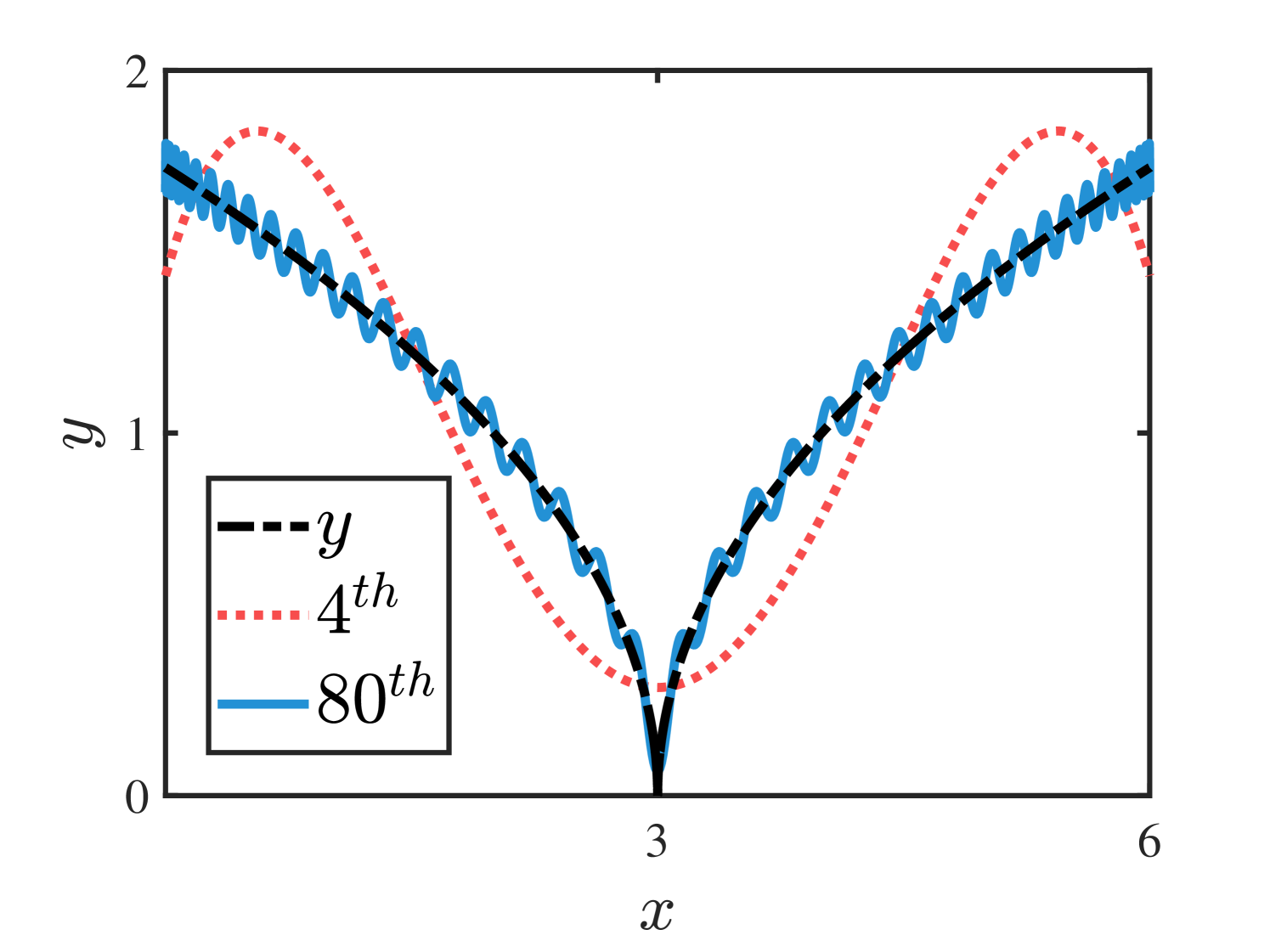
(a)
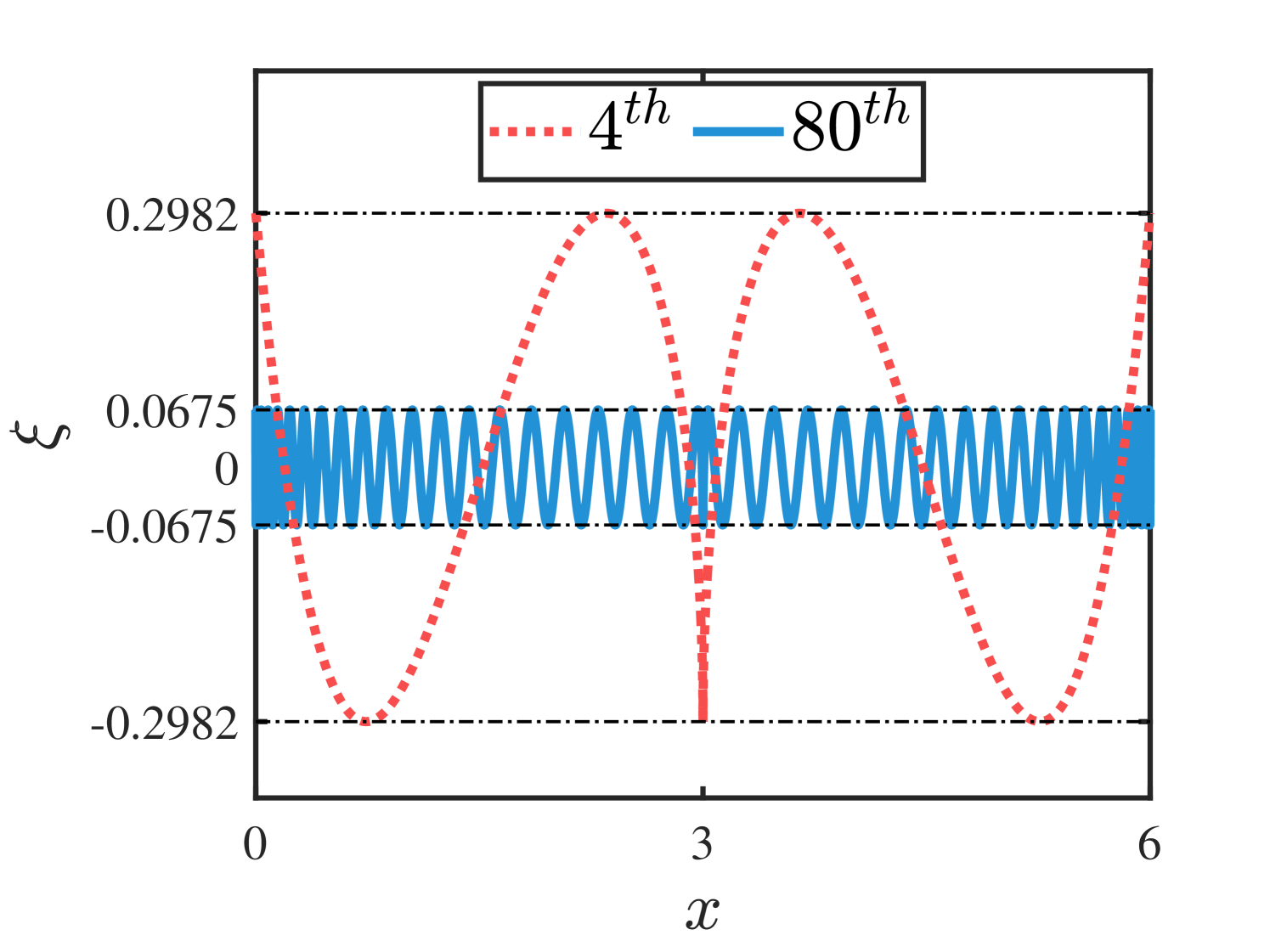
(b)
3.2 Probability Bounds on the GP model
The following result provides the probability bounds in the distribution of a GP model.
Lemma 3.
(Lemma 2 of [17]) Suppose there exist measurements of a bounded function , where denotes the state, denotes the measurement of that corrupted with noise , and denotes the RKHS. Let . For and its inferred GP model holds,
| (11) |
where is a discounting factor, is a norm of , and is a factor denoting the maximum mutual information over the measurements.
Remark 2.
The value of is related to the type of kernels, e.g., RBF kernel, Matérn kernel and linear kernel from [27]. Thus, its sublinear dependent term can be regarded as a constant [18]. In [17], a more correlated statement yields that with more appropriate prior information, the value of will decrease such that the dynamics can be represented by with fewer differences.
3.3 Covariance Oriented Safe Sample Policy
Computing a high-confidence GP model is closely related to the appropriate prior information. If the mean function of a GP model is closer to the prior information, will decrease to get close to the exact dynamics [24]. Therefore, handling the high covariance data will accelerate the learning process. Meanwhile, to maintain the prior information is always safe, we propose a positive sample policy inside an existing ROA as follows,
| (13) |
where denotes the covariance of a trajectory starting from , denotes the estimate ROA and denotes the index number of the total episode . The trajectory of the result in (13) can be used to enrich the GP prior model recursively. The example below shows a comparison of the dynamics between the original system (1) and a learned system (12).
Example : Consider a partially unknown nonlinear system (14) with unknown term as
| (14) |
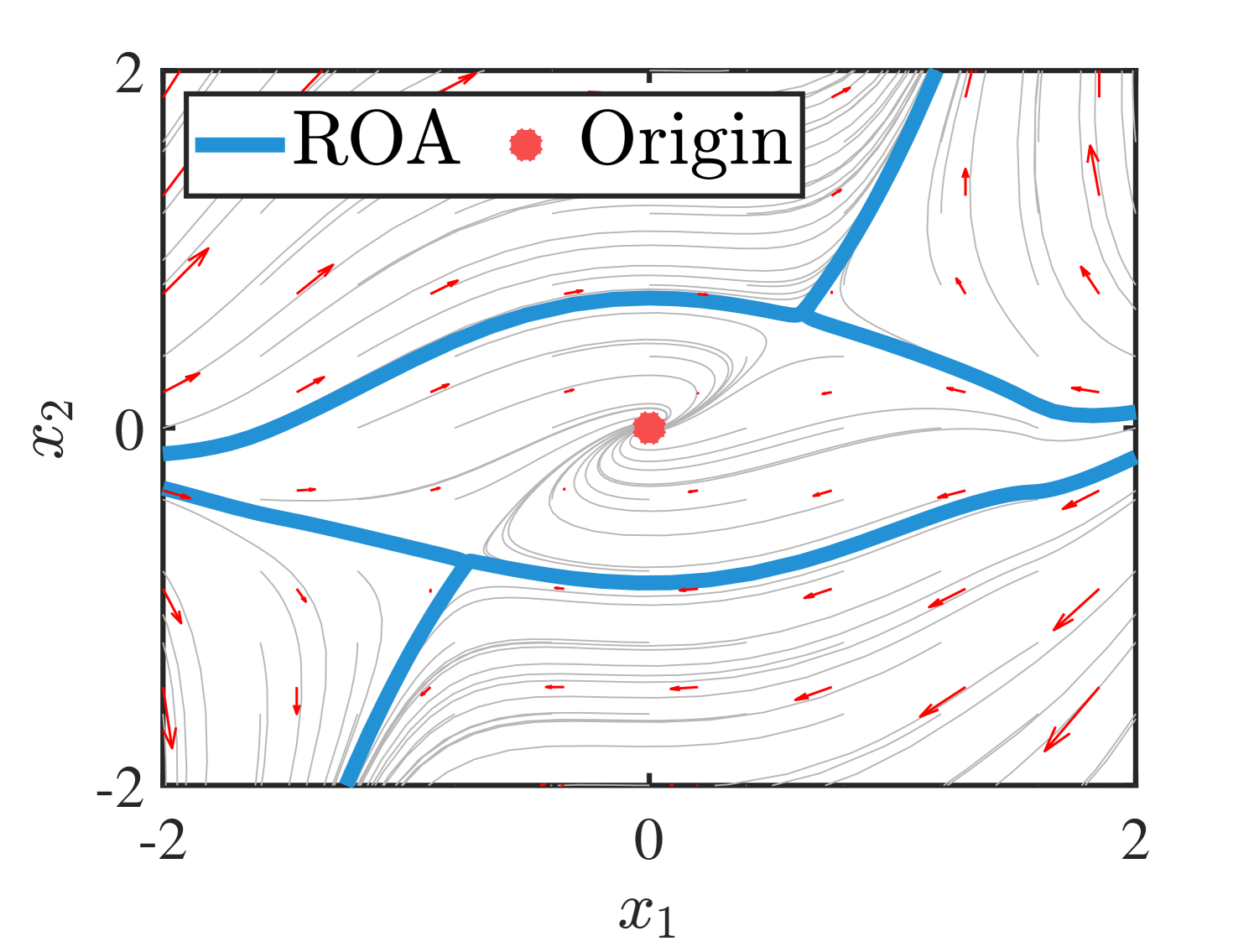
(a)
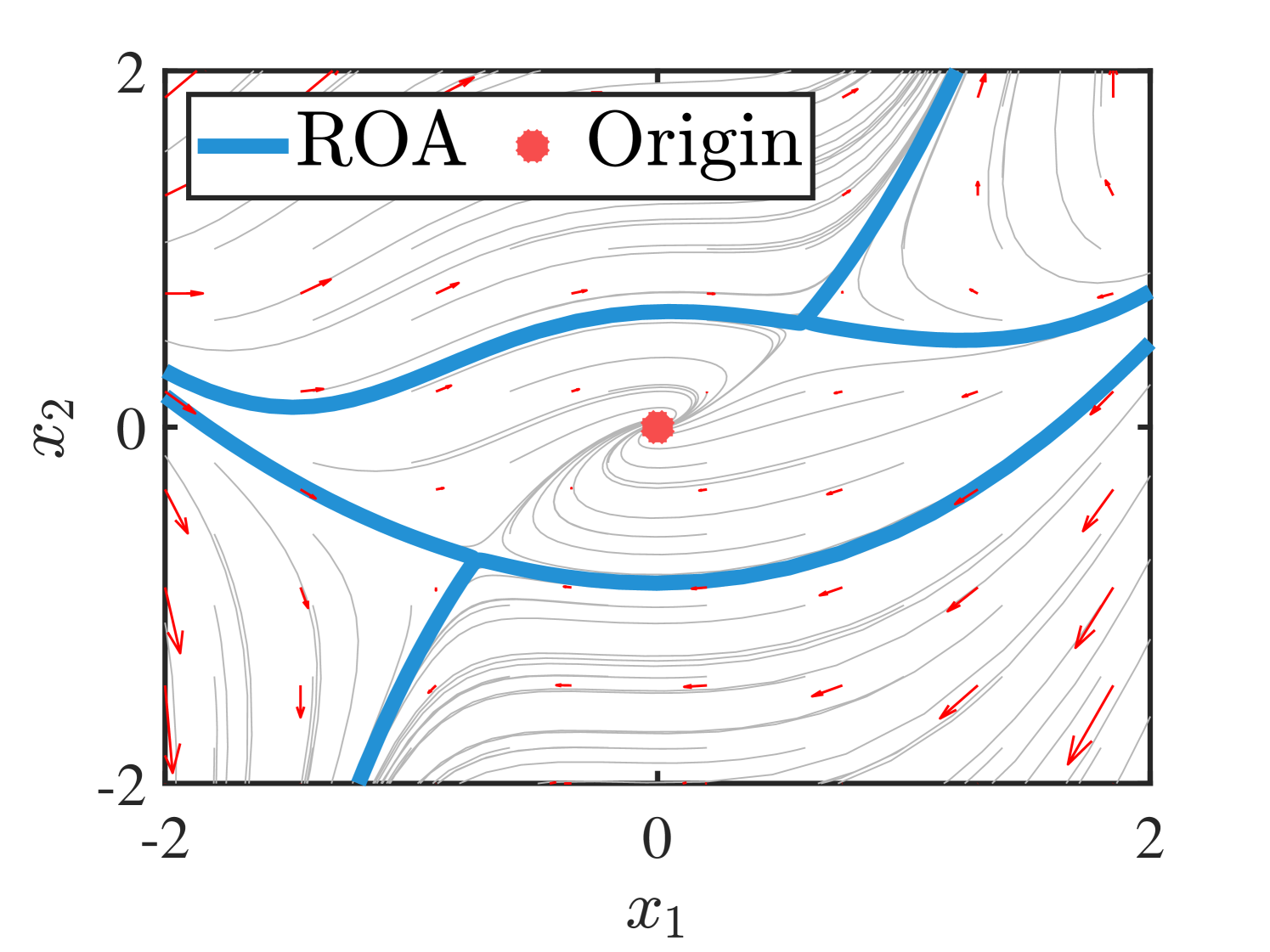
(b)
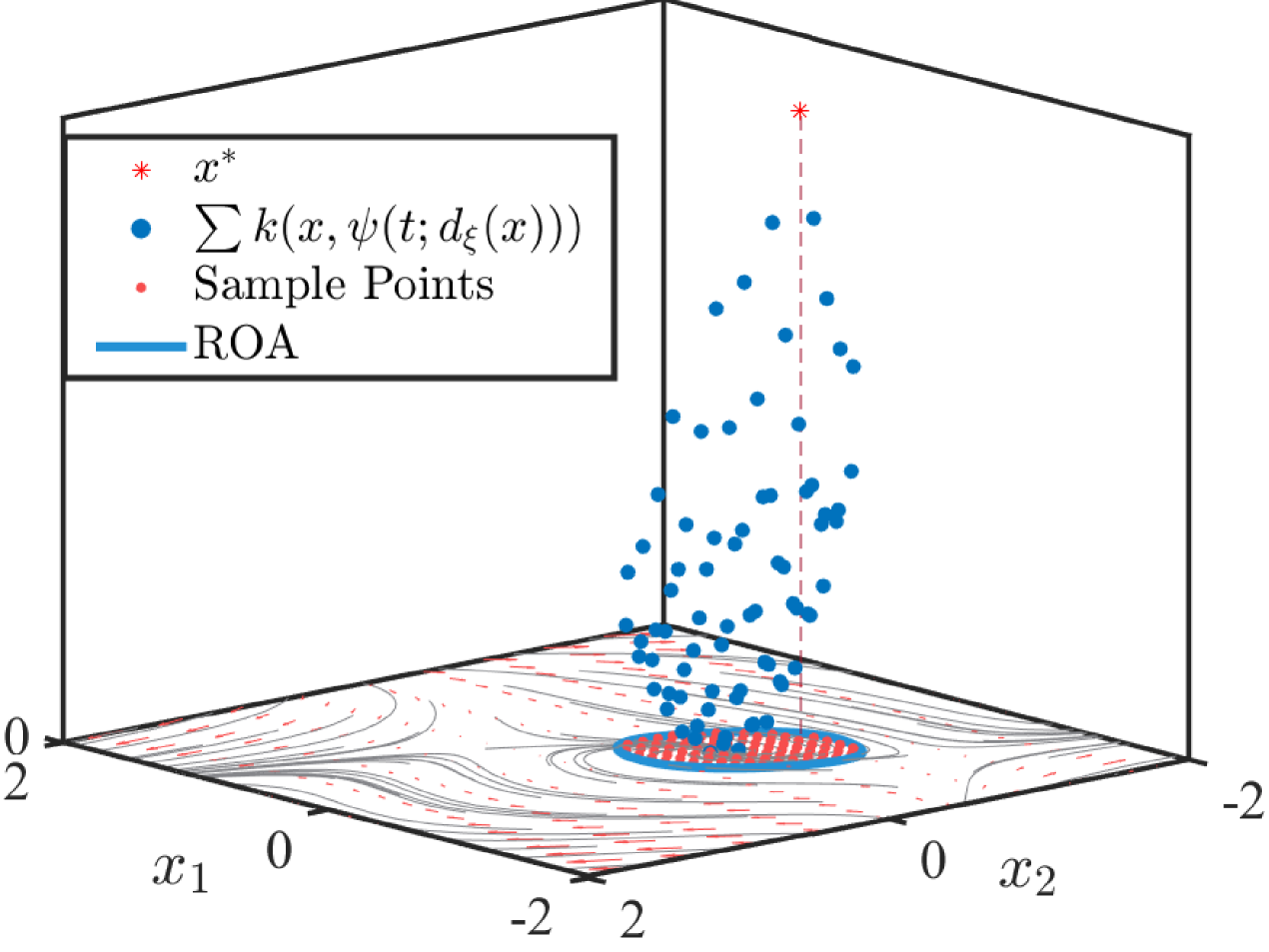
Figure 3(b) shows the learned polynomial system dynamics of (14). The non-polynomial term in (14) is approximated by degree Chebyshev interpolants in , while the state trajectory is used to construct a GP model with degree polynomial mean function. Figure 4 shows the obtained sum of covariance of the learned polynomial system based on (13). Compared to the points around the equilibrium point, those nearby the ROA edge have larger sum of covariance and can be considered with high uncertainty. Thus, the distribution of the sum of covariance in Figure 4 poses a direction to reduce the uncertainty during the learning process.
4 Estimating the Region of Attraction
In this section, we will estimate the ROA of the learned polynomial system (12) via SOSPs . The relationship of estimates between the learned polynomial system and the true dynamics will also be discussed.
4.1 Parameterize the ROA by Barrier Function
The parameterization of a barrier function in (12) via SOSPs is developed in [13]. To deal with the non-negativity constraints, we will introduce the Positivestellensatz (P-satz) here for further SOSPs implementation.
Let be the set of polynomials and be the set of sum of squares polynomials, e.g., where and .
This lemma declared that any strictly positive polynomial is in the cone that generated by polynomials and . Using Lemma 4, the optimal barrier function of the learned polynomial system (12) can be searched in the state space via 3 SOSPs.
1. Obtain the maximum sublevel set of a specified Lyapunov function by a bilinear search,
| (15) | ||||||
| s.t. |
where is an auxiliary factor to relax the non-negativity constraint for the initial barrier function .
2. Search another two auxiliary factors for ,
| (16) | ||||||
| s.t. | ||||||
Meanwhile, can be re-written into the square matrix representation form as , where is a semi-definite coefficient matrix and is a monomial vector [13]. The trace of is used to approximate the volume of barrier certified ROA (BCROA).
3. Enlarge to parameterize a permissive with fixed and ,
| (17) | ||||||
| s.t. | ||||||
The optimal barrier function can be found with a permissive BCROA if the increase of is less than a threshold, otherwise repeat 2 and 3 for a long term.
These 3 SOSPs demonstrate the process to obtain an optimal BCROA directly. Thus, if a ROA exists in the learned polynomial system (9), a permissive BCROA would be computed by these SOSPs directly.
4.2 Existence of Probabilistic BCROA
The relationship of a BCROA in the learned system (12) toward the true dynamics is given in the following theorem.
Theorem 1.
Given measurements of a partially unknown system (9) such that we can obtain a learned system (12) with a probability greater or equal to . Based on the SOSPs (15), (16) and (17), if there exists a BCROA such that
| (18) |
holds for the states , then can be regarded as a BCROA in (9) with probability bounds .
Proof.
Given an arbitrary initial state in the learned system (12), its state trajectory is guaranteed to converge to the origin due to the Lyapunov constraints in (15), (16) and (17). Since the derivative of the barrier function is non-negative over the trajectory , will strictly increase along . Then, the BCROA established a region with the safety and stability guarantee in (12).
4.3 Probabilistic Optimal BCROA Estimate
To illustrate our procedures of finding probabilistic optimal BCROAs, we present an algorithm below and a corresponding flowchart in Figure 5, which both consist of a learned polynomial system and SOSPs. Besides, the following theorem proposes the confidence range of the result from Algorithm 1 over episodes.
Theorem 2.
Algorithm 1 establishes probabilistic ROA with probabilities greater or equal to , where denotes the sample number with index . Then, the following probability bounds are given:
| (19) | ||||
where and denote the union set and the intersection set of these optimal BCROAs, respectively, and denotes the exact ROA of the system (9).
Proof.
After executing the algorithm times, we could get optimal BCROAs with probability bounds toward the dynamical system (9). Since the increasing generates larger information set , when , the GP model can be inferred with the richest such that the lower bound of this probabilistic range is approximating . Let be the intersection set of , which represents the most common part of these optimal BCROAs toward the exact dynamics of (9). Then, a conservative statement about toward the real ROA in (9) establishes with a minimum value of . Therefore, the second equation in (19) about toward establishes in a similar way, which completes the proof. ∎
Theorem 2 presents a probabilistic statement of generated from Algorithm 1. Obviously, a higher degree mean function in (12) could approximate the real dynamics much more precisely. Note that the shape of is various with uncertainty. It is worthy noting that the corresponding Lyapunov function and the barrier function could increase their degrees simultaneously for a better estimate. This is because a higher degree polynomial certified ROA can explore more areas, so the probabilistic bound narrows naturally.
5 Numerical Examples
Based on the Matlab toolbox of Chebfun, GPML, SOSOPT and Mosek solver, we estimate the BCROA of the autonomous partially unknown system by two examples.
5.1 Example 4: A 2D Nonlinear System
Extended to Example 3, we consider the system:
| (20) |
Example 3 shows the construction of the first learned dynamical system in Figure 3(b) and the noise over the system measurement is bounded by . The learned GP models are consisted by a degree polynomial mean function zero, and a RBF kernel function with signal variances and length scale .
At each episode, a given LCROA is considered to the next step, where is a degree polynomial. Besides, we obtained the probability bounds with a fixed discounting factor according to the method in [21]. After episodes, the probability bounds of these optimal BCROAs is , where denotes the exact ROA in (20).
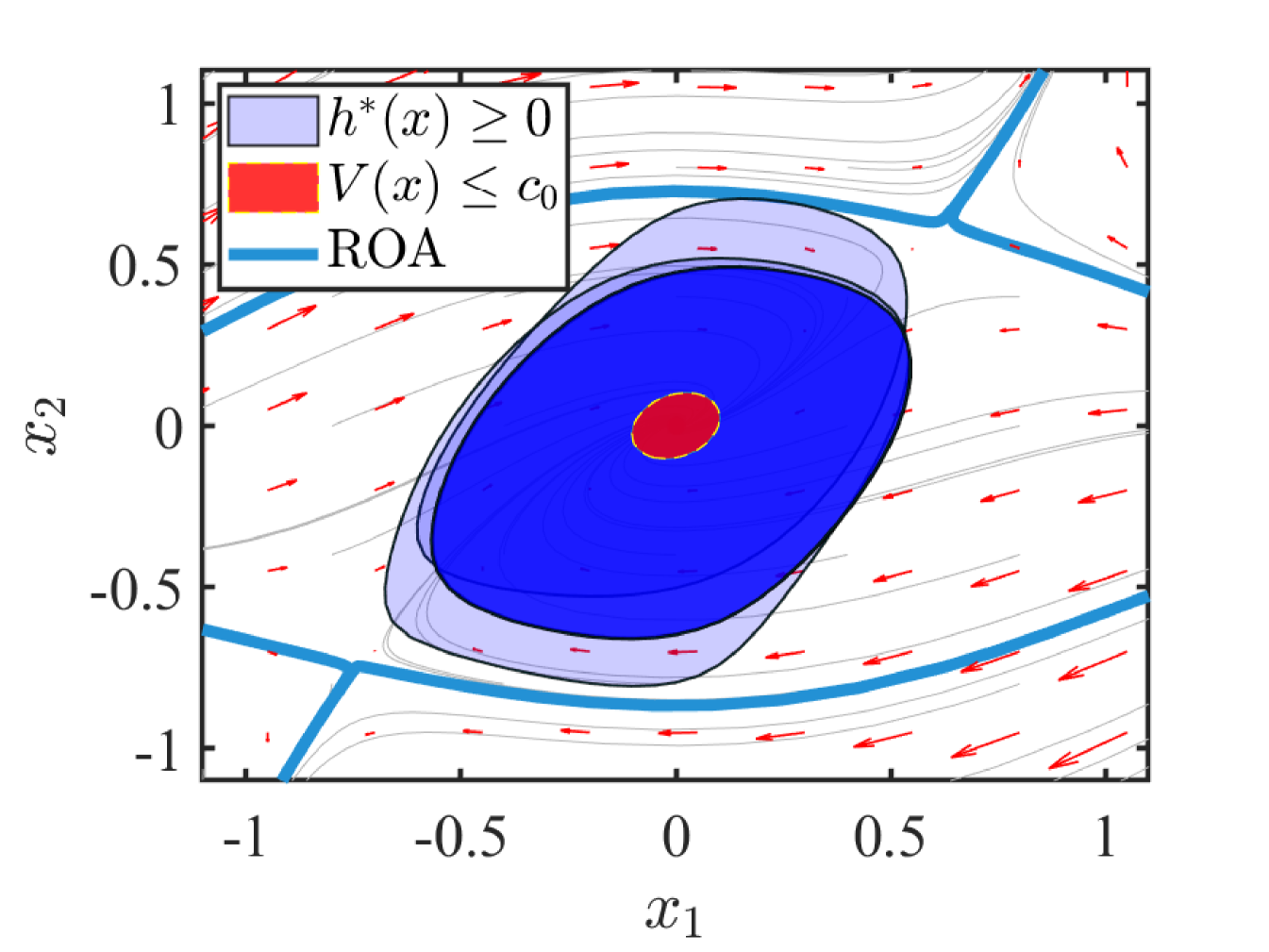
In Figure 6, each computed optimal BCROA is displayed with a fixed transparency. The intersection region of these optimal BCROAs is established with the probability , while the union region of these optimal BCROAs is established with the probability . Therefore, the result of these probabilistic optimal BCROAs in Figure 6 is not only obviously larger than the LCROA, but also guaranteeing the system safety by a clear probability range.
5.2 Example 5: A 3D Nonlinear System
Consider a 3D nonlinear system corrupted with unknown terms as the form of (1),
| (21) |
The non-polynomial terms in (21) are approximated by the degree Chebyshev interpolants in . To learn the system dynamics, we first collect the trajectory starting at , where the noises over and are bounded by . In this case, we use a degree polynomial mean function and a RBF kernel with signal variances and length scale .
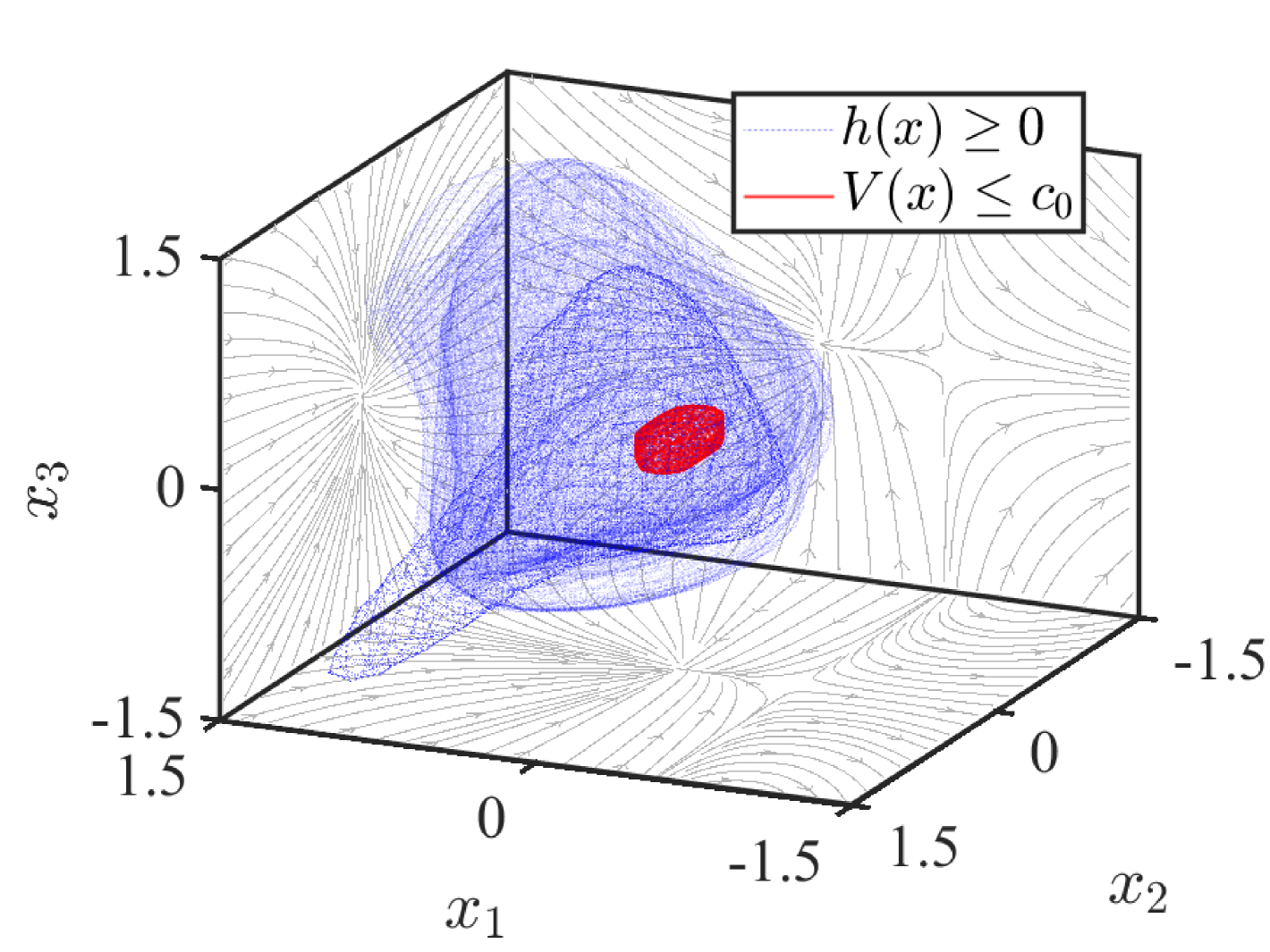
A sublevel set is given to construct the LCROA with a order . Set such that the probability bounds of optimal BCROAs can be computed as .
These optimal BCROAs are displayed in Figure 7 with a fixed transparency. From Figure 7, we see that there are various differences of these optimal BCROAs. Furthermore, as seen in Table 1, with the same hyperparameters, the computation time of Example 5 is greater than Example 4 significantly. However, at the episode 10, Example 5 will first stop learning due to the high computation cost. Although higher dimensional functions find a comparable BCROA, but this is often not the case due to the fragile and changeable dynamics under uncertainty.
| \hhline | Episode 1 | Episode 5 | Episode 10 |
|---|---|---|---|
| Example 4 | |||
| Example 5 | |||
| \hhline |
6 Conclusion
In this work, a method is proposed to compute a barrier certified region of attraction such that the stability and safety can both be guaranteed for a class of partially unknown systems. The proposed method is built based on Chebyshev interpolants, Gaussian processes, sum-of-squares programming and a safe sample policy. The effectiveness of the proposed algorithm has been demonstrated via two numerical examples.
On the other hand, we would like to admit that a large amount of unknown terms may affect the accuracy and efficiency of proposed algorithm. Possible solutions to address this issue could be to construct an efficient sample policy [29] or to exploit local GP regression [30]. Thus, future efforts will be devoted to prior data selection in further enlarging the estimated region of attraction for partially unknown systems [13, 17].
References
- [1] E. Glassman, A. L. Desbiens, M. Tobenkin, M. Cutkosky, and R. Tedrake, “Region of attraction estimation for a perching aircraft: A Lyapunov method exploiting barrier certificates,” in Proceedings of the International Conference on Robotics and Automation, pp. 2235–2242, 2012.
- [2] L. Wang, E. A. Theodorou, and M. Egerstedt, “Safe learning of quadrotor dynamics using barrier certificates,” in Proceedings of the International Conference on Robotics and Automation, pp. 2460–2465, 2018.
- [3] S.-C. Hsu, X. Xu, and A. D. Ames, “Control barrier function based quadratic programs with application to bipedal robotic walking,” in Proceedings of the American Control Conference, pp. 4542–4548, 2015.
- [4] P. Magne, D. Marx, B. Nahid-Mobarakeh, and S. Pierfederici, “Large-Signal Stabilization of a DC-Link Supplying a Constant Power Load Using a Virtual Capacitor: Impact on the Domain of Attraction,” IEEE Transactions on Industry Applications, vol. 48, no. 3, pp. 878–887, 2012.
- [5] G. Chesi, Domain of attraction: Analysis and control via SOS programming, vol. 415. Springer Science & Business Media, 2011.
- [6] V. I. Zubov, Methods of AM Lyapunov and their application. P. Noordhoff, 1964.
- [7] F. Blanchini, “Set invariance in control,” Automatica, vol. 35, no. 11, pp. 1747–1767, 1999.
- [8] A. D. Ames, S. Coogan, M. Egerstedt, G. Notomista, K. Sreenath, and P. Tabuada, “Control barrier functions: Theory and applications,” in Proceedings of the European Control Conference, pp. 3420–3431, 2019.
- [9] A. D. Ames, X. Xu, J. W. Grizzle, and P. Tabuada, “Control barrier function based quadratic programs for safety critical systems,” IEEE Transactions on Automatic Control, vol. 62, no. 8, pp. 3861–3876, 2016.
- [10] P. A. Parrilo, Structured semidefinite programs and semialgebraic geometry methods in robustness and optimization. PhD thesis, California Institute of Technology, 2000.
- [11] I. R. Manchester, M. M. Tobenkin, M. Levashov, and R. Tedrake, “Regions of attraction for hybrid limit cycles of walking robots,” IFAC Proceedings Volumes, vol. 44, no. 1, pp. 5801–5806, 2011.
- [12] A. El-Guindy, D. Han, and M. Althoff, “Estimating the region of attraction via forward reachable sets,” in Proceedings of the American Control Conference, pp. 1263–1270, 2017.
- [13] L. Wang, D. Han, and M. Egerstedt, “Permissive barrier certificates for safe stabilization using sum-of-squares,” in Proceedings of the American Control Conference, pp. 585–590, 2018.
- [14] D. Han, and M. Althoff, “On estimating the robust domain of attraction for uncertain non-polynomial systems: An LMI approach,” in Proceedings of the Conference on Decision and Control, pp. 2176–2183, 2016.
- [15] A. Iannelli, A. Marcos, and P. Seiler, “An equilibrium-independent region of attraction formulation for systems with uncertainty-dependent equilibria,” in Proceedings of the Conference on Decision and Control, pp. 725–730, 2018.
- [16] J. Vinogradska, B. Bischoff, D. Nguyen-Tuong, and J. Peters, “Stability of controllers for Gaussian process dynamics,” The Journal of Machine Learning Research, vol. 18, no. 1, pp. 3483–3519, 2017.
- [17] J. Umlauft, L. Pöhler, and S. Hirche, “An uncertainty-based control Lyapunov approach for control-affine systems modeled by Gaussian process,” IEEE Control Systems Letters, vol. 2, no. 3, pp. 483–488, 2018.
- [18] F. Berkenkamp, R. Moriconi, A. P. Schoellig, and A. Krause, “Safe learning of regions of attraction for uncertain, nonlinear systems with Gaussian processes,” in Proceedings of the Conference on Decision and Control, pp. 4661–4666, 2016.
- [19] J. Umlauft, A. Lederer, and S. Hirche, “Learning stable Gaussian process state space models,” in Proceedings of the American Control Conference, pp. 1499–1504, 2017.
- [20] A. Devonport, H. Yin, and M. Arcak, “Bayesian safe learning and control with sum-of-squares analysis and polynomial kernels,” in Proceedings of the Conference on Decision and Control, pp. 3159–3165, 2020.
- [21] P. Jagtap, G. J. Pappas, and M. Zamani, “Control barrier functions for unknown nonlinear systems using Gaussian processes,” in Proceedings of the Conference on Decision and Control, pp. 3699–3704, 2020.
- [22] D. Han, and M. Althoff, “Estimating the domain of attraction based on the invariance principle,” in Proceedings of the Conference on Decision and Control, pp. 5569–5576, 2016.
- [23] H. K. Khalil, Nonlinear systems; 3rd ed. Prentice-Hall, 2002.
- [24] C. K. Williams and C. E. Rasmussen, Gaussian processes for machine learning, vol. 2. MIT press, 2006.
- [25] V. I. Paulsen and M. Raghupathi, An introduction to the theory of reproducing kernel Hilbert spaces, vol. 152. Cambridge university press, 2016.
- [26] L. N. Trefethen, Approximation Theory and Approximation Practice. SIAM, 2019.
- [27] N. Srinivas, A. Krause, S. M. Kakade, and M. Seeger, “Gaussian process optimization in the bandit setting: No regret and experimental design,” arXiv preprint: 0912.3995, 2009.
- [28] M. Putinar, “Positive polynomials on compact semi-algebraic sets,” Indiana University Mathematics Journal, vol. 42, no. 3, pp. 969–984, 1993.
- [29] J. Umlauft, T. Beckers, A. Capone, A. Lederer, and S. Hirche, “Smart forgetting for safe online learning with Gaussian Processes,” in Learning for Dynamics and Control, pp. 160–169, PMLR, 2020.
- [30] D. Nguyen-Tuong, M. Seeger, and J. Peters, “Model learning with local Gaussian Process regression,” Advanced Robotics, vol. 23, no. 15, pp. 2015–2034, 2009.
- [31] C. Santoyo, M. Dutreix, and S. Coogan, “A barrier function approach to finite-time stochastic system verification and control,” Automatica, vol. 125, p. 109439, 2021.
- [32] H. König, Eigenvalue distribution of compact operators, vol. 16. Birkhäuser, 2013.
Appendix: Proof of Proposition 1
Proof.
First, Mercer’s Theorem [32] allows us to represent a kernel by a kernel basis vector . For this paper, we restrict our attention to the RBF kernel , though our methodology can support more general kernels,
| (22) | ||||
where denotes the signal variance, denotes the length scale and denotes an infinite dimensional vector,
| (23) |
Then, since and its measurement in (1) are bounded in the RKHS, we can formulate,
| (24) |
where denotes the weight vector and denotes the noise. Let be the prior distribution of and let be the posterior distribution of based on and , we can infer their relationship as follows,
| (25) |
Next, let be the weight-independent marginal likelihood . GP is relocating likelihood with measurements as below,
| (26) |
to compute the based on (25) and (26),
| (27) | ||||
where .
By using the Maximum a Posterior estimation, the exact value of the optimal weight can be computed as,
| (28) | ||||
The derivative of in (28) can be computed as,
| (29) |
and the optimal weight can be parameterized directly,
| (30) | ||||
Thus, we can obtain the optimal as (27) shows,
| (31) | ||||
where the predictive output of the query states is,
| (32) |
Because is an infinite vector, which is used to approximate with optimal weight . To avoid the loss of generality, we can truncate by a finite monomial vector without any impact of the inference processes from (26) to (31). This will reshape the mean function in the polynomial form and adjust the second term in (31) as,
| (33) | ||||
where is a kernel Gramian matrix and . Thus, Proposition 1 is obtained, which completes the proof. ∎