On Feature Reduction using Deep Learning
for Trend Prediction in Finance

A Restricted Boltzmann Machine (RBM) is a network made of two layers as shown in Fig.2.

The input layer entails $n$ visible units $\bm{V}=(V_{1},\ldots,V_{n})$ used to represent observable data and $m$ hidden units $\bm{H}=(H_{1},...,H_{m})$ that are used to capture dependencies between observed variables. RBM have been designed to work with binary values in $\{0,1\}$. A weighting matrix $W$ defined over the relation $\bm{V}\times\bm{H}$ is used to quantify the relationship between $\bm{V}$ and $\bm{H}$.

RBM is bidirectional. Indeed, the values given at input and hidden units are given by

$$h_{j}=\sigma\left(b_{j}+\sum_{i=1}^{m}w_{i,j}v_{i}\right)\qquad j=1..m$$

(1)

and

$$v_{i}=\sigma\left(a_{i}+\sum_{j=1}^{n}w_{i,j}h_{j}\right)\qquad i=1..n$$

(2)

where $\sigma$ is the logistic sigmoid, $a_{i}$ and $b_{j}$ the biases.

RBM belongs to the class of energy based models (EBM). Indeed, RBM can be regarded as a Markov random field with associated a bipartite undirected graph. Therefore, the values given at visible and hidden units can be interpreted in terms of conditional probabilities, that is

$$P(H_{j}=1|\bm{V})=h_{j}\qquad j=1..m$$

(3)

and

$$P(V_{i}=1|\bm{H})=v_{i}\qquad i=1..n$$

(4)

Being the RBM based on a bipartite graph, the hidden variables are mutually independent given the visible variables and vice versa. Therefore, the conditional probabilities are given as

$$P(\bm{V}|\bm{H})=\prod\limits_{i=1}^{n}P(V_{i}|\bm{H})$$

(5)

$$P(\bm{H}|\bm{V})=\prod\limits_{j=1}^{m}P(H_{j}|\bm{V})$$

(6)

They can be both expressed in terms of joint probability $P(\bm{V},\bm{H})$ and its marginal probabilities $P(\bm{V})=\sum\limits_{\bm{H}}P(\bm{V},\bm{H})$ and $P(\bm{H})=\sum\limits_{\bm{V}}P(\bm{V},\bm{H})$. Since RBM makes use of the logistic sigmoid, the joint probability distribution is given by the Gibbs distribution

$$P(\bm{V},\bm{H})=\frac{1}{Z}e^{−E(\bm{V},\bm{H})}$$

(7)

where $E(\bm{V},\bm{H})$ is named the energy function and defined as

$$E(\bm{V},\bm{H})=-\sum_{i=1}^{n}a_{i}v_{i}-\sum_{j=1}^{m}b_{j}h_{j}-\sum_{i=1}^{n}\sum_{j=1}^{m}v_{i}w_{i,j}h_{j}$$

(8)

where $Z$ is called partition function and it is a normalizing constant used to assure that probability sums up to 1.

RBM can be adapted to process real-valued visible variables by scaling the input data to the unit interval, so that input values are interpreted as a-priori probabilities $p_{i}\in[0,1]$ that $V_{i}=1$.

RBM can be trained to replicate an input $\bm{v}$. Given the matrix $W$

$$\frac{\partial}{\partial w_{i,j}}log(P(\bm{v}))=v_{i}h_{j}-v^{\prime}_{i}h^{\prime}_{j}$$

(9)

where $h_{j}$ is obtained by Eq.(1) and $v^{\prime}_{i}$ is obtained by Eq.(1). At each step, the procedure makes use of the Gibbs sampling in order to get the vector $h^{\prime}$, while $\bm{v}=\bm{v}_{0}$. Thus, assuming a gradient descendant rule, the update of weights is given as

$$\Delta w_{i,j}=\epsilon(v_{i}h_{j}-v^{\prime}_{i}h^{\prime}_{j})$$

(10)

where $\epsilon$ is the learning rate. In addition, biases are updated using rules $\Delta a=\epsilon(v-v^{\prime})$, $\Delta b=\epsilon(h-h^{\prime})$.

At the end of the training, the hidden units $\bm{h}$ offer a compression of visible inputs $\bm{v}$.

An Auto-Encoder (AE) is a DL network that is trained to reconstruct or approximate the input by itself. For this reason, also AEs make use of unsupervised training. AE structure consists on an input layer, an output layer and one or more hidden layers connecting them. For the purpose of reconstructing the input, the output layer has the same dimension as the input layer, forming a bottleneck structure as depicted in Fig. 3.

An AE consists of two parts: one maps the input to a lower dimensional representation (encoding); the other maps back the latent representation into a reconstruction of the same shape as the input (decoding).

In the simplest structure there is just one single hidden layer. The AE takes the input $\mathbf{x}\in\mathbb{R}^{d}={\mathcal{X}}$ and maps it onto $\mathbf{y}\in\mathbb{R}^{p}$:

$$\mathbf{y}=\sigma_{1}(\mathbf{Wx}+\mathbf{b})$$

(11)

where $\sigma_{1}$ is an element-wise activation function such as a sigmoid function or a rectified linear unit. After that, the latent representation $\mathbf{y}$, usually referred to as code, is mapped back onto the reconstruction $\mathbf{z=x^{\prime}}$ of the same shape as $\mathbf{x}$:

$$\mathbf{z}=\sigma_{2}(\mathbf{W^{\prime}y}+\mathbf{b^{\prime}})$$

(12)

Since we are trying to fit the model for replicating the input, the parameters ($\mathbf{W}$, $\mathbf{W^{\prime}}$, $\mathbf{b}$ and $\mathbf{b}^{\prime}$) are optimized so that the average reconstruction error is minimized. This error can be measured by different ways. Among them the squared error:

$${\mathcal{L}}(\mathbf{x},\mathbf{z})=\|\mathbf{x}-\mathbf{z}\|^{2}=\|\mathbf{x}-\sigma_{2}(\mathbf{W^{\prime}}(\sigma_{1}(\mathbf{Wx}+\mathbf{b}))+\mathbf{b^{\prime}})\|^{2}$$

(13)

Instead if the input is interpreted as either bit vectors, i.e., $x_{i}\in\{0,1\}$ or vectors of bit probabilities, i.e., $x_{i}\in[0,1]$, the cross-entropy of the reconstruction is a suitable solution:

$${\mathcal{L}}(\mathbf{x},\mathbf{z})=-\sum_{k=1}^{d}[x_{k}\log z_{k}+(1-x_{k})\log(1-z_{k})]$$

(14)

In order to force the hidden layer to extract more robust features we train the AE to reconstruct the input from a corrupted version of by discarding some of the values. This is done by setting randomly some of the inputs to zero [5]. This version of AE is called Denoising Auto-Encoder.

Historical data consist of the price series of S&P 500 from 01 Jan 2007 to 01 Jan 2017. The input is made of multiple technical indicators computed over the price series. Table I provides the list of indicators used in our experiments (a detailed description can be found in, e.g., [6, 7, 8]).

Trend labeling of data is performed by assigning at each time $t$ a value $y(t)\in\{+1;-1\}$ for uptrend and downtrend respectively. The rule followed to assign the label makes use of a centered moving average (cMA) of the index at time $t$ using the rolling window $[t-3,t+3]$. After, the following criteria for labeling are applied:

$$y(t)=+1\;\text{if}\;\text{cMA}(t)>\text{close(t)}\;\text{and}\;\text{cMA}(t+3)>\text{cMA(t+1)}$$

$$y(t)=-1\;\text{if}\;\text{cMA}(t)<\text{close(t)}\;\text{and}\;\text{cMA}(t+3)<\text{cMA(t+1)}$$

Otherwise at time $t$ we keep the previous label, i.e., $y(t)=y(t-1)$. In Fig. 4 is shown the close price series and the value of labels.

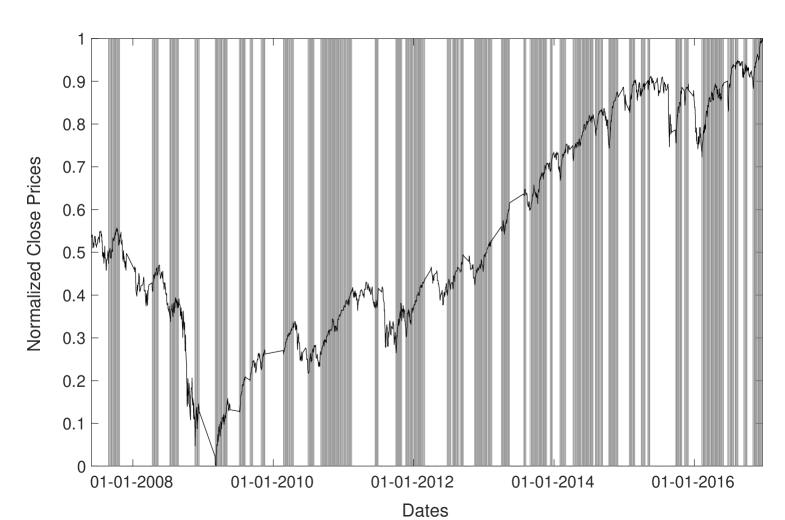
In order to improve the quality of the training set, thus predictability of model, we focus on periods larger enough to outline a trend (at least $10$ days) and consistent with value movements, meaning that an uptrend should entail a positive value increment within the period, while we should have a decrement for downtrends. Periods that do not meet these characteristics are discarded from the training set.

All data available have been used to identify the structure able to compress the input data. Instead the the SVM has been trained using the 90% of available data and tested over the remaining 10%. Comparisons have been performed using the most recent 10% of data for testing. In order to avoid a bias of results due to the selection of most recent period, the final comparison between RBM and AE has been performed using a 10-fold cross validation.

All the experiments are carried out on a workstation equipped with an Intel Xeon Processor E5 v3 Family, $3.5$GHz x$8$, $16$GB RAM and GPU GeForce GTX 980 Ti with $6$GB RAM on board.

The framework has been developed in Python. The implementation of AE and RBM are based on Theano [9], while SVM is based on scikit-learn library for machine learning [10]. All indicators are calculated by using TA-Lib, a technical analysis library [11].

In order to accomplish the feature reduction we make use of AE and RBM as preliminary to a SVM classifier used for prediction. A comparison between AE and RBM have been done in terms of accuracy of prediction and time required to train the network.

The training of AE is based on Backpropagation algorithm with stochastic descendant gradient for updating weights and Cross-Entropy as loss function. The weighting matrix $W$ is initialized with values uniformly sampled in the interval $[-4\sqrt{6/(n_{visible}+n_{hidden})},+4\sqrt{6/(n_{visible}+n_{hidden})}]$ and the biases are initialized to $0$, as suggested by [12] for sigmoid activation functions.

The algorithm used to train the RBM has been the gradient-based persistent contrastive divergence learning procedure[13]. In this case the initial values of the weights are chosen from a zero-mean Gaussian with a standard deviation of $0.01$ as suggested by Hinton in [14]. Hidden and visible biases are initialized to $0$.

In both cases we divide the training set into small mini-batches to accelerate the computation. Also we have introduced an adaptive learning rate that is exponentially decreasing by means of a constant decay-rate, in the expectation of improving both accuracy and efficiency of the training procedures. We use a form of regularization for early-stopping to avoid over-fitting issues.

Alternatives are compared by means of prediction accuracy, that is the number of correct labels over the overall number of labels.First we consider two important aspects regarding input data: diversity and scaling.

Diversity. The first question we consider is how important is to use diverse sources of information, where by ”diverse” we mostly mean independent or uncorrelated. To investigate this aspect we first consider only cross-over indicators obtained by crossing different slower and faster moving averages (MA). In particular, we consider $11$ faster MAs (with all periods within the range $[5,15]$) and $11$ slower MAs (with periods uniformly distributed within the range $[20,30]$). This leads to $121$ indicators obtained by the different combinations of MAs.

In Table II and Fig. 5 we report the accuracy obtained for both AE and RBM with a varying number of hidden neurons. The performance obtained of both AE and RBM are comparable, and it tends to improve by increasing the number of hidden neurons.

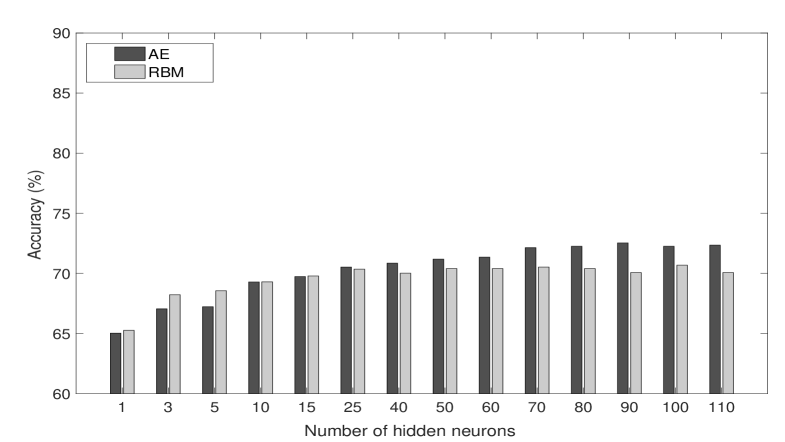
The low accuracy values obtained and the low speed in their improvement by a higher number of neurons suggest that diversity can play a relevant role. Indeed, even an high number of features may convey few information when sources are highly correlated.

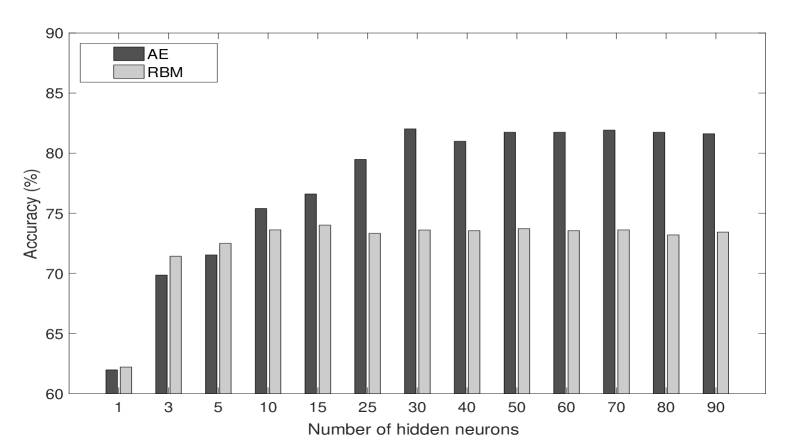
In Table III we report accuracy obtained by using the whole set of available indicators. Some of them are parametric with respect to the look-back period. For those we assumed different periods, namely $n=3,14,30$, in the aim of enriching the available information. We also included the adjusted closing price and volume of the index. This leads to collect a total of $93$ source, each providing a specific day-by-day feature. By looking at the results, we can observe a substantial improvement of accuracy and an initial differentiation between AE and RBM.

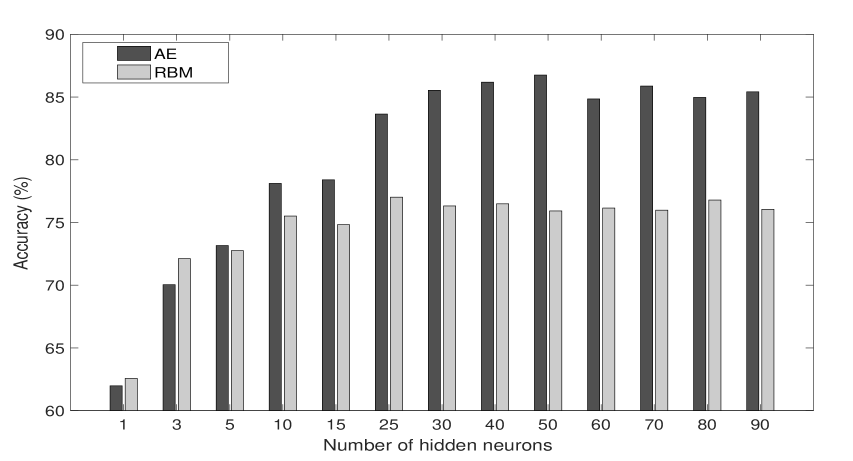
Scaling. AE and RBM require to scale input values. This is generally done by a standard max/min normalization. However, other possibilities are available. Here we consider a rescaling over the unit interval $[0,1]$ obtained by means of the empirical cumulative distribution function (ECDF). The procedure consists in calculating the ECDF for each individual feature and then to assign to each instant of time $t$ its corresponding value of the ECDF. The expectation is that max/min normalization keeps unchanged the density of data points, so that information is not uniformly distributed over the unit interval. Instead, the scaling offered by ECDF is able to better distribute data points and this may contribute to improve performances.

Table  IV and Fig. 7 show the results of this experiment. Accuracy shows an actual improvement, supporting the initial hypothesis that ECDF offers a better scaling than standard normalization.

From all experiments above we can observe how there exists an optimal number of hidden neurons, over that performances do not improve or slightly decrease. That is the optimal dimensionality of the embedding performed by AE and RBM. In general, according to our experience, AE is able to reach higher dimensions. This might be the reason of better performances offered by the feature reduction based on AE.

In order to validate this finding, we compare both the networks in their best case ($50$ hidden neurons for AE and $25$ hidden neurons for RBM, all indicators used as input, rescaled by means of ECDF) using a 10-fold cross validation procedure. In Table V we report the results. They outline a consistent out-performance of AE versus RBM, resulting AE more accurate and faster to train.