¹¹institutetext: Colorado State University, Fort Collins CO 80521, USA

On Finding Lekkerkerker-Boland Subgraphs

Nathan Lindzey lindzey@cs.colostate.edu, Computer Science Department, Colorado State University, Fort Collins, CO, 80523-1873 U.S.A. Ross M. McConnell rmm@cs.colostate.edu, Computer Science Department, Colorado State University, Fort Collins, CO, 80523-1873 U.S.A.

Abstract

Lekkerkerker and Boland characterized the minimal forbidden induced subgraphs for the class of interval graphs. We give a linear-time algorithm to find one in any graph that is not an interval graph. Tucker characterized the minimal forbidden submatrices of matrices that do not have the consecutive-ones property. We give a linear-time algorithm to find one in any matrix that does not have the consecutive-ones property.

1 Introduction

A graph is an interval graph if it is the intersection graph of a set of intervals on a line. Such a set of intervals is known as an interval model of the graph. They are an important subclass of perfect graphs [3], they have been written extensively about and they model constraints in various combinatorial optimization and decision problems [11, 13]. They have a rich structure and history, and interesting relationships to other graph classes. For a survey, see [1].

If $M$ is a 0-1 (binary) matrix, we let $size(M)$ denote the number of rows, columns and 1’s. Such a matrix has the consecutive-ones property if there exists a reordering of its columns such that, in every row, the 1’s are consecutive. A clique matrix of a graph is a matrix that has a row for each vertex, a column for each clique, and a 1 in row $i$ , column $j$ if vertex $i$ is contained in clique $j$ . A graph is an interval graph if and only if its clique matrices have the consecutive-ones property, see, for example [3].

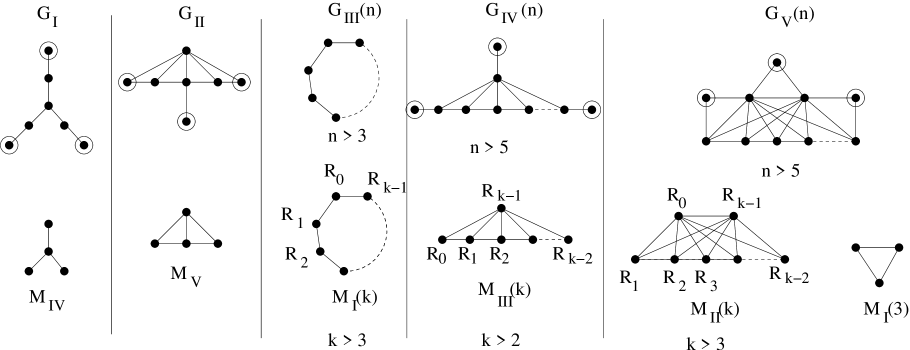
In 1962, Lekkerkerker and Boland described the minimal induced forbidden subgraphs for the class of interval graphs [6], known as the LB graphs (Figure 2). Ten years later, Tucker described the minimum forbidden submatrices for consecutive-ones matrices [16]. These are depicted in Figure 1. Not surprisingly, there is a relationship between the intersection graphs of rows of Tucker matrices and the LB graphs, depicted in Figure 2.

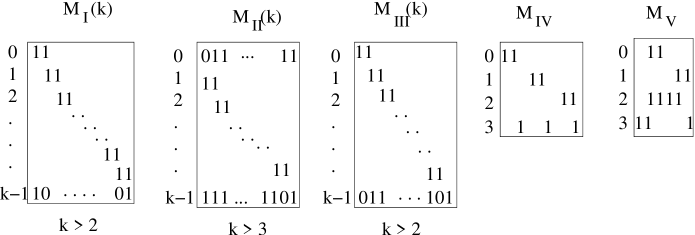
Refer to caption — Figure 1: The Minimal Forbidden Submatrices for Consecutive-Ones Matrices. For $M_{I}$ , $k\geq 3$ , and for $M_{II}$ and $M_{II}$ , $k\geq 4$ . $M_{IV}$ and $M_{I}$ have fixed size.

In this paper, we give a linear time bound for finding one of the LB subgraphs when a graph is not an interval graph. As part of our algorithm, we also give a linear-time $(O(size(M))$ bound for finding one of Tucker’s submatrices in a matrix $M$ that does not have the consecutive-ones property. This latter problem was solved previously in $O(n*size(M))$ time in [2], where $n$ is the number of rows of the matrix.

A graph is chordal if it has no chordless cycle ( $G_{III}$ on four or more vertices). Figure 5 seems to imply that the rows of a given Tucker submatrix of the clique matrix can be extended to an interval model of an LB subgraph by including at most three additional rows of the matrix, giving the rows of vertices that induce an LB subgraph. Figure 5 gives a counterexample. Fortunately, it is true in the case of chordal graphs, but the example illustrates the need for a proof; it does not follow from seemingly obvious considerations, such as that no clique is a subset of any other. This gives an LB subgraph if $G$ is chordal, and when it is not chordal, the algorithm of [15] already gives a $G_{III}$ .

An interval graph is proper if there exists an interval representation where no interval is a subset of another. It is a unit interval graph if there exists an interval representation where all intervals have the same length. These graph classes are the same, and Wegner showed that a graph is a proper interval graph if and only if it does not have a chordless cycle, the special case of $G_{IV}$ or $G_{V}$ for $n=6$ or the claw ( $K_{1,3}$ ) as an induced subgraph [17]. Hell and Huang give an algorithm that produces one of them in linear time [4] . The problem of finding a forbidden subgraph reduces easily to finding an LB subgraph. Each of the LB graphs is either one of Wegner’s forbidden subgraphs or contains an obvious claw, and finding a claw in linear time, given an interval model, is elementary. By itself, this approach has no obvious advantages over Hell and Huang’s elegant algorithm, but such reductions are useful when studying or programming a collection of related algorithms.

A certifying algorithm is an algorithm that provides, with each output, a simple-to-check proof that it has answered correctly [5, 9]. An interval model gives a certificate that a graph is an interval graph, and an LB subgraph gives one if the graph is not an interval graph. However, a certifying algorithm was given previously in [5]. The ability to give a consecutive-ones ordering or a Tucker submatrix in linear time gives a linear-time certifying algorithm for consecutive-ones matrices, but one was given previously in [8]. The previous certificates are easier to check, which is a desirable property for certifying algorithms. However, they are neither minimal nor uniquely characterized. Aside from the theoretical interest in LB subgraphs, it is easy to obtain a minimal certificate of the form given in [5] from an LB subgraph found by the algorithm we describe below. An open question is whether a minimal, unique, especially simple, or otherwise interesting special case of the certificate from [8] can be obtained by applying the algorithm of that paper to a Tucker submatrix obtained by the algorithm of the present paper. Tucker submatrices may be useful in heuristics for finding large submatrices that have the consecutive-ones property, small Tucker matrices, or identifying errors in biological data [14, 2]. Our techniques provide new tools for such heuristics.

2 Preliminaries

Given a graph $G$ , let $V$ denote the number of vertices and $E$ denote the number of edges. If $\emptyset\subset X\subseteq V$ , let $G[X]$ denote the subgraph induced by $X$ . Standard sparse representations of 0-1 matrices take $O(size(M))$ space to represent $M$ . We treat the rows and columns as sets, where each row $R$ is the set of columns where the row has a 1 and each column $C$ is the set of rows where the column has a 1. Suppose ${\cal R}$ is the set of rows of a consecutive-ones ordered matrix and $(C_{1},C_{2},\ldots,C_{m})$ is the ordering of the columns. In linear time, we can find, for each row, the leftmost and rightmost column in the row. Let us call these the left endpoint and right endpoint of the row.

That interval graphs are a subclass of the class of chordal graphs follows from inclusion of $G_{III}$ among the LB subgraphs. Rose, Tarjan and Lueker give an $O(V+E)$ algorithm that finds whether a graph is a chordal graph, and, if so, produces its maximal cliques [12]. Otherwise, the algorithm of [15] produces a chordless cycle ( $G_{III}$ ) in linear time.

When a graph is chordal, the problem of deciding whether it is an interval graph reduces to the problem of deciding whether its clique matrix has the consecutive-ones property. Booth and Lueker further reduced this problem to that of finding a maximal prefix ${\cal R}^{\prime}=\{R_{1},R_{2},\ldots,R_{r}\}$ of the rows of a binary matrix $M$ that has the consecutive-ones property, in $O(size(M))$ time.

Assigning a left-to-right order to children of each internal node of a rooted tree results in a unique left-to-right order of the leaves. Booth and Lueker’s algorithm produces a PQ tree, for ${\cal R}^{\prime}$ . The PQ tree represents all possible consecutive-ones orderings of ${\cal R}^{\prime}$ . There is one leaf $\{c\}$ for each column $c$ . The internal nodes of the PQ tree consists of P nodes and Q nodes. The consecutive-ones ordering of columns are given by the leaf orders obtainable by assigning an arbitrary left-to-right order to children of each P node, and for each Q node, assigning the given left-to-right order or its reverse.

Though the PQ tree can be represented using $O(1)$ space per node, conceptually, we will consider each node of the PQ tree to be set given by the disjoint union of its children; equivalently, it is the union of its leaf descendants.

Definition 1

Let ${\cal S}$ be a collection of subsets of a set $U$ . Two elements of $U$ are in the same Venn class if they are elements of the same set of members of ${\cal S}$ . The unconstrained Venn class consists of those elements of $U$ that are not in any member of ${\cal S}$ ; all others are constrained. Two sets $R_{1},R_{2}$ overlap if their intersection is nonempty, but neither is a subset of the other. The overlap graph of ${\cal S}$ is the undirected graph whose vertices are the members of ${\cal S}$ , and $R_{1},R_{2}\in{\cal S}$ are adjacent if and only if $R_{1}$ and $R_{2}$ overlap.

Lemma 1

[10] A set of columns is a Q node of a consecutive-ones matrix $M$ if and only if it is the union of rows of a connected component of the overlap graph of rows of $M$ . The Venn classes of rows in this component are its children.

3 Breadth-first search on the overlap graph of a collection of sets, given a consecutive-ones ordering

In linear time, we may label each row of a consecutive-ones ordered matrix with its left and right endpoints. We may then label each column $c_{i}$ of a consecutive-ones ordered matrix with the set of rows that have their left endpoints in $c_{i}$ . In linear time, we can then radix sort the list of sets that have their left endpoint at $c_{i}$ in descending order of index of right endpoint, yielding a list ${\cal R}_{i}$ . This is accomplished with a single radix sort that has the index of the left endpoint as its primary sort key and index of the right endpoint as the secondary sort key. By symmetry, we can construct a list ${\cal L}_{i}$ of rows that have their right endpoint in each column $c_{i}$ , sorted in ascending order of index of left endpoint.

This allows us to perform a breadth-first search on the overlap graph of the rows in time linear in the size of the matrix, as follows. The lists ${\cal L}_{i}$ and ${\cal R}_{i}$ are represented with doubly-linked lists. We maintain the invariant that elements that have been placed in the BFS queue have been removed from these lists. When a consecutive-ones ordered set $R$ comes to the front of the queue, we traverse its list $(c_{j},c_{j+1},\ldots,c_{k})$ of columns. For each $c_{h}$ in the list, we remove elements from ${\cal R}_{h}$ and place them in the queue, until we reach an element in ${\cal R}_{i}$ whose right endpoint is no farther to the right than $c_{k}$ . All of the removed elements overlap $R$ . Since ${\cal R}_{h}$ is sorted in descending order of right endpoint, all these elements are a prefix of ${\cal R}_{h}$ , and any remaining elements in the list do not overlap $R$ . When we remove an element from ${\cal R}_{h}$ , we remove it from any list ${\cal L}_{h^{\prime}}$ that it is a member of, to maintain the invariant. This takes $O(1)$ time for each element moved to the BFS queue, plus $O(1)$ time for each column of $R$ . The lists $L_{h}$ are handled symmetrically. Summing over all rows $R$ , the time is $O(size(M))$ .

4 Finding Tucker Submatrices

4.1 Tucker matrices with at most four rows

Lemma 2

If a set ${\cal R}^{\prime}$ of rows has the consecutive-ones property and $Z$ is a row such that ${\cal R}={\cal R}^{\prime}\cup\{Z\}$ does not, then $Z$ is one of the rows of every Tucker submatrix in ${\cal R}$ .

Algorithm 4.1

(See Lemma 3.)

init	ialR	ows	( $M^{\prime},k$ )
	$M:=M^{\prime}$
	$i:=1$ ;
	While $i\leq k+1$ and M has at least $i-1$ rows
		Using Booth and Lueker, find the minimal prefix $(R_{1},R_{2},\ldots,R_{r},Z)$ of rows
			of $M$ that does not have the consecutive-ones property.
		Let $M$ be the matrix whose row sequence is $(Z,R_{1},R_{2},\ldots,R_{r})$ .
	return $M$

Lemma 3

Suppose Algorithm 4.1 is run with parameter $k$ and a matrix $M^{\prime}$ that does not have the consecutive-ones property. If the returned matrix $M$ has at most $k$ rows, then these are the rows of every Tucker matrix of $M$ . Otherwise, $M$ fails to have the consecutive-ones property and every Tucker submatrix in $M$ has at least $k+1$ rows.

Proof

By induction on $i$ , $M$ does not have the consecutive-ones property at the end of iteration $i$ . Also, by induction on $i$ , using Lemma 2, at the end of iteration $i$ , for every Tucker submatrix $M_{T}$ of $M$ , the rows of $M_{T}$ include the first $i$ rows of $M$ . If $M_{T}$ has only $i$ rows, then the first $i$ rows of $M$ do not have the consecutive-ones property, so at the end of iteration $i+1$ , $M$ will have $i$ rows.

We run Algorithm 4.1 for $k=4$ . If it returns a matrix with $j$ rows, where $j\leq 4$ , it is easy to get a linear time bound to get the columns. (One way is to generate all $j!\leq 24$ orderings of rows and for each, to check for the columns of each Tucker matrix of size $j$ .) Otherwise, Algorithm 4.1 returns a matrix $M$ of more than 4 rows. By Lemma 3, $M$ fails to have the consecutive-ones property and every Tucker submatrix of $M$ has at least five rows. This excludes any instances of $M_{IV}$ , $M_{V}$ or the anomalous case of $M_{I}$ on three rows that does not correspond to a chordless cycle.

4.2 Matrices in which all Tucker submatrices have more than four rows

Lemma 4

The overlap graphs of $M_{I}$ , $M_{II}$ , and $M_{III}$ are simple cycles.

Definition 2

Suppose ${\cal R}^{\prime}$ is a set of rows with the consecutive-one property, $Q$ is a Q node of its PQ tree, $(X_{1},X_{2},\ldots,X_{k})$ is the ordering of $Q$ ’s children and $Z$ is a row not in ${\cal R}^{\prime}$ . Let $X_{h},X_{i},X_{j}$ be three children of $Q$ such that $h<i<j$ . They are a 1-0-1 configuration for $Z$ if $X_{h}$ and $X_{j}$ each contain a 1 of row $Z$ and $X_{i}$ contains a 0 of row $Z$ . They are a 0-1-0 configuration for $Z$ if $X_{h}$ and $X_{j}$ each contain a 0 of row $Z$ and $X_{i}$ contains a 1 of row $Z$ .

Lemma 5

If ${\cal R}^{\prime}$ is a set of rows that has the consecutive-ones property and $Z$ is a row not in ${\cal R}^{\prime}$ , then ${\cal R}^{\prime}\cup\{Z\}$ does not have the consecutive-ones property if the PQ tree of ${\cal R}^{\prime}$ has a Q node $Q$ such that either:

1.

$Q$ has a 1-0-1 configuration for $Z$ ;
2.

$Q$ has a 0-1-0 configuration for $Z$ and $Z$ is not a subset of $Q$ .

This test is implicit in Booth and Lueker’s algorithm, where it is a sufficient condition, but not a necessary one. The following is a consequence of Lemma 1.

Lemma 6

[8] The conditions of Lemma 5 are necessary and sufficient if the overlap graph of of ${\cal R}^{\prime}$ is connected.

Lemma 7

If a matrix fails to have the consecutive-ones property and has no Tucker submatrix with fewer than five rows, then when Algorithm 4.1 is run on it with $k=4$ , at the end of one of the five iterations of its loop, the PQ tree of ${\cal R}^{\prime}=\{R_{1},R_{2},\ldots,R_{r}\}$ will have a Q node $Q$ with the following properties:

–

$Q$ has a 1-0-1 configuration $(X_{h},X_{i},X_{j})$ for $Z$ ;
–

There exist $A,B\in{\cal R}^{\prime}$ that are members of the component of the overlap graph on ${\cal R}^{\prime}$ whose union is $Q$ , and such that $A$ contains $X_{h}$ and is disjoint from $X_{i}$ and $X_{j}$ , and $B$ contains $X_{j}$ and is disjoint from $X_{h}$ and $X_{i}$ .

Proof

If ${\cal T}$ is the rows of $M$ that contain a Tucker submatrix $M_{T}$ , at the end of an iteration of the loop of Algorithm 4.1, $Z\in{\cal T}$ by by Lemma 2. By Lemma 4, the overlap graph of ${\cal T}^{\prime}={\cal T}\setminus\{Z\}$ is connected, so ${\cal T}^{\prime}$ is a subset of a component of the overlap graph of ${\cal R}^{\prime}$ , which gives rise to a Q node $Q$ of the PQ tree of ${\cal R}^{\prime}$ , by Lemma 1. Since the children of $Q$ are the Venn classes of the component, no two Venn classes of ${\cal T}^{\prime}$ , hence no two columns of $M_{T}$ , can lie in the same child of the Q node.

For each choice of a last row of a Tucker matrix on at least five rows, Figure 3 gives the possible orderings imposed on the last row by a consecutive-ones ordering of ${\cal T}^{\prime}$ , which is unique up to reversal, by Lemmas 4 and 1. In each case, if row $i\not\in\{0,1,k-2,k-1\}$ is chosen to go last, rows $i-1$ and $i+1$ satisfy the requirements of $A$ and $B$ . $M_{T}$ has at least five rows and no row of $M_{T}$ is contained in $Z$ more than once in the five iterations, so in at least one of the iterations a row $i\not\in\{0,1,k-2,k-1\}$ will go last.

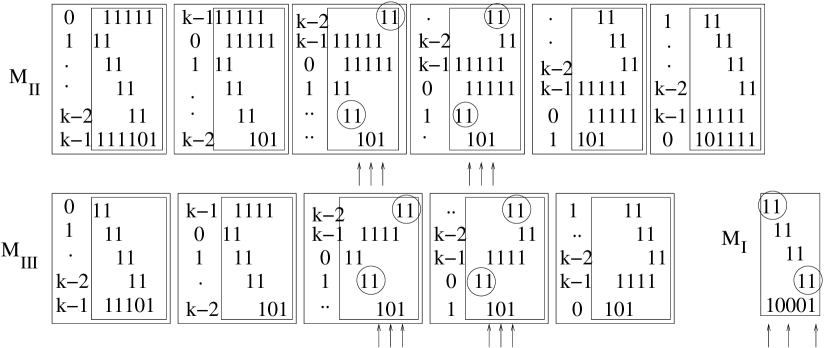
The correctness and linear time bound for the following are the key results of this section:

Algorithm 4.2

Find the rows of a Tucker submatrix when every Tucker submatrix has at least five rows

fin	dRo	ws	( $M$ )
	Run initialRows( $M,4$ ) (Algorithm 4.1) to find ${\cal R}^{\prime}$ , $Z$ , $A$ , $B$
		satisfying the requirements of Lemma 7
	Let $P$ be a shortest path in the overlap graph of ${\cal R}^{\prime}$ from $A$ to $B$
	Let $P_{1}$ be a minimal prefix of $P$ such that the union of $\{Z\}$ and the
		set ${\cal P}_{1}$ of rows of $P_{1}$ does not have the consecutive-ones property.
	Let $P_{2}$ be a minimal suffix of $P_{1}$ such that the union of $\{Z\}$ and the
		set ${\cal P}_{2}$ of rows of $P_{2}$ does not have the consecutive-ones property.
	Return ${\cal P}_{2}\cup\{Z\}$ .

Lemma 8

If $M$ does not have the consecutive-ones property and every Tucker matrix of $M$ has at least five rows, then Algorithm 4.2 returns the set of rows of a Tucker matrix of $M$ .

Proof

Since $A$ and $B$ lie in the same component of the overlap graph of ${\cal R}^{\prime}$ , $P$ exists. Since ${\cal R}^{\prime}$ has the consecutive-ones property, so does ${\cal P}$ . Because ${\cal P}$ has a connected overlap graph, $P$ , $\bigcup{\cal P}$ is a single Q node of the PQ tree of ${\cal P}$ , by Lemma 1. Because of $A$ and $B$ , $X_{h}$ , $X_{i}$ , and $X_{j}$ are contained in distinct Venn classes of ${\cal P}$ , and the ones containing $X_{h}$ and $X_{j}$ are constrained. Since $\bigcup{\cal P}$ is consecutive, it must have a row that contains the $X_{i}$ , hence the Venn class of ${\cal P}$ containing $X_{i}$ is also constrained. Therefore, ${\cal P}\cup\{Z\}$ does not have the consecutive-ones property by Lemma 5, and $P_{1}$ and $P_{2}$ exist. By Lemma 2, all Tucker matrices in ${\cal R}^{\prime}\cup\{Z\}$ contain $Z$ , so this applies also to ${\cal P}_{2}\cup\{Z\}$ .

Suppose there is a proper subset ${\cal R}^{\prime\prime}$ of the rows on $P_{2}$ such that ${\cal R}^{\prime\prime}\cup\{Z\}$ contains a Tucker matrix. The overlap graph of ${\cal R}^{\prime\prime}$ is connected, by Lemma 4. Since $P_{2}$ is a shortest path, it is a chordless path, so ${\cal R}^{\prime\prime}$ is a subpath of $P_{2}$ by Lemma 4. Let ${\cal R}^{\prime}_{1}$ be the rows on $P_{1}$ , excluding the last row on $P_{1}$ . Let ${\cal R}^{\prime}_{2}$ be the rows of $P_{2}$ , excluding the first row on $P_{2}$ . By the minimality of $P_{1}$ and $P_{2}$ , ${\cal R}^{\prime}_{1}\cup\{Z\}$ and ${\cal R}^{\prime}_{2}\cup\{Z\}$ have the consecutive-ones property. Since ${\cal R}^{\prime\prime}$ is a subpath of $P_{2}$ , ${\cal R}^{\prime\prime}\subseteq{\cal R}^{\prime}_{1}$ or ${\cal R}^{\prime\prime}\subseteq{\cal R}^{\prime}_{2}$ , so ${\cal R}^{\prime\prime}\cup\{Z\}$ has the consecutive-ones property, contradicting our assumption that it does not. Therefore, ${\cal P}_{2}\cup\{Z\}$ is the set of rows of a Tucker matrix.

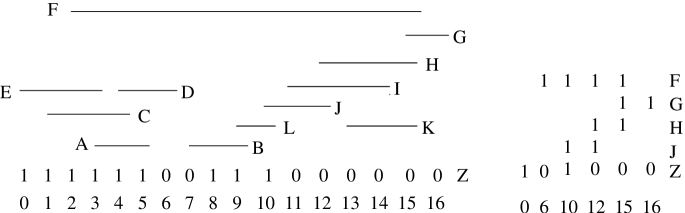
Figure 4 gives an example on which we illustrate some implementation details. $Z$ is given by the 1’s and 0’s above the column numbers in the figure on the left, and ${\cal R}^{\prime}$ is depicted by the intervals. The rows labeled $A$ and $B$ satisfy the requirements of $A$ and $B$ for Lemma 7, and $P=(A,E,F,G,H,J,L,B)$ is a shortest path from $A$ to $B$ in the overlap graph of ${\cal R}^{\prime}$ , found using the BFS algorithm of Section 3.

Using Booth and Lueker’s terminology, we maintain labels on each class indicating whether it is full (contains only 1’s of $Z$ ), empty (contains only 0’s of $Z$ ), or partial (contains both 1’s and 0’s of $Z$ ). The minimal prefix $P_{1}$ of $P$ whose rows, together with $Z$ , do not have the consecutive-ones property, is $(A,E,F,G,H,J)$ . This is detected as follows. It is easy to verify that its sequence of constrained Venn classes is $(\{0,1\}$ , $\{2\}$ , $\{3\}$ , $\{4,5\}$ , $\{6-9\},\{10,11\}$ , $\{12\}$ , $\{13,14\}$ , $\{15\}$ , $\{16\})$ , and their full/partial/empty labels $(F,F,F,F,P,P,E,E,E,E)$ , respectively. Selecting a 1 from a full class, a 0 from the first partial class and a 1 from the second partial class gives a 1-0-1 configuration satisfying Lemma 5. It is the minimal such prefix. A smaller prefix, $(A,E,F)$ has a 0-1-0 configuration, but it does not satisfy Lemma 5 because $Z\subset A\cup E\cup F$ .

The minimal suffix $P_{2}$ of $P_{1}$ that satisfies Lemma 5 is $(F,G,H,J)$ , which is found in the same way by working on the reverse of $P_{1}$ . Its sequence of constrained Venn classes are $(\{2-9\}$ , $\{10,11\}$ , $\{12-14\}$ , $\{15\}$ , $\{16\})$ , labeled $(P,P,E,E,E)$ , respectively. Selecting a 0 from the first partial class, a 1 from the next, and a 0 from an empty class gives a 0-1-0 configuration. It satisfies condition 2 of the lemma, because the unconstrained class, $\{0,1\}$ is partial, hence $Z\not\subseteq F\cup G\cup H\cup J$ .

Therefore, $\{F,G,H,J,Z\}$ is the set of rows of a Tucker submatrix. A minimal set of columns that illustrates that it satisfies the lemma is $\{0,6,10,12,15,16\}$ . On the righthand side of Figure 4 is the resulting Tucker matrix, which matches the final configuration in the sequence for $M_{III}$ in Figure 3.

This example shows that the key to finding $P_{1}$ and $P_{2}$ is maintaining the sequence of constrained Venn classes and their full/partial/empty labels as rows are added in the order in which they occur on $P$ or on the reverse of $P_{1}$ . Since they are added in an order such that every prefix of the order has a connected overlap graph, the sequence is uniquely constrained after each row is added, by Lemma 1. When a row $R_{i}$ is added, if it overlaps a constrained Venn class $X$ , $X$ must be replaced in the sequence with two Venn classes, $(X\setminus R_{i},X\cap R_{i})$ or with $(X\cap R_{i},X\setminus R_{i})$ , whichever is required to maintain consecutiveness of $R_{i}$ . If $R_{i}$ intersects the unconstrained class, $S$ , then $R_{i}\cap S$ must be added at one extreme end of the sequence, whichever maintains consecutiveness of $R_{i}$ . Details are given in [8].

The difference between this algorithm and that of [8] (and Booth and Lueker) is that, instead of testing at each iteration whether the next row $R_{i}$ can be added to those considered so far without undermining the consecutive-ones property, it must repeatedly perform this test on the fixed row $Z$ after each row $R_{i}$ is added. We already know that $R_{i}$ can be added, since ${\cal R}^{\prime}$ has the consecutive-ones property. Like Booth and Lueker, the previous algorithm of [8] applies the full/partial/empty labels for $R_{i}$ to facilitate the test, in $O(|R_{i}|)$ time, and then removes them before considering the next row $R_{i+1}$ . Though we must perform the test on the fixed row $Z$ at each iteration, instead of on $R_{i}$ , we must do it $O(|R_{i}|)$ time, not $O(|Z|)$ time, in order to retain the linear time bound. To do this, we leave the full/partial/empty labelings for $Z$ from one iteration to the next, so that we only have to update them, using $R_{i}$ , rather than re-creating them each time a new row is considered.

To facilitate this, we keep updated labels $c(X)$ and $n(X)$ on each Venn class $X$ , where $c(X)$ denotes the cardinality of $X$ and $n(X)$ is the number of elements of $Z$ in $X$ . Labels only need to be updated when a Venn class is split. It is split into $X\cap R_{i}$ and $X\setminus R_{i}$ . We may find $c(X\cap R_{i})$ and $n(X\cap R_{i})$ by counting them directly, since there are $O(|R_{i}|)$ of these elements. The classes are implemented with doubly-linked lists, and these sets are removed from the list for $X$ , leaving it to represent $X\setminus R_{i}$ . Subtracting $c(X\cap R_{i})$ and $n(X\cap R_{i})$ from the old labels $c(X)$ and $n(X)$ gives the updated labels for $c(X\setminus R_{i})$ and $n(X\setminus R_{i})$ in $O(1)$ time. Each of the new classes is full if its $c()$ and $n()$ labels are equal, empty if its $n()$ label is 0, and partial otherwise.

To evaluate whether one of the conditions of Lemma 5 holds, it is easy to see that it suffices to keep track of transition pairs, which are consecutive pairs such that one contains a 0 and one contains a 1. This happens when their full/partial/empty labels are unequal, or else both partial. When a new transition pair forms, we have touched at least one member of the pair within our $O(|R_{i}|)$ operations, so keeping track of these does not affect this time bound.

Since finding $P$ takes linear time by the BFS of Section 3, it remains only to bound the time required to find the first step, finding the elements $A$ and $B$ of Lemma 7. This is much more straightforward, since we apply it once for each iteration of the loop of Algorithm 4.1, hence we can afford to take $\Theta(size(M))$ time for the test. We can apply the entire set of full/partial/empty labels for $Z$ to the PQ tree within this bound, by working from the leaves to the root.

For each Q node $Q$ , the members of the overlap component whose union is $Q$ are unions of more than one and fewer than all of its children. How to find them in linear time for all Q nodes has been described previously, for example in [7]. We find the rows of the overlap component that contain a Venn child of $Q$ that is labeled full or partial (a “1”). Out of all such rows, let $A^{\prime}$ be the one with a leftmost right endpoint, and let $B^{\prime}$ be the one with the rightmost left endpoint. By a simple greedy swapping argument, the overlap component giving rise to $Q$ contains an $A$ and a $B$ satisfying Lemma 7 if and only if $A^{\prime}$ and $B^{\prime}$ satisfy it, which happens if and only if there is a child between the right endpoint of $A^{\prime}$ and the left endpoint of $B^{\prime}$ that is labeled partial or empty (a “0”). This can also clearly be implemented so that the time bound over all Q nodes takes $O(size(M))$ time.

Once the set ${\cal P}_{2}\cup\{Z\}$ of rows of a Tucker matrix have been found, it remains to find the columns. This is a set of columns, the removal of any one of which would undermine the conditions of Lemma 5, which are satisfied initially by ${\cal P}_{2}\cup\{Z\}$ . Deletion of a column undermines the lemma if and only if does one of the following:

1.

It disconnects the path in overlap graph on ${\cal R}$ ;
2.

It undermines the only remaining 1-0-1 configuration, or 0-1-0 configuration with a 1 in the unconstrained class.

The second test is elementary and omitted because of space constraints. For the first test, recall that $P_{2}=(R_{1},R_{2},\ldots,R_{k})$ is a chordless path in the overlap graph. Let ${\cal A}=\{R_{1}\setminus R_{2}\}\cup\{X|X=R_{i}\cap R_{i+1}$ for $i\in\{1,2,\ldots,k-1\}\}$ $\cup\{Y|Y=R_{i+1}\setminus R_{i}$ for $i\in\{1,2,\ldots,k-1\}\}$ . Each element of ${\cal A}$ is consecutive-ones ordered, the sum of cardinalities of sets in ${\cal A}$ is $O(size(M))$ . The overlap graph remains connected if and only if every member of ${\cal A}$ contains at least one retained column. We give each column a list of members of ${\cal A}$ it is contained in and keep a counter on each element of ${\cal A}$ indicating the number of remaining columns it contains. When removing a column $C$ , the counters can be updated by decrementing the counters of members of ${\cal A}$ in its list. A column cannot be removed if removing it would decrement a counter to 0.

5 Finding a Lekkerkerker-Boland Subgraph

Tucker observed that the smallest graphs whose clique matrices contain a Tucker matrix must be exactly the LB graphs [16]. However, making use of this to find an LB subgraph is not as straightforward as it appears. It is easy to believe from Figure 2 that that the rows of every Tucker submatrix in a clique matrix can be extended to a clique matrix of an LB subgraph by including at most three additional rows. The rows of the result would therefore identify the vertices that induce an LB subgraph.

That this reasoning is flawed is illustrated by Figure 5. Neither does it follow from the fact that no column of the clique matrix is a subset of any other; we discovered the example in the figure when trying to prove it using only this fact. Therefore, though the conclusion is true in the case of chordal graphs, this requires proof.

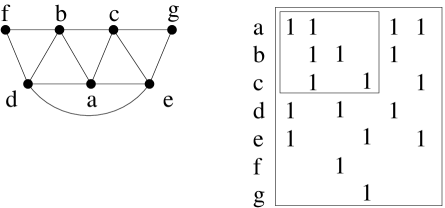
If $G$ is not chordal, we may return a $G_{III}$ by the algorithm of [15]. Henceforth, we may assume that the graph is chordal. A clique tree of a chordal graph is a tree that has one node for each maximal clique, and with the property that for each vertex $v$ of $G$ , the cliques that contain $v$ induce a connected subtree. Every chordal graph has a clique tree, see for example [3]. A vertex is simplicial if its neighbors induce a complete subgraph. The following are immediate from results that appear there:

Lemma 9

Let $T$ be a clique tree for a chordal graph $G$ , and let $K$ be a leaf. Then $K$ contains a simplicial vertex of $G$ . Let $S$ be the simplicial vertices of $K$ , and let $T^{\prime}$ be the result of deleting leaf $K$ from $T$ . Deleting $S$ from $G$ yields an induced subgraph that has $T^{\prime}$ as a clique tree.

Definition 3

By shrinking a clique tree $T$ , let us denote the operation of deleting the set $S$ of simplicial vertices in a leaf $K$ of $T$ , yielding a graph with the smaller clique tree described by the lemma.

Lemma 10

If $G$ is a chordal graph, $T$ is a clique tree of $G$ , and $G[X]$ is connected, then the cliques of $T$ that contain members of $X$ induce a connected subtree of $T$ .

Lemma 11

Let $T$ be a clique tree of a chordal graph $G$ , ${\cal K}$ a collection of cliques of $G$ , and a clique $C\in{\cal K}$ . If every member of ${\cal K}-C$ contains a vertex that $C$ does not have and $G[\bigcup{\cal K}\setminus C]$ is connected, then $C$ does not lie on the path in $T$ between any pair of cliques of ${\cal K}-C$ .

Definition 4

If a Tucker matrix occurs as a submatrix induced by column set ${\cal C}$ and row set ${\cal R}$ of a clique matrix, let a private row for $C\in{\cal C}$ be a row $R\not\in{\cal R}$ that is contained in no column of ${\cal C}$ other than $C$ . Let the special columns of $M_{II}-M_{V}$ be those that are subsets of other columns of these matrices, and let the special columns of an instance of $M_{I}$ on three rows be all three columns.

The special columns are the ones that Tucker identified as “asteroidal column triples” in the bipartite incidence graph of rows and and columns in [16]. However, the existence of simplicial vertices or “asteroidal vertex triples” in a a sense defined in [6] was not examined. The paper dealt with arbitrary consecutive-ones matrices where such rows need not occur.

Lemma 12

Let $G$ be a chordal graph and let $M_{T}$ be a submatrix of a clique matrix that is an instance of $M_{I}$ on three vertices or an instance of $M_{II}-M_{V}$ . Then the clique matrix has a private row for each special column of $M_{T}$ .

Proof

Let ${\cal K}$ be the set of cliques of $G$ that contain the columns of this instance of $M_{T}$ , let $C\in{\cal K}$ contain a special column of the instance, and let $T$ be a clique tree for $G$ . In each case, $C$ does not lie on the unique path in $T$ between any pair of members of ${\cal K}-C$ , by Lemma 11. Therefore, iteratively shrinking $T$ (Definition 3) until it cannot be further shrunk without deleting a clique of ${\cal K}$ results in an induced subgraph $G^{\prime}$ with a clique tree $T^{\prime}$ where $C$ is a leaf. By Lemma 9, $C$ has a simplicial vertex, which must be a private row for $C$ in ${\cal K}$ .

By examination, it is easy to verify in the case of $M_{I}$ on three rows, and $M_{II}-M_{IV}$ that adding the private rows for the special columns to the rows and columns of the submatrix gives an interval model for the corresponding LB subgraph. The resulting set of rows therefore induces an LB subgraph.

References

[1] A. Brandstaedt, V.B. Le, and J.P. Spinrad. Graph Classes: A Survey. SIAM Monographs on Discrete Mathematics, Philadelphia, 1999.
[2] C. Chauve, U.-U. Haus, T. Stephen, and V. P. You. Minimal conflicting sets for the consecutive ones property in ancestral genome reconstruction. Journal of Computational Biology, 17:1167–1181, 2010.
[3] M. C. Golumbic. Algorithmic Graph Theory and Perfect Graphs. Academic Press, New York, 1980.
[4] P. Hell and J. Huang. Certifying LexBFS recognition algorithms for proper inteval graphs and proper interval bigraphs. SIAM J. Discrete Math, 18:554–570, 2004.
[5] D. Kratsch, R.M. McConnell, K. Mehlhorn, and J.P. Spinrad. Certifying algorithms. SIAM Journal on Computing, 36:236–353, 2006.
[6] C. Lekkerker and D. Boland. Representation of finite graphs by a set of intervals on the real line. Fund. Math., 51:45–64, 1962.
[7] G. S. Lueker and K. S. Booth. A linear time algorithm for deciding interval graph isomorphism. J. ACM, 26:183–195, 1979.
[8] R. M. McConnell. A certifying algorithm for the consecutive-ones property. Proceedings of the 15th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA04), 15:761–770, 2004.
[9] R. M. McConnell, K. Mehlhorn, S. Näher, and P. Schweitzer. Certifying algorithms. Computer Science Reviews, 5:119–161, 2011.
[10] J. Meidanis, O. Porto, and G.P. Telles. On the consecutive ones property. Discrete Applied Mathematics, 88:325–354, 1998.
[11] Fred S. Roberts. Graph Theory and Its Applications to Problems of Society. Society for Industrial and Applied Mathematics, Philadelphia, 1978.
[12] D. Rose, R. E. Tarjan, and G. S. Lueker. Algorithmic aspects of vertex elimination on graphs. SIAM J. Comput., 5:266–283, 1976.
[13] J. Spinrad. Efficient Graph Representations. American Mathematical Society, Providence RI, 2003.
[14] J Stoye and R. Wittler. A unified approach for reconstructing ancience gene clusters. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 6:387–400, 2009.
[15] E. E. Tarjan and M. Yannakakis. Addendum: Simple linear-time algorithms to test chordality of graphs, test acyclicity of hypergraphs, and selectively reduce acyclic hypergraphs. SIAM Journal on Computing, 14:254–255, 1985.
[16] A. Tucker. A structure theorem for the consecutive 1’s property. Journal of Combinatorial Theory, Series B, 12:153–162, 1972.
[17] G. Wegner. Eigenschaften der Nerven Homologishe-Einfactor Familien in $R^{n}$ . PhD thesis, Universität Göttingen, 1967.