On Hypothesis Transfer Learning of Functional Linear Models
Abstract
We study the transfer learning (TL) for the functional linear regression (FLR) under the Reproducing Kernel Hilbert Space (RKHS) framework, observing the TL techniques in existing high-dimensional linear regression is not compatible with the truncation-based FLR methods as functional data are intrinsically infinite-dimensional and generated by smooth underlying processes. We measure the similarity across tasks using RKHS distance, allowing the type of information being transferred tied to the properties of the imposed RKHS. Building on the hypothesis offset transfer learning paradigm, two algorithms are proposed: one conducts the transfer when positive sources are known, while the other leverages aggregation techniques to achieve robust transfer without prior information about the sources. We establish lower bounds for this learning problem and show the proposed algorithms enjoy a matching asymptotic upper bound. These analyses provide statistical insights into factors that contribute to the dynamics of the transfer. We also extend the results to functional generalized linear models. The effectiveness of the proposed algorithms is demonstrated on extensive synthetic data as well as a financial data application.
1 Introduction
Advances in technologies enable us to collect and process densely observed data over some temporal or spatial domains, which are coined functional data [Ramsay et al., 2005; Kokoszka and Reimherr, 2017]. While functional data analysis (FDA) has been proven useful in various fields like finance, genetics and etc., and has been researched widely in the statistical community, its effectiveness relies on having sufficient training samples drawn from the same distribution. However, this may not hold for functional data under some applications due to collection expenses or other constraints. Transfer learning (TL)[Torrey and Shavlik, 2010] leverages additional information from some similar (source) tasks to enhance the learning procedure on the original (target) task, and is an appealing mechanism when there is a lack of training samples. The goal of this paper is to develop TL algorithms for functional linear regression (FLR), one of the most prevalent models in the FDA. The FLR concerned in this paper is Scalar-on-Function regression, which takes the form:
where is a scalar response, and are the square-integrable functional predictor and coefficient function respectively over a compact domain , and is a random noise with zero mean.
A classical approach to estimating is to reduce the problem to classical multivariate linear regression by expanding the and under the same finite basis, like deterministic basis functions, e.g. Fourier basis, or the eigenbasis of the covariance function of [Cardot et al., 1999; Yao et al., 2005; Hall and Hosseini-Nasab, 2006; Hall and Horowitz, 2007], which we refer to truncation-based FLR in this paper. Conceptually, the offset transfer learning techniques developed in multivariate/high-dimensional linear regression [Kuzborskij and Orabona, 2013, 2017; Li et al., 2022; Bastani, 2021] can be applied to truncation-based FLR methods, though they lack a theoretical foundation in this context due to the truncation error inherent in a basis expansion of . In particular, a key property distinguishing functional data from multivariate data is that they are inherently infinite-dimensional and generated through smooth underlying processes. Omitting this fact and treating the finite coefficients as multivariate parameters loses the benefit that data are generated from smooth processes, see detailed discussion in Section 2. Observing these limitations we develop the first TL algorithms for FLR with statistical risk guarantees under the supervised learning setting.
We summarize our main contributions as follows.
-
1.
We propose using the Reproducing Kernel Hilbert Space (RKHS) distance between tasks’ coefficients as a measure of task similarity. The transferred information is thus tied to the RKHS’s properties and makes the transfer more interpretable. One can tailor the employed RKHS to the task’s nature, offering flexibility to embed diverse structural elements, like smoothness or periodicity, into TL processes.
-
2.
Built upon the offset transfer learning (OTL) paradigm, we propose TL-FLR, a variant of OTL for multiple positive transfer sources. We establish the minimax optimality for TL-FLR. Intriguingly, the result reveals that the faster statistical rate of TL-FLR, compared to non-transfer learning, not only depends on source sample size and the magnitude of discrepancy across tasks like most existing works, but also the signal ratio between offset and source model.
-
3.
To deal with the practical scenario in which there is no available prior task similarity information, we propose Aggregation-based TL-FLR (ATL-FLR), utilizing sparse aggregation to mitigate negative transfer effects. We establish the upper bound for ATL-FLR and show the aggregation cost decreases faster than the transfer learning risk, demonstrating an ability to identify optimal sources without too much extra cost compared to TL-FLR. We further extend this framework to Functional Generalized Linear Models (FGLM) with theoretical guarantees, broadening its applicability.
-
4.
In developing statistical guarantees, we uncovered unique requirements for making OTL theoretically feasible in the functional data context. These include the necessity for covariate functions across tasks to exhibit similar structural properties to ensure statistical convergence, and the coefficient functions of negative sources can be separated from positive ones within a finite-dimensional space to ensure optimal source identification.
Literature review.
Apart from truncation-based FLR approaches mentioned before, another line of research proposed that one can obtain a smooth estimator, via smoothness regularization [Yuan and Cai, 2010; Cai and Yuan, 2012], and has been widely used in other functional models like the FGLM, functional Cox-model, etc. [Cheng and Shang, 2015; Qu et al., 2016; Reimherr et al., 2018; Sun et al., 2018].
Turning to the TL regime in supervised learning, the hypothesis transfer learning (HTL) framework has become popular [Li and Bilmes, 2007; Orabona et al., 2009; Kuzborskij and Orabona, 2013; Perrot and Habrard, 2015; Du et al., 2017]. Offset transfer learning (OTL) (a.k.a. biases regularization transfer learning) has been widely analyzed and applied as one of the most popular HTL paradigms. It assumes the target’s function/parameter is a summation of the source’s and the offset’s function/parameter. A series of works have derived theoretical analysis under different settings. For example, in Kuzborskij and Orabona [2013, 2017], the authors provide the first theoretical study of OTL in the context of linear regression with stability analysis and generalization bounds. Later, in Wang and Schneider [2015]; Wang et al. [2016] the authors derive similar theoretical guarantees for non-parametric regression via Kernel Ridge Regression. A unified framework that generalizes many previous works is proposed in Du et al. [2017] and the authors also present an excess risk analysis for their framework. Apart from the regression setting, generalization bounds for classification with surrogate losses have been studied in Aghbalou and Staerman [2023]. Other results that study HTL outside OTL can be found in Li and Bilmes [2007]; Cheng and Shang [2015]. Besides, OTL can also be viewed as a case of representation learning [Du et al., 2020; Tripuraneni et al., 2020; Xu and Tewari, 2021] by viewing the estimated source model as a representation for target tasks.
OTL has recently been adopted by the statistics community for various high-dimensional models with statistical risk guarantees. For example, Bastani [2021] proposed using OTL for high-dimensional (generalized) linear regression but only includes one positive transfer source. Later, Li et al. [2022] extended this idea to multiple sources scenario and leveraged aggregation to alleviate negative transfer effects. In Tian and Feng [2022], the learning procedure gets extended to the high-dimensional generalized linear model and the authors also proposed a positive sources detection algorithm via a validation approach. In these works, the similarity among tasks is quantified via -norm, which captures the sparsity structure in high-dimensional parameters. There is no TL for FDA that we are aware of, but the closest work would be in the area of domain adaptation. Zhu et al. [2021] studied the domain adaptation problem between two separable Hilbert spaces by proposing algorithms to estimate the optimal transport mapping between two spaces.
Notation.
For two sequence and , we denotes and if and for some universal constant when . For two random variable sequence and , if for any , there exists and such that , , we say . For a set , let denote its cardinality, denote its complement. For an integer , denote .
We denote the covariance function of as for . For a real, symmetric, square-integrable, and nonnegative kernel, , we denote its associated RKHS on as and corresponding norm as . We also denote its integral operator as for . For two kernels, and , their composition is . For a given kernel and covariance kernel , define bivariate function and its integral operator as and .
2 Preliminaries and Backgrounds
Problem Set-up.
We now formally set the stage for the transfer learning problem in the context of FLR. Consider the following series of FLRs,
| (1) |
for , , where denotes the target model and denotes source models. Denote the sample space as the Cartesian product of the covariate space and response space . For each , we denote . Throughout the paper we assume are i.i.d. across both and with zero mean and finite variance .
As estimating is our primary interest, we assume for simplicity that for all . We assume , a condition commonly validated in most TL literature and numerous practical applications. While our framework is designed primarily for the posterior drift setting, i.e. the marginal distributions of remain the same but vary, the excess risk bounds we establish are based on a comparatively more relaxed condition, see Section 4.
In the absence of source data, estimating is termed as target-only learning and one can obtain a smooth estimator of through the regularized empirical risk minimization (RERM) [Yuan and Cai, 2010; Cai and Yuan, 2012], i.e.
where is an employed kernel and is the loss function. This approach has been proven to achieve the optimal rate in terms of excess risk, and we refer to it as Optimal Functional Linear Regression (OFLR) in this paper, which serves as a non-transfer learning baseline.
Similarity Measure.
We first state the limitations of using -norm as a similarity measure in the truncation-based FLR method, which converts the problem into a classic multivariate one. For a given series of basis functions and truncated number , one can model the -th FLR as
| (2) |
where and . Denote as the coefficient vector in (2), one can then measure the similarity between the target and the -th FLR model by the or norm of like the previous works did for multivariate linear regression. However, from the functional data analysis literature, since the functional data are generated from some structural underlying process, it is well known that one has to have the same kind of structure in the estimator like smoothness for theoretical reliability. For example, when the coefficient functions are smooth, the above approach cannot measure the similarity, since are not necessarily sparse or might require regularization via an -norm, but the employed basis functions might not reflect the desired smoothness. Besides, the basis functions and should be consistent across tasks, which reduces the flexibility of the learning procedure.
To explore the similarity tied to the structure of coefficient functions, one should quantify the similarity between tasks within certain functional spaces that possess the same structures. These structural properties, e.g. continuity/smoothness/periodicity, can be naturally encapsulated via kernels and their corresponding RKHS. Consequently, quantifying the similarity within a certain RKHS provides interpretability since the type of information transferred is tied to the structural properties of the used RKHS. We also note that this method is broadly applicable since the reproducing kernel can be tailored to the application problem accordingly. For example, one can transfer the information about continuity or smoothness by picking to be a Sobolev kernel, and about periodicity by picking periodic kernels like where is the lengthscale and is the period.
Given the reasoning above, for , we assume , and define the -th contrast function . Given a constant , we say the -th source model is “h-transferable” if . The magnitude of characterizes the similarity between the target model and source models. We also define as a subset of , which consists of the indexes of all “h-transferable” source models. It is worth mentioning that the quantity is introduced for theoretical purposes to establish optimality, which is prevalent in recent studies such as Bastani [2021]; Cai and Wei [2021]. But for the implementation of the algorithm, it is not necessary to know the actual value of . We abbreviate as to generally represent the h-transferable sources index.
Learning Framework.
This paper leverages the widely used OTL paradigm, see reviews in Section 1. Formally, in the FLR and single source context, the OTL obtains the target function via where is the estimator trained on source dataset and is obtained from target dataset via following minimization problem:
where the loss function can be square loss [Orabona et al., 2009; Kuzborskij and Orabona, 2013] or surrogate losses [Aghbalou and Staerman, 2023]. The main idea is that the estimator can be learned well given sufficiently large source samples and the simple offset estimator can be learned with much fewer target samples.
3 Methodology
3.1 Transfer Learning with Known
For multiple sources, the idea of data fusion inspires us to obtain a centered source estimator via all source datasets in place of . Therefore, we can generalize single source OTL to the multiple sources scenario as follows.
| (3) |
| (4) |
Since the probabilistic limit of is not consistent with , calibration of is performed in (4). The regularization term in (4) is consistent with our similarity measure, i.e. it restricts to lie in a ball centered at . Therefore, this term pushes the close to while the mean square error loss over the target dataset allows calibration for the bias. Intuitively, if is close to then TL-FLR can boost the learning on the target model.
3.2 Transfer Learning with Unknown
Assuming the index set is known in Algorithm 1 can be unrealistic in practice without prior information or investigation. Moreover, as some source tasks might have little or even a negative contribution to the target one, it could be practically harmful to directly apply Algorithm 1 by assuming all sources belong to . Inspired by the idea of aggregating multiple estimators in Li et al. [2022], we develop ATL-FLR which can be directly applied without knowing while being robust to negative transfer sources.
The general idea of ATL-FLR is that one can first construct a collection of candidates for , named , such that there exists at least one satisfying with high probability and then obtain their corresponding estimators via TL-FLR. Then, one aggregates the candidate estimators in such that the aggregated estimator satisfies the following oracle inequality in high probability,
| (5) |
where , and is the aggregation cost. Thus the can achieve similar performance as TL-FLR up to some aggregation cost. Formally, the proposed aggregation-based TL-FLR is as follows.
-
1.
Obtain by OFLR using and let .
-
2.
For each , obtain by OFLR using and obtain truncated RKHS norm .
-
3.
Set
Remark 1.
While exploring the estimated similarity across sources to the target in Step 2, we use a truncated RKHS norm, which is the distance between and after projecting them onto the space spanned by the first eigenfunctions of . Here, and are the eigenvalues and eigenfunctions of . Such a truncated norm guarantees the identifiability of , see Section 4.2 for detail.
Step 2 ensures the target-only baseline lies in while the construction of ensures thorough exploration of . If can be identified by one of the , then inequality (5) indicates that even without knowing , the can mimic the performance of the TL-FLR estimator, while not being worse than the target-only , up to an aggregation cost.
The sparse aggregation is adopted from Gaîffas and Lecué [2011], see Appendix B. Although we note that other aggregation methods like aggregate with cumulated exponential weights (ACEW) [Juditsky et al., 2008; Audibert, 2009], aggregate with exponential weights (AEW) [Leung and Barron, 2006; Dalalyan and Tsybakov, 2007], and Q-aggregation [Dai et al., 2012] can replace sparse aggregation in Step 4, sparse aggregation is often preferred due to its computational efficiency and ability to eliminate negative transfer effects. Specifically, the final aggregated estimator is usually represented as a convex combination of elements in i.e. . The sparse aggregation sets most of the to zero, which effectively excludes the negative transfer sources. On the other hand, none of the ACEW, AEW, and Q-aggregation will set the to most of the time, meaning that negative transfer sources can still affect . Although one can manually tune temperature parameters in these approaches to shrink the close to zero, they are less computationally efficient given the fact that sparse aggregation does not require such a tuning process. In Section 6, we verify that sparse aggregation outperforms other aggregation methods under various settings.
4 Theoretical Analysis
In this section, we study the theoretical properties of the prediction accuracy of the proposed algorithms. We evaluate the proposed algorithms via excess risk, i.e.
where the expectation is taken over an independent test data point from the target distribution. To study the excess risk of TL-FLR and ATL-FLR, we define the parameter space as
To establish the theoretical analysis of the proposed algorithms, we first state some assumptions. For , denote and as the eigenvalues and eigenfunctions of respectively.
Assumption 1 (Eigenvalue Decay Rate (EDR)).
Suppose that the eigenvalue decay rate (EDR) of is , i.e.
The polynomial EDR assumption is standard in FLR literature like Cai and Yuan [2012]; Reimherr et al. [2018]. RKHSs that satisfy this assumption, like Sobolev spaces, are natural choices when one is concerned about the smoothness being the structural properties in the TL processes.
Assumption 2.
We assume either one of the following conditions holds.
-
1.
commutes with , , i.e. , and
-
2.
Or the following linear operator is Hilbert–Schmidt.
We note that under the posterior drift setting, both conditions in Assumption 2 are satisfied automatically. Although neither condition implies the other, both conditions primarily focus on how the smoothness of the source kernel relates to that of the target kernel . Specifically, Condition 1 implies and not only share the same eigenspace but also have similar magnitudes of the projection onto the -th dimension of the eigenspace, which commonly appears in FDA literature [Yuan and Cai, 2010; Balasubramanian et al., 2022]. This helps us to control the excess risk of over the target domain. Condition 2 implies the probability measures of and are equivalent, see Baker [1973]. Collectively, these conditions indicate the feasibility of OTL for functional data relies on the fact that source covariance function should behave similarly to the target’s . Either a too “smooth” or a too “rough” can degrade the optimality. This aligns with the principles of standard target-only FLR, where the performance of the estimator is jointly determined by the covariance function and reproducing kernel.
4.1 Minimax Excess Risk of TL-FLR
We first provide the upper bound of excess risk on TL-FLR.
Theorem 1 (Upper Bound).
Theorem 1 provides the excess risk upper bound of , which bounds the excess risk of two terms. The first term comes from the transfer step and depends on the sample size of sources in , while the second term is due to only using the target dataset to learn the offset. In the trivial case when , the upper bound becomes , which coincides with the upper bound of target-only baseline OFLR [Cai and Yuan, 2012]. When , compared with the excess risk of the target-only baseline, we can see the sample size in source models and the factor are jointly affecting the transfer learning. The factor represents the relative task signal strength between the source and target tasks. Geometrically, one can interpret as the factor controlling the angle between the source and target models within the RKHS.
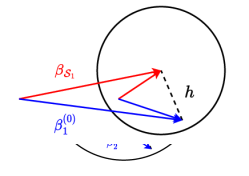
Figure 1 shows how and impact the learning rate. When the and are more concordant ( and ), the angle between them are small and thus so the , making the second term in the upper bound negligible in the excess risk, and thus the risk converges faster compared to baseline given sufficiently large . If and are less concordant ( and ), leveraging will be less effective since a large will make the second term the dominate term.
It is worth noting that most of the existing literature fails to identify how affects the effectiveness of OTL. For example, in Wang et al. [2016]; Du et al. [2017], this factor does not appear in the upper bound, and they claim provide successful transfer from source to target. In high-dimensional linear regression [Li et al., 2022; Tian and Feng, 2022], the authors only identify is proportional to and claims a small can provide a faster convergence rate excess risk. However, our analysis (Figure 1) shows even with the same , the similarity of the two tasks can be different, since the signal strength of will also affect the effectiveness of OTL. To this end, this reveals that one cannot obtain a faster excess risk in OTL by simply including more source datasets (larger ), but should also carefully select or construct the .
Theorem 2 (Lower Bound).
Under the same condition of Theorem 1, for any possible estimator based on , the excess risk of satisfies
| (7) |
4.2 Excess Risk of ATL-FLR
In this subsection, we study the excess risk for ATL-FLR. As we discussed before, making ATL-FLR achieve similar performance to TL-FLR relies on the fact that there exists a such that it equals to the true (so ) with high probability. Therefore, to ensure the constructed in Step 2 of Algorithm 2 satisfies such a property, we impose the following assumption to guarantee the identifiability of and thus ensure the existence of such .
Assumption 3 (Identifiability of ).
Suppose for any , there is an integer such that
where is the truncated version of defined in Algorithm 2.
Assumption 3 ensures that , there exists a finite-dimensional subspace of , such that the norm of the projection of the contrast function, , on this subspace is already greater than . This assumption indeed eliminates the existence of , for , that live on the boundary of the RKHS-ball centered at with radius in . Under Assumption 3, we now show the constructed in Algorithm 2 guarantees the existence of .
Theorem 3.
Remark 2.
Assumption 3 ensures a sufficient gap between those that belong to and those that don’t, which ensures their estimated counterpart will also possess this gap with high probability, making one of the consistent with .
With Proposition 1, which states the cost of sparse aggregation in Appendix C.5, and the excess risk of TL-FLR in Theorem 3, we can establish the excess risk for ATL-FLR.
Theorem 4 (Upper Bound of ATL-FLR).
One interesting note is that the transfer learning risk is the classical nonparametric rate while the aggregation cost is parametric (or nearly parametric). Therefore, the aggregation cost usually decays substantially faster than the transfer learning risk. However, in the high-dimensional linear regression TL, such a faster-decayed aggregation cost is diminished since the transfer learning risk is also parametric, see [Li et al., 2022].
5 Extension to Functional Generalized Linear Models
In this section, we show our approaches in the FLR model can be naturally extended to the functional generalized linear model (FGLM) settings, which includes wider application scenarios like classification. To start, consider the following series of FGLM models similar to the FLR setting (1),
where and , is the canonical parameter. The functions are known, and is either known or out-of-interest parameter that is independent of . In this paper, we consider to take the canonical form, i.e. . The GLMs are characterized by the different . For example, in linear regression with Gaussian response, ; in the logistic regression with binary response, ; and in Poisson regression with non-negative integer response, .
A standard method for addressing GLM involves minimizing the loss function defined as the negative log-likelihood. Therefore, to implement the transfer learning for FGLM, one can naturally substitute the square loss in TL-FLR (Algorithm 1) and ATL-FLR (Algorithm 2) with the negative log-likelihood loss, i.e.
We refer to these transfer learning algorithms for FGLM as TL-FGLM and ATL-FGLM. To establish the optimality of TL-FGLM and ATL-FGLM, the following technical assumptions are required.
Assumption 4.
Assume is Lipschitz continuous on its domain, and .
Assumption 5.
Assume there exist constants such that the function satisfies
Assumption 4 is natural in most GLM literature and is satisfied by many popular exponential families. Assumption 5 restricts the in the bounded region and thus restricts the variance of .
Since the conditional mean for FGLM is , we evaluate the accuracy by excess risk, i.e. .
Theorem 5.
Remark 3.
The error bound of TL-FLR and TL-FGLM are the same, which is consistent with the case in the single-task learning scenario between FLR and FGLM, see Cai and Yuan [2012]; Du and Wang [2014]. However, we note the proof is not a trivial extension of FLR since minimizing the regularized negative likelihood usually will not provide an analytical solution.
Remark 4.
Due to the same upper bound for TL-FLR and TL-FGLM, the upper bound of ATL-FGLM is the same as ATL-TLR, i.e. with the same aggregation cost.
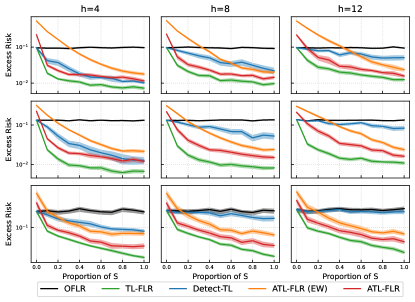
6 Experiments
We illustrate our algorithms for FLR by providing results using simulated data and defer the financial market data application and FGLM results to Appendix E. We consider the following, OFLR, TL-FLR, ATL-FLR, Detection Transfer Learning (Detect-TL) [Tian and Feng, 2022] and Exponential Weighted ATL-FLR (ATL-FLR (EW)). To set up the RKHS, we consider the setting in Cai and Yuan [2012]. Let for and define the reproducing kernel of as .
For the target model, is set to be (1) ; (2) ; (3) . For a specific , let , then we generate source models as follows. We scale each target model such that their RKHS norm is . If , then is set to be with ’s i.i.d. uniform random variable on . If , then is generated from a Gaussian process with mean function with kernel as covariance kernel. The predictors are i.i.d. generated from a Gaussian process with the mean function and the covariance kernels are set to be Matérn kernel [Cressie and Huang, 1999] where the parameter controls the smoothness of . We set the covariance kernel of as for the target tasks and for source tasks, to fulfill Assumptions 2. We note that such a setting is more challenging than assuming that the target and source tasks have the same covariance kernel. All functions are generated on with 50 evenly spaced points and we set and . For each algorithm, we set the regularization parameters as and as the optimal values in Theorem 1 and select the constants using cross-validation. The excess risk for the target tasks is calculated via the Monte-Carlo method by using newly generated predictors .
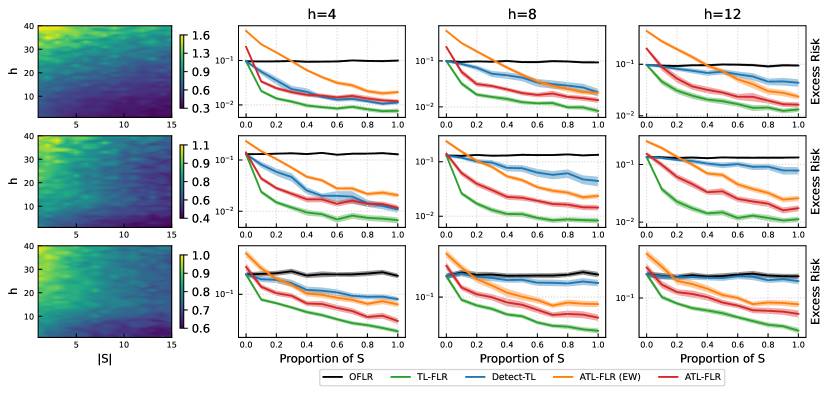
In the left panel of Figure 2 we compare TL-FLR with OFLR by considering relative excess risk, i.e. the ratio of TL-FLR’s excess risk to OFLR’s. We note that since RKHS of is fixed, the magnitude of is proportional to and a large indicates less similarity between sources and target tasks. Overall, the effectiveness of TL-FLR for different presents a consistent pattern, i.e, with more transferable sources involved and smaller (bottom right), TL-FLR has a more significant improvement, while with fewer sources and larger (top left), the transfer may be worse than OFLR.
In the right panel of Figure 2, we evaluate ATL-FLR under unknown cases. We set as a random subset of such that is equal to . We also implement TL-FLR by using true and OFLR as baseline. In all scenarios, ATL-FLR outperforms all its competitors. Comparing ATL-FLR with ATL-FLR(EW), even though ATL-FLR(EW) has similar patterns as ATL-FLR, we can see the gaps between the two curves are larger when the proportion of is small, showing that ATL-FLR(EW) is more sensitive to source tasks in , while ATL-FLR is less affected. Detect-TL only has a considerable reduction on the excess risk with relatively small , but provides limited improvement when is large, indicating its limited learning effect when there is only limited knowledge available in sources.
7 Conclusion
In this paper, we study offset transfer learning in functional regression settings including FLR and FGLM. We derive excess risk and show a faster statistical rate depending on both source sample size and the magnitude of similarity across tasks. Our theoretical analysis will help researchers better understand the transfer dynamic of offset transfer learning. Moreover, we leverage the sparse aggregation to alleviate the negative transfer effect while having faster-decreasing aggregation costs compared to transfer learning risk.
References
- Aghbalou and Staerman [2023] Anass Aghbalou and Guillaume Staerman. Hypothesis transfer learning with surrogate classification losses: Generalization bounds through algorithmic stability. In International Conference on Machine Learning, pages 280–303. PMLR, 2023.
- Audibert [2009] Jean-Yves Audibert. Fast learning rates in statistical inference through aggregation. The Annals of Statistics, 37(4):1591–1646, 2009.
- Baker [1973] Charles R Baker. On equivalence of probability measures. The Annals of Probability, pages 690–698, 1973.
- Balasubramanian et al. [2022] Krishnakumar Balasubramanian, Hans-Georg Müller, and Bharath K Sriperumbudur. Unified rkhs methodology and analysis for functional linear and single-index models. arXiv preprint arXiv:2206.03975, 2022.
- Bastani [2021] Hamsa Bastani. Predicting with proxies: Transfer learning in high dimension. Management Science, 67(5):2964–2984, 2021.
- Cai and Wei [2021] T Tony Cai and Hongji Wei. Transfer learning for nonparametric classification: Minimax rate and adaptive classifier. The Annals of Statistics, 49(1):100–128, 2021.
- Cai and Yuan [2012] T Tony Cai and Ming Yuan. Minimax and adaptive prediction for functional linear regression. Journal of the American Statistical Association, 107(499):1201–1216, 2012.
- Cardot et al. [1999] Hervé Cardot, Frédéric Ferraty, and Pascal Sarda. Functional linear model. Statistics & Probability Letters, 45(1):11–22, 1999.
- Cheng and Shang [2015] Guang Cheng and Zuofeng Shang. Joint asymptotics for semi-nonparametric regression models with partially linear structure. The Annals of Statistics, 43(3):1351–1390, 2015.
- Cressie and Huang [1999] Noel Cressie and Hsin-Cheng Huang. Classes of nonseparable, spatio-temporal stationary covariance functions. Journal of the American Statistical association, 94(448):1330–1339, 1999.
- Dai et al. [2012] Dong Dai, Philippe Rigollet, and Tong Zhang. Deviation optimal learning using greedy -aggregation. The Annals of Statistics, 40(3):1878–1905, 2012.
- Dalalyan and Tsybakov [2007] Arnak S Dalalyan and Alexandre B Tsybakov. Aggregation by exponential weighting and sharp oracle inequalities. In International Conference on Computational Learning Theory, pages 97–111. Springer, 2007.
- Du and Wang [2014] Pang Du and Xiao Wang. Penalized likelihood functional regression. Statistica Sinica, pages 1017–1041, 2014.
- Du et al. [2017] Simon S Du, Jayanth Koushik, Aarti Singh, and Barnabás Póczos. Hypothesis transfer learning via transformation functions. Advances in neural information processing systems, 30, 2017.
- Du et al. [2020] Simon S Du, Wei Hu, Sham M Kakade, Jason D Lee, and Qi Lei. Few-shot learning via learning the representation, provably. arXiv preprint arXiv:2002.09434, 2020.
- Gaîffas and Lecué [2011] Stéphane Gaîffas and Guillaume Lecué. Hyper-sparse optimal aggregation. The Journal of Machine Learning Research, 12:1813–1833, 2011.
- Hall and Horowitz [2007] Peter Hall and Joel L Horowitz. Methodology and convergence rates for functional linear regression. The Annals of Statistics, 35(1):70–91, 2007.
- Hall and Hosseini-Nasab [2006] Peter Hall and Mohammad Hosseini-Nasab. On properties of functional principal components analysis. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 68(1):109–126, 2006.
- Juditsky et al. [2008] Anatoli Juditsky, Philippe Rigollet, and Alexandre B Tsybakov. Learning by mirror averaging. The Annals of Statistics, 36(5):2183–2206, 2008.
- Kokoszka and Reimherr [2017] Piotr Kokoszka and Matthew Reimherr. Introduction to functional data analysis. Chapman and Hall/CRC, 2017.
- Kuzborskij and Orabona [2013] Ilja Kuzborskij and Francesco Orabona. Stability and hypothesis transfer learning. In International Conference on Machine Learning, pages 942–950. PMLR, 2013.
- Kuzborskij and Orabona [2017] Ilja Kuzborskij and Francesco Orabona. Fast rates by transferring from auxiliary hypotheses. Machine Learning, 106:171–195, 2017.
- Leung and Barron [2006] Gilbert Leung and Andrew R Barron. Information theory and mixing least-squares regressions. IEEE Transactions on information theory, 52(8):3396–3410, 2006.
- Li et al. [2022] Sai Li, T Tony Cai, and Hongzhe Li. Transfer learning for high-dimensional linear regression: Prediction, estimation and minimax optimality. Journal of the Royal Statistical Society Series B: Statistical Methodology, 84(1):149–173, 2022.
- Li and Bilmes [2007] Xiao Li and Jeff Bilmes. A bayesian divergence prior for classiffier adaptation. In Artificial Intelligence and Statistics, pages 275–282. PMLR, 2007.
- Orabona et al. [2009] Francesco Orabona, Claudio Castellini, Barbara Caputo, Angelo Emanuele Fiorilla, and Giulio Sandini. Model adaptation with least-squares svm for adaptive hand prosthetics. In 2009 IEEE international conference on robotics and automation, pages 2897–2903. IEEE, 2009.
- Perrot and Habrard [2015] Michaël Perrot and Amaury Habrard. A theoretical analysis of metric hypothesis transfer learning. In International Conference on Machine Learning, pages 1708–1717. PMLR, 2015.
- Qu et al. [2016] Simeng Qu, Jane-Ling Wang, and Xiao Wang. Optimal estimation for the functional cox model. The Annals of Statistics, 44(4):1708–1738, 2016.
- Ramsay et al. [2005] Jim Ramsay, James Ramsay, BW Silverman, et al. Functional Data Analysis. Springer Science & Business Media, 2005.
- Reimherr et al. [2018] Matthew Reimherr, Bharath Sriperumbudur, and Bahaeddine Taoufik. Optimal prediction for additive function-on-function regression. Electronic Journal of Statistics, 12(2):4571–4601, 2018.
- Sun et al. [2018] Xiaoxiao Sun, Pang Du, Xiao Wang, and Ping Ma. Optimal penalized function-on-function regression under a reproducing kernel hilbert space framework. Journal of the American Statistical Association, 113(524):1601–1611, 2018.
- Tian and Feng [2022] Ye Tian and Yang Feng. Transfer learning under high-dimensional generalized linear models. Journal of the American Statistical Association, pages 1–14, 2022.
- Torrey and Shavlik [2010] Lisa Torrey and Jude Shavlik. Transfer learning. In Handbook of research on machine learning applications and trends: algorithms, methods, and techniques, pages 242–264. IGI global, 2010.
- Tripuraneni et al. [2020] Nilesh Tripuraneni, Michael Jordan, and Chi Jin. On the theory of transfer learning: The importance of task diversity. Advances in neural information processing systems, 33:7852–7862, 2020.
- Vaart and Wellner [1996] Aad W Vaart and Jon A Wellner. Weak convergence. In Weak convergence and empirical processes, pages 16–28. Springer, 1996.
- Varshamov [1957] Rom Rubenovich Varshamov. Estimate of the number of signals in error correcting codes. Docklady Akad. Nauk, SSSR, 117:739–741, 1957.
- Wang and Schneider [2015] Xuezhi Wang and Jeff G Schneider. Generalization bounds for transfer learning under model shift. In UAI, pages 922–931, 2015.
- Wang et al. [2016] Xuezhi Wang, Junier B Oliva, Jeff G Schneider, and Barnabás Póczos. Nonparametric risk and stability analysis for multi-task learning problems. In IJCAI, pages 2146–2152, 2016.
- Wendland [2004] Holger Wendland. Scattered data approximation, volume 17. Cambridge university press, 2004.
- Xu and Tewari [2021] Ziping Xu and Ambuj Tewari. Representation learning beyond linear prediction functions. Advances in Neural Information Processing Systems, 34:4792–4804, 2021.
- Yao et al. [2005] Fang Yao, Hans-Georg Müller, and Jane-Ling Wang. Functional linear regression analysis for longitudinal data. The Annals of Statistics, 33(6):2873–2903, 2005.
- Yuan and Cai [2010] Ming Yuan and T Tony Cai. A reproducing kernel hilbert space approach to functional linear regression. The Annals of Statistics, 38(6):3412–3444, 2010.
- Zhu et al. [2021] Jiacheng Zhu, Aritra Guha, Mengdi Xu, Yingchen Ma, Rayleigh Lei, Vincenzo Loffredo, XuanLong Nguyen, and Ding Zhao. Functional optimal transport: Mapping estimation and domain adaptation for functional data. 2021.
Appendix A Appendix: Background of RKHS and Integral Operators
In this section, we will present some facts about the RKHS and also the integral operator of a kernel that are useful in our proof and refer readers to Wendland [2004] for a more detailed discussion.
Let be a compact set of . For a real, symmetric, square-integrable, and semi-positive definite kernel , we denote its associated RKHS as . For the reproducing kernel , we can define its integral operator as
is self-adjoint, positive-definite, and trace class (thus Hilbert-Schmidt and compact). By the spectral theorem for self-adjoint compact operators, there exists an at most countable index set , a non-increasing summable positive sequence and an orthonormal basis of , such that the integrable operator can be expressed as
The sequence and the basis are referred as the eigenvalues and eigenfunctions. The Mercer’s theorem shows that the kernel itself can be expressed as
where the convergence is absolute and uniform.
We now introduce the fractional power integral operator and the composite integral operator of two kernels. For any , the fractional power integral operator is defined as
For two kernels and , we define their composite kernel as
and thus . Given these definitions, for a given reproducing kernel and covariance function , the definition of in the main paper is
If both and are bounded linear operators, the spectral algorithm guarantees the existence of eigenvalues and eigenfunctions .
Appendix B Appendix: Sparse Aggregation Process
We provide the procedure of sparse aggregation in Step 4 of ATL-FLR (Algorithm 2) for readers’ reference and refer readers to Gaîffas and Lecué [2011] for more detail.
The sparse aggregation algorithm is stated in Algorithm 3. For the Oracle inequality and the pre-specified parameter and , we refer the reader to Appendix C.5 for model detail. In general, the final aggregated estimator will only select two of the best-performed candidates from the candidates set . This guarantees some of the incorrectly constructed are not involved in building and thus alleviate the negative transfer sources.
Remark 5.
In Gaîffas and Lecué [2011], the authors indicated has a explicit solution with the form
with and in belongs to and has an analytical form.
Appendix C Appendix: Proof of Section 4
C.1 Proof of Upper Bound for TL-FLR (Theorem 1)
Proof.
We first prove the upper bound under Assumption 2 condition 1 and defer the proof under condition 2 at the end. WLOG, we assume the eigenfunction of and are perfectly aligned, i.e. for all . We also We also recall that we set all the intercept since will not affect the convergence rate of estimating [Du and Wang, 2014].
Let represent the he set of all square integrable functions over . Since , for any , there exist a such that . In following proofs, we denote as ’s corresponding element in . Therefore, we can rewrite the minimization problem in the transfer step and the calibrate step as
where and
Thus the excess risk of can be rewritten as
Define the empirical version of as
and let
To bound the excess risk , by triangle inequality,
where each term at the r.h.s. corresponds to the excess risk from the transfer and calibrate steps respectively.
Transfer Step.
For the transfer step, the solution of minimization is
where is identity operator, and
Besides, the solution of the transfer learning step, , converges to its population version, which is defined by the following moment condition
and therefore leads to the explicit form of as
Define
By triangle inequality
For approximation error, by Lemma 1 and taking , the second term on r.h.s. can be bounded by
Now we turn to the estimation error. We further introduce an intermedia term
We first bound . Based on he fact that
we have
For the first term in the above inequality, by Lemma 3,
For second one, by Lemma 2 and 4,
Therefore,
Finally, we bound . Once again, by the definition of
Thus, by Lemma 2
Combine three parts, we get
by taking and notice the fact that is bounded above (This is a reasonable condition since the signal-to-noise ratio can’t be 0, otherwise one can hardly learn anything from the data), we have
The desired upper bound is proved given the fact that and is bounded above.
Calibrate Step.
The estimation scheme in the calibrate step is in the same form as the transfer step and thus its proof follows the same logic as the transfer step. The solution to the minimization problem in the calibration step is
where
Similarly, define
where is the population version of the estimator, i.e. .
By triangle inequality,
For the second term in r.h.s.,
where .
By Lemma 1 with ,
where the second inequality holds with the fact the . Therefore,
For the first term, we play the same game as transfer step. Define
and the definition of leads to
Therefore,
leading to
where the first term and operator norm comes from Lemma 2 and 3 with , and bounds on comes from transfer step and bias term of calibrate step.
Finally, for , notice that
thus by Lemma 2,
Combine three parts, we get
taking and notice the fact that is bounded above (similar reasoning as the transfer step), we have
Combining the results from transfer step and calibrate step, and reorganizing the constants for each term, we have
To prove the same upper bound under Assumption 2, we only need to show Lemma 1 to Lemma 5 still hold under Assumption 2. Let be the eigen-pairs of . We show that
| (8) |
Consider
Since is Hilbert–Schmidt, then
which leads to
Therefore, Equation (8) holds. One can now replace the common eigenfunctions by in the proofs of Lemma 1 to Lemma 5, and it is not hard to check the results still hold. ∎
C.2 Proof of Lower Bound for TL-FLR (Theorem 2)
In this part, we proof the alternative version for lower bound, i.e.
This alternative form is also proved in other contexts like high-dimensional linear regression or GLM to show optimality. However, the upper bound we derive for TL-FLR can still be sharp since in the TL regime, it is always assumed , and leads to .
On the other hand, one can modify the transfer step in TL-FLR by including the target dataset to estimate , which produces an alternative upper bound , and mathematically aligns with the alternative lower bound we mention above. However, we would like to note that such a modified TL-FLR is not computationally efficient for transfer learning, since for each new upcoming target task, TL-FLR needs to recalculate a new with the huge datasets .
Proof.
Note that any lower bound for a specific case will immediately yield a lower bound for the general case. Therefore, we consider the following two cases.
(1) Consider , i.e.
In this case, all the source model shares the same coefficient function as the target model, i.e. for all , and therefore the estimation process is equivalent to estimate under target model with sample size equal to . The lower bound in Cai and Yuan [2012] can be applied here directly and leads to
(2) Consider where is a ball in RKHS centered at with radius , and for all and . That is all the source datasets contain no information about . Consider slope functions and as the probability distribution of under . Then the KL divergence between and is
Let be any estimator based on and consider testing multiple hypotheses, by Markov inequality and Lemma 6
| (9) | ||||
Our target is to construct a sequence of such that the above lower bound matches with the upper bound. We consider Varshamov-Gilbert bound in Varshamov [1957], which we state as Lemma 7. Now we define,
where . Then,
hence . Besides,
where the last inequality is by Lemma 7, and
Therefore, one can bound the KL divergence by
Using the above results, the r.h.s. of Equation 9 becomes
Taking , which implies , would produce
Combining the lower bound in case (1) and case (2), we obtain the desired lower bound. ∎
C.3 Proof of Consistency (Theorem 3)
Proof.
C.4 Proof of Upper Bound for ATL-FLR (Theorem 4)
C.5 Proposition
Proposition 1 (Gaîffas and Lecué [2011]).
Given a confidence level , assume either setting (1) or (2) holds for a constant ,
-
1.
-
2.
where . Let be the upper bound for . The pre-specified parameter in Algorithm 3 is defined as
Let be the output of Algorithm 2, then
| (10) |
holds with probability at least where
and are some constants depend on .
Remark 6.
We call the setting (1) bounded setting and (2) sub-exponential setting. The latter one is milder but leads to a suboptimal cost. We refer readers to Gaîffas and Lecué [2011] for more detailed discussions about the optimal cost in sparse aggregation.
C.6 Lemmas
In this part, we prove the lemmas that are used in the proof of Theorem 1. We prove them under the Assumption 2 condition 1 and let denote perfectly aligned eigenfunctions of with .
Lemma 1.
Proof.
By the definition of and ,
then
Hence,
By Young’s inequality,
∎
Lemma 2.
Proof.
Let
then
By Cauchy-Schwarz inequality,
Consider , note that
By Jensen’s inequality
thus,
By assumptions of eigenvalues, for some constant . Finally, by Lemma 5
The rest of the proof can be completed by Markov inequality. ∎
Lemma 3.
Proof.
Therefore,
thus by assumption on eigenvalues and Lemma 5 with ,
with the constant proportional to . The rest of the proof can be completed by Markov inequality. ∎
Lemma 4.
Proof.
with the universal constant proportional to . The rest of the proof can be completed by Markov inequality. ∎
Lemma 5.
Proof.
The proof is exactly the same as Lemma 6 in Cai and Yuan [2012] once we know that , which got satisfied under the assumptions of eigenvalues. ∎
Lemma 6 (Fano’s Lemma).
Let be probability measure such that
then for any test function taking value in , we have
Lemma 7.
(Varshamov-Gilbert) For any , there exists at least N-dimenional vectors, such that
Appendix D Appendix: Proof of Section 5
We prove the upper bound and the lower bound of TL-FGLM. We first note that under Assumption 5, the excess risk is equivalent to up to universal constants. Thus we focus on in following proofs.
Although we are focusing on , which is exactly the same as FLR. However, minimizing the regularized negative log-likelihood will not provide an analytical solution of as those in FLR, meaning that the proof techniques we used in proving TL-FLR and ATL-FLR are not applicable. Therefore, we use the empirical process to prove the upper bound.
We abbreviate as in following proofs. We first introduce some notations. Let
and their empirical version are denoted as
Let and be the conditional distribution of and respectively, and and as their empirical version, by define
we get
D.1 Proof of Upper bound for TL-FGLM (Theorem 5)
Proof.
As mentioned before, we are focusing on , i.e.
Therefore, we only need to show is bounded by the error terms in Theorem 5. Notice that
| (11) |
we then bound the two terms in r.h.s. separately. We denote for all and .
We first focus on the transfer learning error. Based on the Theorem 3.4.1 in [Vaart and Wellner, 1996], if the following three conditions hold,
-
1.
;
-
2.
;
-
3.
.
then
For part (1), define
Then and by Cauchy-Schwarz inequality,
To bound the right hand side, by Theorem 2.14.1 in [Vaart and Wellner, 1996], we need to find the covering number of , i.e. . We first show that
Suppose there exist functions such that
Since
thus
where the inequality follows the fact for all , and under Assumption 2. Hence, the covering number of under norm is bounded by covering number of under norm , i.e.
Define , then
Next, we will show can be bounded by covering number for a ball in for some finite integer . Notice that , hence for any ,
which allows one to rewrite as
Let be a truncation number, and define
For any , let be its counterpart, then
Suppose there exist function such that
then by triangle inequality
The above inequality indeed shows that the covering number of with radius can be bounded by the covering of with radius , i.e.
It is known that the covering number for a unit ball in , then the covering number is less than . Therefore,
which leads to
By Dudley entropy integral, we know
Hence, by Theorem 2.14.1 in [Vaart and Wellner, 1996], we finish the proof of (1).
For part (2), let where , then we notice and . We further notice
and thus
Besides, by direct calculation,
By Taylor expansion, there exists a such that
Notice that , and then
and
which leads to
Hence, we get
which proves part (2).
Finally for part (3), we pick which satisfies where . Let , since
hence
Combining part (1)-(3), based on the Theorem 3.4.1 in [Vaart and Wellner, 1996], we know
To bound the second term in the r.h.s. of (11), we follow the same proof procedure as the proof of bounding first term. Specifically, we need to show
-
1.
;
-
2.
;
-
3.
.
It is not hard to check, including the estimator from transfer step into the loss function for debias step defined at the beginning of the proof will not affect the statements (1)-(3). For example, in part (1), the will vanish when calculating ; in part (2), its effect will vanish since our assumption of the second order derivatives of s are bounded from infinity and zero; in part (3), the inequality holds as is the minimizer of the regularized loss function. Therefore, in the end, we have
where .
Combining the bounds of and , we reach to
for some .
∎
D.2 Proof of Lower Bound for TL-FGLM (Theorem 5)
Proof.
Similar to the lower bound of TL-FLR, we consider the following two cases.
(1) Consider , i.e. all the source datasets come from the target domain, and thus for all . This can also be viewed as finding the lower bound of the estimator on with the size of the target dataset as .
We first calculate the Kullback–Leibler divergence between and under the exponential family. By the definition of KL divergence and density function of the exponential family, we have
for some between and . For any estimator based on , by Markov inequality and Fano’s Lemma, we have
| (12) | ||||
To have the lower bound matches with the upper bound, we need to construct the series of such that the r.h.s. of the above inequality is equal to up to a constant. Let be a fixed integer and
Then,
where the last inequality is by Lemma 7, and
Combining the upper and lower bound of with the r.h.s. of (12), we obtain
Taking , which implies , would produce
Now we finish the proof of the first half part of the lower bound. To prove the second half, we consider the following case.
(2) Consider for all , i.e. all the source domains have no useful information about the target domain. Then we know the , and our goal is to show is bounded by up to a constant related to by constructing a sequence of .
Again, let be a fixed integer and
Then similar to case (1), we can prove that
Then for any estimator based on and follows a similar process as case (1),
Again, taking leads to
Combining the lower bound in case (1) and case (2), we obtain the desired lower bound. ∎
Appendix E Appendix: Additional Experiments for TL-FLR/ATL-FLR
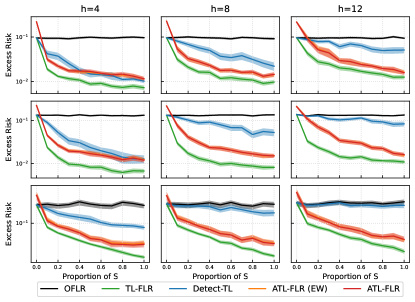
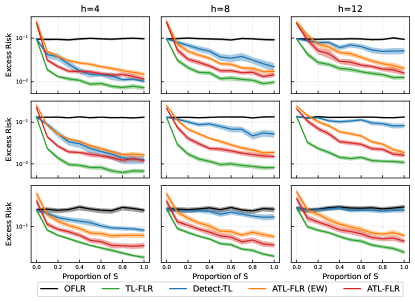
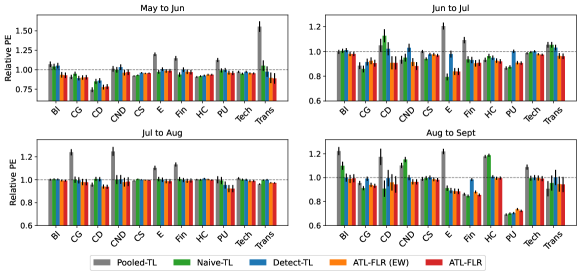
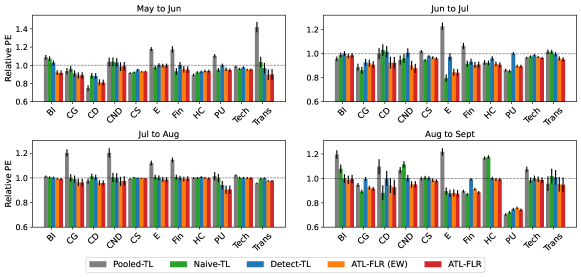
In this section, we explore how the smoothness of the coefficient functions, , for , will affect the performance of ATL-FLR. We also explore how different temperatures will affect the performance of Exponential Weighted ATL-FLR (ATL-FLR (EW)).
We consider the setting that with are generated from a much rougher Gaussian process, i.e. are generated from a Gaussian process with mean function with covariance kernel , which is exactly Wiener process, and thus the s are less smooth than s that are generated from Ornstein–Uhlenbeck process (the one we used in main paper). For ATL-FLR (EW), we consider three different temperatures, i.e. , where a lower temperature will usually produce small aggregation coefficients. All the other settings are the same as the simulation section.
The results are presented in Figure 3. In general, the patterns of using the Wiener process are consistent with using the Ornstein–Uhlenbeck process, which demonstrates the robustness of the proposed algorithms to negative transfer source models. We also note that while the temperature is low (), the small convex combination coefficients will make ATL-FLR(EW) have almost the same performance as ATL-FLR, but it still cannot beat ATL-FLR. While we increase the temperature (), the gap between ATL-FLR(EW) and ATL-FLR increases, especially when the proportion of is small. Therefore, selecting the wrong can hugely degrade the performance of ATL-FLR(EW). This demonstrates the superiority of sparse aggregation in practice since its performance does not depend on the selection of any hyperparameters.
Appendix F Appendix: Real Data Application
In this section, we demonstrate an application of the proposed algorithms in the financial market. The goal of portfolio management is to balance future stock returns and risk, and thus investors can rebalance their portfolios according to their goals. Some investors may be interested in predicting the future stock returns in a specific sector, and transfer learning can borrow market information from other sectors to improve the prediction of the interest.
In this stock data application, for two given adjacent months, we focus on utilizing the Monthly Cumulative Return (MCR) of the first month to predict the Monthly Return (MR) of the subsequent month and improving the prediction accuracy on a certain sector by transferring market information from other sectors. Specifically, suppose for a specific stock, the daily price for the first month is and for the second month is , then the predictors and responses are expressed as
| (13) |
The stock price data are collected from Yahoo Finance (https://finance.yahoo.com/) and we focus on stocks whose corresponding companies have a market cap over Billion. We divide the sectors based on the division criteria on Nasdaq (https://www.nasdaq.com/market-activity/stocks/screener). The raw data obtained from websites are processed to match the format in (13) and both the raw data and processed data are available in https://github.com/haotianlin/TL-FLM.
After pre-processing, the dataset consists of total sectors: Basic Industries (BI), Capital Goods (CG), Consumer Durable (CD), Consumer Non-Durable (CND), Consumer Services (CS), Energy (E), Finance (Fin), Health Care (HC), Public Utility (PU), Technology (Tech), and Transportation (Trans), with the number of stocks in each sector as . The period of the stocks’ price is 05/01/2021 to 09/30/2021.
We compare the performance of Pooled Transfer (Pooled-TL), Naive Transfer (Naive-TL), Detect-TL, ATL-FLR(EW) and ATL-FLR. Naive-TL implements TL-FLR by setting all source sectors belonging to , while the Pooled-TL one omits the calibrate step in Naive-TL, and the other three are the same as the former simulation section. The learning of each sector is treated as the target task each time, and all the other sectors are sources. We randomly split the target sector into the train () and test () set and report the ratio of the four approaches’ prediction errors to OFLR’s on the test set. We consider the Matérn kernel as the reproducing kernel again. Specifically, we set and (where is equivalent to the exponential kernel and is equivalent to Gaussian kernel) which endows with different smoothness properties. The tuning parameters are selected via Generalized Cross-Validation(GCV). Again, we replicate the experiment times and report the average prediction error with standard error in Figure 4.
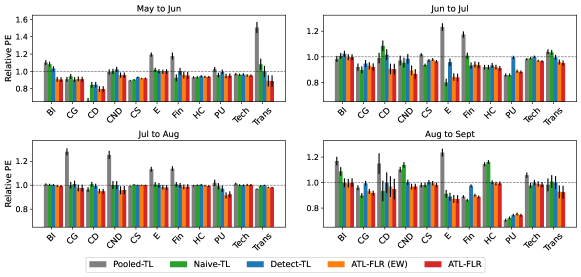
First, we note that the Pooled-TL and Naive-TL only reduce the prediction error in a few sectors, but make no improvement or even downgrade the predictions in most sectors. This implies the effect of direct transfer learning can be quite random, as it can benefit the prediction of the target sector when it shares high similarities with other sectors while having worse performance when similarities are low. Besides, Naive-TL shows an overall better performance compared to the Pooled-TL, demonstrating the importance of the calibrate step. For Detect-TL, all the ratios are close to , showing its limited improvement, which is as expected as it can miss positive transfer sources easily. Finally, both ATL-FLR(EW) and ATL-FLR provide more robust improvements on average. We can see both of them have improvements across almost all the sectors, regardless of the similarity between the target sector and source sectors. Comparing the results from different kernels, we can see the improvement patterns are consistent across all the sectors and adjacent months, showing the proposed algorithms are also robust to different reproducing kernels.