On packet lengths and overhead for random linear coding over the erasure channel

It has been shown that network coding allows a source node to multicast information at a rate approaching the maximum flow of a network as the symbol alphabet size approaches infinity [1, 2]. An infinitely large symbol alphabet would correspond to transmission of infinitely long blocks of data, which is neither possible nor practical. Subsequent works have shown that a finite alphabet is sufficient to achieve the maximum flow and a number of works have provided bounds on the necessary alphabet size. For example, in [3] the alphabet size is upper bounded by the product of the number of sources with the number of receivers, while in [4] a lower bound on the alphabet size is given by the number of receivers.

Random linear coding was proposed to allow for distributed implementation [5]. In random network coding, a randomly generated encoding vector is typically communicated to the receiver by appending it to the header of the transmitted packet. The overhead inherent in communicating the encoding vector becomes negligible as the number of symbols in the packet grows large. Regarding the alphabet size for random network coding, a lower bound of 2 times the number of receivers is given in [4].

The “length” of a transmitted packet (i.e., the number of bits conveyed by the packet) depends on both the symbol alphabet and the number of symbols per packet. From the previous works listed above, it is clear that transmitting sufficiently long packets is crucial to ensuring the existence of network codes and to allowing random linear coding to operate with low overhead.

However, long packets are more susceptible to noise, interference, congestion, and other adverse channel effects. This point has been ignored in previous works on network coding. In particular, a number of previous works [6, 7, 8] consider transmission over an erasure channel, in which a packet is either dropped with a probability $\epsilon$ or received without error. In a wireline network, the erasure channel is used to model dropped packets due to buffer overflows. Clearly, longer packets take up more space in memory, so the erasure probability will increase as the packet length grows. In the case of a wireless network, there are a number of reasons that the erasure probability will increase with the length of the packet, as listed below.

• •

  If we try to fit more bits into the channel using modulation, then for fixed transmission power, points in the signal constellation will move closer together and errors are more likely.

• •

  If we try to fit more bits into the channel by decreasing symbol duration, then we are constrained by bandwidth, a carefully-controlled resource in wireless systems.

• •

  Longer packets are more susceptible to the effects of fading.

In this work, we model the erasure probability as a function of the packet length and investigate the implications on network coding performance. This is somewhat reminiscent of [9], in which the erasure probability is a function of the link distance in a wireless network, and the effect on capacity is investigated. Our emphasis will be on a wireless channel with a fixed bandwidth, for which we will associate erasure probability with the probability of symbol error for a given modulation scheme.

We note that a careful examination of packet lengths in data networks is not a new idea; most notably, many researchers participated in a dispute over the packet size for the Asynchronous Transfer Mode (ATM) standard in the 1980s. And still many tradeoffs are being studied today at the network level regarding the packet length. The interplay between packet lengths and coding arises because of the way that network coding unifies different layers of the protocol stack. Another work which examines a similar problem is [10], in which packet headers and packet lengths are analyzed for Reed-Solomon coding in video applications.

We consider the following setting. A source node has $K$ units of information $\{s_{1},s_{2},\ldots,s_{K}\}$ that it wants to transmit. We will refer to each of these information units as packets and let each packet be given by a vector of $n$ $q$-ary symbols, where $q$ is the symbol alphabet (the size of a finite field) and $n$ is the number of symbols per packet. We consider values of $q$ which are powers of 2, i.e., $q=2^{u}$ for some $u\geq 1$. The length of a packet is given by $n\log_{2}q$ bits. In Section III we will consider the case where $\{s_{1},s_{2},\ldots,s_{K}\}$ are packets of uncoded information, whereas in Section IV we will assume that a (deterministic) error-correcting code has been applied in order to form $\{s_{1},s_{2},\ldots,s_{K}\}$.

The source generates random linear combinations by forming the modulo-$q$ sum $\sum_{i=1}^{K}\alpha_{i}s_{i}$, where $\alpha_{i}$ are chosen randomly and uniformly from the set $\{0,1,2,\ldots,q-1\}$. Note that the resulting random linear combination is a packet with length $n\log_{2}q$ bits. With each random linear combination transmitted, the source appends a packet header identifying $\alpha_{i}$, which requires an additional $K\log_{2}q$ bits of overhead with every $n\log_{2}q$ bits transmitted. A receiver will collect these random linear combinations until it has received enough to decode. For transmission over an erasure channel, decoding can be performed by Gaussian elimination. Let $N$ denote the number of random linear combinations needed for decoding. Each of the $N$ random linear combinations represents a linear equation in $\{s_{1},s_{2},\ldots,s_{K}\}$ and the distribution of $N$ is given by

$$\mbox{Pr}(N{\leq}j)\!=\!\mbox{Pr}\{\mbox{a random $K{\times}j$ matrix has rank }K\}.$$

Note that Pr$(N\leq j)$ is equal to zero for $j<K$. For $j\geq K$, the distribution can be found following the procedure in [11] and is given by

	$\displaystyle\mbox{Pr}(N{\leq}j)$	$\displaystyle\!\!=\!\!$	$\displaystyle\frac{(q^{j}{-}1)(q^{j}{-}q)(q^{j}{-}q^{2})\ldots(q^{j}{-}q^{K{-}1})}{q^{jK}}$
		$\displaystyle\!\!=\!\!$	$\displaystyle\prod_{i=0}^{K-1}(1-q^{-j{+}i})$

The expected value of $N$ can be found from the above distribution and is shown to be given by

	$\displaystyle E[N]$	$\displaystyle=$	$\displaystyle K+\sum_{j=K}^{\infty}\left(1-\prod_{i=0}^{K-1}(1-q^{-j{+}i})\right)$		(1)
		$\displaystyle=$	$\displaystyle\sum_{i=1}^{K}(1-q^{-i})^{-1}$

Clearly, as $q\rightarrow\infty$, $E[N]\rightarrow K$.

We let $\epsilon(n\log_{2}q)$ denote the erasure probability on the channel, which is an increasing function of the packet length $n\log_{2}q$. The expected number of transmissions needed for the receiver to decode the original $K$ packets is given by

$$\frac{E[N]}{1-\epsilon(n\log_{2}q)}.$$

Over the course of these transmissions, the average number of packets received for each transmission is

$$\frac{K(1-\epsilon(n\log_{2}q))}{E[N]}$$

We account for the overhead by scaling the number of packets received per transmission by $n/(n+K)$, which is the ratio of number of information symbols to the total number of symbols (information plus overhead) sent with each transmission. We define $S$ as the effective portion of each transmission which contains message information; $S$ is a measure of throughput in packets per transmission and takes values between 0 and 1.

$$S=\frac{K}{E[N]}\frac{n}{n+K}(1-\epsilon(n\log_{2}q))$$

(2)

If the erasure probability is constant, $\epsilon(n\log_{2}q)=e$, then for $n$, $q$ $\rightarrow\infty$, corresponding to infinitely long packets, the value of $S$ approaches $1-e$, which is the Shannon capacity of the erasure channel.

From the expression in (2), we can identify a tradeoff between the packet length and the throughput. As the number of information symbols per packet $n$ grows large, the effect of overhead becomes negligible, but the erasure probability grows and the transmissions are more likely to fail. Alternatively, if $n$ approaches zero, transmissions are more likely to succeed, but the overwhelming amount of overhead means that no information can be transmitted. In a similar manner, as the alphabet size $q$ grows, the random linear coding becomes more efficient in the sense that $E[N]\rightarrow K$, but again, the erasure probability increases and transmissions are likely to be unsuccessful. This tradeoff demonstrates that the alphabet size, packet length, and overhead must be carefully weighed in determining the performance of random linear coding over the erasure channel.

In this section we consider the case where $\{s_{1},s_{2},\ldots,s_{K}\}$ are uncoded information symbols. We define the data rate in bits per transmission as $R$, where

$$R=Sn\log_{2}q.$$

(3)

The data rate $R$ accounts for the fact that each received packet contains $n\log_{2}q$ bits of information. Since the packets $\{s_{1},s_{2},\ldots,s_{K}\}$ consist of uncoded information, for every random linear combination sent, all $n$ symbols must be received without error. Then

$$\mbox{Pr}(\mbox{erasure})=1-\left(1-\mbox{Pr}(\mbox{symbol error})\right)^{n}$$

and $\mbox{Pr}(\mbox{symbol error})$ will correspond to the symbol error probability for $q$-ary modulation over the channel. We denote the probability of symbol error by $P_{q}$ and note that it is independent of $n$ but depends on $q$ as well as features of the channel such as pathloss, signal-to-noise ratio (SNR), and fading effects. We will consider a wireless channel of limited bandwidth, for which modulation techniques such as pulse amplitude modulation (PAM), phase shift keying (PSK), and quadrature amplitude modulation (QAM) are appropriate. For these modulation techniques, $P_{q}\rightarrow 1$ as $q\rightarrow\infty$ [12].

In this setting, the erasure probability is given by

$$1-\epsilon(n\log_{2}q)=(1-P_{q})^{n}.$$

(4)

From the above expression we note that, as suggested by our discussion on the tradeoff between throughput and packet length, as $n\rightarrow\infty$, both $S$ and $R$ approach zero exponentially fast. Additionally, for the modulation schemes mentioned above, $S$ and $R$ approach zero as $q\rightarrow\infty$, albeit at a slower rate.

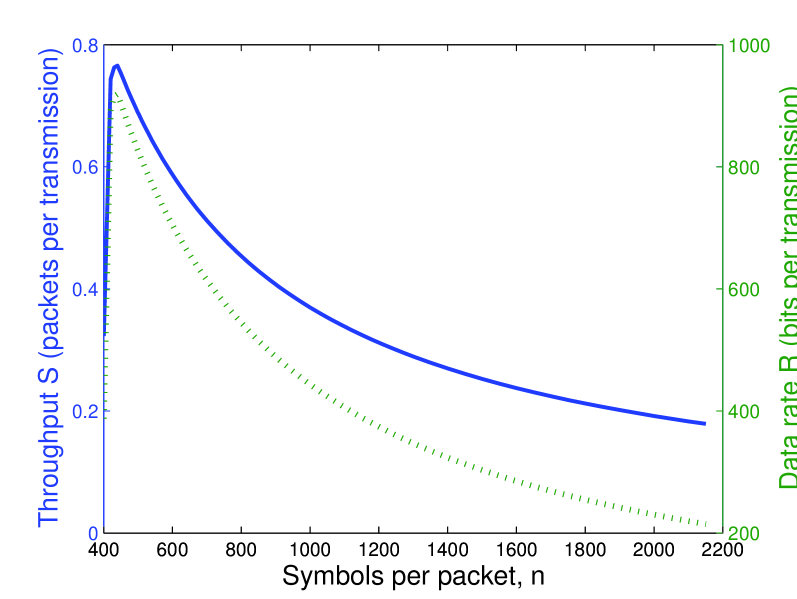
As a numerical example, we have plotted the throughput $S$ and data rate $R$ for QAM modulation over an additive white Gaussian noise (AWGN) channel. In this case the symbol error probability for the optimum detector is approximated by [12]

$$P_{q}\approx 1-\left(1-2\left(1-\frac{1}{\sqrt{q}}\right)Q\left(\frac{3\gamma_{b}\log_{2}q}{q-1}\right)\right)^{2}$$

(5)

where $\gamma_{b}$ is the SNR per bit and $Q$ is the complementary cumulative distribution function for the Gaussian distribution. The above expression for $P_{q}$ holds with equality for $\log_{2}q$ even. The results are shown in Figure 1, where $q$ is fixed and $n$ is varied, and in Figure 2, where $n$ is fixed and $q$ is varied. In all cases, the throughput and data rate are concave functions, admitting optimum values for $n$ and $q$. Furthermore, if $n$ grows large as $q$ is fixed or if $q$ grows large as $n$ is fixed, the throughput approaches zero.

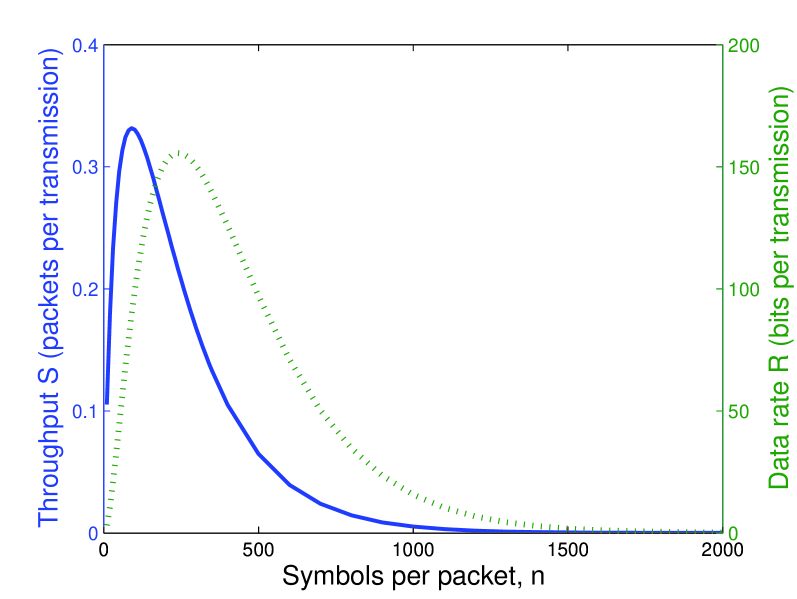
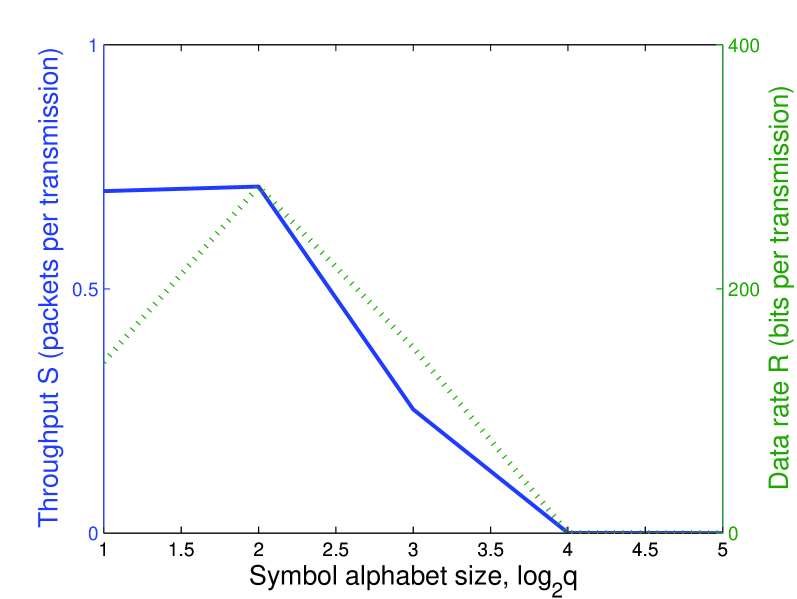
To improve the performance described above, a number of techniques might be employed, including enhanced receivers, diversity techniques, and channel coding.

In this section we examine the effect of using a deterministic pre-code prior to performing random linear coding. We assume that an uncoded packet $\sigma_{i}$, consisting of $k$ $q$-ary information symbols, is passed through an encoder to add redundancy, producing the packet $s_{i}$ consisting of $n$ $q$-ary symbols. Thus a $q$-ary code of rate $R_{pc}=k/n$ is used to produce $\{s_{1},s_{2},\ldots,s_{K}\}$. Random linear coding is again performed on $\{s_{1},s_{2},\ldots,s_{K}\}$ and we assume that the codebook for the pre-code is known to the decoder and does not need to be transmitted over the channel. At the receiver, decoding of the random linear code will be performed first using the coefficients $\alpha_{i}$, $i=1,2,\ldots,K$ sent with each random linear combination. Subsequently the pre-code will be decoded. The use of the pre-code means that the system will be tolerant to some errors in the $n$ symbols sent in each random linear combination.

To account for the pre-code, we modify the throughput $S$ expressed in (2) by multiplying it be $R_{pc}$, which results in

$$S=\frac{K}{E[N]}\frac{k}{n+K}(1-\epsilon(n\log_{2}q)).$$

(6)

To obtain the data rate $R$ in bits per transmission, $S$ is now scaled by $k$, the number of information symbols present in each packet.

$$R=Sk\log_{2}q$$

(7)

We can bound the erasure probability, and thus the throughput $S$ and data rate $R$, using bounds on the error-correcting capabilities of the pre-code. Let $t$ denote the number of symbol errors that the pre-code can correct. For a given code, $t=\lfloor 1/2(d_{min}-1)\rfloor$ errors, where $d_{min}$ is the minimum distance of the code. The erasure probability can be bounded as follows.

	$\displaystyle 1-\epsilon(n\log_{2}q)$	$\displaystyle\stackrel{{\scriptstyle(a)}}{{\geq}}$	$\displaystyle 1-\sum_{i=t+1}^{n}\mbox{Pr}(i\mbox{ symbols in error})$
		$\displaystyle\stackrel{{\scriptstyle(b)}}{{=}}$	$\displaystyle 1-\sum_{i=t+1}^{n}\binom{n}{i}P_{q}^{i}(1-P_{q})^{n-i}$
		$\displaystyle\stackrel{{\scriptstyle(c)}}{{\geq}}$	$\displaystyle\sum_{i=0}^{\lfloor 1/2(d-1)\rfloor}\binom{n}{i}P_{q}^{i}(1-P_{q})^{n-i}$

In the above expression, $(a)$ holds with equality for the class of perfect codes [12], $(b)$ follows by assuming that errors are independent, identically distributed $\sim P_{q}$ among the $n$ symbols, and $(c)$ holds for $d\leq d_{min}$. We make use of the Gilbert-Varshamov bound to provide a lower bound on $d_{min}$ as follows.

$$d=\inf\left\{d_{min}:\sum_{i=0}^{d_{min}-2}\binom{n-1}{i}(q-1)^{i}\geq q^{n-k}\right\}$$

(8)

Lower bounds on the throughput and data rate are given as follows.

$$S_{LB}=\frac{K}{E[N]}\frac{k}{n+K}\sum_{i=0}^{\lfloor 1/2(d-1)\rfloor}\binom{n}{i}P_{q}^{i}(1-P_{q})^{n-i}$$

(9)

$$R_{LB}=S_{LB}k\log_{2}q$$

(10)

For $q\rightarrow\infty$ while all other parameters are fixed, if the modulation scheme has $P_{q}\rightarrow 1$, then $S_{LB},R_{LB}\rightarrow 0$. In the limit of increasing symbols per packet $n$, we identify two different cases. First, if the pre-code rate $R_{pc}$ is fixed (i.e, $k\rightarrow\infty$ as $n\rightarrow\infty$ with fixed ratio between the two) then $S_{LB}\rightarrow R_{pc}$ (multiplied by $K/E[N]\approx 1)$ and $R_{LB}$ increases without bound. On the other hand, if $k$ is fixed (i.e., as $n\rightarrow\infty$, $R_{pc}\rightarrow 0$) then $S_{LB},R_{LB}\rightarrow 0$.

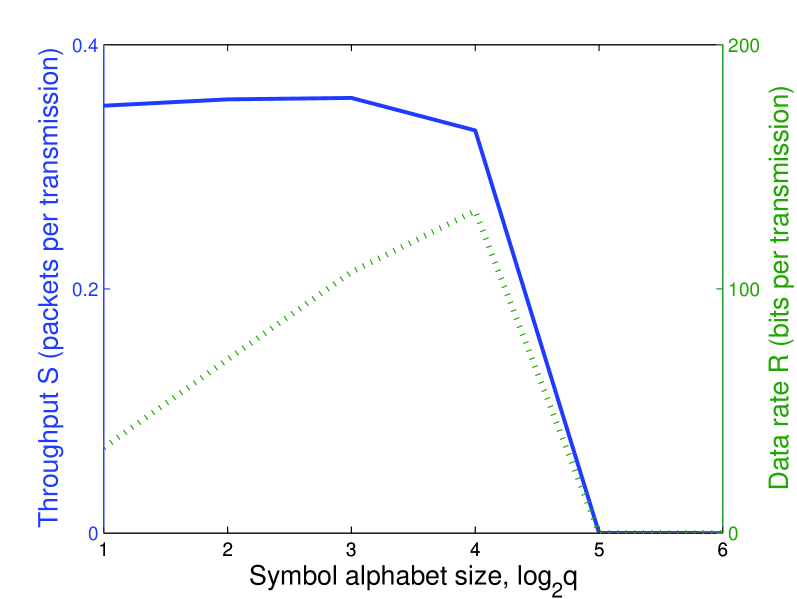
We have computed numerical examples of $S_{LB}$ and $R_{LB}$ assuming QAM modulation with $P_{q}$ as given in (5). In Fig. 3 we display the throughput and data rate as a function of $q$. Clearly, pre-coding allows the system to support higher $q$ with non-zero throughput, although the throughput does eventually go to zero for large $q$. In comparing this result to Fig. 2, note that all other parameters are fixed and the pre-code rate $R_{pc}=1/2$ results in a halving of the throughput and data rate.

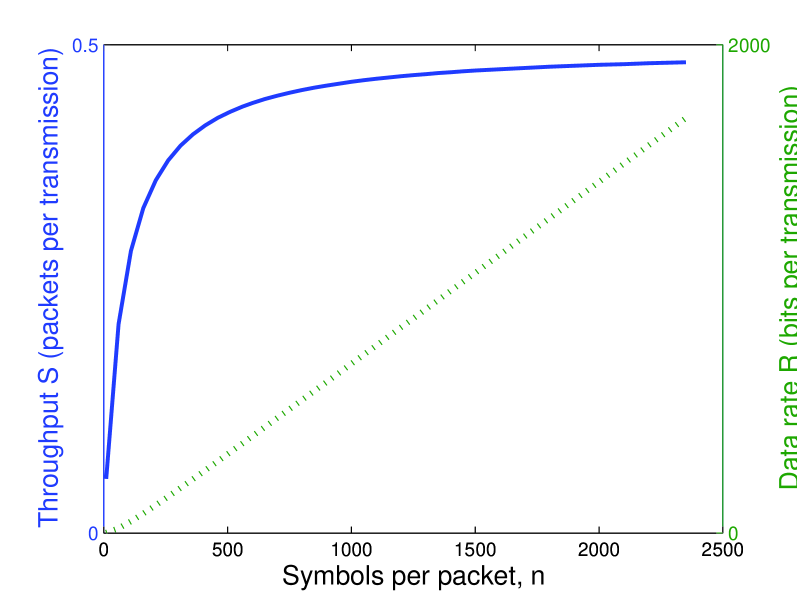
In Fig. 4 we have displayed the two different cases for performance as a function of increasing symbols per packet $n$. In Fig. 4(a), the rate $R_{pc}$ is fixed at $1/2$ and $S_{LB}\rightarrow R_{pc}$ while $R_{LB}$ increases without bound. In this case, pre-coding ensures that the throughput and data rate increase with $n$. However, there is a caveat: the result in Fig. 4(a) requires that $k\rightarrow\infty$, which means that the source must have an infinite supply of uncoded information to be transmitted. On the other hand, if the source has a finite amount of information to be transmitted, as shown in Fig. 4(b), then as $n\rightarrow\infty$, the pre-code rate $R_{pc}\rightarrow 0$ and the data rate also approaches zero. In summary, the use of a pre-code can improve performance on the erasure channel; indeed, pre-coding is the mechanism which allows us to represent a noisy channel as an erasure channel. However, pre-coding can only ensure that the data rate increases with packet length if there is an infinite supply of (uncoded) information at the source. This is a strong assumption for a network, where data often arrives in bursts.

The primary contribution of this work is the elucidation of the fact that the widely-used assumption of the erasure probability being constant as the packet length increases leads to idealized performance that cannot be obtained in a practical scenario. We have shown that the assumption of increasingly long packets, either due to increasingly many symbols per packet or to an increasing alphabet size, can result in a data rate of zero for random linear coding if the erasure probability increases with packet length. While the use of a pre-code prior to performing random linear coding can improve performance, it can only ensure that the throughput increases with packet length if there is an infinite supply of data awaiting transmission at the source. We have also demonstrated that the overhead needed for random linear coding can have a devastating impact on the throughput. We have focused our attention on the erasure channel, but the tradeoff between packet length and throughput will arise in other channels, particularly in wireless channels where these effects can be exacerbated by fading. A number of techniques, such as pre-coding, can be employed to combat the adverse effects of the channel, but in making use of these techniques, the performance gains offered by network coding will be tempered.

This work is supported by the Office of Naval Research through grant N000140610065, by the Department of Defense under MURI grant S0176941, and by NSF grant CNS0626620. Prepared through collaborative participation in the Communications and Networks Consortium sponsored by the U.S. Army Research Laboratory under The Collaborative Technology Alliance Program, Cooperative Agreement DAAD19-01-2-0011. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation thereon. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Laboratory or the U. S. Government.