Relative realizability and the Brundu-Logar normal form \MSC14T05, 14Q10
On realizability of lines on tropical cubic surfaces and the Brundu-Logar normal form
Abstract
We present results on the relative realizability of infinite families of lines on general smooth tropical cubic surfaces. Inspired by the problem of relative realizability of lines on surfaces, we investigate the information we can derive tropically from the Brundu-Logar normal form of smooth cubic surfaces. In particular, we prove that for a residue field of characteristic the tropicalization of the Brundu-Logar normal form is not smooth. We also take first steps in investigating the behavior of the tropicalized lines.
keywords:
cubic surfaces, tropical lines, relative realizability, tropical geometry1 Introduction
Since 1849 it has been a well-known fact that every classical smooth cubic surface contains exactly lines [4, 16]. With the rise of tropical geometry the question about an analogous result about tropical cubic surfaces was inevitable. In 2007 Vigeland proved in [19] that on smooth tropical cubic surfaces, there can be infinitely many tropical lines. Accordingly, the following questions arose:
{que}[Relative Realizability]
For a given pair of a tropical line on a tropical cubic surface , is there a pair of a classical line on a classical cubic surface such that and ?
{que}[Relative Realizability, Lifting Multiplicities]
For a pair and a fixed lift of , how many lines tropicalize to , i.e. what is the lifting multiplicity of with respect to ?
The question of the geometric behavior of the tropical lines and the problem of their relative realizability has been worked on for more than a decade and is not yet completely solved [19, 20, 15, 2, 1, 8, 11, 5, 14].
With respect to the question of lifting multiplicities, there has been a recent new development: in [14] an octanomial model for cubic surfaces is presented, which satisfies that all lines on a tropically smooth cubic in this form have distinct tropicalizations [14, Theorem 3.4], i.e. all lifting multiplicities are one or zero.
Also, the conjecture is posed that the lines on a tropically smooth cubic surface have distinct tropicalizations [14, Conjecture 4.1]. Moreover, according to [14], Kristin Shaw has announced a proof that every tropically smooth family of complex cubic surfaces contains 27 lines with distinct tropicalizations.
By tools introduced in [20, 15] it is possible to divide tropical lines into isolated lines and infinite families. On general smooth tropical cubics there can only occur two types of families; see Proposition 1 and [15, 8]. The lifting behavior of one type of family over characteristic has been investigated in [2, 1]. Our first main result, Theorem 4, is a generalization of this result to fields of arbitrary characteristics, obtained by complementary methods. Also, we present two trend-setting new examples, one for the second family type in Example 4.1 and one on the unsolved case to Theorem 4 in Example 3.
Unfortunately, the computational expenditure to compute the lines on a generic classical smooth surface is very high, impeding an easy access to examples of more complex lifts over arbitrary characteristic. The existence of a normal form of classical cubic surfaces which allows the direct computation of all 27 lines from the parameters of the cubic polynomial by simple formulas seems to present a new perspective to solving this problem. Therefore, we ask {que}[[18, Question 26]] How to compute the Brundu-Logar normal form in practice? What does it tell us tropically?
The first part of this question has been computationally answered for generic cubics over the -adic fields by Avinash Kulkarni [12]. As a smooth cubic is transformed in the Brundu-Logar normal form by projective linear transformations, this question is closely related to {que}[[18, Question 12]] How can we decide if a given polynomial defines a smooth tropical surface after a linear transformation of ? Unfortunately, the Brundu-Logar normal form of a lift of any chosen smooth tropical cubic is itself no longer tropically smooth. More precisely, our second main result is the following theorem:
Theorem (Theorem 9).
If , the tropicalization of any cubic in Brundu-Logar normal form is not tropically smooth.
However, we can still investigate the tropicalization of cubics in Brundu-Logar normal form and look into the behavior of the tropicalizations of the 27 lines. We will see in Section 3.3 that the statement of Theorem 3.4 from [14] does not hold for the Brundu-Logar normal form, as we can have higher lifting multiplicities in this setting, as illustrated in Examples 4.2 and 4.2. These examples prove that [14, Conjecture 4.1] does not hold for non-smooth tropical cubics.
This paper is organized as follows. In Section 2 we present results on the relative realizability of lines on tropical cubic surfaces. In Section 3 we study the tropical Brundu-Logar normal form and its tropicalized lines. Section 4 presents significant examples of realizable lines in tropical cubic surfaces, one of them obtained by transforming to the Brundu-Logar normal form.
Acknowledgments. I am very grateful to Hannah Markwig for her continued support and advice during this project. I warmly thank Diane Maclagan for her support during my research at the University of Warwick. Also I want to thank Marta Panizzut, Michael Joswig and Bernd Sturmfels for insightful and inspiring conversations on cubic surfaces. Very special thanks to Marta Panizzut and Avinash Kulkarni for their ready and generous assistance with the computations.
I also want to thank Sara Lamboglia and the anonymous referee for their helpful comments on the presentation of this paper.
2 Relative realizability of infinite families of lines
Let Denote the facets of with Using the concept of decorations introduced in [20], we can classify lines on surfaces by their way of being contained in the surface: passing through vertices or edges. Decorations allow one to distinguish isolated lines and infinite families of lines contained in the tropical surface. This concept was refined by the theory of motifs introduced in [15], where also a thorough classification of all motifs of lines on general smooth surfaces of varied degree can be found, completing the started classification from [20]. The concept of generality used in this section is the one introduced by [20].
[[15, Definition 6]] A motif of a tropical line on a tropical surface is a pair , where the primal motif is a decoration of the underlying graph of with a finite number of dots and vertical line segments. Every dot stands for a vertex of contained in that cell of corresponding to the decorated edge or vertex of the graph, while a vertical line segment stands for an edge of that intersects in its relative interior with the cell whose corresponding part in the graph is decorated. The dual motif is the subcomplex in the dual subdivision of dual to the union of all cells of that passes through: .
Proposition 1 ([15, Proposition 23], [8, Section 3.2]).
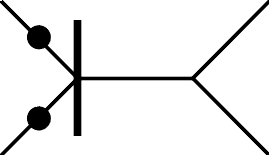
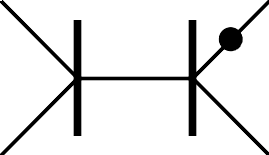
Only the motifs 3I and 3J allow infinite families on general smooth tropical cubic surfaces; see Figure 1.

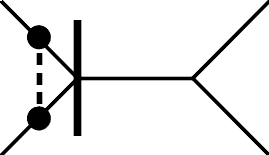
Remark 2.
The dual motif to 3I is a unimodular tetrahedron, which has one edge in and at least a one-dimensional intersection with both and . This is called a -exit tetrahedron. The property of relative realizability of families of motif 3I depends on how the dual motif, a 4-exit tetrahedron, is contained in the subdivision of the Newton polytope of the cubic surface. For smooth cubic surfaces, there are two ways up to coordinate changes to include a 4-exit tetrahedron in .
A family of lines on a smooth cubic surface is of type 3I-1 if it has motif 3I with the dual motif contained in in a position equivalent to up to coordinate changes; see Figure 2(a). It is of type 3I-2 if it is of motif 3I and the dual motif is contained in in a position equivalent by coordinate changes to ; see Figure 2(b).
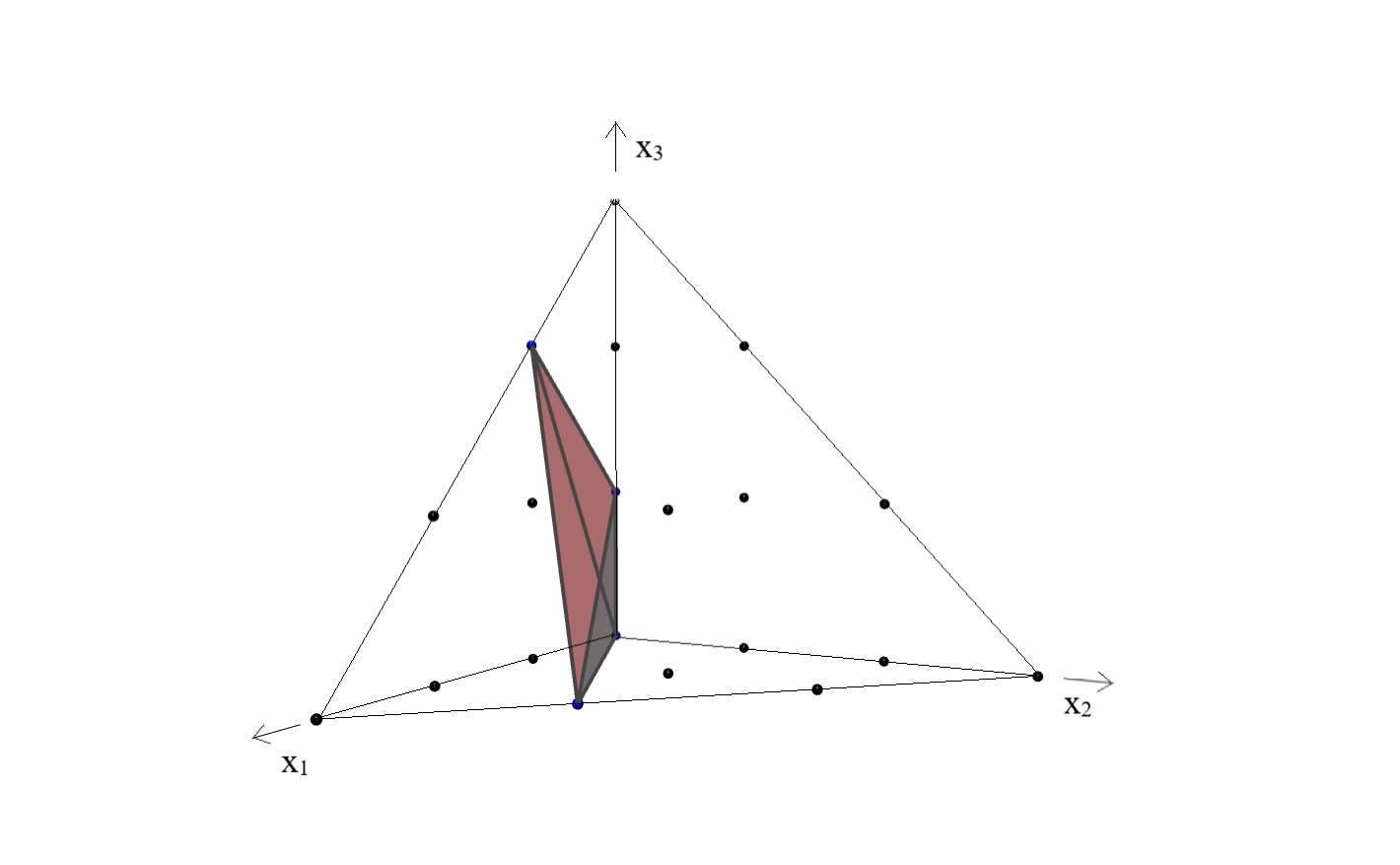
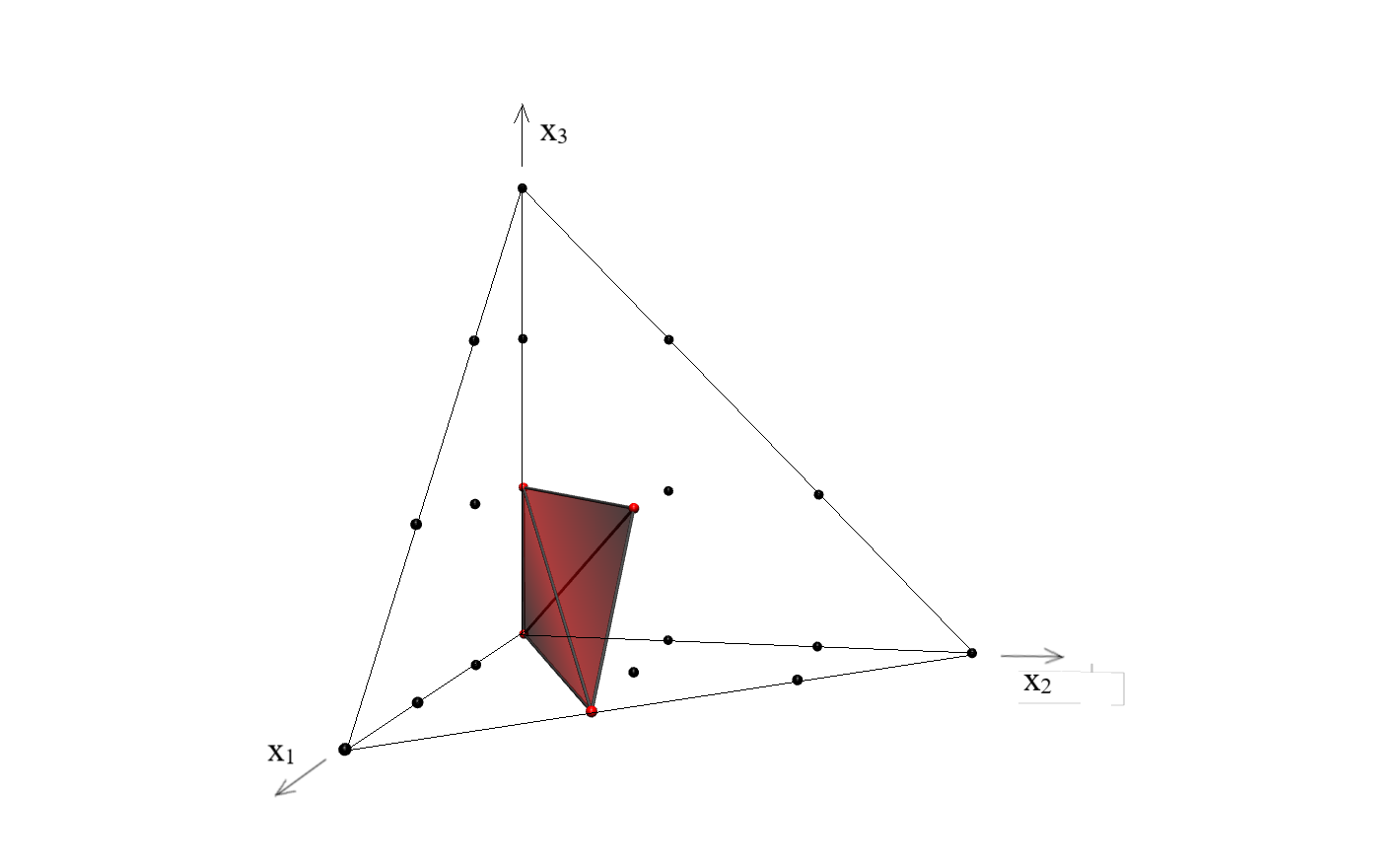
A tropical line is called degenerate, if the bounded middle line segment has length zero.
Proposition 3.
Over a line of motif 3I on a tropical cubic surface lifts if and only if it is degenerate and of type 3I-1.
Proof 2.1.
This is a corollary of Theorem 7.2 in [2] which states, that for an algebraic surface over with Newton polytope a unimodular 4-exit tetrahedron, the tropical line is approximable by a complex algebraic line if and only if and the Newton polytope is of the form . We can assume the vertex of contained in to be and apply this locally to .
Theorem 4 ([8, Theorems 4.1.9 and 4.1.16]).
Let be an algebraically closed field with valuation and let be its residue field. Let be a general smooth tropical cubic surface containing a family of lines .
If the family is of type 3I-1 with
or the family is of type 3I-2, then for any homogeneous with the family cannot be realized as lines on , i.e. the lifting multiplicity of any
non-degenerate member of the family is zero.
Proof 2.2.
Since we consider our cubic homogeneous, we consider everything over .
Without loss of generality we can assume that the monomials corresponding to the vertices of the dual motif of the family have coefficients of valuation zero, while the coefficients of all other monomials in have strictly positive valuation. We write
For let be a linear homogeneous ideal, such that . If the lines are realizable, we have
The initial ideal of in is given as . This basis is a Gröbner basis with the lexicographic order with
If has type 3I-1, we obtain By Gröbner basis theory, we know that there exits a polynomial of support if and only if its polynomial division with the Gröbner basis of has remainder zero. Carrying out the polynomial division, we find the remainder
If , this polynomial is zero if and only if .
For of type 3I-2, The remainder of by polynomial division is
This polynomial is zero if and only if .
Theorem 4 deals with the non-degenerate lines of motif 3I. We can use the same techniques to prove the following theorem.
Theorem 5.
Let be an algebraically closed field with valuation and let be its residue field. Let be a general smooth tropical cubic surface containing a family of lines of type 3I-2. The degenerate line of this family cannot be realized on any lift of , homogeneous.
Proof 2.3.
As before we consider everything over and assume that the monomials corresponding to the vertices of the dual motif of the family have coefficients of valuation zero, while all other coefficients in have strictly positive valuation. Again we denote
Let be the degenerate line of the family of type 3I-2 on and let be a linear homogeneous ideal, such that .
We use the same argument as in the proof of Theorem 4: if the line is realizable, it follows that
The initial ideal of in can only be determined up to a : , given by a Gröbner basis with the lexicographic order with
If is of type 3I-2, we know
By polynomial division of a polynomial of support with the Gröbner basis, we obtain the remainder:
Since , this polynomial is zero if and only if .
Remark 6.
The same techniques do not reveal similar results for type 3I-1. Indeed the lifting behavior of the two types is quite different.
For any member of a family of type 3I-1 on a smooth tropical surface , is there a lift of defined over a field with residue field of containing a lift of ?
It remains to investigate families of motif 3J. Similar to lines of type 3I-1, we can find a lift of a smooth tropical cubic surface defined over , for and each, where a non-degenerate member of the family of motif 3J is realizable. The details are shown in Example 4.1. The arising question is
For any member of a family of motif 3J on a smooth tropical surface , is there a lift of over any algebraically closed field containing a lift of ?
3 The Brundu-Logar normal form and its tropicalization
The fact that the Plücker coordinates of the lines on cubics in Brundu-Logar normal form are known explicitly motivates our study of their tropicalizations. In this section let be algebraically closed,
3.1 The classical Brundu-Logar normal form
A homogeneous cubic polynomial is in Brundu-Logar normal form if
where and is the hypersurface defined by
Theorem 7 ([3, Theorem 1.4 and 1.7]).
Every smooth homogeneous cubic polynomial can be brought into Brundu-Logar normal form by applying projective transformations.
Every cubic in Brundu-Logar normal form is smooth and thus contains exactly lines.
In particular, the points in parametrize all smooth cubics.
The question how to obtain the Brundu-Logar normal form for a given cubic is answered by a Magma script written by Avinash Kulkarni for generic cubics over -adic fields [12].
3.2 Tropicalizing the Brundu-Logar normal form
Let and the cubic in Brundu-Logar normal form defined by . We denote by the corresponding cubic surface. The tropicalization of in Brundu-Logar normal form is:
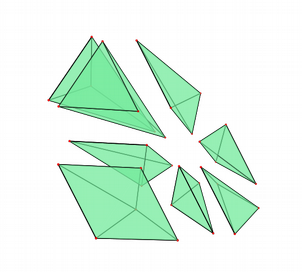
If all parameters of are not zero, the Newton polytope is given by
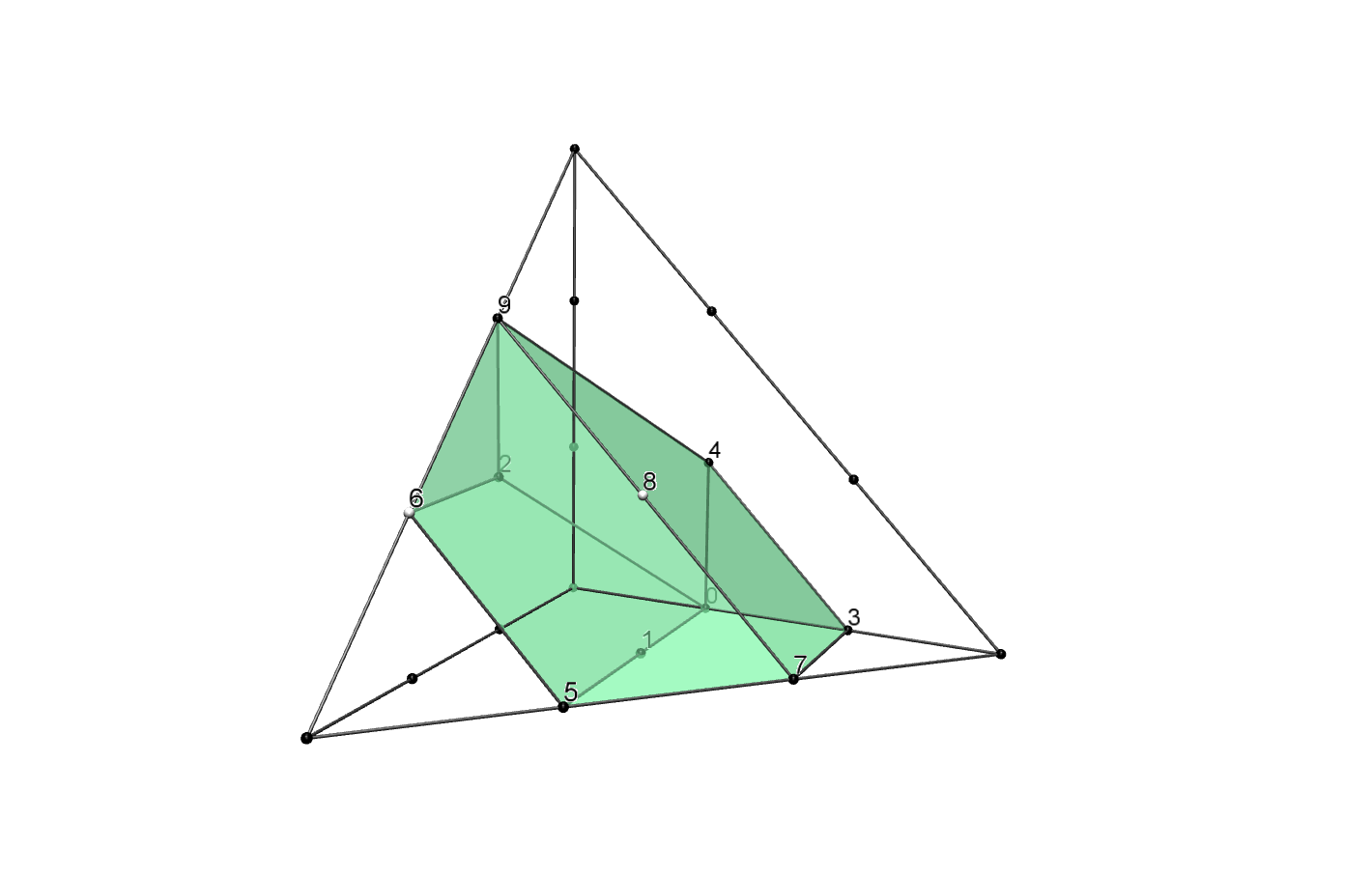
Dehomogenized with respect to and embedded in the tetrahedron this polytope is shown in Figure 3.
The weight vector induced by a cubic in Brundu-Logar normal form with is
Remark 8.
By definition, a tropical variety is smooth if and only if the dual subdivision of is unimodular [13, Section 4.5]. For all coefficients of not zero, we have , so a unimodular triangulation contains exactly tetrahedra.
By [3, Theorem 1.4], every classical Brundu-Logar normal form is smooth. However, the conditions on the weights to a cubic in Brundu-Logar normal form do not allow unimodular triangulations.
Theorem 9.
If , the tropicalization of any cubic in Brundu-Logar normal form is not tropically smooth.
In particular, this statement holds for most choices of fields with a valuation
Proof 3.1.
The idea is to make a case distinction of which combinations of the parameters in have minimal valuation. In every case, we obtain either that too many vertices have minimal valuation, that vertices contained in a plane have minimal valuation or that the vertices of minimal valuation form a tetrahedron of size larger than . These arguments are valid independent of containing zeros or coordinates of being and thus of the exact volume of . In the proof we classify all possible cases. For each case we find obstructions to unimodular triangulations.
For brevity, we abstain from listing all the cases; rather we show the concept by an exemplary case:
Let .
For the numeration of the vertices see Table 1.
Since on the level of minimal valuations we can only have cancellations in either or , at least one of and has value , similar with and . If and have no cancellation, we obtain that the six vertices 0, 2, 4, 5, 7, 9 have the same minimal valuation. But a subdivision of a polytope in can only be unimodular if a maximum of vertices have minimal valuation. We need to have cancellations:
-
1.
Cancellation in .
It follows that Therefore, the vertices with numbers 2, 4, 5, 7 have same minimal valuation. However, these vertices are contained in a plane and therefore induce subpolytopes in the subdivision which are not unimodular. -
2.
Cancellation in .
We obtain So the vertices with numbers 0, 5, 7, 9 form a polytope in the triangulation. However, this tetrahedron is too big, since the edge from vertex number 0 to 5 contains another lattice point in its interior.
In contrast to the octanomial model presented in [14], the tropicalized Brundu-Logar normal form is not smooth for most choices of valuated fields. Additionally in Example 4.2 we will see that an analogous statement to [14, Theorem 3.4] on the bound for lifting multiplicities does not hold for the tropicalized Brundu-Logar normal form.
3.3 Tropicalizing the 27 lines in the Brundu-Logar normal form
For a cubic in Brundu-Logar normal form, [3, Table 2] gives the Plücker coordinates of the 27 lines in terms of , where and satisfy , .
This offers a new perspective on working the problem of relative realizability: tropicalizing the coordinates we can conclude which of the tropical lines in the tropicalized cubic surface in Brundu-Logar normal form are realizable. Further, for any cubic we can determine the transformation bringing it into normal form, apply its inverse to the lines and obtain analogous information.
Table LABEL:tab:plückercoordinates shows the tropicalized Plücker coordinates. We can obtain the vertices of tropical lines from their Plücker coordinates; see [7], [13, Example 4.3.19]. For shorter notation, we write instead of .
Remark 10.
Note that the tropicalizations of the first five lines and are always distinct. These are depicted in Figures 4(a), 4(c).
As of the tropicalized lines on a tropicalized surface in Brundu-Logar normal form contain at least one tropical Plücker coordinate of value , here is a short overview how to visualize these lines: with five Plücker coordinates of value the tropical line is „an edge“of the tetrahedron modelling the tropical projective space [13, Chapter 6], as shown in Figure 4(a). The case of four infinite Plücker coordinates does not occur naturally in Table LABEL:tab:plückercoordinates; it would lead to a line segment in one of the facets of . Three Plücker coordinates of value lead to a tropical half line visible in one of the facets of as in Figure 4(b). Two Plücker coordinates of value lead to a classical line in the interior of , corresponding to the middle line segment of a tropical line of infinite length in the tropical surface; see for example Figure 4(c). One Plücker coordinate of value leads to a tropical half line visible in the finite parts of the surface. This is depicted for Example 4.2 in Figure 6.
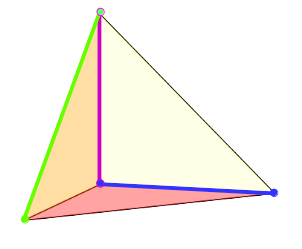
blue: ,
green: ,
magenta:
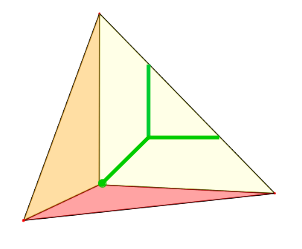
green:
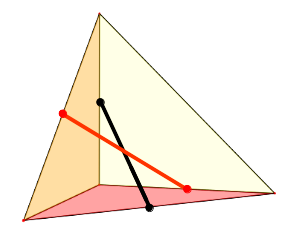
red: ,
black:
Since at least of the tropicalized lines have Plücker coordinates of value , at most classical lines on can have tropicalizations fully visible on In comparison, of the lines on a cubic in octanomial form, only one classical line has finite tropical Plücker coordinates [14].
4 Examples
In this section we show some examples on the theory presented in Sections 2 and 3. We start with two examples on the relative realizability of families of motif 3J and 3I-1 indicating positive answers to Questions 2 and 2. We conclude with examples investigating the behavior of lines on the tropicalized Brundu-Logar normal form.
4.1 Relative Realizability
[Lines of motif 3J] This example indicates that Question 2 might be answerable with yes. In fact it shows a cubic surface on which a member of a family of motif 3J is realizable.
We investigate the cubic surface detected by Hampe and Joswig in [10] containing two families of motif 3I and one of motif 3J. We choose the weight vector as below, which induces a surface containing no lines of non-general motifs and can therefore be considered as generic:
Using the Magma script [17] by Emre Sertoz written for [14] we can compute the lines on a simple lift of the tropical cubic over an -adic field. A simple lift is a cubic where the coefficients are given as , where is either a prime if we are over the -adics, or over the Puiseux series. The following table shows the tropicalized Plücker coordinates of the computed lines for matching those for , indicating that does not have a special role in the lifting behavior of this case. The table also shows the Plücker coordinates of the tropical lines contained in the tropical surface sorted into isolated lines and families as computed by the polymake extension a-tint [9, 10].
| tropicalized lines | tropical lines | motif | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| isolated | 3B | |||||||||||||
| 3A | ||||||||||||||
| 3G | ||||||||||||||
| 3D | ||||||||||||||
| 3G | ||||||||||||||
| 3D | ||||||||||||||
| 3H | ||||||||||||||
| 3F | ||||||||||||||
| 3F | ||||||||||||||
| 3G | ||||||||||||||
| 3G | ||||||||||||||
| 3A | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3D | ||||||||||||||
| 3H | ||||||||||||||
| 3H | ||||||||||||||
| 3H | ||||||||||||||
| 3H | ||||||||||||||
| fam. | 3J, | |||||||||||||
| 3I-2, | ||||||||||||||
| 3I-2, | ||||||||||||||
Investigating the dual subdivision of the surface, we see that the two families of motif 3I have type 3I-2. As proven in Theorems 4 and 5 no member of these families lifts. In particular, all the 27 lines on this simple lift tropicalize to non-degenerate lines. It is notable that all the 26 isolated lines are realizable on our chosen lift of the surface. Furthermore, for this example the statement from [14, Conjecture 4.1] holds: the tropicalizations of the lines are distinct.
Notice that in this example the member for of the family of motif 3J lifts, supporting the idea that we have a different lifting behavior for families of motif 3J than for motif 3I; see Question 2.
[Lines of type 3I-1 over ] We consider an example of a smooth tropical cubic surface containing a family of type 3I-1 and its lifting behavior over and . The results suggest Question 2 might be answered positively and Proposition 3 might be extendable to characteristic . We also compare the lifting of the lines with the corresponding Brundu-Logar normal form to the chosen surface.
Using the Magma script from [12], we can calculate the Brundu-Logar normal form to any generic cubic over the -adics and investigate the behavior of the tropical lines on both sides. We consider the tropical cubic surface given by the weight vector below. This cubic is of interest as it contains a family of type 3I-1. We investigate a simple lift of this surface over , giving an example corroborating a positive answer to Question 2.
The tropicalized Brundu-Logar normal form, , to this cubic contains families, numbered , . We have the weight vector
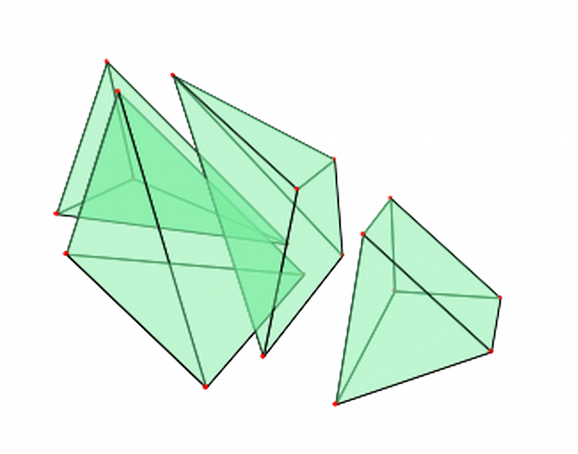
Subdiv()
| tropical Plücker coordinates | |||||||
|---|---|---|---|---|---|---|---|
Computing the tropicalizations of the lines in the Brundu-Logar normal form (right columns in Table LABEL:tab:exHJ) and their inverse images under the transformation leading to the normal form (left columns), we can investigate the lifting behaviour of the tropical lines on both surfaces.
Investigating the Plücker coordinates of the tropicalized lines on , as demonstrated in Table LABEL:tab:exHJ, we obtain two tropicalized lines of higher lifting multiplicity on : a tropical half line of lifting multiplicity and a middle line segment of infinite length of lifting multiplicity . The other lines on have distinct tropicalizations. Comparing Table LABEL:tab:BLNFlines3I-1 with the middle right column of Table LABEL:tab:exHJ, we obtain that three inner members of the family lift and that one inner member of family lifts, while no members of and lift. Additionally, approximates the tropicalized line of lifting multiplicity for .
| lines on | lifting? | lines on | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (3I-1), yes | (e) | ||||||||||||
| yes | (e) | ||||||||||||
| yes | (e) | ||||||||||||
| yes | (d) | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (a), : | ||||||||||||
| yes | (c) | ||||||||||||
| yes | (c) | ||||||||||||
| yes | (a), : | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (b), : | ||||||||||||
| yes | (c) | ||||||||||||
| yes | (d) | ||||||||||||
| yes | (b), : | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (c) | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (c) | ||||||||||||
| yes | (b), : | ||||||||||||
| yes | (a), : | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (a), : | ||||||||||||
| yes | (b) | ||||||||||||
| yes | (b) | ||||||||||||
| (3I-2), no | |||||||||||||
Using polymake, we obtain that the tropical cubic surface contains isolated lines. They are all non-degenerate and lift onto the chosen simple lift of the surface. Additionally, the surface contains two families, both of motif 3I. However, an investigation of the dual subdivision shows that one family is of type 3I-1, while the other is of type 3I-2. As proven in Theorems 4 and 5 the family of type 3I-2 does not lift. Nevertheless, we are in the case that the characteristic of the residue field is equal to , and we observe that for a member of the family of type 3I-1 does lift in this setting.
Comparing these results with a simple lift over , we obtain that in this case in accordance with Theorem 4 the non-degenerate lines of type 3I-1 do not lift. However, the degenerate line of type 3I-1 lifts, suggesting Proposition 3 might hold in different characteristics; see Remark 6. The isolated lines have the same lifting behavior for and .
4.2 Lines on the tropicalized Brundu-Logar normal form
In the following let be the field of Puiseux series over . {exa} This example is tropically very degenerate. Most of the tropicalized lines vanish completely or partly into the infinite boundary, but we observe that some of them can be approximated by families. We also obtain higher lifting multiplicities.
Choose as , , , , , , where .
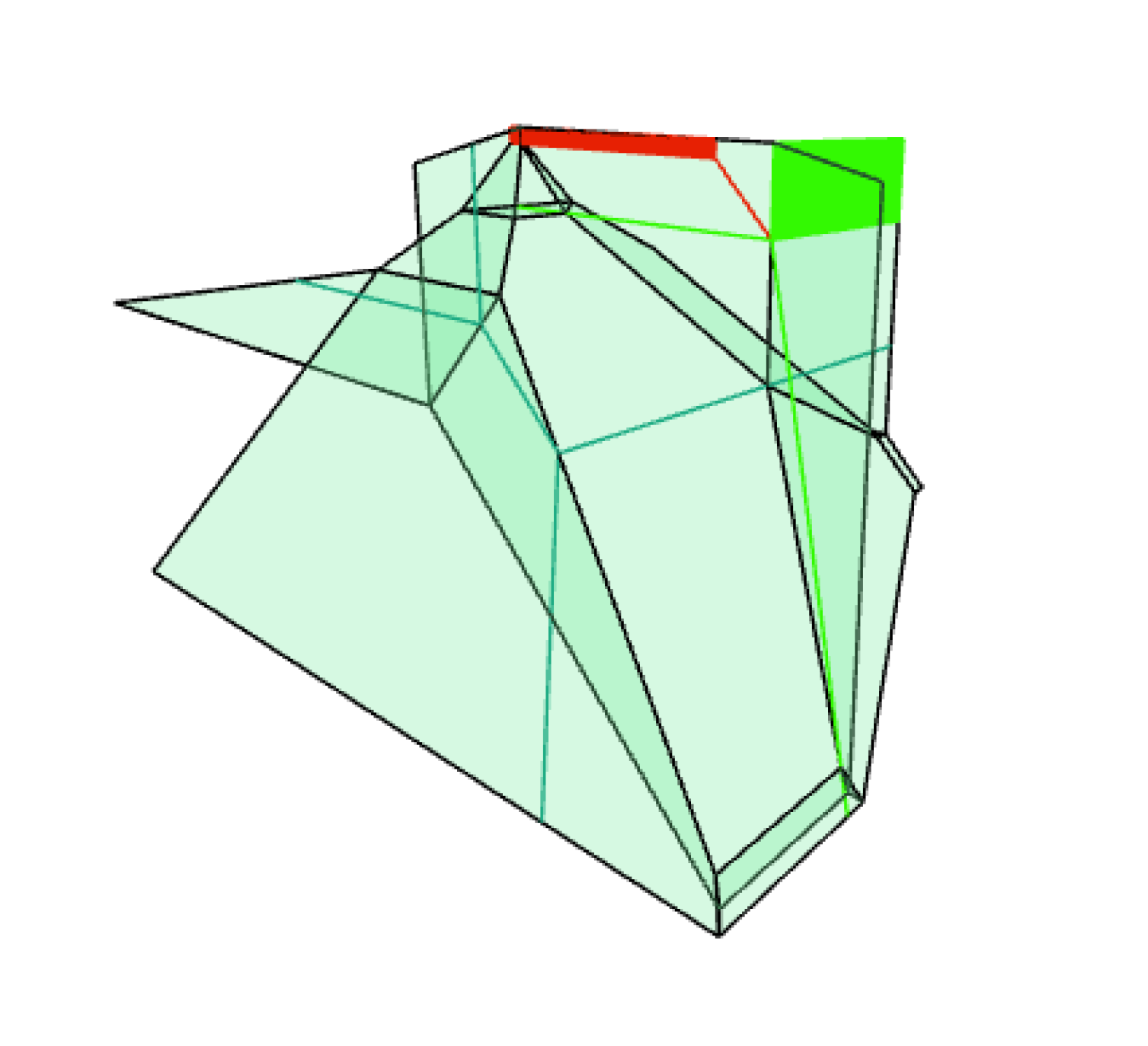
This choice satisfies and , so encodes the Brundu-Logar normal form of some smooth cubic surface. These parameters lead to the trivial subdivision of ; the dual surface is shown in Figure 6(a).
In this case we identify the tropicalizations of all lines.
The tropical surface contains no isolated lines and 7 families, whose tropical Plücker coordinates are as follows with :
| Plücker coordinates | ||||||
|---|---|---|---|---|---|---|
The tropical Plücker coordinates of the lines are shown in Table LABEL:tab:expluck. We see that the lines tropicalize to distinct lines, of which only one has finite Plücker coordinates. The maximal lifting multiplicity observed in this example is ; see Table LABEL:tab:expluck.
By taking the limit of and/or while fixing the other parameter accordingly,
we can approximate some tropicalized lines as an infinite border point of some of the families; see last column of Table LABEL:tab:expluck.
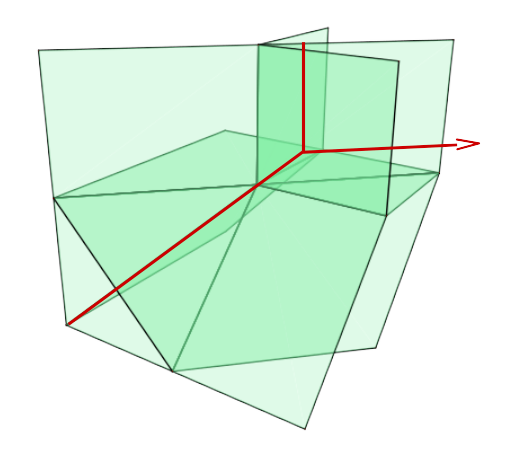
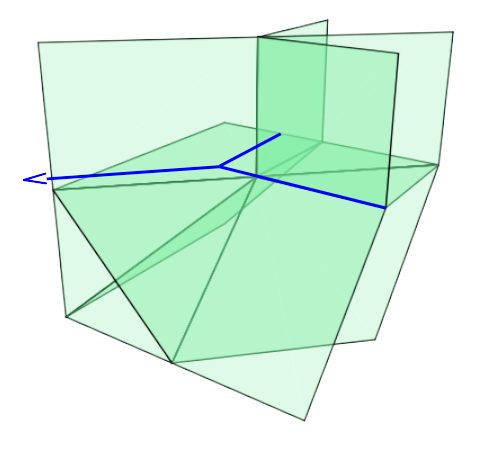
The lines , which are completely in infinity, as shown in Figure 4,
are no limit of any of the families. The tropical lines and have one finite vertex; the other one is in infinity, cf. Remark 10. So only a tropical half line is visible; see Figure 6(b)-6(c). This also does not appear as a limit of the families in this case.
| Plücker coordinates | |||||||
|---|---|---|---|---|---|---|---|
| not approximable | |||||||
| with | |||||||
| with | |||||||
| with | |||||||
| with , | |||||||
| with , | |||||||
| (b) and (b) with , | |||||||
| not approximable | |||||||
| with , | |||||||
| (c) and (a) with , | |||||||
| with | |||||||
| with , | |||||||
| (a) and (a) with , | |||||||
| all families with | |||||||
Note, that the a-tint output for the computation of families has to be checked for redundancies.
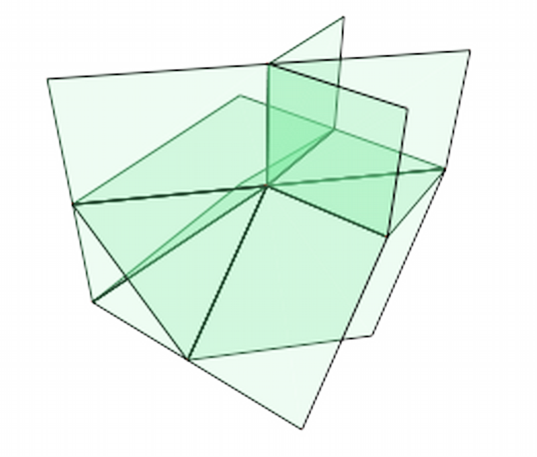
the trivial subdivision
The concluding example is a subdivision relatively close to a unimodular triangulation: it contains only two polytopes of the too large volume . However, we can still observe lifting multiplicities higher than one, but we can no longer approximate lines partly contained in the infinite boundary by families.
We choose the parameters , , , , and obtain the weight vector , which induces a subdivision with maximal cells; see Figure 8(a). The corresponding surface has 1 isolated line and 2 families and , computed using a-tint in polymake:
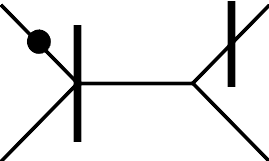
The primal motifs of the two families can be seen in Figure 7. We obtain motifs that are not in the classification of [15], since our surface is not tropically smooth. Only the motif of the isolated line, motif 3A, is one that can occur on general smooth tropical cubics.
Computing the tropicalized lines with finite Plücker coordinates using Table LABEL:tab:plückercoordinates, we obtain that , while tropicalizes to an inner member of given by and tropicalizes to the degenerate representative of with . In this case, we cannot obtain any of the other lines as limits of the families as .
References
- [1] Tristram Bogart - Eric Katz, Obstructions to lifting tropical curves in surfaces in 3-space, SIAM J. Discrete Math. 26, no. 3, 1050–1067. 14T05 (52B20) (2012).
- [2] Erwan Brugallé - Kristin Shaw, Obstructions to approximating tropical curves in surfaces via intersection theory, Canad. J. Math. 67 no. 3 (2015), 527–572.
- [3] Michela Brundu - Alessandro Logar, Parametrization of the orbits of cubic surfaces, Transformation Groups 3 no. 3 (1998), 209–239.
- [4] Arthur Cayley, On the triple tangent planes of surfaces of the third order, Cambridge and Dublin Math. J. 4 (1849), 118–138.
- [5] Maria Angelica Cueto - Anand Deopurkar, Anticanonical tropical cubic del Pezzos contain exactly 27 lines, arXiv:1906.08196, 2019.
- [6] Ewgenij Gawrilow - Michael Joswig, polymake: a framework for analyzing convex polytopes, Polytopes—combinatorics and computation (Oberwolfach, 1997), DMV Sem., vol. 29, Birkhäuser, Basel, 2000, pp. 43–73.
- [7] Alheydis Geiger, Tropical Cubic Surfaces - Enumeration and Lines, Master’s Thesis, University of Tübingen, to appear soon.
- [8] Alheydis Geiger, Realisability of infinite families of tropical lines on general smooth tropical cubic surfaces, Master’s Thesis, University of Warwick, 2018.
- [9] Simon Hampe, a-tint: A polymake extension for algorithmic tropical intersection theory, European Journal of Combinatorics 36 (2014), 579 – 607.
- [10] Simon Hampe - Michael Joswig, Tropical computations in polymake, Algorithmic and experimental methods in algebra, geometry, and number theory, Springer, Cham, 2017, pp. 361–385.
- [11] Michael Joswig - Marta Panizzut - Bernd Sturmfels, The Schläfli Fan, arXiv:1905.11951, 2019.
- [12] Avinash Kulkarni, GitHub, Brundu-Logar.m, https://github.com/a-kulkarn/cubic-surfaces, 2019-09-02.
- [13] Diane Maclagan - Bernd Sturmfels, Introduction to Tropical Geometry, Providence, Rhode Island : American Mathematical Society, 2015.
- [14] Marta Panizzut - Emre Can Sertöz - Bernd Sturmfels, An Octanomial Model for Cubic Surfaces, arXiv:1908.06106, 2019.
- [15] Marta Panizzut - Magnus Dehli Vigeland, Tropical lines on cubic surfaces, arXiv:math.AG/0708.3847v2, 2019.
- [16] George Salmon, On the triple tangent planes to a surface of the third order, Cambridge and Dublin Math. J. 4 (1849), 252–260.
- [17] Emre Sertoz, GitHub, blowdown.mag, https://github.com/emresertoz/pAdicCubicSurface, 2019-09-08.
- [18] Bernd Sturmfels - Kristian Ranestad, Twenty-seven questions about the cubic surface, arXiv:1912.07347, 2019.
- [19] Magnus Dehli Vigeland, Tropical lines on smooth tropical surfaces, arXiv:math.AG/0708.3847, 2007.
- [20] Magnus Dehli Vigeland, Smooth tropical surfaces with infinitely many tropical lines, Ark. Mat., Volume 48, Number 1, 177-206. 0 (2010).