On Regularization of Gradient Descent,
Layer Imbalance and Flat Minima
Abstract
We analyze the training dynamics for deep linear networks using a new metric – layer imbalance – which defines the flatness of a solution. We demonstrate that different regularization methods, such as weight decay or noise data augmentation, behave in a similar way. Training has two distinct phases: 1) ‘optimization’ and 2) ‘regularization’. First, during the optimization phase, the loss function monotonically decreases, and the trajectory goes toward a minima manifold. Then, during the regularization phase, the layer imbalance decreases, and the trajectory goes along the minima manifold toward a flat area. Finally, we extend the analysis for stochastic gradient descent and show that SGD works similarly to noise regularization.
1 Introduction
In this paper, we analyze regularization methods used for training of deep neural networks. To understand how regularization like weight decay and noise data augmentation work, we study gradient descent (GD) dynamics for deep linear networks (DLNs). We study deep networks with scalar layers to exclude factors related to over-parameterization and to focus on factors specific to deep models. Our analysis is based on the concept of flat minima [5]. We call a region in weight space flat, if each solution from that region has a similar small loss. We show that minima flatness is related to a new metric, layer imbalance, which measures the difference between the norm of network layers. Next, we analyze layer imbalance dynamics of gradient descent (GD) for DLNs using a trajectory-based approach [10].
With these tools, we prove the following results:
-
1.
Standard regularization methods such as weight decay and noise data augmentation, decrease layer imbalance during training and drive trajectory toward flat minima.
-
2.
Training for GD with regularization has two distinct phases: (1) ‘optimization’ and (2) ‘regularization’. During the optimization phase, the loss monotonically decreases, and the trajectory goes toward minima manifold. During the regularization phase, layer imbalance decreases and the trajectory goes along minima manifold toward flat area.
-
3.
Stochastic Gradient Descent (SGD) works similarly to implicit noise regularization.
2 Linear neural networks
We begin with a linear regression with mean squared error on scalar samples :
| (1) |
Let’s center and normalize the training dataset in the following way:
| (2) |
The solution for this normalized linear regression is .
Next, let’s replace with a linear network with scalar layers :
| (3) |
Denote . The loss function for the new problem is:
Now the loss is a non-linear (and non-convex) function with respect to the weights . For the normalized dataset (2), network training is equivalent to the following problem:
| (4) |
Such linear networks with depth-2 have been studied in Baldi and Hornik [2], who showed that all minima for the problem (4) are global and that all other critical points are saddles.
2.1 Flat minima
Following Hochreiter et al [5], we are interested in flat minima – “a region in weight space with the property that each weight from that region has similar small error". In contrast, sharp minima are regions where the function can increase rapidly. Let’s compute the loss gradient :
| (5) |
Here we denote for brevity. The minima of loss are located on hyperbola (Fig. 1). Our interest in flat minima is related to training robustness. Training in the flat area is more stable than in the sharp area: the gradient vanishes if is very large, and the gradient explodes if is very small.
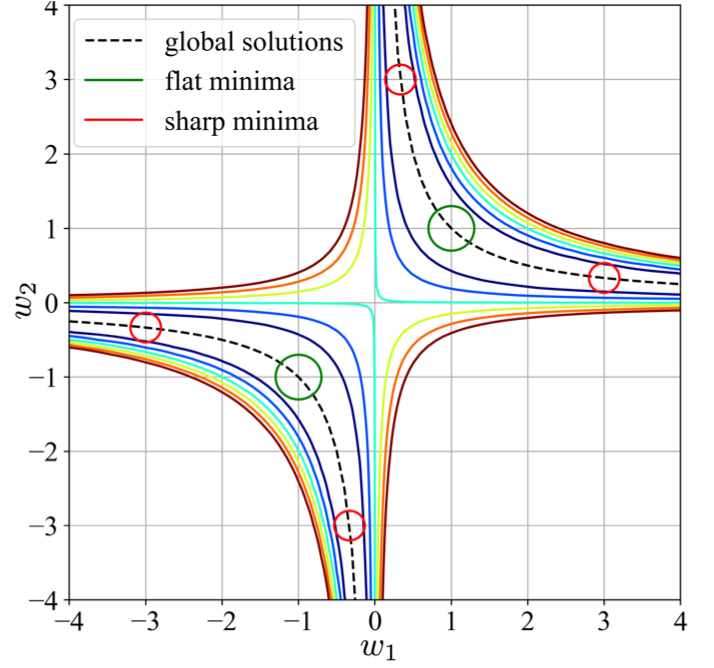
It was suggested by Hochreiter et al [6] that flat minima have smaller generalization errors than sharp minima. Keskar et al. [7] observed that large-batch training tends to converge towards a sharp minima with a significant number of large positive eigenvalues of Hessian. They suggested that sharp minima generalize worse than flat minima, which have smaller eigenvalues. In contrast, Dinh et al. [4] argued that flatness of minima can’t be directly applied to explain generalization; since both flat and sharp minima represent the same function, they perform equally on a validation set.
The question of how minima flatness is related to good generalization is out of scope of this paper.
2.2 Layer imbalance
In this section we define a new metric related to the flatness of the minimizer – layer imbalance.
Dinh [4] showed that minima flatness is defined by the largest eigenvalue of Hessian :
The eigenvalues of the Hessian are . Minima close to the axes are sharp. Minima close to the origin are flat. Note that flat minima are balanced: for all layers.
3 Implicit regularization for gradient descent
In this section, we explore the training dynamics for continuous and discrete gradient descent.
3.1 Gradient descent: convergence analysis
We start with an analysis of training dynamics for continuous GD. By taking a time limit for gradient descent: , we obtain the following DEs [10]:
| (7) |
For continuous GD, the loss function monotonically decreases:
The trajectory for continuous GD is hyperbola: const (see Fig. 2(a)) [10] . The layer imbalance remains constant during training. So if training starts close to the origin, then a final point will also have a small layer imbalance and a minimum will be flat.
Let’s turn from continuous to regular gradient descent:111We omit in the right part for brevity, so means .
| (8) |
We would like to find conditions, which would guarantee that the loss monotonically decreases. For any fixed learning rate, one can find a point , such that the loss will increase after the GD step.222For example, consider the network with 2 layers. The loss after GD step is: For any fixed , one can find with and large enough to make , and therefore the loss will increase: . But we can define an adaptive learning rate which guarantees that the loss decreases.
Theorem 3.1.
Consider discrete GD (Eq. 8). Assume that . If we define an adaptive learning rate , then the loss monotonically converges to 0 with a linear rate.
Proof.
Let’s estimate the loss change for a gradient descent step:
Here is a series with :
Consider the factor . To prove that , we consider two cases.
CASE 1: . In this case, the series can be written as:
where is:
So on the one hand: .
On the other hand: .
CASE 2: . In the series , all terms are now positive. Since , we have that .
On the one hand: .
On the other hand: .
To conclude, in CASE 1 we prove that and in CASE 2 that .
Since , the loss monotonically converges to 0 with rate . ∎
3.2 Gradient descent: implicit regularization
Theorem 3.2.
Consider discrete GD (Eq. 8). Assume that . If we define an adaptive learning rate , then the layer imbalance monotonically decreases.
Proof.
Let’s compute the layer imbalance for the layers and after one GD step:
On the one hand, the factor .
On the other hand:
So and . This guarantees that the layer imbalance decreases. ∎
Note. We proved only that the layer imbalance decreases, but not that converges to . The layer imbalance may stay large, if the loss too fast or if , so the factor . To make the layer imbalance , we should keep the loss in certain range, e.g. . For this, we could increase the learning rate if the loss becomes too small, and decrease learning rate if loss becomes large.
4 Explicit regularization
In this section, we prove that regularization methods, such as weight decay, noise data augmentation, and continuous dropout, decrease the layer imbalance.
4.1 Training with weight decay
As before, we consider the gradient descent for linear network with layers. Let’s add the weight decay (WD) term to the loss: .
The continuous GD with weight decay is described by the following DEs:
| (9) |
Accordingly, the loss dynamics for continuous GD with weight decay is:
The loss decreases when , outside the weight decay band: . The width of this band is controlled by the weight decay .
We can divide GD training with weight decay into two phases: (1) optimization and (2) regularization. During the first phase, the loss decreases until the trajectory gets into the WD-band. During the second phase, the loss can oscillate, but the trajectory stays inside the WD-band (Fig. 2(b)) and goes toward a flat minima area. The layer imbalance monotonically decreases:
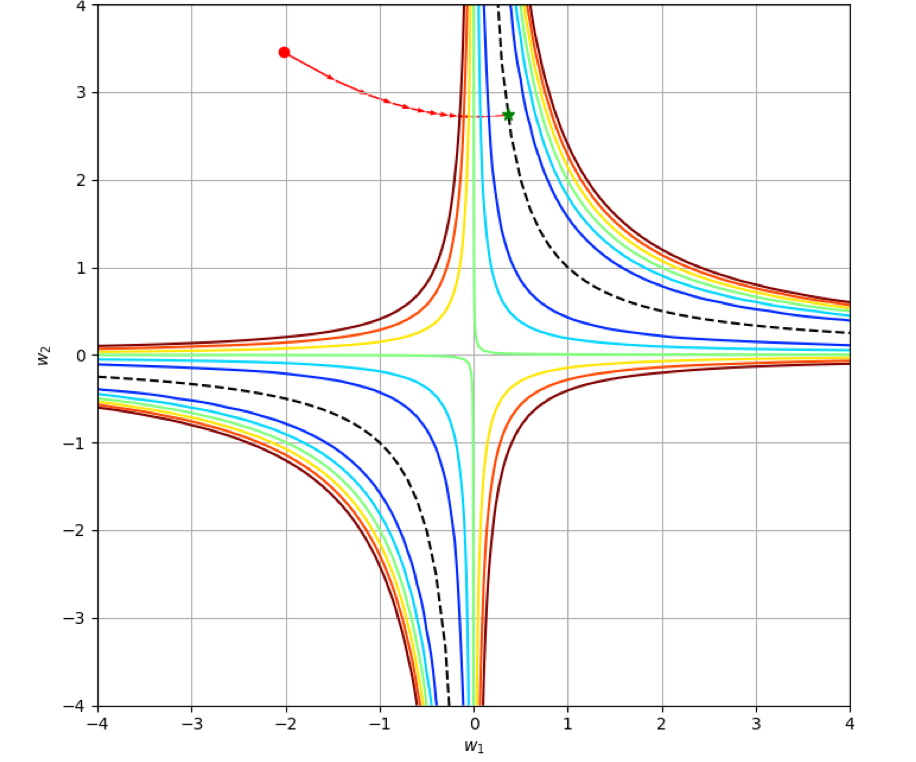
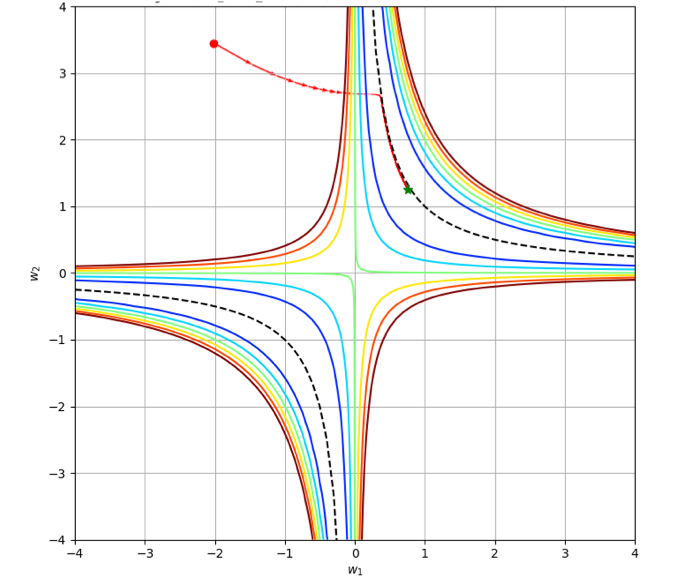
4.2 Training with noise augmentation
Bishop [3] showed that for shallow networks, training with noise is equivalent to Tikhonov regularization. We extend this result to DLNs.
Let’s augment the training data with noise: , where the noise has mean and is bounded: . The DLN with noise augmentation can be written in the following form:
| (10) |
This model also describes continuous dropout [11] when layer outputs are multiplied with the noise: . This model can be also used for continuous drop-connect [8, 12] when the noise is applied to weights: .
The GD with noise augmentation is described by the following stochastic DEs:
Let’s consider loss dynamics:
The loss decreases while the factor , outside of the noise band . The training trajectory is the hyperbola const. When the trajectory gets inside the noise band, it oscillates around the minima manifold, but the layer imbalance remains constant for continuous GD.
Consider now discrete GD with noise augmentation:
| (11) |
For discrete GD, noise augmentation works similarly to weight decay. Training has two phases: (1) optimization and (2) regularization (Fig. 2(c)). During the optimization phase, the loss decreases until the trajectory hits the noise band. Next, the trajectory oscillates inside the noise band, and the layer imbalance decreases. The noise variance defines the band width, similarly to the weight decay .
Theorem 4.1.
Consider discrete GD with noise augmentation (Eq. 11). Assume that the noise has 0-mean and is bounded: . If we define the adaptive learning rate , then the layer imbalance monotonically decreases inside the noise band .
Proof.
Let’s estimate the layer imbalance:
On the one hand, the factor .
On the other hand:
Taking makes , which proves that the layer imbalance decreases. ∎
Note. We can prove that the layer imbalance if we also assume that all layers are uniformly bounded . This implies that there is such that for all the adaptive learning rate , and we can prove that the expectation :
This proves that the layer imbalance with rate .
5 SGD noise as implicit regularization
In this section, we show that SGD works as implicit noise regularization, and that the layer imbalance converges to . As before, we train a DLN with loss on a normalized dataset with samples :
A stochastic gradient for a batch with samples is:
If batch size , then terms and .
So we can write the stochastic gradient in the following form:
The factor works as noise data augmentation, and the term works as label noise. Both and have -mean. When loss is small, we can combine both components into one SGD noise term: . SGD noise has -mean. We assume that SGD noise variance depends on batch size in the following way: . The trajectory for continuous SGD is described by the stochastic DEs:
Let’s start with loss analysis:
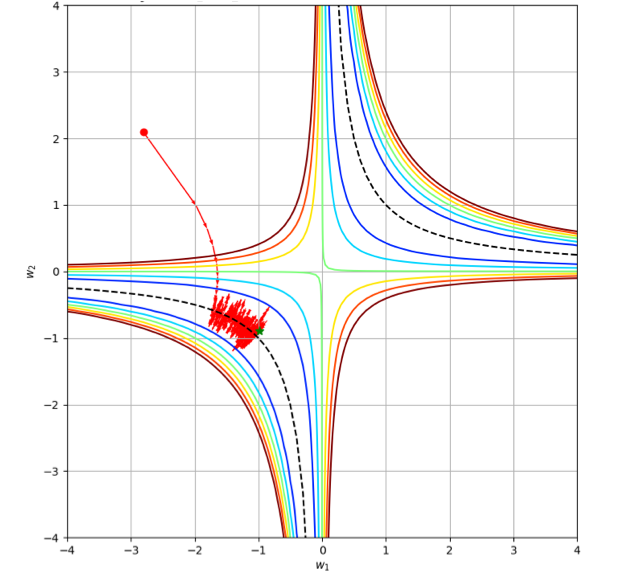
For continuous SGD, the loss decreases anywhere except in the SGD noise band: . The band width depends on : the smaller the batch, the wider the band. The SGD training consists of two parts. First, the loss decreases until the trajectory hits the SGD-noise band. Then the trajectory oscillates inside the noise band. The layer imbalance remains constant for continuous SGD.
Similarly to the noise augmentation, the layer imbalance decreases for discrete SGD:
| (12) |
Theorem 5.1.
Consider discrete SGD (Eq. 12). Assume that , and that SGD noise satisfies . If we define the adaptive learning rate , then the layer imbalance monotonically decreases.
Proof.
Let’s estimate the layer imbalance:
On the one hand, the factor . On the other hand:
Setting makes , which completes the proof. ∎
The layer imbalance at a rate proportional to the variance of SGD noise. It was observed by Keskar et al. [7] that SGD training with a large batch leads to sharp solutions, which generalize worse than solutions obtained with a smaller batch. This fact directly follows from Theorem 5.1. The layer imbalance decreases at a rate . When a batch size increases, , the variance of SGD-noise decreases as . One can compensate for smaller SGD noise with additional generalization: data augmentation, weight decay, dropout, etc.
6 Discussion
In this work, we explore dynamics for gradient descent training of deep linear networks. Using the layer imbalance metric, we analyze how regularization methods such as -regularization, noise data augmentation, dropout, etc, affect training dynamics. We show that for all these methods the training has two distinct phases: optimization and regularization. During the optimization phase, the training trajectory goes from an initial point toward minima manifold, and loss monotonically decreases. During the regularization phase, the trajectory goes along minima manifold toward flat minima, and the layer imbalance monotonically decreases. We derive an analytical proof that noise augmentation and continuous dropout work similarly to -regularization. Finally, we show that SGD behaves in the same way as gradient descent with noise regularization.
This work provides an analysis of regularization for scalar linear networks. We leave the question of how regularization works for over-parameterized nonlinear networks for future research. The work also gives a few interesting insights into training dynamics, which can lead to new algorithms for large batch training, new learning rate policies, etc.
Acknowledgments
We would like to thank Vitaly Lavrukhin, Nadav Cohen and Daniel Soudry for the valuable feedback.
References
- Arora et al. [2019] S. Arora, N. Golowich, N. Cohen, and W. Hu. A convergence analysis of gradient descent for deep linear neural networks. In ICLR, 2019.
- Baldi and Hornik [1989] P. Baldi and K. Hornik. Neural networks and principal component analysis: Learning from examples without local minima. In Neural Networks 2.1, page 53–58, 1989.
- Bishop [1995] C. M. Bishop. Training with noise is equivalent to Tikhonov regularization. Neural Computation, 7:108–116., 1995.
- Dinh et al. [2017] Laurent Dinh, Razvan Pascanu, Samy Bengio, and Yoshua Bengio. Sharp minima can generalize for deep nets. In ICML, 2017.
- Hochreiter and Schmidhuber [1994a] S. Hochreiter and J. Schmidhuber. Simplifying neural nets by discovering flat minima. In NIPS, 1994a.
- Hochreiter and Schmidhuber [1994b] S. Hochreiter and J. Schmidhuber. Flat minima search for discovering simple nets, technical report fki-200-94. Technical report, Fakultat fur Informatik, H2, Technische Universitat Munchen, 1994b.
- Keskar et al. [2016] N. S. Keskar, D. Mudigere, J. Nocedal, M. Smelyanskiy, and P. T. P. Tang. On large-batch training for deep learning: generalization gap and sharp minima. In ICLR, 2016.
- Kingma et al. [2015] D. Kingma, T. Salimans, and M. Welling. Variational dropout and the local reparameterization trick. In NIPS, 2015.
- Neyshabur et al. [2015] Behnam Neyshabur, Ruslan Salakhutdinov, and Nathan Srebro. Path-sgd: Path-normalized optimization in deep neural networks. In NIPS, page 2422–2430, 2015.
- Saxe et al. [2013] Andrew M. Saxe, James L. McClelland, and Surya Ganguli. Exact solutions to the nonlinear dynamics of learning in deep linear neural network. In ICLR, 2013.
- Srivastava et al. [2014] N. Srivastava, G. E. Hinton, A. Krizhevsky, I. Sutskever, and R. Salakhutdinov. Dropout: a simple way to prevent neural networks from overfitting. Journal of Machine Learning Research, 2014.
- Wan et al. [2013] Li Wan, Matthew Zeiler, Sixin Zhang, Yann Le Cun, and Rob Fergus. Regularization of neural networks using dropconnect. In ICML, 2013.