On restrictions of balanced 2-interval graphs
Abstract
The class of 2-interval graphs has been introduced for modelling scheduling and allocation problems, and more recently for specific bioinformatic problems. Some of those applications imply restrictions on the 2-interval graphs, and justify the introduction of a hierarchy of subclasses of 2-interval graphs that generalize line graphs: balanced 2-interval graphs, unit 2-interval graphs, and (,)-interval graphs. We provide instances that show that all the inclusions are strict. We extend the NP-completeness proof of recognizing 2-interval graphs to the recognition of balanced 2-interval graphs. Finally we give hints on the complexity of unit 2-interval graphs recognition, by studying relationships with other graph classes: proper circular-arc, quasi-line graphs, -free graphs, …
Keywords: 2-interval graphs, graph classes, line graphs, quasi-line graphs, claw-free graphs, circular interval graphs, proper circular-arc graphs, bioinformatics, scheduling.
1 2-interval graphs and restrictions
The interval number of a graph, and the classes of -interval graphs have been introduced as a generalization of the class of interval graphs by McGuigan [McG77] in the context of scheduling and allocation problems. Recently, bioinformatics problems have renewed interest in the class of 2-interval graphs (each vertex is associated to a pair of disjoint intervals and edges denote intersection between two such pairs). Indeed, a pair of intervals can model two associated tasks in scheduling [BYHN+06], but also two similar segments of DNA in the context of DNA comparison [JMT92], or two complementary segments of RNA for RNA secondary structure prediction and comparison [Via04].
 |
 |
 |
| (a) | (b) | (c) |
RNA (ribonucleic acid) are polymers of nucleotides linked in a chain through phosphodiester bonds. Unlike DNA, RNAs are usually single stranded, but many RNA molecules have secondary structure in which intramolecular loops are formed by complementary base pairing. RNA secondary structure is generally divided into helices (contiguous base pairs), and various kinds of loops (unpaired nucleotides surrounded by helices). The structural stability and function of non-coding RNA (ncRNA) genes are largely determined by the formation of stable secondary structures through complementary bases, and hence ncRNA genes across different species are most similar in the pattern of nucleotide complementarity rather than in the genomic sequence. This motivates the use of 2-intervals for modelling RNA secondary structures: each helix of the structure is modeled by a 2-interval. Moreover, the fact that these 2-intervals are usually required to be disjoint in the structure naturally suggests the use of 2-interval graphs. Furthermore, aiming at better modelling RNA secondary structures, it was suggested in [CHLV05] to focus on balanced 2-interval sets (each 2-interval is composed of two equal length intervals) and their associated intersection graphs referred as balanced 2-interval graphs. Indeed, helices in RNA secondary structures are most of the time composed of equal length contiguous base pairs parts. To the best of our knowledge, nothing is known on the class of balanced 2-interval graphs.
Sharper restrictions have also been introduced in scheduling, where it is possible to consider tasks which all have the same duration, that is 2-interval whose intervals have the same length [BYHN+06, Kar05]. This motivates the study of the classes of unit 2-interval graphs, and -interval graphs. In this paper, we consider these subclasses of interval graphs, and in particular we address the problem of recognizing them.
A graph of order is a 2-interval graph if it is the intersection graph of a set of unions of two disjoint intervals on the real line, that is each vertex corresponds to a union of two disjoint intervals , ( for “left” and for “right”), and there is an edge between and iff . Note that for the sake of simplicity we use the same letter to denote a vertex and its corresponding 2-interval. A set of 2-intervals corresponding to a graph is called a realization of . The set of all intervals, , is called the ground set of (or the ground set of ).
The class of 2-interval graphs is a generalization of interval graphs, and also contains all circular-arc graphs (intersection graphs of arcs of a circle), outerplanar graphs (have a planar embedding with all vertices around one of the faces [KW99]), cubic graphs (maximum degree 3 [GW80]), and line graphs (intersection graphs of edges of a graph).
Unfortunately, most classical graph combinatorial problems turn out to be NP-complete for 2-interval graphs: recognition [WS84], maximum independent set [BNR96, Via01], coloration [Via01], …Surprisingly enough, the complexity of the maximum clique problem for 2-interval graphs is still open (although it has been recently proven to be NP-complete for 3-interval graphs [BHLR07]).
For practical application, restricted 2-interval graphs are needed. A 2-interval graph is said to be balanced if it has a 2-interval realization in which each 2-interval is composed of two intervals of the same length [CHLV05], unit if it has a 2-interval realization in which all intervals of the ground set have length 1 [BFV04], and is called a -interval graph if it has a 2-interval realization in which all intervals of the ground set are open, have integer endpoints, and length [BYHN+06, Kar05]. In the following sections, we will study those restrictions of 2-interval graphs, and their position in the hierarchy of graph classes illustrated in Figure 2.
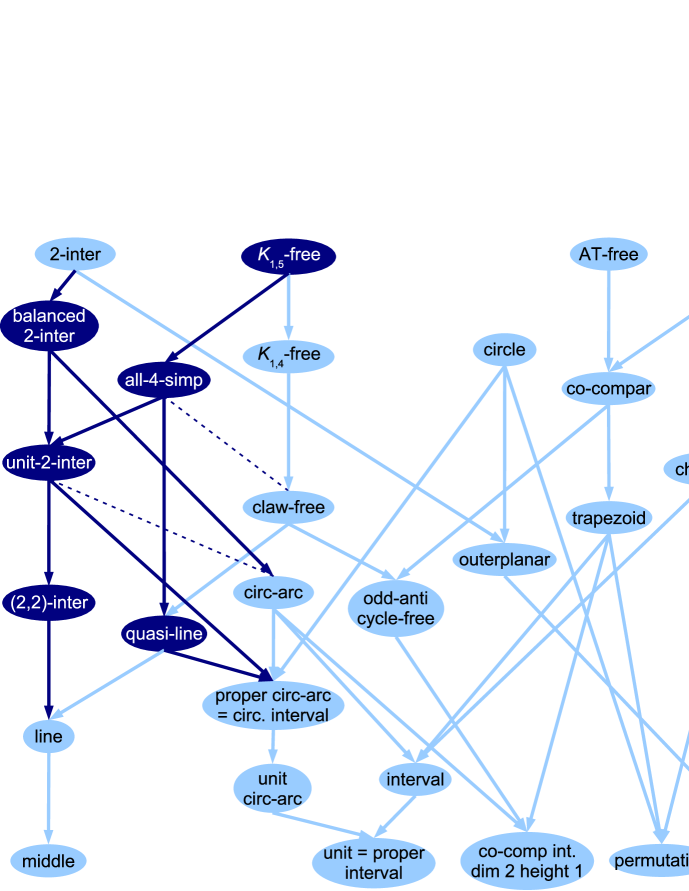
Note that all -interval graphs are unit 2-interval graphs, and that all unit 2-interval graphs are balanced 2-interval graphs. We can also notice that -interval graphs are exactly line graphs: each interval of length 1 of the ground set can be considered as the vertex of a root graph and each 2-interval as an edge in the root graph. This implies for example that the coloration problem is also NP-complete for -interval graphs and wider classes of graphs. It is also known that the complexity of the maximum independent set problem is NP-complete on -interval graphs [BNR96]. Recognition of -union graphs, a related class (restriction of multitrack interval graphs), was also recently proven NP-complete [HK06].
2 Useful gadgets for 2-interval graphs and restrictions
For proving hardness of recognizing 2-interval graphs, West and Shmoys considered in [WS84] the complete bipartite graph as a useful 2-interval gadget. Indeed, all realizations of this graph are contiguous, that is, for any realization, the union of all intervals in its ground set is an interval. Thus, by putting edges between some vertices of a and another vertex , we can force one interval of the 2-interval (or just one extremity of this interval) to be blocked inside the realization of . It is not difficult to see that has a balanced 2-interval realization, for example the one in Figure 3.
 |
 |
 |
| (a) | (b) | (c) |
However, is not a unit 2-interval graph. Indeed, each 2-interval corresponding to a degree 5 vertex intersect disjoint 2-intervals, and hence one of or intersect at least intervals, which is impossible for unit intervals. Therefore, we introduce the new gadget which is a -interval graph with only contiguous realizations.
 |
 |
 |
| (a) | (b) | (c) |
Property 1.
Any 2-interval realization of is contiguous.
Proof.
Write the graph . To study all possible realizations of , let us study all possible realizations of .
As 2-intervals , , and are disjoints, their ground set is a set of eight disjoint intervals. The ground set of , and is a set of six disjoint intervals. Let be the number of intervals of intersecting intervals of . We have directly:
| (1) |
As there are 12 edges in which is bipartite, we also have:
| (2) |
Finally, to build a realization of from a realization of , one must place so as to intersect three disjoint intervals of . Thus one of the intervals of intersects at least two intervals and () of . So there is “a hole between those two intervals”, for example , which is included in one of the intervals of . So we notice that has to fill one of the seven holes of . Thus, the intervals of can not fill more than six holes, and the observation that an interval intersecting consecutive intervals (for ) fills holes, we get:
| (3) |
Equations 1, 2 and 3 are necessary for any valid realization of which gives a valid realization of .
Let’s suppose by contradiction that the union of all intervals of the ground set of is not an interval. Then there is a hole, that is an interval included in the covering interval of , which intersect no . We proceed like for equation 3, with the constraint that another hole cannot be filled by the intervals of , so we get instead:
| (4) |
3 Balanced 2-interval graphs
We show in this section that the class of balanced 2-interval graphs is strictly included in the class of 2-interval graphs, and strictly contains circular-arc graphs. Moreover, we prove that recognizing balanced 2-interval graphs is as hard as recognizing (general) 2-interval graphs.
Property 2.
The class of balanced 2-interval graphs is strictly included in the class of 2-interval graphs.
Proof.
We build a 2-interval graph that has no balanced 2-interval realization. Let’s consider a chain of gadgets (introduced in previous section) to which we add three vertices , , and as illustrated in Figure 5.
| (a) |
 |
| (b) |
 |
In any realization, the presence of holes showed by crosses in the Figure gives the following inequalities for any realization: , , and (or if the realization of the chain of appears in the symmetrical order: , , and ). If this realization was balanced, then we would have (or for the symmetrical case: ) : impossible! So this graph has no balanced 2-interval realization although it has a 2-interval generalization. ∎
Theorem 1.
Recognizing balanced 2-interval graphs is an NP-complete problem.
Proof.
We just adapt the proof of West and Shmoys [WS84, GW95]. The problem of determining if there is a Hamiltonian cycle in a 3-regular triangle-free graph is proven NP-complete, by reduction from the more general problem without the no triangle restriction. So we reduce the problem of Hamiltonian cycle in a 3-regular triangle-free graph to balanced 2-interval recognition.
Let be a 3-regular triangle-free graph. We build a graph which has a 2-interval realization (a special one, very specific, called -representation and which we prove to be balanced) iff has a Hamiltonian cycle.
 |
 |
The construction of , illustrated in Figure 6(a) is almost identical to the one by West and Shmoys, so we just prove that has a balanced realization, shown in Figure 6 (b), by computing lengths for each interval to ensure it. All have a balanced realization as shown in section 1 of total length 79, in particular . We can thus affect length 83 to the intervals of . The intervals of the other can have length 3, and their length 79, so through the computation illustrated in Figure 6, intervals of can have length , that is . We dilate until a hole between two consecutive intervals of its can contain an interval of , that is until the hole has length : so after this dilating, has length . Finally if has a Hamiltonian cycle, then we have found a balanced 2-interval realization of of total length . ∎
It is known that circular-arc graphs are 2-interval graphs, they are also balanced 2-interval.
Property 3.
The class of circular-arc graphs is strictly included in the class of balanced 2-interval graphs.
Proof.
The transformation is simple: if we have a circular-arc representation of a graph , then we choose some point of the circle. We partition in , where intersects all the arcs corresponding to vertices of and none of the arcs of the vertices of . Then we cut the circle at point to map it to a line segment: every arc of becomes an interval, and every arc of becomes a 2-interval. To obtain a balanced realization we just cut in half the intervals of to obtain two intervals of equal length for each. And for each 2-interval of , as both intervals are located on one of the extremities of the realization, we can increase the length of the shortest so that it reaches the length of the longest without changing intersections with the other intervals. The inclusion is strict because is a balanced 2-interval graph (as a subgraph of for example) but is not a circular-arc graph (we can find two in , and only one can be realized with a circular-arc representation). ∎
4 Unit 2-interval and (x,x)-interval graphs
Property 4.
Let . The class of -interval graphs is strictly included in the class of -interval graphs.
Proof.
We first prove that an interval graph with a representation where all intervals have length (and integer open bounds) has a representation where all intervals have length .
We use the following algorithm. Let be initialized as the set of all intervals of length , and let be initially the empty set. As long as is not empty, let be the left-most interval of , remove from each interval such that (including ), add to , and translate by +1 all the remaining intervals in . When is empty, the intersection graph of , where all intervals have length is the same as the intersection graph for the original .
We also build for each a -interval graph which is not a -interval graph. We consider the bipartite graph and a perfect matching . We call the graph obtained from with the following transformations, illustrated in Figure 7(a): remove edges of the perfect matching, add four graphs called , , , (for each , we call and the vertices of degree 3), link and , link all to and , link all to and , and finally add a vertex (resp. ) linked to all , , and to two adjacent vertices of (resp. ) of degree 4. We illustrate in Figure 7(b) that has a realization with intervals of length . We can prove by induction on that has no realization with intervals of length : it is rather technical, so we just give the idea. Any realization of forces the block to share an extremity with the block , so each 2-interval has one interval intersecting the other extremity of , and the other intersecting the other extremity of . Then constraints on the position of vertices force their intervals to appear as two “stairways” as shown in Figure 7(b). So must contain extremities of intervals which have to be different, so it must have length .
(a)
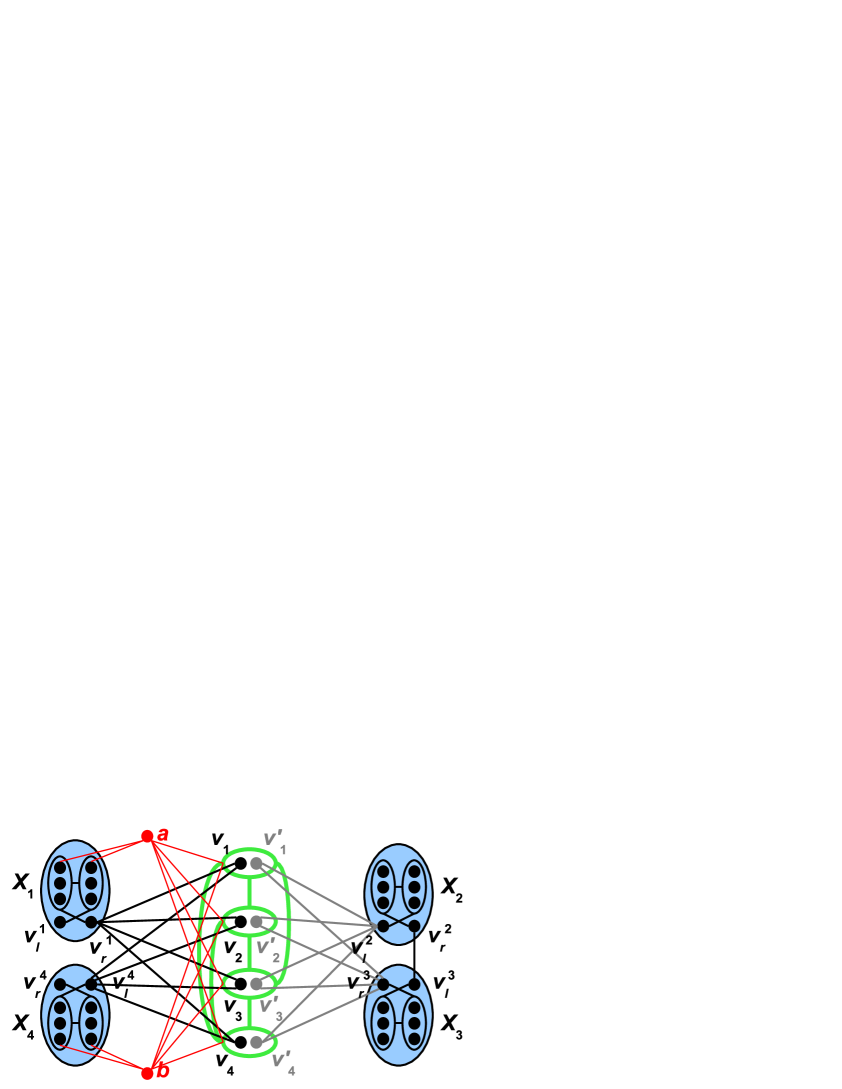
(b)

∎
The complexity of recognizing unit 2-interval graphs and -interval graphs remains open, however the following shows a relationship between those complexities.
Lemma 1.
unit 2-interval graphs-interval graphs.
Proof.
The part is trivial. To prove , let be a unit 2-interval graph. Then it has a realization with 2-intervals, that is intervals of the ground set. So we consider the interval graph of the ground set, which is a unit interval graph. There is a linear time algorithm based on breadth-first search to compute a realization of such a graph where interval endpoints are rational, with denominator [CKN+95]. So by dilating by a factor such a realization, we obtain a realization of where intervals of the ground set have length . ∎
Theorem 2.
If recognizing -interval graphs is polynomial for any integer then recognizing unit 2-interval graphs is polynomial.
5 Investigating the complexity of unit 2-interval graphs
In this section we show that all proper circular-arc graphs (circular-arc graphs such that no arc is included in another in the representation) are unit 2-interval graphs, and we study a class of graphs which generalizes quasi-line graphs and contains unit 2-interval graphs.
Recall that, according to Property 3, circular-arc graphs are balanced 2-interval graphs. However, circular-arc graphs are not necessarily unit 2-interval graphs.
Property 5.
The class of proper circular-arc graphs is strictly included in the class of unit 2-interval graphs.
Proof.
As in the proof of Property 3, we choose a point on the circle of the representation of a proper circular-arc graph , and maps the cut circle into a line segment. We extend the outer extremities of intervals that have been cut so that no interval contains another. Thus we obtain a set of 2-intervals for arcs containing , and a set of intervals for arcs not containing . For each interval of , we add a new interval disjoint of any other to get a 2-interval. If we consider the intersection graph of the ground set of such a representation, it is a proper interval graph. So it is also a unit interval graph [Rob69], which provides a unit 2-interval representation of .
To complete the proof, we notice that the domino (two cycles having an edge in common) is a unit 2-interval graph but not a circular-arc graph. ∎
Quasi-line graphs are those graphs whose vertices are bisimplicial, i.e., the closed neighborhood of each vertex is the union of two cliques. This graph class has been introduced as a generalization of line graphs and a useful subclass of claw-free graphs [Ben81, FFR97, CS05, KR07]. Following the example of quasi-line graphs that generalize line graphs, we introduce here a new class of graphs for generalizing unit 2-interval graphs. Let . A graph is all--simplicial if the neighborhood of each vertex can be partitioned into at most cliques. The class of quasi-line graphs is thus exactly the class of all--simplicial graphs. Notice that this definition is equivalent to the following: in the complement graph of , for each vertex , the vertices that are not in the neighborhood of are -colorable.
Property 6.
The class of unit 2-interval graphs is strictly included in the class of all-4-simplicial graphs.
Proof.
The inclusion is trivial. What is left is to show that the inclusion is strict. Consider the following graph which is all--simplicial but not unit 2-interval: start with the cycle , call its vertices , , add four gadgets called , and for each we connect the vertex to two connected vertices of degree 4 in . This graph is certainly all--simplicial. But if we try to build a 2-interval realization of this graph, then each of the 2-intervals has an interval trapped into the block . So each 2-interval has only one interval to realize the intersections with the other : this is impossible as we have to realize a which has no interval representation. ∎
Property 7.
The class of claw-free graphs is not included in the class of all-4-simplicial graphs.
Proof.
The Kneser Graph is triangle-free, but not 4-colorable [Lov78]. We consider the graph obtained by adding an isolated vertex and then taking the complement graph, i.e., . It is claw-free as is triangle-free. And if it was all--simplicial, then the neighborhood of in , that is , would be a union of at most four cliques, so would be 4-colorable: impossible so this graph is claw-free but not all-4-simplicial. ∎
Property 8.
The class of all--simplicial graphs is strictly included in the class of -free graphs.
Proof.
If a graph contains , then it has a vertex with independent neighbors, and hence is not all--simplicial. The wheel is a simple example of a graph which is -free but in which the center can not have its neighborhood (a ) partitioned into cliques or less. ∎
Unfortunately, all--simplicial graphs do not have a nice structure which could help unit 2-interval graph recognition.
Theorem 3.
Recognizing all--simplicial graphs is NP-complete for .
Proof.
We reduce from the Graph -colorability problem, which is known to be NP-complete for [Kar72]. Let be a graph, and let be the complement graph of to which we add a universal vertex . We claim that is -colorable iff is all--simplicial.
If is -colorable, then the non-neighborhood of any vertex in is -colorable, so the neighborhood of any vertex in is a union of at most cliques. And the neighborhood of is also a union of at most cliques, so is all--simplicial.
Conversely, if is all--simplicial, then in particular the neighborhood of is a union of at most cliques. Let’s partition it into vertex-disjoint cliques . Then, coloring such that two vertices have the same color iff they are in the same leads to a valid -coloring of . ∎
6 Conclusion
Motivated by practical applications in scheduling and computational biology, we focused in this paper on balanced 2-interval graphs and unit 2-intervals graphs. Also, we introduced two natural new classes: -interval graphs and all--simplicial graphs.
We mention here some directions for future works. First, the complexity of recognizing unit 2-interval graphs and -interval graphs remains open. Second, the relationships between quasi-line graphs and subclasses of balanced 2-intervals graphs still have to be investigated. Last, since most problems remains NP-hard for balanced 2-interval graphs, there is thus a natural interest in investigating the complexity and approximation of classical optimization problems on unit 2-interval graphs and -interval graphs.
Acknowledgments
We are grateful to Vincent Limouzy in particular for bringing to our attention the class of quasi-line graphs, and Michael Rao and Michel Habib for useful discussions.
References
- [Ben81] A. Ben Rebea. Étude des stables dans les graphes quasi-adjoints. PhD thesis, Université de Grenoble, 1981.
- [BFV04] G. Blin, G. Fertin, and S. Vialette. New results for the 2-interval pattern problem. In Proceedings of the 15th Symposium on Combinatorial Pattern Matching (CPM’04), 2004.
- [BHLR07] A. Butman, D. Hermelin, M. Lewenstein, and D. Rawitz. Optimization problems in multiple-interval graphs. In Proceedings of the 18th Annual Symposium On Discrete Algorithms (SODA’07), pages 268–277, 2007.
- [BLS+] A. Brandstädt, V. B. Le, T. Szymczak, F. Siegemund, H.N. de Ridder, S. Knorr, M. Rzehak, M. Mowitz, and N. Ryabova. ISGCI: Information System on Graph Class Inclusions. http://wwwteo.informatik.uni-rostock.de/isgci/classes.cgi.
- [BNR96] V. Bafna, B. O. Narayanan, and R. Ravi. Nonoverlapping local alignments (weighted independent sets of axis-parallel rectangles). Discrete Applied Math., 71(1):41–54, 1996.
- [BYHN+06] R. Bar-Yehuda, M. M. Halldórson, J. Naor, H. Shachnai, and I. Shapira. Scheduling split intervals. SIAM Journal on Computing, 36(1):1–15, 2006.
- [CHLV05] M. Crochemore, D. Hermelin, G. M. Landau, and S. Vialette. Approximating the 2-interval pattern problem. In Proceedings of the 13th Annual European Symposium on Algorithms (ESA’05), volume 3669 of LNCS, pages 426–437, 2005.
- [CKN+95] D. G. Corneil, H. Kim, S. Natarajan, S. Olariu, and A. P. Sprague. Simple linear time recognition of unit interval graphs. Information Processing Letters, 55:99–104, 1995.
- [CS05] M. Chudnovsky and P. Seymour. The structure of claw-free graphs. In Surveys in Combinatorics, volume 327 of London. Math. Soc. Lecture Notes, pages 153–172. Cambridge University Press, 2005.
- [FFR97] R. Faudree, E. Flandrin, and Z. Ryjáček. Claw-free graphs - a survey. Discrete Mathematics, 164:87–147, 1997.
- [GW80] J. R. Griggs and D. B. West. Extremal values of the interval number of a graph. SIAM Journal on Algebraic and Discrete Methods, 1:1–7, 1980.
- [GW95] A. Gyárfás and D. B. West. Multitrack interval graphs. Congress Numerantium, 109:109–116, 1995.
- [HK06] M. M. Halldórsson and R. K. Karlsson. Strip graphs: Recognition and scheduling. In Proceedings of the 32nd Workshop on Graph-Theoretic Concepts in Computer Science (WG’06), volume 4271 of LNCS, pages 137–146, 2006.
- [JMT92] D. Joseph, J. Meidanis, and P. Tiwari. Determining DNA sequence similarity using maximum independent set algorithms for interval graphs. In Proceedings of the Third Scandinavian Workshop on Algorithm Theory (SWAT’92), volume 621 of LNCS, pages 326–337, 1992.
- [Kar72] R. M. Karp. Reducibility among combinatorial problems, pages 85–103. Plenum Press, 1972.
- [Kar05] R. Karlsson. A survey of split intervals and related graphs, 2005. Manuscript.
- [KR07] A. King and B. Reed. Bounding in terms of ans for quasi-line graphs, 2007. Article in preparation.
- [KW99] A. V. Kostochka and D. B. West. Every outerplanar graph is the union of two interval graphs. Congress Numerantium, 139:5–8, 1999.
- [Lov78] L. Lovász. Kneser’s conjecture, chromatic number, and homotopy. Journal of Combinatorial Theory Series A, 25:319–324, 1978.
- [McG77] R. McGuigan, 1977. Presentation at NSF-CBMS Conference at Colby College.
- [Rob69] F. S. Roberts. Indifference graphs. In Proof Techniques in Graph Theory, Proceedings of the Second Ann Arbor Graph Theory Conference, pages 139–146, 1969.
- [Via01] S. Vialette. Aspects algorithmiques de la prédiction des structures secondaires d’ARN. PhD thesis, Université Paris 7, 2001.
- [Via04] S. Vialette. On the computational complexity of -interval pattern matching. Theoretical Computer Science, 312(2-3):223–249, 2004.
- [WS84] D. B. West and D. B. Shmoys. Recognizing graphs with fixed interval number is NP-complete. Discrete Applied Math., 8:295–305, 1984.
7 Appendix
Proof of Theorem 1.
Let be a 3-regular triangle-free graph. We build a graph which has a 2-interval realization (a special one, very specific, and which we prove to be balanced) iff has a Hamiltonian cycle.
First we will detail how we build starting from the graph , and adding some vertices, in particular gadgets. The idea is that the edges of will partition into a Hamiltonian cycle and a perfect matching iff all 2-intervals of the realization of can have their left interval realizing the Hamiltonian cycle, and their right interval realizing the perfect matching. A realization with such a placement of the intervals is called an “H-representation” of .
We proceed as illustrated in Figure 6. We choose some vertex of that we call (which will be the “origin” of the Hamiltonian cycle), and the other are called . For each vertex of we link it to a vertex of the of a called (which will block one of the four extremities of the 2-interval ). We link all vertices to a new vertex , which is linked to no except (thus the interval of each intersecting , for , won’t intersect ). We add three , , and : two vertices of the of are linked to , a third one is linked to one vertex of the of , one vertex of the of is linked to , and all vertices of to .
To explain this construction in detail, we study the realization of , if we suppose it is a (balanced) 2-interval graph, and we prove that it leads us to find a Hamiltonian cycle in .
As the realization of and are two contiguous blocks of intervals then one of their extremities must intersect. As is linked to two disjoint vertices of , both intervals of are used to realize those intersections. But one interval of that we call , also has to intersect one vertex of which is not linked to , so intersects the second extremity of the block (the first extremity being occupied by the extremity of ). And as intersects only one interval of , it must be the extremity of . The other interval of is contained in the block , thus can’t intersect neither all the vertices , so all those 2-intervals intersect . And as none of them intersect except , all of them except have an interval contained in , that we call . The other interval of each is linked to a so it has one extremity occupied by , and the other one is free.
Conversely, if has a Hamiltonian cycle, then it is possible to find a -representation, such that all the constraints induced by the edges of are respected, as illustrated with the realization in Figure 6. We have already proved that this realization can be balanced. ∎
Proof of Property 4.
In the following, as we only considering the interval of or located at one extremity of the block , and not the one inside, we will use and to denote those extremity intervals. For each vertex , we call its left interval and its right interval. We do the same for , and call the left extremity of any interval .
We prove by induction that the graph is -interval but not -interval, and that for any unit 2-interval realization, there exists an order such that :
-
•
either and ,
-
•
or the symmetric case: and .
Those two equalities correspond in fact to the “two stairways structure” which
appears in Figure 7.
Base case :
we study all possible unit 2-interval realizations of
to prove that one of the expected inequalities is always true.
We also prove that has no (2,2)-interval realization.
First recall that realizations of subgraphs can only be blocks of contiguous intervals. The edge between and forces the two blocks of and to be contiguous, with intervals and at their extremities. Each 2-interval must intersect both and , so one of its intervals intersects and the other intersects . Thus, one same interval of can not intersect both and which are disjoint, so intersects one interval of (say the one intersecting , the other case being treated symmetrically) and intersects the other one (so, the one intersecting ). Each has to intersect both and , so it has to intersect with its first interval and with the second. But 2-interval must also intersect and which are both disjoint and disjoint to and . So one interval of each must intersect and the other one must intersect .
So we have shown that any unit 2-interval realization of has the following aspect (or the symmetric) : the extremity of the block intersecting all which intersect (or ) which intersects all , which intersect the extremity (or ) which intersects the extremity of (or ), which intersects all , which intersect (or ), which intersects all , which intersect the extremity of .
Now we suppose, by contradiction, that there exists a (2,2)-interval realization of . is an interval of length 2, but one of its two parts of length one has to intersect an element of . The other has to intersect both and . As neither nor can intersect other intervals of , then the first interval of and is the same interval. By proceeding the same way on and , we obtain that the second interval of and is the same interval, so and should correspond to the same 2-interval: it contradicts with the fact that vertices and have a different neighborhood. So has no (2,2)-interval realization.
To obtain the expected inequalities, we have to analyze the possible positions of all and . We only treat the first two inequalities as the second case is symmetric.
Suppose that . As and are non adjacent, then interval is strictly on the left of , so is strictly on the left of . Thus those two intervals do not intersect. But and are adjacent, so and must have intersecting right intervals. But then we have , and the right intervals of and can not intersect. We deduce their left intervals intersect, so .
If we suppose that , we get as well that and . So for any unit 2-interval realization of there exists an order or such that:
-
•
either and ,
-
•
or the symmetric inequalities.
Recursion: suppose that for some , is not -interval but is -interval, and that any -interval realization verifies one of the expected inequalities.
Graph is an induce subgraph of : . So by the induction hypothesis, there exists an order such that for any unit 2-interval realization of :
-
•
either and ,
-
•
or the symmetric case: and .
The position of and remains to be determined. We treat only the case where the first two inequalities are true, as the second case is symmetric.
As and are adjacent, and and are not, then . So we define the following way: is the leftmost interval such that . if there is none, we say . Then we call the permutation defined by:
Then we directly get inequalities:
-
•
-
•
We obtain the expected inequalities by reasoning the same way as in the end of the base case.
So in particular we have and must intersect all those for , but also an interval of which intersects none of the . So it must have length , thus is not a -interval graph
Conclusion: As the base case and the recursion has been proved, expected properties of the graph are true for any . ∎