On the Impossibility of a Perfect Hypervisor
Abstract
We establish a fundamental impossibility result for a perfect hypervisor—one that (1) preserves every observable behavior of any program exactly as on bare metal and (2) adds zero timing or resource overhead.
Within this model we prove two theorems.
(1) Indetectability Theorem. If such a hypervisor existed, no guest-level program, measurement, or timing test could distinguish it from native execution; all traces, outputs, and timings would be identical.
(2) Impossibility Theorem. Despite that theoretical indetectability, a perfect hypervisor cannot exist on any machine with finite computational resources.
These results are architecture-agnostic and extend beyond hypervisors to any virtualization layer—emulators, sandboxes, containers, or runtime-instrumentation frameworks. Together they provide a formal foundation for future work on the principles and limits of virtualization.
Index Terms:
virtualization, hypervisor, virtual machine monitor, impossibility result, timing overhead, detection, nesting, resource constraintsI Introduction
Virtualization underpins much of modern computing, allowing one physical machine to host multiple guest operating systems or processes via a hypervisor, also known as a virtual machine monitor (VMM). Engineers have sought to minimize the overhead and visibility of virtualization using hardware extensions (Intel VT-x [1], AMD-V [2]), paravirtualization, and other optimizations. These efforts have led to considerable improvements but have not closed the gap to the hypothetical perfect hypervisor: one that neither changes observable behavior nor exact timing compared to running on bare metal.
In this paper, we prove two fundamental results regarding this ideal:
-
•
Indetectability of a Perfect Hypervisor: If such a perfect hypervisor existed, it would be impossible for any program to detect its presence, since all execution traces, I/O results, and timing would be identical to those on bare metal.
-
•
Impossibility of a Perfect Hypervisor: No such hypervisor can actually exist on a finite-resource machine, as shown by a contradiction argument involving infinite nesting.
I-A Contributions
-
1.
Perfect Hypervisor Definition. Based on the foundational virtualization framework by Popek and Goldberg [3], we define a hypothetical perfect hypervisor that strictly satisfies two conditions: (1) it preserves every observable behavior of a program exactly as if it were executing on bare metal, and (2) it introduces zero additional timing or resource overhead.
-
2.
We present and prove an Indetectability Theorem showing that, under these strong conditions, the hypothetical perfect hypervisor would be fundamentally undetectable by any algorithmic test.
-
3.
We present and prove an Impossibility Theorem demonstrating that such a perfect hypervisor cannot exist in any physically realizable system with finite resources.
We provide proofs grounded in fundamental principles of computation rather than architectural or technological limitations, highlighting that the impossibility arises inherently at the conceptual level.
I-B Paper Organization
The paper is organized as follows. Section II defines the system model, timing semantics, and the notion of a perfect hypervisor. Section III proves that such a hypervisor would be fundamentally undetectable. Section IV establishes its impossibility under finite-resource constraints. Section V discusses implications for nested and hardware-assisted virtualization. Section VI concludes.
II System Model and Definitions
II-A Machine Model, Execution, and I/O
We assume a physical machine with a finite set of resources: CPU cycles, memory (including cache hierarchy), and I/O devices. Time is discretized into ticks, each representing an indivisible quantum (e.g., a clock cycle or minimal scheduler slice). A bare-metal execution of a program on can thus be represented by a sequence of state transitions
where each step consumes exactly one tick and yields a new system state . These states include the contents of memory, registers, and any relevant I/O buffers.
More formally, a machine state is defined as a tuple:
where:
-
•
is the memory state, modeled as a mapping from memory addresses () to values ().
-
•
is the register state, mapping register identifiers (), including general-purpose registers, special-purpose registers, the program counter, and flags, to values ().
-
•
captures the state of I/O buffers and devices, whenever applicable, including pending operations and device statuses.
Each state transition updates these components deterministically based on the executed instruction or event occurring within that tick.
Each instruction or operation in may also produce observable results, such as output to a display, network packets, or data written to storage. For convenience, we denote all such I/O events collectively as a set of time-stamped outputs , where is the tick at which event occurred.
II-B Hypervisor (Virtual Machine Monitor)
Following the virtualization model of Popek and Goldberg [3], a virtual machine monitor (VMM)—commonly referred to today as a hypervisor—acts as an intermediary layer that presents a virtual machine to the guest program .
Formally, transforms the bare-metal state transitions into transitions that appear identical to a direct execution on physical hardware, but behind the scenes, may intercept privileged instructions, manage memory mappings, handle device I/O, and schedule CPU access.
If itself runs on , the combined sequence of states from the perspective of can be abstractly written as:
Here, each transition may consume some number of machine ticks, depending on how emulates or traps the guest’s requests.
II-C Timing and Overhead: Partial Native Execution
Modern virtualization often executes some instructions natively without trap-and-emulate overhead (e.g., via Intel VT-x, AMD-V). Hence, not all instructions necessarily incur hypervisor overhead. Nonetheless, a perfect hypervisor must ensure that no step—including privileged instructions, memory or device I/O, interrupt handling, etc.—takes longer than it would on bare metal.
Definition 1 (Timing Overhead).
Let be the number of ticks used by program to complete operations on bare metal . Let be the number of ticks used by under hypervisor to complete the same operations. We define the timing overhead as
A hypervisor has zero overhead if and only if
where denotes the space of all computable programs. Equivalently,
Even if some instructions are not executed natively, every instruction and event must preserve exact timing equivalence.
One can also view overhead at the level of individual instructions:
where and are the ticks to run the -th instruction under vs. bare metal, respectively. A perfect hypervisor requires this sum to be zero for every prefix .
II-D Behavioral Equivalence
Definition 2 (Behavioral Equivalence).
A hypervisor provides behaviorally equivalent execution if, for every program and every operation index (), the observable state and the I/O events produced by at step under match exactly those produced when runs on bare metal for steps. Formally, if denotes the system state on bare metal after steps and denotes the hypervisor-based state, then in all observables, and the I/O event history is identical up to step .
II-E Perfect Hypervisor
Definition 3 (Perfect Hypervisor).
In simpler terms, a perfect hypervisor never changes either the time it takes to run up to any step or the external outputs produced by at each step.
II-F Observationally Identical Execution.
Based on Definitions 1 and 2, we say that the execution of a program under a hypervisor is observationally identical to its execution on bare metal if, for every step , the externally visible system state equals , and the time to reach that state matches . This means that observes the same outputs, timings, and side effects under as it would on physical hardware. Consequently, if a hypervisor is perfect (Definition 3), it guarantees observationally identical execution for all programs and all execution prefixes.
III Indetectability of a Perfect Hypervisor
Theorem 1 (Indetectability Theorem).
If is a perfect hypervisor on , then for any detection algorithm executing inside the virtual machine context exposed by , the execution of under is observationally identical to the execution of on bare metal. Consequently, no such detector can reliably distinguish from .
III-A Proof
Let be an arbitrary detection algorithm—or “detector”—executing entirely inside the virtual-machine context provided by . Its goal is to decide whether it is running on bare metal or under a hypervisor. By assumption of a perfect hypervisor, we have two primary invariants: behavioral equivalence and zero timing overhead. Formally,
where
-
•
is the externally visible state of (including any guest-accessible side-channel measurements) at step when running under ;
-
•
is the externally visible state of at the same step when running directly on the bare-metal machine ; and
-
•
and denote the cumulative ticks (or other resource metrics) observable at step in the respective runs.
Because these two runs are observationally equivalent at every step , the entire trace of externally visible states, outputs, and timings accessible to is identical in both environments. Formally, let
and
be the full execution traces (states and timings) of under and on bare metal, respectively. From the above invariants, we have .
Hence, for any function
that might compute from its observable execution trace (including any final decision bit “hypervisor vs. bare metal”), it follows that
In other words, must return the same value in both runs because is evaluated on identical input data in each environment.
Therefore, ’s outcome does not differ between bare metal and hypervisor execution, implying it cannot exceed random guessing in determining whether is present. Thus, no detection algorithm can reliably distinguish from .
A perfect hypervisor is fundamentally undetectable by any guest-level algorithm.
∎
Remark 1.
This result implies that any approach to detect the presence of a “perfect” hypervisor must fail with probability at least as high as random guessing. Such a hypervisor would be intrinsically undetectable, as it offers no measurable or inferable artifact to the guest environment.
IV Impossibility of a Perfect Hypervisor on a Finite-Resource Machine
Theorem 2 (No Perfect Hypervisor on Finite Resources).
IV-A Proof
IV-A1 Step 1: Assume Existence of a Perfect Hypervisor
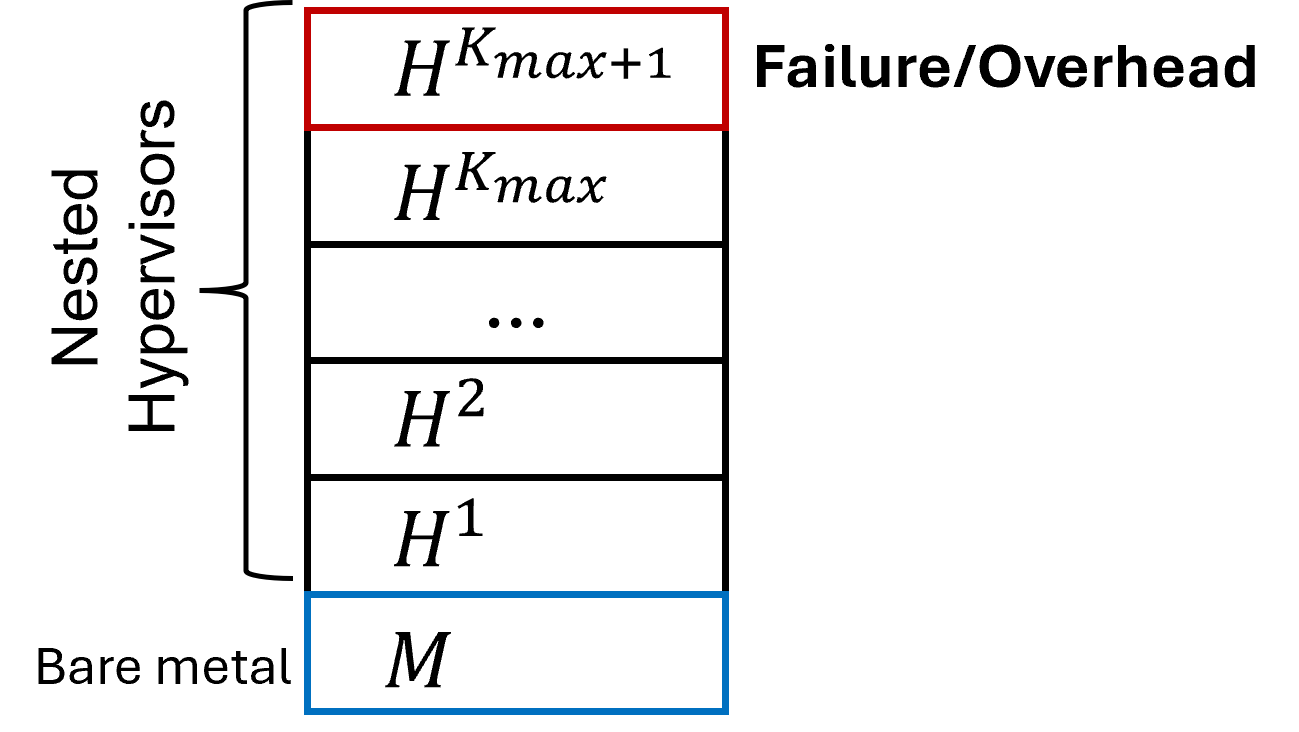
Assumption. Suppose, for contradiction, that there is a hypervisor on satisfying both conditions in Definition 3 for any program . We will show that such cannot coexist with the finiteness of ’s resources.
IV-A2 Step 2: Arbitrary Self-Nesting
Rationale. Under condition (1), is behaviorally indistinguishable from . Hence, if a guest program attempts to install another copy of (i.e., run the hypervisor code within itself), must permit it exactly as if running on real hardware. Refusal to do so would be observable to the guest, violating behavioral equivalence.
Construction. Define , and for each integer , let be an instance of the same hypervisor code running as a guest under . By condition (2) of (3) (Zero Timing Overhead), each also perceives no additional latency or scheduling delay. Formally, for every and every step :
Thus, we can nest arbitrarily many times without introducing any detectable difference compared to bare metal.
IV-A3 Step 3: Contradiction from Finite Resources
Because is explicitly stated to have finite memory and CPU capacity, the possibility of creating infinitely many nested hypervisors leads to a direct conflict (Figure 1).
We make this precise below:
-
a)
Positive Resource Consumption. Every hypervisor instance, however small or optimized, consumes a strictly positive amount of memory and other hardware resources (e.g., control structures, scheduling overhead for intercepts, device virtualization data). Let represent the memory footprint of . The total memory consumed by nested instances is:
where is a lower bound on ’s minimal memory usage. Since has finite memory , there must be some integer beyond which the machine cannot instantiate any additional hypervisor layer (i.e., ).
-
b)
Observable Failure or Resource Multiplexing Overhead. Once we reach nesting depth , the system faces two outcomes, each contradicting one of the perfectness properties in (3):
-
•
Case 1: Failure or Refusal to Launch. If the new hypervisor instance cannot be created due to memory exhaustion, then the guest sees an error or denial absent on true hardware (which would manifest a hardware fault in a specific manner that cannot perfectly mask). This violates the behavioral equivalence requirement (1).
-
•
Case 2: Attempted “Compression,” “Reallocation,”, “Simulation,” etc. Suppose tries to mask the resource exhaustion by strategies such as compressing memory, reallocating CPU time, or by simulating the appearance of a successful launch without actually instantiating it. In all cases, performs additional internal operations that do not occur on bare metal in response to the same guest instructions.
-
–
Timing overhead is introduced. Compression or emulation of nested behavior, as well any other algorithm, must consume CPU cycles or I/O bandwidth. If experiences even small delays (e.g., longer TLB misses, slower I/O), then condition (2) in (3) is violated:
-
–
Visible state changes occur. To mask the presence of , must intercept control transfers, emulate system calls, or simulate internal VM state. These introduce inconsistencies — e.g., incorrect exception codes, unexpected cache behavior, or changes in page table layout — that can detect. This violates behavioral equivalence:
-
–
-
•
Conclusion of the Contradiction. We see that continuing to nest forever on a finite-resource eventually produces an observable distinction in either states or timings, contrary to (3). Hence, our initial assumption that can be perfect for all programs must be false. No hypervisor can satisfy both behavioral equivalence and zero overhead on a finite-resource machine.
No perfect hypervisor exists on a finite-resource machine.
∎
V Discussion
V-A Generalization Beyond Hypervisors
While our proofs explicitly address the impossibility of a perfect hypervisor, the underlying reasoning naturally extends to broader classes of virtualization technologies. Common abstractions beyond hypervisors—such as emulators, sandboxes, containers, runtime instrumentation frameworks, and other execution-isolation environments—share fundamental properties that make the generalization straightforward.
More formally, we observe that any virtualization or isolation layer that satisfies analogous conditions to those described in Definitions 2 and 3—particularly behavioral equivalence and zero timing overhead—must confront the same resource-constraint limitations and contradictions discussed in Section IV. Specifically, the following reasoning applies broadly:
-
(i)
Emulators and Full-System Simulators: Emulators translate and simulate instructions from a guest architecture to a host architecture. Achieving perfect behavioral equivalence and timing fidelity would necessitate precise simulation of CPU pipelines, caches, timing interrupts, and other hardware features at zero overhead. As shown previously, finite resources inherently impose limits on such precise, overhead-free emulation, making a perfect emulator similarly unattainable.
-
(ii)
Sandboxes and Containers: These lighter-weight virtualization mechanisms typically isolate processes or applications by controlling their system calls, network interfaces, or file accesses. Even these seemingly lightweight solutions inevitably require nonzero overhead (e.g., syscall interception, memory isolation mechanisms, cgroup or namespace management), and attempting to completely hide this overhead violates the finite-resource constraint argument. Thus, a sandbox or container environment achieving both perfect equivalence and zero overhead would face precisely the contradictions described earlier.
-
(iii)
Runtime Instrumentation and Debugging Environments: Instrumentation frameworks (e.g., Valgrind, DynamoRIO, PIN) inject additional code or trap instructions to monitor or modify program behavior. Any instrumentation step necessarily adds overhead. Therefore, maintaining observational indistinguishability with uninstrumented execution, particularly in timing-critical applications, is fundamentally impossible under the conditions discussed.
In general, our impossibility result reflects an intrinsic limitation rooted not only in hypervisor technology, but in the concept of virtualization itself. Any software-based abstraction layer placed between hardware and executing programs must inevitably either manifest measurable resource-consumption overhead or fail to reproduce behavioral equivalence with bare-metal execution faithfully. Consequently, the impossibility theorem established in this paper extends naturally and rigorously to all virtualization and isolation layers seeking absolute indistinguishability and zero overhead.
Perfect virtualization is fundamentally impossible under finite-resource constraints.
V-B From Technical to Fundamental Analysis
While many technical studies have extensively analyzed the practical aspects of virtualization overhead, detection techniques, and architecture-specific vulnerabilities [4, 5, 6], this paper intentionally abstracts away from implementation-specific artifacts. Instead, we provide foundational theorems establishing the intrinsic theoretical limits of virtualization itself, independent of the underlying architecture, implementation details, or specific virtualization technology. This approach ensures generalizability, clarity, and rigor, laying the groundwork for deeper theoretical and practical insights into virtualization systems.
V-C Nested Virtualization
Real systems that allow nested virtualization (e.g., KVM on KVM, or VMware on VMware) accumulate overhead with each layer. Our result clarifies why: some overhead is inherent to all layers; otherwise, infinite nesting would be possible with no cost, violating resource constraints.
V-D Hardware-Assisted Virtualization
While CPU extensions (Intel VT-x, AMD-V) reduce overhead for many virtualization operations (often letting non-privileged instructions run at native speed), they cannot eliminate overhead entirely. Theorem 2 applies equally to any hardware-assisted approaches, since even these must handle certain privileged instructions, resource mappings, and interrupts.
VI Conclusion
We have shown that a perfect hypervisor—one that incurs no timing or resource overhead and exhibits no observable behavioral differences—would be undetectable by any guest‐level algorithm (Theorem 1). We then proved that such a hypervisor cannot exist on a finite-resource machine (Theorem 2); allowing infinite, cost-free nesting would contradict basic resource constraints.
This boundary underscores a broader lesson: overhead can be minimized but never completely eliminated across all programs and execution prefixes. Each additional layer of nesting must accumulate some cost, so any claim of “perfect virtualization” must reckon with the impossibility formalised here.
References
- [1] Intel Corp., Intel® Virtualization Technology (VT-x). [Online]. Available: https://www.intel.com/content/www/us/en/virtualization/virtualization-technology/intel-virtualization-technology.html (accessed Jun. 10, 2025).
- [2] AMD Corp., AMD Virtualization (AMD-V)TM Technology. [Online]. Available: https://www.amd.com/en/technologies/virtualization (accessed Jun. 10, 2025).
- [3] G. J. Popek and R. P. Goldberg, “Formal requirements for virtualizable third generation architectures,” Communications of the ACM, vol. 17, no. 7, pp. 412–421, 1974.
- [4] T. Garfinkel, K. Adams, A. Warfield, and J. Franklin, “Compatibility is not transparency: VMM detection myths and realities,” in Proc. 11th Workshop on Hot Topics in Operating Systems (HotOS XI), 2007, pp. 106–111.
- [5] P. Ferrie, “Attacks on virtual machine emulators,” Symantec Security Response, Tech. Rep., 2006.
- [6] J. Rutkowska, “Red Pill (Detecting virtualization),” Black Hat Briefings, 2007.