On the intersection ideal graph of semigroups

First suppose that $S\setminus K$ is an $\mathcal{L}-$class. Let if possible, $K$ is not maximal left ideal of $S$. Then there exists a nontrivial left ideal $K^{\prime}$ of $S$ such that $K\subset K^{\prime}$. There exists $a\in K^{\prime}$ but $a\notin K$. Thus, $L_{a}=S\setminus K$. Consequently, $L_{a}\subset K^{\prime}$ gives $S=K^{\prime}$, a contradiction. Conversely, suppose that $K$ is a maximal left ideal of $S$. For each $a\in S\setminus K$, maximality of $K$ implies $K\cup S^{1}a=S$. Consequently, $a$ $\mathcal{L}$ $b$ for every $a,b\in S\setminus K$. Thus $S\setminus K$ is contained in some $\mathcal{L}-$class and this $\mathcal{L}-$class is disjoint from $K$. It follows that $S\setminus K$ is an $\mathcal{L}-$class. ∎

First suppose that $\Gamma(S)$ is not connected. Then $S$ has at least two nontrivial left ideals, namely $I_{1},I_{2}$. Without loss of generality, assume that $I_{1}\in C_{1}$ and $I_{2}\in C_{2}$, where $C_{1}$ and $C_{2}$ are distinct components of $\Gamma(S)$. If $I_{1}$ is not minimal then there exists at least one nontrivial left ideal $I_{k}$ of $S$ such that $I_{k}\subset I_{1}$ so that their intersection is nontrivial. Therefore, $I_{1}\sim I_{k}$. Now if the intersection of $I_{2}$ and $I_{k}$ is nontrivial then $I_{1}\sim I_{k}\sim I_{2}$, a contradiction. Therefore the intersection of $I_{2}$ and $I_{k}$ is trivial. If $I_{2}\cup I_{k}\neq S$ then $I_{1}\sim I_{2}\cup I_{k}\sim I_{2}$, a contradiction. Thus, $I_{k}\cup I_{2}=S$. It follows that $I_{1}\sim I_{2}$, again a contradiction. Thus $I_{1}$ is minimal. Similarly, we get $I_{2}$ is minimal.

Further assume that $I_{1}$ is not maximal. Then there exists a nontrivial left ideal $I_{k}$ of $S$ such that $I_{1}\subset I_{k}$ so that $I_{1}\sim I_{k}$. If $I_{1}\cup I_{2}\neq S$ then $I_{1}\sim I_{1}\cup I_{2}\sim I_{2}$, a contradiction to the fact that $\Gamma(S)$ is disconnected. It follows that $I_{1}\cup I_{2}=S$ so that the intersection of $I_{k}$ and $I_{2}$ is nontrivial. Thus we have $I_{1}\sim I_{k}\sim I_{2}$, a contradiction. Hence $I_{1}$ is maximal. Similarly, we observe that $I_{2}$ is maximal. The converse follows from the Remark 2.1. ∎

Suppose first that $\Gamma(S)$ is disconnected. Then by Theorem 3.1, each nontrivial left ideal of $S$ is minimal. Suppose $S$ has at least three minimal left ideals, namely $I_{1},I_{2}$ and $I_{3}$. Then $I_{1}\cup I_{2}$ is a nontrivial left ideal of $S$ which is not minimal. Consequently, by Theorem 3.1, we get a contradiction of the fact that $\Gamma(S)$ is disconnected. Thus, $S$ has exactly two minimal left ideals. If $S\neq I_{1}\cup I_{2}$, then $I_{1}\cup I_{2}$ is a nontrivial left ideal which is not minimal, a contradiction ( cf. Theorem 3.1). Thus, $S=I_{1}\cup I_{2}$.

Conversely, suppose $S=I_{1}\cup I_{2}$ where $I_{1}$ and $I_{2}$ are minimal left ideals of $S$. If there exists another nontrivial left ideal $I_{k}$ of $S$ then either $I_{1}\subset I_{k}$ or $I_{2}\subset I_{k}$. Without loss of generality, assume that $I_{1}\subset I_{k}$, we have $I_{1}\sim I_{k}$. Since $I_{1}\cup I_{2}=S$ we get $I_{k}\cup I_{2}=S$. It follows that the intersection of $I_{2}$ and $I_{k}$ is nontrivial. By minimality of $I_{2}$, we can observe that $I_{2}\subset I_{k}$. Consequently, $S\subseteq I_{k}$, a contradiction. Thus, by Theorem 3.1, $\Gamma(S)$ is disconnected.

∎

Let $I_{1},I_{2}$ be two nontrivial left ideals of $S$. If $I_{1}\sim I_{2}$ then $d(I_{1},I_{2})$ = 1. If $I_{1}\nsim I_{2}$ i.e. $I_{1}\cap I_{2}$ is trivial then in the following cases we show that $d(I_{1},I_{2})$$\leq 2$.

Subcase 1. $I_{1}\not\subset I_{k}$ and $I_{k}\not\subset I_{1}$. Since $I_{1}\not\subset I_{k}$ it follows that there exists $x\in I_{k}$ but $x\notin I_{1}$ so that $x\in I_{2}$. Consequently, $I_{2}\cap I_{k}$ is nontrivial. Therefore, we get a path $I_{1}\sim I_{k}\sim I_{2}$ of length two. Thus, $d(I_{1},I_{2})=2$.

Subcase 2. $I_{k}\subset I_{1}$. There exists $x\in I_{1}$ but $x\notin I_{k}$. If $I_{2}\cup I_{k}=S$ then $x\in I_{2}$. Thus, we get $I_{1}\cap I_{2}$ is nontrivial, a contradiction. Consequently, $I_{2}\cup I_{k}\neq S$. Further, we get a path $I_{1}\sim(I_{2}\cup I_{k})\sim I_{2}$ of length two. Thus, $d(I_{1},I_{2})=2$.

Subcase 3. $I_{1}\subset I_{k}$. Since $I_{1}\cup I_{2}=S$ we get $I_{k}\cup I_{2}=S$. Further, the intersection of $I_{k}$ and $I_{2}$ is nontrivial. Consequently, $I_{1}\sim I_{k}\sim I_{2}$ gives a path of length two between $I_{1}$ and $I_{2}$. Thus, $d(I_{1},I_{2})=2$. Hence, $diam(\Gamma(S))$ $\leq$ $2$.

∎

Suppose that $S$ contains a unique minimal left ideal $I_{1}$. Note that every nontrivial left ideal of $S$ contains at least one minimal left ideal. Since $I_{1}$ is unique then it must contained in every nontrivial left ideals of $S$. Thus, the graph $\Gamma(S)$ is complete.

Conversely, suppose that $\Gamma(S)$ is a complete graph. On contrary if $S$ has at least two minimal left ideals, viz. $I_{1},I_{2}$. By Remark 2.1, $I_{1}\nsim I_{2}$, a contradiction to the fact that $\Gamma(S)$ is complete. Thus $S$ has unique minimal left ideal. ∎

First suppose that $\Gamma(S)$ is not a null graph. Let if possible, $S$ has at least two minimal left ideals, namely $I_{1},I_{2}$. Since $\Gamma(S)$ is not a null graph then $I_{1}$ and $I_{1}\cup I_{2}$ forms a nontrivial left ideals of $S$ and $I_{1}\sim(I_{1}\cup I_{2})$. Suppose $J$ is any nontrivial left ideal of $S$ such that $J\sim I_{1}$ then $J\sim(I_{1}\cup I_{2})$. It follows that every nontrivial left ideal of $S$ which is adjacent with $I_{1}$ is also adjacent with $(I_{1}\cup I_{2})$ and $I_{2}\sim I_{1}\cup I_{2}$ but $I_{2}\nsim I_{1}$ implies that $deg(I_{1})<deg(I_{1}\cup I_{2})$, a contradiction. Therefore, $\Gamma(S)$ is a complete graph. ∎

Suppose that $diam(\Gamma(S))=2$. Assume that $I_{1}$ is the only minimal left ideal of $S$. Since $I_{1}$ is unique minimal left ideal then it is contained in all other nontrivial left ideals of $S$. Therefore, for any nontrivial left ideals $J,K$, we have $I_{1}\subset(J\cap K)$. Consequently, $d(J,K)=1$ for any $J,K\in V(\Gamma(S))$. Therefore $S$ has at least two minimal left ideals. Conversely suppose that $S$ has at least two minimal left ideals, viz. $I_{1},I_{2}$. Then by Remark 2.1, we have $I_{1}\nsim I_{2}$. Consequently, by Theorem 3.4, $d(I_{1},I_{2})=2$. Thus, $diam(\Gamma(S))=2$. ∎

If $\Gamma(S)$ is disconnected or a tree, then clearly $g(\Gamma(S))=\infty$. Suppose that the semigroup $S$ has $n$ minimal left ideals. Now we prove the result through following cases.

(i) Suppose that $|{\rm Min}(S)|=4$ with ${\rm Min}(S)=\{I_{1},I_{2},I_{3},I_{4}\}$. Then note that the subgraph induced by the vertices $I_{1},I_{12},I_{123},I_{14}$ and $I_{124}$ is isomorphic to $K_{5}$. Thus, $\Gamma(S)$ is nonplanar.

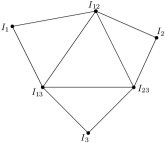
(ii) The proof for $\Gamma(S)$ is nonplanar for $n\geq 4$ follows from part (i). If $n=2$ then by Corollary 3.2 and Theorem 3.3, $\Gamma(S)$ is planar. For $n=3$, $\Gamma(S)$ is planar as shown in Figure 1.

∎

(i) Suppose that $|{\rm Min}(S)|=5$ with ${\rm Min}(S)=\{I_{1},I_{2},I_{3},I_{4},I_{5}\}$. Note that $I_{12}\sim I_{23}\sim I_{34}\sim I_{45}\sim I_{15}\sim I_{12}$ induces a cycle of length 5. Then by Theorem 2.4, $\Gamma(S)$ is not perfect.

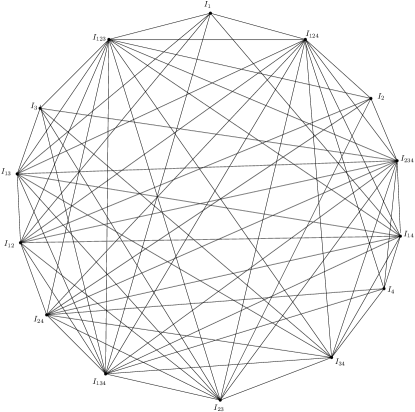
(ii) The proof for $\Gamma(S)$ is not a perfect graph for $n\geq 5$ follows from part (i). If $n=2$ then by Corollary 3.2 and Theorem 3.1, $\Gamma(S)$ is disconnected. Thus, being a null graph, $\Gamma(S)$ is perfect. For $n\in\{3,4\}$, we show that $\Gamma(S)$ does not contain a hole or an antihole of odd length at least five (cf. Theorem 2.4). If $n=3$, $\Gamma(S)$ is perfect as shown in Figure 1. If $n=4$ then from Figure 2 note that $\Gamma(S)$ does not contain a hole or an antihole of odd length at least five.

∎

We prove (ii), (iii) $\Rightarrow$ (iv). The proof of remaining parts is straightforward. Suppose $\Gamma(S)$ is a tree. Then clearly $|{\rm Min}(S)|\leq 2$. Otherwise, for minimal left ideals $I_{1},I_{2},I_{3}$ we have $I_{12}\sim I_{13}\sim I_{23}\sim I_{12}$ a cycle, a contradiction. Suppose that $|{\rm Min}(S)|=1$. Let $I_{1}$ be the unique minimal left ideal of $S$. Consequently, $I_{1}$ is contained in all other nontrivial left ideals of $S$. If $S$ has at least three nontrivial left ideals then we get a cycle, a contradiction. Thus $|V(\Gamma(S))|=2$. Now we assume that $|{\rm Min}(S)|=2$. Let $I_{1},I_{2}$ be two minimal left ideals of $S$. Let if possible, $S=I_{12}$. Then by Corollary 3.2 and Theorem 3.3, $\Gamma(S)$ is disconnected so is not a tree. Thus $S\neq I_{12}$. Then $J=I_{12}$ is a nontrivial left ideal of $S$. Now if $S$ has a nontrivial left ideal $K$ other than $I_{1},I_{2}$ and $J$. Without loss of generality, assume that $I_{1}\subset K$ then we get a cycle $I_{1}\sim I_{12}\sim K\sim I_{1}$, a contradiction. Thus, for $S\neq I_{12}$, we have $V(\Gamma(S))=\{I_{1},I_{2},I_{12}\}$.

(iii) $\Rightarrow$ (iv). If $\Gamma(S)$ is bipartite then we have $|{\rm Min}(S)|\leq 2$. In the similar lines of the work discussed above, (iv) holds. ∎

(i) Suppose that $S\neq I_{12\cdots n}$. It follows that $J=I_{12\cdots n}$ is a nontrivial left ideal of $S$. It is well known that every nontrivial left ideal of $S$ contains at least one minimal left ideal. Consequently, for any nontrivial left ideal $K$ of $S$, we have $J\cap K$ is nontrivial. Thus, $J$ is a dominating vertex. Hence, $\gamma(\Gamma(S))=1$.

(ii) Suppose that $S=I_{12\cdots n}$. Note that there is no dominating vertex in $\Gamma(S)$ so that $\gamma(\Gamma(S))\geq 2$. Now we show that $D=\{I_{1},I_{23\cdots n}\}$ is a dominating set. Since $S$ is the union of $n$ minimal left ideals so any nontrivial left ideal of $S$ is union of these minimal left ideals (cf. Remark 2.2). Let $J\in V(\Gamma(S))\setminus D$ be any nontrivial left ideal of $S$. Then $J$ is union of $k$ minimal left ideals of $S$, where $1\leq k\leq n-1$. If $I_{1}\subset J$, then we are done. If $I_{1}\not\subset J$ then $J$ must be union of $I_{2},I_{3},\ldots,I_{n}$. It follows that intersection of $J$ and $I_{23\cdots n}$ is nontrivial. Consequently, $J\sim I_{23\cdots n}$. Thus $D$ is a dominating set. This completes the proof. ∎

Let ${\rm Min}(S)=\{{I_{i_{1}}:i_{1}\in[n]}\}$ be the set of all minimal left ideals of S. Then, by Remark 2.1, ${\rm Min}(S)$ is an independent set of $\Gamma(S)$. It follows that $\alpha(\Gamma(S))\geq n$. Now we prove that for any arbitrary independent set $U$, we have $|U|\leq n$. Assume that $I\in V(\Gamma(S))$ such that $I\in U$. Since every nontrivial left ideal contains at least one minimal left ideal. Without loss of generality, assume that $I_{{i_{1}}{i_{2}}\cdots{i_{k}}}\subseteq I$ for some $i_{1},i_{2},\cdots,i_{k}\in[n]$. Then note that $|U|\leq n-k+1$. Otherwise, there exist at least two nontrivial left ideals which are adjacent, a contracdiction. Consequently, we have $|U|\leq n$. Thus, $\alpha(\Gamma(S))=n$. ∎

Let $I_{1},I_{2},\ldots,I_{n}$ be $n$ minimal left ideals. Consider $\mathcal{C}=\{I_{{i_{1}}{i_{2}}\cdots{i_{n-1}}}:i_{1},i_{2},\ldots,i_{n-1}\in[n]\}$. Clearly, $|\mathcal{C}|=n$. Notice that for any $J,K\in\mathcal{C}$, we have $J\cap K$ is nontrivial so that $J\sim K$. Thus, $\mathcal{C}$ becomes a clique of size $n$. ∎

First suppose that $\omega(\Gamma(S))=n$. Assume that $S$ has $n(\geq 4)$ minimal left ideals, namely $I_{1},I_{2},\ldots,I_{n}$. Then $\mathcal{C}=\{I_{{i_{1}}{i_{2}}\cdots{i_{n-1}}},I_{{i_{1}}{i_{2}}}:i_{1},i_{2},\ldots,i_{n}\in[n]\}$ forms a clique of size greater than $n$ of $\Gamma(S)$. It follows that $\omega(\Gamma(S))>n$. If $n=3$, assume that $S\neq I_{123}$. Then $\mathcal{C}=\{I_{12},I_{13},I_{23},I_{123}\}$ forms a clique of size four of $\Gamma(S)$. It follows that $S=I_{123}$. For $n=2$, we have either $S=I_{12}$ or $S\neq I_{12}$. For $S=I_{12}$, by Corollary 3.2 and by Theorem 3.3, $\Gamma(S)$ is disconnected. Thus, $\omega(\Gamma(S))<n$. Thus $S\neq I_{12}$. If $S$ has a nontrivial left ideal $K\notin\{I_{1},I_{2},I_{12}\}$ then we get a clique of size three. Therefore, $I_{12}$ is a unique maximal left ideal. Converse follows trivially.∎

We prove the result by showing that if $J,K\in{\rm Max}(S)$ then $J\sim K$. Let if possible, $J\nsim K$. The maximality of $J$ and $K$ follows that $J\cup K=S$. By Lemma 2.3, $S\setminus J$ and $S\setminus K$ are $\mathcal{L}-$classes of $S$. It follows that $J$ and $K$ are only nontrivial left ideals of $S$. Thus, being a null graph $\Gamma(S)$ is disconnected, a contradiction. ∎

Let $J$ be an arbitrary nontrivial left ideal of $S$ such that $J\nsim K$. Note that $J$ is minimal left ideal of $S$. On contrary, suppose that $J$ is not a minimal left ideal of $S$. Then there exists a nontrivial left ideal $J^{\prime}$ of $S$ such that $J^{\prime}\subset J$. Since $K$ is maximal left ideal of $S$. Consequently, $J^{\prime}\cup K=S$. It follows that intersection of $J$ and $K$ is nontrivial, a contradiction. By Remark 2.1, we can color all the vertices which are not adjacent with $K$ with one color. Since $deg(K)$ is finite, we have $\chi(\Gamma(S))<\infty$. ∎

First note that $S$ has $2^{n}-2$ nontrivial left ideals and every nontrivial left ideal of $S$ is of the form $I_{{i_{1}}{i_{2}}\cdots{i_{k}}}$ and $1\leq k\leq n-1$ (cf. Remark 2.2). If $n$ is odd then consider $\mathcal{C}=\{I_{{j_{1}}{j_{2}}\cdots{j_{t}}}:\lceil\frac{n}{2}\rceil\leq t\leq n-1\}$. Note that $\mathcal{C}$ forms a clique of size $2^{n-1}-1$. We may now suppose that $n$ is even. Consider $\mathcal{C}_{1}=\{I_{{j_{1}}{j_{2}}\cdots{j_{t}}}:\frac{n}{2}+1\leq t\leq n-1\}$. Notice that $\mathcal{C}_{1}$ forms a clique. Further, observe that $\mathcal{C}^{{}^{\prime}}=\{I_{{i_{1}}{i_{2}}\cdots{i_{\frac{n}{2}}}}:i_{1},i_{2},\ldots,i_{\frac{n}{2}}\in[n]\}$ do not form a clique because for $j_{1},j_{2},\ldots,j_{\frac{n}{2}}\in[n]\setminus\{i_{1},i_{2},\ldots,i_{\frac{n}{2}}\}$, $I_{{i_{1}}{i_{2}}\cdots{i_{\frac{n}{2}}}}\nsim I_{{j_{1}}{j_{2}}\cdots{j_{\frac{n}{2}}}}$. However, $\mathcal{C}^{{}^{\prime\prime}}=\{I_{{i_{1}}{i_{2}}\cdots{i_{\frac{n}{2}}}}\in\mathcal{C}^{{}^{\prime}}\setminus\{I_{{j_{1}}{j_{2}}\cdots{j_{\frac{n}{2}}}}\}:j_{1},j_{2},\ldots,j_{\frac{n}{2}}\notin\{i_{1},i_{2},\ldots,i_{\frac{n}{2}}\}\}$ forms a clique of size $\frac{|\mathcal{C}^{{}^{\prime}}|}{2}$. Further note that the set $\mathcal{C}_{1}\cup\mathcal{C}^{{}^{\prime\prime}}$ also forms a clique of size $2^{n-1}-1$. Thus, $\omega(\Gamma(S))\geq 2^{n-1}-1$. To complete the proof, we show that $\chi(\Gamma(S))\leq 2^{n-1}-1$. For $I=I_{{i_{1}}{i_{2}}\cdots{i_{k}}}$ and $J=I_{{j_{1}}{j_{2}}\cdots{j_{n-k}}}$, where $i_{1},i_{2},\ldots,i_{k}\in[n]\setminus\{j_{1},j_{2},\ldots,j_{n-k}\}$ we have $I\cap J$ is trivial. Consequently, we can color these vertices with same color so that we can cover all the vertices with $2^{n-1}-1$ colors. Thus $\chi(\Gamma(S))\leq 2^{n-1}-1$. Hence $\omega(\Gamma(S))=\chi(\Gamma(S))=2^{n-1}-1$. ∎