On the origin of the anomalous behaviour of 2+ excitation energies in the neutron-rich Cd isotopes
Abstract
Recent experimental results obtained using decay and isomer spectroscopy indicate an unusual behaviour of the energies of the first excited 2+ states in neutron-rich Cd isotopes approaching the N=82 shell closure. To explain the unexpected trend, changes of the nuclear structure far-off stability have been suggested, namely a quenching of the N=82 shell gap already in 130Cd, only two proton holes away from doubly magic 132Sn. We study the behaviour of the 2+ energies in the Cd isotopes from N=50 to N=82, i.e. across the entire span of a major neutron shell using modern beyond mean field techniques and the Gogny force. We demonstrate that the observed low 2+ excitation energy in 128Cd close to the N=82 shell closure is a consequence of the doubly magic character of this nucleus for oblate deformation favoring thereby prolate configurations rather than spherical ones.
keywords:
Anomaly, Cadmium isotopes, Beyond Mean Field Approach.PACS:
21.60.Jz, 21.10.Re, 21.60.Ev, 27.60.+j, ,
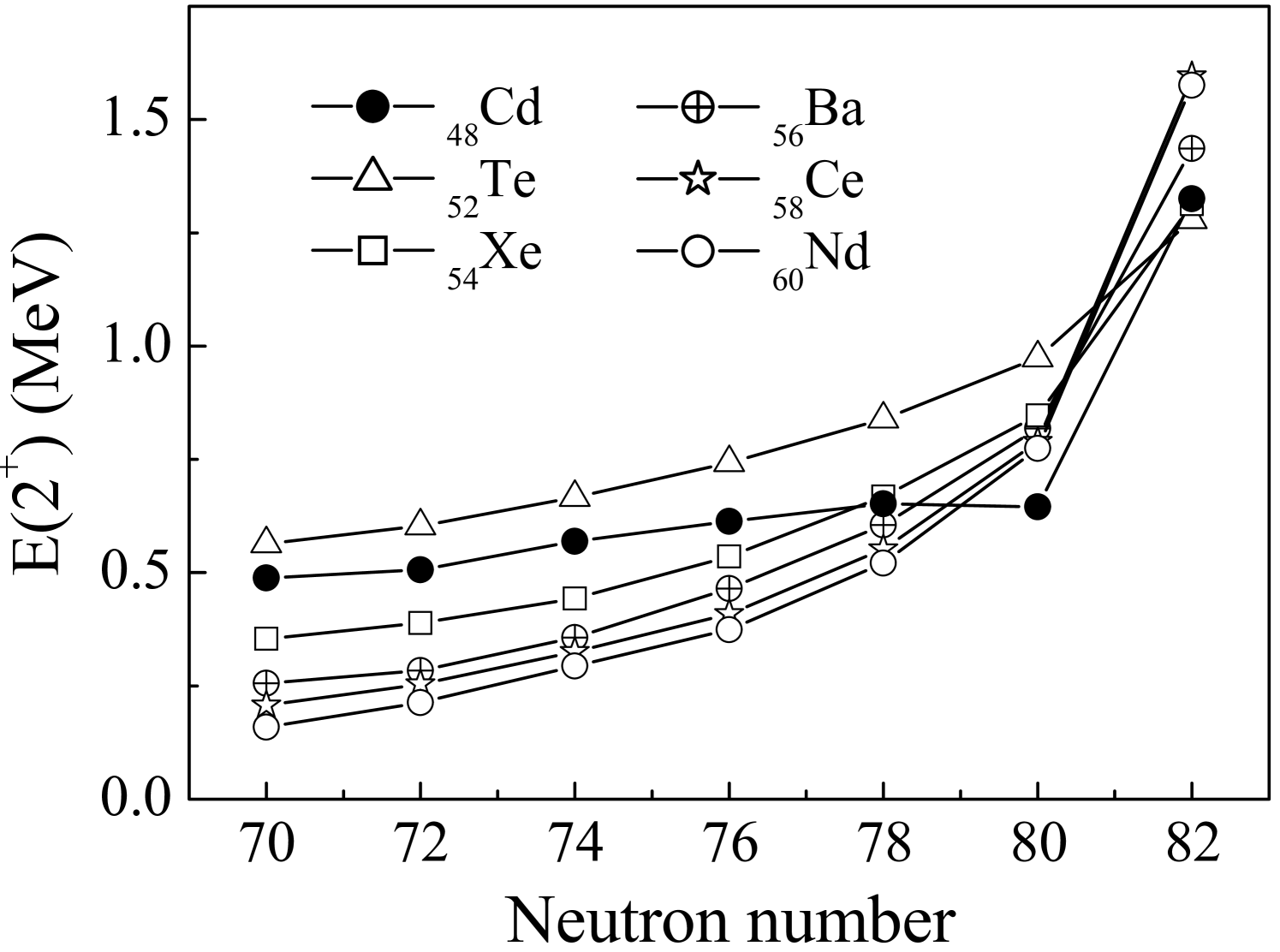
Recent advances in experimental techniques allow to follow the isotopic chains of heavy nuclei and therefore the evolution of nuclear structure over wider and wider isospin ranges, in some cases even across the entire span of a major neutron shell. The Cd isotopes (Z=48) for example are the first case, where experimental information about excited states is now available from the N=50 to the N=82 shell closure, that is from 98Cd to 130Cd gor97 ; jun07 . Approaching the proton and neutron drip lines new facets of nuclear structure are expected DripLineReview to gain relevance due to the increased importance of the coupling to the unbound continuum and changes in the density distributions of protons and neutrons. The availability of experimental information over a wide isospin range therefore allows for the most stringent test of the validity of global nuclear structure models. Besides the nuclear structure aspect, the understanding of the nuclei around the doubly-magic tin isotopes 100Sn and 132Sn is also of astrophysical interest. The rapid proton () capture process of hydrogen burning on the surface of an accreting neutron star ends in a closed SnSbTe cycle near 100Sn sch01 and the dynamics of the process and with it the solar abundance distribution in the mass 130 region is determined by the properties of the N=82 waiting point nuclei below 132Sn kra93 . Already more than ten years ago it was shown that the assumption of a quenching of the N=82 neutron shell closure leads to a considerable improvement in the global abundance fit in process calculations che95 ; pfe97 . Different theoretical calculations indeed predict such a reduction of the shell gap near the neutron drip line dob94 ; sha02 . Unfortunately, this region of very neutron-rich waiting point nuclei is still out of reach experimentally. However, in recent years a number of experimental observations in the 132Sn region have been interpreted as first experimental evidence of the quenching of the N=82 shell closure in 130Cd kau00 ; dil03 , much closer to 132Sn than predicted by any calculation. One of them concerns the anomalous behaviour of the energies of the first excited 2+ states in the heavy Cd isotopes as illustrated in Fig. 1. The 2+ state in the N=80 isotope 128Cd at an excitation energy of 645 keV lies 7 keV lower than the 2+ level in 126Cd kau00 . It is evident from Fig. 1 that the neutron-rich Cd isotopes display a completely different behaviour when approaching N=82 than the Te, Xe, Ba, Ce and Nd isotopes above the Z=50 shell closure. However, the recently observed excitation scheme of 130Cd and its comparison to shell model calculations does not give any evidence for a reduced N=82 gap in this nucleus jun07 . Furthermore, a new direct mass measurement for 134Sn restored the 132Sn shell closure to that expected for a doubly-magic nucleus dwo08 . Previous measurements seemed to indicate a reduced strength of that shell closure. In light of these new experimental results the interpretation of the anomalous behaviour of the 2+ energies as hint to a possible N=82 shell quenching has to be questioned.
In this Letter we study the evolution of 2+ excitation energies in the Cd isotopes between N=50 and N=82 from a theoretical view point in an attempt to unveil the origin of the anomalous behaviour. This endeavor of a realistic calculation across an entire major shell can only be realized in the framework of modern beyond mean field theories with effective interactions BHR.03 ; rod02 ; Ni.06 . An exploratory study of the neutron-rich Cd isotopes has already been presented in jun06 . In that reference, a simplified approach, neglecting some relevant exchange terms of the Gogny force, has been used and only a few isotopes have been investigated. Furthermore, no particle number projection has been performed, neither at the mean field level nor in the configuration mixing approach.
In this work we use the recently proposed symmetry conserving configuration mixing approach rod07 with particle number and angular momentum projection and the finite range density dependent Gogny interaction (D1S parametrization BERGNPA84 ) with all exchange terms included. This interaction has been adjusted to reproduce global properties of nuclear matter more than twenty five years ago and does not invoke any parameter adjustment to certain regions of the nuclear chart. Its strength is the ability to describe in a consistent way a large variety of phenomena such as the erosion of the N=20 shell closure around 32Mg rod02 , the emergence of the new shell closure at N=32 in neutron-rich Ca, Ti, and Cr isotopes rod07 , the shape coexistence in the Pb isotopes egi04 as well as the fission barriers in 254No egi00 . The intention of these calculations is to describe general trends and evolutions of nuclear properties and to help to unravel the basic underlying origins rather than to obtain an as detailed as possible description of a single nucleus of interest.

In our approach rod07 , we first generate the collective subspace of Hartree-Fock-Bogoliubov (HFB) wave functions, , by the quadrupole constrained particle number projection (PNP) before the variation PNP-Gogny , i.e., we minimize the energy
| (1) |
with , where is the projector onto neutron (proton) number and the Lagrange multiplier determined by the constraint , in an obvious notation. The constraint on the operator allows the definition of potential energy surfaces along the most relevant degrees of freedom. In the present calculations we restrict this set to the quadrupole deformation , triaxial shapes, i.e. the degree of freedom, are not considered.
The configuration mixing calculation is performed within the generator coordinate method (GCM) framework taking linear combinations of the particle number projected wave functions obtained in the first step and performing in addition angular momentum projection:
| (2) |
with the angular momentum projector.
Then, the variational principle applied to the weights gives the generalized eigenvalue problem (Hill-Wheeler equation):
| (3) |
with and the Hamiltonian and norm overlaps, respectively (see rod02 for further details). In the calculations we use 11 harmonic oscillator major shells and the D1S parametrization BERGNPA84 of the Gogny force.
It is important to emphasize here that nuclei close to shell closures belong to the weak pairing regime where the HFB approach breaks down. To properly deal with the pairing correlations in nuclei such as 132Te and 128Cd with only a few particles/holes outside a doubly-magic core it is mandatory to apply the so-called Projection Before Variation approach as described above. As a matter of fact we find quantitative differences between the present calculations and those of Ref. jun06 performed also with the Gogny interaction but without PNP and without exchange terms. Furthermore, in order to check the validity of the axial approach used in this work, we have also performed triaxial calculations at the PNP level. The results show that none of the analyzed isotopes exhibits triaxial minima or large softness TL.09 .
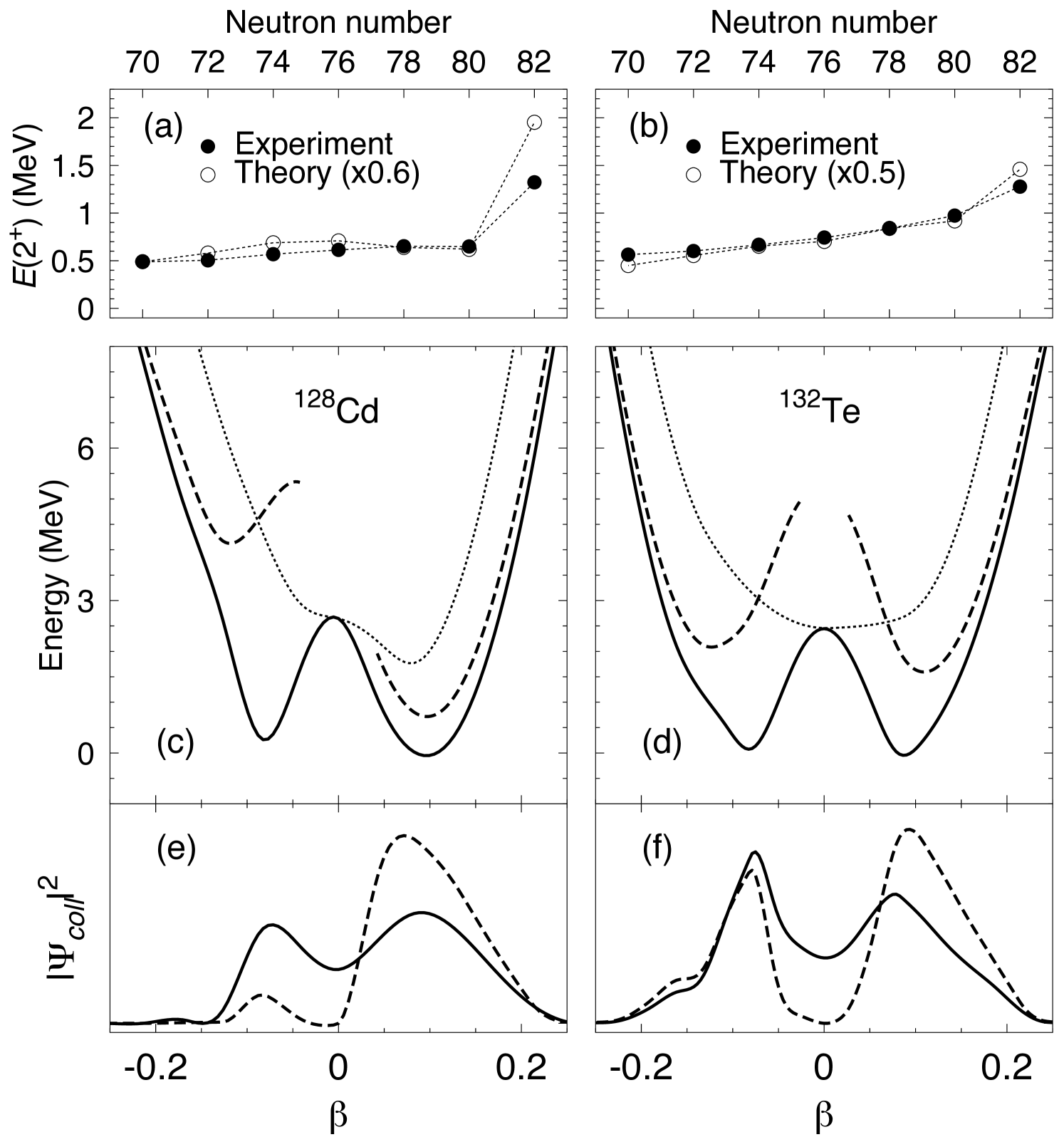
In Fig. 2 we compare the calculated excitation energies of the states (the eigenvalues of Eq. 3 for and ) and the transition strengths for all Cadmium isotopes from the N=50 to the N=82 shell closure to the available experimental information NUCDATA . We find an overall good qualitative agreement between theory and experiment. The general trend as well as the absolute strength of the experimental values are well reproduced by our calculations. For the excitation energies one can distinguish three different regions. In the first one, N=51-58, the parabolic behaviour of the energy roughly corresponds to the successive filling of the g7/2 neutron orbital. In the second region, N=59-70, with a rather flat energy, several smaller sub-shells (d5/2, d5/2, s1/2) are being filled. Finally, from N=71 to 82, the h11/2 orbital is being filled, but at variance from the first region here we observe the unexpected non-parabolic behaviour of the energies. These three regions have an approximate counterpart in the transition probabilities. Though we nicely reproduce these features the calculated energies are too high on an absolute scale. The origin of this scaling is supposedly due to the absence of K-mixing in the calculations. This mixing can be induced in different, non-independent, ways: at the HFB level, by angular momentum projection before variation carlo , by the Coriolis force (cranking) or by admixing of two-quasiparticle states (Tamm-Dancoff) carlo ; sun , and at the configuration mixing level by the consideration of triaxial shapes BH-08 . Within our approach we have investigated the plane and, as mentioned above, none of the nuclei studied show triaxial minima or large softness and it seems that in this case the consideration of K-mixing effects amounts, at least for the lowest lying collective states, to a global, rather constant, change in the mass parameter (either for rotations or vibrations). That means, the ratio between the calculated and experimental energies is nearly constant (about 1.6) over a large range of isotopes. This effect, which is not yet fully understood, has already been observed in previous studies, see for example rod07 . A rather constant ratio has also been obtained in limiting situations evaluating the mass parameter with and without triaxial effects ER.04 and in an exact triaxial angular momentum projection doba . Taking into account this constant factor the calculations reproduce the experimental data even quantitatively. This is shown in Fig. 3(a,b) where the renormalized calculated 2+ excitation energies for the Cd and Te isotopes are compared to experimental data in the region of interest close to N=82. The calculations nicely reproduce the experimental trends, namely the parabola-like behaviour in the Te isotopes and the “pathological” flattening up to N=80 for the Cd isotopes.
To trace back the origin for the different behaviour of the N=76, 78, and 80 Cd and Te isotones we will compare in more detail the different steps of the calculations for the N=80 pair. In Fig. 3(c,d) we present the potential energy curves calculated before configuration mixing as a function of the intrinsic quadrupole deformation . These curves show clear differences between 128Cd and 132Te and shed light on the origin of the different behaviour of the 2+ energies. The energies obtained using the solutions of the PNP equations (see eq. 1) show an intrinsic spherical minimum in 132Te and a slightly prolate one in 128Cd. The results obtained after angular momentum projection, i.e., the energy expectation values calculated with the wave functions , are rather similar for both nuclei for the 0+ state: They present coexisting prolate and oblate minima. However, the results for the 2+ state are rather different: for 128Cd we obtain a deep prolate deformed minimum about 3.5 MeV lower than the oblate one, whereas in 132Te we observe again two symmetric minima as for the 0+ state. Finally, in Fig. 3(e,f) the wave functions of the collective states (eq. 2) with angular momentum 0 and 2, respectively, i.e. the states obtained after configuration mixing, are shown (the corresponding 2+ energies have already been shown in Fig. 3(a,b)). Once more, pronounced differences are observed for the 2+ state: In 132Te this state represents on average a quadrupole oscillation around a spherical shape. In 128Cd, on the other hand, the 2+ state is essentially an oscillation around a prolate deformed shape and therefore strongly coupled to rotation. This is the main reason why the 2+ energies in the heavy Cd isotopes behave differently from those in the heavy Te isotopes.
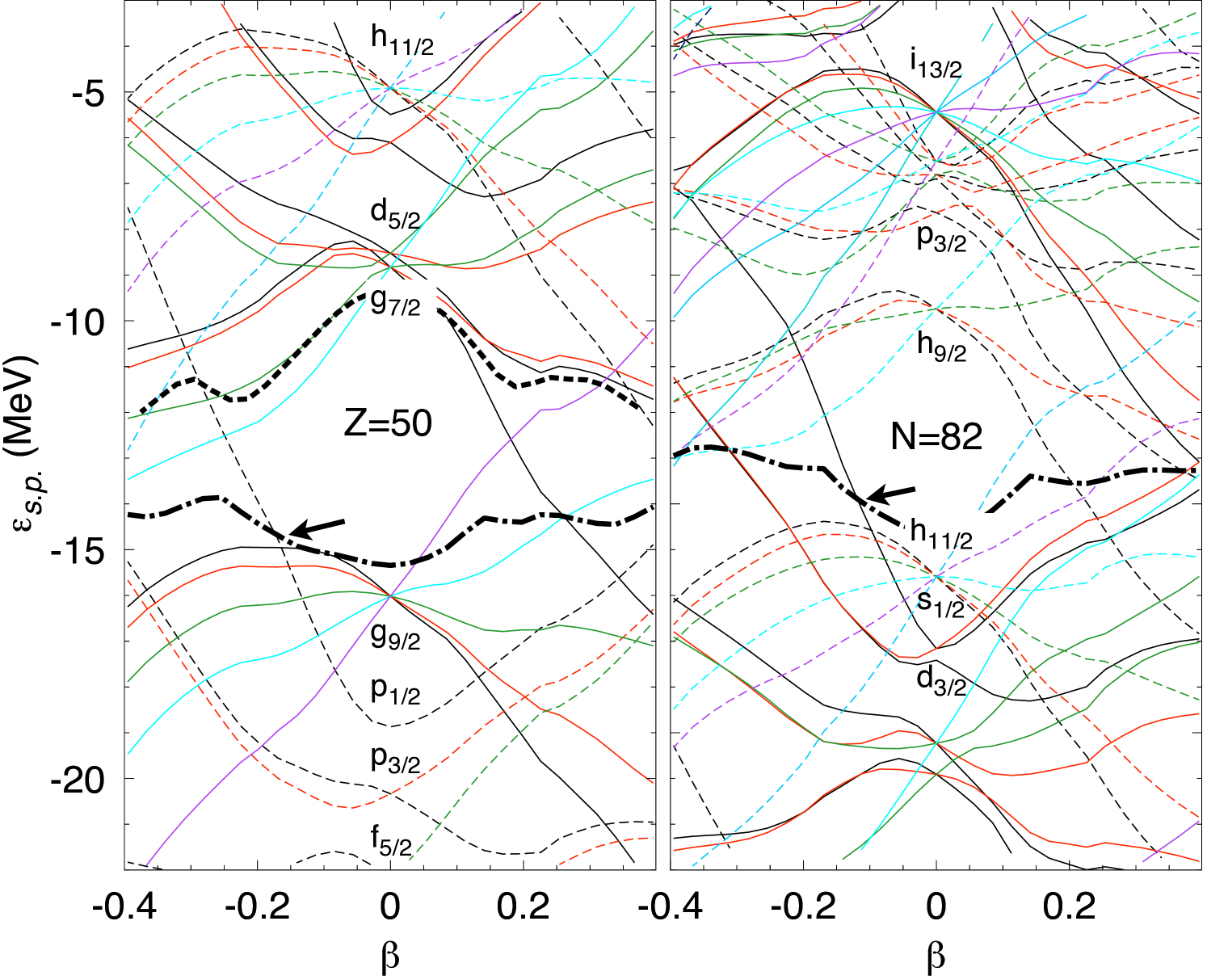
Trying to understand the underlying origin of the differences between the properties of the 2+ states in 128Cd and 132Te we will now have a closer look to the potential energy curves obtained after particle number but before angular momentum projection (dotted lines in Fig.3(c,d)). Already here, a difference between the two nuclei is apparent. On the oblate side (), the energy increases much faster for 128Cd compared to 132Te (=2.5 MeV and 1.0 MeV, respectively). This difference can be understood on the basis of the single particle energies (SPE), represented in Fig. 4 for 128Cd. The SPE for 132Te are not significantly different from these ones. The proton Fermi levels for both nuclei are included in Fig. 4, while for the neutrons we assume the Fermi level to be the same since both nuclei have the same number of neutrons, . At an oblate deformation of about the neutron level is emerging from the Fermi surface, see the corresponding arrow. From here on both N=80 isotones have a completely filled shell. On the proton side, a similar situation occurs around where the proton level is crossing the Fermi surface for 128Cd. That means that for oblate deformations larger than in addition to the full neutron shell the nucleus 128Cd also has a completely filled large intruder proton orbit, namely the shell. To deform this nucleus with closed large intruder shells for both protons and neutrons a lot of energy is required resulting in the very steep PNP curve for 128Cd in Fig. 3(c). Furthermore, the generation of two units of angular momentum to form a 2+ state is very costly for such a stiff configuration since it requires the admixing of orbitals above the or shell closures (compare the curve for curve in Fig. 3(c)). The situation in 132Te is very different. In this case, the proton Fermi level lies above the shell closure and the oblate branch of the proton system can easily be deformed (see Fig. 4) due to the positive slope of the relevant orbitals. This deformation will be directly transfered to the neutron system due to the strong proton-neutron interaction. Even more important, a state can easily be build by coupling two protons (see Fig. 3(d)). To summarize this discussion, we have shown that the prolate deformation of the 2+ state in 128Cd has its origin in a very peculiar coincidence of closed shell proton and neutron configurations for leading to a ”blocking” of the oblate branch of the energy curve, i.e., in this branch the nucleus behaves as a double magic one. Since the proton oblate blocking persist also in the nearby and 78 Cadmium isotopes it is obvious that these isotopes will be on average more deformed than the corresponding Tellurium isotopes, as depicted by the energies in Fig.3(a,b), indicating that the different behavior of the Cadmium and Tellurium isotopes close to the shell closure can be explained by ”standard” nuclear structure effects without invoking shell quenching.
In conclusion we have presented a theoretical study of the origin of the unusual behaviour of 2+ excitation energies in neutron-rich Cadmium isotopes towards the N=82 shell closure using modern beyond mean field techniques and the Gogny force. We have demonstrated that these calculations, which do not dispose of any adjustable parameters, are not only able to describe general features of atomic nuclei across entire major shells, i.e. over wide ranges of isospin, but also to reproduce local features of nuclear structure such as the low 2+ energies in 126,128Cd and unravel their origin. Furthermore, our calculations show that the anomalous behaviour of the 2+ energies in the heavy Cd isotopes is caused by the very special characteristics of the Cd isotopes which favor prolate configurations close to the shell closure. There is no need to assume any changes of nuclear structure far-off stability, i.e. a quenching of the shell closure, to explain the experimental findings.
The authors acknowledge financial support from the Spanish Ministerio de Educación y Ciencia under contracts FPA2005-00696, FPA2007-66069 , by the Spanish Consolider-Ingenio 2010 Programme CPAN (CSD2007-00042) and within the programa Ramón y Cajal (A. Jungclaus).
References
- (1) M. Górska et al., Phys. Rev. Lett. 79, 2415 (1997).
- (2) A. Jungclaus et al., Phys. Rev. Lett. 99, 132501 (2007).
- (3) J. Dobaczewski, N. Michel, W. Nazarewicz, M. Płoszajczak and J. Rotureau, Prog. Part. Nucl. Phys. 56, 432-455 (2007)
- (4) H. Schatz et al., Phys. Rev. Lett. 86, 3471 (2001).
- (5) K.-L. Kratz et al., Astrophys. J. 403, 216 (1993).
- (6) B. Chen et al., Phys. Lett. B 355, 37 (1995).
- (7) B. Pfeiffer, K.-L. Kratz and F.-K. Thielemann, Z. Phys. A 357, 235 (1997).
- (8) J. Dobaczewski, I. Hamamoto, W. Nazarewicz and J.A. Sheik, Phys. Rev. Lett. 72, 981 (1994).
- (9) M.M. Sharma and A.R. Farhan, Phys. Rev. C 65, 044301 (2002).
- (10) T. Kautzsch et al., Eur. Phys. J. A 9, 201 (2000).
- (11) I. Dillmann et al., Phys. Rev. Lett. 91, 162503 (2003).
- (12) M. Dworschak et al., Phys. Rev. Lett. 100, 072501 (2008).
- (13) M. Bender, P.-H. Heenen and P.G. Reinhardt, Rev. Mod. Phys. 75, 121 (2003).
- (14) R. Rodríguez-Guzmán et al, Nucl. Phys. A709, 201 (2002).
- (15) T. Niks̆ić et al, Phys. Rev. C 74, 064309 (2006)
- (16) A. Jungclaus and J.L. Egido, Phys. Scr. T125, 53-56 (2006).
- (17) T.R. Rodríguez and J.L. Egido, Phys. Rev. Lett. 99, 062501 (2007).
- (18) J. F. Berger, M. Girod, D. Gogny, Nucl. Phys. A 428, 23c (1984)
- (19) J.L. Egido, L.M. Robledo and R. Rodríguez-Guzman, Phys. Rev. Lett. 93, 082502 (2004).
- (20) J.L. Egido and L.M. Robledo, Phys. Rev. Lett. 85, 1198 (2000).
- (21) M. Anguiano, J.L. Egido and L.M. Robledo, Nucl.Phys. A696, 467-493 (2001)
- (22) T.R. Rodríguez and J.L. Egido, to be published.
- (23) Evaluated Nuclear Structure Data File, http://www.nndc.bnl.gov/ensdf/
- (24) K.W. Schmid and F. Gruemmer, Rep. Prog. Phys. 50, 731 (1987)
- (25) K. Hara and Y. Sun, Int. J. Mod. Phys. E 4, 637 (1995).
- (26) M. Bender and P.-H. Heenen, Phys. Rev. C (to be published), arXiv:0805.4383[nucl-th]
- (27) J.L. Egido and L.M. Robledo, in Extended density functional in nuclear structure physics, Lect. Notes in Phys. 641, 269-299 (2004).
- (28) H. Zduńczuk, W. Satula, J. Dobaczewski, and M. Kosmulski, Phys. Rev. C 76, 044304 (2007)