On the Stretch Factor of Convex Delaunay Graphs
Abstract
Let be a compact and convex set in the plane that contains the origin in its interior, and let be a finite set of points in the plane. The Delaunay graph of is defined to be the dual of the Voronoi diagram of with respect to the convex distance function defined by . We prove that is a -spanner for , for some constant that depends only on the shape of the set . Thus, for any two points and in , the graph contains a path between and whose Euclidean length is at most times the Euclidean distance between and .
1 Introduction
Let be a finite set of points in the plane and let be a graph with vertex set , in which each edge has a weight equal to the Euclidean distance between and . For a real number , we say that is a -spanner for , if for any two points and of , there exists a path in between and whose Euclidean length is at most . The smallest such is called the stretch factor of . The problem of constructing spanners has received much attention; see Narasimhan and Smid [12] for an extensive overview.
Spanners were introduced in computational geometry by Chew [3, 4], who proved the following two results. first, the -Delaunay graph, i.e., the dual of the Voronoi diagram for the Manhattan metric, is a -spanner. Second, the Delaunay graph based on the convex distance function defined by an equilateral triangle, is a -spanner. We remark that in both these results, the stretch factor is measured in the Euclidean metric. Chew also conjectured that the Delaunay graph based on the Euclidean metric, is a -spanner, for some constant . (If not all points of are on a line, and if no four points of are cocircular, then the Delaunay graph is the well-known Delaunay triangulation.) This conjecture was proved by Dobkin et al. [8], who showed that . The analysis was improved by Keil and Gutwin [9], who showed that .
In this paper, we unify these results by showing that the Delaunay graph based on any convex distance function has bounded stretch factor.
Throughout this paper, we fix a compact and convex set in the plane. We assume that the origin is in the interior of . A homothet of is obtained by scaling with respect to the origin, followed by a translation. Thus, a homothet of can be written as
for some point in the plane and some real number . We call the center of the homothet .
For two points and in the plane, we define
If , then this definition is equivalent to the following: Consider the translate and the ray emanating from that contains . Let be the (unique) intersection between this ray and the boundary of . Then
The function is called the convex distance function associated with . Clearly, we have and for all points and with . Chew and Drysdale [5] showed that the triangle inequality holds. In general, the function is not symmetric, i.e., is not necessarily equal to . If is symmetric with respect to the origin, however, then is symmetric.
Let be a finite set of points in the plane. For each point in , we define
If is not strictly convex, then the set may consist of a closed region of positive area with an infinite ray attached to it. For example, in figure 1, the set consists of the set of all points that are on or to the left of the leftmost zig-zag line, together with the infinite horizontal ray that is at the same height as the point . Also, the intersection of two regions and , where and are distinct points of , may have a positive area. As a result, the collection , where ranges over all points of , does not necessarily give a subdivision of the plane in which the interior of each cell is associated with a unique point of . In order to obtain such a subdivision, we follow the approach of Klein and Wood [10] (see also Ma [11]): first, infinite rays attached to regions of positive area are not considered to be part of the region. Second, a point in that is in the interior of more than one region is assigned to the region of the lexicographically smallest point in for which .
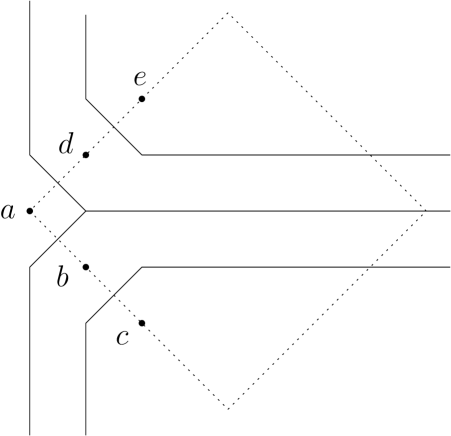
To formally define Voronoi cells, let denote the lexicographical ordering on the set of all points in the plane. Let be the points of , sorted according to this order. Then the Voronoi cells of the points of are defined as
and, for ,
where and denote the closure and the interior of the set , respectively.
Thus, in figure 1, the Voronoi cell consists only of the set of all points that are on or to the left of the leftmost zig-zag line; the infinite horizontal ray that is at the same height as the point is not part of this cell.
The Voronoi diagram of with respect to is defined to be the collection of Voronoi cells , where ranges over all points of . An example is given in figure 1.
As for the Euclidean case, the Voronoi diagram induces Voronoi cells, Voronoi edges, and Voronoi vertices. Each point in the plane is either in the interior of a unique Voronoi cell, in the relative interior of a unique Voronoi edge, or a unique Voronoi vertex. Each Voronoi edge belongs only to the two Voronoi cells that contain on their boundaries. Observe that Voronoi cells are closed.
The Delaunay graph is defined to be the dual of the Voronoi diagram:
Definition 1
Let be a finite set of points in the plane. The Delaunay graph of with respect to is defined to be the dual of the Voronoi diagram . That is, the vertex set of is and two distinct vertices and are connected by an edge in if and only if the Voronoi cells and share a Voronoi edge.
For example, the Delaunay graph for the point set in figure 1 consists of the five edges , , , , and .
We consider the Delaunay graph to be a geometric graph, which means that each edge is embedded as the closed line segment with endpoints and .
Before we can state the main result of this paper, we introduce two parameters whose values depend on the shape of the set . Let and be two distinct points on the boundary of . These points partition into two chains. For each of these chains, there is an isosceles triangle with base and whose third vertex is on the chain. Denote the base angles of these two triangles by and ; see figure 2 (left). We define
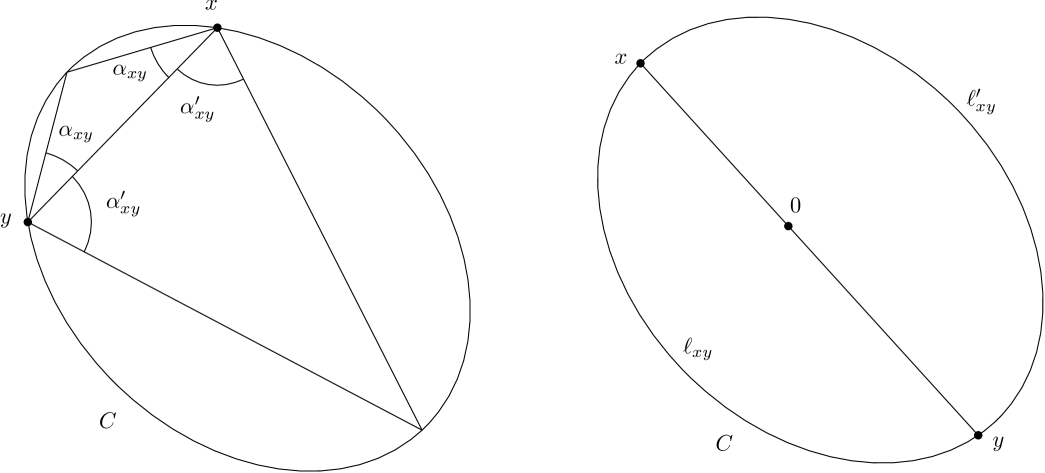
Consider again two distinct points and on , but now assume that , , and the origin are collinear. As before, and partition into two chains. Let and denote the lengths of these chains; see figure 2 (right). We define
Clearly, the convex distance function and, therefore, the Voronoi diagram , depends on the location of the origin in the interior of . Surprisingly, the Delaunay graph does not depend on this location; see Ma [11, Section 2.1.6]. We define
In this paper, we will prove the following result:
Theorem 1
Let be a compact and convex set in the plane with a non-empty interior, and let be a finite set of points in the plane. The stretch factor of the Delaunay graph is less than or equal to
Thus, for any two points and in , the graph contains a path between and whose Euclidean length is at most times the Euclidean distance between and .
We emphasize that we do not make any “general position” assumption; our proof of Theorem 1 is valid for any finite set of points in the plane.
Throughout the rest of this paper, we assume that the origin is chosen in the interior of such that .
The rest of this paper is organized as follows. In Section 2, we prove some basic properties of the Delaunay graph which are needed in the proof of Theorem 1. In particular, we give a formal proof of the fact that this graph is plane. Even though this fact seems to be well known, we have not been able to find a proof in the literature. Section 3 contains a proof of Theorem 1. This proof is obtained by showing that the Delaunay graph satisfies the “diamond property” and a variant of the “good polygon property” of Das and Joseph [6]. The proof of the latter property is obtained by generalizing the analysis of Dobkin et al. [8] for the lengths of so-called one-sided paths.
2 Some properties of the Delaunay graph
Recall that in the Euclidean Delaunay graph, if two points and of are connected by an edge, then there exists a disk having and on its boundary that does not contain any point of in its interior. The next lemma generalizes this result to the Delaunay graph .
Lemma 1
Let and be two points of and assume that is an edge in the Delaunay graph . Then, the following are true.
-
1.
The line segment between and does not contain any point of .
-
2.
For every point in , there exists a real number such that
-
(a)
the homothet contains and on its boundary, and
-
(b)
the interior of does not contain any point of .
-
(a)
Proof. To prove the first claim, assume that the line segment between and contains a point of . Then it follows from Ma [11, Lemma 2.1.4.2] that . Thus, the Voronoi cells of and do not share an edge and, therefore, is not an edge in the Delaunay graph. This is a contradiction.
To prove the second claim, let be an arbitrary point in . Then and for all . Thus, if we define , then , both and are on the boundary of the homothet , and no point of is in the interior of this homothet.
As can be seen in figure 1, Voronoi cells are, in general, not convex. They are, however, star-shaped:
Lemma 2
Let be a point of and let be a point in the Voronoi cell . Then the line segment is completely contained in .
Proof. In [11, Lemma 2.1.4.7], Ma shows that, if is in the interior of , then is completely in the interior of . Clearly, this implies that is in , if (i.e., is in the interior or on the boundary of this Voronoi cell).
It is well known that the Euclidean Delaunay graph is a plane graph; see, for example, de Berg et al. [7, page 189]. The following lemma states that this is true for the Delaunay graph as well.
Lemma 3
The Delaunay graph is a plane graph.
Proof. By the first claim in Lemma 1, does not contain two distinct edges and that are collinear and overlap in a line segment of positive length. Again by the first claim in Lemma 1, does not contain two distinct edges and such that is on the open line segment joining and .
It remains to show that does not contain two edges and that cross properly. The proof is by contradiction. Thus, let , , , and be four pairwise distinct points of , no three of which are collinear, and assume that the line segments and are edges of that have exactly one point in common.
Since is an edge of , there exists a point in the relative interior of . Thus, by the second claim in Lemma 1, there exists a real number , such that the homothet contains and on its boundary and no point of is in the interior of this homothet. Observe that is in the interior of . Let be a Euclidean disk centered at that is contained in the interior of and that is contained in . We define to be the set of all 2-link polygonal chains , with ; see figure 3. Observe that has a positive area. Since and are star-shaped (by Lemma 2), we have . Since is convex, we have ; in fact, the convex hull of is contained in . Thus, neither nor is in the interior of the convex hull of . Since and intersect in a point, the line segment crosses the set .
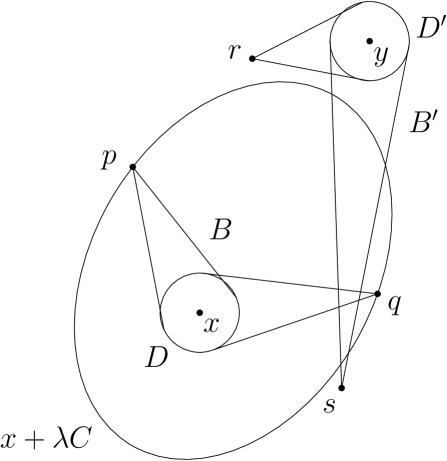
By a symmetric argument, since is an edge of , there exist a point in the relative interior of and a real number , such that contains and on its boundary and no point of is in the interior of this homothet. Let be a Euclidean disk centered at that is contained in the interior of and that is contained in . We define to be the set of all 2-link polygonal chains , with . The set has a positive area, the line segment crosses this set, , and neither nor is in the interior of the convex hull of .
It follows that and overlap in a region of positive area. Since and , however, the area of the intersection is equal to zero. This is a contradiction. It follows that the edges and do not cross.
3 The stretch factor of Delaunay graphs
In this section, we will prove Theorem 1. first, we show that the Delaunay graph satisfies the diamond property and a variant of the good polygon property of Das and Joseph [6]. According to the results of Das and Joseph, this immediately implies that the stretch factor of is bounded. In fact, we will obtain an upper bound on the stretch factor which is better than the one that is implied by Das and Joseph’s result.
3.1 The diamond property
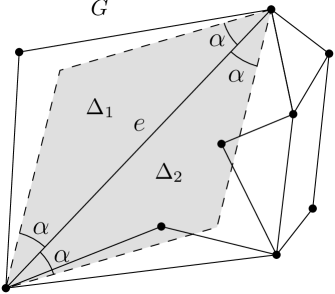
Let be a plane graph with vertex set and let be a real number with . For any edge of , let and be the two isosceles triangles with base and base angle ; see figure 4. We say that satisfies the -diamond property, if at least one of the triangles and does not contain any point of in its interior. The graph is said to satisfy the -diamond property, if every edge of satisfies this property.
Lemma 4
Consider the value that was defined in Section 1. The Delaunay graph satisfies the -diamond property.
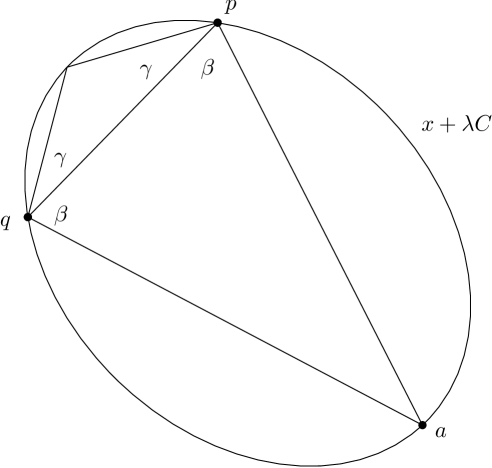
Proof. Let be an arbitrary edge of and let be any point in the relative interior of . By Lemma 1, there exists a real number such that and are on the boundary of the homothet and no point of is in the interior of . The points and partition into two chains. For each of these chains, there is an isosceles triangle with base and whose third vertex is on the chain. We denote the base angles of these two triangles by and ; see figure 5. We may assume without loss of generality that . Let denote the third vertex of the triangle with base angle . If we translate so that coincides with the origin and scale the translated homothet by a factor of , then we obtain the set . This translation and scaling does not change the angles and . Thus, using the notation of Section 1 (see also figure 2), we have . The definition of then implies that
Let be the isosceles triangle with base and base angle such that and the third vertex of are on the same side of . Then is contained in the triangle with vertices , , and . Since the latter triangle is contained in , it does not contain any point of in its interior. Thus, does not contain any point of in its interior. This proves that the edge satisfies the -diamond property.
3.2 The visible-pair spanner property
For a real number , we say that the plane graph satisfies the strong visible-pair -spanner property, if the following is true: For every face of , and for every two vertices and on the boundary of , such that the open line segment joining and is completely in the interior of , the graph contains a path between and having length at most . If for every face of and for every two vertices and on the boundary of , such that the line segment does not intersect the exterior of , the graph contains a path between and having length at most , then we say that satisfies the visible-pair -spanner property. Observe that the former property implies the latter one. Also, observe that these properties are variants of the -good polygon property of Das and Joseph [6]: The -good polygon property requires that contains a path between and that is along the boundary of and whose length is at most ; in the (strong) visible-pair spanner property, the path is not required to be along the boundary of .
In this subsection, we will prove that the Delaunay graph satisfies the visible-pair -spanner property, where is as defined in Section 1. This claim will be proved by generalizing results of Dobkin et al. [8] on so-called one-sided paths.
Let and be two distinct points of and assume that is not an edge of the Delaunay graph . Consider the Voronoi diagram . We consider the sequence of points in whose Voronoi cells are visited when the line segment is traversed from to . If does not contain any Voronoi vertex, then this sequence forms a path in between and . Since, in general, Voronoi cells are not convex, it may happen that this path contains duplicates. In order to avoid this, we define the sequence in the following way.
In the rest of this section, we will refer to the line through and as the -axis, and we will say that is to the left of . This implies a left-to-right order on the -axis, the notion of a point being above or below the X-axis, as well as the notions horizontal and vertical. (Thus, conceptually, we rotate and translate all points of , the set , the Voronoi diagram , and the , such that and are on a horizontal line and is to the left of . Observe that is still defined based on the lexicographical order of the points of S before this rotation and translation.) In the following, we consider the (horizontal) line segment . If this segment contains a Voronoi vertex, then we imagine moving vertically upwards by an infinitesimal amount. Thus, we may assume that does not contain any Voronoi vertex of the (rotated and translated) Voronoi diagram .
The first point in the sequence is . We define to be the point on the line segment such that and is closest to .
Let and assume that the points of and the points in have already been defined, where is the point on the line segment such that and is closest to . If , then the construction is completed. Otherwise, observe that is in the relative interior of a Voronoi edge. We define to be the point of whose Voronoi cell contains on its boundary, and define to be the point on the line segment such that and is closest to .
Let be the sequence of points in obtained in this way. By construction, these points are pairwise distinct and for each with , the Voronoi cells and share an edge. Therefore, by definition, is an edge in . Thus, defines a path in between and . We call this path the direct path between and . If all points are strictly on one side of the line through and , then we say that the direct path is one-sided.
We will show in Lemma 6 that the length of a one-sided path is at most . The proof of this lemma uses a geometric property which we prove first.
Let be a homothet of whose center is on the -axis, and let and be two points on the boundary of that are on or above the -axis. The points and partition the boundary of into two chains. One of these chains is completely on or above the -axis; we denote this chain by . The length of this chain is denoted by .
For two points and on the -axis, we write if is strictly to the left of , and we write if or .
We now state the geometric property, which is illustrated in figure 6. Recall the value that was defined in Section 1.

Lemma 5
Let and be two homothets of whose centers and are on the -axis. Assume that , , and . For , let and be the leftmost and rightmost points of on the -axis, respectively. Assume that and . Let be a point that is on the boundaries of both and and on or above the -axis. Let and . Then
Proof. We define . Let be the homothet of whose center is on the -axis such that the intersection between and the -axis is equal to the line segment , and let ; see figure 6. Observe that, for , is obtained from by a scaling by a factor of . Thus, since , we have
Let be the homothet of whose center is on the -axis such that the intersection between and the -axis is equal to the line segment , and let . Since is obtained from by a scaling by a factor of , we have
Thus, we have
By convexity, we have . Then it follows, again from convexity (see Benson [1, page 42]), that
Thus, we have
which implies that
Since, by the definition of , , the proof is complete.
We are now ready to prove an upper bound on the length of a one-sided path.
Lemma 6
If the direct path between and is one-sided, then its length is at most .
Proof. As above, we assume that and are on the -axis and that is to the left of . Consider the direct path in and the sequence , as defined above. Since the direct path is one-sided, we may assume without loss of generality that the points are strictly above the -axis. We have to show that
| (1) |
Recall that, for each with , is in the relative interior of and is on the line segment . Therefore, by Lemma 1, if we define (which is equal to ), then the homothet contains and on its boundary and no point of is in its interior.
For each with , let and be the leftmost and rightmost points of that are on the -axis, respectively. We will prove that for each with ,
| (2) |
Before we prove (2), we show that . Observe that . Assume that there is an index such that . Since , it follows that . If , then and, therefore, is completely contained in the interior of . This is a contradiction, because is on the boundary of , but no point of is in the interior of . Thus, we have . Since , we have , which is a contradiction.
Thus, we have shown that . By a symmetric argument, it follows that .
Now we are ready to prove (2). The proof is by induction on . For the base case, i.e., when , we have to show that
Since , this inequality follows from the definition of .
Let and assume that (2) holds for . We have to show that (2) holds for , i.e.,
| (3) |
By the induction hypothesis, we have
Thus, (3) holds if we can show that
| (4) |
We distinguish two cases.
Case 1: .
By the triangle inequality, we have
Since is on the boundary of and strictly above the -axis, we have
It follows that
Thus, (4) holds.
Case 2: .
Since is on the boundaries of both and and strictly above the -axis, we can apply Lemma 5 with and obtain
Thus,
We claim that . Assuming this is true, it follows that
i.e., (4) holds.
It remains to prove that . Since and is strictly above the -axis, this is true for . Assume that and . Then, since is strictly above the -axis, is in the relative interior of .
By the definition of the point , there is a point on the -axis such that and the line segment is contained in the Voronoi cell . By Lemma 2, the triangle with vertices , , and is contained in .
Again by the definition of the point , there is a point on the -axis such that and the line segment is contained in the Voronoi cell . By Lemma 2, the triangle with vertices , , and is contained in .
Since and are strictly above the -axis and since is in the relative interior of , the intersection of and has a positive area and is contained in the intersection of and . This is a contradiction, because the area of the intersection of any two Voronoi cells is zero.
We are now ready to prove that the Delaunay graph satisfies the visible-pair spanner property:
Lemma 7
The Delaunay graph satisfies the visible-pair -spanner property.
Proof. Recall from Lemma 3, that the graph is plane. It suffices to prove that satisfies the strong visible-pair -spanner property. Let be a face of and let and be two vertices on such that the open line segment between and is contained in the interior of . We have to show that there is a path in between and whose length is at most .
As before, we assume that and are on the -axis and that is to the left of . Consider the direct path in and the sequence , as defined in the beginning of this section. We will show that the direct path is one-sided. The lemma then follows from Lemma 6.
Since the open line segment between and is in the interior of , none of the points is on the closed line segment . Assume that for some with , is on the -axis. Then is either strictly to the left of or strictly to the right of . We may assume without loss of generality that is strictly to the right of . Consider the point and the homothet as in the proof of Lemma 6. Since is on and in the interior of , and since is on the boundary of , it follows from convexity that is in the interior of , which is a contradiction. Thus we have shown that none of the points is on the -axis.
Assume that the direct path is not one-sided. Then there is an edge on this path such that one of and is strictly below the -axis and the other point is strictly above the -axis. Let be the intersection between and the -axis. By assumption, is not on the open line segment joining and , and by Lemma 1, and . Thus, is either strictly to the left of or strictly to the right of . We may assume without loss of generality that is strictly to the right of . Consider again the point and the homothet as in the proof of Lemma 6. This homothet contains the points , and . Thus, by convexity, contains the triangle with vertices , , and . Since is in the interior of this triangle, it follows that is in the interior of , which is a contradiction.
3.3 The proof of Theorem 1
Das and Joseph [6] have shown that any plane graph satisfying the diamond property and the good polygon property has a bounded stretch factor. The analysis of the stretch factor was slightly improved by Bose et al. [2]. A close inspection of the proof in [2] shows that the following holds: Let be a geometric graph with the following four properties:
-
1.
is plane.
-
2.
satisfies the -diamond property.
-
3.
The stretch factor of any one-sided path in is at most .
-
4.
satisfies the visible-pair -spanner property.
Then, is a -spanner for
We have shown that the Delaunay graph satisfies all these properties: By Lemma 3, is plane. By Lemma 4, satisfies the -diamond property. By Lemma 6, the stretch factor of any one-sided path in is at most . By Lemma 7, satisfies the visible-pair -spanner property. If is a triangulation, then obviously, satisfies the visible-pair -spanner property. Therefore, we have completed the proof of Theorem 1.
4 Concluding remarks
We have considered the Delaunay graph , where is a compact and convex set with a non-empty interior and is a finite set of points in the plane. We have shown that the (Euclidean) stretch factor of is bounded from above by a function of two parameters and that are determined only by the shape of . Roughly speaking, these two parameters give a measure of the “fatness” of the set .
Our analysis provides the first generic bound valid for any compact and convex set . In all previous works, only special examples of such sets were considered. Furthermore, our approach does not make any “general position” assumption about the point set , while most related works on Delaunay graphs do not consider the case when four points are cocircular.
Note that for the Euclidean Delaunay triangulation (i.e., when the set is the disk of radius one, and with no four cocircular points), we have and , and we derive an upper bound on the stretch factor of .
Observe that this is much worse than the currently best known upper bound (as proved by Keil and Gutwin [9]), which is . We leave open the problem of improving our upper bound. In particular, is it possible to generalize the techniques of Dobkin et al. [8] and Keil and Gutwin [9], from the Euclidean metric to an arbitrary convex distance function?
References
- [1] R. V. Benson. Euclidean Geometry and Convexity. McGraw-Hill, New York, NY, 1966.
- [2] P. Bose, A. Lee, and M. Smid. On generalized diamond spanners. In Proceedings of the 10th Workshop on Algorithms and Data Structures, volume 4619 of Lecture Notes in Computer Science, pages 325–336, Berlin, 2007. Springer-Verlag.
- [3] L. P. Chew. There is a planar graph almost as good as the complete graph. In Proceedings of the 2nd ACM Symposium on Computational Geometry, pages 169–177, 1986.
- [4] L. P. Chew. There are planar graphs almost as good as the complete graph. Journal of Computer and System Sciences, 39:205–219, 1989.
- [5] L. P. Chew and R. L. Drysdale. Voronoi diagrams based on convex distance functions. In Proceedings of the 1st ACM Symposium on Computational Geometry, pages 235–244, 1985.
- [6] G. Das and D. Joseph. Which triangulations approximate the complete graph? In Proceedings of the International Symposium on Optimal Algorithms, volume 401 of Lecture Notes in Computer Science, pages 168–192, Berlin, 1989. Springer-Verlag.
- [7] M. de Berg, M. van Kreveld, M. Overmars, and O. Schwarzkopf. Computational Geometry: Algorithms and Applications. Springer-Verlag, Berlin, 2nd edition, 2000.
- [8] D. P. Dobkin, S. J. Friedman, and K. J. Supowit. Delaunay graphs are almost as good as complete graphs. Discrete & Computational Geometry, 5:399–407, 1990.
- [9] J. M. Keil and C. A. Gutwin. Classes of graphs which approximate the complete Euclidean graph. Discrete & Computational Geometry, 7:13–28, 1992.
- [10] R. Klein and D. Wood. Voronoi diagrams based on general metrics in the plane. In Proceedings of the 5th Symposium on Theoretical Aspects of Computer Science, volume 294 of Lecture Notes in Computer Science, pages 281–291, Berlin, 1988. Springer-Verlag.
- [11] L. Ma. Bisectors and Voronoi Diagrams for Convex Distance Functions. Ph.D. thesis, Department of Computer Science, FernUniversität Hagen, Germany, 2000.
- [12] G. Narasimhan and M. Smid. Geometric Spanner Networks. Cambridge University Press, Cambridge, UK, 2007.