On the unification of the graph edit distance and graph matching problems

Graphs are frequently used in various fields of computer science, since they constitute a universal modeling tool which allows the description of structured data. The handled objects and their relations are described in a single and human-readable formalism. Hence, tools for graphs supervised classification and graph mining are required in many applications such as pattern recognition (Riesen, 2015), chemical components analysis, transfer learning (Das and Lee, 2018). In such applications, comparing graphs is of first interest. The similarity or dissimilarity between two graphs requires the computation and the evaluation of the “best” matching between them. Since exact isomorphism rarely occurs in pattern analysis applications, the matching process must be error-tolerant, i.e., it must tolerate differences on the topology and/or its labeling. The Graph Edit Distance (GED)(Riesen, 2015) problem and the Graph Matching problem (GM) (Swoboda et al., 2017) provide two different error models. These two problems have been deeply studied but they have split the research community into two groups of people developing separately quite different methods.

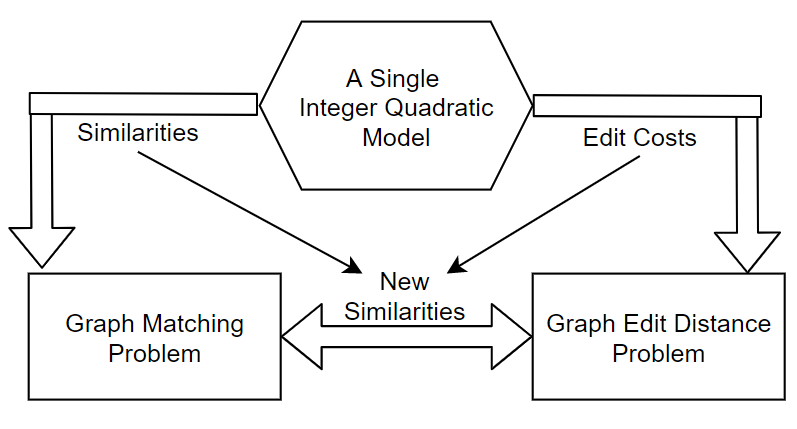
In this paper, we propose to unify the GED problem and the GM problem in order to unify the work force in terms of methods and benchmarks. We show that the GED problem can be equivalent to the GM problem under certain (permissive) conditions. The paper is organized as follows: Section 2, we give the definitions of the problems. Section 3, the state of the art on GM and GED is presented along with the literature comparing GED and GM to other problems. Section 4, a specific related work is detailed since it is the basement of our reasoning. Section 5, our proposal is described and a proof is given. Section 6, experimental results are presented to validate empirically our proposal. Finally, conclusions are drawn.

In this section, we define the problems to be studied. An attributed graph is considered as a set of 4 tuples ($V$,$E$,$\mu$,$\zeta$) such that: $G$ = ($V$,$E$,$\mu$,$\zeta$). $V$ is a set of vertices. $E$ is a set of edges such as $E\subseteq V\times V$. $\mu$ is a vertex labeling function which associates a label to a vertex. $\zeta$ is an edge labeling function which associates a label to an edge.

In this section, the state of the art is presented. First, the solution methods for GED and GM are described. Finally, papers comparing GED to other matching problems are mentioned.

In (Lerouge et al., 2017), an ILP was proposed to model the GED problem. This model will play an important role in our proposal so we propose to give a brief definition of this model. For each type of edit operation, a set of corresponding binary variables is defined in Table 1.

The objective function (4) is the overall cost induced by an edit path $({y},{z},{a},{b},{g},{h})$ that transforms a graph $G_{1}$ into a graph $G_{2}$. In order to get the graph edit distance between $G_{1}$ and $G_{2}$, this objective function must be minimized.

		$\displaystyle C({y,z,a,b,g,h})=\Biggl{(}\sum_{u_{i}\in V_{1}}\sum_{v_{k}\in V_{2}}c(u_{i}\rightarrow v_{k})\cdot y_{i,k}$		(4)
		$\displaystyle+\sum_{e_{ij}\in E_{1}}\sum_{e_{kl}\in E_{2}}c(e_{ij}\rightarrow e_{kl})\cdot z_{ij,kl}+\sum_{u_{i}\in V_{1}}c(u_{i}\rightarrow\epsilon)\cdot a_{i}$
		$\displaystyle+\sum_{v_{k}\in V_{2}}c(\epsilon\rightarrow v_{k})\cdot g_{k}+\sum_{e_{ij}\in E_{1}}c(e_{ij}\rightarrow\epsilon)\cdot b_{ij}$
		$\displaystyle+\sum_{e_{kl}\in E_{2}}c(\epsilon\rightarrow e_{kl})\cdot h_{kl}\Biggr{)}$

Now, the constraints are presented. They are mandatory to guarantee that the admissible solutions of the ILP are edit paths that transform $G_{1}$ in $G_{2}$. The constraint (5a) ensures that each vertex of $G_{1}$ is either mapped to exactly one vertex of $G_{2}$ or deleted from $G_{1}$, while the constraint (5b) ensures that each vertex of $G_{2}$ is either mapped to exactly one vertex of $G_{1}$ or inserted in $G_{1}$:

	$\displaystyle a_{i}+\sum_{v_{k}\in V_{2}}y_{i,k}=1\quad\forall u_{i}\in V_{1}$		(5a)
	$\displaystyle g_{k}+\sum_{u_{i}\in V_{1}}y_{i,k}=1\quad\forall v_{k}\in V_{2}$		(5b)

The same applies for edges:

	$\displaystyle b_{ij}+\sum_{e_{kl}\in E_{2}}z_{ij,kl}=1\quad\forall e_{ij}\in E_{1}$		(6a)
	$\displaystyle h_{kl}+\sum_{e_{ij}\in E_{1}}z_{ij,kl}=1\quad\forall e_{kl}\in E_{2}$		(6b)

The topological constraints defined in Definition 4 can be expressed with the following constraints (7) and (8):

$e_{ij}$ and $e_{kl}$ can be mapped only if their head vertices are mapped:

$$z_{ij,kl}\leq y_{i,k}\quad\forall(e_{ij},e_{kl})\in E_{1}\times E_{2}$$

(7)

$e_{ij}$ and $e_{kl}$ can be mapped only if their tail vertices are mapped:

$$z_{ij,kl}\leq y_{j,l}\quad\forall(e_{ij},e_{kl})\in E_{1}\times E_{2}$$

(8)

The insertions and deletions variables $a$, $b$, $g$ and $h$ help the reader to understand how the objective function and the constraints were obtained, but they are unnecessary to solve the GED problem. In the equation (4), the variables ${a},{b},{g}\text{ and }{h}$ are replaced by their expressions deduced from the equations (5a), (5b), (6a) and (6b). For instance, from the equation (5a), the variable $a$ is deduced: $a_{i}=1-\sum_{v_{k}\in V_{2}}y_{i,k}$ and replaced in the equation (4), the part of the objective function concerned by variable $a$ becomes:

	$\displaystyle\sum_{u_{i}\in V_{1}}c(u_{i}\rightarrow\epsilon)\cdot a_{i}=$	$\displaystyle\sum_{u_{i}\in V_{1}}c(u_{i}\rightarrow\epsilon)$		(9)
		$\displaystyle+\sum_{u_{i}\in V_{1}}\sum_{v_{k}\in V_{2}}-c(u_{i}\rightarrow\epsilon).y_{i,k}$

Consequently, a new objective function is expressed as follows:

	$\displaystyle C^{\prime}({y,z})=$	$\displaystyle\gamma+\sum_{u_{i}\in V_{1}}\sum_{v_{k}\in V_{2}}\Bigl{(}c(u_{i}\rightarrow v_{k})$		(10)
		$\displaystyle-c(u_{i}\rightarrow\epsilon)-c(\epsilon\rightarrow v_{k})\Bigr{)}\cdot y_{i,k}$
		$\displaystyle+\sum_{e_{ij}\in E_{1}}\sum_{e_{kl}\in E_{2}}\Bigl{(}c(e_{ij}\rightarrow e_{kl})$
		$\displaystyle-c(e_{ij}\rightarrow\epsilon)-c(\epsilon\rightarrow e_{kl})\Bigr{)}\cdot z_{ij,kl}$
	$\displaystyle\text{with }\gamma=$	$\displaystyle\sum_{u_{i}\in V_{1}}c(u_{i}\to\epsilon)+\sum_{v_{k}\in V_{2}}c(\epsilon\to v_{k})$
		$\displaystyle+\sum_{e_{ij}\in E_{1}}c(e_{ij}\to\epsilon)+\sum_{e_{kl}\in E_{2}}c(\epsilon\to e_{kl})$

Equation (10) shows that the GED can be obtained without explicitly computing the variables ${a},{b},{g}\text{ and }{h}$. Once the formulation solved, all insertion and deletion variables can be a posteriori deduced from the substitution variables.

The vertex mapping constraints (5a) and (5b) are transformed into inequality constraints, without changing their role in the program. As a side effect, it removes the $a$ and $g$ variables from the constraints:

$$\sum_{v_{k}\in V_{2}}y_{i,k}\leq 1\quad\forall u_{i}\in V_{1}$$

(11)

$$\sum_{u_{i}\in V_{1}}y_{i,k}\leq 1\quad\forall v_{k}\in V_{2}$$

(12)

In fact, the insertions and deletions variables $a$ and $g$ of the equations (5a) and (5b) can be seen as slack variables to transform inequality constraints to equalities and consequently providing a canonical form. The entire formulation is called F2 and described as follows :

$\gamma$ is not a function of $y$ and $z$. It does not impact the minimization problem. However, $\gamma$ is mandatory to obtain the GED value (i.e. $d_{min}(G_{1},G_{2})$ from Problem 3). The topological constraints (7) and (8) are expressed in another way and are replaced by the constraints (13d) and (13e).

In this paragraph, we propose to draw a relation between the graph matching and graph edit distance problems. Especially, we create a link between both problems through a change of similarity functions. Our proposal can be stated as follows:

To intuitively demonstrate the exactness of the proposition, we proceed as follows :

1. 1.

   We start from the GED problem expressed by model F2 (see Model 13).

2. 2.

   We link the similarity function $s$ with the cost function $c$ thanks to a new similarity function $s^{\prime}$.

3. 3.

   With this similarity function $s^{\prime}$, we show that F2 turns to be a maximization problem and we call this new model F2’.

4. 4.

   F2’ is modified by switching from a linear to a quadratic model called GMM’.

5. 5.

   GMM’ is identical to GMM. It is sufficient to show that both models express the same problem, that is to say, the graph matching problem.

Under the condition of Proposition 1, the optimal assignment obtains when solving the graph matching problem can be used to reconstruct an optimal solution of the GED problem. An instance of GED and an instance of GM are presented in Figure 1. Solutions of the GED instance are presented with respect to the cost function $c$ while the graph matching solutions are presented with respect to the similarity function $s^{\prime}$. The optimal matching of both instances are the same.

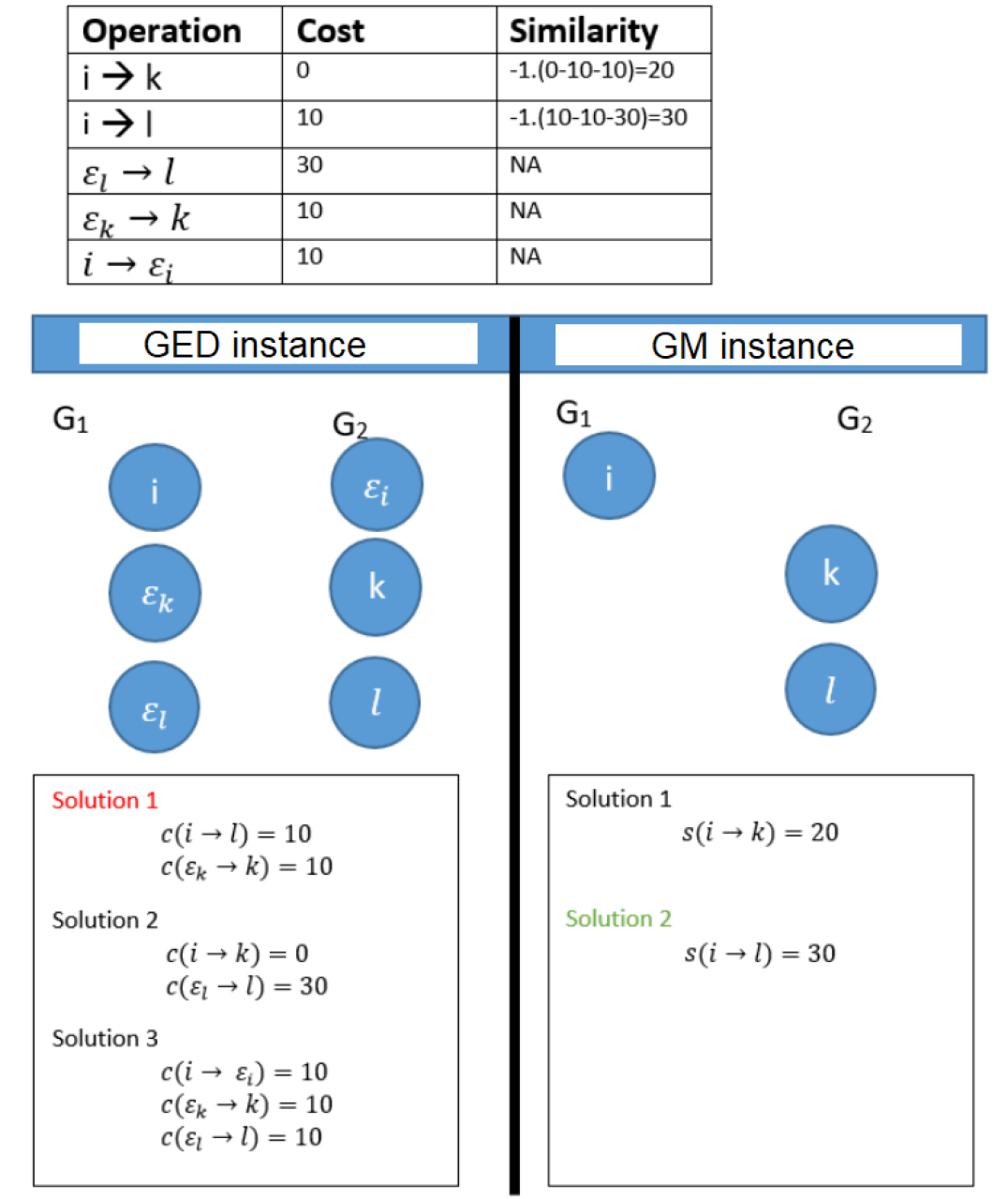
Model GMM’ has $|V_{1}|.|V_{2}|$ variables and $|V_{1}|+|V_{2}|$ constraints. Similarity functions can be represented by a similarity matrix $K$ of size is $|V_{1}|.|V_{2}|\times|V_{1}|.|V_{2}|$.

Proposition 1 is a first attempt toward the unification of two communities working respectively on GED and GM problems. All the methods solving the graph matching problem can be used to solve the graph edit distance problem under a specific similarity function $s^{\prime}(u_{i}\to v_{k})=-\Bigr{(}c(u_{i}\to v_{k})-c(u_{i}\to\epsilon)-c(\epsilon\to v_{k})\Bigr{)}$.

In this section, we show the results of our numerical experiments to validate our proposal that the model GMM’ can model the GED problem if $s^{\prime}(i\to k)=-\{c(i\to k)-c(i\to\epsilon)-c(\epsilon\to k)\}$. We based our protocol on the ICPR GED contest¹¹1 https://gdc2016.greyc.fr/ (Abu-Aisheh et al., 2017). Among the data sets available, we chose the GREC data set for two reasons. First, graphs sizes range from 5 to 20 nodes and these sizes are amendable to compute optimal solutions. Second, the GREC cost function, defined in the contest, is complex enough to cover a large range of matching cases. This cost function is not a constant value and includes euclidean distances between point coordinates. The reader is redirected to (Abu-Aisheh et al., 2017) for the full definition of the cost function. From the GREC database, we chose the subset of graphs called ”MIXED” because it holds 10 graphs of various sizes. We computed all the pairwise comparisons to obtain 100 solutions. We compared the optimal solutions obtained by our Model GMM’ and the optimal solutions found by the straightforward ILP formulation called F1 (Lerouge et al., 2017). We computed the average difference between the GED values and the objective function values of our model GMM’. The average difference is exactly equal to zero. This result corroborates our theoretical statement. Detailed results and codes can be found on the website https://sites.google.com/view/a-single-model-for-ged-and-gm.

In this paper, an equivalence between graph matching and graph edit distance problems was proven under a reformulation of the similarity functions between nodes and edges. These functions should take into account explicitly the deletion and insertion costs. That’s the major difference between GM and GED problems. In the GED problem, costs to delete or to insert vertices or edges are explicitly introduced in the error model. On the other hand, deletion costs are implicitly set to a specific value (that is to say 0) in the GM problem. Many learning methods aim at learning edit costs (Serratosa, 2020; Martineau et al., 2020) or matching similarities (Zanfir and Sminchisescu, 2018; Caetano et al., 2007). Learned matching similarities may include implicitly deletion and insertion costs. Does it help the learning algorithm to learn separately insertion and deletion costs? That is still an open question. However, with this paper, we stand for a rapprochement of the research communities that work on learning graph edit distance and learning graph matching because edit costs can be hidden in the learned similarities.