On the Unique Determination of Modal Multiconductor Transmission-Line Properties

The analysis of TL systems typically begins with extracting their per-unit-length inductance and capacitance matrices ($\left[L\right]$ and $\left[C\right]$, respectively). These matrices detail the terminal-domain values, but for clarity in the following analysis, the subscripts $T$ and $M$ will be used to indicate which domain (terminal or modal) is being used in each matrix, e.g., $\left[L_{T}\right]$ or $\left[C_{M}\right]$.

The transformation between the two domains makes use of similarity transforms, specified in terms of currents and voltages, and which are expressed as (nonsingular) matrices [1, 2]. These transformations are defined as

such that each column of $\left[T_{I}\right]$ and $\left[T_{V}\right]$ corresponds to a particular mode, and for which the entries describe the relative (i.e., with respect to the modal quantities) currents and voltages on each conductor for that mode. The TL wave equations for propagation along $z$ in the terminal domain can be expressed as [1]

where $\left[Z_{T}\right]$ and $\left[Y_{T}\right]$ are the per-unit-length impedance and admittance, respectively, in the terminal domain. The modal-domain equations have the same form; that is

Inserting (1a) and (1b) into (2) yields

which can be re-arranged and compared to (3) to give the relations

Using these definitions, the propagation constants and characteristic impedances can be expressed as

where $\left[\gamma\right]$ is the propagation constant matrix, and $\left[{Z_{c}}\right]$ is the characteristic impedance matrix. Additionally, characteristic impedances can be defined as

Again applying equations (1a) and (1b), and comparing (8a) with (8b) yields the relation

Other TL modal properties may be determined in a similar manner.

Equations (5a) through (9) are well known and unambiguously correct. However, ambiguity is introduced in the solution process – specifically, through the use of (6a) and (6b), which are used to solve for the the transformation matrices $\left[T_{V}\right]$ and $\left[T_{I}\right]$ independent of one another [2]. Specifically, since these two equations are of the form

where $\left[M\right]$ is a matrix to be diagonalized, $\left[Q\right]$ is the diagonalization matrix, and $\left[D\right]$ is a diagonal matrix said to be the diagonalized form of $\left[M\right]$, a regular eigenvalue process is typically used to simultaneously solve for $\left[Q\right]$ and $\left[D\right]$, given $\left[M\right]$. Unfortunately, the matrix $\left[Q\right]$ is not unique. It can be observed that if $\left[Q\right]$ is post-multiplied by a diagonal matrix $\left[g\right]$, such that

then the diagonalization of $\left[M\right]$ by use of $\left[S\right]$ is

and is still valid, since

A diagonal $\left[g\right]$ ensures the diagonality of $\left[D\right]$, since any $\left[Q\right]^{\text{-}1}\left[M\right]\left[Q\right]$ will itself be diagonal (subject to some physical constraints – it has been shown that some physical systems can result in a non-diagonalizable matrix [10], although these are unlikely to be encountered in practice). Furthermore, it can be shown that since $\left[Q\right]^{\text{-}1}\left[M\right]\left[Q\right]$ is diagonal, the product $\left[g\right]^{\text{-}1}\left[Q\right]^{\text{-}1}\left[M\right]\left[Q\right]\left[g\right]$ reduces simply to $\left[Q\right]^{\text{-}1}\left[M\right]\left[Q\right]$, such that the value of $\left[g\right]$ has no bearing on the solution values $\left[D\right]$ and $\left[Q\right]$ in (13) [2].

This fact allows for the correct diagonalization of the propagation constants in (6a) and (6b), regardless of the values of $\left[g\right]$. The problem with this ambiguity arises from attempting to solve any of (5a), (5b), (9), for which $\left[T_{V}\right]$ and $\left[T_{I}\right]$ could each be post-multiplied by an arbitrary diagonal matrix – however, in these equations, the value of $\left[g\right]$ will indeed have a direct impact on the diagonalized results, for example

the solution of which is presently ambiguous. In the following work the correction matrices $\left[g\right]$ will be utilized with the following definitions:

where $\left[T_{I}\right]_{old}$ and $\left[T_{V}\right]_{old}$ are the matrices determined by the original eigenmode solution, and $\left[T_{I}\right]_{new}$ and $\left[T_{V}\right]_{new}$ are the corrected transformation matrices used to produce the correct modal TL properties.

Presently, there exist some strategies for solving the appropriate values of $\left[g_{V}\right]$ and $\left[g_{I}\right]$. Two of the most common are based on simple normalizations that are typically arbitrarily chosen and applied; both were detailed extensively in [6]. The first is the normalization of the product $\left[T_{V}\right]^{T}\left[T_{I}\right]$, for which it was shown that the symmetric nature of $\left[\gamma_{M}\right]^{2}$, $\left[Z_{T}\right]$, $\left[Y_{T}\right]$ leads to the conclusion that

where $\left[D\right]$ is any diagonal matrix, typically chosen to be identity for convenience. This is the introduction of one ambiguity, since the choice is entirely arbitrary. The second method involves a form of self-normalization of the matrix diagonals, such that

This process also introduces some ambiguity, since there is no physical justification for such a method. However, even though these processes are not rigorously justified or correct, they typically result in solutions with tolerable error, and therefore have been widely adopted. Some work has also been done in attempting to normalize via physical quantities such as voltage, current, and power, but this has generally resulted in non-unique solutions [8].

The definition of such a modal-terminal domain transformation relies on the fact that both domains are equally valid representations of the same physical system. Therefore, various physical properties must be equivalent in both domains, foremostly, total energy and total charge. In the frequency domain, these are directly related to total power and current. Accordingly, the following are postulated:

• •

  That the total power being carried by a TL in the modal domain is equal to that carried in the terminal domain. This will be elaborated on in Sec. II-E.
  

• •

  That the total co-directed currents in the modal domain are equal to the total of those in the terminal domain. This will be investigated in Sec. II-F.
  

While the total voltages and currents in the terminal domain ($\vec{V}_{T}$ and $\vec{I}_{T}$, respectively) represent a superposition of excited modes, it will be of interest to examine the effects of a single excited mode in the terminal domain. In this case, these terminal voltages and currents will be expressed as:

where ${V_{M}}_{n}$ and ${I_{M}}_{n}$ are the voltage and current of the excited mode $n$, respectively, and the delta vector $\vec{\delta}_{n}$ is defined as

The complex-conjugate transpose of a matrix or vector will be expressed as

where the over-bar denotes the element-wise complex conjugate. The inner product will be used to represent sums over vectors; that is, for vectors $\vec{a}$ and $\vec{b}$

In this manner, the sum of the elements in a single vector may be expressed as

where $\vec{1}$ is a vector, the entries of which are each unity.

In accordance with the first postulate,

Substituting the terminal to modal domain transforms in (1a) and (1b) yields

to which one of the solutions is the identity matrix $\left[I\right]$. Furthermore, equating the carried power by a single mode to its terminal-domain equivalent yields

from which the scalars can be cancelled to give

which, in conjunction with (24) demonstrates the unique definition of

A similar derivation was investigated in [6], however, this was only for one component of power (the real part), and subsequently an equation such as (26) could not be developed through the cancellation of complex voltage and current terms to demonstrate the identity matrix as the unique solution to (27).

Consider first a single excited mode, $n$, which is modelled via a two-conductor TL. The current magnitude for this mode is expressed, in accordance with the previous definitions, as ${I_{M}}_{n}$. While this is a single quantity, there are of course two currents present: one on each conductor. Let the magnitude of the current on one of the conductors be labelled ${I_{M}}_{n}\left(+\right)$, and the magnitude of the current flowing in the opposite direction – that is, on the other conductor – be labelled ${I_{M}}_{n}\left(-\right)$. The conservation of current enforces the equality of the currents ${I_{M}}_{n}\left(+\right)={I_{M}}_{n}\left(-\right)$.

Consider next a TL with more than two conductors, as described in the terminal domain. Assume for now that the current carried by the reference conductor is included in the set of all currents. It is certain that the conservation of current specifies that the sum of the currents on all conductors must be zero. Similar to the modal domain TL, assume that the current magnitudes may be divided into two sets $\vec{I}_{T}\left(+\right)$ and $\vec{I}_{T}\left(-\right)$, with the membership of the sets being determined by the phase of these currents with respect to the modal currents. Although it may seem intuitive for TEM modes, a proof that only two such contra-directed phases (corresponding to co- and contra-directed currents) exist is supplied in Appendix A. According to the conservation of current, the sums of each group must be equal to each other, that is: $\vec{1}^{T}\vec{I}_{T}\left(+\right)=\vec{1}^{T}\vec{I}_{T}\left(-\right)$. Furthermore, the set of total currents on all conductors is equal to the difference of the two groups, such that

The vector $\vec{I}_{T}\left(+\right)$ will then contain an entry of zero wherever $\vec{I}_{T}\left(-\right)$ has a nonzero entry, and vice-versa, such that all vectors have the same length (which is the number of conductors in the TL).

It is known from (1b) that the distribution of terminal-domain currents is dictated by the transformation matrix $\left[T_{I}\right]$ – that is, if a single mode is excited, the currents on each conductor are uniquely specified by the corresponding column of $\left[T_{I}\right]$. Let the transformation matrix then be separated into two new matrices – one, labelled $\left[T_{I}(+)\right]$, consisting of the components related to the set of currents $\vec{I}_{T}\left(+\right)$ and another labelled $\left[T_{I}(-)\right]$, consisting of the components related to the set of currents $\vec{I}_{T}\left(-\right)$. Then,

The equality of currents between domains specifies that the total co-directed currents must be equal in both the modal and terminal domains. Specifically, for an excited mode $n$, there must exist appropriate sets $\vec{I}_{T}\left(+\right)_{new}$ and $\vec{I}_{T}\left(-\right)_{new}$, such that

Invoking (18b) and (29b) allows the previous expressions to be expanded to

The scalars ${I_{M}}_{n}\left(+\right)$ and ${I_{M}}_{n}\left(-\right)$ can then be cancelled to yield the expressions:

which simply imply that the sum of each column in $\left[T_{I}(+)\right]_{new}$ and $\left[T_{I}(-)\right]_{new}$ must be equal to unity.

The unique correction process may then be determined by substituting (29a) into (15b), and letting the matrices $\left[T_{I}(+)\right]_{old}$ and $\left[T_{I}(-)\right]_{old}$ be specified to contain the same non-zero indices as $\left[T_{I}(+)\right]_{new}$ and $\left[T_{I}(-)\right]_{new}$,

Substituting the previous equations into (32a) and (32b) yields:

which indicates that the entries along the diagonal of the correction matrix $\left[g_{I}\right]$ are simply the inverse of the sum of the corresponding columns in $\left[T_{I}(+)\right]_{old}$ and $\left[T_{I}(-)\right]_{old}$.

Recall that in practical use, the information related to the reference conductor would not be contained directly in $\vec{I}_{Tnew}$, $\left[T_{I}\right]_{new}$, $\left[T_{I}(+)\right]_{new}$, or $\left[T_{I}(-)\right]_{new}$. This is not such a critical issue, as being a single, scalar value, it would, if accounted for, either appear in the set of currents $\vec{I}_{T}\left(+\right)_{new}$ or $\vec{I}_{T}\left(-\right)_{new}$, and subsequently be manifested in either of $\left[T_{I}(+)\right]_{old}$ or $\left[T_{I}(-)\right]_{old}$. This does mean that, in practice, only one of (34a) or (34b) will be correct – but the issue is simply resolved by noting that the correct equation will always correspond to the sum with the larger magnitude. Then,

and hence the current transformation matrix is uniquely defined.

It is worth noting that if the transformation matrices (in their corrected state) are complex, several contradictions may arise with the previously derived equations. To alleviate such concerns, Appendix B offers a proof of the remarkable fact that the transformation matrices must be real – indicating that the terminal-domain voltages and currents must always be in phase with their corresponding modal quantities.

The solution process to determine the corrected, unique transformation matrices is then as follows:

1. 1.

   Find the original, uncorrected, transformation matrices $\left[T_{I}\right]_{old}$ and $\left[T_{V}\right]_{old}$ (for example, via an eigenmode process utilizing (6a) and/or (6b)).

2. 2.

   Apply the equality of currents to obtain $\left[g_{I}\right]$ from $\left[T_{I}\right]_{old}$, utilizing (35).

3. 3.

   Apply (15b) to obtain the correct current transformation matrix $\left[T_{I}\right]_{new}$ from $\left[g_{I}\right]$ and $\left[T_{I}\right]_{old}$.

4. 4.

   Employ the equality of power (27) to obtain the corrected voltage transformation matrix $\left[T_{V}\right]_{new}$, that is, $\left[T_{V}\right]_{new}=\left[T_{I}\right]_{new}^{-1*}$.

A proposed algorithm for correcting the transformation matrices and associated discussion are given in Appendix C.

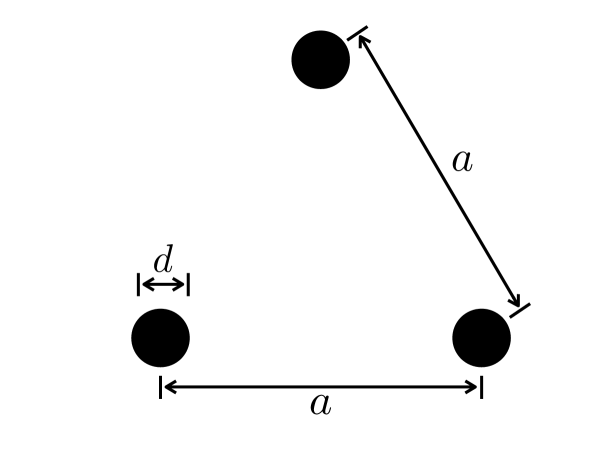
This TL consists of three cylindrical copper conductors of diameter $d$ = 1.00 mm suspended in air and spaced equally apart by a distance $a$ = 3.46 mm, as shown in Fig. 1. Since the system is symmetric, the choice of reference conductor is arbitrary, and the $\left[L_{T}\right]$ and $\left[C_{T}\right]$ matrices are 2$\times$2 in size, with

Employing equations (6a) and (6b) (noting that these two equations are solved independently of one another) yields the modal propagation constants $\left[\gamma_{M}\right]$, as well as the current and voltage transformation matrices:

where it can be noted that the uncorrected transformation matrices within acceptable error satisfy the equality of total power (27). The modal propagation constants agree to within 0.2% with the modal solutions given by HFSS, which are

Subsequently, the terminal and (incorrect) modal characteristic impedances, the latter determined from either (7a) or (7b), are

the latter of which are significantly different from the HFSS modal characteristic impedance values of

exhibiting differences of 39.7% and 40.3%, respectively. This is expected, as the current and voltage transformation matrices $\left[T_{I}\right]$ and $\left[T_{V}\right]$ do not strictly respect current or power equivalence between domains, for which they must be first corrected using the proposed processes.

The correction process is then implemented by utilizing (15a), (15b), (27), and (35). Specifically, implementing the latter gives

Then, it follows that the corrected transformation matrices are

which are well within the acceptable error of being entirely real. Using these new values in (9) gives

which are in much closer agreement (a percent difference of 0.27% for both values on the diagonal) to the modal values given by HFSS (40) than the uncorrected values in (39). For additional verification, it can be shown that, within the given error, $\left[T_{V}\right]_{new}^{T}\left[T_{I}\right]_{new}^{*}=\left[I\right]$, and that $\left[\gamma_{M}\right]$ remains consistent whether solved with (6a) or (6b).

The current and voltage transformation matrices contain information regarding the relative voltage and current distribution of each mode in each column. Observing the first column (mode), it is noted in $\left[T_{I}\right]$ that the relative currents have equal magnitudes and are in the same direction. By deduction, it may be inferred that the reference conductor then carries a relative current with double the magnitude of either of the other two conductors, and from $\left[T_{V}\right]$ it is observed that the two non-reference conductors have the same relative voltage. This mode then corresponds to a “common” mode, where the two-non reference conductors have the same relative current and voltage characteristics. Observing the second mode, it can be seen that in the corresponding second column of $\left[T_{I}\right]$, there are opposite and equal-magnitude relative currents on the non-reference conductors, leading to the conclusion that the relative current on the reference conductor is zero. Since the second column entries in $\left[T_{V}\right]$ are also equal in magnitude, but oppositely directed, it can be inferred that this is a “balanced” (or “differential”) mode.

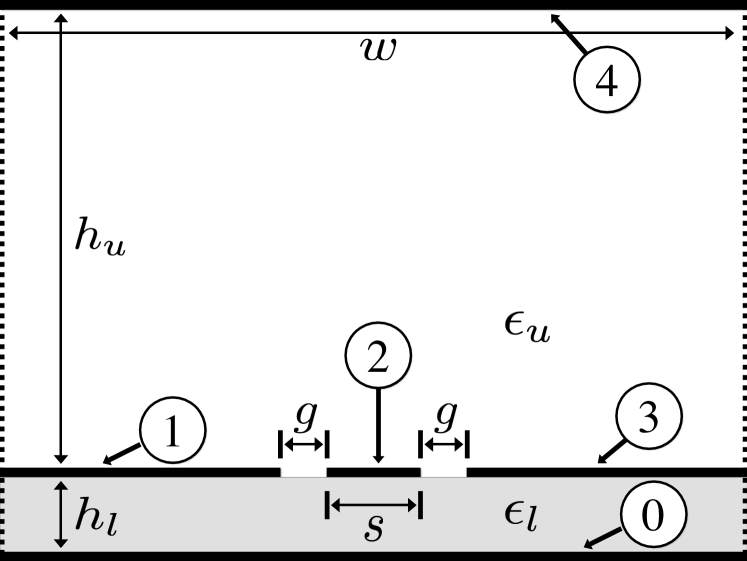
The shielded, conductor-backed coplanar waveguide (S-CBCPW) TL used is shown in Fig. 2. The lower dielectric is RO-3010, and the upper dielectric is air. The boundary conditions used on the vertical sides are (fictitious) perfect magnetic conductors (PMCs), indicated by the dashed lines. The numbers indicate the conductors, with number 0 (the conductor backing) being taken as the reference. Conductors 1 and 3 are the CPW grounds, while conductor 2 is the CPW strip line, and conductor 4 is the shield. The various parameters used were $h_{l}$ = 1.524mm, $h_{u}$ = 100mm, $s$ = 1.00mm, $g$ = 1.00mm, $w$ = 10mm, $\epsilon_{l}$ $\approx$ 10.2, $\epsilon_{u}$ $\approx$ 1.00. The imaginary components of all matrices will be ignored for this example, as they are negligibly small. Simulation in HFSS yields the matrices with real components

These yield modal propagation constants and (uncorrected) transformation matrices

and transformation matrices

The modal propagation constants are once again very close (within 0.2%) to the HFSS-given values, which have imaginary components of

The (real components of the incorrect) modal characteristic impedances derived using the above transformation matrices are

which are not very similar to those given by HFSS:

with percentage differences of 8.6%, 56.7%, 36.5%, and 17.0% respectively. The correction process yields the matrices

which, in turn, allow for the computation of the corrected characteristic impedance matrix, the real values of which are

the values of which are very close to those given by HFSS in (49): percentage differences of 0.17%, 0.06%, 0.63%, and 0.04% respectively.

The nature of the various modes can be determined from observation of the transformation matrices. The first mode (column) is characterized by a relative current value of approximately 0.4 on each of the CPW ground conductors (numbers 1 and 3), and approximately 0.2 on the CPW strip line (conductor 2). There is a negligibly small relative current component on the shield (conductor 4), and the same relative voltage is present on conductors 1 through 4, indicating that there is a negligibly small electric field in the upper region (the region between the plane of conductors 1, 2 and 3, and the plane of conductor 4). Since the same relative voltage exists on the three CPW conductors (1 through 3), it can be concluded that this mode is a parallel-plate-waveguide (PPW)-type mode in the lower dielectric region. The relative current magnitudes are a result of a nearly equally distributed (relative) current density over unequally sized conductors.

The second mode can be analyzed simply, as only two of the conductors – the two CPW ground planes (conductors 1 and 3) – support non-zero relative currents and voltages. This corresponds to the coupled-slotline (CSL) mode, for which there are indeed currents induced on the remaining conductors, but the net currents on each conductor are zero.

The third mode is characterized by a positive relative current on the CPW strip line (conductor 2), and negative relative currents of nearly half that magnitude on each of the CPW grounds (conductors 1 and 3). This is what would be expected of a CPW mode, although it can be observed that the sum of the negative relative currents implies that there is some small relative current component on the reference conductor backing as well. This would be expected from a conductor-backed CPW mode, and also it can be observed from the relative voltages that there is some coupling with the shield as well.

The last mode is similar to the first, in that all of the conductors except for one are equipotential. This, along with the relative currents on all conductors, readily identifies this mode as the PPW-like mode in the upper region.

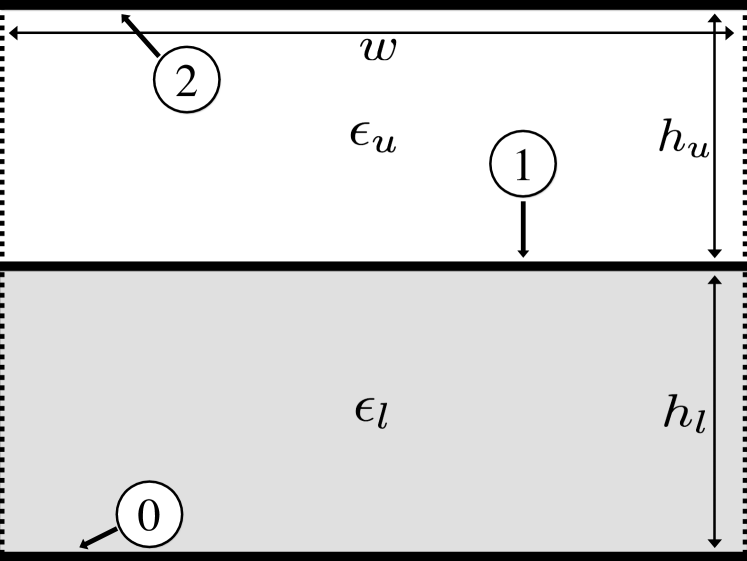
To confirm the validity of the proposed solution, this example will deal with artificially inflated losses. The TL consists of three rectangular conductors, as shown in Fig. 3, which are assumed to be perfectly conducting. It is also assumed that the upper and lower faces of the middle conductor (conductor 1) possess the same voltage and current values, such that there is coupling between the upper and lower regions. The vertical boundary conditions are again modelled as PMCs. Let $w$ = 10 mm, $h_{l}$ = 1.524 mm, $h_{u}$ = 10 mm, $\epsilon_{l}$ = 3.0 $-\ j$3.0, and $\epsilon_{u}$ = 1.0 $-\ j$1.0. Under these conditions, the terminal domain parameters are solved as

These data give modal propagation-constant and (uncorrected) modal characteristic-impedance and transformation matrices of

from which a number of observations may be made. Firstly, the modal propagation constants are in excellent agreement (within 0.03% and 0.4%) of HFSS, which gives

Secondly, the transformation matrices do not satisfy the current equalities, since the sum of the either of the positive or negative currents is not unity, and moreover, one entry of $\left[T_{V}\right]$ has a significant imaginary component. Thirdly, the modal characteristic impedances differ greatly (44.8% and 17.2%, repsectively) from those given by HFSS:

The correction process yields the matrices

from which it can be seen that the transformation matrices are real, and the characteristic impedance values are very close to those given by HFSS (0.03% and smaller than 0.01%), indicating that the modal transformation process proposed in this work is valid even in the presence of extreme loss.