On the use of approximate Bayesian computation Markov chain Monte Carlo with inflated tolerance and post-correction
Abstract.
Approximate Bayesian computation allows for inference of complicated probabilistic models with intractable likelihoods using model simulations. The Markov chain Monte Carlo implementation of approximate Bayesian computation is often sensitive to the tolerance parameter: low tolerance leads to poor mixing and large tolerance entails excess bias. We consider an approach using a relatively large tolerance for the Markov chain Monte Carlo sampler to ensure its sufficient mixing, and post-processing the output leading to estimators for a range of finer tolerances. We introduce an approximate confidence interval for the related post-corrected estimators, and propose an adaptive approximate Bayesian computation Markov chain Monte Carlo, which finds a ‘balanced’ tolerance level automatically, based on acceptance rate optimisation. Our experiments show that post-processing based estimators can perform better than direct Markov chain targetting a fine tolerance, that our confidence intervals are reliable, and that our adaptive algorithm leads to reliable inference with little user specification.
Key words and phrases:
Adaptive, approximate Bayesian computation, confidence interval, importance sampling, Markov chain Monte Carlo, tolerance choice1. Introduction
Approximate Bayesian computation is a form of likelihood-free inference (see, e.g., the reviews Marin et al., 2012; Sunnåker et al., 2013) which is used when exact Bayesian inference of a parameter with posterior density is impossible, where is the prior density and is an intractable likelihood with data . More specifically, when the generative model of observations cannot be evaluated, but allows for simulations, we may perform relatively straightforward approximate inference based on the following (pseudo-)posterior:
| (1) |
where is a ‘tolerance’ parameter, and is a ‘kernel’ function, which is often taken as a simple cut-off , where extracts a vector of summary statistics from the (pseudo) observations.
The summary statistics are often chosen based on the application at hand, and reflect what is relevant for the inference task; see also (Fearnhead and Prangle, 2012; Raynal et al., to appear). Because may be regarded as a smoothed version of the true likelihood using the kernel , it is intuitive that using a too large may blur the likelihood and bias the inference. Therefore, it is generally desirable to use as small a tolerance as possible, but because the computational methods suffer from inefficiency with small , the choice of tolerance level is difficult (cf. Bortot et al., 2007; Sisson and Fan, 2018; Tanaka et al., 2006).
We discuss simple post-processing procedure which allows for consideration of a range of values for the tolerance , based on a single run of approximate Bayesian computation Markov chain Monte Carlo (Marjoram et al., 2003) with tolerance . Such post-processing was suggested in (Wegmann et al., 2009) (in case of simple cut-off), and similar post-processing has been suggested also with regression adjustment (Beaumont et al., 2002) (in a rejection sampling context). The method, discussed further in Section 2, can be useful for two reasons: A range of tolerances may be routinely inspected, which can reveal excess bias in the pseudo-posterior ; and the Markov chain Monte Carlo inference may be implemented with sufficiently large to allow for good mixing.
Our contribution is two-fold. We suggest straightforward-to-calculate approximate confidence intervals for the posterior mean estimates calculated from the post-processing output, and discuss some theoretical properties related to it. We also introduce an adaptive approximate Bayesian computation Markov chain Monte Carlo which finds a balanced during burn-in, using acceptance rate as a proxy, and detail a convergence result for it.
2. Post-processing over a range of tolerances
For the rest of the paper, we assume that the kernel function in (1) has the form
where is any ‘dissimilarity’ function and is a non-increasing ‘cut-off’ function. Typically , where are the chosen summaries, and in case of the simple cut-off discussed in Section 1, . We will implicitly assume that the pseudo-posterior given in (1) is well-defined for all of interest, that is, .
The following summarises the approximate Bayesian computation Markov chain Monte Carlo algorithm of Marjoram et al. (2003), with proposal and tolerance :
Algorithm 1 (abc-mcmc()).
Suppose and are any starting values, such that and . For , iterate:
-
(i)
Draw and .
-
(ii)
With probability accept and set ; otherwise reject and set , where
Algorithm 1 may be implemented by storing only and the related distances , and in what follows, we regard either or as the output of Algorithm 1. In practice, the initial values should be taken as the state of the Algorithm 1 run for a number of initial ‘burn-in’ iterations. We also introduce an adaptive algorithm for parameter tuning later (Section 4).
It is possible to consider a variant of Algorithm 1 where many (possibly dependent) observations are simulated in each iteration, and an average of their kernel values is used in the accept-reject step (cf. Andrieu et al., 2018). We focus here in the case of single pseudo-observation per iteration, following the asymptotic efficiency result of Bornn et al. (2017), but remark that our method may be applied in a straightforward manner also with multiple observations.
Definition 2.
Suppose is the output of abc-mcmc() for some . For any such that for some , and for any function , define
Algorithm 11 in Appendix details how and can be calculated in time simultaneously for all in case of simple cut-off. The estimator approximates and may be used to construct a confidence interval; see Algorithm 5 below. Theorem 4 details consistency of , and relates to the limiting variance, in case the following (well-known) condition ensuring a central limit theorem holds:
Assumption 3 (Finite integrated autocorrelation).
Suppose that and is finite, with , where is a stationary version of the abc-mcmc() chain, and
Theorem 4.
Proof of Theorem 4 is given in Appendix. Inspired by Theorem 4, we suggest to report the following approximate confidence intervals for the suggested estimators:
Algorithm 5.
The confidence interval in Algorithm 5 is straightforward application of Theorem 4, except for using a common integrated autocorrelation estimate for all . This relies on the approximation , which may not always be entirely accurate, but likely to be reasonable, as illustrated by Theorem 6 in Section 3 below. We suggest using a common for all tolerances because direct estimation of integrated autocorrelation is computationally demanding, and likely to be unstable for small .
The classical choice for in Algorithm 5(ii) is windowed autocorrelation, , with some , where is the sample autocorrelation of (cf. Geyer, 1992). We employ this approach in our experiments with where the cut-off lag is chosen adaptively as the smallest integer such that (Sokal, 1996). Also more sophisticated techniques for the calculation of the asymptotic variance have been suggested (e.g. Flegal and Jones, 2010).
We remark that, although we focus here on the case of using a common cut-off for both the abc-mcmc() and the post-correction, one could also use a different cut-off in the simulation phase, as considered by Beaumont et al. (2002) in the regression context. The extension to Definition 2 is straightforward, setting , and Theorem 4 remains valid under a support condition.
3. Theoretical justification
The following result, whose proof is given in Appendix, gives an expression for the integrated autocorrelation in case of simple cut-off.
Theorem 6.
Suppose Assumption 3 holds and , then
where , , is the integrated autocorrelation of and is the rejection probability of the abc-mcmc() chain at .
We next discuss how this loosely suggests that . The weight , and under suitable regularity conditions both and are continuous with respect to , and as . Then, for , we have and therefore . For small , the terms with are of order , and are dominated by the other terms of order . The remaining ratio may be written as
where with . If , then the term is upper bounded by , and we believe it to be often less than , because the latter expression is similar to the contribution of rejections to the integrated autocorrelation; see the proof of Theorem 6.
For general , it appears to be hard to obtain similar theoretical result, but we expect the approximation to be still sensible. Theorem 6 relies on being independent of conditional on , assuming at least single acceptance. This is not true with other cut-offs, but we believe that the dependence of from given is generally weaker than dependence of and , suggesting similar behaviour.
We conclude the section with a general (albeit pessimistic) upper bound for the asymptotic variance of the post-corrected estimators.
Theorem 7.
Theorem 7 follows directly from (Franks and Vihola, 2017, Corollary 4). The upper bound guarantees that a moderate correction, that is, close to and close to , is nearly as efficient as direct abc-mcmc(). Indeed, typically and as , in which case Theorem 7 implies . However, as , the bound becomes less informative.
4. Tolerance adaptation
We propose Algorithm 8 below to adapt the tolerance in abc-mcmc() during a burn-in of length , in order to obtain a user-specified overall acceptance rate . Tolerance optimisation has been suggested earlier based on quantiles of distances, with parameters simulated from the prior (e.g. Beaumont et al., 2002; Wegmann et al., 2009). This heuristic might not be satisfactory in the Markov chain Monte Carlo context, if the prior is relatively uninformative. We believe that acceptance rate optimisation is a more natural alternative, and Sisson and Fan (2018) suggested this as well.
Our method requires also a sequence of decreasing positive step sizes . We used and in our experiments, and discuss these choices later.
Algorithm 8.
Suppose is a starting value with . Initialise where . For , iterate:
-
(i)
Draw and .
-
(ii)
With probability accept and set ; otherwise reject and set .
-
(iii)
.
In practice, we use Algorithm 8 with a Gaussian symmetric random walk proposal , where the covariance parameter is adapted simultaneously (Haario et al., 2001; Andrieu and Moulines, 2006) (see Algorithm 23 of Supplement D). We only detail theory for Algorithm 8, but note that similar simultaneous adaptation has been discussed earlier (cf. Andrieu and Thoms, 2008), and expect that our results could be elaborated accordingly.
The following conditions suffice for convergence of the adaptation:
Assumption 9.
Suppose and the following hold:
-
(i)
with and a constant.
-
(ii)
The domain , , is a nonempty open set and is bounded.
-
(iii)
The proposal is bounded and bounded away from zero.
-
(iv)
The distances where admit densities which are uniformly bounded in .
-
(v)
stays in a set almost surely, where .
-
(vi)
for all .
Theorem 10.
Under Assumption 9, the expected value of the acceptance probability, with respect to the stationary distribution of the chain, converges to .
Polynomially decaying step size sequences as in Assumption 9 (i) are common in adaptation which is of the stochastic approximation type as our approach (Andrieu and Thoms, 2008). Slower decaying step sizes such as often behave better with acceptance rate adaptation (cf. Vihola, 2012, Remark 3).
Simple random walk Metropolis with covariance adaptation (Haario et al., 2001) typically leads to a limiting acceptance rate around (Roberts et al., 1997). In case of a pseudo-marginal algorithm such as abc-mcmc(), the acceptance rate is lower than this, and decreases when is decreased (see Lemma 16 of Supplement C). Markov chain Monte Carlo would typically be necessary when rejection sampling is not possible, that is, when the prior is far from the posterior. In such a case, the likelihood approximation must be accurate enough to provide reasonable approximation . This suggests that the desired acceptance rate should be taken substantially lower than .
The choice of the desired acceptance rate could also be motivated by theory developed for pseudo-marginal Markov chain Monte Carlo algorithms. Doucet et al. (2015) rely on log-normality of the likelihood estimators, which is problematic in our context, because the likelihood estimators take value zero. Sherlock et al. (2015) find the acceptance rate to be optimal under certain conditions, but also in a quite dissimilar context. Indeed, in our context, the guideline assumes a fixed tolerance, and informs about choosing the number of pseudo-data per iteration. As we stick with single pseudo-data per iteration following (Bornn et al., 2017), the guideline cannot be taken too informative. We recommend slightly higher such as to ensure sufficient mixing.
5. Post-processing with regression correction
Beaumont et al. (2002) suggested similar post-processing as in Section 2, applying a further regression correction. Namely, in the context of Section 2, we may consider a function where and is a solution of
where is the stationary distribution of abc-mcmc(), with marginal , given in Appendix. When the latter expectation is replaced by its empirical version, the solution coincides with weighted least squares , with , and with matrix having rows .
We suggest the following confidence interval for in the spirit of Algorithm 5:
where is the integrated autocorrelation estimate for where and , where the first term is included as an attempt to account for the increased uncertainty due to estimated , analogous to weighted least squares. Experimental results show some promise for this confidence interval, but we stress that we do not have better theoretical backing for it, and leave further elaboration of the confidence interval for future research.
6. Experiments
We experiment with our methods on two models, a lightweight Gaussian toy example, and a Lotka-Volterra model. Our experiments focus on three aspects: can abc-mcmc() with larger tolerance and post-correction to a desired tolerance deliver more accurate results than direct abc-mcmc(); does the approximate confidence interval appear reliable; how well does the tolerance adaptation work in practice. All the experiments are implemented in Julia (Bezanson et al., 2017), and the codes are available in https://bitbucket.org/mvihola/abc-mcmc.
Because we believe that Markov chain Monte Carlo is most useful when little is known about the posterior, we apply covariance adaptation (Haario et al., 2001; Andrieu and Moulines, 2006) throughout the simulation in all our experiments, using an identity covariance initially. When running the covariance adaptation alone, we employ the step size as in the original method of Haario et al. (2001), and in case of tolerance adaptation, we use step size .
Regarding our first question, we investigate running abc-mcmc() starting near the posterior mode with different pre-selected tolerances . We first attempted to perform the experiments by initialising the chains from independent samples of the prior distribution, but in this case, most of the chains failed to accept a single move during the entire run. In contrast, our experiments with tolerance adaptation are initialised from the prior, and both the tolerances and the covariances are adjusted fully automatically by our algorithm.
6.1. One-dimensional Gaussian model
Our first model is a toy model with , and . The true posterior without approximation is Gaussian. While this scenario is clearly academic, the prior is far from the posterior, making rejection sampling approximate Bayesian computation inefficient. It is clear that has zero mean for all (by symmetry), and that is more spread for bigger . We experiment with both simple cut-off and Gaussian cut-off .
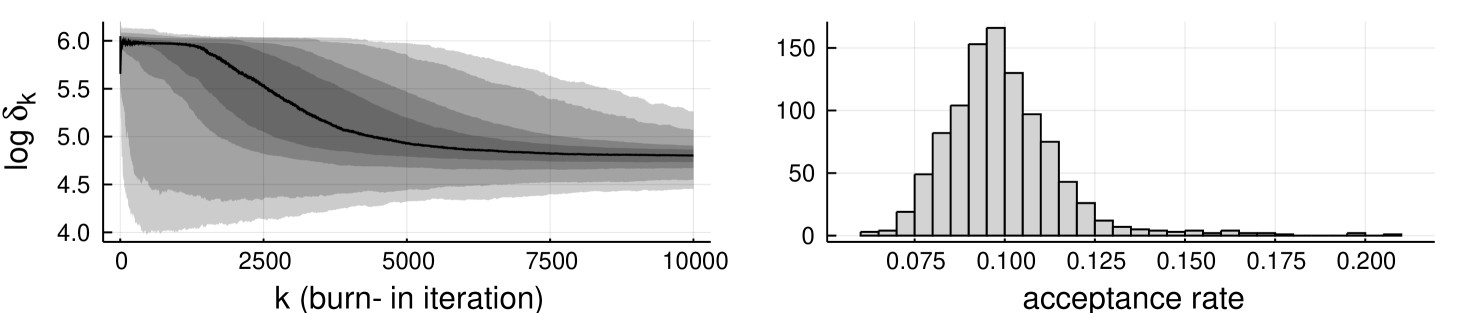
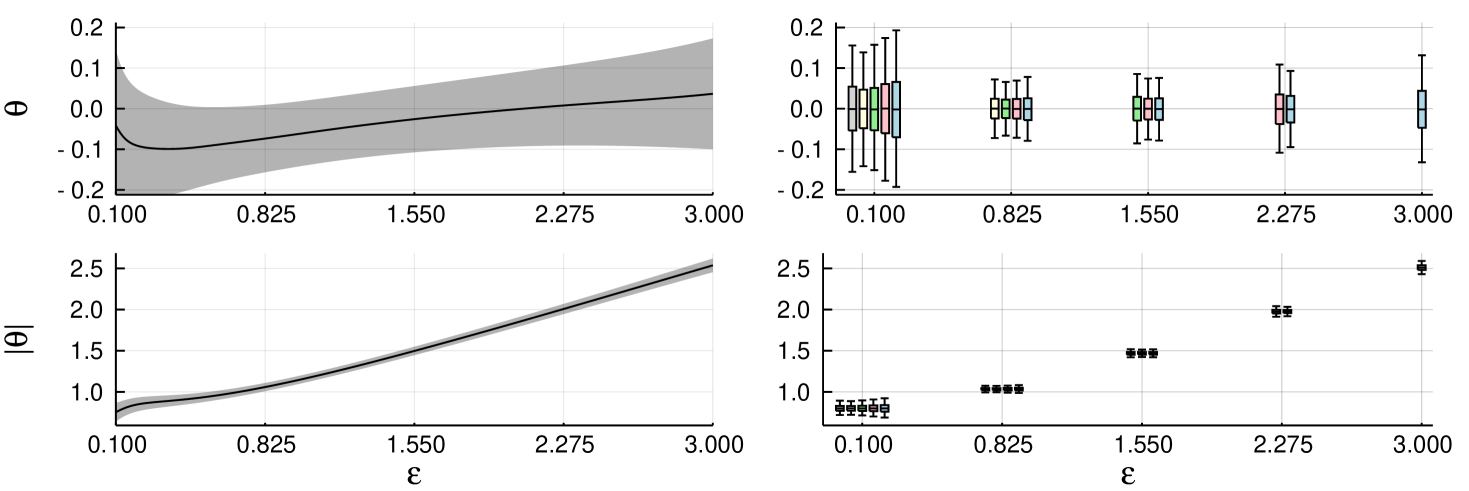
We run the experiments with 10,000 independent chains, each for 11,000 iterations including 1,000 burn-in. The chains were always started from . We inspect estimates for the posterior mean for and . Figure 1 (left) shows the estimates with their confidence intervals based on a single realisation of abc-mcmc(3). Figure 1 (right) shows box plots of the estimates calculated from each abc-mcmc(), with indicated by colour; the rightmost box plot (blue) corresponds to abc-mcmc(3), the second from the right (red) abc-mcmc(2.275) etc. For , the post-corrected estimates from abc-mcmc() and abc-mcmc() appear slightly more accurate than direct abc-mcmc(). Similar figure for Gaussian cut-off, with similar findings, may be found in the Supplement Figure 6.
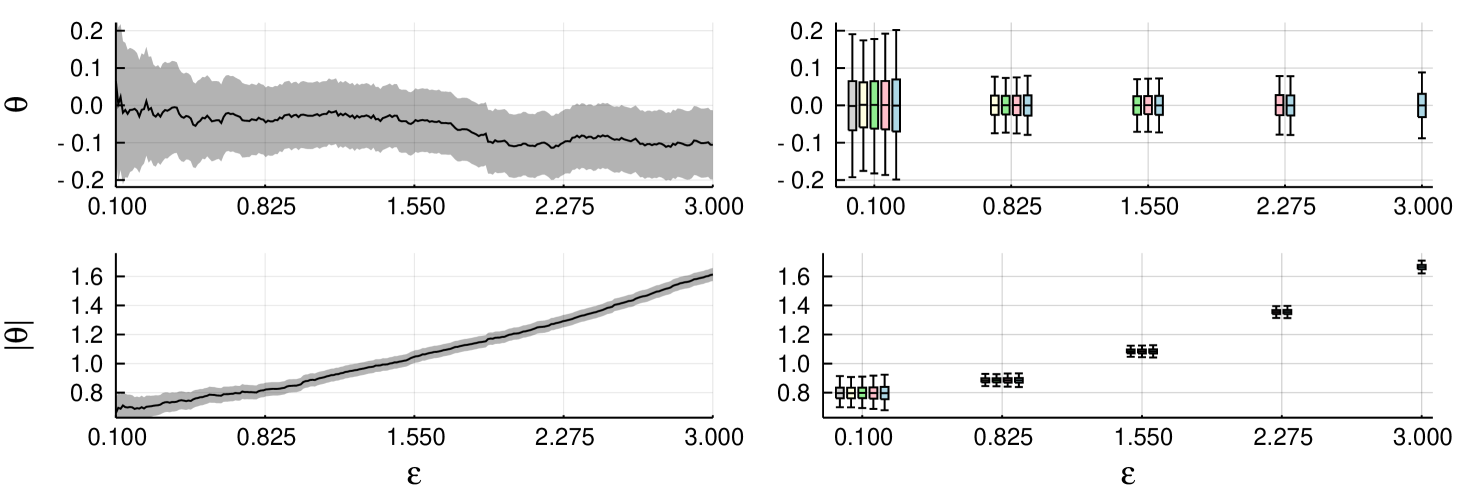
Table 1 shows frequencies of the calculated 95% confidence intervals containing the ‘ground truth’, as well as mean acceptance rates. The ground truth for is known to be zero for all , and the overall mean of all the calculated estimates is used as the ground truth for . The frequencies appear close to ideal with the post-correction approach, being slightly pessimistic in case of simple cut-off as anticipated by the theoretical considerations (cf. Theorem 6 and the discussion below).
| Acc. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cut-off | 0.10 | 0.82 | 1.55 | 2.28 | 3.00 | 0.10 | 0.82 | 1.55 | 2.28 | 3.00 | rate | |
| 0.1 | 0.93 | 0.93 | 0.03 | |||||||||
| 0.82 | 0.97 | 0.95 | 0.95 | 0.94 | 0.22 | |||||||
| 1.55 | 0.97 | 0.97 | 0.95 | 0.96 | 0.95 | 0.95 | 0.33 | |||||
| 2.28 | 0.98 | 0.97 | 0.96 | 0.95 | 0.96 | 0.96 | 0.96 | 0.95 | 0.4 | |||
| 3.0 | 0.98 | 0.98 | 0.97 | 0.97 | 0.95 | 0.96 | 0.96 | 0.96 | 0.95 | 0.95 | 0.43 | |
| 0.1 | 0.93 | 0.93 | 0.05 | |||||||||
| 0.82 | 0.94 | 0.95 | 0.92 | 0.95 | 0.29 | |||||||
| 1.55 | 0.94 | 0.94 | 0.95 | 0.94 | 0.94 | 0.95 | 0.38 | |||||
| 2.28 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.95 | 0.41 | |||
| 3.0 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.95 | 0.95 | 0.95 | 0.42 | |
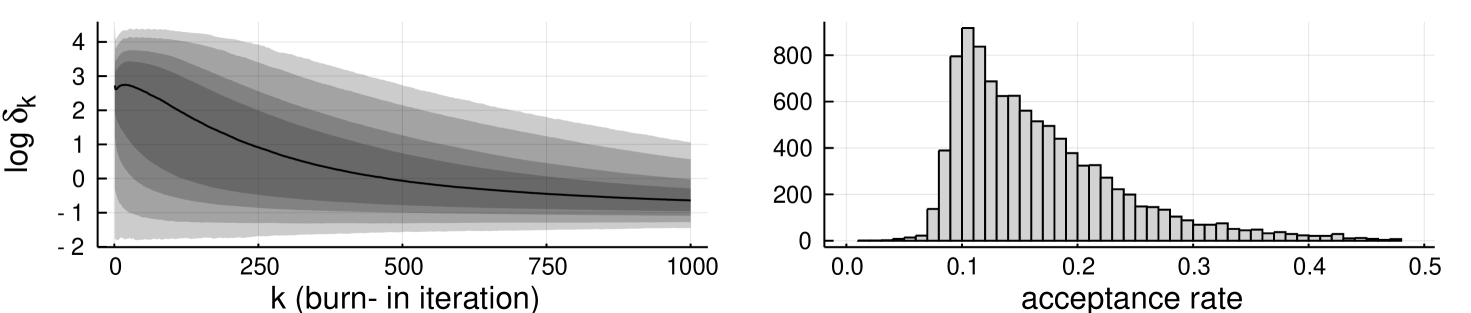
Figure 2 shows progress of tolerance adaptations during the burn-in, and histogram of the mean acceptance rates of the chain after burn-in. The lines on the left show the median, and the shaded regions indicate the 50%, 75%, 95% and 99% quantiles. The figure suggests concentration, but reveals that the adaptation has not fully converged yet. This is also visible in the mean acceptance rate over all realisations, which is for simple cut-off and for Gaussian cut-off (see Figure 7 in the Supplement). Table 2 shows root mean square errors for target tolerance , with both abc-mcmc() with fixed as above, and for the tolerance adaptive algorithm. Here, only the adaptive chains with final tolerance were included (9,998 and 9,993 out of 10,000 chains for and , respectively). Tolerance adaptation (started from prior distribution) appears to be competitive with ‘optimally’ tuned fixed tolerance abc-mcmc().
| Fixed tolerance | Adapt | Fixed tolerance | Adapt | |||||||||
| 0.1 | 0.82 | 1.55 | 2.28 | 3.0 | 0.64 | 0.1 | 0.82 | 1.55 | 2.28 | 3.0 | 0.28 | |
| 9.75 | 8.95 | 9.29 | 9.65 | 10.3 | 9.15 | 7.97 | 7.12 | 7.82 | 8.94 | 9.93 | 7.08 | |
| 5.49 | 5.35 | 5.51 | 5.81 | 6.24 | 5.38 | 4.47 | 4.22 | 4.68 | 5.26 | 5.95 | 4.15 | |
6.2. Lotka-Volterra model
Our second experiment is a Lotka-Volterra model suggested by Boys et al. (2008), which was considered in the approximate Bayesian computation context by Fearnhead and Prangle (2012). The model is a Markov process of counts, corresponding to a reaction network with rate , with rate and with rate . The reaction log-rates are parameters, which we equip with a uniform prior, . The data is a simulated trajectory from the model with until time . The inference is based on the Euclidean distances of five-dimensional summary statistics of the process observed every 5 time units ( and ). The summary statistics are the sample autocorrelation of at lag 2 multiplied by 100, and the 10% and 90% quantiles of and . The observed summary statistics are .
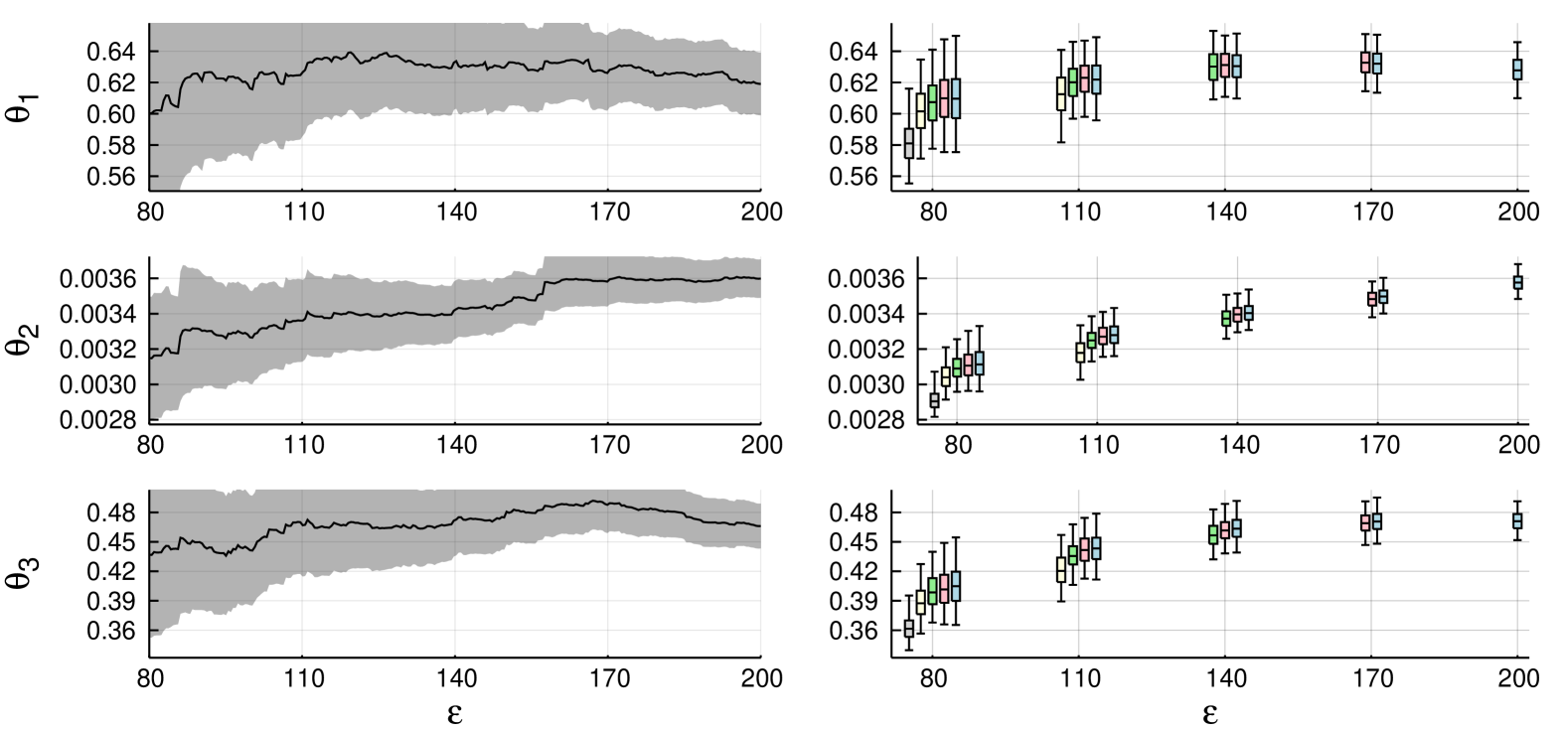
We first run comparisons similar to Section 6.1, but now with 1,000 independent abc-mcmc() chains with simple cut-off. We investigate the effect of post-correction, with 20,000 samples, including 10,000 burn-in, for each chain. All chains were started from near the posterior mode, from . Figure 3
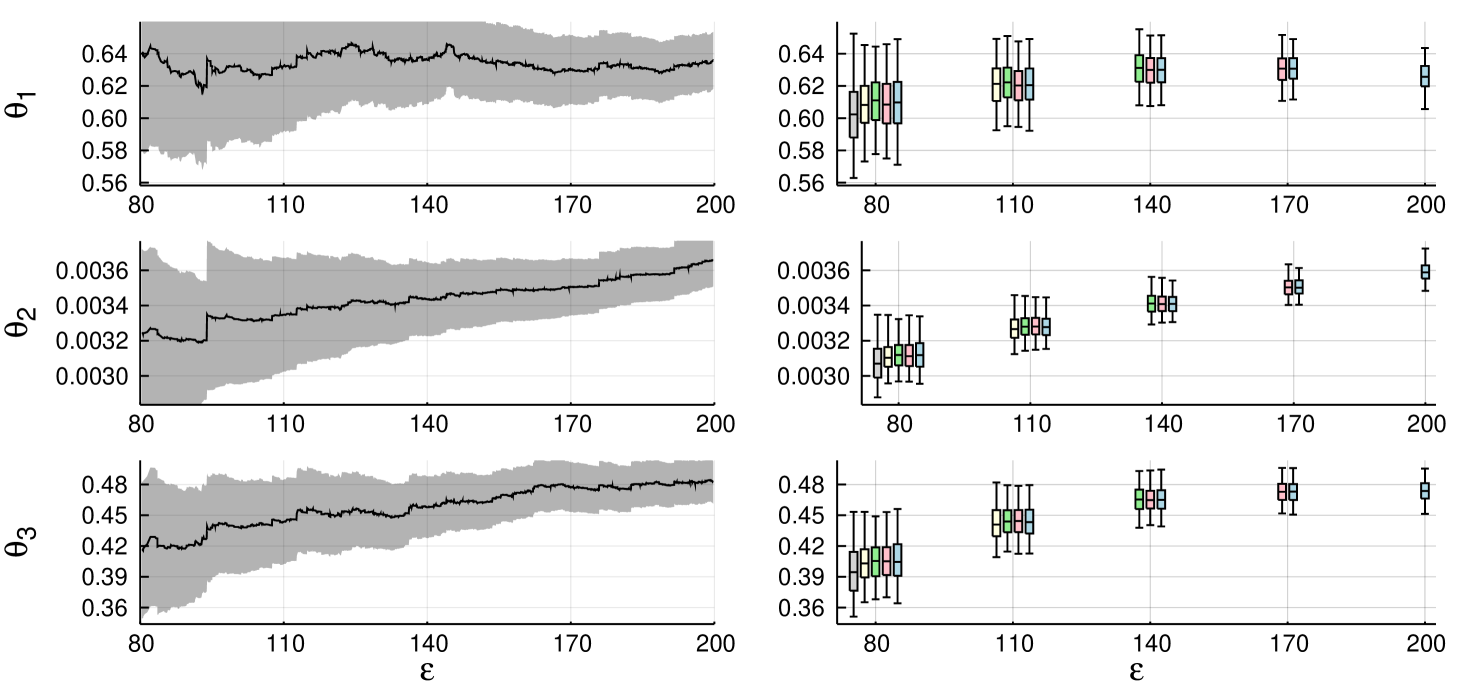
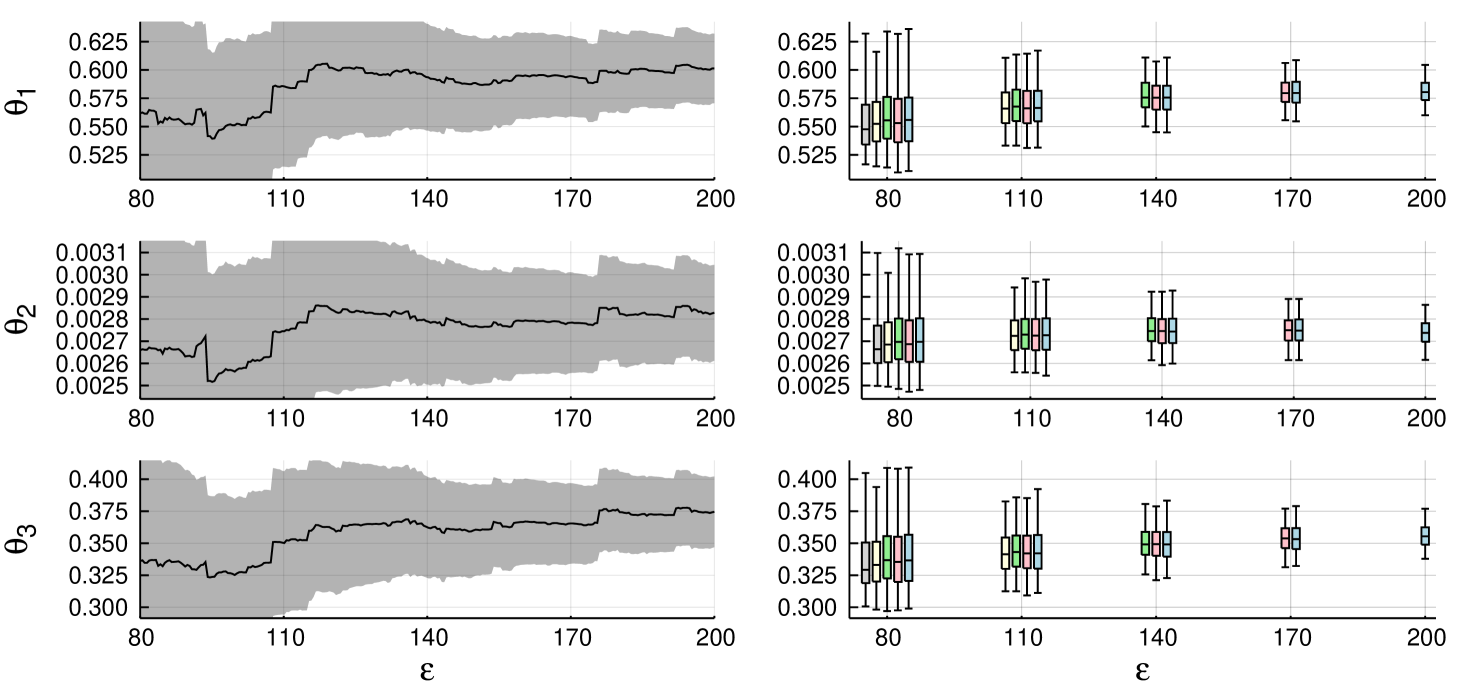
shows results for regression correction with Epanechnikov cut-off (Beaumont et al., 2002). The results suggest that post-correction might provide slightly more accurate estimators, particularly with smaller tolerances. There is also some bias in abc-mcmc() with smaller , when compared to the ground truth calculated from abc-mcmc() chain of ten million iterations. Table 3 shows coverages of confidence intervals.
| Acc. | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | rate | ||
| 80 | 0.8 | 0.73 | 0.74 | 0.05 | |||||||||||||
| 110 | 0.97 | 0.93 | 0.94 | 0.89 | 0.94 | 0.9 | 0.07 | ||||||||||
| 140 | 0.99 | 0.97 | 0.93 | 0.98 | 0.96 | 0.92 | 0.98 | 0.96 | 0.94 | 0.1 | |||||||
| 170 | 0.99 | 0.98 | 0.96 | 0.93 | 0.98 | 0.97 | 0.96 | 0.93 | 0.99 | 0.98 | 0.96 | 0.95 | 0.14 | ||||
| 200 | 1.0 | 0.99 | 0.98 | 0.97 | 0.94 | 0.99 | 0.99 | 0.98 | 0.97 | 0.92 | 0.99 | 0.98 | 0.98 | 0.96 | 0.94 | 0.17 | |
| regr. | 80 | 0.75 | 0.76 | 0.68 | 0.05 | ||||||||||||
| 110 | 0.92 | 0.92 | 0.93 | 0.94 | 0.87 | 0.91 | 0.07 | ||||||||||
| 140 | 0.93 | 0.94 | 0.94 | 0.94 | 0.96 | 0.97 | 0.9 | 0.92 | 0.94 | 0.1 | |||||||
| 170 | 0.93 | 0.95 | 0.95 | 0.95 | 0.96 | 0.97 | 0.97 | 0.98 | 0.92 | 0.94 | 0.94 | 0.95 | 0.14 | ||||
| 200 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.98 | 0.98 | 0.98 | 0.98 | 0.98 | 0.95 | 0.96 | 0.95 | 0.96 | 0.96 | 0.17 | |
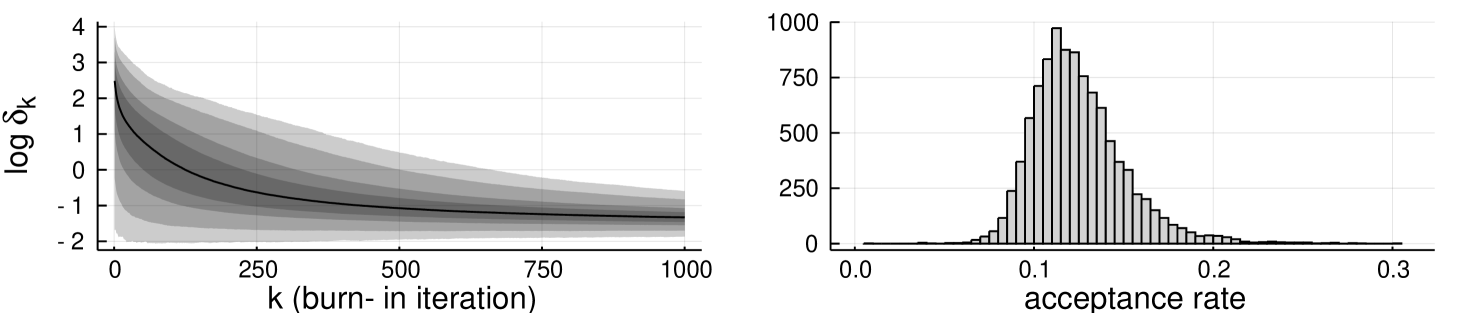
In addition, we experiment with the tolerance adaptation, using also 20,000 samples out of which 10,000 are burn-in. Figure 5
shows the progress of the -tolerance during the burn-in, and histogram of the realised mean acceptance rates during the estimation phase. The realised acceptance rates are concentrated around the mean . Table 4
| Post-correction, simple cut-off | Regression, Epanechnikov cut-off | |||||||||||
| Fixed tolerance | Adapt | Fixed tolerance | Adapt | |||||||||
| 80 | 110 | 140 | 170 | 200 | 122.6 | 80 | 110 | 140 | 170 | 200 | 122.6 | |
| 2.37 | 1.81 | 1.75 | 1.83 | 1.93 | 1.8 | 3.1 | 2.74 | 3.02 | 3.09 | 3.19 | 2.57 | |
| 1.32 | 0.99 | 0.93 | 0.96 | 1.06 | 1.04 | 1.52 | 1.39 | 1.54 | 1.61 | 1.63 | 1.28 | |
| 2.94 | 2.26 | 2.11 | 2.14 | 2.37 | 2.34 | 2.77 | 2.53 | 2.76 | 2.85 | 2.91 | 2.34 | |
shows root mean square errors of the estimators from abc-mcmc() for for fixed tolerance and with tolerance adaptation. Only the adaptive chains with final tolerance were included (999 out of 1,000 chains).
In this case, the chains run with the tolerance adaptation led to better results than those run only with the covariance adaptation (and fixed tolerance). This perhaps surprising result may be due to the initial behaviour of the covariance adaptation, which may be unstable when there are many rejections. Different initialisation strategies, for instance following (Haario et al., 2001, Remark 2), might lead to more stable behaviour compared to using the adaptation of Andrieu and Moulines (2006) from the start, as we do. The different step size sequences ( and ) could also play a rôle. We repeated the experiment for the chains with fixed tolerances, but now with covariance adaptation step size . This led to more accurate estimators for abc-mcmc() with higher , but worse behaviour with smaller . In any case, also here, tolerance adaptation delivered competitive results (see Supplement F).
7. Discussion
We believe that approximate Bayesian computation inference with Markov chain Monte Carlo is a useful approach, when the chosen simulation tolerance allows for good mixing. Our confidence intervals for post-processing and automatic tuning of simulation tolerance may make this approach more appealing in practice.
A related approach by Bortot et al. (2007) makes tolerance an auxiliary variable with a user-specified prior. This approach avoids explicit tolerance selection, but the inference is based on a pseudo-posterior not directly related to in (1). Bortot et al. (2007) also provide tolerance-dependent analysis, showing parameter means and variances with respect to conditional distributions of given . We believe that our approach, where the effect of tolerance in the expectations with respect can be investigated explicitly, can be more immediate to interpret. Our confidence interval only shows the Monte Carlo uncertainty related to the posterior mean, and we are currently investigating how the overall parameter uncertainty could be summarised in a useful manner.
The convergence rates of approximate Bayesian computation has been investigated by Barber et al. (2015) in terms of cost and bias with respect to true posterior, and recently by Li and Fearnhead (2018a, b) in the large data limit, the latter in the context of regression. It would be interesting to consider extensions of these results in the Markov chain Monte Carlo context. In fact, Li and Fearnhead (2018a) already suggest that the acceptance rate must be lower bounded, which is in line with our adaptation rule.
Automatic selection of tolerance has been considered earlier in Ratmann et al. (2007), who propose an algorithm based on tempering and a cooling schedule. Based on our experiments, the tolerance adaptation we present in this paper appears to perform well in practice, and provides reliable results with post-correction. For the adaptation to work efficiently, the Markov chains must be taken relatively long, rendering the approach difficult for the most computationally demanding models.
We conclude with a brief discussion of certain extensions of the suggested post-correction method; more details are given in Supplement E. First, in case of non-simple cut-off, the rejected samples may be ‘recycled’ by using the acceptance probability as weight (Ceperley et al., 1977). The accuracy of the post-corrected estimator could be enhanced with smaller values of by performing further independent simulations from (which may be calculated in parallel). The estimator is rather straightforward, but requires some care because the estimators of the pseudo-likelihood take value zero. The latter extension, which involves additional simulations as post-processing, is similar to the ‘lazy’ version of Prangle (2016, 2015) incorporating a randomised stopping rule for simulation, and to debiased ‘exact’ approach of Tran and Kohn (2015), which may lead to estimators which get rid of -bias entirely.
8. Acknowledgements
This work was supported by Academy of Finland (grants 274740, 284513 and 312605). The authors wish to acknowledge CSC, IT Center for Science, Finland, for computational resources, and thank Christophe Andrieu for useful discussions.
References
- Andrieu and Moulines (2006) C. Andrieu and É. Moulines. On the ergodicity properties of some adaptive MCMC algorithms. Ann. Appl. Probab., 16(3):1462–1505, 2006.
- Andrieu and Thoms (2008) C. Andrieu and J. Thoms. A tutorial on adaptive MCMC. Statist. Comput., 18(4):343–373, Dec. 2008.
- Andrieu et al. (2005) C. Andrieu, É. Moulines, and P. Priouret. Stability of stochastic approximation under verifiable conditions. SIAM J. Control Optim., 44(1):283–312, 2005.
- Andrieu et al. (2018) C. Andrieu, A. Lee, and M. Vihola. Theoretical and methodological aspects of MCMC computations with noisy likelihoods. In S. A. Sisson, Y. Fan, and M. Beaumont, editors, Handbook of Approximate Bayesian Computation. Chapman & Hall/CRC Press, 2018.
- Barber et al. (2015) S. Barber, J. Voss, and M. Webster. The rate of convergence for approximate Bayesian computation. Electron. J. Statist., 9(1):80–105, 2015.
- Beaumont et al. (2002) M. Beaumont, W. Zhang, and D. Balding. Approximate Bayesian computation in population genetics. Genetics, 162(4):2025–2035, 2002.
- Bezanson et al. (2017) J. Bezanson, A. Edelman, S. Karpinski, and V. B. Shah. Julia: A fresh approach to numerical computing. SIAM review, 59(1):65–98, 2017.
- Bornn et al. (2017) L. Bornn, N. Pillai, A. Smith, and D. Woodard. The use of a single pseudo-sample in approximate Bayesian computation. Statist. Comput., 27(3):583–590, 2017.
- Bortot et al. (2007) P. Bortot, S. Coles, and S. Sisson. Inference for stereological extremes. J. Amer. Statist. Assoc., 102(477):84–92, 2007.
- Boys et al. (2008) R. J. Boys, D. J. Wilkinson, and T. B. Kirkwood. Bayesian inference for a discretely observed stochastic kinetic model. Stat. Comput., 18(2):125–135, 2008.
- Burkholder et al. (1972) D. Burkholder, B. Davis, and R. Gundy. Integral inequalities for convex functions of operators on martingales. In Proc. Sixth Berkeley Symp. Math. Statist. Prob, volume 2, pages 223–240, 1972.
- Ceperley et al. (1977) D. Ceperley, G. Chester, and M. Kalos. Monte Carlo simulation of a many-fermion study. Phys. Rev. D, 16(7):3081, 1977.
- Delmas and Jourdain (2009) J.-F. Delmas and B. Jourdain. Does waste recycling really improve the multi-proposal Metropolis–Hastings algorithm? an analysis based on control variates. J. Appl. Probab., 46(4):938–959, 2009.
- Doucet et al. (2015) A. Doucet, M. Pitt, G. Deligiannidis, and R. Kohn. Efficient implementation of Markov chain Monte Carlo when using an unbiased likelihood estimator. Biometrika, 102(2):295–313, 2015.
- Fearnhead and Prangle (2012) P. Fearnhead and D. Prangle. Constructing summary statistics for approximate Bayesian computation: semi-automatic approximate Bayesian computation. J. R. Stat. Soc. Ser. B Stat. Methodol., 74(3):419–474, 2012.
- Flegal and Jones (2010) J. M. Flegal and G. L. Jones. Batch means and spectral variance estimators in Markov chain Monte Carlo. Ann. Statist., 38(2):1034–1070, 2010.
- Franks and Vihola (2017) J. Franks and M. Vihola. Importance sampling correction versus standard averages of reversible MCMCs in terms of the asymptotic variance. Preprint arXiv:1706.09873v3, 2017.
- Geyer (1992) C. J. Geyer. Practical Markov chain Monte Carlo. Statist. Sci., pages 473–483, 1992.
- Haario et al. (2001) H. Haario, E. Saksman, and J. Tamminen. An adaptive Metropolis algorithm. Bernoulli, 7(2):223–242, 2001.
- Li and Fearnhead (2018a) W. Li and P. Fearnhead. On the asymptotic efficiency of approximate Bayesian computation estimators. Biometrika, 105(2):285–299, 2018a.
- Li and Fearnhead (2018b) W. Li and P. Fearnhead. Convergence of regression-adjusted approximate Bayesian computation. Biometrika, 105(2):301–318, 2018b.
- Marin et al. (2012) J.-M. Marin, P. Pudlo, C. P. Robert, and R. J. Ryder. Approximate Bayesian computational methods. Statist. Comput., 22(6):1167–1180, 2012.
- Marjoram et al. (2003) P. Marjoram, J. Molitor, V. Plagnol, and S. Tavaré. Markov chain Monte Carlo without likelihoods. Proc. Natl. Acad. Sci. USA, 100(26):15324–15328, 2003.
- Meyn and Tweedie (2009) S. Meyn and R. L. Tweedie. Markov Chains and Stochastic Stability. Cambridge University Press, 2nd edition, 2009. ISBN 978-0-521-73182-9.
- Prangle (2015) D. Prangle. Lazier ABC. Preprint arXiv:1501.05144, 2015.
- Prangle (2016) D. Prangle. Lazy ABC. Statist. Comput., 26(1-2):171–185, 2016.
- Ratmann et al. (2007) O. Ratmann, O. Jørgensen, T. Hinkley, M. Stumpf, S. Richardson, and C. Wiuf. Using likelihood-free inference to compare evolutionary dynamics of the protein networks of H. pylori and P. falciparum. PLoS Comput. Biol., 3(11):e230, 2007.
- Raynal et al. (to appear) L. Raynal, J.-M. Marin, P. Pudlo, M. Ribatet, C. P. Robert, and A. Estoup. ABC random forests for bayesian parameter inference. Bioinformatics, to appear.
- Roberts et al. (1997) G. Roberts, A. Gelman, and W. Gilks. Weak convergence and optimal scaling of random walk Metropolis algorithms. Ann. Appl. Probab., 7(1):110–120, 1997.
- Roberts and Rosenthal (2006) G. O. Roberts and J. S. Rosenthal. Harris recurrence of Metropolis-within-Gibbs and trans-dimensional Markov chains. Ann. Appl. Probab., 16(4):2123–2139, 2006.
- Rudolf and Sprungk (2018) D. Rudolf and B. Sprungk. On a Metropolis-Hastings importance sampling estimator. Preprint arXiv:1805.07174, 2018.
- Schuster and Klebanov (2018) I. Schuster and I. Klebanov. Markov chain importance sampling - a highly efficient estimator for MCMC. Preprint arXiv:1805.07179, 2018.
- Sherlock et al. (2015) C. Sherlock, A. H. Thiery, G. O. Roberts, and J. S. Rosenthal. On the efficiency of pseudo-marginal random walk Metropolis algorithms. Ann. Statist., 43(1):238–275, 2015.
- Sisson and Fan (2018) S. Sisson and Y. Fan. ABC samplers. In S. Sisson, Y. Fan, and M. Beaumont, editors, Handbook of Markov chain Monte Carlo. Chapman & Hall/CRC Press, 2018.
- Sokal (1996) A. D. Sokal. Monte Carlo methods in statistical mechanics: Foundations and new algorithms. Lecture notes, 1996.
- Sunnåker et al. (2013) M. Sunnåker, A. G. Busetto, E. Numminen, J. Corander, M. Foll, and C. Dessimoz. Approximate Bayesian computation. PLoS computational biology, 9(1):e1002803, 2013.
- Tanaka et al. (2006) M. Tanaka, A. Francis, F. Luciani, and S. Sisson. Using approximate Bayesian computation to estimate tuberculosis transmission parameters from genotype data. Genetics, 173(3):1511–1520, 2006.
- Tran and Kohn (2015) M. N. Tran and R. Kohn. Exact ABC using importance sampling. Preprint arXiv:1509.08076, 2015.
- Vihola (2012) M. Vihola. Robust adaptive Metropolis algorithm with coerced acceptance rate. Statist. Comput., 22(5):997–1008, 2012.
- Vihola et al. (2016) M. Vihola, J. Helske, and J. Franks. Importance sampling type estimators based on approximate marginal MCMC. Preprint arXiv:1609.02541v5, 2016.
- Wegmann et al. (2009) D. Wegmann, C. Leuenberger, and L. Excoffier. Efficient approximate Bayesian computation coupled with Markov chain Monte Carlo without likelihoods. Genetics, 182(4):1207–1218, 2009.
Appendix
The following algorithm shows that in case of simple (post-correction) cut-off, and may be calculated simultaneously for all tolerances efficiently:
Algorithm 11.
Suppose and is the output of abc-mcmc().
-
(i)
Sort with respect to :
-
•
Find indices such that for all .
-
•
Denote .
-
•
-
(ii)
For all unique values , let , and define
(and for , let and .)
The sorting in Algorithm 11(i) may be performed in time, and and may all be calculated in time by forming appropriate cumulative sums.
of Theorem 4.
Algorithm 1 is a Metropolis–Hastings algorithm with compound proposal and with target . The chain is Harris-recurrent, as a full-dimensional Metropolis–Hastings which is -irreducible (Roberts and Rosenthal, 2006). Because is monotone and , we have , and therefore is absolutely continuous with respect to , and , where is a constant. If we denote and , then almost surely by Harris recurrence and invariance (e.g. Vihola et al., 2016). The claim (i) follows because is the marginal density of .
of Theorem 6.
The invariant distribution of abc-mcmc() may be written as where , and that for . Consequently, and , so Hereafter, let and denote and . Clearly, and
Note that with , the acceptance ratio is , where which is independent of , so is marginally a Metropolis–Hastings type chain, with proposal and acceptance probability , and
Using this iteratively, we obtain that
and therefore with ,
We conclude by noticing that . ∎
Supplement B Convergence of the tolerance adaptive ABC-MCMC under generalised conditions
This section details a convergence theorem, under weaker assumptions than that of Theorem 10, for the tolerance adaptation (Algorithm 8) of Section 4.
For convenience, we denote the distance distribution here as , where for . With this notation, and re-indexing , we may rewrite Algorithm 8 as follows:
Algorithm 12.
Suppose is a starting value with . Initialise . , iterate:
-
(i)
Draw and .
-
(ii)
Accept, by setting , with probability
(2) and otherwise reject, by setting .
-
(iii)
.
Let us set , and consider the proposal-rejection Markov kernel
| (3) |
where
Then is the transition of the -coordinate chain of Algorithm 12 with simple cut-off at iteration , obtained by disregarding the -coordinate. It is easily seen to be reversible with respect to the posterior probability given in (1), written here in terms of instead of .
Assumption 13.
Suppose and the following hold:
-
(i)
Step sizes satisfy , ,
-
(ii)
The domain , , is a nonempty open set.
-
(iii)
and are uniformly bounded densities on (i.e. s.t. and for all ), and for .
-
(iv)
admits a uniformly bounded density .
-
(v)
The values remain in some compact subset almost surely.
-
(vi)
for all , where .
-
(vii)
There exists such that the Markov transitions are simultaneously -geometrically ergodic: there exist and s.t. for all and with , it holds that
- (viii)
Theorem 14.
Supplement C Analysis of the tolerance adaptive ABC-MCMC
In this section we aim to prove generalised convergence (Theorem 14 of Section B) of the tolerance adaptation, from which Theorem 10 of Section 4 will follow as a corollary. Throughout, we denote by a constant which may change from line to line.
C.1. Proposal augmentation
Suppose is a Markov kernel which can be written as
| (4) |
where is a jointly measurable function and is a Markov proposal kernel. With , we define the proposal augmentation to be the Markov kernel
| (5) |
It is easy to see that need not be reversible even if is reversible. In this case, however, does leave a probability measure invariant.
Lemma 15.
Suppose a Markov kernel of the form given in (4) is -reversible. Let be its proposal augmentation. Then the following statements hold:
-
(i)
, where .
-
(ii)
If is -geometrically ergodic with constants , then is -geometrically ergodic with constants , where and
Lemma 15 extends (Schuster and Klebanov, 2018, Theorem 4), who consider the case where is a Metropolis–Hastings chain (see also Delmas and Jourdain, 2009; Rudolf and Sprungk, 2018). The extension to the more general class of reversible proposal-rejection chains allows one to consider, for example, jump and delayed acceptance chains, as well as the marginal chain (3) of Section B, which will be important for our analysis of the tolerance adaptation.
of Lemma 15.
Consider now the -coordinate chain presented in (3) of Section B. This transition is clearly a reversible proposal-rejection chain of the form (4). We now consider , its proposal augmentation. This is the chain , formed by disregarding the -parameter as with before, but now augmenting by the proposal . Its transitions are of the form goes to in the ABC-MCMC, with and kernel
C.2. Monotonicity properties
The following result establishes monotonicity of the mean field acceptance rate with increasing tolerance.
Proof.
Since and are uniformly bounded (Assumption 13(iii)), and , differentiation under the integral sign is possible in the following by the dominated convergence theorem. By the quotient rule,
| (6) |
By reversibility of Metropolis–Hastings targeting with proposal ,
With
we can then write (6) as
By the same reversibility property as before, we can write this again as
We then conclude, since
Lemma 17.
C.3. Stochastic approximation framework
To obtain a form common in the stochastic approximation literature (cf. Andrieu et al., 2005), we write the update in Algorithm 12 as
where
noise sequence and conditional expectation
where . We also set for convenience
Lemma 18.
C.4. Contractions
We define for and the -norm We define for a bounded operator on a Banach space of bounded functions , the operator norm .
Lemma 19.
Proof.
By Assumption 13(iv), we have for all ,
We obtain the first inequality for part (i), then, from the bound,
The second, Lipschitz bound follows by a mean value theorem argument for the function , namely
where the last inequality follows by compactness of (Assumption 13(v)).
We now consider part (ii). We have,
For the first term, by Assumption 13(iv), as in (i), we have
For the other term, we have
By the triangle inequality, we have
Each term above is bounded by , as is . Moreover, by Lemma 17(ii), we have for all , and the first inequality in part (ii) follows. The second inequality follows by a mean value theorem argument as before. Proof of (iii) is simpler. ∎
C.5. Control of noise
We state a simple standard fact used repeatedly in the proof of Lemma 21 below, our key lemma.
Lemma 20.
Suppose are random variables with , , and Then, almost surely,
Lemma 21.
Suppose Assumption 13 holds. Then, with we have
Proof.
Similar to (Andrieu et al., 2005, Proof of Prop. 5.2), we write , where
with representing the information obtained through running Algorithm 12 up to and including iteration and then also generating , and
Here, is the Poisson solution defined in Lemma 18(ii), and . We remind that from Section C.3.
We now show for each of the terms individually, which implies the result of the lemma.
(1) Since for all ,
we have that is a -martingale for each . By the Burkholder-Davis-Gundy inequality for martingales (cf. Burkholder et al., 1972), we have
where in the last inequality we have noted that . Since , we get that
Hence, the result follows by Lemma 20.
(2) For , we have for ,
so that is a -martingale, for . By the Burkholder-Davis-Gundy inequality again,
We then use Lemma 18(ii) and , to get, after combining terms,
where we have used Assumption 13(viii) in the last inequality. We then conclude by Lemma 20 as before.
(3) By Lemma 18(ii), the triangle inequality, , and the dominated convergence theorem, we obtain
We then apply Assumption 13(viii) and Jensen’s inequality, and use that go to zero, since , to get that
We now may conclude by Lemma 20.
(4) By Lemma 18(ii) and , we have for ,
where we have used lastly Assumption 13(viii) and Jensen’s inequality. Since this is a telescoping sum, we get
We then conclude by Lemma 20, since .
(5) By Lemma 18(i), where do not depend on . Hence,
where we have used lastly Assumption 13(viii) and Jensen’s inequality. Since was defined to be of order , we have
By the dominated convergence theorem, we then have
Taking the limit , we can then conclude by using Lemma 20.
(6) The proof is essentially the same as for (5).
C.6. Proofs of convergence theorems
of Theorem 14.
We define our Lyapunov function to be the continuously differentiable function . We also have that is continuous, which follows from Lemma 19(iii). One can then check that Assumption 13 and Lemma 21 imply that the assumptions of (Andrieu et al., 2005, Theorem 2.3) hold. The latter result implies , for some satisfying , as desired. ∎
Lemma 22.
Suppose Assumption 9 holds. Then both and are simultaneously -geometrically ergodic (i.e. uniformly ergodic).
Proof.
We have some , and also , for all . Hence, for ,
By Lemma 17(ii), it holds for some for all . Therefore,
where is independent of . As in Nummelin’s split chain construction (cf. Meyn and Tweedie, 2009), we can then define the Markov kernel with . Set . For any , , and , we have
where we have used in the first inequality. Hence, are simultaneously -geometrically ergodic, and thus so are by Lemma 18(i). ∎
Supplement D Simultaneous tolerance and covariance adaptation
Algorithm 23 (TA-AM()).
Suppose is a starting value with and is the identity matrix.
-
1.
Initialise where and . Set .
-
2.
For , iterate:
-
(i)
Draw
-
(ii)
Draw .
-
(iii)
Accept, by setting , with probability
Otherwise reject, by setting .
-
(iv)
-
(v)
-
(vi)
-
(i)
-
3.
Output .
Supplement E Details of extensions in Section 7
In case of non-simple cut-off, the rejected samples may be ‘recycled’ the rejected samples in the estimator (Ceperley et al., 1977). This may improve the accuracy (but can also reduce accuracy in certain pathological cases; see Delmas and Jourdain (2009)). The ‘waste recycling’ estimator is
When is consistent under Theorem 4, this is also a consistent estimator. Namely, as in the proof of Theorem 4, we find that is a Harris recurrent Markov chain with invariant distribution
and , where . Therefore, is a strongly consistent estimator of
See (Rudolf and Sprungk, 2018; Schuster and Klebanov, 2018) for alternative waste recycling estimators based on importance sampling analogues.
A refined estimator may be formed as
where and , for , and where is the number of independent random variables generated before observing . The variables , and with independent . This ensures that
which is sufficient to ensure that is a proper weighting scheme from to ; see (Vihola et al., 2016, Proposition 17(ii)), and consequently the average is a proper weighting.
Supplement F Supplementary results
| Acc. | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cut-off | 0.10 | 0.82 | 1.55 | 2.28 | 3.00 | 0.10 | 0.82 | 1.55 | 2.28 | 3.00 | rate | |
| 0.1 | 9.68 | 5.54 | 0.03 | |||||||||
| 0.82 | 8.99 | 3.81 | 5.38 | 2.14 | 0.22 | |||||||
| 1.55 | 9.21 | 3.66 | 3.59 | 5.5 | 2.17 | 1.96 | 0.33 | |||||
| 2.28 | 9.67 | 3.86 | 3.6 | 3.97 | 5.85 | 2.28 | 2.02 | 2.08 | 0.4 | |||
| 3.0 | 10.36 | 4.03 | 3.71 | 3.98 | 4.51 | 6.21 | 2.42 | 2.12 | 2.16 | 2.26 | 0.43 | |
| 0.1 | 7.97 | 4.47 | 0.05 | |||||||||
| 0.82 | 7.12 | 3.67 | 4.22 | 2.08 | 0.29 | |||||||
| 1.55 | 7.82 | 3.39 | 4.35 | 4.68 | 1.99 | 2.52 | 0.38 | |||||
| 2.28 | 8.94 | 3.59 | 3.81 | 5.52 | 5.26 | 2.2 | 2.29 | 3.29 | 0.41 | |||
| 3.0 | 9.93 | 4.01 | 3.97 | 4.81 | 6.76 | 5.95 | 2.44 | 2.44 | 2.92 | 4.1 | 0.42 | |
| Fixed tolerance | Adapt | Fixed tolerance | Adapt | |||||||||
| 0.1 | 0.82 | 1.55 | 2.28 | 3.0 | 0.64 | 0.1 | 0.82 | 1.55 | 2.28 | 3.0 | 0.28 | |
| 0.93 | 0.97 | 0.97 | 0.98 | 0.98 | 0.96 | 0.93 | 0.94 | 0.94 | 0.95 | 0.95 | 0.93 | |
| 0.92 | 0.95 | 0.96 | 0.96 | 0.96 | 0.96 | 0.93 | 0.92 | 0.94 | 0.95 | 0.95 | 0.92 | |
| Acc. | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | rate | ||
| 80 | 2.37 | 1.32 | 2.94 | 0.05 | |||||||||||||
| 110 | 1.81 | 1.48 | 0.99 | 0.86 | 2.26 | 1.88 | 0.07 | ||||||||||
| 140 | 1.75 | 1.41 | 1.22 | 0.93 | 0.77 | 0.68 | 2.11 | 1.69 | 1.4 | 0.1 | |||||||
| 170 | 1.83 | 1.35 | 1.14 | 1.05 | 0.96 | 0.75 | 0.64 | 0.6 | 2.14 | 1.65 | 1.33 | 1.15 | 0.14 | ||||
| 200 | 1.93 | 1.41 | 1.11 | 0.97 | 0.95 | 1.06 | 0.75 | 0.61 | 0.56 | 0.6 | 2.37 | 1.74 | 1.36 | 1.16 | 1.09 | 0.17 | |
| regr. | 80 | 3.1 | 1.52 | 2.77 | 0.05 | ||||||||||||
| 110 | 2.74 | 1.99 | 1.39 | 1.0 | 2.53 | 1.81 | 0.07 | ||||||||||
| 140 | 3.02 | 2.08 | 1.56 | 1.54 | 1.05 | 0.79 | 2.76 | 1.9 | 1.39 | 0.1 | |||||||
| 170 | 3.09 | 2.13 | 1.6 | 1.31 | 1.61 | 1.09 | 0.83 | 0.69 | 2.85 | 1.95 | 1.46 | 1.16 | 0.14 | ||||
| 200 | 3.19 | 2.2 | 1.68 | 1.36 | 1.15 | 1.63 | 1.1 | 0.84 | 0.71 | 0.63 | 2.91 | 2.04 | 1.52 | 1.21 | 1.01 | 0.17 | |
| Post-correction, simple cut-off | Regression, Epanechnikov cut-off | |||||||||||
| Fixed tolerance | Adapt | Fixed tolerance | Adapt | |||||||||
| 80.0 | 110.0 | 140.0 | 170.0 | 200.0 | 122.6 | 80.0 | 110.0 | 140.0 | 170.0 | 200.0 | 122.6 | |
| 0.8 | 0.97 | 0.99 | 0.99 | 1.0 | 0.93 | 0.75 | 0.92 | 0.93 | 0.93 | 0.96 | 0.9 | |
| 0.73 | 0.94 | 0.98 | 0.98 | 0.99 | 0.84 | 0.76 | 0.93 | 0.94 | 0.96 | 0.98 | 0.9 | |
| 0.74 | 0.94 | 0.98 | 0.99 | 0.99 | 0.86 | 0.68 | 0.87 | 0.9 | 0.92 | 0.95 | 0.83 | |
| Acc. | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | rate | ||
| 80 | 0.32 | 0.11 | 0.11 | 0.07 | |||||||||||||
| 110 | 0.91 | 0.78 | 0.76 | 0.52 | 0.79 | 0.56 | 0.09 | ||||||||||
| 140 | 0.97 | 0.96 | 0.91 | 0.95 | 0.88 | 0.8 | 0.96 | 0.9 | 0.86 | 0.12 | |||||||
| 170 | 0.98 | 0.98 | 0.97 | 0.94 | 0.97 | 0.97 | 0.93 | 0.87 | 0.97 | 0.97 | 0.95 | 0.91 | 0.15 | ||||
| 200 | 0.99 | 0.98 | 0.98 | 0.96 | 0.93 | 0.99 | 0.99 | 0.98 | 0.94 | 0.87 | 0.98 | 0.98 | 0.97 | 0.94 | 0.92 | 0.18 | |
| regr. | 80 | 0.34 | 0.41 | 0.25 | 0.07 | ||||||||||||
| 110 | 0.86 | 0.81 | 0.88 | 0.87 | 0.81 | 0.82 | 0.09 | ||||||||||
| 140 | 0.94 | 0.94 | 0.92 | 0.95 | 0.95 | 0.96 | 0.9 | 0.91 | 0.91 | 0.12 | |||||||
| 170 | 0.95 | 0.95 | 0.95 | 0.95 | 0.96 | 0.97 | 0.97 | 0.97 | 0.92 | 0.94 | 0.94 | 0.95 | 0.15 | ||||
| 200 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 | 0.96 | 0.97 | 0.97 | 0.98 | 0.98 | 0.92 | 0.94 | 0.95 | 0.95 | 0.95 | 0.18 | |
| Acc. | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | 80 | 110 | 140 | 170 | 200 | rate | ||
| 80 | 3.24 | 2.2 | 4.67 | 0.07 | |||||||||||||
| 110 | 2.12 | 2.14 | 1.14 | 1.38 | 2.69 | 3.17 | 0.09 | ||||||||||
| 140 | 1.87 | 1.56 | 1.49 | 0.89 | 0.81 | 0.79 | 2.1 | 1.82 | 1.63 | 0.12 | |||||||
| 170 | 1.77 | 1.27 | 1.05 | 0.96 | 0.87 | 0.68 | 0.59 | 0.59 | 2.14 | 1.6 | 1.31 | 1.19 | 0.15 | ||||
| 200 | 1.94 | 1.45 | 1.2 | 1.11 | 1.08 | 0.95 | 0.69 | 0.59 | 0.54 | 0.57 | 2.44 | 1.95 | 1.68 | 1.58 | 1.52 | 0.18 | |
| regr. | 80 | 2.67 | 1.14 | 2.17 | 0.07 | ||||||||||||
| 110 | 2.88 | 2.18 | 1.27 | 0.9 | 2.36 | 1.76 | 0.09 | ||||||||||
| 140 | 2.67 | 1.98 | 1.61 | 1.38 | 1.02 | 0.83 | 2.57 | 1.91 | 1.54 | 0.12 | |||||||
| 170 | 2.89 | 1.98 | 1.49 | 1.21 | 1.46 | 0.98 | 0.74 | 0.61 | 2.63 | 1.79 | 1.34 | 1.08 | 0.15 | ||||
| 200 | 3.57 | 2.85 | 2.46 | 4.93 | 1.2 | 1.82 | 1.41 | 1.21 | 1.42 | 0.63 | 3.11 | 2.32 | 1.88 | 1.81 | 1.22 | 0.18 | |
| Post-correction, simple cut-off | Regression, Epanechnikov cut-off | |||||||||||
| Fixed tolerance | Adapt | Fixed tolerance | Adapt | |||||||||
| 80 | 110 | 140 | 170 | 200 | 122.6 | 80 | 110 | 140 | 170 | 200 | 122.6 | |
| 3.24 | 2.12 | 1.87 | 1.77 | 1.94 | 1.8 | 2.67 | 2.88 | 2.67 | 2.89 | 3.57 | 2.57 | |
| 2.2 | 1.14 | 0.89 | 0.87 | 0.95 | 1.04 | 1.14 | 1.27 | 1.38 | 1.46 | 1.82 | 1.28 | |
| 4.67 | 2.69 | 2.1 | 2.14 | 2.44 | 2.34 | 2.17 | 2.36 | 2.57 | 2.63 | 3.11 | 2.34 | |