On the Use of Cauchy Prior Distributions for Bayesian Logistic Regression

We denote two disjoint subsets of sample points based on their response values: $A_{0}=\{i:y_{i}=0\}$ and $A_{1}=\{i:y_{i}=1\}$. According to the definition of Albert and Anderson (1984), complete separation occurs in the sample if there exists a vector $\bm{\alpha}=(\alpha_{1},\alpha_{2},\ldots,\alpha_{p})^{T}$, such that for all $i=1,2,\ldots,n$,

Consider a simple example in which we wish to predict whether subjects in a study have a certain kind of infection based on model (1). Let $y_{i}=1$ if the $i$th subject is infected and 0 otherwise. The model includes an intercept ($x_{i1}=1$) and the other covariates are age ($x_{i2}$), gender ($x_{i3}$), and previous records of being infected ($x_{i4}$). Suppose in the sample, all infected subjects are older than 25 ($x_{i2}>25$), and all subjects who are not infected are younger than 25 ($x_{i2}<25$). This is an example of complete separation because (2) is satisfied for $\bm{\alpha}=(-25,1,0,0)^{T}$.

If the sample points cannot be completely separated, Albert and Anderson (1984) introduced another notion of separation called quasicomplete separation. There is quasicomplete separation in the sample if there exists a non-null vector $\bm{\alpha}=(\alpha_{1},\alpha_{2},\ldots,\alpha_{p})^{T}$, such that for all $i=1,2,\ldots,n$,

and equality holds for at least one $i$. Consider the set up of the previous example where the goal is to predict whether a person is infected or not. Suppose we have the same model but there is a slight modification in the dataset: all infected subjects are at least 25 years old ($x_{i2}\geq 25$), all uninfected subjects are no more than 25 years old ($x_{i2}\leq 25$), and there are two subjects aged exactly 25, of whom one is infected but not the other. This is an example of quasicomplete separation because (2) is satisfied for $\bm{\alpha}=(-25,1,0,0)^{T}$ and the equality holds for two observations with age exactly 25.

Let $\mathcal{C}$ and $\mathcal{Q}$ denote the set of all vectors $\bm{\alpha}$ that satisfy (2) and (3), respectively. For any $\bm{\alpha}\in\mathcal{C}$, all sample points must satisfy (2), so $\bm{\alpha}$ cannot lead to quasicomplete separation which requires at least one equality in (3). This implies that $\mathcal{C}$ and $\mathcal{Q}$ are disjoint sets, while both can be non-empty for a certain dataset. Note that Albert and Anderson (1984) define quasicomplete separation only when the sample points cannot be separated using complete separation. Thus according to their definition, only one of $\mathcal{C}$ and $\mathcal{Q}$ can be non-empty for a certain dataset. However, in our slightly modified definition of quasicomplete separation, the absence of complete separation is not required. This permits both $\mathcal{C}$ and $\mathcal{Q}$ to be non-empty for a dataset. In the remainder of the paper, for simplicity we use the term “separation” to refer to either complete or quasicomplete separation, so that $\mathcal{C}\cup\mathcal{Q}$ is non-empty.

When Markov chain Monte Carlo (MCMC) is applied to sample from the posterior distribution, the posterior mean is a commonly used summary statistic. We aim to study whether the marginal posterior mean $E(\beta_{j}\mid\mathbf{y})$ exists under the independent Cauchy priors suggested by Gelman et al. (2008). Let $C(\mu,\sigma)$ denote a Cauchy distribution with location parameter $\mu$ and scale parameter $\sigma$. The default prior suggested by Gelman et al. (2008) corresponds to $\beta_{j}\stackrel{{\scriptstyle\text{ind}}}{{\sim}}C(0,\sigma_{j})$, for $j=1,2,\dots,p$.

For a design matrix with full column rank, Albert and Anderson (1984) showed that a finite maximum likelihood estimate of $\bm{\beta}$ does not exist when there is separation in the data. However, even in the case of separation and/or a rank deficient design matrix, the posterior means for some or all $\beta_{j}$’s may exist because they incorporate the information from the prior distribution. Following Definition 2.2.1 of Casella and Berger (1990, pp. 55), we say $E(\beta_{j}\mid\mathbf{y})$ exists if $E(|\beta_{j}|\mid\mathbf{y})<\infty$, and in this case, $E(\beta_{j}\mid\mathbf{y})$ is given by

Note that alternative definitions may require only one of the integrals in (4) to be finite for the mean to exist, e.g., Bickel and Doksum (2001, pp. 455). However, according to the definition used in this paper, both integrals in (4) have to be finite for the posterior mean to exist. Our main result shows that for each $j=1,2,\ldots,p$, the existence of $E(\beta_{j}\mid\mathbf{y})$ depends on whether the predictor $\mathbf{X}_{j}$ is a solitary separator or not, which is defined as follows:

This definition implies that for a solitary separator $\mathbf{X}_{j}$, if $\alpha_{j}>0$, then $x_{i,j}\geq 0$ for all $i\in A_{1}$, and $x_{i,j}\leq 0$ for all $i\in A_{0}$; if $\alpha_{j}<0$, then $x_{i,j}\leq 0$ for all $i\in A_{1}$, and $x_{i,j}\geq 0$ for all $i\in A_{0}$. Therefore, the hyperplane $\{\mathbf{x}\in\mathbb{R}^{p}:x_{j}=0\}$ in the predictor space separates the data into two groups $A_{1}$ and $A_{0}$ (except for the points located on the hyperplane). The following theorem provides a necessary and sufficient condition for the existence of marginal posterior means of regression coefficients in a logistic regression model.

A proof of Theorem 1 is available in Appendices A and B.

We expand on the second remark with a toy example where a predictor is a solitary separator before centering but not after centering. Consider a dataset with $n=100$, $\mathbf{y}=(\underbrace{0,\dots 0}_{25},\underbrace{1,\dots,1}_{75})^{T}$ and a binary predictor $\mathbf{X}_{j}=(\underbrace{0,\dots 0}_{50},\underbrace{1,\dots,1}_{50})^{T}$. Here $\mathbf{X}_{j}$ is a solitary separator which leads to quasicomplete separation before centering. However, the centered predictor $\mathbf{X}_{j}=(\underbrace{-0.5,\dots-0.5}_{50},\underbrace{0.5,\dots,0.5}_{50})^{T}$ is no longer a solitary separator because after centering the hyperplane $\{\mathbf{x}:x_{j}=-0.5\}$ separates the data but $\{\mathbf{x}:x_{j}=0\}$ does not. Consequently, the posterior mean $E(\beta_{j}\mid\mathbf{y})$ does not exist before centering but it exists after centering.

So far we have mainly focused on the logistic regression model, which is one of the most widely used binary regression models because of the interpretability of its regression coefficients in terms of odds ratios. We now generalize Theorem 1 to binary regression models with link functions other than the logit. Following the definition in McCullagh and Nelder (1989, pp. 27), we assume that for $i=1,2,\ldots,n$, the linear predictor $\mathbf{x}_{i}^{T}\bm{\beta}$ and the success probability $\pi_{i}$ are connected by a monotonic and differentiable link function $g(\cdot)$ such that $g(\pi_{i})=\mathbf{x}_{i}^{T}\bm{\beta}$. We further assume that $g(.)$ is a one-to-one function, which means that $g(.)$ is strictly monotonic. This is satisfied by many commonly used link functions including the probit. Without loss of generality, we assume that $g(\cdot)$ is a strictly increasing function.

Note that (7) in the sufficient condition of Theorem 2 imposes constraints on the link function $g(.)$, and hence the likelihood function. A proof of this theorem is given in Appendix C. Moreover, it is shown that condition (7) holds for the probit link function.

In certain applications, to incorporate available prior information, it may be desirable to use Cauchy priors with nonzero location parameters. The following corollary states that for both logistic and probit regression, the condition for existence of posterior means derived in Theorems 1 and 2 continues to hold under independent Cauchy priors with nonzero location parameters.

A proof of Corollary 1 is available in Appendix D.

In some applications it could be more natural to allow the regression coefficients to be dependent, a priori. Thus in addition to independent Cauchy priors, we also study the existence of posterior means under a multivariate Cauchy prior, with the following density function:

where $\bm{\beta}\in\mathbb{R}^{p}$, $\bm{\mu}$ is a $p\times 1$ location parameter and $\bm{\Sigma}$ is a $p\times p$ positive-definite scale matrix. A special case of the multivariate Cauchy prior is the Zellner-Siow prior (Zellner and Siow 1980). It can be viewed as a scale mixture of $g$-priors, where conditional on $g$, $\bm{\beta}$ has a multivariate normal prior with a covariance matrix proportional to $g(\mathbf{X}^{T}\mathbf{X})^{-1}$, and the hyperparameter $g$ has an inverse gamma prior, $\text{IG}(1/2,n/2)$. Based on generalizations of the $g$-prior to binary regression models (Fouskakis et al. 2009; Sabanés Bové and Held 2011; Hanson et al. 2014), the Zeller-Siow prior, which has a density (8) with $\bm{\Sigma}\propto n(\mathbf{X}^{T}\mathbf{X})^{-1}$, can be a desirable objective prior as it preserves the covariance structure of the data and is free of tuning parameters.

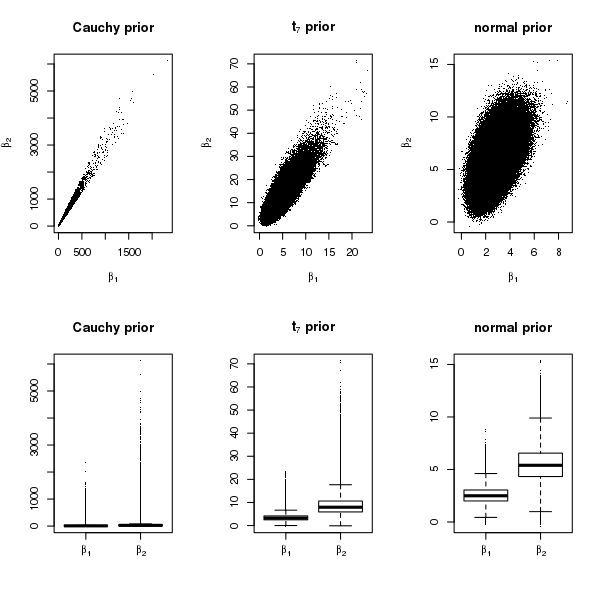
A proof of Theorem 3 is available in Appendices E and F. The study of existence of posterior means under multivariate Cauchy priors in the presence of quasicomplete separation has proved to be more challenging. We hope to study this problem in future work. Note that although under (8), the induced marginal prior of $\beta_{j}$ is a univariate Cauchy distribution for each $j=1,2,\ldots,p$, the multivariate Cauchy prior is different from independent Cauchy priors, even with a diagonal scale matrix $\bm{\Sigma}=\text{diag}(\sigma_{1}^{2},\sigma_{2}^{2},\ldots,\sigma_{p}^{2})$. In fact, as a rotation invariant distribution, the multivariate Cauchy prior places less probability mass along axes than the independent Cauchy priors (see Figure 1). Therefore, it is not surprising that solitary separators no longer play an important role for existence of posterior means under multivariate Cauchy priors, as evident from Theorem 3.

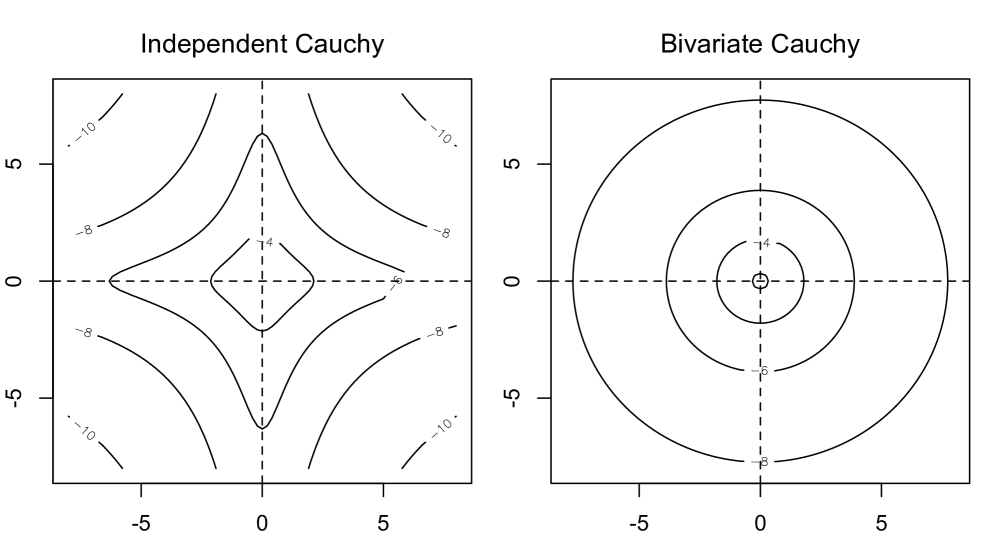
So far we have considered Cauchy priors, which are $t$ distributions with 1 degree of freedom. We close this section with a remark on lighter tailed $t$ priors (with degrees of freedom greater than 1) and normal priors, for which the prior means exist.

Polson et al. (2013) showed that the likelihood for logistic regression can be written as a mixture of normals with respect to a Pólya-Gamma (PG) distribution. Based on this result, they developed an efficient Gibbs sampler for logistic regression with a multivariate normal prior on $\bm{\beta}$. Choi and Hobert (2013) showed that their Gibbs sampler is uniformly ergodic. This guarantees the existence of central limit theorems for Monte Carlo averages of functions of $\bm{\beta}$ which are square integrable with respect to the posterior distribution $p(\bm{\beta}\mid\mathbf{y})$. Choi and Hobert (2013) developed a latent data model which also led to the Gibbs sampler of Polson et al. (2013). We adopt their latent data formulation to develop a Gibbs sampler for logistic regression with independent Student-$t$ priors on $\bm{\beta}$.

Let $U=(2/\pi^{2})\sum_{l=1}^{\infty}W_{l}/{(2l-1)}^{2}$, where $W_{1},W_{2},\dots$ is a sequence of i.i.d. Exponential random variables with rate parameters equal to 1. The density of $U$ is given by

Then for $k\geq 0$, the Pólya-Gamma (PG) distribution is constructed by exponential tilting of $h(u)$ as follows:

A random variable with density $p(u;k)$ has a PG($1,k$) distribution.

Let $t_{v}(0,\sigma_{j})$ denote the Student-$t$ distribution with $v$ degrees of freedom, location parameter 0, and scale parameter $\sigma_{j}$. Since Student-$t$ distributions can be expressed as inverse-gamma (IG) scale mixtures of normal distributions, for $j=1,2,\ldots,p$, we have:

Conditional on $\bm{\beta}$ and $\bm{\Gamma}=\text{diag}(\gamma_{1},\gamma_{2},\ldots,\gamma_{p})$, let $(y_{1},z_{1}),(y_{2},z_{2}),\ldots,(y_{n},z_{n})$ be $n$ independent random vectors such that $y_{i}$ has a Bernoulli distribution with success probability $\exp(\mathbf{x}_{i}^{T}\bm{\beta})/(1+\exp(\mathbf{x}_{i}^{T}\bm{\beta}))$, $z_{i}\sim PG(1,|\mathbf{x}_{i}^{T}\bm{\beta}|)$, and $y_{i}$ and $z_{i}$ are independent, for $i=1,2,\ldots,n$. Let $\bm{Z}_{D}=\text{diag}(z_{1},z_{2},\ldots,z_{n})$, then the augmented posterior density is $p(\bm{\beta},\bm{\Gamma},\bm{Z}_{D}\mid\mathbf{y})$. We develop a Gibbs sampler with target distribution $p(\bm{\beta},\bm{\Gamma},\bm{Z}_{D}\mid\mathbf{y})$, which cycles through the following sequence of distributions iteratively:

1. 1.

   $\bm{\beta}\mid\bm{\Gamma},\bm{Z}_{D},\mathbf{y}\sim\text{N}\left((\mathbf{X}^{T}\bm{Z}_{D}\mathbf{X}+\bm{\Gamma}^{-1})^{-1}\mathbf{X}^{T}\mathbf{\tilde{y}},(\mathbf{X}^{T}\bm{Z}_{D}\mathbf{X}+\bm{\Gamma}^{-1})^{-1}\right)$, where $\tilde{y}_{i}=y_{i}-1/2$ and $\mathbf{\tilde{y}}=(\tilde{y}_{1},\tilde{y}_{2},\ldots,\tilde{y}_{n})^{T}$,

2. 2.

   $\gamma_{j}\mid\bm{\beta},\bm{Z}_{D},\mathbf{y}\stackrel{{\scriptstyle\text{ind}}}{{\sim}}\text{IG}\left(\frac{v+1}{2},\frac{\beta_{j}^{2}+v\sigma_{j}^{2}}{2}\right)$, for $j=1,2,\ldots,p$,

3. 3.

   $z_{i}\mid\bm{\Gamma},\bm{\beta},\mathbf{y}\stackrel{{\scriptstyle\text{ind}}}{{\sim}}\text{PG}(1,|\mathbf{x}_{i}^{T}\bm{\beta}|)$, for $i=1,2,\ldots,n$.

Steps 1 and 3 follow immediately from Choi and Hobert (2013); Polson et al. (2013) and step 2 follows from straightforward algebra. In the next section, for comparison of posterior distributions under Student-$t$ priors with different degrees of freedom, we implement the above Gibbs sampler, and for normal priors we apply the Gibbs sampler of Polson et al. (2013). Both Gibbs samplers can be implemented using the R package tglm, available in the supplement.

Our empirical results in the next section suggest that the Gibbs sampler exhibits extremely slow mixing for posterior simulation under Cauchy priors for data with separation. Thus we consider alternative MCMC sampling algorithms in the hope of improving mixing. A random walk Metropolis algorithm shows some improvement over the Gibbs sampler in the $p=2$ case. However, it is not efficient for exploring higher dimensional spaces. Thus we have been motivated to use the software Stan (Carpenter et al. 2016), which implements the No-U-Turn Sampler (NUTS) of Hoffman and Gelman (2014), a tuning free extension of the Hamiltonian Monte Carlo (HMC) algorithm (Neal 2011).

It has been demonstrated that for continuous parameter spaces, HMC can improve over poorly mixing Gibbs samplers and random walk Metropolis algorithms. HMC is a Metropolis algorithm that generates proposals based on Hamiltonian dynamics, a concept borrowed from Physics. In HMC, the parameter of interest is referred to as the “position” variable, representing a particle’s position in a $p$-dimensional space. A $p$-dimensional auxiliary parameter, the “momentum” variable, is introduced to represent the particle’s momentum. In each iteration, the momentum variable is generated from a Gaussian distribution, and then a proposal of the position momentum pair is generated (approximately) along the trajectory of the Hamiltonian dynamics defined by the joint distribution of the position and momentum. Hamiltonian dynamics changing over time can be approximated by discretizing time via the “leapfrog” method. In practice, a proposal is generated by applying the leapfrog algorithm $L$ times, with stepsize $\epsilon$, to the the current state. The proposed state is accepted or rejected according to a Metropolis acceptance probability. Section 5.3.3 of the review paper by Neal (2011) illustrates the practical benefits of HMC over random walk Metropolis algorithms. The examples in this section demonstrate that the momentum variable may change only slowly along certain directions during leapfrog steps, permitting the position variable to move consistently in this direction for many steps. In this way, proposed states using Hamiltonian dynamics can be far away from current states but still achieve high acceptance probabilities, making HMC more efficient than traditional algorithms such as random walk Metropolis.

In spite of its advantages, HMC has not been very widely used in the Statistics community until recently, because its performance can be sensitive to the choice of two tuning parameters: the leapfrog stepsize $\epsilon$ and the number of leapfrog steps $L$. Very small $\epsilon$ can lead to waste in computational power whereas large $\epsilon$ can yield large errors due to discretization. Regarding the number of leapfrog steps $L$, if it is too small, proposed states can be near current states and thus resemble random walk. On the other hand, if $L$ is too large, the Hamiltonian trajectory can retrace its path so that the proposal is brought closer to the current value, which again is a waste of computational power.

The NUTS algorithm tunes these two parameters automatically. To select $L$, the main idea is to run the leapfrog steps until the trajectory starts to retrace its path. More specifically, NUTS builds a binary tree based on a recursive doubling procedure, that is similar in flavor to the doubling procedure used for slice sampling by Neal (2003), with nodes of the tree representing position momentum pairs visited by the leapfrog steps along the path. The doubling procedure is stopped if the trajectory starts retracing its path, that is making a “U-turn”, or if there is a large simulation error accumulated due to many steps of leapfrog discretization. NUTS consists of a carefully constructed transition kernel that leaves the target joint distribution invariant. It also proposes a way for adaptive tuning of the stepsize $\epsilon$.

We find that by implementing this tuning free NUTS algorithm, available in the freely available software Stan, substantially better mixing than the Gibbs sampler can be achieved in all of our examples in which posterior means exist. We still include the Gibbs sampler in this article for two main reasons. First, it illustrates that Stan can provide an incredible improvement in mixing over the Gibbs sampler in certain cases. Stan requires minimal coding effort, much less than developing a Gibbs sampler, which may be useful information for readers who are not yet familiar with Stan. Second, Stan currently works for continuous target distributions only, but discrete distributions for models and mixed distributions for regression coefficients frequently arise in Bayesian variable selection, for regression models with binary or categorical response variables (Holmes and Held 2006; Mitra and Dunson 2010; Ghosh and Clyde 2011; Ghosh et al. 2011; Ghosh and Reiter 2013; Li and Clyde 2015). Unlike HMC algorithms, Gibbs samplers can typically be extended via data augmentation to incorporate mixtures of a point mass and a continuous distribution, as priors for the regression coefficients, without much additional effort.

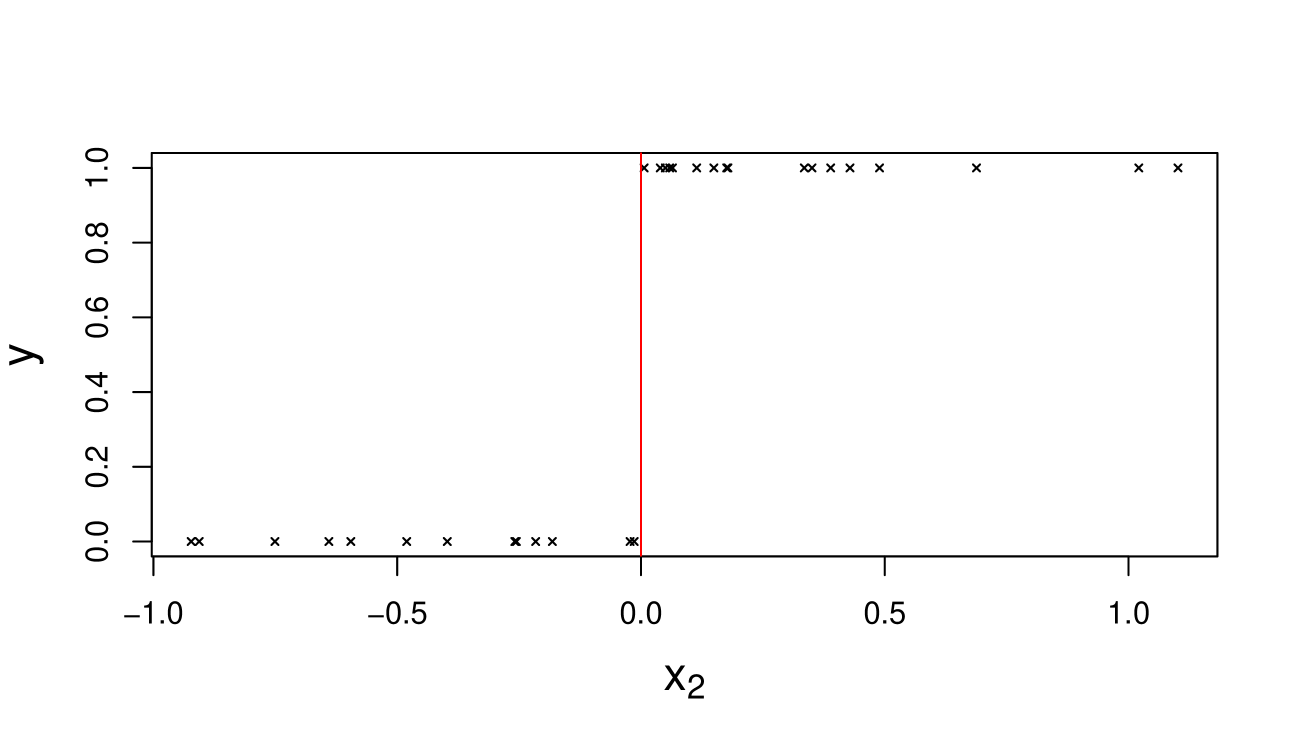
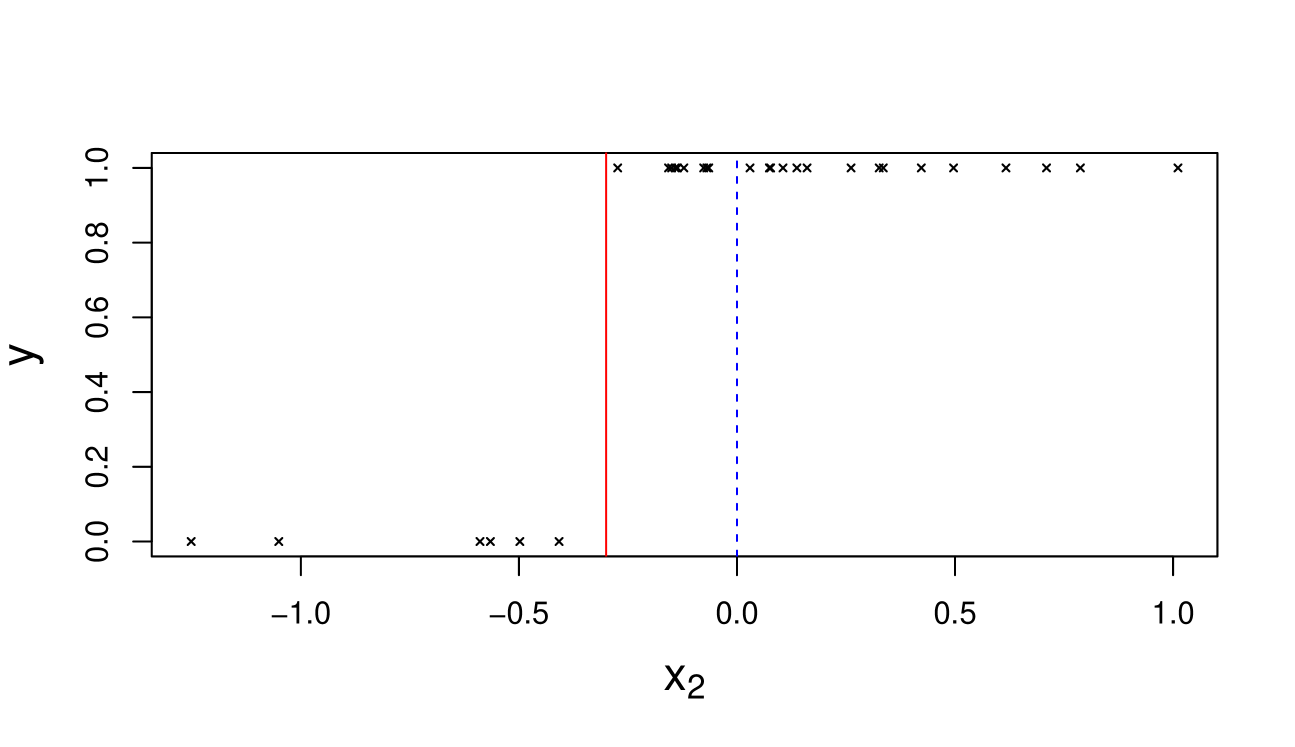
First, we generate a dataset with $p=2$ (including the intercept) and $n=30$. The continuous predictor $\mathbf{X}_{2}$ is chosen to be a solitary separator (after standardizing), which leads to complete separation, whereas the constant term $\mathbf{X}_{1}$ contains all one’s and is not a solitary separator. A plot of $\mathbf{y}$ versus $\mathbf{X}_{2}$ in Figure 2 demonstrates this graphically. So by Theorem 1, under independent Cauchy priors, $E(\beta_{1}\mid\mathbf{y})$ exists but $E(\beta_{2}\mid\mathbf{y})$ does not.

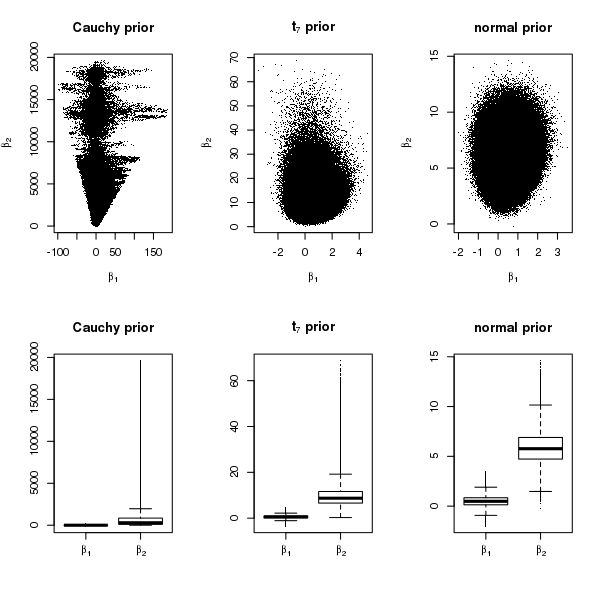
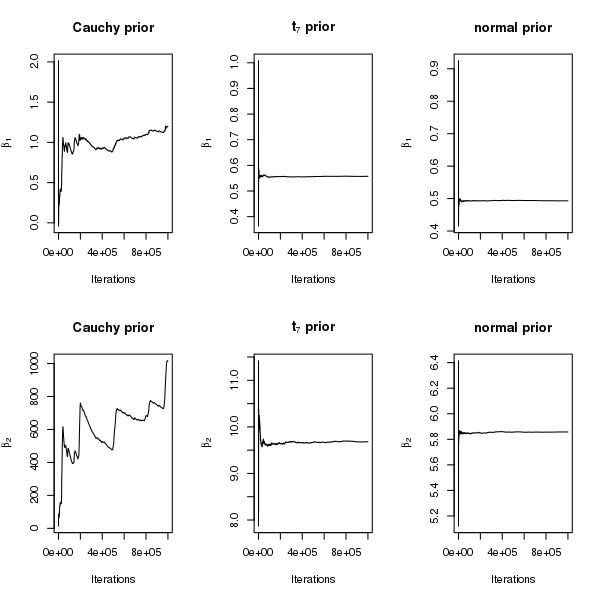
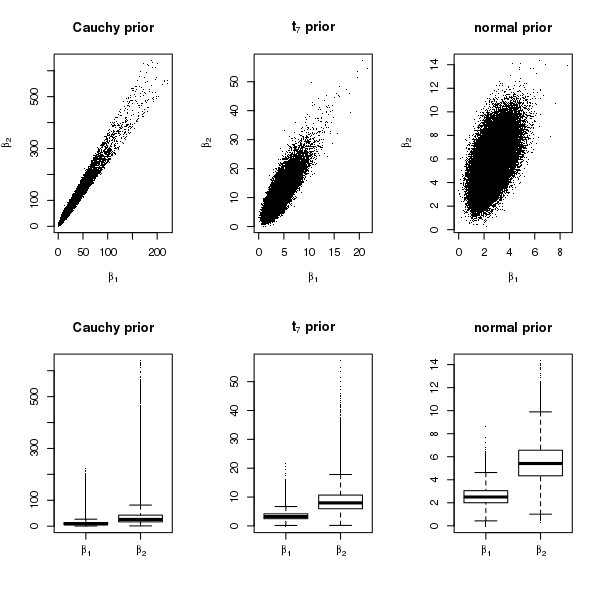
The results from the Gibbs sampler are reported in Figures 3 and 4. Figure 3 shows the posterior samples of $\bm{\beta}$ under the different priors. The scale of $\beta_{2}$, the coefficient corresponding to the solitary separator $\mathbf{X}_{2}$, is extremely large under Cauchy priors, less so under $t_{7}$ priors, and the smallest under normal priors. In particular, under Cauchy priors, the posterior distribution of $\beta_{2}$ seems to have an extremely long right tail. Moreover, although $\mathbf{X}_{1}$ is not a solitary separator, under Cauchy priors, the posterior samples of $\beta_{1}$ have a much larger spread. Figure 4 shows that the running means of both $\beta_{1}$ and $\beta_{2}$ converge rapidly under normal and $t_{7}$ priors, whereas under Cauchy priors, the running mean of $\beta_{1}$ does not converge after a million iterations and that of $\beta_{2}$ clearly diverges. We also ran Stan for this example but do not report the results here, because it gave warning messages about divergent transitions for Cauchy priors, after the burn-in period. Given that the posterior mean of $\beta_{2}$ does not exist in this case, the lack of convergence is not surprising.

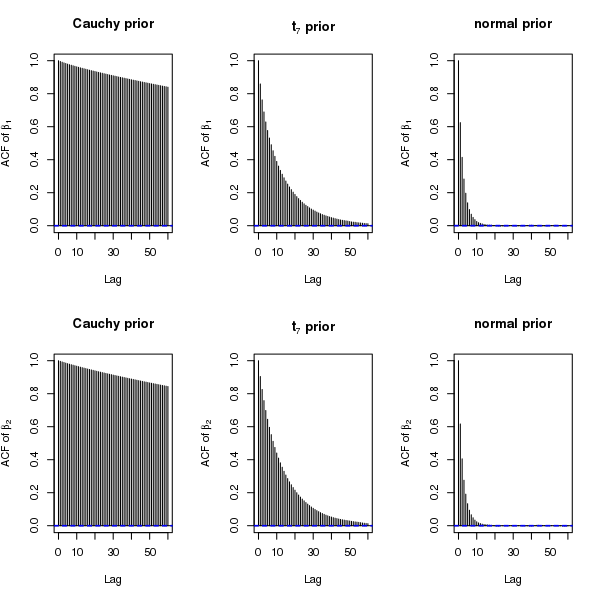
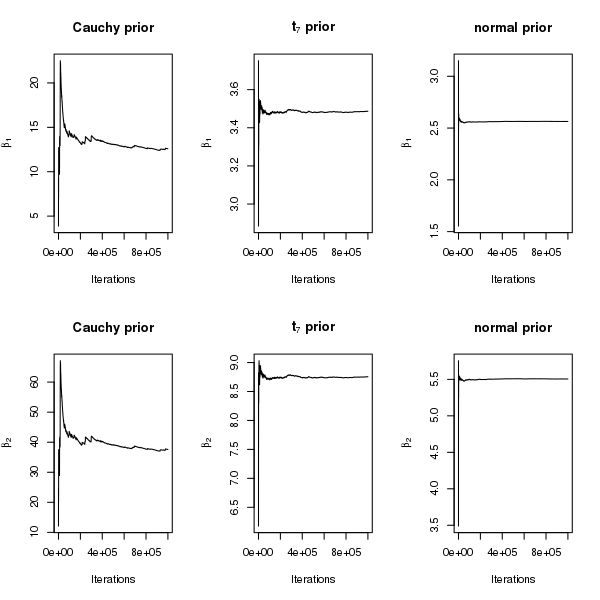
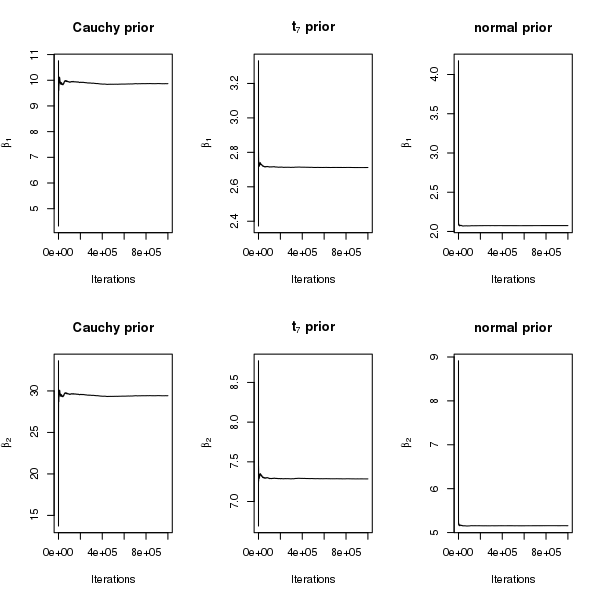
Now we generate a new dataset with $p=2$ and $n=30$ such that there is complete separation but there are no solitary separators (see Figure 5). This guarantees the existence of both $E(\beta_{1}\mid\mathbf{y})$ and $E(\beta_{2}\mid\mathbf{y})$ under independent Cauchy priors. The difference in the existence of $E(\beta_{2}\mid\mathbf{y})$ for the two simulated datasets is reflected by the posterior samples from the Gibbs sampler: under Cauchy priors, the samples of $\beta_{2}$ in Figure 1 in the Appendix are more stabilized than those in Figure 3 in the manuscript. However, when comparing across prior distributions, we find that the posterior samples of neither $\beta_{1}$ nor $\beta_{2}$ are as stable as those under $t_{7}$ and normal priors, which is not surprising because among the three priors, Cauchy priors have the heaviest tails and thus yield the least shrinkage. Figure 2 in the Appendix shows that the convergence of the running means under Cauchy priors is slow. Although we have not verified the existence of the second or higher order posterior moments under Cauchy priors, for exploratory purposes we examine sample autocorrelation plots of the draws from the Gibbs sampler. Figure 6 shows that the autocorrelation decays extremely slowly for Cauchy priors, reasonably fast for $t_{7}$ priors, and rapidly for normal priors.

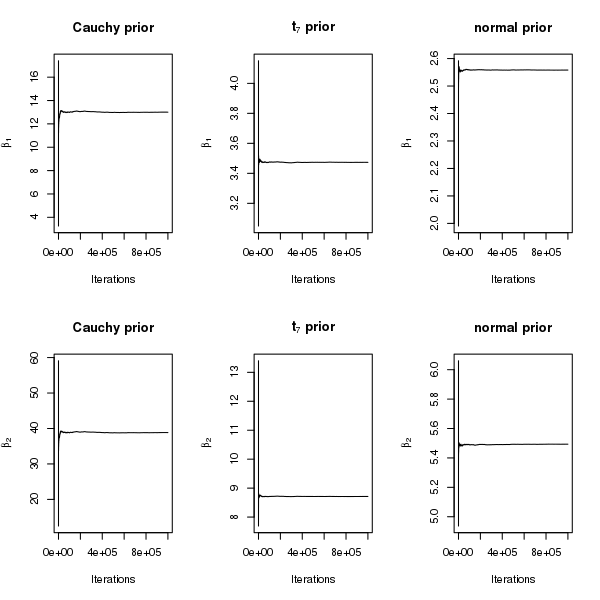
Some results from Stan are reported in Figures 3 and 4 in the Appendix. Figure 3 in the Appendix shows posterior distributions with nearly identical shapes as those obtained using Gibbs sampling in Figure 1 in the Appendix, with the only difference being that more extreme values appear under Stan. This is most likely due to faster mixing in Stan. As Stan traverses the parameter space more rapidly, values in the tails appear more quickly than under the Gibbs sampler. Figures 2 and 4 in the Appendix demonstrate that running means based on Stan are in good agreement with those based on the Gibbs sampler.

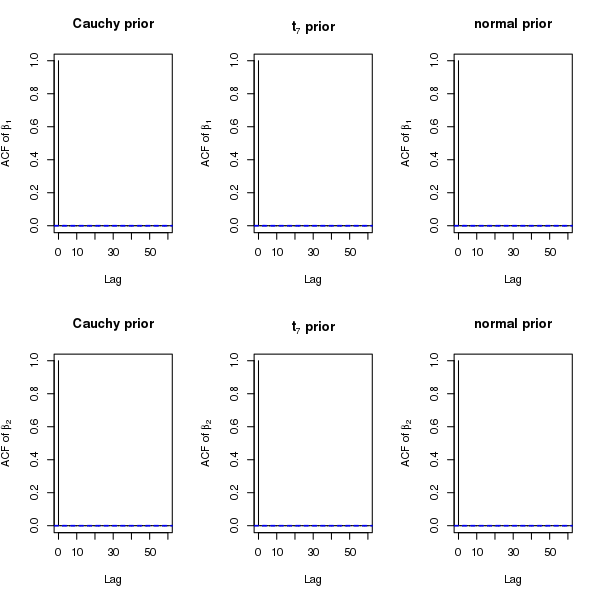
The autocorrelation plots for Stan in Figure 7 demonstrate a remarkable improvement over those for Gibbs in Figure 6 for all priors, and the difference in mixing is the most prominent for Cauchy priors.

To summarize, all the plots unequivocally suggest that Cauchy priors lead to an extremely slow mixing Gibbs sampler and unusually large scales for the regression coefficients, even when all the marginal posterior means are guaranteed to exist. While mixing can be improved tremendously with Stan, the heavy tailed posteriors under Stan are in agreement with those obtained from the Gibbs samplers. One may argue that in spite of the unnaturally large regression coefficients, Cauchy priors could lead to superior predictions. Thus in the next two sections we compare predictions based on posteriors under the three priors for two real datasets. As Stan generates nearly independent samples, we use Stan for MCMC simulations for the real datasets.

The “SPECT” dataset (Kurgan et al. 2001) is available from the UCI Machine Learning Repository¹¹1https://archive.ics.uci.edu/ml/datasets/SPECT+Heart. The binary response variable is whether a patient’s cardiac image is normal or abnormal, according to the diagnosis of cardiologists. The predictors are 22 binary features obtained from the cardiac images using a machine learning algorithm. The goal of the study is to determine if the predictors can correctly predict the diagnoses of cardiologists, so that the process could be automated to some extent.

Prior to centering, two of the binary predictors are solitary quasicomplete separators: $x_{i,j}=0$ $\forall i\in A_{0}$ and $x_{i,j}\geq 0$ $\forall i\in A_{1}$, for $j=18,19$, with $\mathbf{X}_{1}$ denoting the column of ones. Ghosh and Reiter (2013) analyzed this dataset with a Bayesian probit regression model which incorporated variable selection. As some of their proposed methods relied on an approximation of the marginal likelihood based on the MLE of $\bm{\beta}$, they had to drop these potentially important predictors from the analysis. If one analyzed the dataset with the uncentered predictors, by Theorem 1, the posterior means $E(\beta_{18}\mid\mathbf{y})$ and $E(\beta_{19}\mid\mathbf{y})$ would not exist under independent Cauchy priors. However, after centering there are no solitary separators, so the posterior means of all coefficients exist.

The SPECT dataset is split into a training set of 80 observations and a test set of 187 observations by Kurgan et al. (2001). We use the former for model fitting and the latter for prediction. First, for each of the three priors (Cauchy, $t_{7}$, and normal), we run Stan on the training dataset, for 1,000,000 iterations after discarding 100,000 samples as burn-in.

As in the simulation study, MCMC draws from Stan show excellent mixing for all priors. However, the posterior means of the regression coefficients involved in separation are rather large under Cauchy priors compared to the other priors. For example, the posterior means of $(\beta_{18},\beta_{19})$ under Cauchy, $t_{7}$, and normal priors are $(10.02,5.57),(3.24,1.68),$ and $(2.73,1.43)$ respectively. These results suggest that Cauchy priors are too diffuse for datasets with separation.

Next for each $i=1,2,\dots,n_{\text{test}}$ in the test set, we estimate the corresponding success probability $\pi_{i}$ by the Monte Carlo average:

where $\bm{\beta}^{(s)}$ is the sampled value of $\bm{\beta}$ in iteration $s$, after burn-in. Recall that here $n_{\text{test}}=187$ and $S=10^{6}$. We calculate two different types of summary measures to assess predictive performance. We classify the $i$th observation in the test set as a success, if $\widehat{\pi}_{i}^{\text{MC}}\geq 0.5$ and as a failure otherwise, and compute the misclassification rates. Note that the misclassification rate does not fully take into account the magnitude of $\widehat{\pi}_{i}^{\text{MC}}$. For example, if $y_{i}=1$ both $\widehat{\pi}_{i}^{\text{MC}}=0.5$ and $\widehat{\pi}_{i}^{\text{MC}}=0.9$ would correctly classify the observation, while the latter may be more preferable. So we also consider the average squared difference between $y_{i}$ and $\widehat{\pi}_{i}^{\text{MC}}$:

which is always between 0 and 1, with a value closer to 0 being more preferable. Note that the Brier score (Brier 1950) equals $2MSE^{\text{MC}}$, according to its original definition. Since in some modified definitions (Blattenberger and Lad 1985), it is the same as $MSE^{\text{MC}}$, we refer to $MSE^{\text{MC}}$ as the Brier score.

To compare the Monte Carlo estimates with those based on the EM algorithm of Gelman et al. (2008), we also estimate the posterior mode, denoted by $\widetilde{\bm{\beta}}$ under identical priors and hyperparameters, using the R package arm (Gelman et al. 2015). The EM estimator of $\pi_{i}$ is given by:

and $MSE^{\text{EM}}$ is calculated by replacing $\widehat{\pi}_{i}^{\text{MC}}$ by $\widehat{\pi}_{i}^{\text{EM}}$ in (12).

We report the misclassification rates in Table 1 and the Brier scores in Table 2. MCMC achieves somewhat smaller misclassification rates and Brier scores than EM, especially under $t_{7}$ and normal priors. This suggests that a full Bayesian analysis using MCMC may produce estimates that are closer to the truth than modal estimates based on the EM algorithm. The predictions are similar across the three prior distributions with the normal and $t_{7}$ priors yielding slightly more accurate results than Cauchy priors.

We now analyze the “Pima Indians Diabetes” dataset in the R package MASS. This is a classic dataset without separation that has been analyzed by many authors in the past. Using this dataset we aim to compare predictions under different priors, when there is no separation. Using the training data provided in the package we predict the class labels of the test data. In this case the difference between different priors is practically nil. The Brier scores are same up to three decimal places, across all priors and all methods (EM and MCMC). The misclassification rates reported in Table 3 also show negligible difference between priors and methods. Here Cauchy priors have a slightly better misclassification rate compared to normal and $t_{7}$ priors, and MCMC provides slightly more accurate results compared to those obtained from EM. These results suggest that when there is no separation and maximum likelihood estimates exist, Cauchy priors may be preferable as default weakly informative priors in the absence of real prior information.

In the supplementary material, we present additional simulation results for logistic and probit regression with complete separation, along with an appendix that contains the proofs of all theoretical results. The Gibbs sampler developed in the paper can be implemented with the R package tglm, available from the website: https://cran.r-project.org/web/packages/tglm/index.html.

The authors thank the Editor-in-Chief, Editor, Associate Editor and the reviewer for suggestions that led to a greatly improved paper. The authors also thank Drs. David Banks, James Berger, William Bridges, Merlise Clyde, Jon Forster, Jayanta Ghosh, Aixin Tan, and Shouqiang Wang for helpful discussions. The research of Joyee Ghosh was partially supported by the NSA Young Investigator grant H98230-14-1-0126.

Supplementary Material: On the Use of Cauchy Prior Distributions for Bayesian Logistic Regression

In this supplement, we first present an appendix with additional simulation results for logit and probit link functions, and then include an appendix that contains proofs of the theoretical results.

Figures 1 and 2 are based on the posterior samples from a Gibbs sampler under a logit link, whereas Figures 3 and 4 are corresponding results from Stan. A detailed discussion of the results is provided in Section 4.2 of the manuscript.

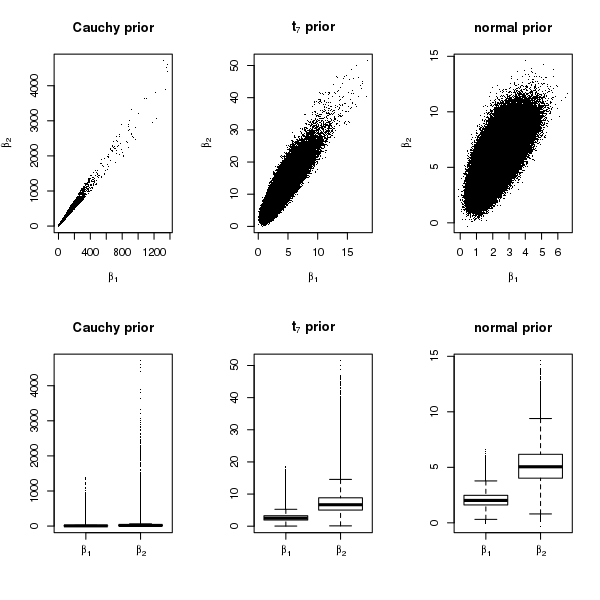
In this section we analyze the simulated dataset described in Section 4.2 of the manuscript under a probit link, while keeping everything else the same. We have shown in Theorem 2, that the theoretical results hold for a probit link. The goal of this analysis is to demonstrate that the empirical results are similar under the logit and probit link functions. For this dataset, Theorem 2 guarantees the existence of both $E(\beta_{1}\mid\mathbf{y})$ and $E(\beta_{2}\mid\mathbf{y})$ under independent Cauchy priors and a probit link function. As in the case of logistic regression the heavy tails of Cauchy priors translate into an extremely heavy right tail in the posterior distributions of $\beta_{1}$ and $\beta_{2}$, compared to the lighter tailed priors (see Figure 5 and 6 here). Thus in the case of separation, normal priors seem to be reasonable for probit regression also.

Here we show that if $\mathbf{X}_{j}$ is a solitary separator, then $E(\beta_{j}\mid\mathbf{y})$ does not exist, which is equivalent to the necessary condition for Theorem 1.

Here we show that if $\mathbf{X}_{j}$ is not a solitary separator, then the posterior mean of $\beta_{j}$ exists.