On the use of stereodynamical effects to control cold chemical reactions: the H + D D + HD case study
Abstract
Quantum calculations are reported for the stereodynamic control of the H + D D + HD chemical reaction in the energy range of 1–50 K. Stereodynamic control is achieved by a formalism similar to that reported by Perreault et al. [Nature Chem. 10, 561 (2018)] in recent experimental works in which the alignment of the molecular bond axis relative to the incident relative velocity is controlled by selective preparations of the molecule in a specific or superposition of magnetic projection quantum numbers of the initial molecular rotational level. The approach presented here generalizes the experimental scheme of Perreault et al. and offers additional degree of control through various experimental preparation of the molecular alignment angle. Illustrative results presented for the H + D2 and D + HD reactions show significant control with the possibility of turning the reaction completely on or off with appropriate stereodynamic preparation of the molecular state. Various scenarios for maximizing and minimizing the reaction outcomes are identified with selective preparation of molecular rotational states.
I Introduction
Stereochemistry Aldegunde et al. (2006, 2011); Cernuto et al. (2018); Ascenzi et al. (2019); Falcinelli et al. (2019, 2021) along with coherent and optimal control of molecular processes Tannor, Kosloff, and Rice (1986); Rice and Zhao (2000); Levis, Menkir, and Rabitz (2001); Shapiro and Brumer (2012) are a manifestation of a long standing goal of controlling chemical reactions. The problem has been addressed independently from the perspective of a variety of research fields; from exploiting ultra–fast light–induced electron dynamics – within an attosecond time scale Cattaneo et al. (2018)– to an ultra–slow sub–Kelvin nuclear dynamics, in the context of either cold or ultracold molecular collisions Krems (2008); Balakrishnan (2016).
In a recent series of seminal experiments, Perreault and co–workers have demonstrated a relatively simple setup in which a co–expansion of two colliding molecules (HD + D2 and HD + H2) in the same beam stream enable cold collisions with relative kinetic energies of about 1 Kelvin Perreault, Mukherjee, and Zare (2017, 2018). The technique, combined with Stark–induced adiabatic Raman passage (SARP) Mukherjee and Zare (2011) allows selective preparation of the alignment of the diatomic internuclear axis relative to the incident velocity vector. This is made possible by a light–assisted spatial polarization of the diatomic angular momentum vector combined with selection of specific –projections, say , along a given quantization axis of choice Dong, Mukherjee, and Zare (2013); Mukherjee, Dong, and Zare (2014). As a consequence, the lower collision energies provided by the co–expansion can selectively discard higher and undesired Perreault, Mukherjee, and Zare (2017) external collisional orbital angular momentum states, , whereas SARP can selectively prepare a specific internal rovibrational state with a given or superposition of states. More recently the same methodology was also applied to cold He + HD and He + D2 collisions with the latter revealing strong signatures of an partial wave resonance Perreault, Mukherjee, and Zare (2019); Zhou et al. (2021). While these experiments have so far been used to study only inelastic processes, they open up new avenues for possible stereodynamic control of cold reactive collisions. Theoretical prospects on that matter have been available for a while Aldegunde et al. (2005, 2006, 2011), and revisited recently in the context of coherent control Devolder, Tscherbul, and Brumer (2020).
It is worthwhile to highlight important aspects of these experiments, beyond requiring a simpler experimental setup compared to current molecule cooling and trapping techniques: (i) it allows controlled low–kinetic energy collisions of spatially–polarized non–polar molecules in a complete field–free environment; (ii) the production of colliding partners described by a single internal quantum state eliminates the need of averaging any observable over a large number of initial states; (iii) due to (i) and (ii), the actual interaction potential can be addressed experimentally as it is, within such physical conditions, mainly driven by the anisotropy caused by the target–projectile relative orientation; and (iv), unveils marked stereodynamical effects previously constrained to scattering experiments using polar molecules de Miranda et al. (2011).
The experiments of Perreault et al. have been accompanied by the theoretical works of Croft et al. Croft et al. (2018); Croft and Balakrishnan (2019) on HD + H2 and Morita et al. Morita and Balakrishnan (2020a, b) on He + HD collisions. Further, Jambrina et al. Jambrina et al. (2019) and Morita et al. Morita et al. (2020) have explored the control of isolated partial wave resonances through stereodynamic preparations of HD + H2 and HCl + H2 collisions, respectively, as in the experiments of Perreault et al. In a recent work, Jambrina et al. examined stereodynamic control of CO + HD collisions in which the HD molecule is prepared in a stereodynamic state but both molecules undergo a change in rotational angular momentum Jambrina et al. (2021). In this work we extend these ideas to low–energy reactive collisions taking the prototypical chemical reactions of H + D D + HD with polarization of the initial rotational state of D2 and HD. Thus, in what follows, we address questions such as (i) the role of bond axis orientation of D2 (HD) relative to the initial relative velocity; (ii) whether it is possible to orient the reactants in a manner to enhance or suppress the production of HD (D2); (iii) can we selectively induce the formation of products in a given internal state by controlling the orientation/alignment of the reactants during the collisions? (iv) identify any propensity rules that accompany these changes. These questions are addressed through a systematic analysis of typical scattering characteristics upon specific choices of so–called stereodynamical parameters – defined in more details below. Collisions are modeled using a time–independent quantum reactive scattering formalism as implemented in the APH3D code Pack and Parker (1987); Kendrick et al. (1999); Kendrick (2003a) that has been used extensively to model atom–diatom reactive collisions, combined with the legacy BKMP2 potential energy surface (PES) for the H3 system Boothroyd et al. (1996). As we shall see below, we have found strong evidence that supports a nearly–total stereodynamic control of a cold chemical reaction, from signifcant enhancement to near complete suppression.
Since the early works of Kuppermann et al. Kuppermann, Schatz, and Baer (1974) the H + H2 exchange reaction and its isotopic variants have been extensively studied in the literature both experimentally and theoretically and we shall focus mainly on aspects related to stereodynamic preparations and collisional outcomes. Interested readers are referred to recent works of Goswami et al. Goswami et al. (2020) who reported wavepacket calculations of the H + H2 exchange reaction; Desrousseaux et al. Desrousseaux et al. (2018) on rotational excitation in H + HD collisions at temperatures in the range of 10–1000 K; recent prediction of a Feshbach resonance on H + HD collisions by Zhou et al. Zhou et al. (2020); and quasi–classical trajectories simulations by Bossion et al. Bossion et al. (2018, 2020). Kendrick and co–workers have reported extensive studies of geometric phase (GP) effects in cold and ultracold H + H2, H + HD and D + HD collisions with vibrationally excited reactants that revealed a new interference mechanism that controls reactivity in the ultracold regime Hazra, Kendrick, and Balakrishnan (2016); Kendrick, Hazra, and Balakrishnan (2016a, b). Non–adiabatic effects in the H + H2 and H + HD reactions with vibrationally excited H2 and HD molecules for vibrational levels 4–9 have also been reported by Kendrick Kendrick (2018a, b, 2019). Several theoretical and combined experiment–theory studies on H + D2 are also available Wrede and Schnieder (1997); Banares et al. (1998); Kendrick et al. (1999); Fernández-Alonso, Bean, and Zare (1999); Kendrick (2000, 2001); Harich et al. (2002); Kendrick (2003b); Pomerantz et al. (2004).
II Theoretical approach
The methodology used herein is, in many aspects, very similar to that utilized in the previous works of Croft et al. Croft et al. (2018); Croft and Balakrishnan (2019) and Morita et al. Morita and Balakrishnan (2020a, b) except that reactive channels are also taken into consideration as a collision–induced outcome. Thus, upon a H + D reactive collision (or likewise D + HD), the probability of detecting a scattered HD product (or D2) by a detector placed at , at a given collision energy , is governed by the state–to–state scattering amplitude Kendrick (2003a) , i.e.
| (1) |
where we have multiplied the original scattering amplitude expression of Kendrick, Eq. (22) Kendrick (2003a), by and have explicitly expressed the spherical harmonic in terms of the Wigner –function. We note that the total scattering amplitude is obtained by summing up all of the contributions from each value of the total angular momentum :
| (2) |
Also, the sums over and effectively average over the azimuthal angle so that Eq. (1) is independent of . The initial and final states are denoted by and with denoting the different atom–diatom arrangements, i.e. for H + D2 and for D + HD; are the vibration, rotation and rotational projection quantum numbers, respectively. Moreover, the vector–coupling coefficients, , are the well known Clebsch–Gordan coefficients and the scattering angle measures the deflection between the asymptotic velocity vectors of H (relative to D2) and of D (relative to HD); is the energy–dependent scattering matrix for a given total angular momentum, written in the –representation , and is the magnitude of the wave vector associated to the entrance channel of the reactants,
| (3) |
where denotes the corresponding diatomic eigenvalue, is the total energy, and is the reduced mass of the reactants.
In the space–fixed (SF) reference frame, used for evaluating the scattering matrix, the coordinate origin lies at the center–of–mass (COM) of the triatomic system. Often, a body–fixed (BF) reference frame is convenient for the scattering calculations in which the BF quantization axis lies parallel to the atom–diatom relative motion coordinate and coincides with the direction of the initial relative velocity vector. Thus, in this set of coordinates, the rotational projection quantum number of the molecular state , prepared experimentally, corresponds to a coherent superposition of all possible pure projections , in , i.e.
| (4) |
where is the angle between the internuclear axis of D2 (or HD) and the incident velocity vector. In the experiments of Perreault et al. denotes the orientation between the polarization lasers and the molecular beam axis; where choices of correspond to either a parallel orientation , known as a H–SARP preparation, or a perpendicular orientation , a V–SARP preparation. Here, H– and V– denote horizontal and vertical polarizations, respectively. A cross polarization state, referred to as X–SARP, corresponding to a superposition of , was also adopted in their recent work on He + HD and He + D2 collisions Perreault, Mukherjee, and Zare (2019); Zhou et al. (2021). For exploring possible control scenarios, several values of within are considered below.
As discussed by Croft and Balakrishnan Croft and Balakrishnan (2019), since the experimental results correspond to an integral over the azimuthal angle , one can express the differential cross sections (DCS) for any SARP–prepared state as a sum of contributions from each –state weighted by . For the state–to–state DCS, this yields
| (5) |
where, . Likewise, for the integral cross section (ICS),
| (6) |
Figure (1) shows the –dependence of the Wigner’s reduced rotation matrices for the hypothetical cases of along with their pair of values (negative values are not shown). Upon a simple inspection of Fig. (1), the following aspects are apparent: (i) For , whenever off–diagonal elements are concerned, i.e. ; (ii) similarly, , for diagonal terms at and, as a consequence, parallel orientations of the reactants are likely to be composed by terms driven by , i.e. ; (iii) in the particular case of and , due to (ii), the expansion of Eq. (4) collapses to a single and isotropic term in which ; (iv) for any value of – not shown in Fig. (1) – and, thus, as expected, processes associated to rotationless reactants are invariant upon changes of .
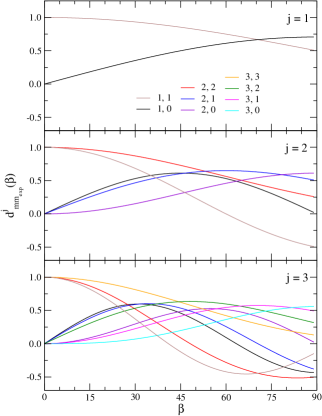
For the sake of clarity, it is worthwhile to illustrate at least a few possible linear combinations shown by Eq. (4). Consider a reactant prepared in the rotational state of a given vibrational manifold with a projection , and subjected to two orientations of its internuclear axis relative to the incoming relative velocity vector: and . The first case, , has been addressed above and the resultant state is simply . Often, the contribution in the ICS (DCS), for uncontrolled collisions, is dominant but suppressed by the typical average made up of all initial –terms. Thus, we may expect that a fixed orientation of for a preparation, in which only contributes, to enhance substantially the collision–induced state–to–state branching ratio of interest. If, instead, a alignment is made, the same preparation is expected to be composed by a broad mixture of all –terms, namely:
| (7) |
which is now mainly dominated by contributions from and with a minor contribution from . Note that in Eq.(7) (and in similar expressions below) we have used numerical values of matrix elements corresponding to the chosen values. If a preparation is considered at the same alignment, the linear combination of –terms yields
| (8) |
In this case, the prepared state is mostly composed of and , and the term. The preparation for , at the two typical orientations of and (V–SARP and H–SARP) has been discussed in great detail by Perreault et al. Perreault, Mukherjee, and Zare (2017, 2018).
The scattering amplitudes in Eq. (1) are computed using a numerically exact time–independent quantum reactive scattering formalism based on hyperspherical coordinates as implemented in the APH3D code Pack and Parker (1987); Kendrick et al. (1999); Kendrick (2000, 2001, 2003b). Details of the computational formalism have been discussed in great detail in prior works of Kendrick Kendrick et al. (1999); Kendrick (2000, 2001, 2003b) and in recent works of Kendrick et al. Kendrick, Hazra, and Balakrishnan (2016b) on the D + HD and H + D2 reactions. We shall remark only on some key details here. The hyper–radius describing the radial motion of the triatomic system is divided into an inner region where all three atoms are in close proximity and an outer region where the different atom–diatom arrangement channels are uncoupled. In the inner region the three–body Hamiltonian is expressed in the adiabatically adjusting principal axis hyperspherical (APH) method of Pack and Parker Pack and Parker (1987). Smith–Johnson hyperspherical coordinates Smith (1962); Kendrick et al. (1999) are used in this region where collision–induced re–arrangements are more likely to occur, and Delves hyperspherical coordinates Delves (1958, 1960); Parker et al. (2002) are used in the outer region. An in–depth discussion of the hyperspherical coupled channel equations and numerical strategies to solve them are available elsewhere Kendrick et al. (1999); Kendrick (2000, 2001, 2003b). Briefly, the six–dimensional three–body problem is reduced to a set of one–dimensional coupled equations along the scattering coordinate , that is discretized in a grid of sectors. The eigenvalue problem associated to the remaining five (internal) degrees of freedom is solved adiabatically, at each sector, yielding an effective set of coupled potentials driving the relative motion along . The five–dimensional (5D) eigenvalue problem is solved in the APH region by means of an implicitly restarted Lanczos method for sparse matrices as implemented in the PARPACK library Sorensen (1992); Maschhoff and Sorensen (1996). The corresponding eigenvalues within the Delves region are evaluated using a 1D Numerov propagator Johnson (1977). Once the eigenvalue problem is solved in both regions for all sectors and the sector–to–sector overlap and transformation matrices evaluated, the resulting set of radial coupled equations are solved using Johnson’s log–derivative method Johnson (1973), first from to . At the numerical solutions, from the outermost sector of the APH region, are projected onto solutions at the innermost sector of the Delves region. The propagation is continued from to , a sufficiently large value of where the interaction potential is negligible. At all channels (from all arrangements) are numerically decoupled, and scattering boundary conditions are applied to the log–derivative matrix in order to evaluate the scattering S–matrix. This involves projecting the log–derivative matrix onto solutions associated with each asymptotic diatomic state, in appropriate Jacobi coordinates, yielding the matrix Pack and Parker (1987). The procedure is repeated independently for each value of the total angular momentum quantum number , –parity (good quantum numbers in the absence of external forces) and, each –parity for the D2 molecule. It should be noted that the basis sets for both APH and Delves regions are independent of collision energy and, therefore, evaluated only once for each sets. Also, both the APH and Delves solutions are properly symmetrized with respect to the identical particle permutation symmetry (e.g., the two nuclei in HD2).
As both H + D2 and D + HD chemical reactions (as well as other isotopic combinations) have been modeled with the APH3D code in the past Kendrick (2001), the optimal set of parameters required to extract fairly converged () scattering characteristics are well established. In this work we follow closely the parameterization used previously by our group Kendrick (2000, 2001, 2003b); Kendrick, Hazra, and Balakrishnan (2016a, b). Thus, the APH region ranges from to with 64 sectors varying logarithmically with a step size of . The Delves region, starting at , extends to with 350 sectors varying linearly with a step size . Reactions such as H + D2 are known to require a few dozens of partial waves whenever collision energies exceed 1 eV Kendrick (2001, 2003b). Here however, we shall simulate the reaction at low and moderate collision energies, between 1 K (about 10-5 eV), a typical value in the experiments of Perreault and co–workers, and 50 K (about 10-3 eV). Thus, to reduce computational efforts associated with nonzero initial rotational levels, we limit our calculations to sets of 4, 7 and 9 depending on the entrance channel taken into consideration. Numerical convergence is estimated within and, as we shall see below, most of the interesting physics is captured at resonant energies where the discrete contribution of specific (and often lower) values of is more relevant.
In order to compute the APH basis set, the 64 sectors between and are further subdivided into five groups each of which with increasing maximum values of and (not to be confused with the orbital angular momentum and its projection quantum numbers), two parameters that define the primitive basis sets used in the APH region Kendrick et al. (1999): (i) , for 1.6–2.9; (ii) , for 2.9–3.7; (iii) , for 3.7–4.6; (iv) , for 4.6–5.8; and, (v) , for 5.8–7.8. Finally, 350 , 650 , 950 , 1250 , 1550 and 1850 channels are propagated for batches of 50 collision energies at each of the entrance channels described below and every parity of and . For the case a parity–adapted basis–set is utilized: 2170 , 2700 channels for even ; 1860 , 2400 and 3000 channels for odd .
III Results
In what follows the collision–induced exothermic reaction and inelastic de–excitation are studied for the reactants in the initial rovibrational state 1, 2 , 3 and 4 ; whereas the internal states of the products are chosen to be either or as well as 0–3. Choices of initial and final states are somewhat arbitrary and intended as representative cases upon which an actual experiment could be designed. However, it should be noted that, as pointed out by Hazra et al. Hazra, Kendrick, and Balakrishnan (2016), the effective reaction pathway along the set of adiabatic coupled potentials, for hydrogen exchange reactions, becomes barrierless for the vibrational manifolds above , which is the primary motivation underlying the choice of herein, since a natural boost in terms of reactivity is expected for low energy collisions Kendrick, Hazra, and Balakrishnan (2016b).
From an experimental perspective there is a growing effort towards addressing even higher vibrational states Perreault, Mukherjee, and Zare (2016); Mukherjee, Perreault, and Zare (2017) in order to explore the inherent delocalization of such weakly–bound systems Perreault et al. (2020). Indeed, Perreault et al. have recently reported complete transfer of population of H) to H via the SARP method opening pathways for collisional experiments involving highly vibrationally excited H2. From a theoretical standpoint however, the description of highly excited vibrational levels during collisions would likely require a treatment which takes into consideration either (i) couplings to higher electronic states or (ii) geometric phase effects whenever the nuclear motion encircles the conical intersection between the two lowest electronic states. In particular, Kendrick and co–workers have discussed both the sources of geometrical phase effects and their consequences on the title reactions for reactants prepared at and below Kendrick (2000); Kendrick, Hazra, and Balakrishnan (2016a, b). The effects are found to play a negligible role for exchange reactions at collision energies above 1 K but to have a somewhat stronger influence on the inelastic outcome in the cold and ultracold regimes.
Previous studies of Croft et al. Croft et al. (2018); Croft and Balakrishnan (2019) and Morita et al. Morita and Balakrishnan (2020a, b) have shown that collision–induced resonances are more sensitive to the relative orientation of the colliding partners. Therefore, we have first scanned collision energies for the various entrance channels mentioned above to survey for any resonances. To our knowledge resonances in the domain up to 50 K above the thresholds of D2 and HD have not yet been reported. We have identified several instances of these and, given the energy regimes involved, are likely to be shape resonances. A detailed characterization in terms of the angular momentum partial waves, width, lifetime and bound state structure of the effective potential well will be addressed elsewhere. Here, we focus on the sensitivity of these resonances to stereodynamic preparation, in particular, to choices of both and in a manner to simulate physical conditions that resemble typical experimental conditions of Perreault et al. Despite strict choices of , and 1–5 K in the experiments reported so far, we take some (theoretical) freedom to explore other possibilities.
III.1 Integral cross sections
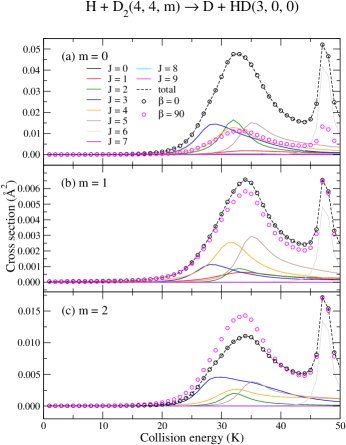
Panels (a)–(c) of Fig. (2) present the –dependent ICS as functions of the collision energy for the H + D D + HD reaction, where solid lines are used for each –contribution of a given –value ( and negative values are not shown for the sake of clarity). Needless to say, both resonant features depicted at about 32 K and 47 K are mostly dominated by the component (panel a) of mid–range partial waves, 2–6, whereas the term alone is responsible for the resonance at 47 K. Also, it is worthwhile to notice that 7–9 provide just a minor correction which suggests that numerical convergence is attained at .
Yet panels (a)–(c) offer a first glimpse on the stereodynamical effects underlying the reaction where hollow symbols denote the ICS for which the initial rotational state of D2, , is prepared in a specific projection , hence a weighted sum of various –terms in contribute, as shown in Eq. (5). Results are shown for internuclear axis orientation (black circles) and (magenta circles) with respect to the incoming relative velocity vector. Regardless of the choice of , the orientation of the internuclear axis alone is capable of modulating the ICS and, as we shall see below, the appropriate choice of a given and combined, can effectively enhance (suppress) the chemical reaction at the resonant energy. The and (panel a) represents the special case, mentioned in the previous section, in which all off–diagonal elements of are zero, whenever , i.e. . Therefore, the ICS expansion is reduced to a sole term associated to , where . In order to better visualize why the same preparation yields a much smaller cross section at , panels (a)–(b), we invoke Eq. (4) again to inspect the actual linear expansion for the prepared state:
| (9) |
Where, we note that , and as a result, and do not contribute to the prepared state. Thus, inspecting panel (a) of Fig. (2) it becomes clear how a perpendicular orientation composed of a broader mixture of contributions that favor and yields a smaller ICS for . The prepared state has only a smaller contribution from that features the largest ICS. A similar analysis applies to results in panels (b) and (c) of Fig. (2) for 1 and 2. In the particular case of panel (c), the relatively smaller component is now mostly favored by the mixture created with a alignment (comparing the magenta circles and the dashed black curve of panel c). As we shall see below, higher values are systematically favored by higher –values.
For convenience, in the remainder of this paper, results presented will correspond to a sum over all –values. However, whenever appropriate, we shall address the various partial wave contributions in terms of the orbital angular momentum quantum number with .
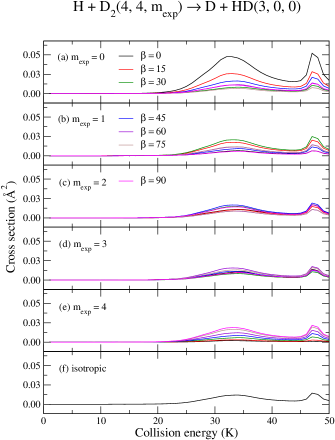
Panels (a)–(e) of Fig (3) present the ICSs for each case of and –, whereas panel (f) shows the so–called isotropic ICS, usually evaluated in ordinary studies of reactive scattering and represents a collision with no control imposed upon the rotational state . The isotropic case corresponds, therefore, to an ICS summed over all final (in this particular example happens to be only due to ) and averaged over all initial –values. The peak predicted at about 32 K is mostly composed of partial waves 0–7 whereas the one at 47 K is mainly composed by even terms, 2, 4, 6 and 8. All contributions from partial waves higher than are negligible.
Inspection of panels (a)–(e), unveils a propensity in which reactivity associated to lower projections of , 0–1, may be significantly enhanced by near parallel orientations of the reactants, say , whereas higher projection values, , are boosted by higher orientation angles. Almost full suppression of the chemical reaction is attained by preparing the reactants in an appropriate superposition of rotational projection states corresponding to specific orientation of its internuclear axis (with respect the incident relative velocity vector). Typical cases are depicted in Fig (3), namely: , (panel a, brown curve); , (panel b, magenta curve); and, , (panel e, black curve).
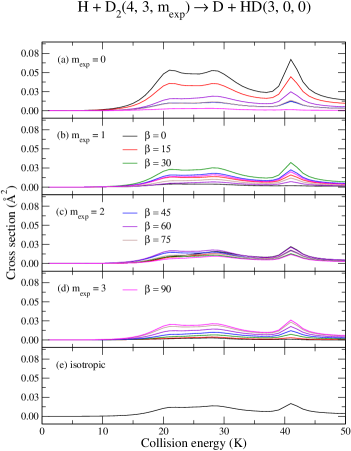
Figure (4) displays the result for the rotational state of D2 for all relevant values of and selected values of , yielding HD molecules in the rotational state . For this case is used and satisfactory numerical convergence is obtained with .
Results presented in panels (a)–(e) of Fig. (4) show a strong stereodynamical effect for different choices of and as for the case. It is worthwhile to reiterate that this dynamical feature is entirely driven by the properties of the Wigner coefficients, , regardless of other scattering characteristics under consideration, such as collision energy. Thus, at the main resonant peak ( 41 K), reactivity is subjected to an enhancement of about a factor of 6 for a , preparation and a complete suppression for , . Likewise, reactivity may be effectively suppressed by a , preparation while enhanced at , . The main partial wave contributions for the broad double–peaked resonant structure are 2–5 whereas the peak at about 41 K is mostly composed of 4 and 6.
The resonance structures depicted in Figs. (2–4) span a somewhat larger range of collision energies, in which a non–negligible number of partial waves contribute. For the SARP experiments, where four–vector correlation measurements are used to extract scattering properties, lower collision energies (and a limited number of partial waves) are desirable Perreault, Mukherjee, and Zare (2017). Below we present results for D2 prepared in the rotational state () that depict several resonances in the 5–10 K regime accessible in a SARP experiment.
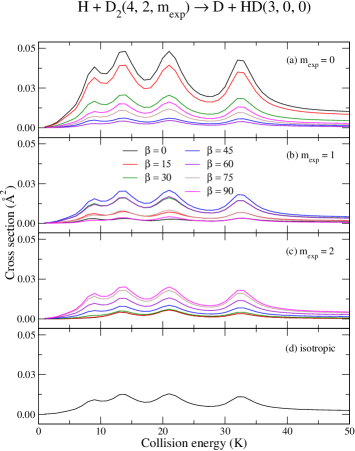
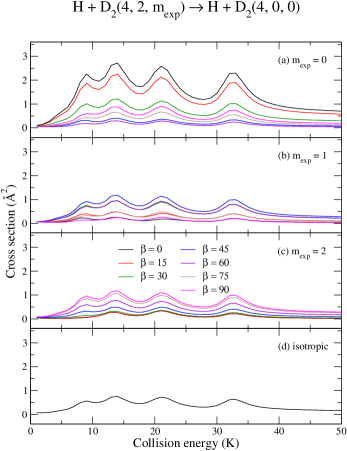
Panels (a)–(d) of Fig. (5) show the energy dependence of the ICS for the H + D D + HD reaction, whereas those panels of Fig. (6) present the ICS associated to the collision–induced de–excitation of D2, from to . The first resonance occurs at about 9 K whose composition is dominated by and with a minor background contribution from . At about 13 K a second (and more intense) peak is predicted to be formed from 0, 2 and 4, followed by another occurrence at 20 K and 32 K . At energies as low as 1 K, most of the contribution is expected from and followed by a minor, yet significant, contribution from . In terms of an actual experimental realization at –10 K, therefore, is likely to offer the best conditions when considering H + D2 collisions.
Cross sections for the inelastic process – panels (a)–(d) of Fig. (6) – are presented to illustrate how the exact same machinery described so far applies in these cases as well. The inelastic cross sections are about a factor of 60 larger than their reactive counterparts, due in part, to the direct and completely barrierless pathway for the inelastic process. Panel (c) of both figures unveil another intriguing aspect, where the first resonant feature ( 9 K) is suppressed entirely for a , preparation. As before, from Eq. (4), a state is expected for a parallel orientation , whereas at would yield
| (10) | ||||
which is strongly dominated by the component. However, at about 9 K, for and , the most relevant contributions arise from and for 1–4, whereas for , contributions from become more relevant above 10 K. Hence, all resonances above 10 K predicted for a D2 state prepared with shall survive mostly due to their character. Therefore, these calculations suggests that controlling the relative orientations of reactants can be also exploited in terms of addressing specific resonances, systematically, due to their –, – and –composition, even if they happen to occur in a band composed of overlapping structures. Moreover, an inspection of the energy dependence of –dependent ICS presented up to this point reveals an intricate competition among different values. As the energy varies, the actual branching ratio in the S–matrix is likely to vary whereas, at same time, controls the weight of various –terms in a given preparation. Morita and Balakrishnan noted a similar observation Morita and Balakrishnan (2020a), in terms of an interference effect due to cross terms in the square of the scattering amplitude, in their analysis of stereodynamical effects in rotationally inelastic collisions of HD and He.
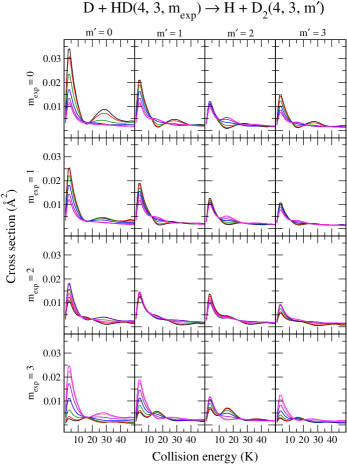
We wrap up the discussion of ICSs by presenting results for the reverse reaction, D + HD H + D2, Fig. (7), in which HD is prepared in () with for all values discussed previously. We limit our analysis to of D2 to inspect all 16 possible –cases, where (negative values are not shown for the sake of simplicity).
Many aspects of the results highlighted for H + D2 are also observed here, and some are highlighted below:
(i) In panel , the maximum enhancement of reactivity is observed for the preparation and cross sections are suppressed for higher values.
(ii) In panel : enhancement is found for higher values.
(iii) In panel : a unique resonant feature at about 15 K is predicted to emerge from the case, whereas smaller traces of it are also expected for other cases.
(iv) In panels : selective suppression of a specific resonance occurs with increase in at 20–40 K as varies from 0 to 90∘.
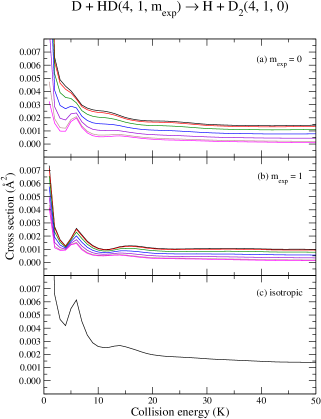
The richness, in terms of resonant and stereodynamical features, manifested in the ICS for a collision of D with HD, with HD prepared in , offers various handles for stereodynamic control of this reaction, in particular, for those experiments targeting collision energies near 1 K. Similarly, the rotational levels from both HD and D2 are also predicted to yield higher reactivity due to a dominant and contribution near K. This is illustrated in Fig. (8) for the D + HD H + D reaction (). A second resonant feature, whose properties are modulated by and a partial wave, occurs at about 6 K. This resonance is also very sensitive to a preparation (comparing black curves from panels (a) and (b)). Due to such a marked characteristic and presence of an isolated partial wave occurrence, a collision of D + HD at about 6 K, with and preparations, appears to be a good candidate for an experimental study. Panel (c) of Fig. (8) depicts the isotropic cross section, where a smaller resonance is also expected to occur at about 14 K ().
In Fig. (9) we present the partial wave composition for the isotropic ICS (summed over –4) for the D + HD H + D and H + D D + HD reactions. Panel (a) depicts results for and ; panel (b) for and ; and, panel (c) for and . The different panels show peaks associated with specific partial waves where dominates near 1 K followed by smaller contributions of . Therefore, is predicted as an ideal case for experimental investigations of both D + HD and H + D2 reactions near 1 K whereas is preferred for measurements from 5 K ( and ) to about 35 K ( and ). We would like to stress that the marked resonance profiles discussed in this work are a manifestation of a given entrance channel . Thus, other choices of exit channels, , shall present a similar energy–dependent behavior and no compromise has been made by choosing a specific or product state.
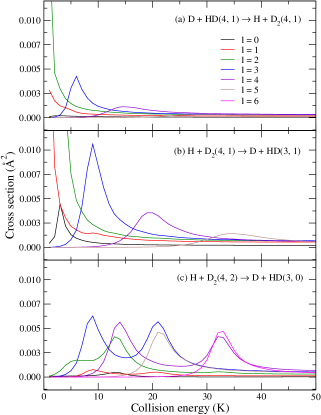
III.2 Differential cross sections
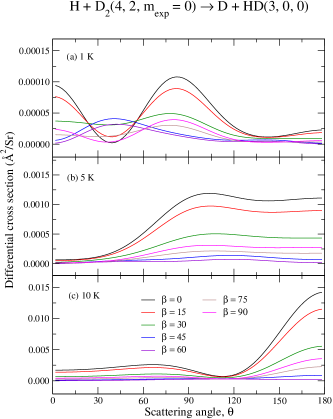
Now we consider how the relative orientation of reactants influences the deflection of products towards a given scattering angle . To this end we shall focus on the preparation as it has been shown to provide the largest enhancements, upon proper choices of . As energy–dependent measurements of scattering processes are inherently more complicated, we shall also fix the collision energies to 1 K, 5 K and 10 K.
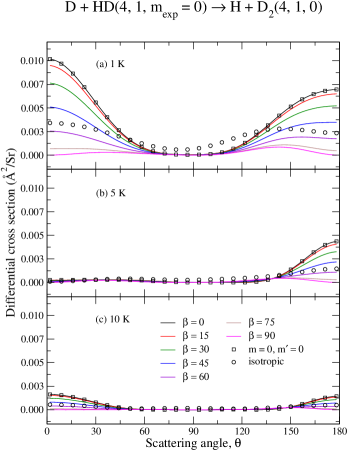
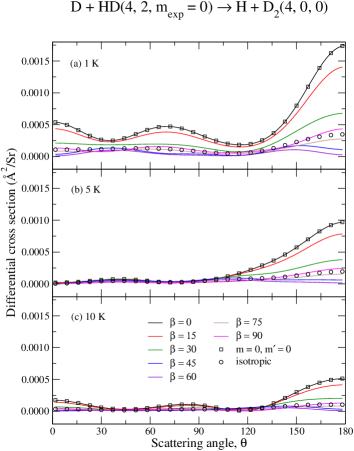
Panels (a)–(c) from Fig. (10) present the –dependency of the DCS for the D + HD H + D reaction, whereas panels (a)–(c) of Fig. (11) present a similar result for the and case. As before, for comparison purposes, circles are used for the averaged isotropic DCS and squares are used for the pure component (summed over 0–4). A comparison between the isotropic case (circles) and the –to– component (squares) unveils once again a similar mechanism discussed above in terms of ICS: i.e., the collision–induced branching ratio associated to lower –values, mainly , is likely to contribute the most but is often suppressed due to the typical average over all –terms. However, the dominant contribution from is unlocked by choosing (black curves). As the molecular alignment angle changes from , the relative contributions of become smaller in yielding, therefore, an overall smaller cross section.
The preference for (backward) forward scattering is seen to be mostly captured by the component and this preference is either magnified or suppressed by a given choice of . By comparing results depicted by circles and squares again, one notices that the small isotropic DCS value at includes a negligible, if any, contribution from the component. Thus, the DCS is the smallest and almost independent of the scattering angle for .
For the sake of completeness, Fig. (12) illustrates a typical DCS for the H + D D + HD reaction. In this case, the DCS at 1 K is peaked near 90∘ but fairly negligible overall. As the collision energy increase to 5 K and 10 K, the scattering becomes preferentially backward with maximum reactivity attained at 10 K, in which case, from Fig. (9), a character is predicted. At all three energies favors the reaction.
IV Conclusion and prospects
In this work we report extensive quantum dynamics calculations of the H + D2 and D + HD chemical reactions with an aim of controlling the reaction outcome through stereodynamic preparation of the molecular rotational state. Our approach extends the formalism presented in recent experimental studies of Perreault et al. Perreault, Mukherjee, and Zare (2017, 2018, 2019); Zhou et al. (2021) applied to rotational quenching of HD by H2, D2 and He and D2 by He to state–to–state chemistry for the first time. We report vast control through stereodynamic preparation of the molecular state, essentially allowing switching the reaction on or off through appropriate alignment of the molecular bond axis relative to the direction of the incident relative velocity vector.
The computations are performed using a state–of–the–art time–independent quantum reactive scattering formalism in hyperspherical coordinates at a moderate range of collision energies, 1–50 K. Both diatomic molecules were prepared in excited rovibrational states, 1–4, and several resonant features have been predicted to occur. Intensities of these resonances were found to be strongly sensitive to the stereodynamic preparation of the molecular rotational states. Several partial wave resonances were identified in this study with 0–2 dominating at lower collision energies (below 10 K) and 4–6 at higher energies. To our knowledge, resonances for the initial states considered here are predicted for the first time and deserve additional investigations in order to characterize properties such as lifetime, quantum numbers etc. Our findings are significant in light of recent experimental progress in preparing vibrationally excited H2 in the vibrational level through the SARP techniques allowing the prospects of studying chemical reactions involving highly vibrationally excited molecules that are also prepared in a stereodynamic state Perreault et al. (2020).
Our results reveal the following aspects which may or may not be universal to the specific system investigated here:
(i) The isotropic reactive cross section, associated to freely rotating reactants, is composed of contributions from smaller –values, in particular, . However, as one averages over all initial states, these higher contributions are often washed out.
(ii) By imposing a certain spatial polarization on the rotational state of reactants, a particular – contribution (denoted by in this work) can be filtered by rotating its internuclear axis.
(iii) The stereodynamically prepared state becomes a pure state as , i.e., as , where is the alignment angle of the molecular bond axis relative to the incident velocity vector, i.e. orientation of the SARP polarization lasers relative to the molecular beam in the experiments of Perreault et al.
(iv) The prepared state becomes a broad mixture of all –terms as .
(v) Due to (iii), the contribution (largest for the present system) are accessible by a preparation, which generally enhances the collision–induced branching ratio of interest. This is equivalent to the H–SARP preparation in the SARP experiments.
(vi) Likewise, due to (iv), in order to enhance unfavored branching ratios, often associated to higher (and ) values, a preparation combining higher with can be used.
(vii) A lower value of combined with a higher value of (and vice–versa) mostly suppresses the reaction.
Possibly, without loss of generality, points (i)–(vii) can be viewed as a set of propensity rules that might be exploited to effectively control any cold chemical reaction, as well as inelastic collisions.
At collision energies above a few Kelvin a diverse array of stereodynamical effects are predicted to occur due to the participation of various partial waves and different –components of the rotationally excited states that allow additional control of the reaction outcome. Our results show that both the collision energy and the alignment angle have a strong effect on the branching ratios and the –composition of a given state, respectively. Likewise, we have found strong evidences suggesting that particular resonances can be selectively controlled, by means of orienting the reactant appropriately, due to their specific partial wave, and compositions.
Such a degree of control of a chemical reaction involving neutral systems, in a completely field–free environment, requires only ro–vibratational excitation, which is relatively easy to realize experimentally and it is also a universal property in contrast to, for instance, the need of working with electrically polar molecules. In particular, two–body losses in ultracold traps , due to chemical reactions and inelastic collisions, have been a long standing problem, mostly circumvent by means of an elegant use of external fields that prevents the colliding partners to approach one another Avdeenkov, Bortolotti, and Bohn (2006); Wang and Quéméner (2015); González-Martínez, Bohn, and Quéméner (2017). Besides their effectiveness, most of these methods are not general and a given molecular system of interest must comply with specific electric properties. In contrast, we have demonstrated here how appropriate choices of and – namely, lower (higher) and higher (lower) – is mostly effective in “turning off” the chemical reaction in a very general fashion.
Finally, in terms of actual experimentation using H + D2 and D + HD, our calculations suggest that choices of either or are the best compromises in order to explore resonances at sufficiently low energies, where only few partial waves contribute. In particular, near 1 K, preparing either D + HD or H + D2 with is a promising choice. However, if the presence of higher partial waves are less of a problem experimentally, and higher collisional energies are of interest, then and are better candidates as they are predicted to possess a series of overlapping resonant structures over a broader range of collision energies.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements.
N.B. acknowledges support from NSF grant No. PHY-1806334 & PHY-2110227 as well as ARO MURI grant No. W911NF-19-1-0283. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. Specifically, it used the Bridges-2 system, which is supported by NSF award number PHY-200034 (N.B.) at the Pittsburgh Supercomputing Center (PSC). B.K.K. acknowledges that part of this work was done under the auspices of the US Department of Energy under Project No. 20170221ER of the Laboratory Directed Research and Development Program at Los Alamos National Laboratory. This work used resources provided by the Los Alamos National Laboratory Institutional Computing Program. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (Contract No. 89233218CNA000001).Data availability statement
The data that support the findings of this study are available within the article.
References
- Aldegunde et al. (2006) J. Aldegunde, J. M. Alvariño, M. P. de Miranda, V. Sáez Rábanos, and F. J. Aoiz, The Journal of Chemical Physics 125, 133104 (2006).
- Aldegunde et al. (2011) J. Aldegunde, P. G. Jambrina, M. P. de Miranda, V. S. Rábanos, and F. J. Aoiz, Phys. Chem. Chem. Phys. 13, 8345 (2011).
- Cernuto et al. (2018) A. Cernuto, F. Pirani, L. M. Martini, P. Tosi, and D. Ascenzi, ChemPhysChem 19, 51 (2018).
- Ascenzi et al. (2019) D. Ascenzi, M. Scotoni, P. Tosi, D. Cappelletti, and F. Pirani, Frontiers in Chemistry 7, 390 (2019).
- Falcinelli et al. (2019) S. Falcinelli, F. Pirani, P. Candori, B. G. Brunetti, J. M. Farrar, and F. Vecchiocattivi, Frontiers in Chemistry 7, 445 (2019).
- Falcinelli et al. (2021) S. Falcinelli, F. Vecchiocattivi, J. M. Farrar, and F. Pirani, The Journal of Physical Chemistry A 125, 3307 (2021).
- Tannor, Kosloff, and Rice (1986) D. J. Tannor, R. Kosloff, and S. A. Rice, The Journal of Chemical Physics 85, 5805 (1986).
- Rice and Zhao (2000) S. A. Rice and M. Zhao, Optical Control of Molecular Dynamics (Wiley, New York, 2000).
- Levis, Menkir, and Rabitz (2001) R. J. Levis, G. M. Menkir, and H. Rabitz, Science 292, 709 (2001).
- Shapiro and Brumer (2012) M. Shapiro and P. Brumer, Quantum Control of Molecular Processes (Wiley-VCH, Weinheim, 2012).
- Cattaneo et al. (2018) L. Cattaneo, J. Vos, R. Y. Bello, A. Palacios, S. Heuser, L. Pedrelli, M. Lucchini, C. Cirelli, F. Martín, and U. Keller, Nature Phys , 733 (2018).
- Krems (2008) R. V. Krems, Phys. Chem. Chem. Phys. 10, 4079 (2008).
- Balakrishnan (2016) N. Balakrishnan, The Journal of Chemical Physics 145 (2016).
- Perreault, Mukherjee, and Zare (2017) W. E. Perreault, N. Mukherjee, and R. N. Zare, Science 358, 356 (2017).
- Perreault, Mukherjee, and Zare (2018) W. E. Perreault, N. Mukherjee, and R. N. Zare, Nature Chem 10, 561 (2018).
- Mukherjee and Zare (2011) N. Mukherjee and R. N. Zare, The Journal of Chemical Physics 135, 024201 (2011).
- Dong, Mukherjee, and Zare (2013) W. Dong, N. Mukherjee, and R. N. Zare, The Journal of Chemical Physics 139, 074204 (2013).
- Mukherjee, Dong, and Zare (2014) N. Mukherjee, W. Dong, and R. N. Zare, The Journal of Chemical Physics 140, 074201 (2014).
- Perreault, Mukherjee, and Zare (2019) W. E. Perreault, N. Mukherjee, and R. N. Zare, The Journal of Chemical Physics 150, 174301 (2019).
- Zhou et al. (2021) H. Zhou, W. E. Perreault, N. Mukherjee, and R. N. Zare, J. Chem. Phys. 154, 104309 (2021).
- Aldegunde et al. (2005) J. Aldegunde, M. P. de Miranda, J. M. Haigh, B. K. Kendrick, V. Sáez-Rábanos, and F. J. Aoiz, The Journal of Physical Chemistry A 109, 6200 (2005).
- Devolder, Tscherbul, and Brumer (2020) A. Devolder, T. Tscherbul, and P. Brumer, Phys. Rev. A 102, 031303 (2020).
- de Miranda et al. (2011) M. H. G. de Miranda, A. Chotia, B. Neyenhuis, D. Wang, G. Quéméner, S. Ospelkaus, J. L. Bohn, J. Ye, and D. S. Jin, Nature Phys , 502 (2011).
- Croft et al. (2018) J. F. E. Croft, N. Balakrishnan, M. Huang, and H. Guo, Phys. Rev. Lett. 121, 113401 (2018).
- Croft and Balakrishnan (2019) J. F. E. Croft and N. Balakrishnan, The Journal of Chemical Physics 150, 164302 (2019).
- Morita and Balakrishnan (2020a) M. Morita and N. Balakrishnan, The Journal of Chemical Physics 153, 091101 (2020a).
- Morita and Balakrishnan (2020b) M. Morita and N. Balakrishnan, The Journal of Chemical Physics 153, 184307 (2020b).
- Jambrina et al. (2019) P. G. Jambrina, J. F. E. Croft, H. Guo, M. Brouard, N. Balakrishnan, and F. J. Aoiz, Phys. Rev. Lett. 123, 043401 (2019).
- Morita et al. (2020) M. Morita, Q. Yao, C. Xie, H. Guo, and N. Balakrishnan, Phys. Rev. Research 2, 032018 (2020).
- Jambrina et al. (2021) P. G. Jambrina, J. F. E. Croft, N. Balakrishnan, and F. J. Aoiz, Phys. Chem. Chem. Phys. 23, 19364 (2021).
- Pack and Parker (1987) R. T. Pack and G. A. Parker, J. Chem. Phys. 87, 3888 (1987).
- Kendrick et al. (1999) B. K. Kendrick, R. T. Pack, R. B. Walker, and E. F. Hayes, The Journal of Chemical Physics 110, 6673 (1999).
- Kendrick (2003a) B. K. Kendrick, The Journal of Physical Chemistry A 107, 6739 (2003a).
- Boothroyd et al. (1996) A. I. Boothroyd, W. J. Keogh, P. G. Martin, and M. R. Peterson, The Journal of Chemical Physics 104, 7139 (1996).
- Kuppermann, Schatz, and Baer (1974) A. Kuppermann, G. C. Schatz, and M. Baer, The Journal of Chemical Physics 61, 4362 (1974).
- Goswami et al. (2020) S. Goswami, J. Sahoo, S. K. Paul, T. R. Rao, and S. Mahapatra, The Journal of Physical Chemistry A 124, 9343 (2020).
- Desrousseaux et al. (2018) B. Desrousseaux, C. M. Coppola, M. V. Kazandjian, and F. Lique, The Journal of Physical Chemistry A 122, 8390 (2018).
- Zhou et al. (2020) B. Zhou, B. Yang, N. Balakrishnan, B. K. Kendrick, and P. C. Stancil, The Journal of Physical Chemistry Letters 11, 4970 (2020).
- Bossion et al. (2018) D. Bossion, Y. Scribano, F. Lique, and G. Parlant, Monthly Notices of the Royal Astronomical Society 480, 3718 (2018).
- Bossion et al. (2020) D. Bossion, S. Ndengué, H.-D. Meyer, F. Gatti, and Y. Scribano, The Journal of Chemical Physics 153, 081102 (2020).
- Hazra, Kendrick, and Balakrishnan (2016) J. Hazra, B. K. Kendrick, and N. Balakrishnan, Journal of Physics B: Atomic, Molecular and Optical Physics 49, 194004 (2016).
- Kendrick, Hazra, and Balakrishnan (2016a) B. K. Kendrick, J. Hazra, and N. Balakrishnan, The Journal of Chemical Physics 145, 164303 (2016a).
- Kendrick, Hazra, and Balakrishnan (2016b) B. K. Kendrick, J. Hazra, and N. Balakrishnan, New Journal of Physics 18, 123020 (2016b).
- Kendrick (2018a) B. K. Kendrick, The Journal of Chemical Physics 148, 044116 (2018a).
- Kendrick (2018b) B. K. Kendrick, Chemical Physics 515, 387 (2018b).
- Kendrick (2019) B. K. Kendrick, The Journal of Physical Chemistry A 123, 9919 (2019).
- Wrede and Schnieder (1997) E. Wrede and L. Schnieder, The Journal of Chemical Physics 107, 786 (1997).
- Banares et al. (1998) L. Banares, F. J. Aoiz, V. J. Herrero, M. J. D’Mello, B. Niederjohann, K. Seekamp-Rahn, E. Wrede, and L. Schnieder, The Journal of Chemical Physics 108, 6160 (1998).
- Fernández-Alonso, Bean, and Zare (1999) F. Fernández-Alonso, B. D. Bean, and R. N. Zare, The Journal of Chemical Physics 111, 1035 (1999).
- Kendrick (2000) B. K. Kendrick, The Journal of Chemical Physics 112, 5679 (2000).
- Kendrick (2001) B. K. Kendrick, The Journal of Chemical Physics 114, 8796 (2001).
- Harich et al. (2002) S. A. Harich, D. Dai, X. Yang, S. D. Chao, and R. T. Skodje, The Journal of Chemical Physics 116, 4769 (2002).
- Kendrick (2003b) B. K. Kendrick, The Journal of Chemical Physics 118, 10502 (2003b).
- Pomerantz et al. (2004) A. E. Pomerantz, F. Ausfelder, R. N. Zare, S. C. Althorpe, F. J. Aoiz, L. Bañares, and J. F. Castillo, The Journal of Chemical Physics 120, 3244 (2004).
- Smith (1962) F. T. Smith, Journal of Mathematical Physics 3, 735 (1962).
- Delves (1958) L. M. Delves, Nuclear Physics 9, 391 (1958).
- Delves (1960) L. M. Delves, Nuclear Physics 20, 275 (1960).
- Parker et al. (2002) G. A. Parker, R. B. Walker, B. K. Kendrick, and R. T Pack, The Journal of Chemical Physics 117, 6083 (2002).
- Sorensen (1992) D. C. Sorensen, SIAM Journal on Matrix Analysis and Applications 13, 357 (1992).
- Maschhoff and Sorensen (1996) K. J. Maschhoff and D. C. Sorensen, Applied Parallel Computing Industrial Computation and Optimization, , 478 (1996).
- Johnson (1977) B. R. Johnson, J. Chem. Phys. 67, 4086 (1977).
- Johnson (1973) B. Johnson, Journal of Computational Physics 13, 445 (1973).
- Perreault, Mukherjee, and Zare (2016) W. E. Perreault, N. Mukherjee, and R. N. Zare, The Journal of Chemical Physics 145, 154203 (2016).
- Mukherjee, Perreault, and Zare (2017) N. Mukherjee, W. E. Perreault, and R. N. Zare, Journal of Physics B: Atomic, Molecular and Optical Physics 50, 144005 (2017).
- Perreault et al. (2020) W. E. Perreault, H. Zhou, N. Mukherjee, and R. N. Zare, Phys. Rev. Lett. 124, 163202 (2020).
- Avdeenkov, Bortolotti, and Bohn (2006) A. V. Avdeenkov, D. C. E. Bortolotti, and J. L. Bohn, Phys. Rev. A 74, 012709 (2006).
- Wang and Quéméner (2015) G. Wang and G. Quéméner, New Journal of Physics 17, 035015 (2015).
- González-Martínez, Bohn, and Quéméner (2017) M. L. González-Martínez, J. L. Bohn, and G. Quéméner, Phys. Rev. A 96, 032718 (2017).