On weakly -convex and weakly -semiconvex sets
1991 Mathematics Subject Classification:
MSC 52A30Abstract. The present work concerns generalized convex sets in the real multi-dimensional Euclidean space, known as weakly -convex and weakly -semiconvex sets. An open set is called weakly -convex (weakly -semiconvex) if, through every boundary point of the set, there passes a straight line (a closed ray) not intersecting the set. A closed set is called weakly -convex (weakly -semiconvex) if it is approximated from the outside by a family of open weakly -convex (weakly -semiconvex) sets. A point of the complement of a set to the whole space is a -nonconvexity (-nonsemiconvexity) point of the set if every straight line passing through the point (every ray emanating from the point) intersects the set. It is proved that if the collection of all -nonconvexity (-nonsemiconvexity) points corresponding to an open weakly -convex (weakly -semiconvex) set is non-empty, then it is open. It is also proved that the non-empty interior of a closed weakly -convex (weakly -semiconvex) set in the space is weakly -convex (weakly -semiconvex).
Keywords: convex set, weakly -convex set, -nonconvexity-point set, weakly -semiconvex set, -nonsemiconvexity-point set, real Euclidean space
1. Introduction
The weakly -convex and weakly -semiconvex sets, , in the real space , , with the Euclidean norm, can be seen as a generalization of convex sets. The notions were coined by Yurii Zelinskii [11], [12]. First, recall the following definitions.
Any -dimensional affine subspace of , , , is called an -dimensional plane. A -dimensional plane is also known as a straight line.
One of two parts of an -dimensional plane, , of the space , , into which it is divided by any of its -dimensional planes (herewith, the points of the -dimensional plane are included) is said to be an -dimensional half-plane. A -dimensional half-plane is also known as a ray.
Definition 1 (Zelinskii [11], [12]).
An open subset , , is called weakly -convex (weakly -semiconvex), , if for any point , there exists an -dimensional plane (-dimensional half-plane ) such that and .
They say that a set is approximated from the outside by a family of open sets , , if is contained in , and ([1]).
It can be proved that any set approximated from the outside by a family of open sets is closed.
Definition 2 (Zelinskii [11], [12]).
A closed subset , , is called weakly -convex (weakly -semiconvex), , if it can be approximated from the outside by a family of open weakly -convex (weakly -semiconvex) sets.
The class of weakly -convex sets in is denoted by and the class of weakly -semiconvex sets in is denoted by .
The properties of the class of generalized convex sets on Grassmannian manifolds which are closely related to the properties of the conjugate sets (see [12, Definition 2]) are investigated in [12]. This class includes . The geometric and topological properties of weakly -convex sets are also investigated in [2], [3].
The theory of weakly -semiconvex sets is newish and it is based on the research of some subclass as well as further investigation of weakly -convex sets also focuses on the similar subclass. In order to determine these subclasses, we need to set the following definition.
Definition 3.
A point is called an -nonconvexity (-nonsemiconvexity) point of a subset if every -dimensional plane (-dimensional half-plane) passing through intersects . The set of all -nonconvexity (-nonsemiconvexity) points of a subset is called the -nonconvexity-point (-nonsemiconvexity-point) set corresponding to and is denoted by (). Moreover, , .
The class of weakly -convex sets in with non-empty -nonconvexity-point set is denoted by and the class of weakly -semiconvex sets with non-empty -nonsemiconvexity-point set in is denoted by .
The disconnectedness of any open weakly -semiconvex set with non-empty -nonsemiconvexity-point set in the plane was established by Zelinskii [11, Theorem 7]. Moreover, the following result is true.
Lemma 1 (Dakhil [2], Osipchuk [8]).
An open set or a closed set belonging to the class consists of not less than three connected components.
Interestingly, the number of components of a set belonging to the class is also affected by the smoothness of its boundary.
Lemma 2 (Osipchuk [4]).
Suppose that an open bounded subset with smooth boundary belongs to the class . Then consists of not less than four connected components.
Lemma 3 (Osipchuk [8]).
Suppose that a closed bounded subset with smooth boundary and such that is not -semiconvex belongs to the class . Then consists of not less than four connected components.
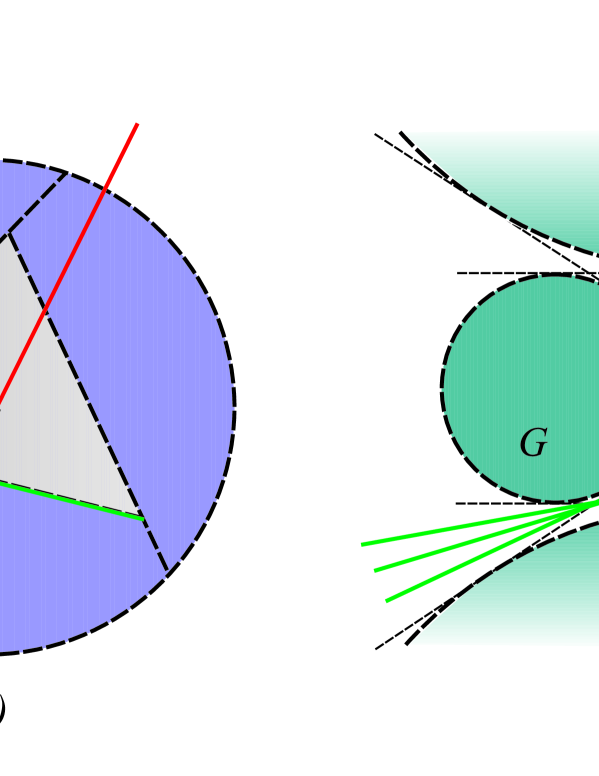
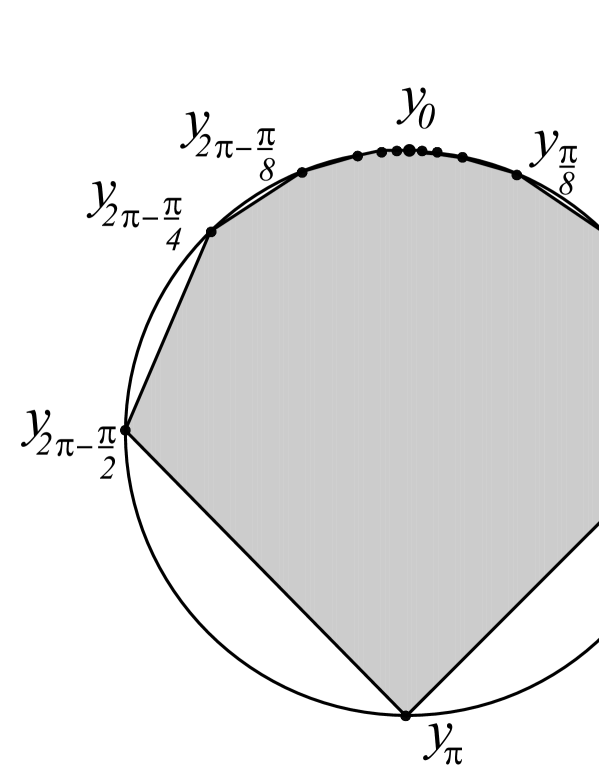
The example of an open set consisting of three components is in Figure 1 a), and an open set with smooth boundary and four components is in Figure 1 b). Moreover, if we want to construct an open set belonging to the class with countably infinite number of components, then, instead of a triangle inside a convex set, we should throw away a closed convex generalized polygon (the convex hull of a bounded countably infinite set of points in the plane with boundary containing countably infinite number of vertices). The example of a closed convex generalized polygon is the convex hull of the points
in Figure 2 a). And also cut the obtained set along rays containing the polygon sides and the accumulation points of the polygon vertices as it is shown in Figure 2 b).
Examples of closed sets belonging to with non-smooth or smooth boundary see in [8].
Notice that the above properties of weakly -semiconvex sets could so far be established only in the plane, in contrast to weakly -convex sets.
Lemma 4 (Dakhil [2], Osipchuk [6]).
An open set or a closed set that belongs to the class consists of not less than three connected components.
But unlike weakly -semiconvex sets with smooth boundary, any open weakly -convex set in with smooth boundary does not have -nonconvexity points [2, Proposition 2.3.7].
An example of sets belonging to the class can be constructed by cutting an open convex set without closed convex polygon or generalized polygon in Figures 1 a) and 2 b) along the straight lines containing the sides and the accumulation points of vertices of the polygons instead of rays. Examples of open and closed sets belonging to see in [5].
For and , the disconnectedness property is violated both for weakly -convex and for weakly -semiconvex sets.
Lemma 5 (Osipchuk [6, 8]).
There exist domains and closed connected sets in the space , , belonging to the class (), .
Of special interest are the properties of -nonconvexity-point sets corresponding to weakly -convex sets and -nonsemiconvexity-point sets corresponding to weakly -semiconvex sets. The following results were obtained.
Lemma 6 (Osipchuk [7, 10]).
Suppose that an open subset belongs to the class . Let , , be the components of . Then
-
(a)
is open and weakly -convex;
-
(b)
, , are convex (bounded or unbounded);
Lemma 7 (Osipchuk [9]).
Suppose that an open subset belongs to the class . Let , , be the components of . Then
-
(a)
is open and weakly -semiconvex;
-
(b)
, , are convex and bounded;
-
(c)
any connected subset of , , consisting of only smooth points is a line segment or a point;
-
(d)
there exists a collection of rays , , such that
-
-
the set does not contain rays emanating from ,
-
-
In other words, Lemma 7 shows that the -nonsemiconvexity-point set corresponding to a flat weakly -semiconvex set is the union of open convex polygons and open convex generalized polygons. But they cannot be arbitrarily placed in the plane. Their arrangement is constrained by property (d).
The methods developed to prove item (a) in Lemmas 6 and 7 allow us to obtain the following result for the closed weakly -convex (weakly -semiconvex) sets in the plane.
Lemma 8 (Osipchuk [9, 10]).
Let be a closed subset such that . If is weakly -convex (weakly -semiconvex), then is weakly -convex (weakly -semiconvex).
In this study, we focus on establishing the general topological properties of the -nonconvexity-point set corresponding to an open weakly -convex set and the -nonsemiconvexity-point set corresponding to an open weakly -semiconvex set in , .
First, we prove that The -nonsemiconvexity-point set corresponding to an open set , , is open. Therefore, we generalize Lemma 7 (a) on the real Euclidean space of any dimension . The proof algorithm is similar to the proof of Lemma 7 (a). Its essence is to find, for every fixed point and each ray emanating from , points , , on these rays, and the number such that the points are contained in together with open balls of the same radii . This allows us to assert that any ray emanating from an open ball with center at and radius intersects the union of the balls contained in . Thus, we show that is an inner point of .
To find , , it was used the connectedness of the components of . Namely, there were constructed the finite number of curves contained in and such that every ray emanating from intersects the union of the curves. Moreover, it was shown that points are actually placed on those curves and is the minimum value of the restrictions of the distance functions defined on the components of to the respective curves. This trick fails for the set in the spaces of higher dimensions, obviously. But we are lucky to find not one-dimensional compacts that meet our requirements.
Using the same algorithm, we also prove that The -nonconvexity-point set corresponding to an open set , , is open. But in this case, we show that, for every fixed point and each straight line passing through , there exist points , , on these lines, and the number such that the points are contained in together with open balls of the same radii .
The consequents of these two statements are that is weakly -semiconvex for and is weakly -convex for , .
The methods developed to prove the first two results allow us to generalize Lemma 8 on closed weakly -semiconvex and closed weakly -convex sets in , .
Property (d) of Lemma 7 easily extends to all spaces with dimensions , and is also inherent to weakly -convex sets of those spaces.
Our final result refutes the validity of Lemma 6 (b) and Lemma 7 (b) for the spaces , , as we construct examples of simultaneously weakly -convex and weakly -semiconvex open sets in , , which non-empty -nonconvexity-point sets are non-convex, bounded (or unbounded) and coincide with their -nonsemiconvexity-point sets.
We give here briefly some directions for further research. Probably the most natural next question to study would be to investigate the general topological properties of , , and , , for , . We expect and to be open (closed) if and are open (closed). In addition, the question of estimating the number of components of the sets belonging to the class remains open for .
2. Main results
Given two points , we will denote by the open line segment between those points and by its length. Let also
Lemma 9.
Suppose that a subset is open and (). Let (). Then for any ray (for any straight line ), , there exist points () such that , where depends on only and does not depend on .
Proof..
Let be the origin. Consider the homeomorphism defined by the formula
Let also be the central projection on the sphere, i.e.,
Then is open.
Fix an arbitrary point (). Without loss of generality, suppose that .
Let be an arbitrary fixed point of (of ), . Since is open, there exist open balls , , such that . Then the images , , are open subsets of (open subsets of the projective space ). Moreover,
is a cover of the unit sphere (of the projective space ). By the Heine-Borel theorem, there exists a subcover
of (of ).
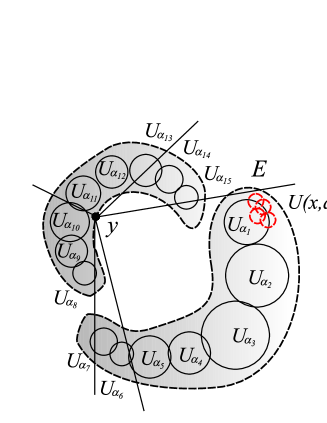
Let , , be the components of . Then for any there exists such that .
Consider the distance functions
They are continuous in the domains , . Then their restrictions to the compacts attain their minimum values on that compacts, i.e.,
Since is finite, there exists
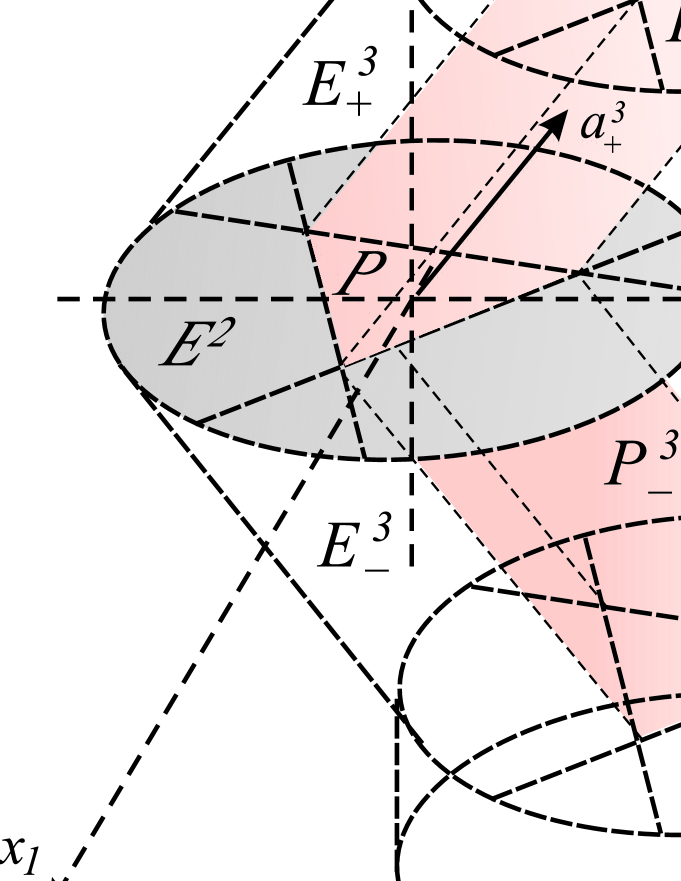
Then for any point , ; see Figure 3. And for any , there exists such that () by the construction. ∎
Theorem 1.
Suppose that an open subset belongs to the class . Then is open.
Proof.
Fix an arbitrary point and show that it is an inner point of .
Since is weakly -semiconvex, it follows that . Then there exists a number such that ).
By Lemma 9, for the fixed there exist points , , and a constant such that .
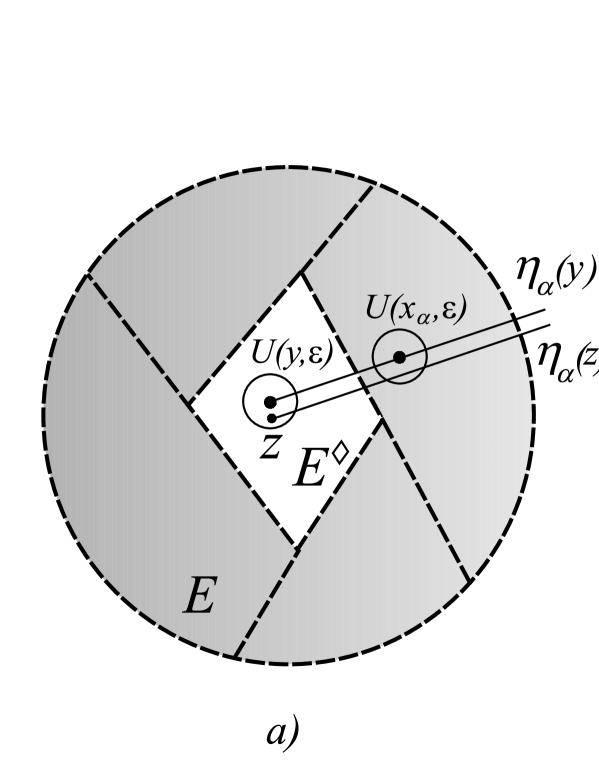
Let . Consider the neighborhood of the point . Let and let , , be an arbitrary ray with initial point at . Draw the ray parallel to the ray . Since for the point correspondent to , it follows that and, therefore, for any ; see Figure 4 a). Thus, is a -nonsemiconvexity point of . Since is arbitrary, it implies that all points of are -nonsemiconvexity points of . Hence, is an inner point of . ∎
Corollary 1.
Suppose that an open subset belongs to the class . Then is weakly -semiconvex.
Proof..
Since is open, then for any point , there exists a ray , , not intersecting . Then by Definition 3. Thus, is weakly -semiconvex. ∎
Theorem 2.
Suppose that an open subset belongs to the class . Then is open.
Proof..
The scheme of proving this theorem is exactly the same as for Theorem 1. We fix an arbitrary point of and show that there exists a neighborhood of this point which belongs to . To do so, we use Lemma 9 with respect to the points and the straight lines , , and we also replace the rays with the straight lines everywhere in the proof of Theorem 1. ∎
Corollary 2.
Suppose that an open subset belongs to the class . Then is weakly -convex.
Theorem 3.
Let be a closed subset such that . If is weakly -semiconvex, then is weakly -semiconvex.
Proof.
Suppose that is not weakly -semiconvex. Then there exists a -nonsemiconvexity point of the set .
By Lemma 9, for the point , there exist points , , and a constant such that .
Consider the neighborhood of the point ; see Figure 4 b). Since is weakly -semiconvex, there exists a family of open weakly -semiconvex sets , , approximating from the outside. Then there exists an index such that for all . For each , choose a point and draw an arbitrary ray , , with initial point at . Consider the ray parallel to . Since for the point correspondent to , it follows that and, therefore, . Since , , then , .
Since the ray is arbitrary, the point is a -nonsemiconvexity point of for all , which gives a contradiction. ∎
Theorem 4.
Let be a closed subset such that . If is weakly -convex, then is weakly -convex.
Proof.
Proposition 1.
Suppose that an open subset belongs to the class . Then there exists a collection of rays such that
-
the set does not contain rays emanating from ,
-
Proof.
Since is open, for any point , there exists a ray such that . Moreover, does not contain any ray emanating from , otherwise, a ray , , does not intersect , which contradicts the definition of -nonsemiconvexity point. ∎
Proposition 2.
Suppose that an open subset belongs to the class . Then there exists a collection of straight lines such that
-
the set does not contain straight lines passing through ,
-
Proof.
The statements are similar to the proof of Proposition 1. We only consider straight lines instead of rays. ∎
Lemma 10.
There exists an open set such that the set is bounded, connected, and non-convex.
Proof.
Let
where is an open bounded convex subset, is an open convex polygon such that , , , is the finite collection of lines passing through the polygon sides. Then and .
Consider the line segment , where is such that the angle between the vector and the unit vector of the axis belongs to the interval .
Let be a bounded oblique cylinder with the set at the base and elements parallel to , i.e.,
Let also be the oblique cylinder symmetric to with respect to the coordinate plane ; see Figure 5 a).
Let be the height of , and be the orthogonal projection of the set onto . Consider the following cylinders:
and that is the cylinder symmetric to with respect to the coordinate plane .
Consider also the following polygonal oblique prisms:
where is the vector symmetric to with respect to the coordinate plane . Prove that
First, show that
Consider an arbitrary point . Then , . Let be an arbitrary ray emanating from . Show that .
-
1.
If intersects a lateral face of , then consider the projection, parallel to , of onto the coordinate plane . It is a ray that we define by . The ray emanates from the point which is the projection of onto . Since is a flat weakly -semiconvex set, it implies that , which gives that , therefore, .
-
2.
If intersects a base of , then it intersects either , which immediately gives that , or it intersects a lateral face of the other prism , , , by the construction, and further considerations are the same as in item 1, but for , a point , and the ray . Then , therefor, .
Moreover, if , then .
Now, prove that and, thus, , and
It is enough to show that if then . Let be the plane passing through parallel to the coordinate plane . Then the intersection is either 1) empty or 2) congruent to , or 3) congruent to .
1) Any straight line passing through in does not intersect .
2) Since is convex in , there exists a straight line passing through in and not intersecting , therefore, not intersecting .
3) and with respect to . Since , there exists a straight line passing through in and not intersecting , therefore, not intersecting .
The set is bounded, connected, and non-convex, obviously.
∎
Lemma 11.
There exists an open set such that the set is unbounded, connected, and non-convex.
Proof.
Consider the oblique cylinders
| (1) | |||||
| (2) | |||||
where
Consider the following polygonal oblique prisms.
where
At this point, we choose such that the set does not contain any ray.
Prove that
First, show that
Define the bottom base of each prism , , by . Consider an arbitrary point . Then , . Let be an arbitrary ray emanating from .
-
1.
If intersects a lateral face of the prism , then consider the projection, parallel to the lateral edges of , of onto the plane . It is a ray that we define by . The ray emanates from the point which is the projection of onto . Since is a flat weakly -semiconvex set as a set congruent to , it implies that , which gives that , therefore, .
-
2.
If intersects a base of , then it intersects either , which immediately gives that , or it intersects a lateral face of another prism , , by the construction, and further considerations are the same as in item 1, but for a point and the ray . Then , therefor, .
Moreover, if , then .
Theorem 5.
There exists an open set , , such that the set is bounded (or unbounded), connected, and non-convex.
Proof.
Prove theorem by the induction. For , the theorem holds by Lemmas 10 and 11. Suppose that, for , an open set , and is bounded (or unbounded), connected, and non-convex.
Consider the following sets:
where is the convex hull of ,
First, show that
Consider an arbitrary point , and an arbitrary ray emanating from . If , then . If , then consider the orthogonal projection of onto the coordinate subspace . It is a ray emanating from the point which is the orthogonal projection of onto . Therefore, , which gives that . Then .
Moreover, if , then .
Now, prove that , therefore, , and
It is enough to show that if
then . Let be the -dimensional plane passing through parallel to the coordinate subspace . Then the intersection is either 1) empty or 2) congruent to , or 3) congruent to .
1) Any straight line passing through in does not intersect .
2) Since is convex in , there exists a straight line passing through in and not intersecting , therefore, not intersecting .
3) and with respect to . Since , there exists a straight line passing through in and not intersecting , therefore, not intersecting .
The set is bounded (or unbounded), connected, and non-convex, obviously. ∎
Declarations
This work was supported by a grant from the Simons Foundation (1290607,T.M.O.). The author declare no potential conflict of interest with respect to the research, authorship and publication of this article. All necessary data are included into the paper.
References
- [1] L. A. Aizenberg. Decomposition of holomorphic functions of several complex variables into partial fractions. Siberian Mathematical Journal, 8(5):859–872, sep 1967.
- [2] H. K. Dakhil. The shadows problems and mappings of fixed multiplicity. candthesis, Institute of Mathematics of NAS of Ukraine, Kyiv, 2017. (in Ukrainian).
- [3] B. A. Klishchuk H. K. Dakhil, Yu. B. Zelinskii. On weakly -convex sets. Dopovidi NANU, (4):3–6, 2017.
- [4] T. M. Osipchuk. On semiconvexity of open sets with smooth boundary in the plane. Proceedings of the International Geometry Center, 12(4):69–88, 2019.
- [5] T. M. Osipchuk. Topological properties of weakly -convex sets. Proceedings of IAMM of NAS of Ukraine, 34:75–84, 2020.
- [6] T. M. Osipchuk. On closed weakly m-convex sets. Proceedings of the International Geometry Center, 15(1):50–65, jun 2022.
- [7] T. M. Osipchuk. Topological and Geometric Properties of the Set of 1-Nonconvexity Points of a Weakly 1-Convex Set in the Plane. Ukrainian Mathematical Journal, 73(12):1918–1936, may 2022.
- [8] T. M. Osipchuk. Topological properties of closed weakly m-semiconvex sets. Journal of Mathematical Sciences, 260(5):678–692, feb 2022.
- [9] T. M. Osipchuk. Topological and geometric properties of 1-nonsemiconvexity-point sets corresponding to open weakly 1-semiconvex subsets of the plane. Journal of Mathematical Sciences, November 2024.
- [10] T. M. Osipchuk, M. V. Tkachuk. On weakly 1-convex sets in the plane. Proceedings of the International Geometry Center, 16(1):42–49, may 2023.
- [11] Yu. B. Zelinskii. Variations to the ”shadow” problem. Zbirn. Prats Inst. Math. NANU, 14(1):163–170, 2017. (in Ukrainian).
- [12] Yu. B. Zelinskii, I. V. Momot. On -convex sets. Ukr. Math. J., 53:482–487, 2001.