On weighted covering numbers and the Levi-Hadwiger conjecture
Abstract
We define new natural variants of the notions of weighted covering and separation numbers and discuss them in detail. We prove a strong duality relation between weighted covering and separation numbers and prove a few relations between the classical and weighted covering numbers, some of which hold true without convexity assumptions and for general metric spaces. As a consequence, together with some volume bounds that we discuss, we provide a bound for the famous Levi-Hadwiger problem concerning covering a convex body by homothetic slightly smaller copies of itself, in the case of centrally symmetric convex bodies, which is qualitatively the same as the best currently known bound. We also introduce the weighted notion of the Levi-Hadwiger covering problem, and settle the centrally-symmetric case, thus also confirm the equivalent fractional illumination conjecture [19, Conjecture 7] in the case of centrally symmetric convex bodies (including the characterization of the equality case, which was unknown so far).
1 Introduction
1.1 Background and Motivation
Covering numbers can be found in various fields of mathematics, including combinatorics, probability, analysis and geometry. They often participate in the solution of many problems in quite a natural manner.
In the combinatorial world, the idea of fractional covering numbers is well-known and utilized for many years. In [2], the authors introduced the weighted notions of covering and separation numbers of convex bodies and shed new light on the relations between the classical notions of covering and separation, as well as on the relations between the classical and weighted notions. In this note we propose a variant of these numbers which is perhaps more natural and discuss these numbers in more detail, revealing more useful relations, as well as some applications. To state our main results, we need some definitions. The impatient reader may skip the following section and go directly to Section 1.3 where the main results are stated.
Apart from deepening our understanding of these notions, and revealing more useful relations, we also consider this work as a first step towards the functionalization of covering and separation numbers; in the past decade, various parts from the theory of convex geometry have been gradually extended to the realm of log-concave functions. Numerous results found their functional generalizations. One natural way to embed convex sets in into the class of log-concave functions is to identify every convex set with its characteristic function . Besides being independently interesting, such extensions may sometimes be applied back to the setting of convex bodies. For further reading, we refer the reader to [1, 3, 4, 14, 15]. Since covering numbers play a considerable part in the theory of convex geometry, their extension to the realm of log-concave functions seems to be an essential building block for this theory. Our results using functional covering numbers will be published elsewhere.
1.2 Definitions
Let be compact and let be compact with non-empty interior. The classical covering number of by is defined to be the minimal number of translates of such that their union covers , namely
Here and in the sequel we assume that the covered set is compact and the covering set has non-empty interior so that the covering number will be finite. However, one may remove these restriction so long as we are content also with infinite outcomes.
A well-known variant of the covering number is obtained by considering only translates of that are centered in , namely
Clearly, , and it is easy to check that for convex bodies111by convex body we mean, here and in the sequel, a compact convex set with non-empty interior and , we have . Furthermore, if is a Euclidean ball then .
The classical notion of the separation number of in is closely related to covering numbers and is defined to be the maximal number of non-overlapping translates of which are centered in ;
It is a standard equivalence relation that . We also define the less conventional
Note that the condition
is equivalent to which means that .
Moreover, it is easily checked that for a convex and for a centrally
symmetric convex body (i.e., ) we have
and thus by the last remark
for any convex body . In the sequel, we will define weighted counterparts
for and which
will not necessarily be equal, even in the convex and centrally symmetric
case.
In order to define the weighted versions, let denote the indicator function of a set, equal to if and if .
Definition 1.1.
A sequence of pairs of points and weights is said to be a weighted covering of by if for all we have . The total weight of the covering is denoted by . The weighted covering number of by is defined to be the infimal total weight over all weighted coverings of by and is denoted by .
One may consider only coverings
with centers of in . The corresponding weighted covering
number for such coverings, denoted here by
is defined to be the infimal total weight over such coverings. Clearly,
. The weighted notions
of covering and separation numbers corresponding to
and were introduced in [2].
In this note, we shall focus on the weighted versions of
and .
Let us reformulate the above definitions in the language of measures. Note that the covering condition for all is equivalent to where is the discrete measure with masses centered at and where stands for the convolution
Let denote all non-negative discrete and finite measures on and let denote the support of a measure on . Thus, the weighted covering numbers of by can be written as
and
It is this natural to extend this notion of covering to general non-negative measures. Let denote all non-negative Borel regular measures on .
Definition 1.2.
Let be compact and let be compact with non-empty interior. A non-negative measure is said to be a covering measure of by if . The corresponding weighted covering number is defined by
Clearly, . In Proposition 2.6, we show that the above infimum is actually a minimum, that is, there exists an optimal covering Borel measure of by . Note that the set of optimal covering measures is clearly convex.
The weighted notions of the separation are defined similarly; a measure is said to be separated if . The weighted separation numbers, corresponding to , and are respectively defined by:
and
where again clearly .
1.3 Main Results
Our first main result is a strong duality between weighted covering and separation numbers; it turns out that and can be interpreted as the outcome of two dual problems in the sense of linear programming. Indeed, as in [2], this observation is a key ingredient in the proof of our first main result below which states that the outcome of these dual problems is the same (we call this “strong duality”).
Theorem 1.3.
Let be compact and let be a compact with non-empty interior. Then
Remark 1.4.
As a consequence of Theorem 1.3, together with the well-known homothety equivalence between classical covering and separation numbers , we immediately get the following equivalence relation between the classical and weighted covering numbers (which has also appeared in [2] for the pair ).
Corollary 1.5.
Let be compact and let be compact with non-empty interior. Then Then
We remark that Corollary 1.5 is actually
implied by the weak duality
which we prove in Proposition 2.1 below, the proof
of which is relatively simple. Similarly, we shall prove in Proposition
2.1 that
providing an alternative short proof for the weak duality result in
[2, Theorem 6].
For a centrally symmetric convex set , Corollary 1.5 reads . Although this “constant homothety” equivalence of classical and weighted covering is useful, it turns out to be insufficient in certain situations. To that end, we introduce our second main result, in which the homothety factor is replaced by a factor with arbitrarily close to . This gain is diminished by an additional logarithmic factor; such a result is a reminiscent of Lovï¿œsz’s [17] well-known inequality for fractional covering numbers of hypergraphs.
Theorem 1.6.
Let be compact and let be compact with non-empty interior. Then
1.4 Additional inequalities
Let denote the Lebesgue volume of a set . The classical covering and separation numbers satisfy simple volume bounds. Such volume bounds also hold for the weighted case, and turn out to be quite useful.
Theorem 1.7.
Let be compact and let be compact with non-empty interior. Then
Remark 1.8.
Let us show, by using the above volume bounds, that classical and weighted covering numbers are not equal in general, even for centrally symmetric convex bodies such as a cube and a ball (for a simple dimensional example, see the last part of Remark 2.7). Namely, we show that where is the unit ball in and for a large enough . Indeed, it was shown in [11] that the lower limit of the density of covering a cube by balls, defined as the limit of the ratio , as tends to infinity is bounded from below by where as . However, by our volume bounds in Theorem 1.7, it follows that the weighted covering density approaches as . Note that by Proposition 2.1 below, this also means that for a large enough cube and dimension.
1.5 An application
A famous conjecture, known as the Levi-Hadwiger or the Gohberg-Markus covering problem, was posed in [16], [13] and [12]. It states that in order to cover a convex set by slightly smaller copies of itself, one needs at most copies.
Conjecture.
Let be a convex body with non empty interior. Then there exists such that
Equivalently, . Moreover, equality holds if and only if is a parallelotope.
This problem has drawn much attention over the years, but only little has been unraveled so far. We mention that Levi confirmed the conjecture for the plane, and that Lassak confirmed it for centrally symmetric bodies in . The currently best known general upper bound for is and the best bound for centrally symmetric convex bodies is , both of which are simple consequences of Rogers’ bound for the asymptotic lower densities for covering the whole space by translates of a general convex body, see [20]. For a comprehensive survey of this problem and the aforementioned results see [8].
It is natural, after introducing weighted covering, to formulate the Levi-Hadwiger covering problem for the case of weighted covering.
Conjecture 1.9.
Let be a convex body. Then Moreover, equality holds if and only if is a parallelotope.
For centrally symmetric convex bodies, we verify Conjecture 1.9, including the equality case. We show
Theorem 1.10.
Let be a convex body. Then
Moreover, for centrally symmetric , if and only if is a parallelotope.
It is worth mentioning that the classical covering problem of Levi-Hadwiger
is equivalent to the problem of the illumination of a convex body
(for surveys see [18, 6]) which asks how many
directions are required to illuminate the entire boundary of a convex
body (a direction is said to illuminate a point
in the boundary of if the ray emanating from in direction
intersects the interior of ). A fractional version of the
illumination problem was considered in [19], where it
was proven that the fractional illumination number of a convex body
, denoted by , satisfies that
and that for all centrally symmetric
bodies (with parallelotopes attaining equality). It was further conjectured
[19, Conjecture 7] that
for all convex bodies and that equality is attained only for parallelotopes.
However, as no relation between fractional and usual illumination
numbers was proposed, this result remained isolated. Also, it seems
that the equality conditions were not analyzed. In fact, one may
verify that the proof of the equivalence between the illumination
problem and the Levi-Hadwiger covering problem (see [7, Theorem 7])
carries over to the fractional setting and conclude that .
Thus, Theorem 1.10 actually verifies the aforementioned
results about fractional illumination and also verifies [19, Conjecture 7]
for the case of centrally symmetric convex bodies, including the equality
hypothesis.
Combining the inequality in Theorem 1.6 with the volume inequality in Theorem 1.7, we prove the following bound for the classical Levi-Hadwiger problem, in the case of centrally symmetric convex bodies, which is the same as the aforementioned (best known) general bound of Rogers.
Corollary 1.11.
Let be a centrally symmetric convex body. Then for all ,
We remark that the above bound and Rogers’ bound are asymptotically equivalent, and that in both cases the constant above may be improved by performing more careful computations, improving and optimizing over various constants. We avoid such computations as they will not affect the order of magnitude of this bound, and complicate the exposition.
Acknowledgments
We thank Prof. Noga Alon, Prof. Mark Meckes and
Prof. Boris Tsirelson for their valuable comments and suggestions.
We also thank Prof. Rolf Schneider for his proof of Lemma 3.1
and for translating for us the entire paper [9]
from German.
This research was supported in part by ISF grant number 247/11.
The remainder of this note is organized as follows. In Section 2.1 we show weak duality between weighted covering and separation numbers. In Section 2.2 we prove Theorem 1.3. In Section 2.3 we discuss the existence of optimal covering measures. In Section 2.4 we discuss the approximation of uniform covering measures by discrete covering measures. In 2.5 we prove Theorem 1.7. In Section 2.6 we prove Theorem 1.6. In Section 2.7 we discuss the weighted notions of covering and separation in the setting of general metric spaces. In Section 3 we discuss both the classical and weighted versions of the Levi-Hadwiger covering problems, proving Theorem 1.10 and Corollary 1.11.
2 Weighted covering and separation
2.1 Weak duality
Proposition 2.1.
Let be compact and let be compact with non-empty interior. Then
In particular, we also have that
Proof.
Let be a covering measure of by . Let be a separated measure. By our assumptions we have that and . Thus
and so . Similarly, by considering only on and which must be supported only on , the exact same inequality yields . ∎
2.2 Strong duality
We start with the discretized versions of our weighted covering and separation notions. Let be some finite set, which will be chosen later, and define:
and
In this setting, linear programming duality gives us an equality of the form
| (2.1) |
Indeed, define the vectors by
and the matrix by
Note that
Let denote the standard Euclidean inner product in . Then, in the language of vectors and matrices, the above discretized weighted covering and separation notions read
which are equal by the well-known duality theorem of linear programming,
see e.g., [5].
Next, we shall use this observation with a specific family of sets A set is said to be a net of a set if for every there exists for which . In other words, . We shall make use of the two following simple lemmas, corresponding to [2, Lemmas 14-15].
Lemma 2.2.
Let be compact, compact with non-empty interior and let be some net for . Then
Proof.
Indeed, we have that
∎
Lemma 2.3.
Let be compact, be compact with non-empty interior and let be some net for . Then
Proof.
Suppose that satisfies the condition in the definition of , namely for all we have that . Then it is also weighted separated in the usual sense (that is, satisfying for all that ). Indeed, otherwise we would have a point in such that . Since , it follows that and so there exists a point for which which means that , a contradiction to our assumption. ∎
Finally, to prove Theorem 1.3 we shall need the following continuity result for weighted covering numbers:
Proposition 2.4.
Let be compact and let be compact with non-empty interior. Then
Proof.
Clearly we have that
For the opposite direction, let and let be a sequence of continuous functions satisfying so that point-wise monotonically. Let be a sequence of covering Borel regular measures of by (the definition is straightforward: replace in the original definition by ) such that with . By the well-known Banach-Alaoglu theorem and passing to a subsequence we may assume without loss of generality that for some non-negative regular Borel measure. We claim that is a covering measure of by . Indeed, let . For we have that
By the weak* convergence of to , taking the limit implies that and hence, by the monotone convergence theorem, taking the limit implies that . Thus, is a covering measure of by . This means that
which in turn implies the equality , as claimed. ∎
Proof of Theorem 1.3.
Remark 2.5.
In [2], Proposition 22 is analogous to Proposition 2.4 above with instead of . We mention that replacing by is of no significance because any two bodies in fixed dimension are equivalent.
The proof presented in [2] is not correct, as it is based on [2, Lemma 20] which contains an error.
Note, however, that since the function is monotone in , it is clearly continuous almost everywhere. This, combined with the reasoning in [2, Proof of Theorem 7] (or, similarly, the reasoning above for ) implies that for almost every we have
By taking the limit as we get that
which, combined with Theorem 1.3), we get the following row of equalities (as , and so also , are continuous), holding for all convex bodies
2.3 Optimal measures
Proposition 2.6.
Let be compact and let be compact with non-empty interior. Then there exists a (non-empty) convex set of optimal regular Borel covering measures of by . That is, for every we have that and
Proof.
Since by Theorem 1.3 , we may take a sequence of discrete covering measures of by satisfying
Since the unit ball of the space of regular Borel measures is sequentially compact in the weak* topology, there exists a subsequence and a regular Borel measure such that (this is the well-known Banach-Alaoglu’s theorem). Let us show that . Indeed, let and let be a compactly supported continuous function. Then
Taking a monotone sequence of compactly supported continuous functions satisfying and point-wise converging to , it follows by the monotone convergence theorem that , as needed. Since the covering condition is preserved under convex combinations, as is the total measure, it follows that the set of optimal covering measures of by is convex.∎
Remark 2.7.
One might be tempted to ask whether there exists a measure which is simultaneously optimal-separating and optimal-covering, this turns out to be, in general, not correct. Indeed, one may consider the following example. Let be the cross polytope in , that is, , and let (where denotes the convex hull of ). That is, is a two dimensional triangle in . Clearly, . However, if there existed a measure which was both optimal-separating and optimal-covering then in particular it would have had to be supported in , therefore we would get that the weighted covering of by the central section of with the plane is also . This section, which can also be written as , is the hexagon . We claim, however, that . Indeed, the vertex , for example, is covered by the copies of centered at the triangle and similarly define . By the assumption of covering, . On the other hand, if it were true that we would get, for example, that
As this would also apply to , it is a contradiction. Note that this argument actually shows that and further that the only optimal weighted covering of by is given by the measure . Moreover, note that and satisfy that , hence providing a simple example for the fact that classical and weighted covering numbers are not equal in general. By Proposition 2.1, and also provide a simple example for the fact that classical covering and separation numbers are not equal in general.
2.4 A Glivenko-Cantelli class
In this section our goal is somewhat technical. We wish to use a uniform measure to bound , however it is not a member of . We claim that if we find some uniform covering measure of a set by a convex set (supported on some compact Borel set) with total mass , then . This is because uniform measures can be approximated well by discrete ones, and requires a proof. To this end, we need to recall the definition of a Glivenko-Cantelli class. Let be a sequence of i.i.d -valued random vectors having common distribution . The empirical measure is formed by placing mass at each of the points . A class of Borel subsets of is said to be a Glivenko-Cantelli class for if
In the following lemma, we will invoke a Glivenko-Cantelli theorem for the class of convex subsets of . Namely, in [10, Example 14] it is shown that if a probability distribution satisfies that for all then is a Glivenko-Cantelli class for .
Lemma 2.8.
Let and let be a convex set. Let be a uniform measure on some compact Borel set , that is for some . Suppose that is a covering measure of by . Then
Proof.
Let . We need to show that there exists a finite discrete measure such that
and . To this end, let be the uniform probability measure on , let be a sequence of i.i.d valued random vectors having common distribution , and let be the corresponding empirical measure. The assumption that is a covering measure of by is equivalent to the condition that for all . Since for all , it is implied by [10, Example 14] that is a Glivenko-Cantelli class for and so, for some ,
almost surely. In particular, there exists a discrete measure (one of the ’s) for which
for all . Thus the measure is a covering measure of by with , as required. ∎
2.5 Volume bounds
In this section we divide the proof Theorem 1.7 into the following two propositions.
Proposition 2.9.
Let be compact and let be compact with non-empty interior. Then
Additionally, if is convex then
Proof.
By Theorem 1.3, it suffices to prove that . Let be a -separated measure, that is, . Then
and so as claimed.
Alternatively, one may verify that the measure is a covering measure of by , from which the claim also follows. By Lemma 2.8, the latter argument implies that
∎
Proposition 2.10.
Let be compact and let be compact with non-empty interior. Then
Proof.
By Theorem 1.3, it suffices to prove that . Let be a covering measure of by , that is . Then
and so . Moreover, let . Then
and so .
Alternatively, one may verify that the measure is separated in , from which the claim also follows. The fact that also follows from
∎
2.6 An equivalence between classical and weighted covering
In this section we prove Theorem 1.6
Proof of Theorem 1.6.
Fix . Let be a finite weighted discrete covering of by with
Without loss of generality we may assume that are rational numbers and moreover, by allowing repetitions of the covering points, we may assume that for all , for some arbitrarily large . Denote and let be small enough so that . Our aim is to generate a classical covering of by from the above fractional covering by a random process, with cardinality not larger than
To this end, let be an integer to be determined later and let be some real number also to be determined later. Each point will be chosen independently with probability . We claim that with positive probability, for and , the generated set is a covering of by and at the same time the cardinality of the generated set is not greater than
First, we bound the probability that more than will turn out positive. Let denote the Bernoulli random variable corresponding to and let denote their sum. Note that there are at most trials as . Denote the cardinality of by . A standard Chernoff bound tells us that this probability can be bounded as follows. For any
where at the third equality the minimum is attained at and the last step holds for sufficiently large compared with . Set , then for , one can verify that
Next, we show that with sufficiently high probability our generated set is a covering of by To this end, pick a minimal covering (we insist the points of the net belong to ) of by . The cardinality of such a minimal net is . If every point is covered by a translate then the whole of is covered by the translates of our randomly generated set, as we desire. Let us consider one specific point and check the probability that it is covered by our randomly generated set. Since we insisted that we know that
which means that at least of the original translates include . Therefore, the probability that is not covered is less than or equal to . Thus, the probability that one or more of the covering points is not covered is bounded from above by .
To summarize the above, we bounded the probability that either is not covered or the generated set consists of more than points by
and so it is left to choose and so that this bound is less than As one can verify, the choices and satisfy this requirement. Thus, is bounded by
∎
2.7 The metric-space setting
The notions of covering and separation make sense also in the metric space setting. Let be a metric space (with the induced metric topology), and some compact subset. We shall denote the -covering number of by
where . Similarly
The corresponding notion of the separation number is defined to be the maximal number of non-overlapping -balls centered in ;
In this case it makes sense also to define
and one should note that in the case these notions of course coincide. Also note that the metric setting is inherently centrally symmetric. However, since we no longer work in a linear space, some of the arguments in the preceding sections need to be altered.
Let us define weighted covering and separation in the metric setting, and list the relevant theorems corresponding to those proved in previous sections which hold in this setting. We shall remark only on the parts of the proofs which are not identical to those from the linear realm.
Definition 2.11.
Let be a metric space and compact. A sequence of pairs with points and weights is said to be an weighted -covering of if for all , . The total weight of the covering is denoted by . The weighted -covering number of is defined to be the infimal total weight over all weighted -coverings of and is denoted by .
Similarly, we may define (in a slightly different language)
where denotes all non-negative finite discrete measures on . Let denote all non-negative Borel measures on . The weighted covering number with respect to general measures is defined by
The weighted notions of the separation number are defined similarly; a measure is said to be -separated if for all , and -separated in if for all . The weighted separation numbers, corresponding to , and are respectively defined by:
and
Our first result is a weak duality between weighted covering and separation numbers;
Theorem 2.12.
Let be a metric space, compact and let . Then
Proof.
The first and last inequalities follow by definition, and so we should only prove the center inequality. To this end let be a weighted -covering measure of and let be a weighted -separated measure. By our assumptions we have that and for all . Thus
and so . Similarly, one may show that . ∎
As a corollary of Theorem 2.12, we immediately get the following equivalence relation between the classical and weighted covering numbers:
Corollary 2.13.
Let be a metric space, compact and let . Then
Proof.
By Theorem 2.12, and so we only need to verify the inequality . Indeed, let be -separated. Hence, for every there exists some such that which by the triangle inequality means that . Thus, is a -covering of and so , as needed. ∎
3 The Levi-Hadwiger problem
In this section we prove Theorem 1.10 and Corollary 1.11. To this end, we shall need some preliminary results, and before that, some notation.
3.1 Preliminary results
Denote the Euclidean open ball of radius and centered at by . For Denote the segment between two vectors by . Let denote the boundary of a set .
3.1.1 A Homothetic intersection
We will need the following lemma, the proof of which was kindly shown to us by Rolf Schneider and is reproduced here.
Lemma 3.1.
[Schneider] Let be a centrally-symmetric convex body. Let and let be the intersection point of with the ray emanating from and passing through a. Assume that is homothetic to . Then there exists a closed convex cone (with vertex ) such that .
Proof.
Denote the homothety defined by . Since is centrally symmetric, it follows that is symmetric about , and since is homothetic to it follows that , where . Thus , which means that is the center of homothety of .
Define the cone
and denote its closure by . Let us prove that ; assume towards a contradiction that there exists such that . Let be the points for which
and Consider the quadrangle in with vertices .
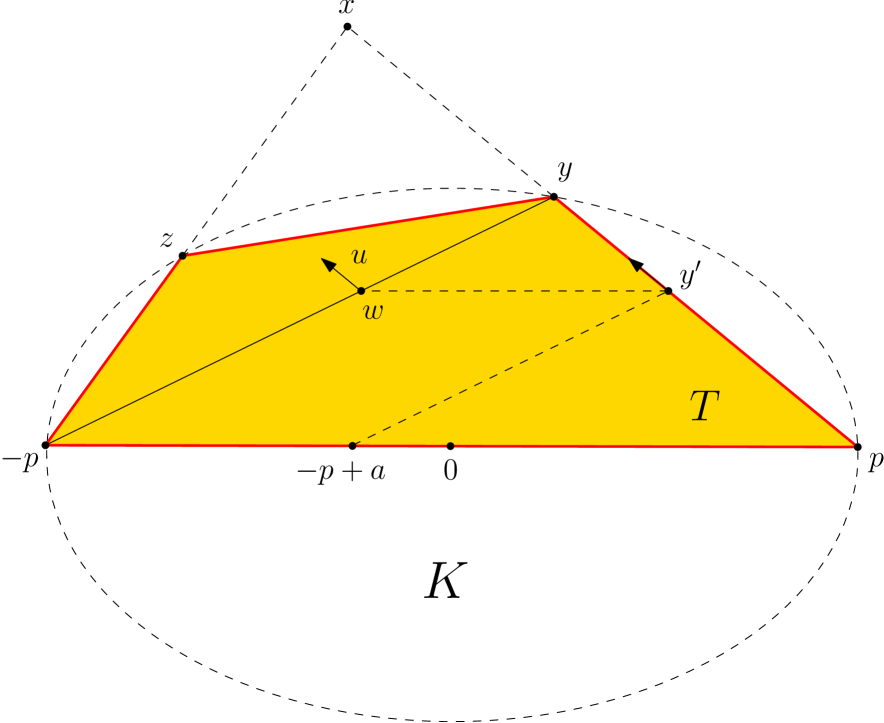
Since is the center of homothety of , the point belongs to the boundary of . However, since the point is in the interior of , it follows that, for some , both and , where (see Figure 3.1). Since , it follows that , and hence , a contradiction to the fact that .
We have proved that and hence . The inclusion trivially holds, and thus . ∎
We remark that if is not centrally symmetric, one may slightly adjust Lemma 3.1 and its proof in order to conclude the following lemma.
Lemma 3.2.
Let be a convex body containing the origin in its interior. Let and assume that the intersection point of with the ray emanating from and passing through a is an exposed point of , denoted by . Let denote the point in for which . Assume that is homothetic to . Then there exist closed convex cones (both with vertex ) such that .
The main difference between the proof of Lemma 3.1 and the proof of Lemma 3.2 is that, in the latter, in order to prove that is the center of homothety of , we need to use the assumption that is an exposed point of . This is done by using the exact same argument as in the equality case of Rogers-Shepard inequality in [21]. We shall not have use of Lemma 3.2 in this note, and we omit the proof’s details.
3.1.2 Covering a convex body by its interior
It will be convenient to work with the weighted covering number of a set by its interior : . The definition of this number is literally the same as for compact sets;
We claim that covering a compact set, fractionally, by its interior is the limit of fractionally covering it by infinitesimally smaller homothetic copies of itself. More precisely, we prove the following.
Lemma 3.3.
Let be compact with non-empty interior. Then
Proof.
Assume without loss of generality that . The inequality
is straightforward by definition. For the opposite direction, let be a covering measure of by , i.e., Note that if , for some set of indices , then
for some open ball . Since , it follows that for all we also have
Hence, as is compact, there exists such that for all ,
where . Therefore, for some , and so
from which the desired equality is implied. ∎
3.1.3 Antipodal sets
In this section we recall a beautiful result by Danzer and Grünbaum, which we will need to invoke later on. To state their result, recall that given a convex body , a set of points is said to be an antipodal set in if for each distinct pair of points in there is a pair of distinct parallel supporting hyperplanes of , each containing one of the two points.
Danzer and Grünbaum [9] proved the following theorem.
Theorem 3.4.
[Danzer and Grünbaum] The maximal cardinality of an antipodal set in a convex body is bounded from above by . Moreover, equality holds if and only if is a parallelotope.
3.2 Completing the proofs
We turn to prove the weighted version of the Levi-Hadwiger problem.
Proof of Theorem 1.10.
Suppose first that is not centrally symmetric. Then the volume inequality in Theorem 1.7, immediately implies that
as required. Of course, in the symmetric case the same argument gives the bound . But we proceed differently so as to be able to analyze the equality case.
Suppose that is centrally symmetric. Without loss of generality, we assume that has non-empty interior and that an open ball of radius is contained in . By Lemma 3.3, we may work with the weighted covering number of by its interior , and by Lemma 2.8 we may also consider uniform covering measures to bound from above. Indeed, consider the uniform measure on with density , that is
| (3.1) |
Let us verify that is a covering measure of by Indeed, let . Then
Since
| (3.2) |
it follows that
| (3.3) |
as required. This means that To address the equality case, assume that for some centrally symmetric convex body we have . In particular, for no is (for given in (3.1)) a covering measure of by . Therefore, the inequality in (3.3) must be an equality for some . Indeed, if not, a standard compactness argument shows that there exists such that for all ,
which means that is a covering measure of by , a contradiction to the assumption .
Next, note that the inequality (3.3) is strict if and only if at least one of the inclusions in (3.2) is strict and, moreover, the rightmost inclusion in (3.2) is strict as long as is not an extremal point of . Thus, the preceding two arguments imply that has at least one extremal point for which
Our aim for the remaining part of the proof, is to show that actually has at least extremal points such that for all , and use the characterization given in Lemma 3.1 for in order to deduce that is an antipodal set of . Finally, we shall invoke Theorem 3.4 to conclude that is a parallelotope.
Assume that there exists exactly extremal points of such that
for all . Then, by using the same compactness argument as before, it follows that there exists such that for all ,
Since , we have that and so it follows that the measure
is a covering measure of by . Therefore, the equality assumption implies that which implies that Concluding the above, there exist at least extremal points in such that for all . By Lemma 3.1, for each there exists a closed convex cone such that .
Let us next prove that if then belongs to the boundary of . Indeed, if belonged to the interior of then it would have to belong to the boundary of as it belongs to . However since . there exists a segment on the ray emanating from and passing through which contains . Together with the assumption that belongs to the interior of , it follows that there exists a segment which both contains and is contained in , a contradiction to the fact that is an extremal point of .
It remains to show that is an antipodal set of . Indeed, since belongs to the boundary of , the segment is contained in the boundary of and so there exists a supporting hyperplane of which contains both and . In particular, supports . In other words, there exists a vector such that for all ,
Hence, for all ,
which means that
contains , supports , and in particular supports . Thus, we conclude that is an antipodal set of . By Theorem 3.4, the maximal cardinality of an antipodal set of a convex body is and equality holds only for parallelotopes, and thus is a parallelotope. ∎
References
- [1] S. Artstein-Avidan, B. Klartag, and V. Milman, The Santaló point of a function, and a functional form of the Santaló inequality, Mathematika 51 (2004), no. 1-2, 33–48.
- [2] S. Artstein-Avidan and O. Raz, Weighted covering numbers of convex sets, Advances in Mathematics 227 (2011), no. 1, 730–744.
- [3] K. Ball, Logarithmically concave functions and sections of convex sets in , Studia Math. 88 (1988), no. 1, 69–84.
- [4] F. Barthe, On a reverse form of the Brascamp-Lieb inequality, Invent. Math. 134 (1998), no. 2, 335–361.
- [5] A. Barvinok, A course in convexity, Graduate Studies in Mathematics, vol. 54, American Mathematical Society, Providence, RI, 2002. MR 1940576 (2003j:52001)
- [6] K. Bezdek, The illumination conjecture and its extensions, Period. Math. Hungar. 53 (2006), no. 1-2, 59–69. MR 2286460 (2007j:52018)
- [7] Boltjansky, V. G. and I. Gohberg, Results and Problems in Combinatorial Geometry, Cambridge University Press, 1985.
- [8] P. Brass, W. Moser, and J. Pach, Research problems in discrete geometry, Springer, New York, 2005.
- [9] L. Danzer and B. Grünbaum, Über zwei Probleme bezüglich konvexer Körper von P. Erdős und von V. L. Klee, Math. Z. 79 (1962), 95–99.
- [10] J. Elker, D. Pollard, and W. Stute, Glivenko-Cantelli theorems for classes of convex sets, Advances in Applied Probability 11 (1979), no. 4, pp. 820–833 (English).
- [11] P. Erdös and C. A. Rogers, The covering of n-dimensional space by spheres, J. London Math. Soc. 28 (1953), 287–293.
- [12] I. Gohberg and A. Markus, A problem on covering of convex figures by similar figures (in Russian), Izv. Mold. Fil. Akad. Nauk SSSR 10 (1960), no. 76, 87–90.
- [13] H. Hadwiger, Ungelöstes Probleme Nr. 20, Elem. Math. 12 (1957), no. 6, 121.
- [14] B. Klartag, Marginals of geometric inequalities, Geometric Aspects of Functional Analysis (VitaliD. Milman and Gideon Schechtman, eds.), Lecture Notes in Mathematics, vol. 1910, Springer Berlin Heidelberg, 2007, pp. 133–166.
- [15] B. Klartag and V. D. Milman, Geometry of log-concave functions and measures, Geometriae Dedicata 112 (2005), no. 1, 169–182.
- [16] F. W. Levi, Überdeckung eines Eibereiches durch Parallelverschiebung seines offenen Kerns, Arch. Math. (Basel) 6 (1955), 369–370.
- [17] L. Lovász, On the ratio of optimal integral and fractional covers, Discrete Mathematics 13 (1975), no. 4, 383–390.
- [18] H. Martini and V. Soltan, Combinatorial problems on the illumination of convex bodies, Aequationes Math. 57 (1999), no. 2-3, 121–152.
- [19] M. Naszódi, Fractional illumination of convex bodies, Contributions to Discrete Mathematics 4 (2009), no. 2, 83–88.
- [20] C. A. Rogers and C. Zong, Covering convex bodies by translates of convex bodies, Mathematika 44 (1997), no. 1, 215–218.
- [21] R. Schneider, Convex bodies: the Brunn-Minkowski theory, Encyclopedia of Mathematics and its Applications, vol. 44, Cambridge University Press, Cambridge, 1993.
Tel Aviv University
shiri@post.tau.ac.il
boazslom@post.tau.ac.il