Opinion Optimization in Directed Social Networks

Let $\mathcal{G}=(V,E)$ denote an unweighted simple directed graph (digraph) with $n=|V|$ nodes (vertices) and $m=|E|$ directed edges (arcs), where $V=\{v_{1},v_{2},\cdots,v_{n}\}$ is the set of nodes, and $E=\{(v_{i},v_{j})\in V\times V\}$ is the set of directed edges. The existence of arc $(v_{i},v_{j})\in E$ means that there is an arc pointing from node $v_{i}$ to node $v_{j}$. In what follows, $v_{i}$ and $i$ are used interchangeably to represent node $v_{i}$ if incurring no confusion. An isolated node is a node with no arcs pointing to or coming from it. Let $N(i)$ denote the set of nodes that can be accessed by node $i$. In other words, $N(i)=\{j:(i,j)\in E\}$. A path $P$ from node $v_{1}$ to $v_{k}$ is an alternating sequence of nodes and arcs $v_{1}$,$(v_{1},v_{2})$,$v_{2}$,$\cdots$, $v_{j-1},(v_{j-1}$,$v_{j})$, $v_{j}$ in which nodes are distinct and every arc $(v_{i},v_{i+1})$ is from $v_{i}$ to $v_{i+1}$. A loop is a path plus an arc from the ending node to the starting node. A digraph is (strongly) connected if for any pair nodes $v_{x}$ and $v_{y}$, there is a path from $v_{x}$ to $v_{y}$, and there is a path from $v_{y}$ to $v_{x}$ at the same time. A digraph is called weakly connected if it is connected when one replaces any directed edge $(i,j)$ with two directed edges $(i,j)$ and $(j,i)$ in opposite directions. A tree is a weakly connected graph with no loops. An isolated node is considered as a tree. A forest is a particular graph that is a disjoint union of trees.

The connections of digraph $\mathcal{G}=(V,E)$ are encoded in its adjacency matrix $\bm{\mathit{A}}=(a_{ij})_{n\times n}$, with the element $a_{ij}$ at row $i$ and column $j$ being $1$ if $(v_{i},v_{j})\in E$ and $a_{ij}=0$ otherwise. For a node $i$ in digraph $\mathcal{G}$, its in-degree $d^{+}_{i}$ is defined as $d^{+}_{i}=\sum_{j=1}^{n}a_{ji}$, and its out-degree $d^{-}_{i}$ is defined as $d^{-}_{i}=\sum_{j=1}^{n}a_{ij}$. In the sequel, we use $d_{i}$ to represent the out-degree $d_{i}^{-}$. The diagonal out-degree matrix of digraph $\mathcal{G}$ is defined as ${\bm{\mathit{D}}}={\rm diag}(d_{1},d_{2},\ldots,d_{n})$, and the Laplacian matrix of digraph $\mathcal{G}$ is defined to be ${\bm{\mathit{L}}}={\bm{\mathit{D}}}-{\bm{\mathit{A}}}$. Let $\mathbf{1}$ and $\mathbf{0}$ be the two $n$-dimensional vectors with all entries being ones and zeros, respectively. Then, by definition, the sum of all entries in each row of $\bm{\mathit{L}}$ is equal to $0$ obeying $\bm{\mathit{L}}\mathbf{1}=\mathbf{0}$. Let $\bm{\mathit{I}}$ be the $n$-dimensional identity matrix.

In a digraph $\mathcal{G}$, if for any arc $(i,j)$, the arc $(j,i)$ exists, $\mathcal{G}$ is reduced to an undirected graph. When $\mathcal{G}$ is undirected, $a_{ij}=a_{ji}$ holds for an arbitrary pair of nodes $i$ and $j$, and thus $d^{+}_{i}=d^{-}_{i}$ holds for any node $i\in V$. Moreover, in undirected graph $\mathcal{G}$ both adjacency matrix $\bm{\mathit{A}}$ and Laplacian matrix $\bm{\mathit{L}}$ of $\mathcal{G}$ are symmetric, satisfying $\bm{\mathit{L}}\mathbf{1}=\mathbf{0}$.

The Friedkin-Johnsen (FJ) model (Friedkin and Johnsen 1990) is a popular model for opinion evolution and formation. For the FJ opinion model on a digraph $\mathcal{G}=(V,E)$, each node/agent $i\in V$ is associated with two opinions: one is the internal opinion $s_{i}$, the other is the expressed opinion $z_{i}(t)$ at time $t$. The internal opinion $s_{i}$ is in the closed interval $[0,1]$, reflecting the intrinsic position of node $i$ on a certain topic, where 0 and 1 are polar opposites of opinions regarding the topic. A higher value of $s_{i}$ signifies that node $i$ is more favorable toward the topic, and vice versa. During the process of opinion evolution, the internal opinion $s_{i}$ remains constant, while the expressed opinion $z_{i}(t)$ evolves at time $t+1$ as follows:

Let $\bm{\mathit{s}}=(s_{1},s_{2},\cdots,s_{n})^{\top}$ denote the vector of internal opinions, and let $\bm{\mathit{z}}(t)=(z_{1}(t),z_{2}(t),\cdots,z_{n}(t))^{\top}$ denote the vector of expressed opinions at time $t$.

Let $\omega_{ij}$ be the element at the $i$-th row and the $j$-th column of matrix $\mathbf{\Omega}\triangleq\left(\bm{\mathit{I}}+\bm{\mathit{L}}\right)^{-1}$, which is called the fundamental matrix of the FJ model for opinion dynamics (Gionis, Terzi, and Tsaparas 2013). The fundamental matrix has many good properties (Chebotarev and Shamis 1997, 1998). It is row stochastic, since $\sum_{j=1}^{n}\omega_{ij}=1$. Moreover, $0\leq\omega_{ji}<\omega_{ii}\leq 1$ for any pair of nodes $i$ and $j$. The equality $\omega_{ji}=0$ holds if and only if $j\neq i$ and there is no path from node $j$ to node $i$; and $\omega_{ii}=1$ holds if and only if the out-degree $d_{i}$ of nodes $i$ is 0. Then, according to Lemma 3.1, for every node $i\in V$, its expressed opinion $z_{i}$ is given by $z_{i}=\sum^{n}_{j=1}\omega_{ij}s_{j}$, a convex combination of the internal opinions for all nodes.

For the FJ model in digraph $\mathcal{G}=(V,E)$, the overall expressed opinion is defined as the sum $z_{\rm sum}$ of expressed opinions $z_{i}$ of every node $i\in V$ at equilibrium. By Lemma 3.1, $z_{i}=\sum^{n}_{j=1}\omega_{ij}s_{j}$ and $z_{\rm sum}=\sum_{i=1}^{n}z_{i}=\sum_{i=1}^{n}\sum_{j=1}^{n}\omega_{ji}s_{i}$. Given the vector for the equilibrium expressed opinions $\bm{\mathit{z}}$, we use $g(\bm{\mathit{z}})$ to denote the average expressed opinion. By definition,

Since $g(\bm{\mathit{z}})=z_{\rm sum}/n$, related problems and algorithms for $g(\bm{\mathit{z}})$ and $z_{\rm sum}$ are equivalent to each other. In what follows, we focus on the quantity $g(\bm{\mathit{z}})$.

Equation (2) tells us that the average expressed opinion $g(\bm{\mathit{z}})$ is determined by two aspects: the internal opinion of every node, as well as the network structure characterizing interactions between nodes encoded in matrix $\mathbf{\Omega}$, both of which constitute the social structure of opinion system for the FJ model. The former is an intrinsic property of each node, while the latter is a structure property of the network, both of which together determine the opinion dynamics system. Concretely, for the equilibrium expressed opinion $z_{i}=\sum_{j=1}^{n}\omega_{ij}s_{j}$ of node $i$, $\omega_{ij}$ indicates the convex combination coefficient or contribution of the internal opinion for node $j$. And the average of the $j$-th column elements of $\mathbf{\Omega}$, denoted by $\rho_{j}\triangleq\frac{1}{n}\sum_{i=1}^{n}\omega_{ij}$, measures the contribution of the internal opinion of node $j$ to $g(\bm{\mathit{z}})$. We call $\rho_{j}$ as the structure centrality (Friedkin 2011) of node $j$ in opinion dynamics modelled by the FJ model, since it catches the long-run structure influence of node $j$ on the average expressed opinion. Note that matrix $\mathbf{\Omega}$ is row stochastic and $0\leq\omega_{ij}\leq 1$ for any pair of nodes $i$ and $j$, $0\leq\rho_{j}\leq 1$ holds for every node $j\in V$, and $\sum_{j=1}^{n}\rho_{j}=1$.

Using structure centrality, the average expressed opinion $g(\bm{\mathit{z}})$ is expressed as $g(\bm{\mathit{z}})=\sum_{i=1}^{n}\rho_{i}s_{i}$, which shows that the average expressed opinion $g(\bm{\mathit{z}})$ is a convex combination of the internal opinions of all nodes, with the weight for $s_{i}$ being the structure centrality $\rho_{i}$ of node $i$.

As shown above, for a given digraph $\mathcal{G}=(V,E)$, its node centrality remains fixed. For the FJ model on $\mathcal{G}=(V,E)$ with initial vector $\bm{\mathit{s}}=(s_{1},s_{2},\cdots,s_{n})^{\top}$ of internal opinions, if we choose a set $T\subset V$ of $k$ nodes and persuade them to change their internal opinions to 0, the average equilibrium opinion, denoted by $g_{T}(\bm{\mathit{z}})$, will decrease. It is clear that for $T=\emptyset$, $g_{\emptyset}(\bm{\mathit{z}})=g(\bm{\mathit{z}})$. Moreover, for two node sets $H$ and $T$, if $T\subset H\subset V$, then $g_{T}(\bm{\mathit{z}})\geq g_{H}(\bm{\mathit{z}})$. Then the problem OpinionMin of opinion minimization arises naturally: How to optimally select a set $T$ with a small number of $k$ nodes and change their internal opinions to 0, so that their influence on the overall equilibrium opinion is maximized. Mathematically, it is formally stated as follows.

Similarly, we can define the problem OpinionMax for maximizing the average equilibrium opinion by optimally selecting a set $T$ of $k$ nodes and changing their internal opinions to 1. The goal of problem OpinionMin is to drive the average equilibrium opinion $g_{T}(\bm{\mathit{z}})$ towards the polar value 0, while the of goal of problem OpinionMax is to drive $g_{T}(\bm{\mathit{z}})$ towards polar value 1. Although the definitions and formulations of problems OpinionMin and OpinionMax are different, we can prove that they are equivalent to each other. In the sequel, we only consider the OpinionMin problem.

Although the OpinionMin problem is seemingly combinatorial, we next show that there is an exact algorithm optimally solving the problem in $O(n^{3})$ time.

Proof.  Since the modifying of the internal opinions does not change the structure centrality $\rho_{i}$ of any node $i$, the optimal set $T$ of nodes for the OpinionMin problem satisfies

which finishes the proof.  $\Box$

Theorem 4.1 shows that the key to solve Problem 1 is to compute $\rho_{i}$ for every node $i$. In Algorithm 1, we present an algorithm Exact, which computes $\rho_{i}$ exactly. The algorithm first computes the inverse $\mathbf{\Omega}$ of matrix $\bm{\mathit{I}}+\bm{\mathit{L}}$, which takes $O(n^{3})$ time. Based on the obtained $\mathbf{\Omega}=(\omega_{ij})_{n\times n}$, the algorithm then computes $\rho_{i}s_{i}$ for each $i\in V$ in $O(n^{2})$ time, by using the relation $\rho_{i}s_{i}=\frac{1}{n}\sum_{j=1}^{n}\omega_{ji}s_{i}$. Finally, Algorithm 1 constructs the set $T$ of $k$ nodes with the largest value of $\rho_{i}s_{i}$, which takes $O(kn)$ time. Therefore, the total time complexity of Algorithm 1 is $O(n^{3})$.

Due to the high computation complexity, Algorithm 1 is computationally infeasible for large graphs. In the next section, we will give a fast algorithm for Problem 1, which is scalable to graphs with twenty million nodes.

For a digraph $\mathcal{G}=(V,E)$, a spanning subgraph of $\mathcal{G}$ is a subgraph of $\mathcal{G}$ with node set being $V$ and edge set being a subset of $E$. A converging tree is a weakly connected digraph, where one node, called the root node, has out-degree 0 and all other nodes have out-degree 1. An isolated node is considered as a converging tree with the root being itself. A spanning converging forest of digraph $\mathcal{G}$ is a spanning subdigraph of $\mathcal{G}$, where all weakly connected components are converging trees. A spanning converging forest is in fact an in-forest in (Agaev and Chebotarev 2001; Chebotarev and Agaev 2002).

Let $\mathcal{F}$ be the set of all spanning converging forests of digraph $\mathcal{G}$. For a spanning converging forest $\phi\in\mathcal{F}$, let $V_{\phi}$ and $E_{\phi}$ denote its node set and arc set, respectively. By definition, for each node $i\in V_{\phi}$, there is at most one node $j\in V_{\phi}$ obeying $(i,j)\in E_{\phi}$. For a spanning converging forest $\phi$, define $\mathcal{R}(\phi)=\{i:(i,j)\notin\phi,\forall j\in V_{\phi}\}$, which is actually the set of roots of all converging trees that constitute $\phi$. Since each node $i$ in $\phi$ belongs to a certain converging tree, we define function $r_{\phi}(i):V\rightarrow\mathcal{R}(\phi)$ to map node $i$ to the root of the converging tree including $i$. Thus, if $r_{\phi}(i)=j$ we conclude that $j\in\mathcal{R}(\phi)$, and nodes $i$ and $j$ belong to the same converging tree in $\phi$. Define $\mathcal{F}_{ij}$ to be the set of those spanning converging forests, where for each spanning converging forest nodes $i$ and $j$ are in the same converging tree rooted at node $j$. That is, $\mathcal{F}_{ij}=\{\phi:r_{\phi}(i)=j,\phi\in\mathcal{F}\}$. Then, we have $\mathcal{F}_{ii}=\{\phi:i\in\mathcal{R}(\phi),\phi\in\mathcal{F}\}$.

Spanning converging forests have a close connection with the fundamental matrix of the FJ model, which is in fact the in-forest matrix of a digraph $\mathcal{G}$ introduced (Chebotarev and Shamis 1997, 1998). Using the approach in (Chaiken 1982), it is easy to derive that the entry $\omega_{ij}$ of the fundamental matrix $\mathbf{\Omega}$ can be written as $\omega_{ij}=|\mathcal{F}_{ij}|/|\mathcal{F}|$.

With the notions mentioned above, we now provide an interpretation and another expression of structure centrality $\rho_{i}$ for any node $i$. For the convenience of description, we introduce some more notations. For a node $i\in V$ and a spanning converging forest $\phi\in\mathcal{F}$ of digraph $\mathcal{G}=(V,E)$, let $M(\phi,i)$ be a set defined by $M(\phi,i)=\{j:r_{\phi}(j)=i\}$. By definition, for any $\phi\in\mathcal{F}$, if $i\notin\mathcal{R}(\phi)$, $M(\phi,i)=\emptyset$; if $i\in\mathcal{R}(\phi)$, $|M(\phi,i)|$ is equal to the number of nodes in the converging tree in $\phi$, whose root is node $i$. For two nodes $i$ and $j$ and a spanning converging forest $\phi$, define $s(\phi,j,i)$ as a function taking two values, 0 or 1:

Then, the structure centrality $\rho_{i}$ of node $i$ is recast as

which indicates that $\rho_{i}$ is the average number of nodes in the converging trees rooted at node $i$ in all $\phi\in\mathcal{F}$, divided by $n$.

We first give a brief introduction to the loop-erasure operation to a random walk (Lawler and Gregory 1980), which is a process obtained from the random walk by performing an erasure operation on its loops in chronological order. Concretely, for a random walk $P=v_{1},(v_{1},v_{2}),v_{2},\ldots,v_{k-1},(v_{j-1},v_{j}),v_{j}$, the loop-erasure $P_{\rm LE}$ to $P$ is an alternating sequence $\widetilde{v}_{1},(\widetilde{v}_{1},\widetilde{v}_{2}),\widetilde{v}_{2}\ldots,\widetilde{v}_{q-1},(\widetilde{v}_{q-1},\widetilde{v}_{q}),\widetilde{v}_{q}$ of nodes and arcs obtained inductively in the following way. First set $\widetilde{v}_{1}=v_{1}$ and append $\widetilde{v}_{1}$ to $P_{\rm LE}$. Suppose that sequence $\widetilde{v}_{1}$, $(\widetilde{v}_{1},\widetilde{v}_{2})$, $\widetilde{v}_{2}$, $\ldots$, $\widetilde{v}_{h-1}$, $(\widetilde{v}_{h-1},\widetilde{v}_{h})$, $\widetilde{v}_{h}$ has been added to $P_{\rm LE}$ for some $h\geq 1$. If $\widetilde{v}_{h}=v_{j}$, then $q=h$ and $\widetilde{v}_{h}$ is the last node in $P_{\rm LE}$. Otherwise, define $\widetilde{v}_{h+1}=v_{r+1}$, where $r=\max\{i:v_{i}=\widetilde{v}_{h}\}$.

Based on the loop-erasure operation on a random walk, Wilson proposed an algorithm to generate a uniform spanning tree rooted at a given node (Wilson 1996; Wilson and Propp 1996). Following the three steps below, we introduce Wilson’s algorithm to get a spanning tree $\tau=(V_{\tau},E_{\tau})$ of a connected digraph $\mathcal{G}=(V,E)$, which is rooted at node $u$. (i) Set $\tau=(\{u\},\emptyset)$ with $V_{\tau}=\{u\}$. Choose $i\in V\setminus V_{\tau}$. Then create an unbiased random walk starting at node $i$. At each time step, the walk jumps to a neighbor of current position with identical probability. The walk stops, when the whole walk $P$ reaches some node in $\tau$. (ii) Perform loop-erasure operation on the random walk $P$ to get $P_{\rm LE}=\widetilde{v}_{1}$, $(\widetilde{v}_{1},\widetilde{v}_{2})$, $\widetilde{v}_{2}$, $\ldots$, $(\widetilde{v}_{q-1},\widetilde{v}_{q})$, $\widetilde{v}_{q}$, and add the nodes and arcs in $P_{\rm LE}$ to $\tau$. Then update $V_{\tau}$ with the nodes in $\tau$. (iii) If $V_{\tau}\neq V$, repeat step (ii), otherwise end circulation and return $\tau$.

For a digraph $\mathcal{G}=(V,E)$, connected or disconnected, we can also apply Wilson’s Algorithm to get a spanning converging forest $\phi_{0}\in\mathcal{F}$, by using the method similar to that in (Avena and Gaudillière 2018; Pilavcı et al. 2021), which includes the following three steps. (i) We construct an augmented digraph $\mathcal{G}^{\prime}=(V^{\prime},E^{\prime})$ of $\mathcal{G}=(V,E)$, obtained from $\mathcal{G}=(V,E)$ by adding a new node $\Delta$ and some new edges. Concretely, in $\mathcal{G}^{\prime}=(V^{\prime},E^{\prime})$, $V^{\prime}=V\cup\{\Delta\}$ and $E^{\prime}=E\cup\{(i,\Delta)\}\cup\{(\Delta,i)\}$ for all $i\in V$. (ii) Using Wilson’s algorithm to generate a uniform spanning tree $\tau$ for the augmented graph $\mathcal{G}^{\prime}$, whose root node is $\Delta$. (iii) Deleting all the edges $(i,\Delta)\in\tau$ we get a spanning forest $\phi_{0}\in\mathcal{F}$ of $\mathcal{G}$. Assigning $\mathcal{R}(\phi_{0})=\{i:(i,\Delta)\in\tau\}$ as the set of roots for trees $\phi_{0}$ makes $\phi_{0}$ become a converging spanning forest of $\mathcal{G}$.

The spanning converging forest $\phi_{0}$ obtained using the above steps is uniformly selected from $\mathcal{F}$ (Avena and Gaudillière 2018). In other words, for any spanning converging forest $\phi$ in $\mathcal{F}$, we have $\mathbb{P}(\phi_{0}=\phi)=1/|\mathcal{F}|$. Following the three steps above for generating a uniform spanning converging forest of digraph $\mathcal{G}$, in Algorithm 2 we present an algorithm to generate a uniform spanning converging forest $\phi$ of digraph $\mathcal{G}$, which returns a list RootIndex with the $i$-th element RootIndex[$i$] recording the root of the tree in $\phi$ node $i$ belongs to. That is, RootIndex[$i$]=$r_{\phi}(i)$.

Below we give a detailed description for Algorithm 2. InForest is a list recording whether a node is in the forest or not in the random walk process. In line 1, we initialize InForest$[i]$ to false, for all $i\in V$. If node $i$ is not a root of any tree in the forest $\phi$, Next[$i$] is the node $j$ satisfying $(i,j)\in\phi$; if node $i$ belongs to the root set $\mathcal{R}(\phi)$, Next[$i$] $=-1$. We initialize Next[$i$] $=-1$ in line 2. We start a random walk at node $u$ in the extended graph $\mathcal{G}^{\prime}$ in line 5 to create a forest branch of $\mathcal{G}$. The probability of visiting node $\Delta$ starting from $u$ is $1/(1+d_{u})$. In line 7, we generate a random real number in $(0,1)$ using function Rand(). If the random number satisfies the inequality in line 8, the walk jumps to node $\Delta$ at this step. According to the previous analysis, in extended graph $\mathcal{G}^{\prime}$, those nodes that point directly to $\Delta$ belong to the root set $\mathcal{R}(\phi)$. In lines 9-11, we set the node $u$ as a root node and update InForest[$u$], Next$[u]$, and RootIndex$[u]$. If the inequality in line 8 does not hold, we use function RandomSuccessor($u,\mathcal{G}$) to return a node randomly selected from the neighbors of $u$ in $\mathcal{G}$ in line 13. Then we update $u$ to Next[$u$] and go back to line 6. The $\mathbf{for}$ loop stops when the random walk goes to a node already existing in the forest. When the loop stops, we get a newly created branch. In lines 15-20, we add the loop-erasure of the branch to the forest and then update RootIndex.

We now analyze the time complexity of Algorithm 2. Before doing this, we present some properties of the diagonal element $\omega_{ii}$ of matrix $\mathbf{\Omega}$ for all nodes $i\in V$.

Proof.  Wilson showed that the expected running time of generating a uniform spanning tree of a connected digraph $\mathcal{G}$ rooted at node $u$ is equal to a weighted average of commute time between the root and the other nodes (Wilson 1996). Marchal rewrote this average of commute time in terms of graph matrices in Proposition 1 in (Marchal 2000). According to Marchal’s result, the expected running time of Algorithm 2 is equal to the trace $\sum_{i=1}^{n}\omega_{ii}(1+d_{i})$ of matrix $\mathbf{\Omega}(\bm{\mathit{I}}+\bm{\mathit{D}})$. Using Lemma 5.2, we have $\sum_{i=1}^{n}\omega_{ii}(1+d_{i})\leq\sum_{i=1}^{n}\frac{2+2d_{i}}{2+d_{i}}\leq 2n\left(1-\frac{1}{n+1}\right).$ Thus, the expected time complexity of Algorithm 2 is $O(n)$.  $\Box$

Here by using (5.1), we present an efficient sampling-based algorithm Fast to estimate $\rho_{i}$ for all $i\in V$ and approximately solve the problem OpinionMin in linear time.

The ingredient of the approximation algorithm Fast is the variation of Wilson’s algorithm introduced in the preceding subsection. The details of algorithm Fast are described in Algorithm 3. First, by applying Algorithm 2 we generate $l$ random spanning converging forests $\phi_{1},\phi_{2},\ldots,\phi_{l}$. Then, we compute $\widehat{\rho}_{i}=\frac{1}{nl}\sum_{j=1}^{l}|M(\phi_{j},i)|$ for all $i\in V$. Note that each of these $l$ spanning converging forests has the same probability of being created from all spanning converging forests in $\mathcal{F}$ (Avena and Gaudillière 2018). Thus, we have $\mathbb{E}\left(\frac{1}{nl}\sum_{j=1}^{l}\left|M(\phi_{j},i)\right|\right)=\rho_{i}$, which implies that $\widehat{\rho}_{i}$ in Algorithm 3 is an unbiased estimation of $\rho_{i}$. Then, $\widehat{\rho}_{i}s_{i}$ is an unbiased estimation of $\rho_{i}s_{i}$. Finally, we choose $k$ nodes from $V$ with the top-$k$ values of $\widehat{\rho}_{i}s_{i}$.

Running Algorithm 2 requires determining the number of sampling $l$, which determines the accuracy of $\widehat{\rho}_{i}s_{i}$ as an approximation of $\rho_{i}s_{i}$. In general, the larger the value of $l$, the more accurate the estimation of $\widehat{\rho}_{i}s_{i}$ to $\rho_{i}s_{i}$. Next, we bound the number $l$ of required samplings of spanning converging forests to guarantee a desired estimation precision of $\widehat{\rho}_{i}s_{i}$ by applying the Hoeffding’s inequality (Hoeffding and Wassily 1963).

We now demonstrate that with a proper choice of $l$, $\widehat{\rho}_{i}s_{i}$ as an estimator of $\rho_{i}s_{i}$ has an approximation guarantee for all $i\in V$. Specifically, we establish an $(\epsilon,\delta)$-approximation of $\widehat{\rho}_{i}s_{i}$: for any small parameters $\epsilon>0$ and $\delta>0$, the approximation error $\widehat{\rho}_{i}s_{i}$ is bounded by $\epsilon$ with probability at least $1-\delta$. Theorem 5.4 shows how to properly choose $l$ so that $\widehat{\rho}_{i}s_{i}$ is an $(\epsilon,\delta)$-approximation of $\rho_{i}s_{i}$.

Recall that our problem aims to determine the optimal set $T$, which consists of $k$ nodes with the largest $\rho_{i}s_{i}$. To avoid calculating $\rho_{i}$ directly, we propose a fast algorithm (Algorithm 3), which returns a set $\widehat{T}$ containing top $k$ nodes of the highest $\hat{\rho}[i]s_{i}$. Based on the result of Theorem 5.4, we can get a union bound between $g_{\widehat{T}}(\bm{\mathit{z}})$ and $g_{T}(\bm{\mathit{z}})$, as stated in the following theorem.

Proof.  According to Theorem 5.4, we suppose now inequalities $|\widehat{\rho}[i]s_{i}-\rho_{i}s_{i}|>\epsilon$ hold for any $i\in V$. Since the nodes in set $T$ have the top value of $\rho_{i}s_{i}$, we have

By Theorem 5.4, one obtains

which completes the proof.  $\Box$

Therefore, for any fixed $k$, the number of samples does not depend on $n$.

We first compare the effectiveness of our algorithms Exact and Fast with four baseline schemes for node selection: Random, In-degree, Internal opinion, and Expressed opinion. Random selects $k$ nodes at random. In-degree chooses $k$ nodes with the largest in-degree, since a node with a high in-degree may has a strong influence on other nodes (Xu et al. 2020). For Internal opinion and Expressed opinion, they have been used in (Gionis, Terzi, and Tsaparas 2013). Internal opinion returns $k$ nodes with the largest original internal opinions, while Expressed opinion selects $k$ nodes with the largest equilibrium expressed opinions in the FJ model corresponding to the original internal opinion vector.

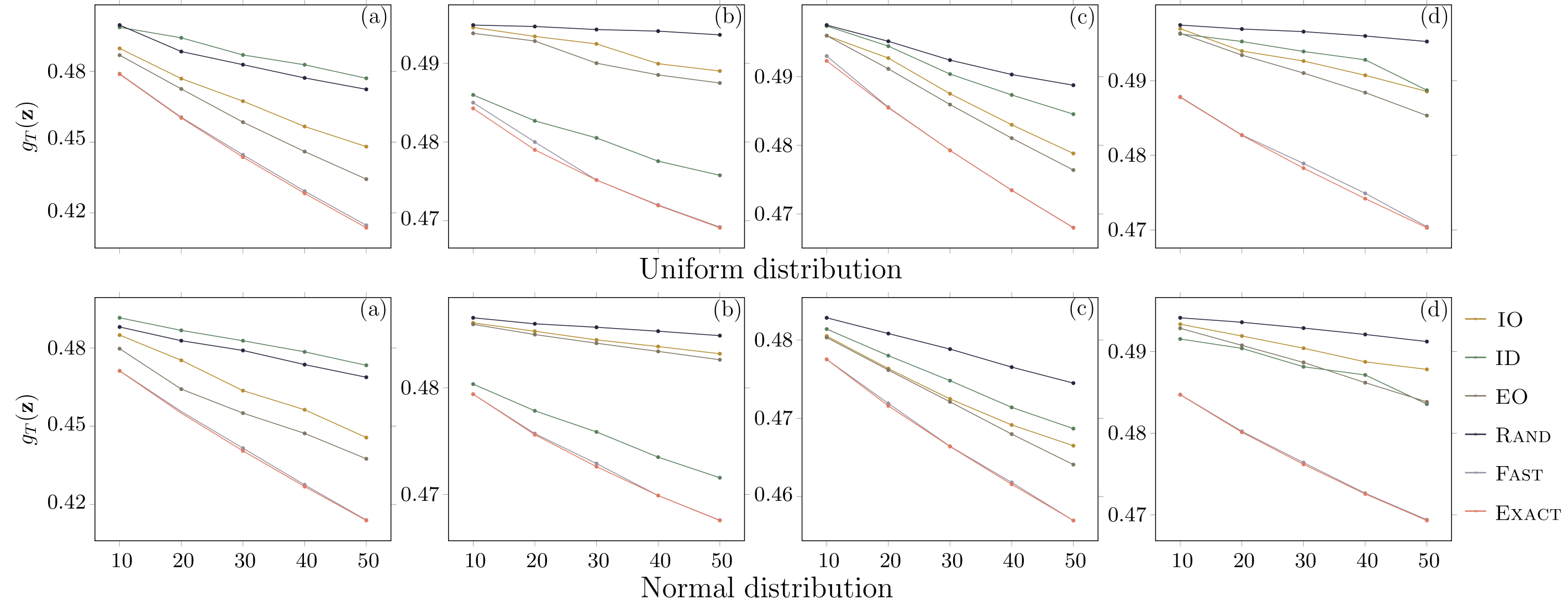
In our experiment, the number $l$ of samplings in algorithm Fast is set be $500$. For each node $i$, its internal opinion $s_{i}$ is generated uniformly in the interval $[0,1]$. For each real network, we first calculate the equilibrium expressed opinions of all nodes and their average opinion for the original internal opinions. Then, using our algorithms Exact and Fast and the four baseline strategies, we select $k=10,20,30,40,50$ nodes and change their internal opinions to 0, and recompute the average expressed opinion associated with the modified internal opinions. We also execute experiments for other distributions of internal opinions. For example, we consider the case that the internal opinions follow a normal distribution with mean $0$ and variance $1$. For this case, we perform a linear transformation, mapping the internal opinions into interval $[0,1]$, so that the smallest internal opinion is mapped to 0, while the largest internal opinion corresponds to 1. As can be seen from Figure 1, for each network algorithm Fast always returns a result close to the optimal solution corresponding to algorithm Exact for both uniform distribution and standardized normal distribution, outperforming the four other baseline strategies.

For the cases that internal opinions obey power-law distribution or exponential distribution, here we do not report the results since they are similar to that observed in Figure 1.

As shown above, algorithm Fast has similar effectiveness to that of algorithm Exact. Below we will show that algorithm Fast is more efficient than algorithm Exact. To this end, in Table 1 we compare the performance of algorithms Exact and Fast. First, we compare the running time of the two algorithms on the real-life directed networks listed in Table 1. For our experiment, the internal opinion of all nodes in each network obeys uniform distribution from $[0,1]$, $k$ is equal to 50, and $l$ is chosen to be 500, 1000, and 2000. As shown in Table 1, Fast is significantly faster than Exact for all $l$, which becomes more obvious when the number of nodes increases. For example, Exact fails to run on the last 11 networks in Table 1, due to time and memory limitations. In contrast, Fast still works well in these networks. Particularly, algorithm Fast is scalable to massive networks with more than twenty million nodes, e.g., FullUSA with over $2.9\times 10^{7}$ nodes.

Table 1 also reports quantitative comparison of the effectiveness between algorithms Exact and Fast. Let $g_{T}$ and $g_{\widehat{T}}$ denote the average opinion obtained, respectively, by algorithms Exact and Fast, and let $\gamma=|g_{T}-g_{\widehat{T}}|/g_{T}$ be the relative error of $g_{\widehat{T}}$ with respect to $g_{T}$. The last three columns of Table 1 present the relative errors for different real networks and various numbers $l$ of samplings. From the results, we can see that for all networks and different $l$, the relative error $\gamma$ is negligible, with the largest value being less than $0.0014$. Moreover, for each network, $\gamma$ is decreased when $l$ increases. This again indicates that the results returned by Fast are very close to those corresponding to Exact. Therefore, algorithm Fast is both effective and efficient, and scales to massive graphs.