Optimal designs in regression with correlated errors

Holger Dette
Ruhr-Universität Bochum
Fakultät für Mathematik
44780 Bochum
Germany Andrey Pepelyshev, Anatoly Zhigljavsky
School of Mathematics
Cardiff University
Cardiff, CF24 4AG
UK

Abstract

This paper discusses the problem of determining optimal designs for regression models, when the observations are dependent and taken on an interval. A complete solution of this challenging optimal design problem is given for a broad class of regression models and covariance kernels.
We propose a class of estimators which are only slightly more complicated than the ordinary least-squares estimators. We then demonstrate that we can design the experiments, such that asymptotically the new estimators achieve the same precision as the best linear unbiased estimator computed for the whole trajectory of the process. As a by-product we derive explicit expressions for the BLUE in the continuous time model and analytic expressions for the optimal designs in a wide class of regression models. We also demonstrate that for a finite number of observations the precision of the proposed procedure, which includes the estimator and design, is very close to the best achievable. The results are illustrated on a few numerical examples.

Keywords and Phrases: linear regression, correlated observations, signed measures, optimal design, BLUE, Gaussian processes, Doob representation

AMS Subject classification: Primary 62K05; Secondary 31A10

1 Introduction

Optimal design theory is a classical field of mathematical statistics with numerous applications in life sciences, physics and engineering. In many cases the use of optimal or efficient designs yields to a reduction of costs by a statistical inference with a minimal number of experiments without loosing any accuracy. Most work on optimal design theory concentrates on experiments with independent observations. Under this assumption the field is very well developed and a powerful methodology for the construction of optimal designs has been established [see for example the monograph of Pukelsheim, (2006)]. While important and elegant results have been derived in the case of independence, there exist numerous situations where correlation between different observations is present and these classical optimal designs are not applicable.

The theory of optimal design for correlated observations is much less developed and explicit results are only available in rare circumstances. The challenging difficulty consists here in the fact that - in contrast to the independent case - correlations yield to non-convex optimization problems and classical tools of convex optimization theory are not applicable. Some exact optimal designs for specific linear models have been studied in Dette et al., (2008); Kiselak and Stehlík, (2008); Harman and Štulajter, (2010). Because explicit solutions of optimal design problems for correlated observations are rarely available, several authors have proposed to determine optimal designs based on asymptotic arguments [see for example Sacks and Ylvisaker, (1966, 1968), Bickel and Herzberg, (1979), Näther, 1985a , Zhigljavsky et al., (2010)], where the references differ in the asymptotic arguments used to embed the discrete (non-convex) optimization problem in a continuous (or approximate) one. However, in contrast to the uncorrelated case, this approach does not simplify the problem substantially and due to the lack of convexity the resulting approximate optimal design problems are still extremely difficult to solve. As a consequence, optimal designs have mainly been determined analytically for the location model (in this case the optimization problems are in fact convex) and for a few one-parameter linear models [see Boltze and Näther, (1982), Näther, 1985a , Ch. 4, Näther, 1985b , Pázman and Müller, (2001) and Müller and Pázman, (2003) among others]. Only recently, Dette et al., (2013) determined (asymptotic) optimal designs for least squares estimation in models with more parameters under the additional assumption that the regression functions are eigenfunctions of an integral operator associated with the covariance kernel of the error process. However, due to this assumption, the class of models for which approximate optimal designs can be determined explicitly is rather small.

The present paper provides a complete solution of this challenging optimal design problem for a broad class of regression models and covariance kernels. Roughly speaking, we determine (asymptotic) optimal designs for a slightly modified ordinary least squares estimator (OLSE), such that the new estimate and the corresponding optimal design achieve the same accuracy as the best unbiased linear estimate (BLUE) with corresponding optimal designs.

To be more precise, consider a general regression observation scheme given by

\displaystyle y(t_{j})=\theta^{T}f(t_{j})+\varepsilon(t_{j}),~~\quad j=1,\dots,N\,,

(1.1)

where $\mathbb{E}[\varepsilon(t_{j})]=0,$ $K(t_{i},t_{j})=\mathbb{E}[\varepsilon(t_{i})\varepsilon(t_{j})]$ denotes the covariance between observations at the points $t_{i}$ and $t_{j}$ . ( $i,j=1,\dots,N$ ), $\theta=(\theta_{1},\ldots,\theta_{m})^{T}$ is a vector of unknown parameters, $f(t)=(f_{1}(t),\ldots,f_{m}(t))^{T}$ is a vector of linearly independent functions, the explanatory variables $t_{1},\dots,t_{N}$ vary in a compact interval, say $[a,b]$ . Parallel to model (1.1) we also consider its continuous time version

\displaystyle y(t)=\theta^{T}f(t)+\varepsilon(t)~,~~t\in[a,b],

(1.2)

where the full trajectory of the process $\{y(t)|t\in[a,b]\}$ can be observed and $\{\varepsilon(t)|t\in[a,b]\}$ is a centered Gaussian process with covariance kernel $K$ , i.e. $K(s,t)=\mathbb{E}[\varepsilon(s)\varepsilon(t)]$ . This kernel is assumed to be continuous throughout this paper.

We pay much attention to the one-parameter case and develop a general method for solving the optimal design problem in model (1.2) explicitly for the OLSE, perhaps slightly modified. The new estimate and the corresponding optimal design achieve the minimal variance among all linear estimates (obtained by the BLUE). In particular, our approach allows to calculate this optimal variance explicitly. As a by-product we also identify the BLUE in the continuous time model (1.2). Based on these asymptotic considerations, we consider the finite sample case and suggest designs for a new estimation procedure (which is very similar to OLSE) with an efficiency very close to the best possible (obtained by the BLUE and the corresponding optimal design), for any number of observations. In doing this, we show how to implement the optimal strategies from the continuous time model in practice and demonstrate that even for very small sample sizes the loss of efficiency with respect to the best strategies based on the use of BLUE with a corresponding optimal design can be considered as negligible. We would like to point out at this point that - even in the one-dimensional case - the problem of numerically calculating optimal designs for the BLUE for a fixed sample size is an extremely challenging one due to the lack of convexity of the optimization problem.

In our approach, the importance of the one-parameter design problem is also related to the fact that the optimal design problem for multi-parameter models can be reduced component-wisely to problems in the one-parameter models. This gives us a way to generate analytically constructed universally optimal designs for a wide range of continuous time multi-parameter models of the form (1.2). Our technique is based on the observation that for a finite number of observations we can always emulate the BLUE in model (1.1) by a different linear estimator. To achieve that theoretically we assign signs to the support points of a discrete design and not only weights in the one-parameter models, but in the multi-parameter case we use matrix weights. We then determine “optimal” signs and weights and consider the weak convergence of these ‘designs” and estimators as the sample size converges to infinity. Finally, we prove the (universal) optimality of the limits in the continuous time model (1.2).

Theoretically, we construct a sequence of designs for either the pure or a modified OLSE, say $\hat{\theta}_{N}$ , such that its variance or covariance matrix satisfies $\mbox{Var}(\hat{\theta}_{N})\to D^{*}$ as the sample size $N$ converges to infinity, where $D^{*}$ is the variance (if $m=1$ ) or covariance matrix (if $m>1$ ) for the BLUE in the continuous time model (1.2). In other words, $D^{*}$ is the smallest possible variance (or covariance matrix with respect to the Loewner ordering) of any unbiased linear estimator and any design. This makes the designs derived in this paper very competitive in applications against the designs proposed by Sacks and Ylvisaker, (1966) and optimal designs constructed numerically for the BLUE (using the Brimkulov-Krug-Savanov algorithm, for example). We emphasize once again that due to non-convexity the numerical construction of optimal designs for the BLUE is extremely difficult. An additional advantage of our approach is that we can analytically compute the BLUE with the corresponding optimal variance (covariance matrix) $D^{*}$ in the continuous time model (1.2) and therefore monitor the proximity of different approximations to the optimal variance $D^{*}$ obtained by the BLUE.

The methodology developed in this paper results in a non-standard estimation and optimal design theory and consists in a delicate interplay between new linear estimators and designs in the models (1.1) and (1.2). For this reason let us briefly introduce various estimators, which we will often refer to in the following discussion. Consider the model (1.1) and suppose that $N$ observations are taken at experimental conditions $t_{1},\ldots,t_{N}$ . For the corresponding vector of observations $\mathbf{Y}=(y(t_{1}),\ldots,y(t_{N}))^{T}$ , a general weighted least squares estimator (WLSE) of $\theta$ is defined by

\displaystyle\mathrm{WLSE:}

\displaystyle\widehat{\theta}_{WLSE}=(\mathbf{X}^{T}\mathbf{W}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{W}\mathbf{Y},

(1.3)

where $\mathbf{X}=(f_{i}(t_{j}))^{i=1,\ldots,m}_{j=1,\ldots,N}$ is an $N\!\times\!m$ design matrix and $\mathbf{W}$ is some $N\times N$ matrix such that $(\mathbf{X}^{T}\mathbf{W}\mathbf{X})^{-1}$ exists. For any such $\mathbf{W}$ the estimator (1.3) is obviously unbiased. The covariance matrix of the estimator (1.3) is given by

\displaystyle\mathrm{Var}(\widehat{\theta}_{WLSE})

\displaystyle=~(\mathbf{X}^{T}\mathbf{W}\,\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{W}\,\mathbf{\Sigma}\mathbf{W}^{T}\,\mathbf{X}(\mathbf{X}^{T}\mathbf{W}^{T}\,\mathbf{X})^{-1},

(1.4)

where $\mathbf{\Sigma}=(K(t_{i},t_{j}))_{i,j=1,\ldots,N}$ is an $N\!\times\!N$ matrix of variances/covariances. For the standard WLSE the matrix $\mathbf{W}$ is symmetric non-negative definite; in this case $\widehat{\theta}_{WLSE}$ minimizes the weighted sum of squares $SS_{\mathbf{W}}(\theta)=(\mathbf{Y}-\mathbf{X}\theta)^{T}\mathbf{W}(\mathbf{Y}-\mathbf{X}\theta)$ with respect to $\theta$ . Important particular cases of estimators of the form (1.3) are the OLSE, the best unbiased linear estimate (BLUE) and the signed least squares estimate (SLSE):

$\displaystyle\mathrm{OLSE:}$	$\displaystyle\widehat{\theta}_{OLSE}=(\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{Y},$	(1.5)
$\displaystyle\mathrm{BLUE:}$	$\displaystyle\widehat{\theta}_{BLUE}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{\Sigma}^{-1}\mathbf{Y},$	(1.6)
$\displaystyle\mathrm{SLSE:}$	$\displaystyle\widehat{\theta}_{SLSE}=(\mathbf{X}^{T}\mathbf{S}\,\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{S}\,\mathbf{Y}.$	(1.7)

Here $\mathbf{S}$ is an $N\!\times\!N$ diagonal matrix with entries $+1$ and $-1$ on the diagonal; note that if $\mathbf{S}\neq\mathbf{I}_{N}$ then SLSE is not a standard WLSE. While the use of BLUE and OLSE is standard, the SLSE is less common. It was introduced in Boltze and Näther, (1982) and further studied in Chapter 5.3 of Näther, 1985a . In the content of the present paper, the SLSE will turn out to be very useful for constructing optimal designs for OLSE and the BLUE in the model (1.2) with one parameter, where the full trajectory can be observed. Another estimate of $\theta$ , which is not a special case of the WLSE, will be introduced in Section 3 and used in the multi-parameter models.

The remaining structure of the paper is as follows. In Section 2 we derive optimal designs for continuous time one-parameter models and discuss how to implement the designs in practice. In Section 3 we extend the results of Section 2 to multi-parameter models. In Appendix B we discuss transformations of regression models and associated designs, which are a main tool in the proofs of our result but also of own interest. In particular, we provide an extension of the famous Doob representation for Gaussian processes [see Doob, (1949) and Mehr and McFadden, (1965)], which turns out to be a very important ingredient in proving the design optimality results of Sections 2 and 3. Finally, in Appendix A we collect some auxiliary statements and proofs for the main results of this paper.

2 Optimal designs for one-parameter models

In this section we concentrate on the one-parameter model

y(t_{j})=\theta f(t_{j})+\varepsilon(t_{j});\qquad j=1,\dots,N,

(2.1)

on the interval $[a,b]$ and its continuous time analogue, where $\mathbb{E}[\varepsilon(t)]=0$ and $\mathbb{E}[\varepsilon(t)\varepsilon(t^{\prime})]=K(t,t^{\prime})$ . Our approach uses some non-standard ideas and estimators in linear models and therefore we begin this section with a careful explanation of the logic of the material.

Sect. 2.1. Under the assumption that the design space is finite we show in Lemma 2.1 that by assigning weights and signs to the observation points $\{t_{1},\dots,t_{N}\}$ we can construct a WLSE which is equivalent to the BLUE. Then, we derive in Corollary 2.1 an explicit form for the optimal weights for a broad class of covariance kernels, which are called triangular covariance kernels.
Sect. 2.2. We demonstrate in Theorem 2.1 that the optimal designs derived in Sect. 2.1 converge weakly to a signed measure, if the cardinality of the design space converges to infinity.
Sect. 2.3. We consider model (2.1) under the assumption that the full trajectory of the process $\{y(t)|t\in[a,b]\}$ can be observed. For the specific case of Brownian motion, that is $K(t,t^{\prime})=\min\{t,t^{\prime}\}$ , we prove analytically the optimality of the signed measure derived in Theorem 2.1 for OLSE. Then, in Theorem 2.3 we establish optimality of the asymptotic measures from Theorem 2.1 for general covariance kernels. As a by-product we also identify the BLUE in the continuous time model (1.2) (in the one-dimensional case). For this purpose, we introduce a transformation which maps any regression model with a triangular covariance kernel into another model with different triangular kernels. These transformations allow us to reduce any optimization problem to the situation considered in Theorem 2.2, which refers to the case of Brownian motion. The construction of this map is based on an extension of the celebrated Doob’s representation which will be developed in Appendix B.
Sect. 2.4. We provide some examples of asymptotic optimal measures for specific models.
Sect. 2.5. We introduce a practical implementation of the asymptotic theory derived in the previous sections. For a finite sample size we construct WLSE with corresponding designs which can achieve very high efficiency compared to the BLUE with corresponding optimal design. It turns out that these estimators are slightly modified OLSE, where only observations at the end-points obtain a weight (and in some cases also a sign).
Sect. 2.6. We illustrate the new methodology in several examples. In particular, we give a comparison with the best known procedures based on BLUE and show that the loss in precision for the procedures derived in this paper is negligible with our procedures being much simpler and more robust than the procedures based on BLUE.

2.1 Optimal designs for SLSE on a finite design space

In this section, we suppose that the design space for model (2.1) is finite, say ${\cal T}=\{t_{1},\ldots,t_{N}\}$ , and demonstrate that in this case the approximate optimal designs for the SLSE (1.7) can be found explicitly. Since we consider the SLSE (1.7) rather than the OLSE (1.5), a generic approximate design on the design space ${\cal T}=\{t_{1},\ldots,t_{N}\}$ is an arbitrary discrete signed measure $\xi=\{t_{1},\ldots,t_{N};w_{1},\ldots,w_{N}\}$ , where $w_{i}=s_{i}p_{i}$ , $s_{i}\in\{-1,1\}$ , $p_{i}\geq 0$ ( $i=1,\dots,N$ ) and $\sum_{i=1}^{N}p_{i}=1$ . We assume that the support $t_{1},\ldots,t_{N}$ of the design is fixed but the weights $p_{1},\ldots,p_{N}$ and signs $s_{1},\ldots,s_{N}$ , or equivalently the signed weights $w_{i}$ , will be chosen to minimize the variance of the SLSE (1.7). In view of (1.4), this variance is given by

\displaystyle D(\xi)=\sum^{N}_{i=1}\sum^{N}_{j=1}K(t_{i},t_{j})w_{i}w_{j}f(t_{i})f(t_{j})\Big{/}\Big{(}\sum^{N}_{i=1}w_{i}f^{2}(t_{i})\Big{)}^{2}.

(2.2)

Note that this expression coincides with the variance of the WLSE (1.2), where the matrix $\mathbf{W}$ is defined by $\mathbf{W}=\mbox{diag}(w_{1},\dots,w_{N})$ .

We assume that $f(t_{i})\neq 0$ for all $i=1,\ldots,N$ . If $f(t_{j})=0$ for some $j$ then the point $t_{j}$ can be removed from the design space $\mathcal{T}$ without changing the SLSE estimator, its variance and the corresponding value $D(\xi)$ . In the above definition of the weights $w_{i}$ , we have $\sum^{N}_{i=1}|w_{i}|=\sum^{N}_{i=1}p_{i}=1$ . Note, however, that the value of the criterion (2.2) does not change if we change all the weights from $w_{i}$ to $cw_{i}$ ( $i=1,\ldots,N$ ) for arbitrary $c\neq 0$ .

Despite the fact that the functional $D$ in (2.2) is not convex as a function of $(w_{1},\dots,w_{N})$ , the problem of determining the optimal design can be easily solved by a simple application of the Cauchy-Schwarz inequality. The proof of the following lemma is given in Appendix A [see also Theorem 5.3 in Näther, 1985a , where this result was proved in a slightly different form].

Lemma 2.1

Assume that the matrix $\mathbf{\Sigma}=(K(t_{i},t_{j}))_{i,j=1,\ldots,N}$ is positive definite and $f(t_{i})\neq 0$ for all $i=1,\ldots,N$ . Then the optimal weights $w_{1}^{*},\dots,w_{N}^{*}$ minimizing (2.2) subject to the constraint $\sum^{N}_{i=1}|w_{i}|=1$ are given by

\displaystyle w_{i}^{*}=c\frac{\mathbf{e}_{i}^{T}\mathbf{\Sigma}^{-1}\mathbf{f}}{f(t_{i})};\qquad i=1,\dots,N,

(2.3)

where $\mathbf{f}=(f(t_{1}),\ldots,f(t_{N}))^{T}$ , $\mathbf{e}_{i}=(0,0,\ldots,0,1,0,\ldots,0)^{T}\in\mathbb{R}^{N}$ is the $i$ -th unit vector, and

c=\Bigl{(}\sum^{N}_{i=1}|\mathbf{e}_{i}^{T}\mathbf{\Sigma}^{-1}\mathbf{f}/f(t_{i})|\Bigr{)}^{-1}.

Moreover, for the design $\xi^{*}=\{t_{1},\ldots,t_{N};w_{1}^{*},\ldots,w_{N}^{*}\}$ with weights (2.3) we have $D(\xi^{*})=D^{*}$ , where $D^{*}=1/(\mathbf{f}^{T}\,\mathbf{\Sigma}^{-1}\mathbf{f})$ , the variance of the BLUE defined in (1.6) using all observations $t_{1},\ldots,t_{N}$ .

Lemma 2.1 shows, in particular, that the pair {SLS estimate, corresponding optimal design $\xi^{*}$ } provides an unbiased estimator with the best possible variance for the one-parameter model (2.1). This results in a WLSE (1.2) with $\mathbf{W}^{*}=\mbox{diag}(w^{*}_{1},\dots,w^{*}_{N})$ which is BLUE. In other words, by a slight modification of the OLSE we are able to emulate the BLUE using the appropriate design or WLSE.

While the statement of Lemma 2.1 holds for arbitrary kernels, we are able to determine the optimal weights $w_{i}^{*}$ more explicitly for a broad class, which are called triangular kernels and are of the form

\displaystyle K(t,t^{\prime})=u(t)v(t^{\prime})\;\;\;{\rm for}\;\;t\leq t^{\prime},

(2.4)

where $u(\cdot)$ and $v(\cdot)$ are some functions on the interval $[a,b]$ . Note that the majority of covariance kernels considered in literature belong to this class, see for example Näther, 1985a ; Zhigljavsky et al., (2010) or Harman and Štulajter, (2011). The following result is a direct consequence of Lemma A.1 from Appendix A .

Corollary 2.1

Assume that the covariance kernel $K(\cdot,\cdot)$ has the form (2.4) so that the matrix $\mathbf{\Sigma}=(K(t_{i},t_{j}))_{i,j=1,\ldots,N}$ is positive definite and has the entries $K(t_{i},t_{j})=u_{i}v_{j}$ for $i\leq j$ , where for $k=1,\ldots,N$ we denote $u_{k}=u(t_{k})$ , $v_{k}=v(t_{k})$ , and also $f_{k}=f(t_{k})$ , $q_{k}=u_{k}/v_{k}$ . If $f_{1}\neq 0\ (i=1,\dots,N)$ , the weights in (2.3) can be represented explicitly as follows:

$\displaystyle w_{1}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}}\left(\tilde{\sigma}_{11}{f_{1}}+\tilde{\sigma}_{12}{f_{2}}\right)=\frac{c\,u_{2}}{f_{1}v_{1}v_{2}(q_{2}-q_{1})}\Bigl{(}\frac{f_{{1}}}{u_{1}}-\frac{f_{2}}{u_{2}}\Bigr{)}\,,$	(2.5)
$\displaystyle w_{N}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{N}}\left(\tilde{\sigma}_{N,N}{f_{N}}+\tilde{\sigma}_{N-1,N}{f_{N-1}}\right)=\frac{c}{f_{N}v_{N}(q_{N}-q_{N-1})}\Bigl{(}\frac{f_{N}}{v_{N}}-\frac{f_{N-1}}{v_{N-1}}\Bigr{)}\,,$	(2.6)
$\displaystyle w_{i}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{i}}\left(\tilde{\sigma}_{i,i}f_{i}+\tilde{\sigma}_{i-1,i}f_{i-1}+\tilde{\sigma}_{i,i+1}f_{i+1}\right)$
	$\displaystyle=$	$\displaystyle\frac{c}{f_{i}v_{i}}\Bigl{(}\frac{(q_{i+1}-q_{i-1})f_{i}}{v_{i}(q_{i+1}-q_{i})(q_{i}-q_{i-1})}-\frac{f_{i-1}}{v_{i-1}(q_{i}-q_{i-1})}-\frac{f_{i+1}}{v_{i+1}(q_{i+1}-q_{i})}\Bigr{)}\,,$

for $i=2,\ldots,N-1$ . In formulas (2.5), (2.6) and (2.1), the quantity $\tilde{\sigma}_{ij}$ denotes the element in the position $(i,j)$ of the matrix $\mathbf{\Sigma}^{-1}=(\tilde{\sigma}_{ij})_{i,j=1,\ldots,N}$ .

2.2 Weak convergence of designs

In this section, we consider the asymptotic properties of designs with weights (2.5) - (2.1). Recall that the design space is an interval, say $[a,b]$ , and that we assume a triangular covariance function of the form (2.4). According to the discussion of triangular covariance kernels provided in Section 4.1 of Appendix B, the functions $u(\cdot)$ and $v(\cdot)$ are continuous and strictly positive on the interval $(a,b)$ and the function $q(\cdot)=u(\cdot)/v(\cdot)$ is positive, continuous and strictly increasing on $(a,b)$ . We also assume that the regression function $f$ in (2.1) is continuous and strictly positive on the interval $(a,b)$ . We define the transformation

Q(t)={q(t)-q(a)\over q(b)-q(a)}

(2.8)

and note that the function $Q:[a,b]\to[0,1]$ is increasing on the interval $[a,b]$ with $Q(a)=0$ and $Q(b)=1$ , that is $Q(\cdot)$ is a cumulative distribution function (c.d.f.). For fixed $N$ and $i=1,\ldots,N$ , define $z_{i,N}=(i-\frac{1}{2})/N$ and the design points

\displaystyle t_{i,N}=Q^{-1}\left(z_{i,N}\right),\;\;i=1,\ldots,N\,.

(2.9)

Theorem 2.1

Consider the optimal design problem for the model (2.1), where the error process $\varepsilon(t)$ has the covariance kernel $K(t,s)$ of the form (2.4). Assume that $u(\cdot)$ , $v(\cdot)$ , $f(\cdot)$ and $q(\cdot)$ are strictly positive, twice continuously differentiable functions on the interval $[a,b]$ . Consider the sequence of signed measures

\xi_{N}=\{t_{1,N},\ldots,t_{N,N};w_{1,N},\ldots,w_{N,N}\},

where the support points $t_{i,N}$ are defined in (2.9) and the weights $w_{i,N}$ are assigned to these points according to the rule (2.3) of Lemma 2.1. Then the sequence of measures $\{\xi_{N}\}_{N\in\mathbb{N}}$ converges in distribution to a signed measure $\xi^{*}$ , which has masses

\displaystyle P_{a}=\frac{c}{f(a)v^{2}(a)q^{\prime}(a)}\Big{[}\frac{f(a)u^{\prime}(a)}{u(a)}-f^{\prime}(a)\Big{]}\,,\;\;P_{b}=c\cdot\frac{h^{\prime}(b)}{f(b)v(b)q^{\prime}(b)}

(2.10)

at the points $a$ and $b$ , respectively, and the signed density

\displaystyle p(t)=-\frac{c}{f(t)v(t)}\Big{[}\frac{h^{\prime}(t)}{q^{\prime}(t)}\Big{]}^{\prime}\,

(2.11)

(that is, the Radon-Nikodym derivative of $\xi^{*}$ with respect to the Lebesque measure) on the interval $(a,b)$ , where the function $h(\cdot)$ is defined by $h(t)=f(t)/v(t)$ .

The proof of Theorem 2.1 is technically complicated and therefore given in Appendix A. The constant $c\neq 0$ in (2.10) and (2.11) is arbitrary. If a normalization $|\xi^{*}|([a,b])=1$ is required, then $c$ can be found from the normalizing condition

\int^{b}_{a}\xi^{*}(dt)=|P_{a}|+|P_{b}|+\int_{a}^{b}|p(t)|dt=1\,.

Throughout this paper we write the limiting designs of Theorem 2.1 in the form

\xi^{*}(dt)=P_{a}\delta_{a}(dt)+P_{b}\delta_{b}(dt)+p(t)dt\,,

(2.12)

where $\delta_{a}(dt)$ and $\delta_{b}(dt)$ are the Dirac-measures concentrated at the points $a$ and $b$ , respectively, and the function $p(\cdot)$ is defined by (2.11). Note also that under the assumptions of Theorem 2.1, the function $p(\cdot)$ is continuous on the interval $[a,b]$ . In the case of Brownian motion, the limiting design of Theorem 2.1 is particularly simple.

Example 2.1

If the error process $\varepsilon$ in model (2.1) is the Brownian motion on the interval $[a,b]$ with $0<a<b<\infty$ , then $K(t,s)=\min(t,s)$ and hence $u(t)=t$ , $v(t)=1$ , $q(t)=t$ . This implies that the limiting design of Theorem 2.1 is given by (2.12) with

\displaystyle P_{a}=c\ \frac{f(a)-f^{\prime}(a)a}{af(a)}\,,\;\;P_{b}=c\ \frac{f^{\prime}(b)}{f(b)}\qquad{\rm{and}}\qquad p(t)=-c\frac{f^{\prime\prime}(t)}{f(t)}\,.

(2.13)

2.3 Optimal designs and the BLUE

In this section we consider the continuous time model (1.2) in the case $m=1$ and demonstrate that the limiting designs derived in Theorem 2.1 are in fact optimal. A linear estimator for the parameter $\theta$ in model (1.2) is defined by $\hat{\theta}_{\mu}=\int^{b}_{a}y(t)\mu(dt)$ , where $\mu$ is a signed measure on the interval $[a,b]$ . Special cases include the OLSE and SLSE $\widetilde{\theta_{\xi}}=\int^{b}_{a}y(t)f(t)\xi(dt)/\int^{b}_{a}f^{2}(t)\xi(dt)$ , where $\xi$ is a measure or a signed measure on the interval $[a,b]$ , respectively. Note that $\hat{\theta}_{\mu}$ is unbiased if and only if $\int^{b}_{a}f(t)\mu(dt)=1$ and $\widetilde{\theta_{\xi}}$ is unbiased by construction. The BLUE (in the continuous time model (1.2)) minimizes

\Phi(\mu)=\mbox{Var}(\hat{\theta}_{\mu})=\int^{b}_{a}\int^{b}_{a}K(x,y)\mu(dx)\mu(dy)

in the class of all signed measures $\mu$ satisfying $\int^{b}_{a}f(t)\mu(dt)=1$ , and

\displaystyle D^{*}=\inf\{\Phi(\mu)\mid\mu\ \ \mbox{signed measure on}\ [a,b]\}

(2.14)

denotes the best possible variance of all linear unbiased estimators in the continuous time model (1.2).

Similarly, a signed measure $\xi^{*}$ on the interval $[a,b]$ is called optimal for least squares estimation in the one-parameter model (1.2), if it minimizes the functional

\displaystyle D(\xi)=\mbox{Var}(\widetilde{\theta_{\xi}})={\int_{a}^{b}\int_{a}^{b}K(t,s)f(t)f(s)\xi(dt)\xi(ds)}\Big{/}{\Big{(}\int_{a}^{b}f^{2}(t)\xi(dt)\Big{)}^{2}}\,,

(2.15)

in the set of all signed measures $\xi$ on the interval $[a,b]$ , such that $\int_{a}^{b}f^{2}(t)\xi(dt)\neq 0$ . In the case of a Brownian motion, we are able to establish the optimality of the design of Example 2.1. A proof of the following result is given in Appendix A.

Theorem 2.2

Let $\{\varepsilon(t)\,|\,t\in[a,b]\}$ be a Brownian motion, so that $K(t,t^{\prime})=\min\{t,t^{\prime}\}$ , and $f$ be a positive, twice continuously differentiable function on the interval $[a,b]\subset\mathbb{R^{+}}$ . Then the signed measure $\xi^{*}$ , defined by (2.12) and (2.13) with arbitrary $c\neq 0$ , minimizes the functional (2.15). The minimal value in (2.15) is obtained as

D(\xi^{*})=\min_{\xi}D(\xi)=\Big{[}\frac{f^{2}(a)}{a}+\int^{b}_{a}(f^{\prime}(t))^{2}dt\Big{]}^{-1}.

Moreover, the BLUE in model (1.2) is given by $\hat{\theta}_{\mu^{*}}$ , where $\mu^{*}(dt)=f(t)\xi^{**}(dt)$ and $\xi^{**}$ is the signed measure defined by (2.12) and (2.13) with constant $c^{*}=D(\xi^{*})$ . This further implies $D^{*}=D(\xi^{*})=\Phi(\mu^{*}).$

Based on the design optimality established in Theorem 2.2 for the special case of Brownian motion and the technique of transformation of regression models described in Appendix B, we can establish the optimality of the asymptotic designs derived in Theorem 2.1 for more general covariance kernels; see Appendix A for the proof.

Theorem 2.3

Under the conditions of Theorem 2.1, the optimal design $\xi^{*}$ minimizing the functional (2.15) is defined by the formulas (2.10) - (2.12) with arbitrary $c\neq 0$ . The minimal value in (2.15) is obtained as

\displaystyle D(\xi^{*})=\Big{[}\frac{\tilde{f}^{2}(q(a))}{q(a)}+\int^{q(b)}_{q(a)}(\tilde{f}^{\prime}(t))^{2}dt\Big{]}^{-1}\,,

(2.16)

where $\tilde{f}(t)=f(q^{-1}(s))/v(q^{-1}(s))$ . Moreover, the BLUE in model (1.2) is given by $\hat{\theta}_{\mu^{*}}$ , where $\mu^{*}(dt)=f(t)\xi^{**}(dt)$ , $\xi^{**}$ is the signed measure defined in (2.10) - (2.12) with constant $c^{*}=D(\xi^{*})$ , and $D^{*}=\Phi(\mu^{*})=D(\xi^{*}).$

2.4 Examples of optimal designs

In this section, we provide the values of $P_{a}$ , $P_{b}$ and the function $p(\cdot)$ in the general expression (2.12) for the optimal designs in a number of important special cases for the one-parameter continuous time model (1.2), where the design space is ${\cal T}=[a,b]$ . Specifically, optimal designs are given in Table 1 for the location model, in Table 2 for the linear model, in Table 3 for a quadratic model and in Table 4 for a trigonometric model. The last named model was especially chosen to demonstrate the existence of optimal designs with a density $p$ which changes sign in the interval $(a,b)$ . In the tables several triangular covariance kernels are considered. The parameters of these covariance kernels satisfy the constraints $c_{2}>\pm c_{1}$ , $\mp c_{2}\not\in[a,b]$ , $\gamma>\omega$ , $\lambda>0$ . For the sake of a transparent presentation, we use the factor $c=1$ in all tables, but we emphasize once again that the optimal designs do not depend on the scaling factor.

As an example, if $K(t,t^{\prime})=e^{-\lambda|t-t^{\prime}|}$ for some $\lambda>0$ , we have from the last row of Table 2 that the optimal design for the continuous time model $\{\theta t+\varepsilon(t)|t\in[1,2]\}$ is $\xi^{*}(dt)=(\lambda-1)\delta_{1}(dt)+(\lambda+\frac{1}{2})\delta_{2}(dt)+\lambda^{2}dt$ , and as a consequence, $D^{*}=(\frac{5}{2}+\frac{1}{2\lambda}+\frac{7}{6}\lambda)^{-1}$ .

Table 1: Optimal designs for the location model:

f(t)=1

t\in[a,b]

$u(t)$	$v(t)$	$P_{a}$	$P_{b}$	$p(t)$
any	$1$	1	0	0
$c_{1}+t$	$c_{2}\pm t$	$\displaystyle\frac{1}{a+c_{1}}$	$\displaystyle\frac{-1}{b\pm c_{2}}$	$0$
$t^{\gamma}$	$t^{\omega}$	$-\gamma a^{-\gamma-\omega}$	$\omega b^{-\gamma-\omega}$	$\gamma\omega t^{-1-\gamma-\omega}$
$e^{\lambda t}$	$e^{-\gamma t}$	$\lambda e^{a(\gamma-\lambda)}$	$\gamma e^{b(\gamma-\lambda)}$	$\lambda\gamma e^{t(\gamma-\lambda)}$

Table 2: Optimal designs for the linear regression model through the origin:

f(t)=t

t\in[a,b]

$u(t)$	$v(t)$	$P_{a}$	$P_{b}$	$p(t)$
$t$	$1$	0	1	0
$c_{1}+t$	$c_{2}\pm t$	$\displaystyle\frac{-c_{1}}{(a+c_{1})a}$	$\displaystyle\frac{\pm c_{2}}{(b\pm c_{2})b}$	0
$t^{\gamma}$	$t^{\omega}$	$-\!(\gamma\!-\!1)a^{-\gamma-\omega}$	$(\omega\!-\!1)b^{-\gamma-\omega}$	$(1\!-\!\gamma)(1\!-\!\omega)t^{-1-\gamma-\omega}$
$e^{\lambda t}$	$1$	$\displaystyle\frac{(a\lambda-1)e^{-a\lambda}}{a}$	$\displaystyle\frac{e^{-b\lambda}}{b}$	$\displaystyle\frac{\lambda e^{-t\lambda}}{t}$
$e^{\lambda t}$	$e^{-\gamma t}$	$\displaystyle\frac{a\lambda-1}{a}e^{a(\gamma-\lambda)}$	$\displaystyle\frac{b\gamma+1^{\rule{0.0pt}{8.53581pt}}}{b}e^{b(\gamma-\lambda)}$	$\displaystyle\frac{\lambda\gamma t-\gamma+\lambda}{t}e^{t(\gamma-\lambda)}$

Table 3: Optimal designs for the quadratic regression model:

f(t)=t^{2}+\nu

t\in[a,b]

$u(t)$	$v(t)$	$P_{a}f(a)$	$P_{b}f(b)$	$p(t)f(t)$
$t$	$1$	$\displaystyle(a^{2}-\nu)/a$	$\displaystyle-2b$	$\displaystyle 2$
$c_{1}+t$	$c_{2}\pm t$	$\displaystyle\frac{(a^{2}-\nu+2ac_{1})}{a+c_{1}}$	$\displaystyle\frac{\mp(b^{2}-\nu\pm 2bc_{2})}{b\pm c_{2}}$	$\displaystyle 2$
$t^{\gamma}$	$t^{\omega}$	${\small{((2\!-\!\gamma)a^{2}\!-\!\gamma\nu)a^{-\gamma-\omega}}}$	${\small{((\omega\!-\!2)b^{2}\!+\!\omega\nu)b^{-\gamma-\omega}}}$	${((2\!-\!\omega\!)(2\!-\!\gamma)\!+\!\nu\gamma\omega)t^{1-\gamma-\omega}}$
$e^{\lambda t}$	$1$	$\displaystyle{(2a-(a^{2}+\nu)\lambda)e^{-a\lambda}}$	$\displaystyle-2{be^{-b\lambda}}$	$\displaystyle{2(1-t\lambda)e^{-t\lambda}}$
$e^{\lambda t}$	$e^{-\lambda t}$	$\displaystyle{(2a-(a^{2}+\nu)\lambda)}$	$\displaystyle-{((b^{2}+\nu)\lambda+2b^{\rule{0.0pt}{8.53581pt}})}$	$\displaystyle\left(2-\lambda^{2}(t^{2}+\nu)\right)$

Table 4: Optimal designs for the trigonometric regression model:

f(t)=1+\frac{1}{2}\sin(2\pi t)

t\in[1,2]

$u(t)$	$v(t)$	$P_{a}$	$P_{b}$	$p(t)f(t)$
$t$	$1$	$\displaystyle(1-\pi)$	$\displaystyle\pi$	$\displaystyle 2\pi^{2}\sin(2\pi t)$
$c_{1}+t$	$c_{2}\pm t$	$\displaystyle\frac{1-\pi c_{1}-\pi}{c_{1}+1}$	$\displaystyle\mp\frac{1\mp\pi c_{2}-2\pi}{c_{2}\pm 2}$	$\displaystyle 2\pi^{2}\sin(2\pi t)$
$t^{2}$	$t$	$\displaystyle(2-\pi)$	$\displaystyle(2\pi-1)/{8}$	$\displaystyle 2t^{-4}{((\pi^{2}t^{2}\!-\!1)\sin(2\pi t)\!+\!\pi t\cos(2\pi t)\!-\!1)}{}$
$e^{\lambda t}$	$1$	$\displaystyle(\lambda-\pi)e^{-\lambda}$	$\displaystyle\pi e^{-2\lambda}$	$\displaystyle(2\pi^{2}\sin(2\pi t)+\pi\lambda\cos(2\pi t))e^{-\lambda t}$
$e^{\lambda t}$	$e^{-\lambda t}$	$\displaystyle(\lambda-\pi)$	$\displaystyle(\lambda+\pi)$	$\displaystyle((2\pi^{2}+\lambda^{2}/2)\sin(2\pi t)+\lambda^{2})$

2.5 Practical implementation: designs for finite sample size

In practice, efficient designs and corresponding estimators for the model (1.1) have to be derived from the optimal solutions in the continuous time model (1.2), and in this section a procedure with a good finite sample performance is proposed. Roughly speaking, it consists of a slight modification of the ordinary least squares estimator and a discretization of a continuous signed measure with the asymptotic optimal density in (2.11) .

We assume that the experimenter can take $N\!+\!2$ observations with $N$ observations inside the interval $[a,b]$ . In principle, any probability measure on the interval can be approximated by an $(N\!+\!2)$ -point measure with weights $1/(N\!+\!2)$ and similarly any finite signed measure can be approximated by an $(N\!+\!2)$ -point signed measure with equal weights (in absolute value). We hence could use a direct approximation of the optimal signed measures of the form (2.12) by a sequence of $(N\!+\!2)$ -point signed measures with equal weights (in absolute value). For an increasing sample size this sequence will eventually converge to the optimal measure of Theorem 2.3. However, this convergence will typically be very slow, where we measure the speed of convergence by the differences between the variances $D(\xi)$ of the corresponding estimates and the optimal value $D^{*}$ defined in (2.16). The main difficulty lies in the fact that a typical optimal measure has masses at the boundary points $a$ and $b$ , in addition to some density on the interval $(a,b)$ . The convergence of discrete measures with equal (in absolute value) weights to such a measure will be very slow, especially in view of the fact that in our approximating measures the points cannot be repeated. Summarizing, approximation of the optimal signed measures by measures with equal weights is possible but cannot be accurate for small $N$ .

In order to improve the rate of convergence we propose a slight modification of the ordinary least squares procedure. In particular, we propose a WLSE with weights at the points $a$ and $b$ (the end-points of the interval $[a,b]$ ), which correspond to the masses $P_{a}$ and $P_{b}$ of the asymptotic optimal design. We thus only need to approximate the continuous part of the optimal signed measure, which has a density on $(a,b)$ , by an $N$ -point design with equal masses. To be precise, consider an optimal measure of the form (2.12). We assume that the density $p(\cdot)$ is not identically zero on the interval $(a,b)$ and choose the constant $c$ such that $\int_{a}^{b}|p(t)|dt=1$ . Note that unless $p(\cdot)$ changes sign in $(a,b)$ , we can choose $p(t)\geq 0$ for all $t\in(a,b)$ . Define $\varphi(t)=|p(t)|$ for $t\in(a,b)$ and denote by $F(t)=\int_{a}^{t}\varphi(s)ds$ the corresponding distribution function. The $N$ -point design we use as an $N$ -point approximation to the measure with density $\varphi(t)$ is $\hat{\xi}_{N}=\{t_{1,N},\ldots,t_{N,N};1/N,\ldots,1/N\}$ , where $t_{i,N}=F^{-1}(z_{i,N})$ with $z_{i,N}=i/(N+1)$ , $i=1,2,\ldots,N$ . If $p(t)=0$ on a sub-interval of $[a,b]$ and $F^{-1}(z_{i,N})$ is not uniquely defined then we choose the smallest element from the set $F^{-1}(z_{i,N})$ as $t_{i,N}$ . Finally, the design we suggest as an ( $N\!+\!2$ )-point approximation to the optimal measure in (2.12) is

\xi^{*}_{N\!+\!2}=P_{a}\delta_{a}+P_{b}\delta_{b}+P\bar{\xi}_{N},

where $P=1-|P_{a}|-|P_{b}|$ , $\bar{\xi}_{N}=\{t_{1,N},\ldots,t_{N,N};s_{1,N}/N,\ldots,s_{N,N}/N\}$ and $s_{i,N}={\rm sign}(p(t_{i,N})),$ $i=1,\ldots,N$ .
The matrix $\mathbf{W}$ , which corresponds to the design $\xi_{N\!+\!2}$ and is used in the corresponding WLSE (1.3), is a diagonal matrix $\mathbf{W}_{N}={\rm diag}(NP_{a},s_{1,N}P,s_{2,N}P,\ldots,s_{N,N}P,NP_{b})$ of size $(N\!+\!2)\!\times\!(N\!+\!2)$ . The set of $N\!+\!2$ design points, where the observations should be taken, is given by $\{a,t_{1,N},t_{2,N},\ldots,t_{N,N},b\}$ and the resulting estimate is defined by

\displaystyle\widehat{\theta}_{WLSE,N}=(\mathbf{X}^{T}\mathbf{W}_{N}\mathbf{X})^{-1}\mathbf{X}^{T}\mathbf{W}_{N}\mathbf{Y}.

(2.17)

It follows from (1.4), (2.15) and the discussion of the previous paragraph that

\lim_{N\to\infty}\mathrm{Var}(\hat{\theta}_{\rm WLSE,N})=\lim_{N\to\infty}D(\xi^{*}_{N\!+\!2})=D^{*},

where $D^{*}$ is defined in (2.14).

2.6 Some numerical results

Consider the regression model (2.1) with $f(t)=t^{2}+1$ , $t\in[1,2]$ , where the error process is given by the Brownian motion. The optimal design for this model can be obtained from Table 3, and we have $P_{a}=0$ , $P_{b}=-0.55$ , $P=0.45$ and $p(t)=1.38/(t^{2}+1)$ . By computing the quantiles from the c.d.f. corresponding to $p$ we can easily obtain support points of $(N\!+\!2)$ -point designs. For example, $\mathrm{supp}\,(\xi^{*}_{4})=\{1,1.24,1.56,2\}$ , $\mathrm{supp}\,(\xi_{5}^{*})=\{1,1.18,1.39,1.65,2\}$ and $\mathrm{supp}\,(\xi_{6}^{*})=\{1,1.14,1.30,1.49,1.71,2\}$ .

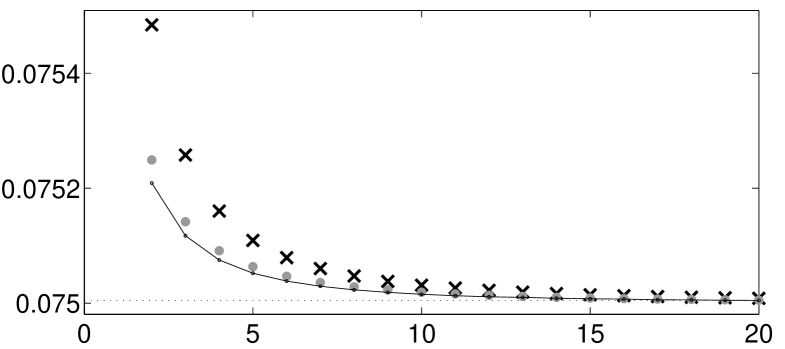
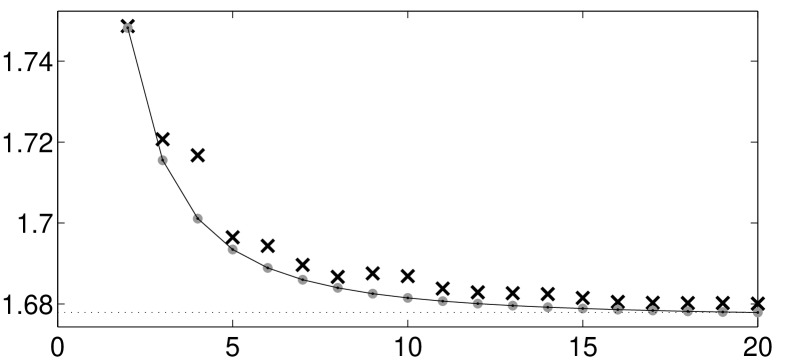
In Figure 1 we display the variance of various linear unbiased estimators for different sample sizes. We observe that the variance of the WLSE defined by (2.17) for the proposed $(N\!+\!2)$ -point design $\xi^{*}_{N+2}$ is slightly larger than the variance of the BLUE for the proposed $(N\!+\!2)$ -point design, which is very close to the variance of the BLUE with corresponding optimal $(N\!+\!2)$ -point design. The calculation of these designs is complicated and has been performed numerically by the Nelder-Mead algorithm in MATLAB. We also note that due to the non-convexity of the optimization problem it is not clear that the algorithm finds the optimal design. However, by Theorem 2.2 and 2.3 we determined the optimal value (2.14), which is $D^{*}\simeq 0.075004$ . This means that for the proposed designs WLSE has almost the same precision as BLUE.

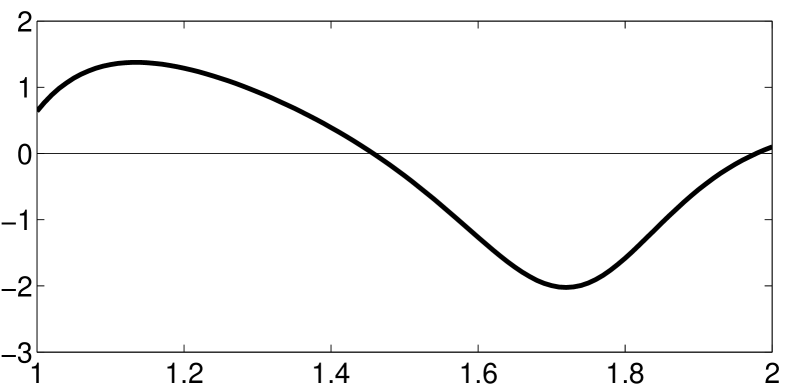
Refer to caption — Figure 1: The variance of the WLSE defined in (2.17) for the proposed $(N\!+\!2)$ -point designs $\xi^{*}_{N+2}$ (crosses), of the BLUE for the proposed $(N\!+\!2)$ -point designs (grey circles) and of the BLUE with corresponding optimal $(N\!+\!2)$ -point designs (line). The error process in model (2.1) is given by the Brownian motion and the regression function is $f(t)=t^{2}+1$ , $t\in[1,2]$ .

In our second example we compare the proposed optimal designs with the designs from Sacks and Ylvisaker, (1966), which are constructed for the BLUE. For this purpose we consider the model (2.1) with regression function $f(t)=1+0.5\sin(2\pi t)$ , $t\in[1,2]$ , and triangular covariance kernel of the form (2.4) with $u(t)=t^{2}$ and $v(t)=t$ . The optimal design in the continuous time model can be obtained from Table 4 and its density is depicted in Figure 2.

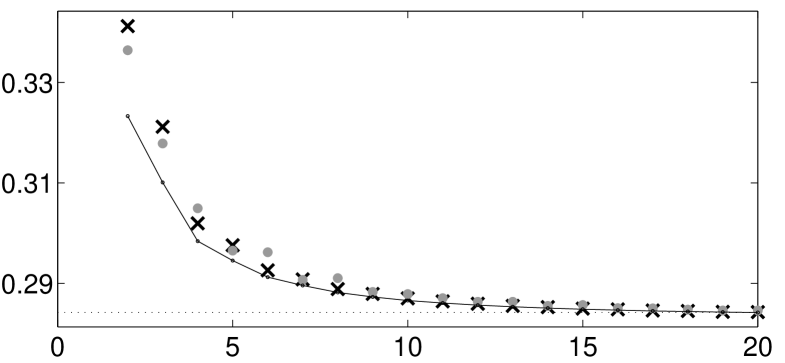
By computing quantiles using this optimal design, we obtain that the 4-point design $\xi^{*}_{4}$ is supported at points 1, 1.27, 1.68 and 2. For $\xi^{*}_{4}$ , the variance of the BLUE is $\simeq 0.6129$ . Using the optimal density from Sacks and Ylvisaker, (1966), we obtain the 4-point design $\xi^{SY}_{4}$ supported at 1, 1.25, 1.63 and 2. For $\xi^{SY}_{4}$ , the variance of the BLUE is $\simeq 0.6200$ . For $N=2,3,\ldots,20$ , the variances of the BLUE for the proposed $(N+2)$ -point designs, the $(N+2)$ -point designs from Sacks and Ylvisaker, (1966) and the optimal $(N+2)$ -point designs for the BLUE are depicted in Figure 3. We observe that for $N=2,3,4$ the new designs yield a smaller variance of the BLUE, while for $N=5$ the design of Sacks and Ylvisaker, (1966) shows a better performance. In all other cases the results for both designs are very similar. In particular, for $N\geq 6$ the variances from the optimal $(N\!+\!2)$ -point designs proposed in this paper and in the paper of Sacks and Ylvisaker, (1966) are only slightly worse than the variances of the BLUE with corresponding best $(N\!+\!2)$ -point designs (which is computed by direct optimization).

3 Multi-parameter models

In this section we discuss optimal design problems for models with more than one parameter. The structure of this section is somewhat similar to the structure of Section 2. In Section 3.1 we introduce a new class of linear estimators of the parameters in model (1.3), which we call matrix-weighted estimators (MWE) and show in Lemma 3.3 that for some special choices of the matrix weights the MWE can always emulate the BLUE. In Section 3.2 matrix-weighted designs associated with the MWE are defined. Then, for the case of triangular kernels, in Corollary 3.1 we derive the asymptotic forms for the sequence of designs that are associated with the version of the MWE which emulates the BLUE. In Section 3.3 we prove optimality of the asymptotic matrix-weighted measure derived in Corollary 3.1 in the continuous time model (1.2) (see Theorem 3.1), while some examples of asymptotically optimal measures are provided in Section 3.4. Finally, the practical implementation of the asymptotic measures is discussed in Section 3.5 and numerical examples are provided in Section 3.6.
The proofs of many statements in this section use the results of Section 2. This is possible as there is a lot of freedom in choosing the form of the MWE to emulate the BLUE and we choose a special form which could be considered as component-wise SLSE. Correspondingly, the resulting matrix-weighted designs (including the asymptotic ones) become combinations of designs for one-parameter models.

3.1 Matrix-weighted estimators and designs

Consider the regression model (1.1) and assume that $N$ observations at points $t_{j}$ ( $j=1,\ldots,N$ ) have been made. Let $\mathbf{O}_{j}$ be an $m\times m$ matrix associated with the observation point $t_{j}$ ; $j=1,\ldots,N.$ Recall the definition of the design matrix $\mathbf{X}=(f_{i}(t_{j}))^{i=1,\ldots,m}_{j=1,\ldots,N}$ and the definition of $\mathbf{Y}=(y(t_{1}),\ldots,y(t_{N}))^{T}.$ We introduce the $m\times N$ matrix $\mathbf{C}=(\mathbf{O}_{1}f(t_{1}),\ldots,\mathbf{O}_{N}f(t_{N}))\,,$ whose $j$ -th column is $\mathbf{O}_{j}f(t_{j})$ . Assuming that the $m\times m$ matrix

\displaystyle\mathbf{M}=\mathbf{C}\mathbf{X}=\sum_{j=1}^{N}\mathbf{O}_{j}f(t_{j})f^{T}(t_{j})

(3.1)

is non-singular we define the linear estimator

\displaystyle\widehat{\theta}_{MWE}=(\mathbf{C}\mathbf{X})^{-1}\mathbf{C}\mathbf{Y}

(3.2)

for the vector $\theta$ in model (1.1). We call this estimator the matrix-weighted estimator (MWE), because each column of the matrix $\mathbf{X}$ is multiplied by a matrix weight. It is easy to see that for any $\mathbf{C}$ the MWE $\widehat{\theta}_{MWE}$ is unbiased and its covariance matrix is given by

\displaystyle\mbox{Var}(\widehat{\theta}_{MWE})=\mathbf{M}^{-1}\mathbf{C}\mathbf{\Sigma}\mathbf{C}^{T}(\mathbf{M}^{-1})^{T},

(3.3)

where $\mathbf{\Sigma}=(K(t_{i},t_{j}))_{i,j=1,\ldots,N}$ is the $N\!\times\!N$ matrix of covariances of the errors. Note that the matrix $\mathbf{M}$ defined in (3.1) generalizes the standard information matrix $\mathbf{X^{T}X}$ and that $\mathbf{M}$ is not necessarily a symmetric matrix. The following result shows that different matrices $\mathbf{O}_{1},\ldots,\mathbf{O}_{N}$ may yield the same matrix-weighted estimator $\widehat{\theta}_{MWE}$ . Its proof is obvious and therefore omitted.

Lemma 3.1

Consider the regression model (1.1) and assume that the matrix $\mathbf{M}$ defined in (3.1) is non-singular. Then the estimator $\widehat{\theta}_{MWE}$ defined in (3.2) coincides with the estimator $\widehat{\theta}_{MWE,\Lambda}=(\mathbf{C}_{\Lambda}\mathbf{X})^{-1}\mathbf{C}_{\Lambda}\mathbf{Y}\,,$ where $\mathbf{C}_{\Lambda}=\Lambda\mathbf{C}$ and $\Lambda$ is an arbitrary non-singular $m\times m$ matrix.

The estimator $\widehat{\theta}_{MWE,\Lambda}$ introduced in Lemma 3.1 is the MWE defined by the matrix weights $\Lambda\mathbf{O}_{1},\ldots,\Lambda\mathbf{O}_{N}$ . Lemma 3.1 implies that the $\widehat{\theta}_{MWE}$ is exactly the same for any set of matrices $\{\Lambda\mathbf{O}_{1},\ldots,\Lambda\mathbf{O}_{N}\}$ as long as $\Lambda$ is non-singular. In the asymptotic considerations below it will be convenient to interpret the combination of the set of experimental conditions $\{t_{1},\ldots,t_{N}\}$ and the set of corresponding matrices $\{\mathbf{O}_{1},\ldots,\mathbf{O}_{N}\}$ in the MWE as an $N$ -point matrix-weighted design.

Definition 3.1

Any combination of $N$ points $\{t_{1},\ldots,t_{N}\}$ and $m\times m$ matrices $\{\mathbf{O}_{1},\ldots,\mathbf{O}_{N}\}$ will be called $N$ -point matrix-weighted design and denoted by

\displaystyle\xi_{N}=\big{\{}t_{1},\ldots,t_{N};\frac{1}{N}\mathbf{O}_{1},\ldots,\frac{1}{N}\mathbf{O}_{N}\big{\}}\,.

(3.4)

The covariance matrix $\mathbf{D}(\xi_{N})$ of a matrix-weighted design $\xi_{N}$ is defined as the covariance matrix ${\rm Var}(\widehat{\theta}_{MWE})$ in (3.3) of the corresponding estimate $\widehat{\theta}_{MWE}$ .

The estimator $\widehat{\theta}_{MWE}$ is not necessarily a least-squares type estimator; that is, it may not be representable in the form (1.3) for some $N\times N$ weight matrix $\mathbf{W}$ and hence there may be no associated weighted sum of squares which is minimized by the MWE. However, for any given $\mathbf{W}$ , we can always find matrices $\mathbf{O}_{j}$ such that

\displaystyle\mathbf{C}=\mathbf{X}^{T}\mathbf{W}

(3.5)

and therefore achieve $\widehat{\theta}_{MWE}=\widehat{\theta}_{WLSE}$ . The following result gives a constructive solution to the matrix equations (3.5).

Lemma 3.2

Assume that $f_{1}(t)\neq 0$ for all $t\in[a,b]$ . Define $\mathbf{O}_{j}=\omega_{j}e_{1}^{T}$ ,

\displaystyle\omega_{j}=\frac{1}{f_{1}(t_{j})}(\mathbf{X}^{T}\mathbf{W})_{j}\in\mathbb{R}^{m}\,,

(3.6)

where $e_{1}=(1,0,\ldots,0)^{T}\in\mathbb{R}^{m}$ is the first unit vector and $(\mathbf{X}^{T}\mathbf{W})_{j}$ denotes the $j$ -th column of the $m\times N$ matrix $\mathbf{X}^{T}\mathbf{W}$ . Then the corresponding matrix-weighted estimator satisfies $\widehat{\theta}_{MWE}=\widehat{\theta}_{WLSE}$ .

Proof. The matrix equation (3.5) can be written as $N$ vector equations

\displaystyle\mathbf{O}_{j}f(t_{j})=(\mathbf{X}^{T}\mathbf{W})_{j};\qquad j=1,\dots,N,

(3.7)

with respect to the matrices $\mathbf{O}_{j}$ . Assume that $\mathbf{O}_{j}=\omega_{j}e_{1}^{T}$ for some $\omega_{j}\in\mathbb{R}^{m}$ . Then

\displaystyle\mathbf{O}_{j}f(t_{j})=\omega_{j}e_{1}^{T}f(t_{j})=\omega_{j}f_{1}(t_{j})

and equation (3.7) has the unique solutions (3.6). $\Box$

The form $\mathbf{O}_{j}=\omega_{j}e_{1}^{T}$ for the matrices $\mathbf{O}_{j}$ considered in Lemma 3.2 means that the matrix $\mathbf{O}_{j}$ has the vector $\omega_{j}$ as its first column while all other entries in this matrix are zero. We shall refer to this form as the one-column form. We can choose other forms for the matrices $\mathbf{O}_{j}$ , but then we would require different, somewhat stronger, assumptions regarding the vector $f(t)$ . For example, if $f(t)\neq(0,\ldots,0)^{T}$ for all $t\in[a,b]$ , then we can always choose diagonal matrices $\mathbf{O}_{j}$ to satisfy (3.5) (see Lemma 3.5 below).

The following choices for $\mathbf{O}_{j}$ ensure coincidence of $\widehat{\theta}_{MWE}$ with the three popular estimators defined in the Introduction.

If $\mathbf{O}_{j}=\mathbf{I}_{m}$ for all $j$ , then $\widehat{\theta}_{MWE}=\widehat{\theta}_{OLSE}$ .

If $\mathbf{O}_{j}=s_{j}\mathbf{I}_{m}$ for all $j$ , then $\widehat{\theta}_{MWE}=\widehat{\theta}_{SLSE}$ .

If $\mathbf{W}=\mathbf{\Sigma}^{-1}$ and $\mathbf{O}_{j}=\omega_{j}e_{1}^{T}$ with $\omega_{j}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1})_{j}/{f_{1}(t_{j})}$ , then $\widehat{\theta}_{MWE}=\widehat{\theta}_{BLUE}$ .

We shall call any MWE $\widehat{\theta}_{MWE}$ optimal if it coincides with the BLUE. In view of the importance of the last case, the corresponding result is summarized in the following lemma.

Lemma 3.3

Consider the regression model (1.1) and let $f_{1}(t)\neq 0$ for all $t\in[a,b]$ . For a given set of $N$ observation points $\{t_{1},\ldots,t_{N}\}$ the MWE $\widehat{\theta}_{MWE}$ defines a BLUE if $\mathbf{O}_{j}=\omega_{j}^{*}e_{1}^{T}$ with $\omega_{j}^{*}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1})_{j}/{f_{1}(t_{j})}$ .

If the covariance kernel of the error process has triangular form (2.4) then we can derive the explicit form for the optimal MWE. The result follows by a direct application of Lemma A.1.

Lemma 3.4

Assume that the covariance kernel $K(\cdot,\cdot)$ has the form (2.4) and that the matrix $\mathbf{\Sigma}=(K(t_{i},t_{j}))_{i,j=1,\ldots,N}$ is positive definite with entries $K(t_{i},t_{j})=u_{i}v_{j}$ for $i\leq j$ , where for $k=1,\ldots,N$ we denote $u_{k}=u(t_{k})$ , $v_{k}=v(t_{k})$ and $q_{k}=u_{k}/v_{k}$ . Then we have the following representation for the optimal vectors $\omega_{j}^{*}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1})_{j}/{f_{1}(t_{j})}\in\mathbb{R}^{m}$ introduced in Lemma 3.3:

$\displaystyle\omega_{1}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}(t_{1})}\left(\tilde{\sigma}_{11}f(t_{1})+\tilde{\sigma}_{12}{f(t_{2})}\right)=\frac{c\,u_{2}}{f_{1}(t_{1})v_{1}v_{2}(q_{2}-q_{1})}\left(\frac{f(t_{1})}{u_{1}}-\frac{f(t_{2})}{u_{2}}\right)\,,$	(3.8)
$\displaystyle\omega_{N}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}(t_{N})}\left(\tilde{\sigma}_{N,N}{f(t_{N})}+\tilde{\sigma}_{N-1,N}{f(t_{N-1})}\right)$
	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}(t_{N})v_{N}(q_{N}-q_{N-1})}\left(\frac{f(t_{N})}{v_{N}}-\frac{f(t_{N-1})}{v_{N-1}}\right)\,,$
$\displaystyle\omega_{i}^{*}$	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}(t_{i})}\left(\tilde{\sigma}_{i,i}f(t_{i})+\tilde{\sigma}_{i-1,i}f(t_{i-1})+\tilde{\sigma}_{i,i+1}f(t_{i+1})\right)$
	$\displaystyle=$	$\displaystyle\frac{c}{f_{1}(t_{i})v_{i}}\left(\frac{(q_{i+1}-q_{i-1})f(t_{i})}{v_{i}(q_{i+1}-q_{i})(q_{i}-q_{i-1})}-\frac{f(t_{i-1})}{v_{i-1}(q_{i}-q_{i-1})}-\frac{f(t_{i+1})}{v_{i+1}(q_{i+1}-q_{i})}\right)\,,$

for $i=2,\ldots,N-1$ . Here in formulas (3.8), (3.4) and (3.4) $\tilde{\sigma}_{ij}$ denote the elements of the matrix $\mathbf{\Sigma}^{-1}=(\tilde{\sigma}_{ij})_{i,j=1,\ldots,N}$ .

The following provides a result similar to Lemmas 3.2 and 3.3 in the case where the matrices $\mathbf{O}_{j}$ are diagonal. An extension of Lemma 3.4 to the matrices $\mathbf{O}_{j}$ of the diagonal form is straightforward and omitted for the sake of brevity.

Lemma 3.5

Consider the regression model (1.1) and let $f_{k}(t)\neq 0$ for all $t\in[a,b]$ and all $k=1,\ldots,m$ . For each $j=1,\ldots,N$ , define the diagonal matrix $\mathbf{O}_{j}$ by its diagonal elements

\displaystyle(\mathbf{O}_{j})_{k,k}=\frac{1}{f_{k}(t_{j})}(\mathbf{X}^{T}\mathbf{W})_{k,j};\qquad k=1,\ldots,m\,,

where $(\mathbf{X}^{T}\mathbf{W})_{k,j}$ denotes the $(k,j)$ -th element of the matrix $\mathbf{X}^{T}\mathbf{W}$ . Then $\widehat{\theta}_{MWE}=\widehat{\theta}_{WLSE}$ .

If additionally $\mathbf{W}=\mathbf{\Sigma}^{-1}$ so that $(\mathbf{O}_{j})_{k,k}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1})_{k,j}/f_{k}(t_{j})$ , then $\widehat{\theta}_{MWE}=\widehat{\theta}_{BLUE}$ .

3.2 Weak convergence of matrix-weighted designs

Let $Q:[a,b]\to[0,1]$ be an increasing function on the interval $[a,b]$ with $Q(a)=0$ and $Q(b)=1$ so that $Q(\cdot)$ is a c.d.f. For a fixed $N$ and $j=1,\ldots,N$ , define the points $t_{1,N},\dots,t_{N,N}$ by (2.9). Suppose that with each $t\in[a,b]$ we can associate an $m\times m$ matrix $\mathbf{O}(t)$ and consider an $N$ -point matrix-weighted design $\xi_{N}$ of the form (3.4) with $t_{j}=t_{j,N}$ and $\mathbf{O}_{j}=\mathbf{O}(t_{j,N})$ . In view of (3.1) and (3.3) this design has the covariance matrix

\mathbf{D}(\xi_{N})=\mathbf{M}^{-1}(\xi_{N})\mathbf{B}(\xi_{N})\left(\mathbf{M}^{-1}(\xi_{N})\right)^{T}\,,

where the matrices $M(\xi_{N})$ and $B(\xi_{N})$ are defined by

	$\displaystyle\mathbf{M}(\xi_{N})$	$\displaystyle=$	$\displaystyle\frac{1}{N}\sum_{j=1}^{N}\mathbf{O}(t_{j,n})f(t_{j,n})f^{T}(t_{j,n}),$
	$\displaystyle\mathbf{B}(\xi_{N})$	$\displaystyle=$	$\displaystyle\frac{1}{N^{2}}\sum_{i=1}^{N}\sum_{j=1}^{N}K(t_{i,n},t_{j,n})\mathbf{O}(t_{i,n})f(t_{i,n})f^{T}(t_{j,n})\mathbf{O}^{T}(t_{j,n}).$

In addition to the sequence of matrix-weighted designs $\xi_{N}$ consider the sequence of uniform distributions on the set $\{t_{1,N},\ldots,t_{N,N}\}.$ As $N\to\infty$ , this sequence converges weakly to the design (probability measure) $\zeta$ on the interval $[a,b]$ with distribution function $Q$ . This implies

\lim_{N\to\infty}\mathbf{M}(\xi_{N})=\mathbf{M}(\xi)=\int_{a}^{b}\mathbf{O}(t)f(t)f^{T}(t)\zeta(dt)

\lim_{N\to\infty}\mathbf{B}(\xi_{N})=\mathbf{B}(\xi)=\int_{a}^{b}\int_{a}^{b}K(t,s)\mathbf{O}(t)f(s)f^{T}(t)\mathbf{O}^{T}(s)\zeta(dt)\zeta(ds)\,,

and

\displaystyle\lim_{N\to\infty}\mathbf{D}(\xi_{N})=\mathbf{D}(\xi)=\mathbf{M}^{-1}(\xi)\mathbf{B}(\xi)\left(\mathbf{M}^{-1}(\xi)\right)^{T}

(3.11)

under the assumptions that the vector-valued function $f$ , the matrix-valued function $\mathbf{O}$ , the kernel $K$ are continuous on the interval $[a,b]$ and the generalized information matrix $\mathbf{M}(\xi)$ are non-singular. Moreover, the sequence of estimators (3.2) converges (almost surely as $N\to\infty$ ) to

\displaystyle\widehat{\theta}_{MWE,\infty}=\mathbf{M}^{-1}(\xi)\int_{a}^{b}\mathbf{O}(t)f(t)y(t)\zeta(dt)\,,

(3.12)

where $\{y(t)\,|\,t\in[a,b]\}$ is the stochastic process in the continuous time model (1.2). Bearing these limiting expressions in mind we say that the sequence of matrix-weighted designs $\xi_{N}$ defined by (3.4) converges to the limiting matrix-weighted design $\xi(dt)=\mathbf{O}(t)\zeta(dt)$ as $N\to\infty$ . This relation justifies the notation $\mathbf{M}(\xi),\mathbf{B}(\xi)$ and $\mathbf{D}(\xi)$ of the previous paragraph.

The (optimal) limiting matrix-weighted designs which will be constructed below will have a similar structure as the signed measures in (2.12). They will assign matrix weights $\mathbf{O}_{a}$ and $\mathbf{O}_{b}$ to the end-points of the interval $[a,b]$ and a ‘matrix density’ $\mathbf{O}(t)$ to the points $t\in(a,b)$ ; that is, these designs will have the form

\xi(dt)=\mathbf{O}_{a}\delta_{a}(dt)+\mathbf{O}_{b}\delta_{b}(dt)+\mathbf{O}(t)dt\,.

(3.13)

In view of (3.12), the MWE in the continuous time model (1.2) associated with any design of the form (3.13) can be written as

\displaystyle\widehat{\theta}_{MWE}(\xi)=\mathbf{M}^{-1}(\xi)\Big{[}\mathbf{O}_{a}f(a)y(a)+\mathbf{O}_{b}f(b)y(b)+\int_{a}^{b}\mathbf{O}(t)f(t)y(t)dt\Big{]}\,,

(3.14)

where $\mathbf{M}(\xi)=\mathbf{O}_{a}f(a)f^{T}(a)+\mathbf{O}_{b}f(b)f^{T}(b)+\int_{a}^{b}\mathbf{O}(t)f(t)f^{T}(t)dt$ . In the particular case associated with Lemma 3.4, we have the following structure of the matrices $\mathbf{O}_{a}$ and $\mathbf{O}_{b}$ and the matrix function $\mathbf{O}(t)$ in (3.13):

\mathbf{O}_{a}=\omega_{a}e_{1}^{T},\;\mathbf{O}_{b}=\omega_{b}e_{1}^{T},\;\,\mathbf{O}(t)=\omega(t)e_{1}^{T}\,\;{\rm for\;}t\in(a,b),

(3.15)

where $\omega_{a}$ and $\omega_{b}$ are some $m$ -dimensional vectors and $\omega(t)\in\mathbb{R}^{m}$ is some vector-valued function defined on the interval $(a,b)$ . Note that $\omega(t)$ does not have to approach $\omega_{a}$ and $\omega_{b}$ as $t\to a$ and $t\to b$ , respectively.

When the sequence of matrix-weighted designs is defined by the formulas of Lemma 3.3 we can compute the limiting matrix-weighted design. The proof follows by similar arguments as given in the proof of Theorem 2.1 and is therefore omitted.

Corollary 3.1

Consider model (1.1), where the error process $\{\varepsilon(t)|\,t\in[a,b]\}$ has a covariance kernel $K$ of the form (2.4). Assume that $u(\cdot)$ , $v(\cdot)$ , $q(\cdot)$ are strictly positive, twice continuously differentiable functions on the interval $[a,b]$ and that the vector-valued function $f(\cdot)$ is twice continuously differentiable with $f_{1}(t)\neq 0$ for all $t\in[a,b]$ . Consider the matrix-weighted design $\xi_{N}$ of the form (3.4), where the support points $t_{j}=t_{j,N}$ are generated by (2.9) and the matrix weights $\mathbf{O}_{j}=\mathbf{O}_{j,N}$ are defined in Lemma 3.3. The sequence $\{\xi_{N}\}_{N\in\mathbb{N}}$ converges (in the sense defined above in the previous paragraph) to a matrix-weighted design $\xi$ defined by (3.13) and (3.15) with

\displaystyle\omega_{a}\!=\!\frac{c}{f_{1}(a)v^{2}(a)q^{\prime}(a)}\left[\frac{f(a)u^{\prime}(a)}{u(a)}-f^{\prime}(a)\right],\;\omega_{b}\!=\!\frac{c\;h^{\prime}(b)}{f_{1}(b)v(b)q^{\prime}(b)},\;\omega(t)\!=\!\frac{-c}{f_{1}(t)v(t)}\left[\frac{h^{\prime}(t)}{q^{\prime}(t)}\right]^{\prime}\;\;\;\;

(3.16)

where $h(t)=f(t)/v(t)$ and the constant $c\neq 0$ is arbitrary.

In Corollary 3.1, the one-column representation of the matrices $\mathbf{O}_{j}$ is used. The following statement contains a similar result for the case where the matrices $\mathbf{O}_{j}$ are diagonal.

Corollary 3.2

Let the conditions of Corollary 3.1 hold and assume additionally that $f_{k}(t)\neq 0$ for all $t\in[a,b]$ and all $k=1,\ldots,m$ . Consider the matrix-weighted design $\xi_{N}$ of the form (3.4), where the support points $t_{j}=t_{j,N}$ are generated by (2.9) and the matrices $\mathbf{O}_{j}=\mathbf{O}_{j,N}$ are defined in Lemma 3.5 with diagonal elements given by $(\mathbf{O}_{j})_{k,k}=(\mathbf{X}^{T}\mathbf{\Sigma}^{-1})_{k,j}/f_{k}(t_{j})$ . Then the sequence $\{\xi_{N}\}_{N\in\mathbb{N}}$ converges to the optimal matrix-weighted design $\xi^{*}$ of the form (3.13), where the diagonal elements of the matrices $\mathbf{O}_{a}=\mathrm{diag}(\mathbf{O}_{a,11},\ldots,\mathbf{O}_{a,mm})$ , $\mathbf{O}_{b}=\mathrm{diag}(\mathbf{O}_{b,11},\ldots,\mathbf{O}_{b,mm})$ and $\mathbf{O}(t)=\mathrm{diag}(\mathbf{O}_{11}(t),\ldots,\mathbf{O}_{mm}(t))$ are given by

\mathbf{O}_{a,jj}\!=\!\frac{c}{f_{j}(a)v^{2}(a)q^{\prime}(a)}\!\left[\frac{f_{j}(a)u^{\prime}(a)}{u(a)}\!-\!f^{\prime}_{j}(a)\right],\;\mathbf{O}_{b,jj}\!=\!\frac{c\;h^{\prime}_{j}(b)}{f_{j}(b)v(b)q^{\prime}(b)},\;\mathbf{O}_{jj}(t)\!=\!\frac{-c}{f_{j}(t)v(t)}\!\left[\frac{h^{\prime}_{j}(t)}{q^{\prime}(t)}\right]^{\prime}\;\;\;\;\;\;

respectively, $h_{j}(t)=f_{j}(t)/v(t)$ , $j=1,\ldots,m$ and the constant $c\neq 0$ is arbitrary.

3.3 Optimal designs and best linear estimators

In this section we consider again the continuous time model (1.2), where the full trajectory of the process $\{y(t)|~t\in[a,b]\}$ can be observed. We start recalling some known facts concerning best linear unbiased estimation. For details we refer the interested reader to the work of Grenander, (1950) or Section 2.2 in Näther, 1985a . Any linear estimator of $\theta$ can be written in the form of the integral

\displaystyle\widehat{\theta}_{\mu}=\int_{a}^{b}y(t)\mu(dt),

(3.17)

where $\mu(t)=(\mu_{1}(t),\ldots,\mu_{m}(t))^{T}$ is a vector of signed measures on the interval $[a,b]$ . For given $\mu$ , the estimator $\widehat{\theta}_{\mu}$ is unbiased if and only if $\int_{a}^{b}f(t)\mu^{T}(dt)=\mathbf{I}_{m}$ , where $\mathbf{I}_{m}$ denotes the $m$ -dimensional identity matrix. Theorem 2.3 in Näther, 1985a states that the estimator $\widehat{\theta}_{\mu^{*}}$ is BLUE if and only if $\int_{a}^{b}f(t){\mu^{*}}^{T}(dt)=\mathbf{I}_{m}$ and the identity

\int_{a}^{b}K(u,v)\mu^{*}(dv)=\mathbf{A}f(u)

holds for all $u\in[a,b]$ , where $\mathbf{A}$ is some $m\times m$ matrix. The matrix $\mathbf{A}$ is uniquely defined and coincides with the matrix

\mathbf{D}^{*}=\mbox{Var}(\widehat{\theta}_{\mu^{*}})=\inf\Big{\{}\int_{a}^{b}\int_{a}^{b}K(u,v)\mu(du){\mu}^{T}(dv)~\Big{|}~\mu\mbox{ vector of signed measures}\Big{\}}~.

(3.18)

The Gauss-Markov theorem further implies that $\mathbf{D}^{*}\leq\mbox{Var}(\widehat{\theta})$ , where $\widehat{\theta}$ is any other linear unbiased estimator of $\theta.$

Definition 3.2

A matrix-weighted design $\xi^{*}$ is called optimal if $\mathbf{D}(\xi^{*})=\mathbf{D}^{*}$ , where $\mathbf{D}(\xi)$ is defined in (3.11) and $\mathbf{D}^{*}$ is defined in (3.18).

The designs we consider have the form (3.13) and the corresponding MWE are expressed by (3.14). The estimator (3.14) can be expressed in the form (3.17), that is $\widehat{\theta}_{MWE}(\xi)=\hat{\theta}_{\mu}$ with

\mu(dt)=\mathbf{M}^{-1}(\xi)\bigl{[}\mathbf{O}_{a}f(a)\delta_{a}(dt)+\mathbf{O}_{b}f(b)\delta_{b}(dt)+\mathbf{O}(t)f(t)dt\bigr{]}\,.

The estimators defined in (3.14) are always unbiased and the following result provides the matrix-weighted optimal design and the BLUE in the continuous time model (1.2). The proof follows by similar arguments as given in the proof of Theorem 2.2 and 2.3 and is therefore omitted.

Theorem 3.1

Let $K(t,s)$ be a covariance kernel of the form (2.4) and the vector-function $f(\cdot)$ be twice continuously differentiable with $f_{1}(t)\neq 0$ for all $t\in[a,b]$ . Under the assumptions of Corollary 3.1 the matrix-weighted design $\xi^{*}$ defined by the formulas (3.13) and (3.16) with $c=1$ is optimal in the sense of Definition 3.2. Moreover, if

\mu^{*}(dt)=\mathbf{M}^{-1}(\xi^{*})\bigl{[}\omega_{a}e_{1}^{T}f(a)\delta_{a}(dt)+\omega_{b}e_{1}^{T}f(b)\delta_{b}(dt)+\omega(t)e_{1}^{T}f(t)dt\bigr{]}\,,

then $\hat{\theta}_{\mu^{*}}$ defines the BLUE in model (1.2). Additionally, we have

\displaystyle\mathbf{D}(\xi^{*})=\mathbf{D}^{*}=\int_{a}^{b}\int_{a}^{b}K(s,t)\mu^{*}(ds)\mu^{*}(dt)=\mathbf{M}^{-1}(\xi^{*}),

where the matrix $\mathbf{M}(\xi^{*})$ is given by

\displaystyle\mathbf{M}(\xi^{*})=\frac{\tilde{f}(q(a))\tilde{f}^{T}(q(a))}{q(a)}+\int_{q(a)}^{q(b)}\tilde{f}^{\prime}(s)\tilde{f}^{\prime T}(s)ds

and $\tilde{f}(s)=f(q^{-1}(s))/v(q^{-1}(s))$ .

In Theorem 3.1 we have used the one-column representation for the matrices $\mathbf{O}(t)$ . Similar arguments establish the optimality of the matrix-weighted designs $\xi^{*}$ defined in Corollary 3.2 where the diagonal representation for the matrices $\mathbf{O}(t)$ is used. The details are omitted for the sake of brevity.

3.4 Examples of optimal matrix-weighted designs

Consider the polynomial regression model with $f(t)=(1,t,t^{2},\ldots,t^{m-1})^{T}$ , $t\in[a,b]$ and the covariance kernel of the Brownian motion $K(t,s)=\min(t,s)$ . For the construction of matrix-weighted designs we use matrices $\mathbf{O}(t)$ in the one-column and diagonal representations.

For the one-column representation we have from Corollary 3.1 and Theorem 3.1 that the optimal matrix weighted design has masses $\mathbf{O}_{a}=\omega_{a}e_{1}^{T}$ and $\mathbf{O}_{b}=\omega(b)e_{1}^{T}$ at points $a$ and $b$ , respectively, and the density $\mathbf{O}(t)=\omega(t)e_{1}^{T}$ . Here the vectors $\omega_{a},\omega_{b}$ and $\omega(t)$ are given by

$\displaystyle\omega_{a}$	$\displaystyle=$	$\displaystyle(1/a,0,-a,\ldots,(2-m)a^{m-2})^{T},$
$\displaystyle\omega_{b}$	$\displaystyle=$	$\displaystyle(0,1,2b,3b^{2},\ldots,(m-1)b^{m-2})^{T},$
$\displaystyle\omega(t)$	$\displaystyle=$	$\displaystyle(0,0,-2,-3\cdot 2t,\ldots,-(m-1)(m-2)t^{m-3})^{T},~t\in(a,b),$

respectively. For the diagonal representation we have from Corollary 3.2 (and an analogue of Theorem 3.1) that the optimal matrix weighted design has masses $\mathbf{O}_{a}$ and $\mathbf{O}_{b}$ at points $a$ and $b$ , respectively, and the density $\mathbf{O}(t)$ , where

$\displaystyle\mathbf{O}_{a}$	$\displaystyle=$	$\displaystyle\mathrm{diag}(1/a,0,-1/a,\ldots,(2-m)/a),$
$\displaystyle\mathbf{O}_{b}$	$\displaystyle=$	$\displaystyle\mathrm{diag}(0,1/b,2/b,\ldots,(m-1)/b),$
$\displaystyle\mathbf{O}(t)$	$\displaystyle=$	$\displaystyle\mathrm{diag}(0,0,-2/t^{2},\ldots,-(m-1)(m-2)/t^{2}),~t\in(a,b).$

Note that in this case all non-vanishing diagonal elements of the matrix $\mathbf{O}(t)$ are proportional to the function $1/t^{2}$ . According to Lemma 3.1, we can use $\Lambda\mathbf{O}(t)$ instead of $\mathbf{O}(t)$ , for any non-singular $m\times m$ matrix $\Lambda$ . By taking the matrix

\Lambda=\mathrm{diag}(1,1,-1/2,\ldots,-1/[(m-1)(m-2)]),

we obtain

$\displaystyle\Lambda\mathbf{O}(a)\;$	$\displaystyle=$	$\displaystyle\mathrm{diag}(1/a,0,1/(2a),\ldots,1/[(m-1)a]),$
$\displaystyle\Lambda\mathbf{O}(b)\;$	$\displaystyle=$	$\displaystyle\mathrm{diag}(0,1/b,-1/b,\ldots,-1/[(m-2)b]),$
$\displaystyle\Lambda\mathbf{O}(t)$	$\displaystyle=$	$\displaystyle\mathrm{diag}(0,0,1/t^{2},\ldots,1/t^{2}),~t\in(a,b).$

As another example, consider the polynomial regression model with $f(t)=(1,t,t^{2},\ldots,t^{m-1})^{T}$ , $t\in[a,b]$ , and the triangular covariance kernel of the function (2.4) with $u(t)=t^{\gamma}$ and $v(t)=t^{\omega}$ .

For the diagonal representation we have from Corollary 3.2 that the optimal matrix weighted design has masses $\mathbf{O}_{a}$ and $\mathbf{O}_{b}$ at points $a$ and $b$ , respectively, and the density $\mathbf{O}(t)$ , where

$\displaystyle\mathbf{O}_{a}$	$\displaystyle=$	$\displaystyle a^{-\gamma-\omega}\mathrm{diag}(-\gamma,1-\gamma,2-\gamma,\ldots,m-1-\gamma),$
$\displaystyle\mathbf{O}_{b}$	$\displaystyle=$	$\displaystyle b^{-\gamma-\omega}\mathrm{diag}(\omega,\omega-1,\omega-2b,\ldots,\omega+1-m),$
$\displaystyle\mathbf{O}(t)$	$\displaystyle=$	$\displaystyle t^{-1-\gamma-\omega}\mathrm{diag}(\tau_{1},\tau_{2},\ldots,\tau_{m}),~t\in(a,b),$

with $\tau_{i}=(i-1-\gamma)(i-1-\omega)$ , $i=1,\ldots,m$ . If we further use $\Lambda=\mathrm{diag}(1/\tau_{1},1/\tau_{2},\ldots,1/\tau_{m})$ then we obtain $\Lambda\mathbf{O}(t)=t^{-1-\gamma-\omega}\mathrm{diag}(1,1,\ldots,1),~t\in(a,b)$ ; that is, all components of the matrix $\Lambda\mathbf{O}(t)$ have exactly the same density.

3.5 Practical implementation

Here we only consider the diagonal representation of the matrices $\mathbf{O}_{a}$ , $\mathbf{O}_{b}$ and $\mathbf{O}(t)$ ; the case of one-column representation of the matrices $\mathbf{O}$ can be treated similarly. We assign matrix weights $\mathbf{O}_{a}$ and $\mathbf{O}_{b}$ to the boundary points $a$ and $b$ and use an $N$ -point approximation to an absolutely continuous probability measure on $(a,b)$ with some density $\varphi(t)$ . The density $\varphi(t)$ is defined to be either the uniform density on $(a,b)$ (if nonzero elements of different components of $\mathbf{O}(t)$ are not proportional to each other) or $\varphi(t)=c|\mathbf{O}_{l,l}(t)|$ for some $l\in\{1,\dots,m\}$ (if nonzero elements of different components of $\mathbf{O}(t)$ are proportional to each other), where $c$ is the normalization constant and $l$ is such that the density $\varphi(t)$ is not identically zero on the interval $(a,b)$ . Denote by $F(t)=\int_{a}^{t}\varphi(s)ds$ the corresponding c.d.f. For given $N$ , we calculate an $N$ -point approximation $\{t_{1,N},\ldots,t_{N,N};1/N,\ldots,1/N\}$ , where $t_{i,N}=F^{-1}(z_{i,N})$ with $z_{i,N}=i/(N+1)$ , $i=1,2,\ldots,N$ , to the probability measure with density $\varphi(t)$ .

To each point $t_{j,N}$ we assign a vector of weights $s_{j}=(s_{j,N,1},\ldots,s_{j,N,m})^{T}$ such that $s_{j,N,k}\in\{-1,0,1\}$ ( $k=1,\ldots,m$ ). The values $s_{j,N,k}=\mathrm{sign}(\mathbf{O}_{k,k}(t_{j}))=\pm 1$ correspond to the sign of the point $t_{j,N}$ in the estimation of $\theta_{k}$ exactly as in the procedure for one-parameter models described in Section 2.5. Some of the values $s_{j,N,k}$ could be 0. If $s_{j,N,k}=0$ for some $k$ then the point $t_{j,N}$ is not used for the estimation of $\theta_{k}$ . By assigning zero weight to a point $t_{j,N}$ in the $k$ -th estimation direction, we perform a thinning of the sample of points $t_{1,N},\ldots,t_{N,N}$ in $k$ -th direction and thus achieve a required density in the each estimation direction. This is a deterministic version of the well-known ‘rejection method’ widely used to generate samples from various probability distributions. If the nonzero components of the matrix weight $\mathbf{O}(t)$ are proportional to each other then for these components $s_{j,N,k}=1$ for all $j$ and $N$ .

The resulting estimator $\hat{\theta}$ has the form (3.2) where

	$\displaystyle\mathbf{C}$	$\displaystyle=$	$\displaystyle\Big{(}N\mathbf{O}_{a}f(a),\mathbf{S}_{1}\mathbf{P}f(t_{1})\ldots,\mathbf{S}_{N}\mathbf{P}f(t_{N}),N\mathbf{O}_{b}f(b)\Big{)},$
	$\displaystyle\mathbf{S}_{j}$	$\displaystyle=$	$\displaystyle\mathrm{diag}(s_{j,N,1},\ldots,s_{j,N,m})\in\mathbb{R}^{m\times m}$

and $\mathbf{P}$ is the diagonal $m\times m$ matrix whose diagonal elements are given by

\mathbf{P}_{k,k}=\frac{N}{\sum_{j=1}^{N}|s_{j,N,k}|}\int_{a}^{b}\mathbf{O}_{k,k}(t)dt.

If nonzero elements of different components of the matrix weight $\mathbf{O}(t)$ are proportional to each other (as was the case in the examples of Section 3.4) then the $(N\!+\!2)$ -point approximations to the limiting design are very similar to the approximations in the one-parameter case considered in Section 2.5; their accuracy is also very high. Otherwise, when the diagonal elements of $\mathbf{O}(t)$ are possibly non-proportional, the accuracy of approximations will depend on the degree of non-homogeneity of components of the matrix weight $\mathbf{O}(t)$ .

3.6 Some numerical results

For comparison of competing matrix weighted designs for multiparameter models it is convenient to consider a functional of the covariance matrix. Exemplarily we investigate in this Section the classical $D$ -optimality criterion defined as $\Psi(\mathbf{D}(\xi))=(\det\mathbf{D}(\xi))^{1/m}$ which has to be minimized.
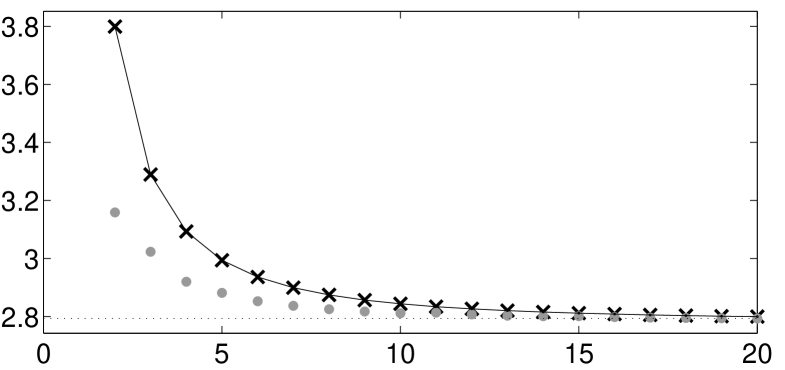
As an example where all nonzero elements of the matrix $\mathbf{O}(t)$ are proportional to each other, let us consider the cubic regression model with $f(t)=(1,t,t^{2},t^{3})^{T}$ and the Brownian motion error process. The optimal value in the continuous time model (1.2) is $\Psi(\mathbf{D}^{*})\simeq 2.7927$ . In Figure 4 we display the $D$ -criterion of the covariance matrices of the MWE and the BLUE for the proposed $(N\!+\!2)$ -point designs and the covariance matrix of the BLUE with corresponding optimal $(N\!+\!2)$ -point designs. We can see that the $D$ -efficiency of the proposed matrix-weighted design is very high, even for small $N$ .

The second example of this section considers a situation where nonzero elements of the matrix $\mathbf{O}(t)$ are not proportional to each other. For this purpose we consider the model (2.1) with $f(t)=(1,t,t^{2})^{T}$ , $t\in[1,2]$ and covariance kernel $K(t,t^{\prime})=e^{-|t-t^{\prime}|}$ with $u(t)=e^{t}$ and $v(t)=e^{-t}$ . Using the diagonal representation, we obtain for the optimal matrix-weighted designs

\displaystyle\mathbf{O}_{a}=\mathrm{diag}(1,0,-1),\;\;\mathbf{O}_{b}=\mathrm{diag}(1,1.5,2),\;\;\mathbf{O}(t)=\mathrm{diag}(1,1,1-2/t^{2}),~t\in(1,2).

The optimal value in the continuous time model (1.2) is given by $\Psi(\mathbf{D}^{*})\simeq 1.6779$ . Since some diagonal elements of $\mathbf{O}(t)$ are constant functions, we take the support points of the design $\xi_{N+2}$ to be equidistant: $t_{i,N}=i/(N+1)$ for $i=1,\ldots,N$ . Then we have $s_{j,N,k}=1$ for all $j=1,\ldots,N$ and $k=1,2$ . However, some elements of $(s_{1,N,3},\ldots,s_{N,N,3})$ should be zero because $\mathbf{O}_{3,3}(t)$ is not proportional to $\mathbf{O}_{1,1}(t)$ . For example, for $N=10$ the vector of signs $(s_{1,N,3},\ldots,s_{N,N,3})$ is $(-1,-1,0,0,0,1,0,0,1,0)$ and for $N=30$ it is
$(-1,0,-1,-1,0,-1,0,0,-1,0,0,0,0,0,0,0,0,1,0,0,0,1,0,0,1,0,0,1,0,1)\,.$

In Figure 5 we depict the $D$ -optimality criterion of the covariance matrices for various estimators. We observe that in this example for all $N$ the $D$ -optimality criterion of the covariance matrices of the MWE is slightly larger than the $D$ -optimality criterion of the covariance matrices of the BLUE. However, we can also see that the proposed $(N\!+\!2)$ -point designs are very efficient compared to the BLUE with corresponding $D$ -optimal $(N\!+\!2)$ -point designs even for small $N$ .

Acknowledgements. This work has been supported in part by the Collaborative Research Center “Statistical modeling of nonlinear dynamic processes” (SFB 823, Teilprojekt C2) of the German Research Foundation (DFG). The research of H. Dette reported in this publication was also partially supported by the National Institute of General Medical Sciences of the National Institutes of Health under Award Number R01GM107639. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. We would also like to thank Martina Stein who typed parts of this paper with considerable technical expertise. The work of Andrey Pepelyshev was partly supported by Russian Foundation of Basic Research, project 12-01-00747.

Appendix A Proof of main results

A.1 Explicit form of the inverse of the covariance matrix of errors

Here we state an auxiliary result, which gives an explicit form for the inverse of the matrix $\mathbf{\Sigma}=(K(t_{i},t_{j}))^{N}_{i,j=1}$ , with a triangular covariance kernel $K$ . We did not find this result (as formulated below) in the literature. Versions of Lemma A.1, however, have been derived independently by different authors; see, for example, Lemma 7.3.2 in Zhigljavsky, (1991) and formula (8) in Harman and Štulajter, (2011). The proof follows from straightforward checking the condition $\mathbf{\Sigma}^{-1}\mathbf{\Sigma}=\mathbf{\Sigma}\mathbf{\Sigma}^{-1}=\mathbf{I}$ .

Lemma A.1

Consider a symmetric $N\times N$ matrix $\mathbf{\Sigma}=(\sigma_{i,j})_{i,j=1,\dots,N}$ which elements are defined by the formula ${\sigma}_{i,j}=u_{i}v_{j}$ for $1\leq i\leq j\leq N$ . Assume that $q_{1}<q_{2}<\ldots<q_{N}$ where $q_{i}=u_{i}/v_{i}$ . Then the inverse matrix $\widetilde{\mathbf{\Sigma}}=\mathbf{\Sigma}^{-1}$ is a symmetric tri-diagonal matrix and its elements $\widetilde{{\sigma}}_{i,j}$ with $i\leq j$ can be computed as follows:

\displaystyle\widetilde{{\sigma}}_{1,1}={\frac{u_{2}}{u_{1}v_{1}v_{2}\left(q_{2}-q_{1}\right)}}\,,\;\;\;\widetilde{{\sigma}}_{N,N}=\frac{1}{v_{N}^{2}\left(q_{N}-q_{{N-1}}\right)}\,,

\displaystyle\widetilde{{\sigma}}_{i,i}=\frac{q_{{i+1}}-q_{{i-1}}}{v_{i}^{2}(q_{{i}}-q_{i-1})(q_{{i+1}}-q_{i})}\,\;(i=2,\ldots,N-1)\,,

\displaystyle\widetilde{{\sigma}}_{i,i+1}=-\frac{1}{v_{i}v_{i+1}(q_{i+1}-q_{i})}\,\;(i=1,\ldots,N-1)\,,

\displaystyle\widetilde{{\sigma}}_{i,i+k}=0\,\;(i=1,\ldots,N-2,\;\;k\geq 2)\,.

In our applications of Lemma A.1 we assume that $\sigma_{i,j}=K(t_{i},t_{j})$ with the covariance kernel $K$ having the form (2.4).

A.2 Proof of Lemma 2.1

Denote $K_{ij}=K(t_{i},t_{j})$ , $f(t_{i})=f_{i}$ , $a_{i}=f_{i}w_{i}$ , $i,j=1,\ldots,N$ , $\mathbf{a}=(a_{1},\ldots,a_{N})^{T}$ . Then for any signed measure $\xi=\{t_{1},\ldots,t_{N};w_{1},\ldots,w_{N}\}$ we have

\displaystyle D(\xi)=\frac{\sum_{i}\sum_{j}K_{ij}f_{i}f_{j}w_{i}w_{j}}{(\sum_{i}f_{i}^{2}w_{i})^{2}}=\frac{\sum_{i}\sum_{j}K_{ij}a_{i}a_{j}}{(\sum_{i}f_{i}a_{i})^{2}}=\frac{\mathbf{a}^{T}\mathbf{\Sigma}\mathbf{a}}{(\mathbf{a}^{T}\mathbf{f})^{2}}.

Since $\mathbf{\Sigma}$ is symmetric and $\mathbf{\Sigma>0}$ , there exists $\mathbf{\Sigma}^{-1}$ and a symmetric matrix $\mathbf{\Sigma}^{1/2}>0$ such that $\mathbf{\Sigma}=\mathbf{\Sigma}^{1/2}\mathbf{\Sigma}^{1/2}$ . Denote $\mathbf{b}=\mathbf{\Sigma}^{1/2}\mathbf{a}$ and $\mathbf{d}=\mathbf{\Sigma}^{-1/2}\mathbf{f}$ . Then we can write the design optimality criterion $D(\xi)$ as $D(\xi)=\mathbf{b}^{T}\mathbf{b}/(\mathbf{b}^{T}\mathbf{d})^{2}$ . The Cauchy-Schwartz inequality gives for any two vectors $\mathbf{b}$ and $\mathbf{d}$ the inequality $(\mathbf{b}^{T}\mathbf{d})^{2}\leq(\mathbf{b}^{T}\mathbf{b})(\mathbf{d}^{T}\mathbf{d})$ , that is, $\mathbf{b}^{T}\mathbf{b}/(\mathbf{b}^{T}\mathbf{d})^{2}\geq 1/(\mathbf{d}^{T}\mathbf{d})$ . This inequality with $\mathbf{b}$ and $\mathbf{d}$ as above is equivalent to $D(\xi)\geq{1}/{\mathbf{f}^{T}\,\mathbf{\Sigma}^{-1}\mathbf{f}}$ for all $\xi$ . Equality is attained if the vector $\mathbf{b}$ is proportional to the vector $\mathbf{d}$ ; that is, if $b_{i}=cd_{i}$ for all $i$ and any $c\neq 0$ . Finally, the equality $b_{i}=cd_{i}$ can be rewritten in the form $w_{i}=c{(\mathbf{\Sigma}^{-1}\mathbf{f})_{i}}/{f(t_{i})}$ .

A.3 Proof of Theorem 2.1

Before starting the main proof we recall the definition of the design points (2.9) and prove the following auxiliary result.

Lemma A.2

Assume that $q(\cdot)=u(\cdot)/v(\cdot)$ is a twice continuously differentiable function on the interval $[a,b]$ . Then for all $i=1,\ldots,N-1$ , we have

	$\displaystyle t_{i+1,N}-t_{i,N}$	$\displaystyle=$	$\displaystyle\frac{1}{NQ^{\prime}(t_{i,N})}+O\Bigl{(}\frac{1}{N^{2}}\Bigr{)}\;\;{\rm as}\;N\to\infty.$		(A.1)
	$\displaystyle\Delta_{n}=(t_{i+1,N}-t_{i-1,N})/2$	$\displaystyle=$	$\displaystyle\frac{1}{NQ^{\prime}(t_{i,N})}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,\;{\rm as}\;N\to\infty.$		(A.2)

Proof of Lemma A.2. Recall the definition $z_{i,N}=(i-1/2)/N$ ( $i=1,\ldots,N$ ) and set

m=q(a)=\min_{t\in[a,b]}q(t)~,~~M=q(b)=\max_{t\in[a,b]}q(t).

From the definition of the function $Q$ in (2.8) we have

\displaystyle q(t_{i+1,N})-q(t_{i,N})=(M-m)(z_{i+1,N}-z_{i,N})=\frac{M-m}{N}\,

(A.3)

for all $i=1,\ldots,N-1$ . Observing Taylor’s formula yields for any $z$

Q^{-1}(z+\delta)=Q^{-1}(z)+\delta\cdot{(Q^{-1})}^{\prime}(z)+O(\delta^{2})\;\;{\rm as}\;\delta\to 0.

In this formula, set $z=z_{i,N}$ and $\delta_{N}=1/N$ so that $z+\delta=z_{i+1,N}$ . We thus obtain

t_{i+1,N}-t_{i,N}=Q^{-1}(z_{i+1,N})=Q^{-1}(z_{i,N})+\frac{1}{N}\cdot{(Q^{-1})}^{\prime}(z_{i,N})+O\Bigl{(}\frac{1}{N^{2}}\Bigr{)}\;\;{\rm as}\;N\to\infty.

By using (2.9) and the relation ${\left(Q^{-1}\right)}^{\prime}(z)=1/Q^{\prime}(Q^{-1}(z))$ we can rewrite this in the form (A.1). The second statement obviously follows from (A.1).

Proof of Theorem 2.1. In view of Lemma 2.1 and (2.5) - (2.1) we have

\displaystyle w_{1,N}=\frac{c_{N}u_{2}}{f_{1}v_{1}v_{2}}\Bigl{(}\frac{f_{{1}}}{u_{1}}-\frac{f_{2}}{u_{2}}\Bigr{)}\,\,,\;\;\;w_{N,N}=\frac{c_{N}}{f_{N}v_{N}}\Bigl{(}\frac{f_{N}}{v_{N}}-\frac{f_{N-1}}{v_{N-1}}\Bigr{)}\,,

\displaystyle w_{i,N}=\frac{c_{N}}{f_{i}v_{i}}\Bigl{(}\frac{2f_{i}}{v_{i}}-\frac{f_{i-1}}{v_{i-1}}-\frac{f_{i+1}}{v_{i+1}}\Bigr{)}\,\;\;\mbox{ for $i=2,\ldots,N-1$},

where we have used the relations (A.3). Here $c_{N}$ is the normalization constant providing $\sum_{i=1}^{N}|w_{i,N}|=1$ and we use the notation $u_{i}=u(t_{i,N})$ , $v_{i}=(t_{i,N})$ and $f_{i}=f(t_{i,N})$ .

Consider first $w_{1,N}$ . Denote $g(t)=f(t)/u(t)$ , then

\displaystyle w_{1,N}/c_{N}=\frac{u(t_{2,N})}{f(t_{1,N})v(t_{1,N})v(t_{2,N})}\left(g(t_{1,N})-g(t_{2,N})\right)\,,

(A.4)

which gives

\displaystyle\frac{u(t_{2,N})}{f(t_{1,N})v(t_{1,N})v(t_{2,N})}=\frac{u(a)}{f(a)v^{2}(a)}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,,

(A.5)

\displaystyle g(t_{1,N})-g(a)=g^{\prime}(a)\left(t_{1,N}-a\right)+O\left(\left(t_{1,N}-a\right)^{2}\right)=g^{\prime}(a)\cdot\frac{1}{2NQ^{\prime}(a)}+O\Bigl{(}\frac{1}{N^{2}}\Bigr{)}

as $N\to\infty$ . Similarly

\displaystyle g(t_{2,N})-g(a)=g^{\prime}(a)\frac{3}{2NQ^{\prime}(a)}+O\Bigl{(}\frac{1}{N^{2}}\Bigr{)}

yielding

\displaystyle g(t_{1,N})-g(t_{2,N})=-g^{\prime}(a)\frac{1}{NQ^{\prime}(a)}+O\Bigl{(}\frac{1}{N^{2}}\Bigr{)}\,.

(A.6)

Combining (A.4), (A.5) and (A.6) we obtain

	$\displaystyle\frac{w_{1,N}}{c_{N}}$	$\displaystyle=$	$\displaystyle-\frac{1}{N}\cdot\frac{u(a)g^{\prime}(a)}{f(a)v^{2}(a)Q^{\prime}(a)}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}$		(A.7)
		$\displaystyle=$	$\displaystyle\frac{1}{N}\cdot\frac{1}{v^{2}(a)Q^{\prime}(a)}\Bigl{[}\frac{u^{\prime}(a)}{u(a)}-\frac{f^{\prime}(a)}{f(a)}\Bigr{]}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}$		(A.7)

as $N\to\infty$ . Similarly to (A.7) we get the asymptotic expression for $w_{N,N}$ :

\displaystyle\frac{w_{N,N}}{c_{N}}=\frac{1}{N}\cdot\frac{h^{\prime}(b)}{f(b)v(b)Q^{\prime}(b)}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}

(A.8)

as $N\to\infty$ . Consider now the weights

\displaystyle w_{i,N}=c_{N}\frac{2h(t_{i,N})-h(t_{i-1,N})-h(t_{i+1,N})}{f(t_{i,N})v(t_{i,N})}\,\;\;\mbox{ ($i=2,\ldots,N-1$)}.

(A.9)

Assume $N\to\infty$ and $i=i(N)$ is such that $i(N)/N=z+O(1/N)$ as $N\to\infty$ for some $z\in(0,1)$ , and set $t=Q^{-1}(z)$ .

We are going to prove that

$\displaystyle\frac{w_{i,N}}{c_{N}}$	$\displaystyle=$	$\displaystyle\frac{2h(t_{i,N})-h(t_{i-1,N})-h(t_{i+1,N})}{f(t_{i,N})v(t_{i,N})}\,$
	$\displaystyle=$	$\displaystyle\frac{1}{N^{2}(Q^{\prime}(t))^{2}f(t)v(t)}\Bigl{[}\frac{h^{\prime}(t)Q^{\prime\prime}(t)}{Q^{\prime}(t)}-h^{\prime\prime}(t)\Bigr{]}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,$
	$\displaystyle=$	$\displaystyle-\frac{1}{N^{2}Q^{\prime}(t)f(t)v(t)}\Bigl{[}\frac{h^{\prime}(t)}{Q^{\prime}(t)}\Bigr{]}^{\prime}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,.$	(A.11)

First, in view of (2.9) we have $t_{i,n}=t+O\left(\frac{1}{N}\right)$ and hence

f(t_{i,N})v(t_{i,N})=f(t)v(t)\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\;\;{\rm as}\;N\to\infty\,.

Consider the numerator in (A.3) and rewrite it as follows:

\displaystyle 2h(t_{i,N})-h(t_{i-1,N})-h(t_{i+1,N})=\left[2h(\tilde{t}_{i,N})-h(t_{i-1,N})-h(t_{i+1,N})\right]+2\left[h({t}_{i,N})-h(\tilde{t}_{i,N})\right]

where $\tilde{t}_{i,N}=(t_{i-1,N}+t_{i+1,N})/2\,.$ We obviously have $t_{i+1,N}=\tilde{t}_{i,N}+\Delta_{N}$ and $t_{i-1,N}=\tilde{t}_{i,N}-\Delta_{N},$ where $\Delta_{N}=(t_{i+1,N}-t_{i-1,N})/2$ is defined in (A.2). This yields

\displaystyle\frac{2h(\tilde{t}_{i,N})-h(t_{i-1,N})-h(t_{i+1,N})}{\Delta_{N}^{2}}=-h^{\prime\prime}(t)\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,.

(A.12)

Next we consider

\displaystyle\frac{h({t}_{i,N})-h(\tilde{t}_{i,N})}{\Delta_{N}^{2}}=\frac{h({t}_{i,N})-h(\tilde{t}_{i,N})}{{t}_{i,N}-\tilde{t}_{i,N}}\cdot\frac{{t}_{i,N}-\tilde{t}_{i,N}}{\Delta_{N}^{2}}.

For the first factor we have

\displaystyle\frac{h({t}_{i,N})-h(\tilde{t}_{i,N})}{{t}_{i,N}-\tilde{t}_{i,N}}=h^{\prime}(t)\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}\,,

while the second factor gives

$\displaystyle\frac{{t}_{i,N}-\tilde{t}_{i,N}}{\Delta_{N}^{2}}$	$\displaystyle=$	$\displaystyle 2\frac{2t_{i,N}-t_{i+1,N}-t_{i-1,N}}{(t_{i+1,N}-t_{i-1,N})^{2}}$
	$\displaystyle=$	$\displaystyle 2\frac{2Q^{-1}(z_{i,N})-Q^{-1}(z_{i+1,N})-Q^{-1}(z_{i-1,N})}{1/N^{2}}\Big{(}\frac{1/N}{Q^{-1}(z_{i+1,N})-Q^{-1}(z_{i-1,N})}\Big{)}^{2}$
	$\displaystyle=$	$\displaystyle-2{(Q^{-1})}^{\prime\prime}(z)/(2{(Q^{-1})}^{\prime}(z))^{2}\Big{(}1+O\Big{(}\frac{1}{N}\Big{)}\Big{)}=Q^{\prime\prime}(t)/(2Q^{\prime}(t))\Big{(}1+O\Big{(}\frac{1}{N}\Big{)}\Big{)}\,,$

where we have used the relation ${\left(Q^{-1}\right)}^{\prime\prime}(z)=-Q^{\prime\prime}(z)/(Q^{\prime}(z))^{3}$ in the last equation. This gives, as $N\to\infty$ ,

\displaystyle 2\frac{h({t}_{i,N})-h(\tilde{t}_{i,N})}{\Delta_{N}^{2}}=2\frac{h({t}_{i,N})-h(\tilde{t}_{i,N})}{{t}_{i,N}-\tilde{t}_{i,N}}\cdot\frac{{t}_{i,N}-\tilde{t}_{i,N}}{\Delta_{N}^{2}}=\frac{h^{\prime}(t)Q^{\prime\prime}(t)}{Q^{\prime}(t)}\Bigl{(}1+O\Bigl{(}\frac{1}{N}\Bigr{)}\Bigr{)}.\;\;\;

(A.13)

Combining the expressions (A.2), (A.3), (A.12) and (A.13) yields the asymptotic expression (A.11) for ${w_{i,N}}/{c_{N}}$ .

By noting that $c_{N}=NC\left(1+O\left(\frac{1}{N}\right)\right)$ as $N\to\infty$ and that the asymptotic density of the points $t_{i,N}$ ( $i=1,\ldots,N$ ) is $Q^{\prime}(t)$ on the interval $[a,b]$ , we deduce the statement of the theorem as a consequence of the asymptotic formulas (A.7), (A.8) and (A.11) for ${w_{1,N}}/{c_{N}}$ , ${w_{N,N}}/{c_{N}}$ and ${w_{i,N}}/{c_{N}}$ respectively.

A.4 Proof of Theorem 2.2

By Theorem 3.3 in Dette et al., (2013) a design minimizes the functional (2.15) if the identity

\displaystyle\int_{a}^{b}\min(s,t)f(t)d\xi(t)=\lambda f(s)

(A.14)

holds $\xi\!-\!a.e.$ , where $\lambda$ is some constant. We consider the design $\xi=\xi^{*}$ defined by (2.12) and (2.13) and verify for this design the condition (A.14). To do this we calculate by partial integration

$\displaystyle\frac{1}{c}\int_{a}^{b}\min(s,t)f(t)p(t)dt$	$\displaystyle=$	$\displaystyle\int^{s}_{a}t(-f^{\prime\prime}(t))dt+\int^{b}_{s}s(-f^{\prime\prime}(t))dt$
	$\displaystyle=$	$\displaystyle-\Bigl{\{}tf^{\prime}(t)\Big{\|}^{s}_{a}-\int^{s}_{a}f^{\prime}(t)dt\Bigr{\}}-s\Bigl{\{}f^{\prime}(b)-f^{\prime}(s)\Bigr{\}}$
	$\displaystyle=$	$\displaystyle(af^{\prime}(a)-f(a))-sf^{\prime}(b)+f(s).$

Observing the definition of the masses in (2.13), the identify (A.14) follows with $\lambda=c$ . This proves the first part of Theorem 2.2.

For a proof of the second statement consider a linear unbiased estimator $\hat{\theta}_{\mu^{*}}$ in model (2.1) based on the full trajectory, where $\mu^{*}(dt)=f(t)\xi^{*}(dt)$ and $\xi^{*}$ is the design in (2.12), (2.13) with a constant $c$ chosen such that $\hat{\theta}_{\mu^{*}}$ is unbiased, that is

c^{*}=\Big{[}\frac{f^{2}(a)}{a}+\int^{b}_{a}(f^{\prime}(t))^{2}dt\Big{]}^{-1}.

Standard arguments of optimal design theory show that $\mu^{*}$ minimizes $\Phi$ (that is, $\hat{\theta}_{\mu^{*}}$ is BLUE in model (2.1) where the full trajectory can be observed) if and only if the inequality

\displaystyle\Phi(\mu^{*},\nu)=\int^{b}_{a}\int^{b}_{a}K(x,y)\mu^{*}(dx)\nu(dy)\geq\Phi(\mu^{*})

(A.15)

holds for all signed measures $\nu$ satisfying $\int^{b}_{a}f(t)\nu(dt)=1$ . Observing this condition and the identity (A.14) we obtain

\Phi(\mu^{*},\nu)=c^{*}\int^{b}_{a}f(s)\nu(ds)=\Bigl{[}\frac{f^{2}(a)}{a}+\int^{b}_{a}(f^{\prime}(t))^{2}dt\Bigr{]}^{-1}=\Phi(\mu^{*})

for all signed measures $\nu$ on $[a,b]$ with $\int^{b}_{a}f(t)\nu(dt)=1$ . By (A.15) $\mu^{*}$ minimizes $\Phi$ . Consequently, the corresponding estimator $\hat{\theta}_{\mu^{*}}$ is BLUE with minimal variance

D^{*}=c^{*}=\Bigl{[}\frac{f^{2}(a)}{a}+\int^{b}_{a}(f^{\prime}(t))^{2}dt\Bigr{]}^{-1}.

A.5 Proof of Theorem 2.3

Let $\{\tilde{\varepsilon}(s)|s\in[\tilde{a},\tilde{b}]$ be a Brownian motion on the interval $[\tilde{a},\tilde{b}]$ and consider the regression model (2.1) with some function $\tilde{f}(s)$ and the error process. By Theorem 2.2 the optimal design is given by

\tilde{\xi}^{*}(ds)=\tilde{P}_{\tilde{a}}\delta_{\tilde{a}}(ds)+\tilde{P}_{\tilde{b}}\delta_{\tilde{b}}(ds)+\tilde{p}(s)ds

with

\tilde{P}_{\tilde{a}}=c\ \frac{\tilde{f}(a)-\tilde{f}^{\prime}(\tilde{a})\tilde{a}}{\tilde{a}\tilde{f}(\tilde{a})}\,,\;\;\tilde{P}_{\tilde{b}}=c\ \frac{\tilde{f}^{\prime}(\tilde{b})}{\tilde{f}(\tilde{b})}\qquad{\rm{and}}\qquad\tilde{p}(s)=-c\frac{\tilde{f}^{\prime\prime}(s)}{\tilde{f}(s)}\,.

We shall now use Theorem B.1 to derive the optimal design $\xi^{*}(dt)$ for the original regression model (2.1) with regression function $f(t)$ and covariance kernel $K(t,t^{\prime})$ from the design $\tilde{\xi}^{*}(ds)$ for the function $\tilde{f}(s)=h(q^{-1}(s))$ , where $h(t)=f(t)/v(t)$ .

For the Brownian motion, the covariance function is defined by (B.4) with $\tilde{v}(t)=1$ and $\tilde{q}(t)=t$ so that by (B.6) we have $\beta(t)=q(t)$ , $\alpha(t)=v(t)$ and $\tilde{\alpha}(t)=1/v(q^{-1}(t)).$ According to (B.14) the optimal design $d\tilde{\xi}^{*}(s)$ transforms to $d\xi^{*}(t)=\tilde{\alpha}^{2}(\beta(t))d\tilde{\xi}^{*}(\beta(t))=d\tilde{\xi}^{*}(q(t))/\nu(t)$ .

Consider first the mass at $b$ . We have $\tilde{P}_{\tilde{b}}=c{\tilde{f}^{\prime}(\tilde{b})}/{\tilde{f}(\tilde{b})}$ . By using the transformation of $t$ into $s=q^{-1}(t)$ , we obtain

P_{b}=\frac{\tilde{P}_{b}}{v^{2}(b)}=c\frac{\tilde{f}^{\prime}(\tilde{b})}{\tilde{f}(\tilde{b})v^{2}(b)}=c\frac{h^{\prime}(b)}{q^{\prime}(b)v^{2}(b)h(b)}=c\frac{h^{\prime}(b)}{q^{\prime}(b)v(b)f(b)}\,,

as required. From the representation of $\tilde{P}_{\tilde{a}}$ we obtain by similar arguments

P_{a}=\frac{\tilde{P}_{a}}{v^{2}(a)}=c\ \frac{h(a)-ah^{\prime}(a)/q^{\prime}(a)}{q^{\prime}(a)v^{2}(a)h(a)}.

Let us now consider the density $\tilde{p}(s),$ $s\in[\tilde{a},\tilde{b}]$ , and rewrite $d\tilde{\xi}^{*}_{p}(\beta(t))$ , the absolutely continuous part of the measure $\tilde{\xi}^{*}$ . The transformation of the variable $s$ into $t=q^{-1}(s)\in[a,b]$ induces the density

\displaystyle d\tilde{\xi}^{*}_{p}(\beta(t))=\tilde{p}(q(t))q^{\prime}(t)=-cq^{\prime}(t)\frac{\tilde{f}^{\prime\prime}(q(t))}{\tilde{f}(q(t))}\,.

(A.16)

Differentiating the equality $\tilde{f}(s)=h(q^{-1}(s))$ , we have

\displaystyle\tilde{f}^{\prime\prime}(s)=\left(h^{\prime}(q^{-1}(s))\cdot(q^{-1}(s))^{\prime}\right)^{\prime}=h^{\prime\prime}(q^{-1}(s))\cdot\left((q^{-1}(s))^{\prime}\right)^{2}+h^{\prime}(q^{-1}(s))\cdot\left(q^{-1}(s)\right)^{\prime\prime}.

Now we obtain

\displaystyle\tilde{f}^{\prime\prime}(q(t))=\frac{h^{\prime\prime}(t)}{(q^{\prime}(t))^{2}}-h^{\prime}(t)\cdot\frac{q^{\prime\prime}(t)}{(q^{\prime}(t))^{3}}

Inserting this into (A.16) and taking into account that $\tilde{f}(q(t))=h(t)$ , we obtain the density

\displaystyle d\tilde{\xi}^{*}_{p}(\beta(t))=c\,\frac{1}{h(t)q^{\prime}(t)}\Bigl{(}h^{\prime}(t)\cdot\frac{q^{\prime\prime}(t)}{q^{\prime}(t)}-h^{\prime\prime}(t)\Bigr{)}=-\frac{c}{h(t)}\left[\frac{h^{\prime}(t)}{q^{\prime}(t)}\right]^{\prime}\,.

(A.17)

In view of the relation $d\xi^{*}(t)=\tilde{\alpha}^{2}(\beta(t))d\tilde{\xi}^{*}(\beta(t))$ we need to divide the right hand side in (A.17) by $v^{2}(t)$ and obtain the expression for the density (2.11). This completes the proof of Theorem 2.3.

Appendix B Gaussian processes with triangular covariance kernels

B.1 Extended Doob’s representation

Assume that $\{\varepsilon(t)|\;t\in[a,b]\}$ is a Gaussian process with covariance kernel $K$ of the form (2.4); that is, $K(t,t^{\prime})=u(t)v(t^{\prime})$ for $t\leq t^{\prime}$ , where $u(\cdot)$ and $v(\cdot)$ are functions defined on the interval $[a,b]$ . According to the terminology introduced in Mehr and McFadden, (1965) kernels of the form (2.4) are called triangular. An alternative way of writing these covariance kernels is

\displaystyle K(t,t^{\prime})=v(t)v(t^{\prime})\min\{q(t),q(t^{\prime})\}\;\;{\rm for}\;\;t,t^{\prime}\in[a,b]\,,

(B.1)

where $q(t)=u(t)/v(t)$ . We assume that $\varepsilon(t)$ is non-degenerate on the open interval $(a,b)$ , which implies that the function $q$ is strictly increasing and continuous on the interval $[a,b]$ [see Mehr and McFadden, (1965), Remark 2]. Moreover, this function is also positive on the interval $(a,b)$ [see Remark 1 in Mehr and McFadden, (1965)], which yields that the functions $u$ and $v$ must have the same sign and can be assumed to be positive on the interval $(a,b)$ without loss of generality. We repeatedly use the following extension of the celebrated Doob’s representation [see Doob, (1949)], which relates to two Gaussian processes (on compact intervals) by a time-space transformation.

Lemma B.1

Let $\{\varepsilon(t)|\;t\in[a,b]\}$ be a non-degenerate Gaussian process with zero mean and covariance function (B.1) and let $\tilde{v}$ and $\tilde{q}$ be continuous positive functions on $[\tilde{a},\tilde{b}]$ , such that $\tilde{q}$ is strictly increasing and $\tilde{q}([\tilde{a},\tilde{b}])=q([a,b])$ . Define the transformations $\tilde{\beta}:[\tilde{a},\tilde{b}]\to[a,b]$ and $\tilde{\alpha}:[\tilde{a},\tilde{b}]\to\mathbb{R}_{+}$ by

\displaystyle\tilde{\beta}(s)=q^{-1}(\tilde{q}(s))\,,\;\;\;\tilde{\alpha}(s)=\tilde{v}(s)/v(\tilde{\beta}(s))\,.

(B.2)

Then the Gaussian process $\{\tilde{\varepsilon}(t)|\;t\in[\tilde{a},\tilde{b}]\}$ defined by

\displaystyle\tilde{\varepsilon}(s)=\tilde{\alpha}(s)\varepsilon(\tilde{\beta}(s))\,

(B.3)

has zero mean and the covariance function is given by

\displaystyle\tilde{K}(s,s^{\prime})=\mathbb{E}[\tilde{\varepsilon}(s)\tilde{\varepsilon}(s^{\prime})]=\tilde{v}(s)\tilde{v}(s^{\prime})\min(\tilde{q}(s),\tilde{q}(s^{\prime}))\,.

(B.4)

Conversely, the Gaussian process $\varepsilon(t)$ can be expressed via $\tilde{\varepsilon}(s)$ by the transformation

\displaystyle\varepsilon(t)=\alpha(t)\tilde{\varepsilon}(\beta(t))\,,

(B.5)

where

\displaystyle\beta(t)=\tilde{q}^{-1}(q(t))\,,\;\;\alpha(t)=v(t)/\tilde{v}(\beta(t))\,.

(B.6)

Proof. Since $\{\varepsilon(t)|t\in[a,b]\}$ is Gaussian and has zero mean, the process defined by (B.3) is also Gaussian and has zero mean. For the covariance function of the process (B.3) we have

$\displaystyle\mathbb{E}\left[\tilde{\varepsilon}(s)\tilde{\varepsilon}(s^{\prime})\right]$	$\displaystyle=$	$\displaystyle\tilde{\alpha}(s)\tilde{\alpha}(s^{\prime})\mathbb{E}\left[\varepsilon(\tilde{\beta}(s))\varepsilon(\tilde{\beta}(s^{\prime}))\right]$
	$\displaystyle=$	$\displaystyle\tilde{\alpha}(s)\tilde{\alpha}(s^{\prime})v(\tilde{\beta}(s))v(\tilde{\beta}(s^{\prime}))\min\left[q(\tilde{\beta}(s)),\,q(\tilde{\beta}(s^{\prime}))\right]$
	$\displaystyle=$	$\displaystyle{\tilde{v}(s)}{\tilde{v}(s^{\prime})}\min\left[\tilde{q}(s),\,\tilde{q}(s^{\prime})\right]=\tilde{K}(s,s^{\prime})\,.$

The second part of the proof follows by the same arguments and the details are therefore omitted. $\Box$

Remark B.1

(a) The classical result of Doob is a particular case of (B.5) when $\tilde{\varepsilon}(t)=W(t)$ is the Brownian motion with covariance function $\tilde{K}(t,s)=\min(t,s)$ . In this case we have $\tilde{v}(t)=1$ , $\tilde{q}(t)=t$ , $\alpha(t)=v(t)$ and $\beta(t)=q(t)$ . Specifically, the Doob’s representation is given by $\varepsilon(t)=v(t)W(q(t))$ [see Doob, (1949)].

(b) Both functions $\beta:\;[a,b]\to[\tilde{a},\tilde{b}]$ and $\tilde{\beta}:[\tilde{a},\tilde{b}]\to[a,b]$ are positive strictly increasing functions and are inverses of each other; that is,

\displaystyle\beta(t)=\tilde{\beta}^{-1}(t)\,,\;\;\forall~t\in[a,b]\,.

(B.7)

\displaystyle\alpha(t)\cdot\tilde{\alpha}(\beta(t))=\frac{v(t)}{\tilde{v}(\beta(t))}\cdot\frac{\tilde{v}(\beta(t))}{v(\tilde{\beta}(\beta(t)))}=1\,,\;\;\forall~t\in[a,b].

(B.8)

(d) The properties (b) and (c) imply that the transformation $\tilde{\varepsilon}\to\varepsilon$ defined by (B.5) is the inverse of the transformation $\varepsilon\to\tilde{\varepsilon}$ defined in (B.3).

B.2 Transformation of regression models

Associated with the transformation of the triangular covariance kernels there exists a canonical transformation for the corresponding regression models. To be precise, consider the regression model (1.1) or its continuous time version (1.2), where the covariance kernel $K(\cdot,\cdot)$ has the form (B.1). Recall the definition of the transformation $\beta:\;[a,b]\to[\tilde{a},\tilde{b}]$ defined in (B.6), which maps the observation points $t_{j}$ to $\tilde{t}_{j}=\beta(t_{j})$ , $j=1,\ldots,N$ and define

\displaystyle\tilde{f}(s)=\frac{f(\tilde{\beta}(s))}{\alpha(\tilde{\beta}(s))},~\tilde{\varepsilon}(s)=\frac{\varepsilon(\tilde{\beta}(s))}{\alpha(\tilde{\beta}(s))},~\tilde{y}(\tilde{t}_{j})=\frac{y(t_{j})}{\alpha(t_{j})}\,,

(B.9)

where $s\in[\tilde{a},\tilde{b}]$ so that $\tilde{\beta}(s)\in[a,b]$ . The regression model (1.1) can now be rewritten in the form

\displaystyle\tilde{y}(\tilde{t}_{j})=\theta^{T}\tilde{f}(\tilde{t}_{j})+\tilde{\varepsilon}(\tilde{t}_{j}),~\tilde{t}_{j}\in[\tilde{a},\tilde{b}],~j=1,\ldots,N.

(B.10)

The errors $\tilde{\varepsilon}(\tilde{t}_{j})$ in (B.10) have zero mean and, by Lemma B.1 and the identity (B.8), their covariances are given by

\displaystyle~\mathbb{E}[\tilde{\varepsilon}(\tilde{t}_{i})\tilde{\varepsilon}(\tilde{t}_{j})]=\tilde{K}(\tilde{t}_{i},\tilde{t}_{j}).

(B.11)

Hence we have transformed the regression observation scheme (1.1) with error covariances $\mathbb{E}[\varepsilon(t_{i})\varepsilon(t_{j})]=K(t_{i},t_{j})$ to the scheme (B.10) with covariances (B.11). Conversely, we can transform the model (B.10) with covariances (B.11) to the model (1.1) using the transformations

\displaystyle f(t)=\frac{\tilde{f}(\beta(t))}{\tilde{\alpha}(\beta(t))}\,,\;\;\varepsilon(t)=\frac{\tilde{\varepsilon}(\beta(t))}{\tilde{\alpha}(\beta(t))}\,,\;t\in[a,b]\,.

(B.12)

Lemma B.2

The transformation $f\to\tilde{f}$ defined in (B.9) is an inverse to the transformation $\tilde{f}\to f$ defined in (B.12).

Proof. Inserting the expression for $\tilde{f}$ from (B.9) into (B.12), we have

\displaystyle f(t)=\frac{\tilde{f}(\beta(t))}{\tilde{\alpha}(\beta(t))}=\frac{f(\tilde{\beta}(\beta(t)))}{\alpha(\tilde{\beta}(\beta(t)))\,\tilde{\alpha}(\beta(t))}=\frac{f(t)}{\alpha(t)\,\tilde{\alpha}(\beta(t))}=f(t),

where we have used the identities $\tilde{\beta}(\beta(t))=t$ , see (B.7), and $\alpha(t)\,\tilde{\alpha}(\beta(t))=1$ , see (B.8).

B.3 Transformation of designs

In this section we consider a transformation of the matrix-weighted designs under a given transformation of the regression models. In the one-parameter case with $m=1$ , these matrix-weighted designs become signed measures; that is, signed designs as considered in Section 2. In this section, it is convenient to define all integrals as Lebesgue-Stieltjes integrals with respect to the distribution functions of the measures $\zeta$ and $\tilde{\zeta}$ .

To be precise, let $d\xi(t)=\mathbf{O}_{\xi}(t)d\zeta(t)$ be a matrix-weighted design on the interval $t\in[a,b]$ . Recalling the definition of $\alpha,\tilde{\alpha}$ and $\beta,\tilde{\beta}$ in (B.2) and (B.6) we define a matrix-weighted design $d\tilde{\xi}(s)=\tilde{\mathbf{O}}_{\tilde{\xi}}(s)d\tilde{\zeta}(s)$ by

\displaystyle d\tilde{\zeta}(s)=d\zeta(\tilde{\beta}(s))\,\;\;{\rm and}\;\;\tilde{\mathbf{O}}_{\tilde{\xi}}(s)=\alpha^{2}(\tilde{\beta}(s))\mathbf{O}_{\xi}(\tilde{\beta}(s))\,.

(B.13)

Note that $\tilde{\zeta}$ and $\zeta$ are probability measures on the intervals $[\tilde{a},\tilde{b}]$ and $[a,b]$ , respectively. Similarly, for a given matrix-weighted design $d\tilde{\xi}(s)=\tilde{\mathbf{O}}_{\tilde{\xi}}(s)d\tilde{\zeta}(s)$ on the interval $[\tilde{a},\tilde{b}]$ we define a matrix-weighted design $d\xi(t)=\mathbf{O}_{\xi}(t)d\zeta(t)$ on the interval $[a,b]$ by

\displaystyle d\zeta(t)=d\tilde{\zeta}(\beta(t))\,\;\;{\rm and}\;\;\mathbf{O}_{\xi}(t)=\tilde{\alpha}^{2}(\beta(t))\tilde{\mathbf{O}}_{\tilde{\xi}}(\beta(t)).

(B.14)

Similar to Lemma B.2 we can see that the transformation $\tilde{\xi}\to\xi$ defined by (B.14) is the inverse to the transformation $\xi\to\tilde{\xi}$ defined by (B.13).

For the following discussion we recall the definition of the covariance matrix $\mathbf{D}(\xi)$ in (3.11). For the model (B.10), the covariance matrix of the design $d\tilde{\xi}(s)=\tilde{\mathbf{O}}_{\tilde{\xi}}(s)d\tilde{\zeta}(s)$ , defined by (B.13), is given by

\displaystyle\tilde{\mathbf{D}}(\tilde{\xi})=\tilde{\mathbf{M}}^{-1}(\tilde{\xi})\tilde{\mathbf{B}}(\tilde{\xi})(\tilde{\mathbf{M}}^{-1}(\tilde{\xi}))^{T},

(B.15)

where

\displaystyle\tilde{\mathbf{B}}(\tilde{\xi})=\int_{\tilde{a}}^{\tilde{b}}\int_{\tilde{a}}^{\tilde{b}}\tilde{K}(t,s){\tilde{\mathbf{O}}}_{\tilde{\xi}}(t)\tilde{f}(t)({\tilde{\mathbf{O}}}_{\tilde{\xi}}(s)\tilde{f}(s))^{T}d\tilde{\zeta}(t)d\tilde{\zeta}(s),\;\;\tilde{\mathbf{M}}(\tilde{\xi})=\int_{\tilde{a}}^{\tilde{b}}{\tilde{\mathbf{O}}}_{\tilde{\xi}}(t){\tilde{f}}(t){\tilde{f}}^{T}(t)d\tilde{\zeta}(t)\,

and the kernel $\tilde{K}$ is defined by (B.4).

Theorem B.1

For any matrix-weighted design $d\xi(t)=\mathbf{O}_{\xi}(t)d\zeta(t)$ and the corresponding matrix-weighted design $\tilde{\xi}$ defined by (B.13), we have $\mathbf{D}(\xi)=\tilde{\mathbf{D}}(\tilde{\xi}).$ In particular, $\mathbf{D}^{*}=\tilde{\mathbf{D}}^{*}$ , where $\mathbf{D}^{*}$ and $\tilde{\mathbf{D}}^{*}$ are the covariance matrices of the BLUE in the continuous time models (1.2) and in the model $\{\theta^{T}\tilde{f}(s)+\tilde{\varepsilon}(s)|s\in[\tilde{a},\tilde{b}]\}$ , respectively.

Proof. Using the variable transformation $\tilde{\beta}(s)=t$ and (B.9), we have

	$\displaystyle\tilde{\mathbf{M}}(\tilde{\xi})$	$\displaystyle=$	$\displaystyle\int{\tilde{\mathbf{O}}}_{\tilde{\xi}}(s){\tilde{f}}(s){\tilde{f}}^{T}(s)d\tilde{\zeta}(s)=\int\frac{\mathbf{O}_{\xi}(\tilde{\beta}(s))f(\tilde{\beta}(s))}{\alpha(\tilde{\beta}(s))}\frac{f^{T}(\tilde{\beta}(s))}{\alpha(\tilde{\beta}(s))}\cdot\alpha^{2}(\tilde{\beta}(s))d\zeta(\tilde{\beta}(s))$
		$\displaystyle=$	$\displaystyle\int\mathbf{O}_{\xi}(t)f(t)f^{T}(t)d\zeta(t)=\mathbf{M}(\xi).$

Next, we calculate the corresponding expression for $\tilde{\mathbf{B}}(\tilde{\xi})$ , that is

$\displaystyle\tilde{\mathbf{B}}(\tilde{\xi})$	$\displaystyle=$	$\displaystyle\int\int\tilde{K}(x,y)\tilde{\mathbf{O}}_{\tilde{\xi}}(x)\tilde{f}(x)(\tilde{\mathbf{O}}_{\tilde{\xi}}(y)\tilde{f}(y))^{T}d\tilde{\zeta}(x)d\tilde{\zeta}(y)$
	$\displaystyle=$	$\displaystyle\int\int\tilde{v}(x)\tilde{v}(y)\min(\tilde{q}(x),\tilde{q}(y))\tilde{\mathbf{O}}_{\tilde{\xi}}(x)\tilde{f}(x)(\tilde{\mathbf{O}}_{\tilde{\xi}}(y)\tilde{f}(y))^{T}d\tilde{\zeta}(x)d\tilde{\zeta}(y)$
	$\displaystyle=$	$\displaystyle\int\int\tilde{v}(x)\tilde{v}(y)\min(\tilde{q}(x),\tilde{q}(y))\frac{\mathbf{O}_{\xi}(\tilde{\beta}(x))f(\tilde{\beta}(x))}{\alpha(\tilde{\beta}(x))}\frac{(\mathbf{O}_{\xi}(\tilde{\beta}(y))f(\tilde{\beta}(y)))^{T}}{\alpha(\tilde{\beta}(y))}\times$
		$\displaystyle\alpha^{2}(\tilde{\beta}(x))d\zeta(\tilde{\beta}(x))\alpha^{2}(\tilde{\beta}(y))d\zeta(\tilde{\beta}(y))$

Define $s=\tilde{\beta}(x)$ and $t=\tilde{\beta}(y)$ so that $x=\tilde{\beta}^{-1}(s)=\beta(s)$ and similarly $y=\beta(t)$ . Changing the variables in the integrals above we obtain

\displaystyle\tilde{B}(\tilde{\xi})

\displaystyle\!\!=\!\!

\displaystyle\int\!\int\tilde{v}(\beta(s))\tilde{v}(\beta(t))\min(\tilde{q}(\beta(s)),\tilde{q}(\beta(t)))\mathbf{O}_{\xi}(s)f(s)(\mathbf{O}_{\xi}(t)f(t))^{T}\alpha(s)\alpha(t)d\zeta(s)d\zeta(t).

Using the definition of $\beta$ in (B.6) yields $\tilde{q}(\beta(t))=\tilde{q}(\tilde{q}^{-1}(q(t)))=q(t)$ and by the definition of $\alpha$ in (B.6) we finally get

	$\displaystyle\tilde{\mathbf{B}}(\tilde{\xi})$	$\displaystyle=$	$\displaystyle\int\!\int\tilde{v}(\beta(s))\tilde{v}(\beta(t))\min(q(s),q(t))\mathbf{O}_{\xi}(s)f(s)(\mathbf{O}_{\xi}(t)f(t))^{T}\frac{v(s)}{\tilde{v}(\beta(s))}\frac{v(t)}{\tilde{v}(\beta(t))}d\zeta(s)d\zeta(t)$
		$\displaystyle=$	$\displaystyle\int\!\int\min(q(s),q(t))\mathbf{O}_{\xi}(s)f(s)(\mathbf{O}_{\xi}(t)f(t))^{T}v(s)v(t)d\zeta(s)d\zeta(t)=\mathbf{B}(\xi)\,.$

The result $\mathbf{D}(\xi)=\tilde{\mathbf{D}}(\tilde{\xi})$ follows now from the definitions (3.11) and (B.15).

References

Bickel and Herzberg, (1979) Bickel, P. J. and Herzberg, A. M. (1979). Robustness of design against autocorrelation in time I: Asymptotic theory, optimality for location and linear regression. Annals of Statistics, 7(1):77–95.
Boltze and Näther, (1982) Boltze, L. and Näther, W. (1982). On effective observation methods in regression models with correlated errors. Math. Operationsforsch. Statist. Ser. Statist., 13:507–519.
Dette et al., (2008) Dette, H., Kunert, J., and Pepelyshev, A. (2008). Exact optimal designs for weighted least squares analysis with correlated errors. Statistica Sinica, 18(1):135–154.
Dette et al., (2013) Dette, H., Pepelyshev, A., and Zhigljavsky, A. (2013). Optimal design for linear models with correlated observations. The Annals of Statistics, 41(1):143–176.
Doob, (1949) Doob, J. L. (1949). Heuristic approach to the Kolmogorov-Smirnov theorems. The Annals of Mathematical Statistics, 20(3):393–403.
Grenander, (1950) Grenander, U. (1950). Stochastic processes and statistical inference. Ark. Mat., 1:195–277.
Harman and Štulajter, (2010) Harman, R. and Štulajter, F. (2010). Optimal prediction designs in finite discrete spectrum linear regression models. Metrika, 72(2):281–294.
Harman and Štulajter, (2011) Harman, R. and Štulajter, F. (2011). Optimality of equidistant sampling designs for the Brownian motion with a quadratic drift. Journal of Statistical Planning and Inference, 141(8):2750–2758.
Kiselak and Stehlík, (2008) Kiselak, J. and Stehlík, M. (2008). Equidistant $D$ -optimal designs for parameters of Ornstein-Uhlenbeck process. Statistics and Probability Letters, 78:1388–1396.
Mehr and McFadden, (1965) Mehr, C. and McFadden, J. (1965). Certain properties of Gaussian processes and their first-passage times. Journal of the Royal Statistical Society. Series B (Methodological), pages 505–522.
Müller and Pázman, (2003) Müller, W. G. and Pázman, A. (2003). Measures for designs in experiments with correlated errors. Biometrika, 90:423–434.
(12) Näther, W. (1985a). Effective Observation of Random Fields. Teubner Verlagsgesellschaft, Leipzig.
(13) Näther, W. (1985b). Exact design for regression models with correlated errors. Statistics, 16:479–484.
Pázman and Müller, (2001) Pázman, A. and Müller, W. G. (2001). Optimal design of experiments subject to correlated errors. Statist. Probab. Lett., 52(1):29–34.
Pukelsheim, (2006) Pukelsheim, F. (2006). Optimal Design of Experiments. SIAM, Philadelphia.
Sacks and Ylvisaker, (1966) Sacks, J. and Ylvisaker, N. D. (1966). Designs for regression problems with correlated errors. Annals of Mathematical Statistics, 37:66–89.
Sacks and Ylvisaker, (1968) Sacks, J. and Ylvisaker, N. D. (1968). Designs for regression problems with correlated errors; many parameters. Annals of Mathematical Statistics, 39:49–69.
Zhigljavsky et al., (2010) Zhigljavsky, A., Dette, H., and Pepelyshev, A. (2010). A new approach to optimal design for linear models with correlated observations. Journal of the American Statistical Association, 105:1093–1103.
Zhigljavsky, (1991) Zhigljavsky, A. A. (1991). Theory of Global Random Search. Springer, Netherlands.