Optimal investment with a noisy signal of future stock prices
Abstract.
We consider an investor who is dynamically informed about the future evolution of one of the independent Brownian motions driving a stock’s price fluctuations. With linear temporary price impact the resulting optimal investment problem with exponential utility turns out to be not only well posed, but it even allows for a closed-form solution. We describe this solution and the resulting problem value for this stochastic control problem with partial observation by solving its convex-analytic dual problem.
Y. Dolinsky is supported in part by the GIF Grant 1489-304.6/2019 and the ISF grant 230/21.
- Mathematical Subject Classification (2010):
-
91G10, 91B16
- Keywords:
-
optimal control with partial observation, exponential utility maximization, noisy price signals, duality, temporary price impact
1. Introduction
Information is arguably a key driver in stochastic optimal control problems as policy choice strongly depends on assessments of the future evolution of a controlled system and on how these can be expected to change over time. This is particularly obvious in Finance where information drives price fluctuations and where the question how it affects investment decisions is still a topic of great interest for financial economics and mathematics alike.
In part this may be due to the many ways information can be modeled and due to the various difficulties that come with each such model choice. If, as we are setting out to do in this paper, one seeks to understand how imperfect signals on future stock price evolution can be factored into present investment decisions, one needs to specify how the signal and the stock price are connected and work out the trading opportunities afforded by the signal. For a dynamic specification of the signal and its noise such as ours, this often leads to challenging combinations of filtering and optimal control and we refer to [8, 12, 7, 20, 2] for classical and more recent work in this direction.
The present paper contributes to this literature with a simple Bachelier stock price model driven by two independent Brownian motions. The investor dynamically gets advanced knowledge about the evolution of one of these over some time period, but the noise arising from the other Brownian motion makes perfect prediction of stock price fluctuations impossible. Accounting in addition for temporary price impact from finite market depth (cf. [16]) as suggested in the Almgren-Chriss model [1], we arrive at a viable expected utility maximization problem. In fact, for exponential utility we follow an approach similar to the one of [4], where the case of perfect stock price predictions is considered, and we work out explicitly the optimal investment strategy and maximum expected utility in this case. We can even allow for dynamically varying horizons over which peeks ahead are possible, thus extending beyond the fixed horizon setting of [4] (which is still included as a special case).
Our model also complements the literature on optimal order execution where different forms of market signals have been studied. For instance, [9] add a Markovian drift to the stock price evolution to model market trends as perceived by the agent; latent factors are added in [10]. With transient price impact rather than temporary one as in our setting, [17] and [19] study such signals and [6] adds a version with non-Markovian finite variation signals. Yet another version of market signals is considered in [5] who use Meyer -fields to model ultra short-term signals on the jumps in the order flow.
Describing how signals are specifically processed into strategies is a challenge for each of these models. In our setting, we find that the investor should optimally weigh her noisy signals of future stock price evolution and aggregate these weights into a projection of its fluctuations. The difference of this projection with the present stock price determines the signal-based part of her investment strategy. The relevant projection weights are computed explicitly and we analyze how they depend on the signal to noise ratio. On top of that, the investor also is interested in chasing the risk premium afforded by the stock and thus aims to take her portfolio to the Merton ratio, well-known from standard expected utility maximization. In addition, we investigate the value of reductions in noise and show that it is convex in signal quality. In other words, incentives for signal improvement turn out to be skewed in favor of investors who are already good at sniffing out the market’s evolution. Finally, we also use the flexibility in the signal horizon of our model to investigate when our investor would most like to be peek ahead if she can do so only once and how much of an advantage a continually probing investor has over her more relaxed counterpart who does so only periodically.
Mathematically, our method is based on the general duality result given in [4]. Here, however, we need to understand how changes of measures can be optimized when two Brownian motions are affected. Fortunately, we again find the problem to reduce to deterministic variational problems, which, albeit more involved, remain quadratic and thus can still be solved explicitly. The time-dependent knowledge horizon adds further challenges, but also affords us the opportunity to show that the problem is continuous with respect to perturbations in signal reach.
The present paper generalizes [4] and, while similar in its line of attack, the method of solution here differs in essential ways. Indeed, both papers apply the dual approach and do not deal with the primal infinite dimensional stochastic control problem directly. But the current paper decomposes the information flow into independent parts and passes to a conditional model driven by independent Brownian motions in the ‘usual’ way. This approach does not require applying the results from the theory of Gaussian Volterra integral equations [15, 14] and readily accommodates time-dependent signal specifications and noise.
2. Problem formulation
Consider an investor who can invest over some time horizon both in the money market at zero interest (for simplicity) and in stock. The price of the stock follows Bachelier dynamics
| (2.1) |
where denotes the initial stock price, describes the stock’s risk premium and its volatility; and parameterize the correlation between the stock price process and its drivers , , two independent Brownian motions specified on a complete probability space . On top of the information flow from present and past stock prices as captured by the augmented filtration generated by , the investor is assumed to have access to a signal which at any time allows her to deduce the future evolution of (but not of ) over a time window where is a right-continuous, nondecreasing time shift satisfying throughout. In other words, the investor is able to partially predict the evolution of future stock prices, albeit with some uncertainty. The uncertainty is described by a noise whose variance accrues over solely from at the rate and accrues from both and at the joint rate afterwards. As a result, the investor can draw on the information flow given by the filtration
| (2.2) |
when making her investment decisions.
In case all noise is wiped out from the stock price signal and so the investor gets perfect knowledge of some future prices, affording her obvious arbitrage opportunities. But even for the complementary case it is easy to check that is not a semimartingale and, by the Fundamental Theorem of Asset Pricing of [11], there is a free lunch with vanishing risk (and in fact even a strong arbitrage as can be shown by a Borel-Cantelli argument similar to the one in [18]). As a consequence, we need to curb the investor’s trading capabilities in order to maintain a viable financial model. In line with the economic view of the role and effect of arbitrageurs, we choose to accomplish this by taking into account the market impact from the investor’s trades. These cause execution prices for absolutely continuous changes in the investor’s position to be given by
| (2.3) |
So, when marking to market her position in the stock accrued by time , the investor will consider her net profit to be
| (2.4) | ||||
| (2.5) |
As a consequence, the investor will have to choose her turnover rates from the class of admissible strategies
| (2.6) |
Assuming for convenience constant absolute risk aversion , the investor would then seek to
| (2.7) |
Remark 2.1.
The special case of no signal noise () and constant peek ahead period (i.e., , , for some ) was solved in [4].
3. Main results and their financial-economic discussion
The paper’s main results are collected in the following theorem.
Theorem 3.1.
The investor’s unique optimal strategy is to average out the risk-premium adjusted stock price estimates
| (3.1) |
to obtain the risk- and liquidity-weighted projection of prices
| (3.2) |
where
| (3.3) |
with . With the projection at hand, the investor should then take at time into view her present stock holdings and choose to turn her position over at the rate
| (3.4) |
Finally, the maximum utility the investor can expect is
| (3.5) | ||||
| (3.6) | ||||
| (3.7) |
where , , denotes the right-continuous inverse of .
Let us briefly collect some financial-economic observations from this result. First, similar to the case without signal noise discussed in [4], an average of future price proxies is formed, but here weights are time-inhomogenous. In fact, the weights used in this averaging are determined in terms of the function and interestingly depend on the peek-ahead horizon only through its present value . As a consequence, when deciding about the time turnover rate , the investor does not care if her information horizon is going to stall or to jump all the way to soon. The reason for this is the investor’s exponential utility which makes investment decisions insensitive to present wealth and thus does not require planning ahead. It would be interesting to see how this changes with different utility functions. Unfortunately, our method to obtain an explicit solution to the optimal investment problem strongly depends on our choice of exponential utility, leaving this a challenge for future research.
Second, it is interesting to assess the impact of signal noise on investment decisions. Here, we observe that the emphasis that the projection puts on the last learned signal decreases when noise gets stronger due to an increase in . This reflects the investor’s reduced trust in this most noisy of her signals when noise becomes more prominent.
Third, we can assess how the presence of noise affects the value of the signal . To this end, let us consider the certainty equivalent
| (3.8) | ||||
| (3.9) |
that an agent, who can eliminate a fraction from the variance in stock price noise by observing part of , gains compared to her peer without that privilege (whence her terminal wealth is determined by , , instead of ). Contributions to this quantity from times long before the investment horizon ( large) when the signal has been received for a long time ( large), depend on by a factor of about . This factor increases from 0 to 1 as increases from 0 (no signal) to 1 (noiseless signal), with the steepest increase at , indicating limited, but ever higher returns from noise reductions. Conversely, an increase in noise is making itself felt the most when the signal is already quite reliable.
Finally, the flexibility concerning the form of the peek-ahead length given by affords one to account for periods when predictions are harder to make over periods where they are easier. Moreover, this flexibility also allows us to shed light on some natural questions such as the following ones:
-
(i)
When best to peek ahead? Suppose that the investor has an opportunity to choose a (deterministic) moment of time when, for one time only, she can peek ahead over some period into the future. What time should she choose? We can formalize this as an optimization problem over the family of time changes
Clearly, the corresponding inverse function is given by
Hence, in view of (3.8) we need to maximize over the value of
Observe that
We conclude that the optimal time is and so one should peek ahead immediately.
-
(ii)
How much of an advantage does continual probing have over periodic probing? For this we can compare the continual probing where we keep predicting what is going to happen over the next time units with its discrete counter part where we only peek ahead every units:
where denotes the floor function. Clearly, the continual probing is superior to periodic probing, but its advantage depends on the probing period length . Indeed, Figure 1 below shows the difference in certainty equivalents for the choices corresponding to updates in the periodic case. We see that, for the considered parameters, the periodically updating investor will be at the greatest disadvantage compared to her more diligent, continually probing counterpart when updating about 80 times for periods of length .
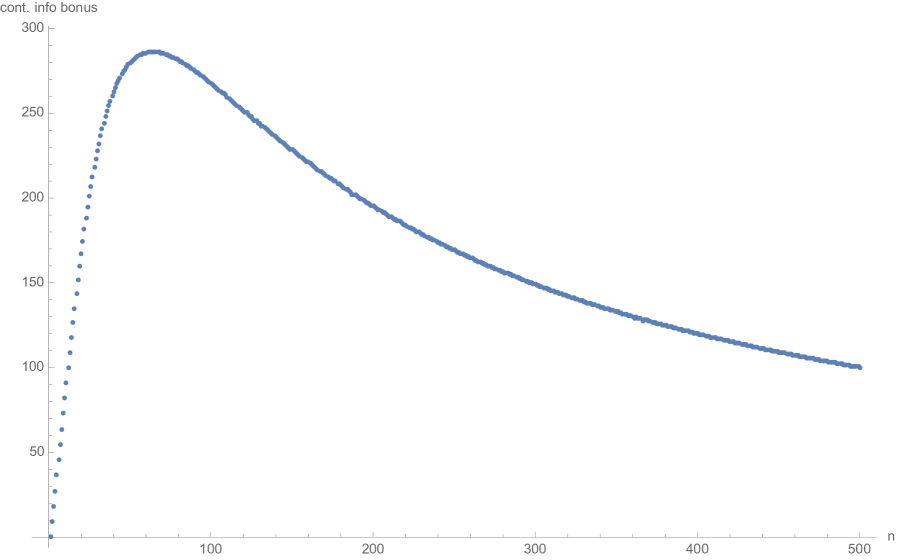
Figure 1. Continual vs. periodic probing: Difference of certainty equivalents for , , when , , , .
4. Proof
We start this section by outlining the main steps of the proof. The first step in Section 4.1 deals with simplifying the general setup to obtain a notationally and computationally more convenient special case of our problem. The second step (Section 4.2) consists of the main idea which is to apply duality theory. We show that the dual problem can be reduced to the solution of three separate deterministic variational problems. The third step (Section 4.3) is to solve these deterministic problems, which are quite involved and for which we therefore compute only their values and the essential properties of the corresponding optimal control. The fourth step (Section 4.4) combines the second and the third step to solve the dual problem. The last step (Section 4.5) uses duality and the Markovian structure of our problem to finally construct the solution to the primal problem from the dual solution.
4.1. Simplification of our setting
Parameter reduction.
Let us first note that it suffices to treat the special case where , , , :
Lemma 4.1.
If is optimal when starting with the initial position in the baseline model with parameters , , , and , then the optimal strategy in the model with general parameters , , , , and is given by
| (4.1) |
where is the measurable functional on for which . Morevorer, the maximum expected utility is times as high as the maximum utility in the baseline model.
Proof.
Let be the representation of an arbitrary admissible strategy as a functional of the underlying Brownian motions and . Then , is a standard two-dimensional Brownian motion under with , and we can write the expected utility from as
| (4.2) |
where is the terminal wealth generated in the baseline model from the initial position by the strategy given by
| (4.3) |
In the baseline model, is optimal by assumption and we obtain an upper bound for the maximum utility in the general model. This bound is sharp since it is attained by as in the formulation of the lemma. ∎
Reduction to differentiable, increasing time changes.
Let us argue next why we can assume without loss of generality that
| (4.4) |
and that it suffices to do the computation of the value of the problem (3.5) for satisfying, in addition, .
In fact, using that the description of optimal policies from Theorem 3.1 holds for satisfying (4.4) and that (3.5) holds when, in addition, (which we will prove independently below), we can even prove that the optimization problem depends continuously on and thus it suffices to consider smooth with (4.4):
Lemma 4.2.
If for and for every continuity point of (i.e., if weakly as Borel measures on ), then the optimal terminal wealth associated with converges almost surely to the one associated with and the problem value for converges to the one of .
Proof.
Let us denote by the value of our problem in dependence on and by its claimed value from the right-hand side of (3.5). Similarly, denote by the optimal terminal wealth (if it exists) for and by our candidate described in Theorem 3.1. Let us furthermore denote by the class of all satisfying (4.4) and by those which in addition satisfy . We will assume that for and for as these statements will be derived below independently from this lemma.
Let us observe first that both and continuously depend on . For this readily follows from (3.5) by dominated convergence; for this is due to the stability of the linear ODE (3.4) and the continuous dependence of its coefficients on .
Let us next argue why an optimal control for general exists and its terminal wealth is . For this take converging to from above and observe that . By Fatou’s lemma we conclude that . Because , any competitor is also in and thus . In conjunction with the preceding estimate, this shows that the candidate for general is indeed optimal with value .
Let us conclude by arguing why it suffices to compute the problem value for . For this choose to converge to a general from below. From the above, we know that . To see that conversely (and conclude), take a risk-aversion and observe that the corresponding (candidate) problem values and satisfy
| (4.5) |
Indeed, the first identity is due to the stability of the right-hand side of (3.5) in ; the estimate holds because the optimal strategy for risk-aversion is also admissible for risk-aversion ; the final identity holds because of uniform integrability which in turn follows from boundedness in with :
| (4.6) |
Letting in (4.5), its left-hand side converges to by continuous dependence on of the right-side of (3.5); the right-hand side in (4.5) converges by monotone convergence to and we are done. ∎
Decomposing the filtration into independent Brownian parts and passage to a conditional model.
For time changes satisfying (4.4), we can introduce
| (4.7) |
and readily check that it is a Brownian motion stopped at time which is independent of both and . Moreover, using that for , we can write the stock price dynamics as
| (4.8) |
and view the insider’s filtration as generated by the following independent components:
| (4.9) |
for and with denoting the collection of -nullsets. So, maximizing expected utility conditional on amounts to maximizing an unconditional expected utility in a model with probability where, by a slight abuse of notation, asset prices evolve according to
| (4.10) |
for some deterministic path segment , a -Brownian motion stopped at time and a standard -Brownian motion which generate the filtration
specifying the information flow for admissible strategies.
4.2. Duality
For the unconditional expected utility maximization under the measure identified above, we can apply Proposition A.2 in [4] to deduce that we can proceed by solving the dual problem with value
| (4.11) |
where and is the set of all probability measures with finite relative entropy . Said proposition also yields that the unique solution to the dual problem allows us to construct the solution to the primal problem considered under as
| (4.12) |
Following the path outlined in the special case treated in [4], we need to rewrite the dual target functional (4.11). For this it will be convenient to introduce the functionals and given by
| (4.13) | ||||
| (4.14) | ||||
| (4.15) | ||||
| and | ||||
| (4.17) | ||||
Lemma 4.3.
The dual infimum in (4.11) coincides with the one taken over all whose densities take the form
| (4.18) |
for some bounded, -adapted and changing values only at finitely many deterministic times. For such , we have the Girsanov -Brownian motions
| (4.19) | ||||
| (4.20) |
which allow for Ito representations
| (4.21) | ||||
| (4.22) |
for suitable and suitable -predictable processes , , , . In terms of these, the dual target value associated with is
| (4.23) |
Proof.
For any the martingale representation property of Brownian motion gives us a predictable with
such that (4.18) holds. Using this density to rewrite the dual target functional as an expectation under , we can use standard density arguments to see that the infimum over can be realized by considering the induced by simple as described in the lemma’s formulation via (4.18). As a consequence, the Itô representations of can be chosen in such a way that the resulting are also measurable in ; in fact they only change when change their values, i.e., at finitely many deterministic times. This measurability property will be used below for applying Fubini’s theorem.
4.3. Solving the deterministic variational problems
Lemma 4.3 above suggests to consider the minimization of the functionals , , and specified there. This amounts to solving deterministic variational problems and the following lemmas sum up the main findings.
Lemma 4.4.
Proof.
For a given and introduce the functions
| (4.27) | |||
| (4.28) |
Clearly, almost surely the functions are absolutely continuous in for almost every with boundary values
| (4.29) |
Changing variables we note
where denotes the derivative with respect to and so
for
| (4.30) | ||||
Minimization of can thus be carried out separately for each . So we fix such an and seek to determine the absolutely continuous which minimizes under the boundary condition (4.29). To this end, observe fist that the functional is strictly convex and so existence of a minimizer follows by a standard Komlos-argument.
In the computation of the minimum value, let us, for ease of notation, put , . We first focus on the contributions to from its integrals over the interval , assuming of course; for we can directly proceed with the minimization over as carried out below with . Clearly if is given then the minimum of is obtained for which satisfy . Hence, the optimal solution will satisfy
for some function which satisfies . Hence the functional to be minimized is really
Its Euler–Lagrange reads ; c.f., e.g., Section 1 in [13]. Since , we conclude that
| (4.31) | ||||
| (4.32) |
for some which is yet to be determined optimally.
Next, we treat the interval . The Euler–Lagrange equation for minimizing the functional
subject to the boundary condition (which we infer from (4.32)) is
Hence,
| (4.33) | ||||
| (4.34) |
for some which we still need to choose optimally.
We plug (4.31)–(4.33) into (4.30) to obtain
Simple computations show that, for , the minimal value of the above positive definite quadratic pattern in is equal to
and is attained for some constants and which depend continuously on . For , we have and the minimization over leads again to this last expression which thus holds for any . Upon integration over , we thus find
and (4.26) follows by the substitution .
∎
Lemma 4.5.
The functional given for square-integrable by (4.13) is minimized by for some continuous functional . This minimizer satisfies
| (4.35) | ||||
| (4.36) |
where and are given in Theorem 3.1.
Moreover, in the special case the minimum value is
| (4.37) |
Proof.
Similar arguments as in Lemma 4.4 give the uniqueness of the minimizer.
For a given introduce the functions
| (4.38) | ||||
| (4.39) |
Clearly, are absolutely continuous and satisfy
| (4.40) |
From a change of variables we obtain
and so for
| (4.41) | ||||
| (4.42) | ||||
| (4.43) | ||||
| (4.44) |
We aim to find absolutely continuous functions which minimize the right hand side of (4.41) under the boundary condition (4.40).
Using the same arguments as in Lemma 4.4, we obtain that a unique minimizer exists. Focusing first on minimizing the contributions to collected over (if ), we moreover find that it satisfies
| (4.45) | ||||
| (4.46) |
for some which we still need to optimize over.
For the contributions to over the interval , i.e., for the minimization of
| (4.47) |
over subject to the yet to be optimally chosen starting value and the terminal value fixed above, we apply Theorem 3.2 in [3] for our present deterministic setup. This result shows that
| (4.48) | ||||
| (4.49) |
allows us to describe the minimizer as the solution to the linear ODE
| (4.50) |
and the minimum value is
| (4.51) | ||||
for
| (4.52) | ||||
Minimizing over in (4.51) we obtain
| (4.53) |
and we find the corresponding minimum value to be
| (4.54) | ||||
| (4.55) | ||||
| (4.56) | ||||
Next, we plugin (4.45)–(4.46) and (4.54) into (4.41). The result is
| (4.57) | ||||
| (4.58) | ||||
| (4.59) |
and from (4.48) (for ) it follows that the minimum over is achieved for
| (4.60) |
The minimizer can now be recovered from (4.38)–(4.39), (4.45)–(4.50), (4.52) and (4.60) and turns out to be a continuous functional of . From (4.45), (4.48), (4.53)
where the last equality follows from (4.52), (4.60) and the Fubini theorem. This together with (4.38)–(4.39) gives (4.35). Finally, (4.37) follows from (4.57)–(4.60). ∎
Lemma 4.6.
The functional given by (4.17) is minimized by which yields the minimum value .
Proof.
The statement is obvious since and if and only if . ∎
4.4. Construction of the solution to the dual problem
Having found the minimum values for the functionals , , and from Lemma 4.3, we conclude that their sum yields a lower bound for the value of the dual problem (4.11). In fact, this lower bound is sharp since we can construct a measure whose dual target value coincides with it. For this consider the resolvent kernel associated with via
| (4.61) |
This kernel allows us to construct the solution
| (4.62) |
to the Volterra equation
| (4.63) |
Now, the probability given by (4.18) with of (4.62) and
| (4.64) |
induces the Girsanov -Brownian motion of (4.19) and, using that solves the Volterra equation (4.63), we find the Ito representations
| (4.65) | ||||
| (4.66) |
As a consequence, , , , , , and , are related exactly in the same way as the corresponding quantities in Lemma 4.3. By the same calculation as in the proof of this lemma, the dual target value thus turns out to be
| (4.67) |
where in the last line we are allowed to drop the expectation because the quantity there is deterministic anyway. It follows that indeed attains the lower bound for the dual problem.
4.5. Construction of the solution to the primal problem
Having constructed the dual optimizer , we now can use (4.12) to compute the optimal primal solution . For , we use the representation of from (4.8) and the fact that and have, respectively, drift and under . Hence, upon taking expectation with respect to , we find
| (4.72) | ||||
| (4.73) | ||||
| (4.74) |
where the last identity is just (4.35). It follows that the optimal initial turnover rate is
| (4.75) |
Invoking the same dynamic programming argument as in Lemma 3.5 of [4], we conclude that the analogous formula holds for arbitrary . This establishes optimality of the strategy described in Theorem 3.1.
References
- Almgren and Chriss [2001] R. Almgren and N. Chriss. Optimal execution of portfolio transactions. J. Risk, 3:5–39, 2001.
- Bandini et al. [2019] E. Bandini, A. Cosso, M. Fuhrman, and H. Pham. Randomized filtering and Bellman equation in Wasserstein space for partial observation control problem. Stochastic Processes and Applications, 129:674–711, 2019.
- Bank et al. [2017] P. Bank, H.M. Soner, and M. Voß. Hedging with temporary price impact. Mathematics and Financial Economics, 11:215–239, 2017.
- Bank et al. [2022] P. Bank, Y. Dolinsky, and M. Rásonyi. What if we knew what the future brings? Optimal investment for a frontrunner with price impact. Applied Mathematics and Optimization, 86:article 25, 2022.
- Bank et al. [2023] P. Bank, Á. Cartea, and L. Körber. Optimal execution and speculation with trade signals, 2023. URL https://doi.org/10.48550/arXiv.2306.00621.
- Belak et al. [2018] C. Belak, J. Muhle-Karbe, and K. Ou. Optimal trading with general signals and liquidation in target zone models. 2018.
- Bensoussan [1992] A. Bensoussan. Stochastic Control of Partially Observable Systems. Cambridge University Press,, Cambridge, UK., 1992.
- Bismut [1982] J.-M. Bismut. Partially observed diffusions and their control. SIAM Journal of Control and Optimization, 20:302–309, 1982.
- Cartea and Jaimungal [2016] Á. Cartea and S. Jaimungal. Incorporating order-flow into optimal execution. Mathematics and Financial Economics, 10(3):339–364, 2016.
- Casgrain and Jaimungal [2019] P. Casgrain and S. Jaimungal. Trading algorithms with learning in latent alpha models. Mathematical Finance, 29(3):735–772, 2019. doi: 10.1111/mafi.12194. URL https://ideas.repec.org/a/bla/mathfi/v29y2019i3p735-772.html.
- Delaben and Schachermayer [1994] F. Delaben and W. Schachermayer. A general version of the fundamental theorem of asset pricing,. Mathematische Annalen, 300:463–520, 1994.
- Fleming and Pardoux [1982] W. Fleming and E. Pardoux. Optimal control for partially observed diffusions. SIAM Journal of Control and Optimization, 20:261–285, 1982.
- Gelfand and Fomin [1963] I.M. Gelfand and S.V. Fomin. Calculus of variations. Prentice Hall, International, 1963.
- Hida and Hitsuda [1993] T. Hida and M. Hitsuda. Gaussian Processes. American Mathematical Society, 1993.
- Hitsuda [1968] M. Hitsuda. Representation of gaussian processes equivalent to wiener process. Osaka Journal of Mathematics, 5:299–312, 1968.
- Kyle [1985] A.S. Kyle. Continuous auctions and insider trading. Econometrica, 53:1315–1335, 1985.
- Lehalle and Neuman [2019] C.A. Lehalle and E. Neuman. Incorporating signals into optimal trading. Finance and Stochastics, 23(1):275–311, 2019.
- Levental and Skorohod [1995] S. Levental and A.V. Skorohod. A necessary and sufficient condition for absence of arbitrage with tame portfolios. Annals of Applied Probability, 5:463–520, 1995.
- Neuman and Voß [2022] E. Neuman and M. Voß. Optimal signal-adaptive trading with temporary and transient price impact. SIAM Journal on Financial Mathematics, 13(2):551–575, 2022. doi: 10.1137/20M1375486. URL https://doi.org/10.1137/20M1375486.
- Tang [1998] S. Tang. The maximum principle for partially observed optimal control of stochastic differential equations. SIAM Journal of Control and Optimization, 36:1596–1617, 1998.