University of Waterloo, Canadaxiaohu@uwaterloo.cahttps://orcid.org/0000-0002-7890-665X University of Waterloo, Canadazhiang.wu@uwaterloo.cahttps://orcid.org/0009-0004-8647-1416 {CCSXML} <ccs2012> <concept> <concept_id>10002978.10003018.10003020</concept_id> <concept_desc>Security and privacy Management and querying of encrypted data</concept_desc> <concept_significance>500</concept_significance> </concept> <concept> <concept_id>10002951.10002952.10003190.10003192.10003426</concept_id> <concept_desc>Information systems Join algorithms</concept_desc> <concept_significance>500</concept_significance> </concept> </ccs2012> \ccsdesc[500]Security and privacy Management and querying of encrypted data \ccsdesc[500]Information systems Join algorithms \EventEditors \EventNoEds2 \EventLongTitle28th International Conference on Database Theory (ICDT 2025) \EventShortTitleICDT 2025 \EventAcronymICDT \EventYear2025 \EventDate \EventLocation \EventLogo \SeriesVolume \ArticleNo
Optimal Oblivious Algorithms for Multi-way Joins
Abstract
In cloud databases, cloud computation over sensitive data uploaded by clients inevitably causes concern about data security and privacy. Even when encryption primitives and trusted computing environments are integrated into query processing to safeguard the actual contents of the data, access patterns of algorithms can still leak private information about the data. Oblivious RAM (ORAM) and circuits are two generic approaches to address this issue, ensuring that access patterns of algorithms remain oblivious to the data. However, deploying these methods on insecure algorithms, particularly for multi-way join processing, is computationally expensive and inherently challenging.
In this paper, we propose a novel sorting-based algorithm for multi-way join processing that operates without relying on ORAM simulations or other security assumptions. Our algorithm is a non-trivial, provably oblivious composition of basic primitives, with time complexity matching the insecure worst-case optimal join algorithm, up to a logarithmic factor. Furthermore, it is cache-agnostic, with cache complexity matching the insecure lower bound, also up to a logarithmic factor. This clean and straightforward approach has the potential to be extended to other security settings and implemented in practical database systems.
keywords:
oblivious algorithms, multi-way joins, worst-case optimality1 Introduction
In outsourced query processing, a client entrusts sensitive data to a cloud service provider, such as Amazon, Google, or Microsoft, and subsequently issues queries to the provider. The service provider performs the required computations and returns the results to the client. Since these computations are carried out on remote infrastructure, ensuring the security and privacy of query evaluation is a critical requirement. Specifically, servers must remain oblivious to any information about the underlying data throughout the computation process. To achieve this, advanced cryptographic techniques and trusted computing hardware are employed to prevent servers from inferring the actual contents of the data [34, 19]. However, the memory accesses during execution may still lead to information leakage, posing an additional challenge to achieving comprehensive privacy. For example, consider the basic (natural) join operator on two database instances: and for some , where each pair of tuples can be joined if and only if they have the same -value. Suppose each relation is sorted by their -values. Using the merge join algorithm, there is only one access to between two consecutive accesses to , but there are accesses to between two consecutive accesses to . Hence, the server can distinguish the degree information of join keys of the input data by observing the sequence of memory accesses. Moreover, if the server counts the total number of memory accesses, it can further infer the number of join results of the input data.
The notion of obliviousness was proposed to formally capture such a privacy guarantee on the memory access pattern of algorithms [31, 30]. This concept has inspired a substantial body of research focused on developing algorithms that achieve obliviousness in practical database systems [55, 24, 20, 17]. A generic approach to achieving obliviousness is Oblivious RAM (ORAM) [31, 41, 29, 52, 23, 48, 7], which translates each logical access into a poly-logarithmic (in terms of the data size) number of physical accesses to random locations of the memory. but the poly-logarithmic additional cost per memory access is very expensive in practice [15]. Another generic approach involves leveraging circuits [53, 26]. Despite their theoretical promise, generating circuits is inherently complex and resource-intensive, and integrating such constructions into database systems often proves to be inefficient. These challenges highlight the advantages of designing algorithms that are inherently oblivious to the input data, eliminating the need for ORAM frameworks or circuit constructions.
In this paper, we take on this question for multi-way join processing, and examine the insecure worst-case optimal join (WCOJ) algorithm [43, 44, 50], that can compute any join queries in time proportional to the maximum number of join results. Our objective is to investigate the intrinsic properties of the WCOJ algorithm and transform it into an oblivious version while preserving its optimal complexity guarantee.
1.1 Problem Definition
Multi-way join. A (natural) join query can be represented as a hypergraph [1], where models the set of attributes, and models the set of relations. Let be the domain of attribute . An instance of is a function that maps each to a set of tuples , where each tuple specifies a value in for each attribute . The result of a join query over an instance , denoted by , is the set of all combinations of tuples, one from each relation , that share the same values in their common attributes, i.e.,
Let be the input size of instance , i.e., the total number of tuples over all relations. Let be the output size of the join query over instance . We study the data complexity [1] of join algorithms by measuring their running time in terms of input and output size of the instance. We consider the size of , i.e., and , as constant.
Model of computation.
We consider a two-level hierarchical memory model [40, 18]. The computation is performed within trusted memory, which consists of registers of the same width. For simplicity, we assume that the trusted memory size is , where is a constant. This assumption will not change our results by more than a constant factor. Since we assume the query size as a constant, the arity of each relation is irrelevant. Each tuple is assumed to fit into a single register, with one register allocated per tuple, including those from input relations as well as intermediate results. We further assume that tuples from any set of relations can fit into the trusted memory. Input data and all intermediate results generated during the execution are encrypted and stored in an untrusted memory of unlimited size. Both trusted and untrusted memory are divided into blocks of size . One memory access moves a block of consecutive tuples from trusted to untrusted memory or vice versa. The complexity of an algorithm is measured by the number of such memory accesses.
An algorithm typically operates by repeating the following three steps: (1) read encrypted data from the untrusted memory into the trusted memory, (2) perform computation inside the trusted memory, and (3) Encrypt necessary data and write them back to the untrusted memory. Adversaries can only observe the address of the blocks read from or written to the untrusted memory in (1) and (3), but not data contents. They also cannot interfere with the execution of the algorithm. The sequence of memory accesses to the untrusted memory in the execution is referred to as the “access pattern” of the algorithm. In this context, we focus on two specific scenarios of interest:
-
•
Random Access Model (RAM). This model can simulate the classic RAM model with and , where the trusted memory corresponds to registers and the untrusted memory corresponds to the main memory. The time complexity in this model is defined as the number of accesses to the main memory by a RAM algorithm.
-
•
External Memory Model (EM). This model can naturally simulate the classic EM model [3, 51], where the trusted memory corresponds to the main memory and the untrusted memory corresponds to the disk. Following prior work [28, 21, 18], we focus on the cache-agnostic EM algorithms, which are unaware of the values of (memory size) and (block size), a property commonly referred to as cache-oblivious in the literature. To avoid ambiguity, we use the terms “cache-agnostic” to refer to “cache-oblivious” and “oblivious” to refer to “access-pattern-oblivious” throughout this paper. The advantages of cache-agnostic algorithms have been extensively studied, particularly in multi-level memory hierarchies. A cache-agnostic algorithm can seamlessly adapt to operate efficiently between any two adjacent levels of the hierarchy. We adopt the tall cache assumption, and further 111In this work, always means and should be distinguished from . for an arbitrarily small constant , and the wide block assumption, . These are standard assumptions widely adopted in the literature of EM algorithms [3, 51, 6, 28, 21, 18]. The cache complexity in this model is defined as the number of accesses to the disk by an EM algorithm.
Oblivious Algorithms. The notion of obliviousness is defined based on the access pattern of an algorithm. Memory accesses to the trusted memory are invisible to the adversary and, therefore, have no impact on security. Let be an algorithm, a join query, and an arbitrary input instance of . We denote as the sequence of memory accesses made by to the untrusted memory when given as the input, where each memory access is a read or write operation associated with a physical address. The join query and the size of the input instance are considered non-sensitive information and can be safely exposed to the adversary. In contrast, all input tuples are considered sensitive information and should be hidden from adversaries. This way, the access pattern of an oblivious algorithm should only depend on and , ensuring no leakage of sensitive information.
Definition 1.1 (Obliviousness [30, 31, 14]).
An algorithm is oblivious for a join query , if given an arbitrary parameter , for any pair of instances of with input size , , where is a negligible function in terms of . Specifically, for any positive constant , there exists such that for any . The notation indicates the statistical distance between two distributions is at most .
This notion of obliviousness applies to both deterministic and randomized algorithms. For a randomized algorithm, different execution states may arise from the same input instance due to the algorithm’s inherent randomness. Each execution state corresponds to a specific sequence of memory accesses, allowing the access pattern to be modeled as a random variable with an associated probability distribution over the set of all possible access patterns. The statistical distance between two probability distributions is typically quantified using standard metrics, such as the total variation distance. A randomized algorithm is indeed oblivious if its access pattern exhibits statistically indistinguishable distributions across all input instances of the same size. Relatively simpler, a deterministic algorithm is oblivious if it displays an identical access pattern for all input instances of the same size.
1.2 Review of Existing Results
Oblivious RAM. ORAM is a general randomized framework designed to protect access patterns [31]. In ORAM, each logical access is translated into a poly-logarithmic number of random physical accesses, thereby incurring a poly-logarithmic overhead. Goldreich et al. [31] established a lower bound on the access overhead of ORAMs in the RAM model. Subsequently, Asharov et al. [7] proposed a theoretically optimal ORAM construction with an overhead of in the RAM model under the assumption of the existence of a one-way function, which is rather impractical [47]. It remains unknown whether a better cache complexity than can be shown for such a construction. Path ORAM [48] is currently the most practical ORAM construction, but it introduces an overhead and requires trusted memory. In the EM model, one can place the tree data structures for ORAM in an Emde Boas layout, resulting in a memory access overhead of .
Insecure Join Algorithms.
The WCOJ algorithm [43] have been developed to compute any join query in time222A hashing-based algorithm achieves time in the worst case using the lazy array technique [27]., where is the fractional edge cover number of the join query (formally defined in Section 2.1). The optimality is implied by the AGM bound [8]. 333The maximum number of join results produced by any instance of input size is , which is also tight in the sense that there exists some instance of input size that can produce join results. However, these WCOJ algorithms are not oblivious. In Section 4, we use triangle join as an example to illustrate the information leakage from the WCOJ algorithm. Another line of research also explored output-sensitive join algorithms. A join query can be computed in time [54, 2], where subw is the submodular-width of the join query. For example, if and only if the join query is acyclic [11, 25]. These algorithms are also not oblivious due to various potential information leakages. For instance, the total number of memory accesses is influenced by the output size, which can range from a constant to a polynomially large value relative to the input size. A possible mitigation strategy is worst-case padding, which involves padding dummy accesses to match the worst case. However, this approach does not necessarily result in oblivious algorithms, as their access patterns may still vary significantly across instances with the same input size.
In contrast, there has been significantly less research on multi-way join processing in the EM model. First of all, we note that an EM version of the WCOJ algorithm incurs at least cache complexity since there are join results in the worst case and all join results should be written back to disk. For the basic two-way join, the nested-loop algorithm has cache complexity and the sort-merge algorithm has cache complexity . For multi-way join queries, an EM algorithm with cache complexity has been achieved for Berge-acyclic joins [37], -acyclic joins [36, 39], graph joins [38, 22] and Loomis-Whitney joins [39].444Some of these algorithms have been developed for the Massively Parallel Computation (MPC) model [10] and can be adapted to the EM model through the MPC-to-EM reduction [39]. These results were previously stated without including the output-dependent term since they do not consider the cost of writing join results back to disk. Again, even padding the output size to be as large as the worst case, these algorithms remain non-oblivious since their access patterns heavily depend on the input data. Furthermore, even in the insecure setting, no algorithm with a cache complexity is known for general join queries.
Oblivious Join Algorithms.
Oblivious algorithms have been studied for join queries in both the RAM and EM models. In the RAM model, the naive nested-loop algorithm can be transformed into an oblivious one by incorporating some dummy writes, as it enumerates all possible combinations of tuples from input relations in a fixed order. This algorithm runs in time, where is the number of relations in the join query. Wang et al. [53] designed circuits for conjunctive queries - capturing all join queries as a special case - whose time complexity matches the AGM bound up to poly-logarithmic factors. Running such a circuit will automatically yield an oblivious join algorithm with time complexity. By integrating the insecure WCOJ algorithm [44] with the optimal ORAM [7], it is possible to achieve an oblivious algorithm with time complexity, albeit under restrictive theoretical assumptions. Alternatively, incorporating the insecure WCOJ algorithm into the Path ORAM yields an oblivious join algorithm with time complexity.
In the EM model, He et al. [35] proposed a cache-agnostic nested-loop join algorithm for the basic two-way join with cache complexity, which is also oblivious. Applying worst-case padding and the optimal ORAM construction to the existing EM join algorithms, we can derive an oblivious join algorithm with cache complexity for specific cases such as acyclic joins, graph joins and Loomis-Whitney joins. However, these algorithms are not cache-agnostic. For general join queries, no specific oblivious algorithm has been proposed for the EM model, aside from results derived from the oblivious RAM join algorithm. These results yield cache complexities of either or , as they rely heavily on retrieving tuples from hash tables or range search indices.
| Previous Results | New Results | |
|---|---|---|
| RAM model | [44, 7] | |
| (one-way function assumption) | (no assumption) | |
| Cache-agnostic | ||
| EM model | ||
| (no assumption) | (tall cache and wide block assumptions) |
Relaxed Variants of Oblivious Join Algorithms.
Beyond fully oblivious algorithms, researchers have explored relaxed notions of obliviousness by allowing specific types of leakage, such as the join size, the multiplicity of join values, and the size of intermediate results. One relevant line of work examines join processing with released input and output sizes. For example, integrating an insecure output-sensitive join algorithm into an ORAM framework produces a relaxed oblivious algorithm with time complexity. It is noted that relaxed oblivious algorithm with the same time complexity have been proposed without requiring ORAM [5, 40] for the basic two-way join as well as acyclic joins. Although not fully oblivious, these algorithms serve as fundamental building blocks for developing our oblivious algorithms for general join queries. Another line of work considered differentially oblivious algorithms [14, 12, 18], which require only that access patterns appear similar across neighboring input instances. However, differentially oblivious algorithms have so far been limited to the basic two-way join [18]. This paper does not pursue this direction further.
1.3 Our Contribution
Our main contribution can be summarized as follows (see Table 1):
-
•
We give a nested-loop-based algorithm for general join queries with time complexity and cache complexity, where and are the fractional and integral edge cover number of the join query, respectively (formally defined in Section 2.1). This algorithm is also cache-agnostic. For classes of join queries with , such as acyclic joins, even-length cycle joins and boat joins (see Section 3), this is almost optimal up to logarithmic factors.
-
•
We design an oblivious algorithm for general join queries with time complexity, which has matched the insecure counterpart by a logarithmic factor and recovered the previous ORAM-based result, which assumes the existence of one-way functions. This algorithm is also cache-agnostic, with cache complexity. This cache complexity can be simplified to when for some sufficiently large constant . This result establishes the first worst-case near-optimal join algorithm in the insecure EM model when all join results are returned to disk.
-
•
We develop an improved algorithm for relaxed two-way joins with better cache complexity, which is also cache-agnostic. By integrating our oblivious algorithm with generalized hypertree decomposition [33], we obtain a relaxed oblivious algorithm for general join queries with time complexity and cache complexity, where fhtw is the fractional hypertree width of the input query.
Roadmap. This paper is organized as follows. In Section 2, we introduce the preliminaries for building our algorithms. In Section 3, we show our first algorithm based on the nested-loop algorithm. While effective, this algorithm is not always optimal, as demonstrated with the triangle join. In Section 4, we use triangle join to demonstrate the leakage of insecure WCOJ algorithm and show how to transform it into an oblivious algorithm. We introduce our oblivious WCOJ algorithm for general join queries in Section 5, and conclude in Section 6.
2 Preliminaries
2.1 Fractional and Integral Edge Cover Number
For a join query , a function is a fractional edge cover for if for any . An optimal fractional edge cover is the one minimizing , which is captured by the following linear program:
| (1) |
The optimal value of (1) is the fractional edge cover number of , denoted as . Similarly, a function is an integral edge cover if for any . The optimal integral edge cover is the one minimizing , which can be captured by a similar linear program as (1) except that is replaced with . The optimal value of this linear program is the integral edge cover number of , denoted as .
2.2 Oblivious Primitives
We introduce the following oblivious primitives, which form the foundation of our algorithms. Each primitive displays an identical access pattern across instances of the same input size.
Linear Scan.
Given an input array of elements, a linear scan of all elements can be done with time complexity and cache complexity in a cache-agnostic way.
Sort [4, 9].
Given an input array of elements, the goal is to output an array according to some predetermined ordering. The classical bitonic sorting network [9] requires time. Later, this time complexity has been improved to [4] in 1983. However, due to the large constant parameter hidden behind , the classical bitonic sorting is more commonly used in practice, particularly when the size is not too large. Ramachandran and Shi [45] showed a randomized algorithm for sorting with time complexity and cache complexity under the tall cache assumption.
Compact [32, 46].
Given an input array of elements, some of which are distinguished as , the goal is to output an array with all non-distinguished elements moved to the front before any , while preserving the ordering of non-distinguished elements. Lin et al. [42] showed a randomized algorithm for compaction with time complexity and cache complexity under the tall cache assumption.
We use the above primitives to construct additional building blocks for our algorithms. To ensure obliviousness, all outputs from these primitives include a fixed size equal to the worst-case scenario, i.e., , comprising both real and dummy elements. All these primitives achieve time complexity and cache complexity. Further details are provided in Appendix B.
SemiJoin.
Given two input relations , of at most tuples and their common attribute(s) , the goal is to output the set of tuples in that can be joined with at least one tuple in .
Project.
Given an input relation of tuples defined over attributes , and a subset of attributes , the goal is to output , ensuring no duplication.
Intersect.
Given two input arrays of at most elements, the goal is to output .
Augment.
Given a relation and additional relations (each with at most tuples) sharing common attribute(s) , the goal is to attach each tuple the number of tuples in (for each ) that can be joined with on .
We note that any sequential composition of oblivious primitives yields more complex algorithms that remain oblivious, which is the key principle underlying our approach.
2.3 Oblivious Two-way Join
NestedLoop. Nested-loop algorithm can compute with time complexity, which iterates all combinations of tuples from and writes a join result (or a dummy result, if necessary, to maintain obliviousness). He et al. [35] proposed a cache-agnostic version in the EM model with cache complexity, which is also oblivious.
Theorem 2.1 ([35]).
For , there is a cache-agnostic algorithm that can compute with time complexity and cache complexity, whose access pattern only depends on and .
RelaxedTwoWay. The relaxed two-way join algorithm [5, 40] takes as input two relations and a parameter , and output a table of elements containing join results of , whose access pattern only depends on and . This algorithm can also be easily transformed into a cache-agnostic version with time complexity and cache complexity. In Appendix C, we show how to improve this algorithm with better cache complexity without sacrificing the time complexity.
Theorem 2.2.
For and a parameter , there is a cache-agnostic algorithm that can compute with time complexity and cache complexity under the tall cache and wide block assumptions, whose access pattern only depends on and .
3 Beyond Oblivious Nested-loop Join
Although the nested-loop join algorithm is described for the two-way join, it can be extended to multi-way joins. For a general join query with relations, the nested-loop primitive can be recursively invoked times, resulting in an oblivious algorithm with cache complexity. Careful inspection reveals that we do not necessarily feed all input relations into the nested loop; instead, we can restrict enumeration to combinations of tuples from relations included in an integral edge cover of the join query. Recall that for , an integral edge cover of is a function , such that holds for every . While enumerating combinations of tuples from relations “chosen” by , we can apply semi-joins using remaining relations to filter intermediate join results.
As described in Algorithm 1, it first chooses an optimal integral edge cover of (line 1), and then invokes the NestedLoop primitive to iteratively compute the combinations of tuples from relations with (line 7), whose output is denoted as . Meanwhile, we apply the semi-join between and the remaining relations (line 8).
Below, we analyze the complexity of this algorithm. First, as , the intermediate join results materialized in the while-loop is at most . After semi-join filtering, the number of surviving results is at most . In this way, the number of intermediate results materialized by line 7 is at most . Putting everything together, we obtain:
Theorem 3.1.
For a general join query , there is an oblivious and cache-agnostic algorithm that can compute for an arbitrary instance of input size with time complexity and cache complexity under the tall cache and wide block assumptions, where and are the optimal fractional and integral edge cover number of , respectively.
It is important to note that any oblivious join algorithm incurs a cache complexity of , so Theorem 3.1 is optimal up to a logarithmic factor for join queries where . Below, we list several important classes of join queries that exhibit this desirable property:
Example 3.2 (-acyclic Join).
A join query is -acyclic [11, 25] if there is a tree structure of such that (1) there is a one-to-one correspondence between relations in and nodes in ; (2) for every attribute , the set of nodes containing form a connected subtree of . Any -acyclic join admits an optimal fractional edge cover that is integral [36].
Example 3.3 (Even-length Cycle Join).
An even-length cycle join is defined as for some even integer . It has two integral edge covers and , both of which are also an optimal fractional edge cover. Hence, .
Example 3.4 (Boat Join).
A boat join is defined as . It has an integral edge cover that is also an optimal fractional edge cover. Hence, .
4 Warm Up: Triangle Join
The simplest join query that oblivious nested-loop join algorithm cannot solve optimally is the triangle join , which has and . While various worst-case optimal algorithms for the triangle join have been proposed in the RAM model, none of these are oblivious due to their inherent leakage of intermediate statistics. Below, we outline the issues with existing insecure algorithms and propose a strategy to make them oblivious.
Insecure Triangle Join Algorithm 2.
We start with attribute . Each value induces a subquery . Moreover, a value is heavy if is greater than , and light otherwise. If is light, is computed by materializing the Cartesian product between and , and then filter the intermediate result by a semi-join with . Every surviving tuple forms a join result with , which will be written back to untrusted memory. If is heavy, is computed by applying the semi-joins between with and . This algorithm achieves a time complexity of (see [43] for detailed analysis), but it leaks sensitive information through the following mechanisms:
-
•
is leaked by the number of for-loop iterations in line 2;
-
•
and are leaked by the number of for-loop iterations in line 4;
-
•
The sizes of heavy and light values in are leaked by the if-else condition in lines 3 and 6;
To protect intermediate statistics, we pad dummy tuples to every intermediate result (such as , and ) to match the worst-case size . To hide heavy and light values, we replace conditional if-else branches with a unified execution plan by visiting every possible combination of and every tuple of . By integrating these techniques, this strategy leads to memory accesses, hence destroying the power of two choices that is a key advantage in the insecure WCOJ algorithm.
Inject Obliviousness to Algorithm 2.
To inject obliviousness into Algorithm 2, Algorithm 3 leverages oblivious primitives to ensure the same access pattern across all instances of the input size. Here’s a breakdown of how this is achieved and why it works. We start with computing by the Intersect primitive. Then, we partition values in into two subsets , depending on the relative order between and . We next compute the following two-way joins and by invoking the RelaxedTwoWay primitive separately, each with the upper bound . At last, we filter intermediate join results by the SemiJoin primitive and remove unnecessary dummy tuples by the Compact primitive.
Analysis of Algorithm 3.
It suffices to show that and , which directly follows from the query decomposition lemma [44]:
All other primitives have time complexity and cache complexity. Hence, this whole algorithm incurs time complexity and cache complexity. As each step is oblivious, the composition of all these steps is also oblivious.
Insecure Triangle Join Algorithm 4.
We start with attribute . We first compute the candidate values in that appear in some join results, i.e., . For each candidate value , we retrieve the candidate values in that can appear together with in some join results, i.e., . Furthermore, for each candidate value , we explore the possible values in that can appear together with in some join results. More precisely, every value appears in as well as forms a triangle with . This algorithm runs in time (see [44] for detailed analysis). Similarly, it is not oblivious as the following intermediate statistics may be leaked:
-
•
is leaked by the number of for-loop iterations in line 2;
-
•
is leaked by the number of for-loop iterations in line 3;
-
•
is leaked by the number of for-loop iterations in line 4;
To achieve obliviousness, a straightforward solution is to pad every intermediate result with dummy tuples to match the worst-case size . However, this would result in memory accesses, which is even less efficient than the nested-loop-based algorithm in Section 3.
Inject Obliviousness to Algorithm 4.
We transform Algorithm 4 into an oblivious version, presented as Algorithm 5, by employing oblivious primitives. The first modification merges the first two for-loops (lines 2–3 in Algorithm 4) into one step (line 1 in Algorithm 5). This is achieved by applying the semi-joins on using separately. Then, the third for-loop (line 4 in Algorithm 4) is replaced with a strategy based on the power of two choices. Specifically, for each surviving tuple , we first compute the size of two lists, and , and put into either or , based on the relative order between and . We next compute the following two-way joins and by invoking the RelaxedTwoWay primitive, each with the upper bound separately. Finally, we filter intermediate join results by the SemiJoin primitive and remove unnecessary dummy tuples by the Compact primitive.
Complexity of Algorithm 5.
It suffices to show that and , which directly follows from the query decomposition lemma [44]:
All other primitives incur time complexity and cache complexity. Hence, this algorithm incurs time complexity and cache complexity. As each step is oblivious, the composition of all these steps is also oblivious.
Theorem 4.1.
For triangle join , there is an oblivious and cache-agnostic algorithm that can compute for any instance of input size with time complexity and cache complexity under the tall cache and wide block assumptions.
5 Oblivious Worst-case Optimal Join Algorithm
In this section, we start with revisiting the insecure WCOJ algorithm in Section 5.1 and then present our oblivious algorithm in Section 5.2 and present its analysis in Section 5.3. Subsequently, in Section 5.4, we explore the implications of our oblivious algorithm for relaxed oblivious algorithms designed for cyclic join queries.
5.1 Generic Join Revisited
In a join query , for a subset of attributes , we use to denote the sub-query induced by attributes in , where . For each attribute , we use to denote the set of relations containing . The insecure WCOJ algorithm described in [44] is outlined in Algorithm 6, which takes as input a general join query and an instance . In the base case, when only one attribute exists, it computes the intersection of all relations. For the general case, it partitions the attributes into two disjoint subsets, and , such that and . The algorithm first computes the sub-query , induced by attributes in , whose join result is denoted . Then, for each tuple , it recursively invokes the whole algorithm to compute the sub-query induced by attributes in , over tuples that can be joined with . The resulting join result for each tuple is denoted as . Finally, it attaches each tuple in with , representing the join results in which participates. The algorithm ultimately returns the union of all join results for tuples in . However, Algorithm 6 exhibits significant leakage of data statistics that violates the obliviousness constraint, for example:
-
•
is leaked in line 1;
-
•
for each relation is leaked in line 3;
-
•
, , and for each tuple are leaked in line 4.
More importantly, this algorithm heavily relies on hashing indexes or range search indexes for retrieving tuples, such that the intersection at line 1 can be computed in time. However, these indexes do not work well in the external memory model since naively extending this algorithm could result in cache complexity, which is too expensive. Consequently, designing a WCOJ algorithm that simultaneously maintains cache locality and achieves obliviousness remains a significant challenge.
5.2 Our Algorithm
Now, we extend our oblivious triangle join algorithms from Section 4 to general join queries, as described in Algorithm 7. It is built on a recursive framework:
Base Case: . In this case, the join degenerates to the set intersection of all input relations, which can be efficiently computed by the Intersect primitive.
General Case: .
In general, we partition into two subsets and , but with the constraint that or but the two attributes in must satisfy and . Similar to Algorithm 6, we compute the sub-query by invoking the whole algorithm recursively, whose join result is denoted as . To prevent the potential leakage, we must be careful about the projection of each relation involved in this subquery, which is computed by the Project primitive. We further distinguish two cases based on :
General Case 1: .
Suppose . Recall that for each tuple , Algorithm 6 computes the intersection on in the base case. To ensure this step remains oblivious, we must conceal the size of . To achieve this, we augment each tuple with its degree in , which is defined as , using the Augment primitive. Then, we partition tuples in into subsets based on their smallest degree across all relations in . The details are described in Algorithm 8. Let denote the set of tuples whose degree is the smallest in , i.e., for each . Whenever we write one tuple to one subset, we also write a dummy tuple to the other subsets. At last, for each , we compute by invoking the RelaxedTwoWay primitive (line 9), with upper bound , and further filter them by remaining relations with semi-joins (line 10).
General Case 2: .
Suppose . Consider an arbitrary tuple . Algorithm 6 computes the residual query . Like the case above, we first compute its degree in as , by the Augment primitive. We then partition tuples in into subsets based on their degrees, but more complicated than Case 1. The details are described in Algorithm 9. More specifically, for each , let
and for each pair , let
For each , we compute by invoking the RelaxedTwoWay primitive iteratively (line 16-17), with the upper bound , and filter these results by remaining relations with semi-joins (line 18). For each , we compute by invoking the RelaxedTwoWay primitive (line 20), with the upper bound , and filter these results by remaining relations with semi-joins (line 21).
5.3 Analysis of Algorithm 7
Base Case: . The obliviousness is guaranteed by the Intersect primitive. The cache complexity is . In this case, . Hence, Theorem 5.1 holds.
General Case: .
By hypothesis, the recursive invocation of ObliviousGenericJoin at line 4 takes time and cache complexity, since . We then show the correctness and complexity for all invocations of RelaxedTwoWay primitive. Let be an optimal fractional edge cover of . The real size of the two-way join at line 9 can be first rewritten as:
where the inequalities follow the facts that , , and the query decomposition lemma [44]. Hence, is valid upper bound for for each . The real size of the two-way join at lines 18-19 and line 22 can be rewritten as
| (2) |
Let , and . Note as is a valid fractional edge cover for both and . For each tuple , we have
where the first inequality follows from for and , and the third inequality follows from . Now, we can further bound (5.3) as
where the second last inequality follows the query decomposition lemma [44].
Theorem 5.1.
For a general join query , there is an oblivious and cache-agnostic algorithm that can compute for any instance of input size with time complexity and cache complexity under the tall cache and wide block assumptions, where is the optimal fractional edge cover number of .
5.4 Implications to Relaxed Oblivious Algorithms
Our oblivious WCOJ algorithm can be combined with the generalized hypertree decomposition framework [33] to develop a relaxed oblivious algorithm for general join queries.
Definition 5.2 (Generalized Hypertree Decomposition (GHD)).
Given a join query , a GHD of is a pair , where is a tree as an ordered set of nodes and is a labeling function which associates to each vertex a subset of attributes in , , such that (1) for each , there is a node such that ; (2) For each , the set of nodes forms a connected subtree of . The fractional hypertree width of is defined as .
The pseudocode of our algorithm is given in Appendix D. Suppose we take as input a join query , an instance , and an upper bound on the output size . Let be an arbitrary GHD of . We first invoke Algorithm 7 to compute the subquery defined by each node , where , and materialize its join result as one relation. We then apply the classic Yannakakis algorithm [54] on the materialized relations by invoking the SemiJoin primitive for semi-joins and the RelaxedTwoWay primitive for pairwise joins. After removing dangling tuples, the size of each two-way join is upper bound by the size of the final join results and, therefore, . This leads to a relaxed oblivious algorithm whose access pattern only depends on and .
Theorem 5.3.
For a join query , an instance of input size , and parameter , there is a cache-agnostic algorithm that can compute with time complexity and cache complexity, whose access pattern only depends on and , where is the fractional hypertree width of .
6 Conclusion
This paper has introduced a general framework for oblivious multi-way join processing, achieving near-optimal time and cache complexity. However, several intriguing questions remain open for future exploration:
-
•
Balancing Privacy and Efficiency: Recent research has investigated improved trade-offs between privacy and efficiency, aiming to overcome the challenges of worst-case scenarios, such as differentially oblivious algorithms [14].
-
•
Emit model for EM algorithms. In the context of EM join algorithms, the emit model - where join results are directly outputted without writing back to disk - has been considered. It remains open whether oblivious, worst-case optimal join algorithms can be developed without requiring all join results to be written back to disk.
-
•
Communication-oblivious join algorithm for MPC model. A natural connection exists between the MPC and EM models in join processing. While recent work has explored communication-oblivious algorithms in the MPC model [13, 49], extending these ideas to multi-way join processing remains an open challenge.
References
- [1] S. Abiteboul, R. Hull, and V. Vianu. Foundations of databases, volume 8. Addison-Wesley Reading, 1995.
- [2] M. Abo Khamis, H. Q. Ngo, and A. Rudra. Faq: questions asked frequently. In PODS, pages 13–28, 2016.
- [3] A. Aggarwal and S. Vitter, Jeffrey. The input/output complexity of sorting and related problems. Communications of the ACM, 31(9):1116–1127, 1988.
- [4] M. Ajtai, J. Komlós, and E. Szemerédi. An 0 (n log n) sorting network. In STOC, pages 1–9, 1983.
- [5] A. Arasu and R. Kaushik. Oblivious query processing. ICDT, 2013.
- [6] L. Arge, M. A. Bender, E. D. Demaine, B. Holland-Minkley, and J. Ian Munro. An optimal cache-oblivious priority queue and its application to graph algorithms. SIAM Journal on Computing, 36(6):1672–1695, 2007.
- [7] G. Asharov, I. Komargodski, W.-K. Lin, K. Nayak, E. Peserico, and E. Shi. Optorama: Optimal oblivious ram. In Eurocrypt, pages 403–432. Springer, 2020.
- [8] A. Atserias, M. Grohe, and D. Marx. Size bounds and query plans for relational joins. In FOCS, pages 739–748. IEEE, 2008.
- [9] K. E. Batcher. Sorting networks and their applications. In Proceedings of the April 30–May 2, 1968, spring joint computer conference, pages 307–314, 1968.
- [10] P. Beame, P. Koutris, and D. Suciu. Communication steps for parallel query processing. JACM, 64(6):1–58, 2017.
- [11] C. Beeri, R. Fagin, D. Maier, and M. Yannakakis. On the desirability of acyclic database schemes. JACM, 30(3):479–513, 1983.
- [12] A. Beimel, K. Nissim, and M. Zaheri. Exploring differential obliviousness. In APPROX/RANDOM, 2019.
- [13] T. Chan, K.-M. Chung, W.-K. Lin, and E. Shi. Mpc for mpc: secure computation on a massively parallel computing architecture. In ITCS. Schloss Dagstuhl-Leibniz-Zentrum für Informatik, 2020.
- [14] T. H. Chan, K.-M. Chung, B. M. Maggs, and E. Shi. Foundations of differentially oblivious algorithms. In SODA, pages 2448–2467. SIAM, 2019.
- [15] Z. Chang, D. Xie, and F. Li. Oblivious ram: A dissection and experimental evaluation. Proc. VLDB Endow., 9(12):1113–1124, 2016.
- [16] Z. Chang, D. Xie, F. Li, J. M. Phillips, and R. Balasubramonian. Efficient oblivious query processing for range and knn queries. TKDE, 2021.
- [17] Z. Chang, D. Xie, S. Wang, and F. Li. Towards practical oblivious join. In SIGMOD, 2022.
- [18] S. Chu, D. Zhuo, E. Shi, and T.-H. H. Chan. Differentially Oblivious Database Joins: Overcoming the Worst-Case Curse of Fully Oblivious Algorithms. In ITC, volume 199, pages 19:1–19:24, 2021.
- [19] V. Costan and S. Devadas. Intel sgx explained. Cryptology ePrint Archive, 2016.
- [20] N. Crooks, M. Burke, E. Cecchetti, S. Harel, R. Agarwal, and L. Alvisi. Obladi: Oblivious serializable transactions in the cloud. In OSDI, pages 727–743, 2018.
- [21] E. D. Demaine. Cache-oblivious algorithms and data structures. Lecture Notes from the EEF Summer School on Massive Data Sets, 8(4):1–249, 2002.
- [22] S. Deng and Y. Tao. Subgraph enumeration in optimal i/o complexity. In ICDT. Schloss Dagstuhl–Leibniz-Zentrum für Informatik, 2024.
- [23] S. Devadas, M. v. Dijk, C. W. Fletcher, L. Ren, E. Shi, and D. Wichs. Onion oram: A constant bandwidth blowup oblivious ram. In TCC, pages 145–174. Springer, 2016.
- [24] S. Eskandarian and M. Zaharia. Oblidb: Oblivious query processing for secure databases. Proc. VLDB Endow., 13(2).
- [25] R. Fagin. Degrees of acyclicity for hypergraphs and relational database schemes. JACM, 30(3):514–550, 1983.
- [26] A. Z. Fan, P. Koutris, and H. Zhao. Tight bounds of circuits for sum-product queries. SIGMOD, 2(2):1–20, 2024.
- [27] J. Flum, M. Frick, and M. Grohe. Query evaluation via tree-decompositions. JACM, 49(6):716–752, 2002.
- [28] M. Frigo, C. E. Leiserson, H. Prokop, and S. Ramachandran. Cache-oblivious algorithms. In FOCS, pages 285–297. IEEE, 1999.
- [29] C. Gentry, K. A. Goldman, S. Halevi, C. Julta, M. Raykova, and D. Wichs. Optimizing oram and using it efficiently for secure computation. In PETs, pages 1–18. Springer, 2013.
- [30] O. Goldreich. Towards a theory of software protection and simulation by oblivious rams. In STOC, pages 182–194, 1987.
- [31] O. Goldreich and R. Ostrovsky. Software protection and simulation on oblivious rams. JACM, 43(3):431–473, 1996.
- [32] M. T. Goodrich. Data-oblivious external-memory algorithms for the compaction, selection, and sorting of outsourced data. In SPAA, pages 379–388, 2011.
- [33] G. Gottlob, N. Leone, and F. Scarcello. Hypertree decompositions and tractable queries. JCSS, 64(3):579–627, 2002.
- [34] H. Hacigümüş, B. Iyer, C. Li, and S. Mehrotra. Executing sql over encrypted data in the database-service-provider model. In SIGMOD, pages 216–227, 2002.
- [35] B. He and Q. Luo. Cache-oblivious nested-loop joins. In CIKM, pages 718–727, 2006.
- [36] X. Hu. Cover or pack: New upper and lower bounds for massively parallel joins. In PODS, pages 181–198, 2021.
- [37] X. Hu, M. Qiao, and Y. Tao. I/o-efficient join dependency testing, loomis–whitney join, and triangle enumeration. JCSS, 82(8):1300–1315, 2016.
- [38] B. Ketsman and D. Suciu. A worst-case optimal multi-round algorithm for parallel computation of conjunctive queries. In PODS, pages 417–428, 2017.
- [39] P. Koutris, P. Beame, and D. Suciu. Worst-case optimal algorithms for parallel query processing. In ICDT. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik, 2016.
- [40] S. Krastnikov, F. Kerschbaum, and D. Stebila. Efficient oblivious database joins. VLDB, 13(12):2132–2145, 2020.
- [41] E. Kushilevitz, S. Lu, and R. Ostrovsky. On the (in) security of hash-based oblivious ram and a new balancing scheme. In SODA, pages 143–156. SIAM, 2012.
- [42] W.-K. Lin, E. Shi, and T. Xie. Can we overcome the n log n barrier for oblivious sorting? In SODA, pages 2419–2438. SIAM, 2019.
- [43] H. Q. Ngo, E. Porat, C. Ré, and A. Rudra. Worst-case optimal join algorithms. JACM, 65(3):1–40, 2018.
- [44] H. Q. Ngo, C. Ré, and A. Rudra. Skew strikes back: New developments in the theory of join algorithms. Acm Sigmod Record, 42(4):5–16, 2014.
- [45] V. Ramachandran and E. Shi. Data oblivious algorithms for multicores. In SPAA, pages 373–384, 2021.
- [46] S. Sasy, A. Johnson, and I. Goldberg. Fast fully oblivious compaction and shuffling. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security, pages 2565–2579, 2022.
- [47] E. Shi. Path oblivious heap: Optimal and practical oblivious priority queue. In 2020 IEEE Symposium on Security and Privacy (SP), pages 842–858. IEEE, 2020.
- [48] E. Stefanov, M. V. Dijk, E. Shi, T.-H. H. Chan, C. Fletcher, L. Ren, X. Yu, and S. Devadas. Path oram: an extremely simple oblivious ram protocol. JACM, 65(4):1–26, 2018.
- [49] Y. Tao, R. Wang, and S. Deng. Parallel communication obliviousness: One round and beyond. Proceedings of the ACM on Management of Data, 2(5):1–24, 2024.
- [50] T. L. Veldhuizen. Leapfrog triejoin: A simple, worst-case optimal join algorithm. In ICDT, 2014.
- [51] J. S. Vitter. External memory algorithms and data structures: Dealing with massive data. ACM Computing surveys (CsUR), 33(2):209–271, 2001.
- [52] X. Wang, H. Chan, and E. Shi. Circuit oram: On tightness of the goldreich-ostrovsky lower bound. In CCS, pages 850–861, 2015.
- [53] Y. Wang and K. Yi. Query evaluation by circuits. In PODS, 2022.
- [54] M. Yannakakis. Algorithms for acyclic database schemes. In VLDB, pages 82–94, 1981.
- [55] W. Zheng, A. Dave, J. G. Beekman, R. A. Popa, J. E. Gonzalez, and I. Stoica. Opaque: An oblivious and encrypted distributed analytics platform. In NSDI 17, pages 283–298, 2017.
Appendix A Missing Materials in Section 1
Graph Joins. A join query is a graph join if for each , i.e., each relation contains at most two attributes.
Loomis-Whitney Joins.
A join query is a Loomis-Whitney join if and .
Appendix B Oblivious Primitives in Section 2
We provide the algorithm descriptions and pseudocodes for the oblivious primitives declared in Section 2.2. For the local variables used in these primitives, key, val, and , we do not need to establish obliviousness for them because they are stored in the trusted memory during the entire execution of the algorithms and the adversaries cannot observe the access pattern to them. But for all the temporal sets with non-constant size, and , they are stored in the untrusted memory.
SemiJoin.
Given two input relations , and their common attribute(s) , the goal is to replace each tuple in that cannot be joined with any tuple in with a dummy tuple , i.e., compute . As shown in Algorithm 10, we first sort all tuples by their join values and break ties by putting -tuples before -tuples if they share the same join value in . We then perform a linear scan, using an additional variable key to track the largest join value of the previous tuple that is no larger than the join value of the current tuple visited. More specifically, we distinguish two cases on . Suppose . If , we just write to the result array . Otherwise, we write a dummy tuple to . Suppose . We simply write a dummy tuple to and update key with . At last, we compact the elements in to move all to the last and keep the first tuples in .
ReduceByKey.
Given an input relation , some of which are distinguished as , a set of key attribute(s) , a weight function , and an aggregate function , the goal is to output the aggregation of each key value, which is defined as the function over the weights of all tuples with the same key value. This primitive can be used to compute degree information, i.e., the number of tuples displaying a specific key value in a relation.
As shown in Algorithm 11, we sort all tuples by their key values (values in attribute(s) ) while moving all distinguished tuples to the last of the relation. Then, we perform a linear scan, using an additional variable key to track the key value of the previous tuple, and val to track the aggregation over the weights of tuples visited. We distinguish three cases. If , the remaining tuples in are all distinguished as , implied by the sorting. We write a dummy tuple to in this case. If and , we simply write a dummy tuple to , and increase val by . If and , the values of all elements with key key are already aggregated into val. In this case, we need to write to and update val with , i.e., the value of current tuple, and key with . At last, we compact the tuples in by moving all to the last and keep the first tuples in for obliviousness.
Annotate.
Given an input relation , where each tuple is associated with a key, and a list of key-value pairs, where each pair is associated with a distinct key, the goal is to attach, for each tuple in , the value of the corresponding distinct pair in matched by the key. As shown in Algorithm 12, we first sort all tuples in and by their key values in attribute , while moving all to the last of the relation and breaking ties by putting all -tuples before -tuples when they have the same key value. We then perform a linear scan, using another two variables to track the -tuple with the largest key but no larger than the key of the current tuple visited. We distinguish the following cases. If is a -tuple and , we update with . If is a -tuple and , we attach val to by writing to . We write a dummy tuple to in the remaining cases. Finally, we compact the tuples in to remove unnecessary dummy tuples.
MultiNumber.
Given an input relation , each associated with a key attribute(s) , the goal is to attach consecutive numbers to tuples with the same key.
As shown in Algorithm 13, we first sort all tuples in by attribute . We then perform a linear scan, using two additional variables to track the key of the previous tuples, and the number assigned to the previous tuple. Consider as the current element visited. If , we simply increase val by . Otherwise, we set val to and update key with . In both cases, we assign val to tuple and writw to .
Project.
Given an input relation defined over attributes , and a subset of attributes , the goal is to output the list (without duplication). This primitive can be simply solved by sorting by attribute(s) and then removing duplicates by a linear scan.
Intersect.
Given two input arrays of distinct elements separately, the goal is to output the common elements appearing in both and . This primitive can be done with sorting by attribute(s) , and then a linear scan would suffice to find out common elements.
Augment.
Given two relations of at most tuples and their common attribute(s) , the goal is to attach each tuple the number of tuples in that can be joined with on . The Augment primitive can be implemented by the ReduceByKey and Annotate primitives. See Algorithm 14.
Appendix C RelaxedTwoWay Primitive
Given two relations of tuples and an integral parameter , where and , the goal is to output a relation of size whose first tuples are the join results and the remaining tuples are dummy tuples. Arasu et al. [5] first proposed an oblivious algorithm for , but it involves rather complicated primitive without giving complete details [16]. Krastnikov et al. [40] later showed a more clean and effective version, but this algorithm does not have a satisfactory cache complexity. Below, we present our own version of the relaxed two-way join. We need one important helper primitive first.
Expand Primitive.
Given a sequence of and a parameter , the goal is to expand each tuple with copies and output a table of tuples. The naive way of reading a pair and then writing copies does not preserve obliviousness since the number of consecutive writes can leak the information. Alternatively, one might consider writing a fixed number of tuples after reading each pair. Still, the ordering of reading pairs is critical for avoiding dummy writes and avoiding too many pairs stored in trusted memory (this strategy is exactly adopted by [5]).
We present a simpler algorithm by combining the oblivious primitives. Suppose is the output table of , such that contains copies of , and any tuple comes before if . As described in Algorithm 15, it consists of four phases:
-
•
(lines 1-4). for each pair with , attach the beginning position of in , which is . For the remaining pairs with , replace them with and attach with the infinite position as these tuples will not participate in any join result;
-
•
(lines 5-7) pad dummy tuples and attach them with consecutive numbers ; after sorting the well-defined positions, each tuple will be followed by dummy tuples, and all dummy tuples with infinite positions are put at last;
-
•
(lines 8-14) for each tuple , we replace it with but the following dummy tuples with . After moving all dummy tuples to the end, the first elements are the output.
It can be easily checked that the access pattern of Expand only depends on the values of and . Moreover, Expand is cache-agnostic since they are constructed by sequential compositions of cache-agnostic primitives (Scan, Sort and Compact).
Lemma C.1.
Given a relation of input size and a parameter , the Expand primitive is cache-agnostic with time complexity and cache complexity, whose access pattern only depends on and .
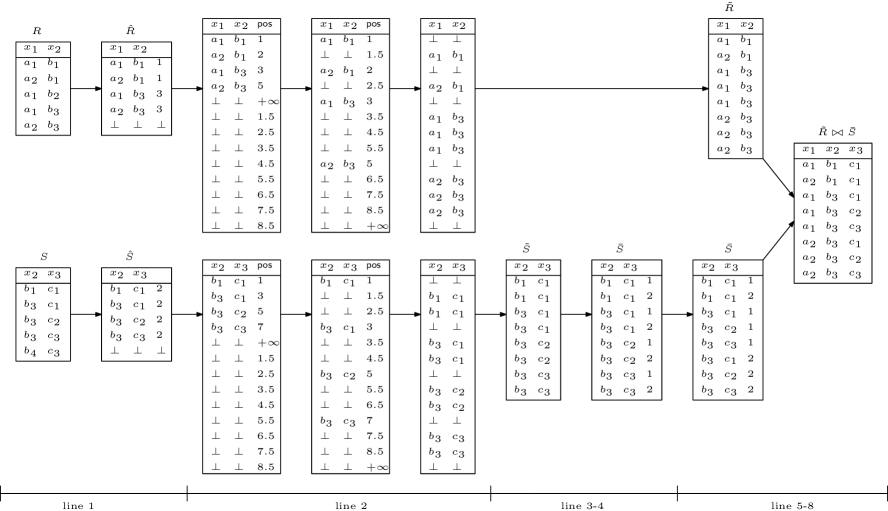
Now, we are ready to describe the algorithmic details of RelaxedTwoWay primitive. The high-level idea is to simulate the sort-merge join algorithm without revealing the movement of pointers in the merge phase. Let be the join results sorted by lexicographically. The idea is to transform into a sub-relation of by keeping attributes separately, without removing duplicates. Then, doing a one-to-one merge to obtain the final join results suffices. As described in Algorithm 16, we construct these two sub-relations from the input relations via the following steps (a running example is given in Figure 1):
-
•
(line 1) attach each tuple with the number of tuples it can be joined in the other relation;
-
•
(line 2) expand each tuple to the annotated number of copies;
-
•
(lines 3-4) prepare the expanded and with the “correct” ordering, as it appears in the final sort-merge join results;
-
•
(lines 5-8) perform a one-to-one merge of ordered tuples in and ;
As a sequential composition of (relaxed) oblivious primitives, RelaxedTwoWay is cache-agnostic, with time complexity and cache complexity, whose access pattern only depends on and .