Optimized Dirac Woods-Saxon basis for covariant density functional theory
Abstract
The Woods-Saxon basis has achieved great success in both nonrelativistic and covariant density functional theories in recent years. Due to its nonanalytical nature, however, applications of the Woods-Saxon basis are numerically complicated and computationally time consuming. In this paper, based on the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc), we check in detail the convergence with respect to the basis space in the Dirac sea. An optimized Dirac Woods-Saxon basis is proposed, whose corresponding potential is close to the nuclear mean field. It is shown that the basis space of the optimized Dirac Woods-Saxon basis required for convergence is substantially reduced compared with the original one. In particular, it does not need to contain the bases from continuum in the Dirac sea. The application of the optimized Woods-Saxon basis would greatly reduce computing resource for large-scale density functional calculations.
I Introduction
The study of exotic nuclei far from the stability line has been at the forefront of nuclear physics research since the discovery of the first halo nucleus 11Li in the 1980s Tanihata et al. (1985). In addition to halos, novel phenomena found in exotic nuclei include the pygmy resonance Adrich et al. (2005), the disappearance of traditional magic numbers and the emergence of new ones Ozawa et al. (2000). These phenomena not only promote the worldwide development of radioactive ion beam facilities but also challenge conventional nuclear models.
The nuclear density functional theory (DFT) is able to provide a unified description for almost all nuclei in the nuclear chart and has become one of the most important microscopic methods for the study of nuclear structure Bender et al. (2003). Its relativistic version, i.e., the covariant density functional theory (CDFT), has attracted wide attention in recent years for many advantages, such as the automatic inclusion of the nucleonic spin degree of freedom and the spin-orbital interaction Ren and Zhao (2020), the explanation of the pseudospin symmetry in the nucleon spectrum Ginocchio (1997); Meng et al. (1998, 1999); Chen et al. (2003); Ginocchio (2005); Liang et al. (2015) and the spin symmetry in the antinucleon spectrum Zhou et al. (2003a); He et al. (2006); Liang et al. (2015), and the natural inclusion of the nuclear magnetism Koepf and Ring (1989), which plays an important role in nuclear magnetic moments Yao et al. (2006); Arima (2011); Li et al. (2011a, b); Li and Meng (2018) and nuclear rotations Meng et al. (2013); König and Ring (1993); Afanasjev et al. (2000); Afanasjev and Ring (2000); Afanasjev and Abusara (2010); Zhao et al. (2011a, b, 2012, 2015); Wang (2017, 2018); Ren et al. (2019, 2020).
In the nuclear DFT, the equations of motion for (quasi)nucleons are either solved in coordinate space or transformed into a matrix diagonalization problem in a complete basis, e.g., the harmonic oscillator (HO) basis. As a good approximation for the mean field of stable nuclei, the HO potential can be solved analytically, and the HO wave function in analytical form may bring convenience in the calculation of some matrix elements, e.g., the separable pairing force Tian et al. (2009). Due to the incorrect asymptotic behavior of HO wave functions, however, the expansion in a localized HO basis is incapable of describing nuclei with very diffuse spatial density distributions. To improve the asymptotic behavior of HO wave functions, a transformed HO basis has been proposed in Refs. Stoitsov et al. (1998a, b) via a local scaling transformation.
Solutions in coordinate space can describe properly the asymptotic behavior of wave functions. When dealing with systems having small separation energy, the coordinate-space calculations in large boxes were found to be more effective than the transformed HO basis Zhang et al. (2013). In the CDFT, the relativistic Hartree equation that neglects pairing correlations has been successfully solved on a three-dimensional lattice Ren et al. (2017). For the treatment of pairing correlations in weakly bound nuclei, it was shown that the Bogoliubov transformation is more suitable than the widely used Bardeen-Cooper-Schrieffer (BCS) method Dobaczewski et al. (1984); Meng (1998). However, the relativistic Hartree-Bogoliubov equation in coordinate space has only been solved by assuming spherical symmetry Meng and Ring (1996); Pöschl et al. (1997); Meng and Ring (1998). Solving the deformed relativistic Hartree-Bogoliubov equation in coordinate space is extremely difficult if not impossible Zhou et al. (2000).
A Woods-Saxon basis was proposed in Ref. Zhou et al. (2003b) as a reconciler between the HO basis and coordinate space. It is obtained by solving the Schrödinger equation or the Dirac equation containing spherical Woods-Saxon potentials with box boundary conditions, and is correspondingly referred to as the Schrödinger Woods-Saxon (SWS) or Dirac Woods-Saxon (DWS) basis. The Woods-Saxon basis has the advantage in providing appropriate asymptotic behaviors of wave functions because of the nature of the Woods-Saxon type potential Woods and Saxon (1954). It was shown in Ref. Zhou et al. (2003b) that for spherical systems the solution of the relativistic Hartree equations in the Woods-Saxon basis is almost equivalent to the solution in coordinate space. Up to the present, the SWS basis has been applied to the spherical Hartree-Fock-Bogoliubov theory Schunck and Egido (2008a, b), and the DWS basis to the spherical relativistic Hartree theory Zhou et al. (2003b), spherical relativistic Hartree-Fock-Bogoliubov theory Long et al. (2010a, b), deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) Zhou et al. (2010); Li et al. (2012), deformed relativistic Hartree-Fock theory Geng et al. (2020), and deformed relativistic Hartree-Fock-Bogoliubov theory Geng and Long (2022).
Recently, the DRHBc theory has been successful in studying deformed halo nuclei Zhou et al. (2010); Li et al. (2012); Sun et al. (2018); Zhang et al. (2019); Sun et al. (2020); Yang et al. (2021); Sun (2021); Zhong et al. (2022), investigating the deformation effects on the location of the neutron drip line In et al. (2021), predicting stability peninsulas beyond the primary neutron drip line Zhang et al. (2021); Pan et al. (2021); He et al. (2021), exploring rotational excitations of exotic nuclei with the angular momentum projection Sun and Zhou (2021a, b), and revealing the shape coexistence from light to heavy nuclei In et al. (2020); Choi et al. (2022); Kim et al. (2022). In particular, stimulated by the success of the fist nuclear mass table with continuum effects Xia et al. (2018), many efforts have been made to construct an upgraded mass table including simultaneously deformation and continuum effects based on the DRHBc theory Zhang et al. (2020), and the DRHBc mass table for even-even nuclei has just been published Zhang et al. (2022). The next step of the DRHBc mass table is the systematical calculation of odd-mass and odd-odd nuclei in the nuclear chart Pan et al. (2022). As mentioned in Ref. Zhang et al. (2020), since the DRHBc theory with the DWS basis is numerically very complicated, large-scale DRHBc calculations are extremely time consuming, especially for odd nuclei where the blocking effects should be considered.
This paper is devoted to exploring methods to reduce the computing cost of the DRHBc theory from the perspective of the DWS basis space. On the one hand, the DWS basis space includes both bases in the Fermi sea and in the Dirac sea for completeness Zhou et al. (2003b). In order to guarantee the convergence with respect to the basis space, it was suggested to take the number of DWS bases in the Dirac sea as the same as that in the Fermi sea Zhou et al. (2010); Li et al. (2012), and later all DRHBc studies followed this way. However, in the spherical relativistic Hartree-Fock-Bogoliubov Long et al. (2010a, b) and deformed relativistic Hartree-Fock Geng et al. (2020) calculations, the number of DWS bases in the Dirac sea is only about one third of that in the Fermi sea. On the other hand, usually the Woods-Saxon potential for the basis is parameterized Koepf and Ring (1991). It is natural to consider the possibility of an optimized DWS basis whose corresponding potential is closer to the mean field of the calculated nucleus, and as a result the basis space required for convergence would be reduced. Following this idea we examine in detail the convergence behavior against the basis truncation in the Dirac sea and propose an optimized Woods-Saxon basis for the large-scale DRHBc calculations as well as other DFT calculations in the present paper.
II Theoretical framework
The details of the DRHBc theory with meson-exchange and point-coupling density functionals can be found in Refs. Li et al. (2012) and Zhang et al. (2020) respectively. In the DRHBc theory, the relativistic Hartree-Bogoliubov (RHB) equation reads Kucharek and Ring (1991)
| (1) |
where is the Fermi energy, and and are the quasiparticle energy and wave function, respectively. is the Dirac Hamiltonian,
| (2) |
is the pairing potential,
| (3) |
with a density-dependent force of zero range,
| (4) |
and the pairing tensor Ring and Schuck (1980). In principle, the zero-range pairing force is not naturally converged with the pairing window, and both appropriate pairing strength and pairing window are significant in the present DRHBc calculations Zhang et al. (2020). It is expected to implement the finite-range pairing force, e.g., the Gogny Meng (1998) or separable pairing force Tian et al. (2009), in the DRHBc theory in future work.
In the DRHBc theory, the scalar potential and vector potential in Eq. (2) are expanded in terms of the Legendre polynomials,
| (5) |
so are the pairing potential and various densities. In order to properly describe the large spatial extension of weakly bound nuclei, the RHB equation, (1), is solved in the DWS basis Zhou et al. (2003b). After solving the RHB equations self-consistently, the total energy, rms radii, quadrupole deformation, and other physical quantities can be calculated.
The wave function of the DWS basis can be written as
| (6) |
where , , and are its quantum numbers, which will be introduced below. , , and are spatial coordinate, spin, and index ( or ) for upper or lower component. is the radial wave function,
| (7) |
satisfying the radial Dirac equations
| (8) | ||||
where is the eigenvalue (energy), and is the node number. and are parameterized Woods-Saxon potentials for the basis,
| (9) | |||
where , , and depict the depth, width, and diffuseness of the potential, respectively. A usual choice of the parametrization can be found in Ref. Koepf and Ring (1991). is the spinor spherical harmonic,
| (10) |
where is the spherical harmonic function, is the spin wave function, is the orbital angular momentum, is the total angular momentum, and , , and are the third components of , , and , respectively. The quantum number is given by the parity and , , running over positive and negative integers . The orbital angular momenta for upper and lower components are
| (11) |
respectively.
III Numerical details
Taking light 20Ne, medium-heavy 112Mo, and heavy 300Th nuclei as examples, a detailed convergence check of the total energy against the energy cutoff in the Dirac sea will be performed. The radial Dirac equations for the DWS basis, (8), are solved with a box size fm and a mesh size fm Zhou et al. (2003b); Zhang et al. (2020). The angular momentum cutoff for the DWS basis is Zhang et al. (2020). The Legendre expansion truncations in Eq. (5) are chosen as and for nuclei with and , respectively Pan et al. (2019); Zhang et al. (2020). The above numerical details are the same as those used in the DRHBc mass table calculations for even-even nuclei Zhang et al. (2022). Since a zero-range pairing interaction (4) is adopted in the DRHBc theory, in the numerical check of the convergence with respect to the basis space pairing correlations should be neglected. In the DRHBc mass table calculations Zhang et al. (2022), the energy cutoff for the DWS basis in the Fermi sea MeV and the number of DWS bases in the Dirac sea is the same as that in the Fermi sea, which are able to give converged results as shown in Ref. Zhang et al. (2020) and thus are taken as the benchmark in the following.
IV Results and discussion
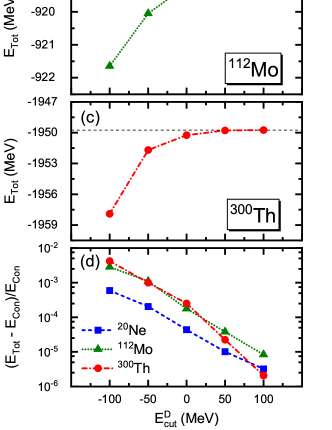
Figure 1 shows the convergence of the total energy with respect to the energy cutoff in the Dirac sea (whose zero point is set to be the continuum threshold in the Dirac sea) for 20Ne, 112Mo, and 300Th. From panels (a), (b), and (c) one finds that, although the total energies of the three nuclei are very different, they show a similar convergence trend with the increase of . When MeV, the difference of the calculated total energy from the converged one (horizontal dashed line) becomes marginal in their respective scale. It is clearly seen in panel (d) that their relative differences from the converged results are on the order of . Therefore, MeV for the DWS basis can lead to a satisfactory accuracy in the DRHBc calculation. The value greater than zero suggests that the contribution of the bases from continuum in the Dirac sea is non-negligible with the adopted DWS basis. A similar conclusion was found in a recent study based on the axially deformed relativistic Hartree-Fock-Bogoliubov theory with the density functional PKA1 Geng and Long (2022).

To compare the number of bases in the Dirac sea with MeV and that in the Fermi sea with MeV, Fig. 2 exhibits and the ratio as functions of the absolute value of the quantum number in the calculations of 20Ne, 112Mo, and 300Th. The as a function of is shown in Fig. 2(a), where the basis numbers for neutrons/protons and positive/negative parities are close to each other and summed. First, we can see that the s are not very different for 20Ne, 112Mo, and 300Th because of the large energy cutoff MeV, and they decrease slowly and almost linearly with . Second, as shown in Figs. 2(b) and 2(c), all the ratios of are smaller than 1, meaning that the basis space in the Dirac sea is not necessarily as large as that in the Fermi sea in order to obtain converged results. Third, the ratio of shows an odd-even staggering with the increase of . This is because, for the same , the orbital angular momentum of the basis in the Fermi sea and that in the Dirac sea differs by , e.g., for positive parity the ratio is calculated in the sequence of , , , for . In a basis space truncated by energy, the number of bases corresponding to spin-orbit partners is in general the same, and it decreases with the increasing . As a result, the numerator and denominator do not decrease synchronously, leading to the odd-even staggering. Fourth, the ratio decreases with on the whole, which reflects the influence of the different depths of the potentials in the Fermi sea and Dirac sea. Finally, the ratios of for the heavy nucleus 300Th are larger than those for lighter ones 20Ne and 112Mo, which shows that the bases in the Dirac sea are more important for heavy nuclei and is consistent with the finding in Ref. Geng and Long (2022). It is also noted that the ratios for protons are obviously larger than those for neutrons in the calculation of 300Th, which will be further discussed below.
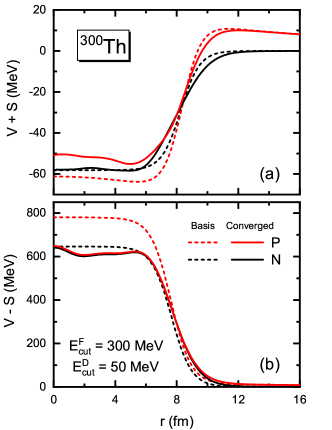
Is it possible to optimize the usual DWS basis to achieve a better performance? We note that Ref. Zhou et al. (2003b) has found when the Woods-Saxon potentials for the basis become more different from the converged mean-field potentials of the calculated nucleus, the contribution of the basis in the Dirac sea will be larger. To illustrate this difference in potentials, Fig. 3 compares for 300Th the Woods-Saxon potentials for the basis and the converged mean-field ones, and for the latter the angular dependence has been averaged. For the potential of neutrons, the difference mainly appears in 6 12 fm and is not remarkable. For the potential of neutrons, distinguishable difference can also be found in 0 6 fm. For protons, however, one finds significant differences in both and potentials. The depth of the potential differs by about 10 MeV, and the difference in that of the potential is larger than 100 MeV. This explains why the ratios for protons are obviously larger than those for neutrons in Fig. 2(c).
According to the above discussion, a possible way to optimize the DWS basis and reduce the basis space is using the Woods-Saxon potentials close to the converged mean-field ones to generate a new basis replacing the original DWS basis. As an attempt, for deformed nuclei, we solve a Dirac equation containing the angle averaged converged mean-field potentials to obtain the new basis, referred to as the optimized Dirac Woods-Saxon (ODWS) basis. This optimized basis is in spirit somewhat similar to the method proposed in Refs. Zhang and Onley (1988, 1991), where deformed relativistic Hartree equations are solved by expanding the Dirac spinors in terms of basis functions calculated from the self-consistent spherical Hartree potential of the same or a nearby nucleus. At the end of this section, we will see the unique advantage making the ODWS basis superior to the recipe in Refs. Zhang and Onley (1988, 1991).
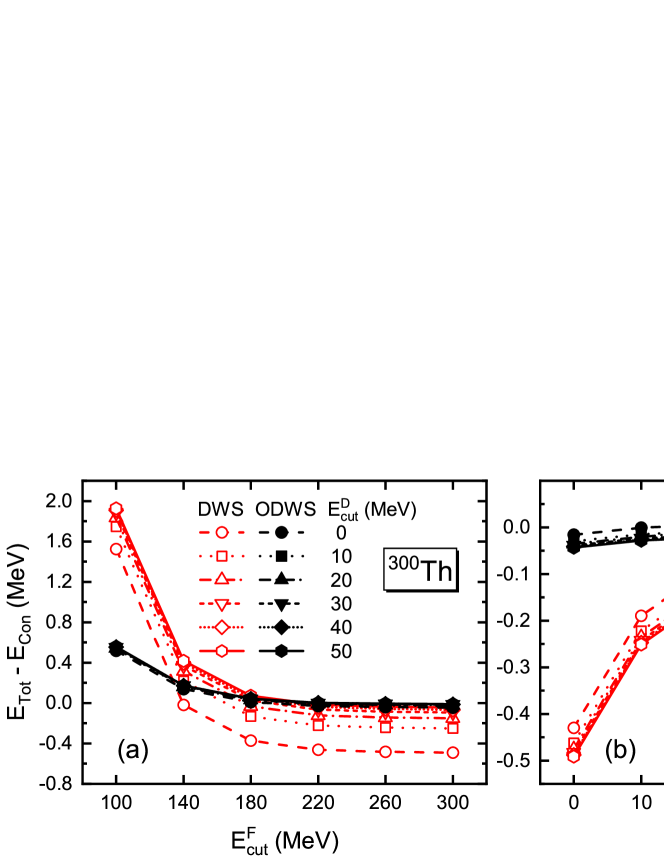
To test the performance of the ODWS basis with respect to the convergence behavior, Fig. 4(a) shows the difference of the total energy from the converged result as a function of in both calculations with the DWS and ODWS bases for 300Th. It is easy to see that although both calculations lead to convergence with increasing cutoff energies, the results obtained with the ODWS basis are always closer to the converged one. In particular, when MeV, the total energy calculated with the ODWS basis is MeV lower than that with the DWS basis. The results with the ODWS basis not only exhibit better convergence with the increasing , but also hardly change with the increasing . This suggests that we can obtain converged results even without the bases from continuum in the Dirac sea, which would significantly reduce the basis space.
To more finely evaluate the convergence with respect to , in Fig. 4(b) we reduce the range of from [100, 300] MeV in Fig. 4(a) to [200, 300] MeV, and thus we rescale the vertical axis. It is found that for the usual DWS basis, the calculated total energy changes by about 0.5 MeV from to 50 MeV, suggesting the importance of the bases from continuum in the Dirac sea. In contrast, for the ODWS basis, the calculated total energy is almost a constant under different cutoff energies. For example, the difference between the results from MeV, MeV and MeV, MeV is only 0.005 MeV, about of its total energy. Therefore, the calculation using the ODWS basis can provide converged total energies for heavy nuclei such as 300Th, with MeV and MeV that are both smaller than those required for the DWS basis. We have further reduced to negative values to see if a smaller ODWS basis space in the Dirac sea could give converged results. It turns out that MeV leads to a ground-state deformation completely different from the converged one, and the difference between the total energy from MeV and the converged one is more than 0.3 MeV. This indicates that some bound bases within 50 MeV from the continuum threshold in the Dirac sea are important for convergence. Thus, an energy cutoff of MeV, i.e., the truncation right at the continuum threshold in the Dirac sea, is suggested for the ODWS basis to guarantee convergence for different nuclei.
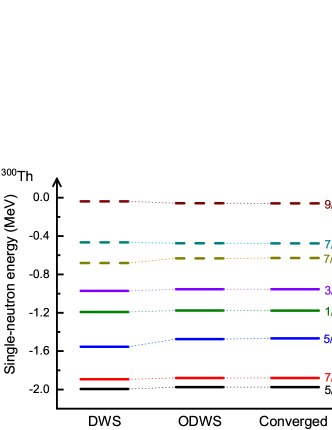
It is also interesting to check whether the ODWS basis space truncated by MeV and MeV can guarantee the convergence of single-particle properties. Figure 5 compares the single-neutron levels of 300Th near the continuum threshold calculated using DWS and ODWS bases as well as those from the converged result. Distinguishable differences can be seen between the result from the DWS basis and the other two. For example, the difference for the single-neutron energy of the state is nearly 0.1 MeV. On the other hand, the result from the ODWS basis and the converged one are almost the same, with the largest difference less than 0.01 MeV. Therefore, according to this comparison and the convergence of the total energy in Fig. 4, MeV and MeV for the ODWS basis are enough to give converged results in the DRHBc calculation. They correspond to a certainly smaller basis space than that of the DWS basis and, thus, require less computing resource.
Finally, one may argue that using the converged mean-field potentials to construct the ODWS basis makes little sense, since one never knows a priori the converged potentials of the calculated nucleus. This is not true. A natural way out is to construct a new basis set with new potentials in each step of the iterative solution of RHB equations. This has been done and can lead to the same results as those calculated by the ODWS basis, but it is found that the reconstruction of the basis in each step is time consuming. In practice, we find that during the iteration only one reconstruction of the basis is enough to get the same results. Here the reconstruction happens when a reference parameter MeV, in which means the largest difference of the mean-field potentials between the present step and the previous step during the iteration. (When is less than a certain value, e.g., MeV, the self-consistent iteration converges.) Note that there is no need to change the cutoff energies during the iteration in the above approach; namely, MeV and MeV are used for the original DWS basis from the beginning and for the ODWS basis after MeV, up to convergence. It is also worthwhile to mention that, although this approach replaces bases during the iteration, there is almost no difference in the convergence steps compared with the calculation using only the DWS basis. Therefore, the ODWS basis is practicable, and its application to large-scale DRHBc mass table calculations is expected.
V Summary
In summary, based on the deformed relativistic Hartree-Bogoliubov theory in continuum, we check in detail the convergence with respect to the basis space in the Dirac sea, and propose an optimized Woods-Saxon basis for nuclear density functional theory. By checking the convergence with respect to the energy cutoff, we demonstrate that the basis space in the Dirac sea is not necessarily as large as that in the Fermi sea in order to obtain results with a satisfactory convergence accuracy of . Then we use the converged mean-field potential to generate a new basis set, referred to as the optimized Dirac Woods-Saxon basis. It is found that the new basis can lead to convergence in both total energy and single-particle levels with a basis space truncated by the energy cutoff MeV in the Fermi sea and MeV in the Dirac sea, which is substantially smaller than the original basis space required for convergence. Finally, we suggest a method to construct the optimized Dirac Woods-Saxon basis during the iterative solution of relativistic Hartree-Bogoliubov equations, which guarantees the practicability of the new basis with a suitable basis space.
The application of the optimized Dirac Woods-Saxon basis to large-scale mass-table-type calculations based on the covariant density functional theory is expected to significantly reduce computing resource. Similarly, its counterpart, the optimized Schrödinger Woods-Saxon basis, is also available for nonrelativistic density functional theory.
Acknowledgements.
Helpful discussions with members of the DRHBc Mass Table Collaboration are highly appreciated. This work was partly supported by the National Natural Science Foundation of China (Grants No. 11935003, No. 11875075, No. 11975031, and No. 12070131001), the National Key R&D Program of China (Contracts No. 2017YFE0116700 and No. 2018YFA0404400), the State Key Laboratory of Nuclear Physics and Technology, Peking University (Grant No. NPT2020ZZ01), and High-performance Computing Platform of Peking University.References
- Tanihata et al. (1985) I. Tanihata, H. Hamagaki, O. Hashimoto, Y. Shida, N. Yoshikawa, K. Sugimoto, O. Yamakawa, T. Kobayashi, and N. Takahashi, Phys. Rev. Lett. 55, 2676 (1985).
- Adrich et al. (2005) P. Adrich, A. Klimkiewicz, M. Fallot, K. Boretzky, T. Aumann, D. Cortina-Gil, U. D. Pramanik, T. W. Elze, H. Emling, H. Geissel, M. Hellström, K. L. Jones, J. V. Kratz, R. Kulessa, Y. Leifels, C. Nociforo, R. Palit, H. Simon, G. Surówka, K. Sümmerer, and W. Waluś (LAND-FRS Collaboration), Phys. Rev. Lett. 95, 132501 (2005).
- Ozawa et al. (2000) A. Ozawa, T. Kobayashi, T. Suzuki, K. Yoshida, and I. Tanihata, Phys. Rev. Lett. 84, 5493 (2000).
- Bender et al. (2003) M. Bender, P.-H. Heenen, and P.-G. Reinhard, Rev. Mod. Phys. 75, 121 (2003).
- Ren and Zhao (2020) Z. X. Ren and P. W. Zhao, Phys. Rev. C 102, 021301(R) (2020).
- Ginocchio (1997) J. N. Ginocchio, Phys. Rev. Lett. 78, 436 (1997).
- Meng et al. (1998) J. Meng, K. Sugawara-Tanabe, S. Yamaji, P. Ring, and A. Arima, Phys. Rev. C 58, R628(R) (1998).
- Meng et al. (1999) J. Meng, K. Sugawara-Tanabe, S. Yamaji, and A. Arima, Phys. Rev. C 59, 154 (1999).
- Chen et al. (2003) T. S. Chen, H. F. Lü, J. Meng, S. Q. Zhang, and S. G. Zhou, Chin. Phys. Lett. 20, 358 (2003).
- Ginocchio (2005) J. N. Ginocchio, Phys. Rep. 414, 165 (2005).
- Liang et al. (2015) H. Liang, J. Meng, and S.-G. Zhou, Phys. Rep. 570, 1 (2015).
- Zhou et al. (2003a) S.-G. Zhou, J. Meng, and P. Ring, Phys. Rev. Lett. 91, 262501 (2003a).
- He et al. (2006) X. T. He, S. G. Zhou, J. Meng, E. G. Zhao, and W. Scheid, Eur. Phys. J. A 28, 265 (2006).
- Koepf and Ring (1989) W. Koepf and P. Ring, Nucl. Phys. A 493, 61 (1989).
- Yao et al. (2006) J. M. Yao, H. Chen, and J. Meng, Phys. Rev. C 74, 024307 (2006).
- Arima (2011) A. Arima, Sci. China Phys. Mech. Astron. 54, 188 (2011).
- Li et al. (2011a) J. Li, J. Meng, P. Ring, J. M. Yao, and A. Arima, Sci. China Phys. Mech. Astron. 54, 204 (2011a).
- Li et al. (2011b) J. Li, J. M. Yao, J. Meng, and A. Arima, Prog. Theor. Phys. 125, 1185 (2011b).
- Li and Meng (2018) J. Li and J. Meng, Front. Phys. 13, 132109 (2018).
- Meng et al. (2013) J. Meng, J. Peng, S. Q. Zhang, and P. W. Zhao, Front. Phys. 8, 55 (2013).
- König and Ring (1993) J. König and P. Ring, Phys. Rev. Lett. 71, 3079 (1993).
- Afanasjev et al. (2000) A. V. Afanasjev, P. Ring, and J. Konig, Nucl. Phys. A 676, 196 (2000).
- Afanasjev and Ring (2000) A. V. Afanasjev and P. Ring, Phys. Rev. C 62, 031302(R) (2000).
- Afanasjev and Abusara (2010) A. V. Afanasjev and H. Abusara, Phys. Rev. C 82, 034329 (2010).
- Zhao et al. (2011a) P. W. Zhao, J. Peng, H. Z. Liang, P. Ring, and J. Meng, Phys. Rev. Lett. 107, 122501 (2011a).
- Zhao et al. (2011b) P. W. Zhao, S. Q. Zhang, J. Peng, H. Z. Liang, P. Ring, and J. Meng, Phys. Lett. B 699, 181 (2011b).
- Zhao et al. (2012) P. W. Zhao, J. Peng, H. Z. Liang, P. Ring, and J. Meng, Phys. Rev. C 85, 054310 (2012).
- Zhao et al. (2015) P. W. Zhao, N. Itagaki, and J. Meng, Phys. Rev. Lett. 115, 022501 (2015).
- Wang (2017) Y. K. Wang, Phys. Rev. C 96, 054324 (2017).
- Wang (2018) Y. K. Wang, Phys. Rev. C 97, 064321 (2018).
- Ren et al. (2019) Z. X. Ren, S. Q. Zhang, P. W. Zhao, N. Itagaki, J. A. Maruhn, and J. Meng, Sci. China Phys. Mech. Astron. 62, 112062 (2019).
- Ren et al. (2020) Z. Ren, P. Zhao, S. Zhang, and J. Meng, Nucl. Phys. A 996, 121696 (2020).
- Tian et al. (2009) Y. Tian, Z. Ma, and P. Ring, Phys. Lett. B 676, 44 (2009).
- Stoitsov et al. (1998a) M. V. Stoitsov, W. Nazarewicz, and S. Pittel, Phys. Rev. C 58, 2092 (1998a).
- Stoitsov et al. (1998b) M. Stoitsov, P. Ring, D. Vretenar, and G. A. Lalazissis, Phys. Rev. C 58, 2086 (1998b).
- Zhang et al. (2013) Y. N. Zhang, J. C. Pei, and F. R. Xu, Phys. Rev. C 88, 054305 (2013).
- Ren et al. (2017) Z. X. Ren, S. Q. Zhang, and J. Meng, Phys. Rev. C 95, 024313 (2017).
- Dobaczewski et al. (1984) J. Dobaczewski, H. Flocard, and J. Treiner, Nucl. Phys. A 422, 103 (1984).
- Meng (1998) J. Meng, Nucl. Phys. A 635, 3 (1998).
- Meng and Ring (1996) J. Meng and P. Ring, Phys. Rev. Lett. 77, 3963 (1996).
- Pöschl et al. (1997) W. Pöschl, D. Vretenar, G. A. Lalazissis, and P. Ring, Phys. Rev. Lett. 79, 3841 (1997).
- Meng and Ring (1998) J. Meng and P. Ring, Phys. Rev. Lett. 80, 460 (1998).
- Zhou et al. (2000) S.-G. Zhou, J. Meng, S. Yamaji, and S.-C. Yang, Chin. Phys. Lett. 17, 717 (2000).
- Zhou et al. (2003b) S.-G. Zhou, J. Meng, and P. Ring, Phys. Rev. C 68, 034323 (2003b).
- Woods and Saxon (1954) R. D. Woods and D. S. Saxon, Phys. Rev. 95, 577 (1954).
- Schunck and Egido (2008a) N. Schunck and J. L. Egido, Phys. Rev. C 77, 011301(R) (2008a).
- Schunck and Egido (2008b) N. Schunck and J. L. Egido, Phys. Rev. C 78, 064305 (2008b).
- Long et al. (2010a) W. H. Long, P. Ring, N. V. Giai, and J. Meng, Phys. Rev. C 81, 024308 (2010a).
- Long et al. (2010b) W. H. Long, P. Ring, J. Meng, N. Van Giai, and C. A. Bertulani, Phys. Rev. C 81, 031302(R) (2010b).
- Zhou et al. (2010) S.-G. Zhou, J. Meng, P. Ring, and E.-G. Zhao, Phys. Rev. C 82, 011301(R) (2010).
- Li et al. (2012) L. Li, J. Meng, P. Ring, E.-G. Zhao, and S.-G. Zhou, Phys. Rev. C 85, 024312 (2012).
- Geng et al. (2020) J. Geng, J. Xiang, B. Y. Sun, and W. H. Long, Phys. Rev. C 101, 064302 (2020).
- Geng and Long (2022) J. Geng and W. H. Long, Phys. Rev. C 105, 034329 (2022).
- Sun et al. (2018) X.-X. Sun, J. Zhao, and S.-G. Zhou, Phys. Lett. B 785, 530 (2018).
- Zhang et al. (2019) K. Y. Zhang, D. Y. Wang, and S. Q. Zhang, Phys. Rev. C 100, 034312 (2019).
- Sun et al. (2020) X.-X. Sun, J. Zhao, and S.-G. Zhou, Nucl. Phys. A 1003, 122011 (2020).
- Yang et al. (2021) Z. H. Yang, Y. Kubota, A. Corsi, K. Yoshida, X.-X. Sun, J. G. Li, M. Kimura, N. Michel, K. Ogata, C. X. Yuan, Q. Yuan, G. Authelet, H. Baba, C. Caesar, D. Calvet, A. Delbart, M. Dozono, J. Feng, F. Flavigny, J.-M. Gheller, J. Gibelin, A. Giganon, A. Gillibert, K. Hasegawa, T. Isobe, Y. Kanaya, S. Kawakami, D. Kim, Y. Kiyokawa, M. Kobayashi, N. Kobayashi, T. Kobayashi, Y. Kondo, Z. Korkulu, S. Koyama, V. Lapoux, Y. Maeda, F. M. Marqués, T. Motobayashi, T. Miyazaki, T. Nakamura, N. Nakatsuka, Y. Nishio, A. Obertelli, A. Ohkura, N. A. Orr, S. Ota, H. Otsu, T. Ozaki, V. Panin, S. Paschalis, E. C. Pollacco, S. Reichert, J.-Y. Roussé, A. T. Saito, S. Sakaguchi, M. Sako, C. Santamaria, M. Sasano, H. Sato, M. Shikata, Y. Shimizu, Y. Shindo, L. Stuhl, T. Sumikama, Y. L. Sun, M. Tabata, Y. Togano, J. Tsubota, F. R. Xu, J. Yasuda, K. Yoneda, J. Zenihiro, S.-G. Zhou, W. Zuo, and T. Uesaka, Phys. Rev. Lett. 126, 082501 (2021).
- Sun (2021) X.-X. Sun, Phys. Rev. C 103, 054315 (2021).
- Zhong et al. (2022) S. Y. Zhong, S. S. Zhang, X. X. Sun, and M. S. Smith, Sci. China Phys. Mech. Astron. 65, 262011 (2022).
- In et al. (2021) E. J. In, P. Papakonstantinou, Y. Kim, and S.-W. Hong, Int. J. Mod. Phys. E 30, 2150009 (2021).
- Zhang et al. (2021) K. Zhang, X. He, J. Meng, C. Pan, C. Shen, C. Wang, and S. Zhang, Phys. Rev. C 104, L021301 (2021).
- Pan et al. (2021) C. Pan, K. Y. Zhang, P. S. Chong, C. Heo, M. C. Ho, J. Lee, Z. P. Li, W. Sun, C. K. Tam, S. H. Wong, R. W.-Y. Yeung, T. C. Yiu, and S. Q. Zhang, Phys. Rev. C 104, 024331 (2021).
- He et al. (2021) X.-T. He, C. Wang, K.-Y. Zhang, and C.-W. Shen, Chin. Phys. C 45, 101001 (2021).
- Sun and Zhou (2021a) X.-X. Sun and S.-G. Zhou, Sci. Bull. 66, 2072 (2021a).
- Sun and Zhou (2021b) X.-X. Sun and S.-G. Zhou, Phys. Rev. C 104, 064319 (2021b).
- In et al. (2020) E. J. In, Y. Kim, P. Papakonstantinou, and S.-W. Hong, J. Korean Phys. Soc. 77, 966 (2020).
- Choi et al. (2022) Y.-B. Choi, C.-H. Lee, M.-H. Mun, and Y. Kim, Phys. Rev. C 105, 024306 (2022).
- Kim et al. (2022) S. Kim, M.-H. Mun, M.-K. Cheoun, and E. Ha, Phys. Rev. C 105, 034340 (2022).
- Xia et al. (2018) X. W. Xia, Y. Lim, P. W. Zhao, H. Z. Liang, X. Y. Qu, Y. Chen, H. Liu, L. F. Zhang, S. Q. Zhang, Y. Kim, and J. Meng, Atom. Data Nucl. Data Tabl. 121-122, 1 (2018).
- Zhang et al. (2020) K. Zhang, M.-K. Cheoun, Y.-B. Choi, P. S. Chong, J. Dong, L. Geng, E. Ha, X. He, C. Heo, M. C. Ho, E. J. In, S. Kim, Y. Kim, C.-H. Lee, J. Lee, Z. Li, T. Luo, J. Meng, M.-H. Mun, Z. Niu, C. Pan, P. Papakonstantinou, X. Shang, C. Shen, G. Shen, W. Sun, X.-X. Sun, C. K. Tam, Thaivayongnou, C. Wang, S. H. Wong, X. Xia, Y. Yan, R. W.-Y. Yeung, T. C. Yiu, S. Zhang, W. Zhang, and S.-G. Zhou (DRHBc Mass Table Collaboration), Phys. Rev. C 102, 024314 (2020).
- Zhang et al. (2022) K. Zhang, M.-K. Cheoun, Y.-B. Choi, P. S. Chong, J. Dong, Z. Dong, X. Du, L. Geng, E. Ha, X.-T. He, C. Heo, M. C. Ho, E. J. In, S. Kim, Y. Kim, C.-H. Lee, J. Lee, H. Li, Z. Li, T. Luo, J. Meng, M.-H. Mun, Z. Niu, C. Pan, P. Papakonstantinou, X. Shang, C. Shen, G. Shen, W. Sun, X.-X. Sun, C. K. Tam, Thaivayongnou, C. Wang, X. Wang, S. H. Wong, J. Wu, X. Wu, X. Xia, Y. Yan, R. W.-Y. Yeung, T. C. Yiu, S. Zhang, W. Zhang, X. Zhang, Q. Zhao, and S.-G. Zhou (DRHBc Mass Table Collaboration), Atom. Data Nucl. Data Tabl. 144, 101488 (2022).
- Pan et al. (2022) C. Pan, M.-K. Cheoun, Y.-B. Choi, J. Dong, X. Du, X.-H. Fan, W. Gao, L. Geng, E. Ha, X.-T. He, J. Huang, K. Huang, S. Kim, Y. Kim, C.-H. Lee, J. Lee, Z. Li, Z.-R. Liu, Y. Ma, J. Meng, M.-H. Mun, Z. Niu, P. Papakonstantinou, X. Shang, C. Shen, G. Shen, W. Sun, X.-X. Sun, J. Wu, X. Wu, X. Xia, Y. Yan, T. C. Yiu, K. Zhang, S. Zhang, W. Zhang, X. Zhang, Q. Zhao, R. Zheng, and S.-G. Zhou (DRHBc Mass Table Collaboration), Phys. Rev. C 106, 014316 (2022).
- Koepf and Ring (1991) W. Koepf and P. Ring, Z. Phys. A 339, 81 (1991).
- Kucharek and Ring (1991) H. Kucharek and P. Ring, Z. Phys. A 339, 23 (1991).
- Ring and Schuck (1980) P. Ring and P. Schuck, The Nuclear Many-body Problem (Springer-Verlag, Berlin, 1980).
- Pan et al. (2019) C. Pan, K. Zhang, and S. Zhang, Int. J. Mod. Phys. E 28, 1950082 (2019).
- Zhang and Onley (1988) J.-K. Zhang and D. Onley, Phys. Lett. B 209, 145 (1988).
- Zhang and Onley (1991) J.-K. Zhang and D. Onley, Nucl. Phys. A 526, 245 (1991).