Optimizing Closed-Loop Performance with Data from Similar Systems:
A Bayesian Meta-Learning Approach
Abstract
Bayesian optimization (BO) has demonstrated potential for optimizing control performance in data-limited settings, especially for systems with unknown dynamics or unmodeled performance objectives. The BO algorithm efficiently trades-off exploration and exploitation by leveraging uncertainty estimates using surrogate models. These surrogates are usually learned using data collected from the target dynamical system to be optimized. Intuitively, the convergence rate of BO is better for surrogate models that can accurately predict the target system performance. In classical BO, initial surrogate models are constructed using very limited data points, and therefore rarely yield accurate predictions of system performance. In this paper, we propose the use of meta-learning to generate an initial surrogate model based on data collected from performance optimization tasks performed on a variety of systems that are different to the target system. To this end, we employ deep kernel networks (DKNs) which are simple to train and which comprise encoded Gaussian process models that integrate seamlessly with classical BO. The effectiveness of our proposed DKN-BO approach for speeding up control system performance optimization is demonstrated using a well-studied nonlinear system with unknown dynamics and an unmodeled performance function.
1 Introduction
Performance-driven optimization of closed-loop control systems often involves optimizing system-specific performance functions. Some performance functions lack a complete mathematical representation, or exhibit such complex models to represent accurately, that standard model-based techniques cannot be deployed without oversimplifying assumptions or introducing conservativeness in the design. As argued in [1, 2], Bayesian optimization (BO) possesses some clear advantages that have led to its adoption for closed-loop performance optimization [3, 4, 5, 6]. Concretely, BO is a gradient-free, global optimization method that works well in data-limited settings while concurrently learning a probabilistic approximation of the underlying performance function from data. This has led BO to be implemented in a range of engineering applications, including energy systems [7, 8, 9], vehicles [10], robotics [11], and aerospace [12].
In the performance-driven BO literature, a standard assumption is that the target system to be optimized is available for closed-loop experimentation. Therefore, at design time, one can evaluate the performance of the target system by changing some parameters such as controller gains or setpoints, and observing the system response. Often, at the start of the BO tuning procedure, the amount of data available from the target system is very limited. Approximating a performance function using very limited data generally results in an inaccurate surrogate model, which needs to be improved in subsequent BO iterations by exploring the search space [13]. Though data available from the target system under consideration may be scarce, in many industrial applications there is often data collected from previous performance optimization tasks on ‘similar systems’ [14]. We posit that this previously collected data, combined with the limited target system data, can warm-start BO by estimating a good initial surrogate model, potentially improving the convergence of BO for the target task.
To this end, we propose the use of few-shot meta-learning (or just meta-learning for brevity), wherein a machine learning model is trained on a variety of related ‘source’ optimization tasks so that it can make accurate predictions for a new target task, in spite of the paucity of target task data. Modern meta-learning algorithms typically require solving a bi-level optimization problem, where the outer level is dedicated to extracting task-independent features across a set of source tasks, and the inner level is devoted to adapting to a specific optimization task with few iterations and limited data. This bi-level training loop is the basis of model-agnostic meta-learning (MAML) [15]. However, MAML is not always easy to train and often exhibits numerical instabilities [16]. In addition, MAML does not generate uncertainty estimates around the predictions since it is a deterministic algorithm. Consequently, we adopt a Bayesian meta-learning approach in this work, which builds on the methodology proposed in [17, 18, 19]. To the best of our knowledge, this paper is the first to propose a Bayesian meta-learning algorithm for closed-loop system optimization capable of leveraging data from similar systems.
Our main contribution in this work is to propose a meta-learned Bayesian optimization methodology for rapidly optimizing closed-loop performance of systems with dynamics and performance functions whose mathematical representations are unknown, but can be evaluated by experiment/simulation. Specifically, we employ Bayesian meta-learning to systematically learn using data collected from a variety of systems that are different to a target system to be optimized, and leverage this disparate dataset to generate a good surrogate model for the target system performance function, despite having very few data samples from the target system. Our Bayesian meta-learning framework is implemented using deep kernel networks (DKNs) which have the advantage of requiring single-level optimization for training as the inner training loop is replaced by a Gaussian process (GP) base kernel. Additionally, our approach is simple to implement using standard deep learning toolkits such as PyTorch. The choice of GPs as the base learner lends itself to classical BO, where the default choice of probabilistic surrogate model is a GP. We demonstrate via simulation experiments that this performance-driven meta-learned BO can generate near-optimal solutions with fewer online experiments than classical BO for systems with unmodeled dynamics, without requiring explicit parameter estimation. While meta-learning has recently been explored in the context of adaptive control in [20, 21, 22], our work differs from these works in a few key aspects: (i) we propose a framework for meta-learning to optimize closed-loop performance rather than controller gain adaptation for tracking/regulation, and (ii) we adopt Bayesian deep learning for meta-learning and instead of adaptive controllers; and, (iii) we do not assume any modeling knowledge on the closed-loop dynamics, controller structure, or performance function.
The rest of the paper is organized as follows. The closed-loop performance optimization problem is formalized in Section 2 and the meta-learning setup is explained therein. In Section 3, we provide a brief overview of BO and deep kernel networks, and describe how they are used for meta-learned BO in Section 4. We demonstrate the effectiveness of the proposed approach using a numerical example in Section 5, and conclude in Section 6.
2 Motivation
We consider a class of stable closed-loop systems of the form
| (1) |
where denote the current and updated state of the system, respectively, is a control parameter to be tuned (e.g., a setpoint or controller gain), and denotes unknown system parameters. The admissible sets of control parameters and system parameters: and , respectively, are known. Additionally, we assume that for each and each , the closed-loop system (1) is globally asymptotically stable to a parameter-dependent equilibrium state , and that the map is continuous on .
To determine how the closed-loop system performs, we define a continuous function . The performance output is available for measurement. Note that for our purposes, it suffices that and are smooth and can be evaluated either by simulation or experiments—however, we do not assume access to a mathematical representation of these functions, nor can we compute their gradients analytically. In other words, no knowledge of or is used in the algorithm. However, is assumed to lie in the reproducing kernel Hilbert space (RKHS) of common (e.g., Gaussian or Matérn) kernels so that it can be approximated reasonably by kernel methods.
For a target system of the form (1) with unknown system parameter , our target optimization task is to compute the control parameter
| (2) |
that optimizes the performance of the closed-loop system (1) directly from data. We will do this without estimating , which would prove difficult since is unknown, and is not measured.
In practical applications that involve optimization of closed-loop performance, it is often the case that the optimization task has been performed before, most likely for similar, but not necessarily identical, systems. While solving these source optimization tasks, one has likely generated optimization-relevant data that can prove valuable to the target optimization task, even if the target system is not exactly the same as one of the systems encountered before. In BO-based tuning, such source data (data obtained while solving source optimization tasks) is typically ignored, and the target system is optimized from scratch [1]. This can lead to slow convergence of BO since the algorithm’s initial estimate of the target performance function, constructed with very few target data points, is often inaccurate or highly uncertain. In this work, we propose meta-learning from similar systems’ source data and integrating the information extracted from the source data to the target optimization task. In the sequel, we will show that meta-learning from disparate sources of data can enable optimization of closed-loop performance in a few-shot manner (i.e., with very limited target system data) and thereby lead to significant acceleration of the target optimization procedure.
Example 1.
As a motivating example, consider a common task in sustainable building design: to minimize energy consumption of a newly constructed target building by tuning controllable variables in space heating/cooling systems [7]. At design time, it is likely that very little useful data has been collected from the target building, and using classical BO will require first exploring the search space until a good estimate of the energy function is learned. Conversely, we posit that the designer could have access to larger quantities of source data from other buildings that are similar in architectural style, location, occupancy, and HVAC equipment. Even if the energy functions learned from those source tasks are not identical to the energy function of the target building, a learner can extract information (e.g., curvature, regions in the parameter space likely to contain optima) about building energy functions, which can be used to rapidly optimize energy in the target building. ∎
Concretely, we assume that a dataset is available, comprising data collected from source optimization tasks performed in the past. Here,
| (3) |
is a data sequence of pairs collected over optimization iterations from the -th source task. Each -th source data pair consists of the control parameter , and the corresponding performance output evaluated on a source system with dynamics modeled by (1) with system parameter , where each is unique. We reiterate that we do not assume access to the source systems or the system parameters . For the target task, our objective is to compute (2) by learning a variety of performance functions from the source dataset and generating a good estimate of the performance function for the target optimization task, despite having access to a very limited target dataset
where .
To this end, we propose the use of Bayesian meta-learning to learn a distribution of performance functions from the source data, and predict the target performance function by conditioning on the target data. With successful meta-learning, we expect that the estimated target task performance function will be significantly more accurate than an initial estimate that uses only the limited target dataset, and in turn, expect this to improve the convergence of BO. Our meta-learning framework comprises a deep kernel network (DKN). Deep kernel networks contain a latent encoder and a Gaussian process (GP) output layer. The latent encoder takes an input and transforms it to a latent variable of user-defined size, thereby lending itself to target systems with a large number of control parameters. Since the final layer is a GP regressor, it integrates seamlessly into classical BO procedures and well-studied acquisition functions can be used with the DKN without modification.
3 Preliminaries
In this section, we explain how classical Bayesian optimization is typically used to solve (2) for the closed-loop system (1) for a fixed , using only target task data. We also describe deep kernel networks that will be used in the next section for meta-learning.
3.1 Bayesian Optimization (BO)
Classical BO comprises two main components: (1) a probabilistic surrogate model that maps for , and (2) an acquisition functions that balances exploration and exploitation to propose new candidate control parameters that are likely to optimize , based on estimates of the surrogate model. Since classical BO starts with no initial data available for the system under consideration, one generally requires some random sampling on to initialize a surrogate model. For each such control parameter , , the closed-loop system (1) is allowed to achieve a steady-state after some suitable wait time , after which a measurement is taken. This steady-state performance output acts as a proxy for the objective function value for the corresponding , that is, . This enables us to obtain an initial set of pairs from which a probabilistic surrogate model can be trained to estimate on .
In particular, classical BO methods utilize Gaussian process (GP) regression [23] to construct the surrogate model. The Gaussian process framework works on the principle that the performance is a random variable and the joint distribution of all for the training data instances is a multivariate Gaussian distribution. This implies that the GP can be characterized entirely by a mean function and a covariance function ; that is, . A common choice is to set , and to represent the covariance function using kernels such as squared exponential kernels or Matérn kernels, which are parameterized by hyperparameters such as length-scales and variances. At inference, for predicting the performance of a new instance , the assumption that the predictions are jointly Gaussian with respect to the training instances yields an estimate with posterior mean and variance given by
| (4) |
where with being an estimate of the variance of the noise corrupting the performance output measurement, , and . Clearly, the accuracy of the predictions depends on the choice of kernel and the kernel hyperparameters . In classical BO, is computed by maximizing a log-marginal likelihood function
| (5) |
where is a constant. Although this problem is non-convex in , one can employ stochastic gradient ascent to search for optimal hyperparameters.
The selection of a next best candidate in classical BO is performed via an acquisition function . The acquisition function uses the predictive distribution given by the GP to compute the utility of performing an evaluation of the objective at each , given the data obtained thus far. The next at which the objective has to be evaluated is obtained by solving the maximization problem . Commonly used acquisition functions include expected improvement (EI) and upper confidence bound (UCB) [13]. With the new control parameter candidate , we wait seconds to obtain and iteratively perform the surrogate model retraining and the acquisition function evaluation steps with the training set augmented each BO iteration with the new pair . This process is repeated ad infinitum.
3.2 Deep Kernel Networks (DKNs)
While commonly used kernel functions have shown good performance in some applications, there are advantages to directly learning the kernel function from data. This is the idea proposed in deep kernel learning [24], where a base kernel with hyperparameters is used to transform the control parameters to a latent space via a non-linear map induced by a deep neural network, parameterized by weights .
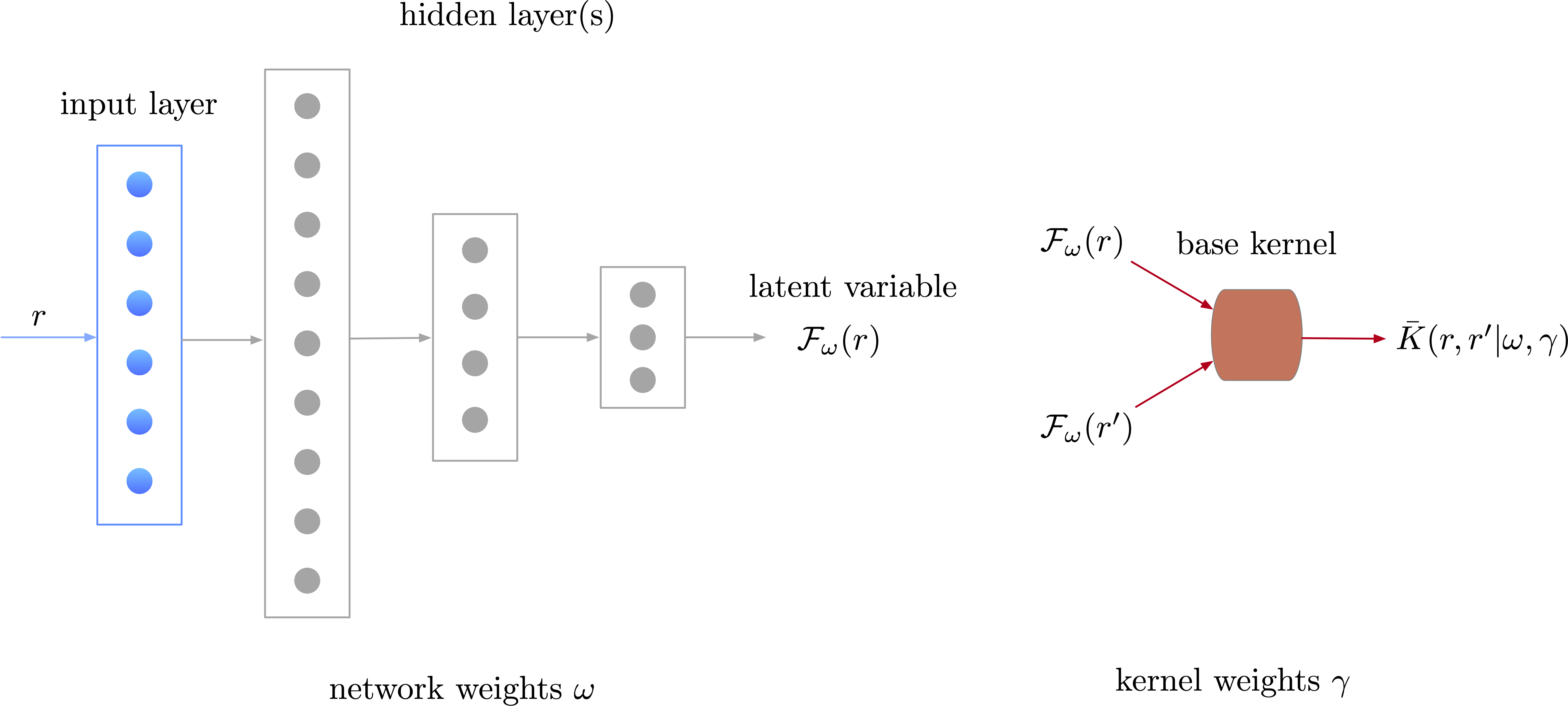
The deep kernel
| (6) |
is trained by maximizing a log marginal likelihood, similar to (5), to concurrently compute and . A noteworthy benefit of deep kernels is that they can be defined on a latent space whose dimension may be significantly lower than the dimensionality of the input, allowing the learning to be applied on problems where the dimensionality of the control parameters is large. A simple example of the DKN architecture is shown in Fig. 1.
4 Meta-Learned Bayesian Optimization with Deep Kernel Networks (DKN-BO)
Recall that is a collection of data obtained from source tasks, where the data of the -th source task is described in (3). Most recent Bayesian meta-learning paradigms [18, 19] work under the assumption that all the source tasks (and the target task) share a set of task-independent hidden parameters and (the reasons for using two symbols here will be explained shortly), and a set of task-specific parameters . Given an input from an unseen task, the Bayesian treatment for inference requires estimating the task-independent parameters and from the source task dataset, and then estimating two distributions: the posterior of the task-specific parameters and the posterior for the output . However, as argued in [17], handling these two distributions requires sampling or amortized distributions, resulting in significantly complex network architectures, and bi-level learning has been shown to require higher-order derivative information, in spite of which the training might suffer from instabilities. By using deep kernel networks, one can marginalize out the task-specific parameters with kernel functions defined in the latent space, which leads to a simple architecture (see Fig. 1), allows for quantification of uncertainty during inference, all the while avoiding the numerical conditioning issues that are reported to occur [16] during training via bi-level optimization (e.g., in MAML).
Training
The marginal likelihood of the Bayesian meta-learning module conditioned on and is given by
| (7) |
where
represents the marginalization over sets of task-specific parameters. We approximate the Bayesian integral above using a Gaussian process prior with kernel ; this is a commonly used approach for tackling similar integrals that are implicitly solved via Bayesian quadrature methods, see for example, [25, 17].
Consequently, one can cast the meta-learning problem as learning the parameters and that characterize a deep kernel network (6), which is tantamount to optimizing (maximizing) the log-marginal likelihood
| (8) |
where , is a vector of all labels of the -th source task, and is a constant scalar. In each training iteration, a source task is selected at random from the set of source tasks, and a random subset of batch data from this source task is selected. The log-marginal likelihood is computed using (7), and well-known variants of stochastic gradient descent methods are used to minimize the negative of . In other words, the learnable parameters are updated by back-propagation
where and are the step sizes of the neural network component and the base kernel component of the deep kernel network, respectively. By optimizing the entire DKN in mini-batches, we can also limit the computational expenditure of the determinant and inverse operations during loss function evaluation, without losing guarantees of convergence of the training loss (up to a small neighborhood of a critical point of the loss function), as demonstrated in [26, Theorem 3.1]. We denote and as the parameters of the DKN learned at the termination of the training loop.
Inference
As in the few-shot optimization setting, we assume that very few data points are initially available from a target task . To predict the control performance on for the target task, and subsequently compute a next candidate with Bayesian optimization, we rely primarily on the optimized task-independent parameters and , as the trained DKN is expected to have learned a suitable surrogate model of from the set of source tasks. By conditioning on the target data, we encourage the predictions of the DKN
to be biased towards to the target task. Under the assumption that the target task is similar to the source tasks, we expect the predictions of the DKN conditioned on limited target task data to be more accurate and exhibit lower uncertainty than a regressor trained solely on the target data.
Analogous to the classical BO algorithm described in Section 3.1, we use the DKN surrogate to predict the control performance at samples in , and use these predictions to optimize an acquisition function. Optimizing the acquisition function yields the next best control input candidate, given the target task data collected so far. In subsequent DKN-BO iterations, even if and are kept constant, since the kernel covariance matrix is appended with new target task data (obtained by evaluating the performance of the target task with candidate control inputs ), the DKN predictions gradually tighten around the true performance function of the target task. A full pseudocode of DKN-BO is provided in Algorithm 1.
The authors in [27] propose a method for introducing scale invariance during training of DKNs so that the target task labels do not need to be normalized to the unit line (which would be impossible, since the target task’s maximum and minimum is unknown). In particular, the proposed method involves computing and , which are the minimum and maximum performance output observed over all source tasks, respectively. Each time a batch is sampled during training, the labels are rescaled to , which, over a large number of training iterations allows the learner to learn trends from the source tasks that are scale independent, enabling inference for the unseen target task without normalization.
Empirically, we have noticed improvements in DKN-BO performance when retraining the base kernel parameters online (as in classical BO) while keeping the neural network weights, i.e. , fixed. However, this approach is closer in spirit to transfer learning than meta-learning, and thus, we do not retrain the base kernel in the following subsection, to avoid online training expenditure.
5 Simulation Results
We consider the following nonlinear system, previously studied in [28, 29]:
| (9a) | ||||
| (9b) | ||||
| (9c) | ||||
where , is a control policy that renders the closed-loop system stable. For the target system, the true parameters are and the optimal control parameter is at which the system attains its maximum ; this is not known to the designer. We choose and .
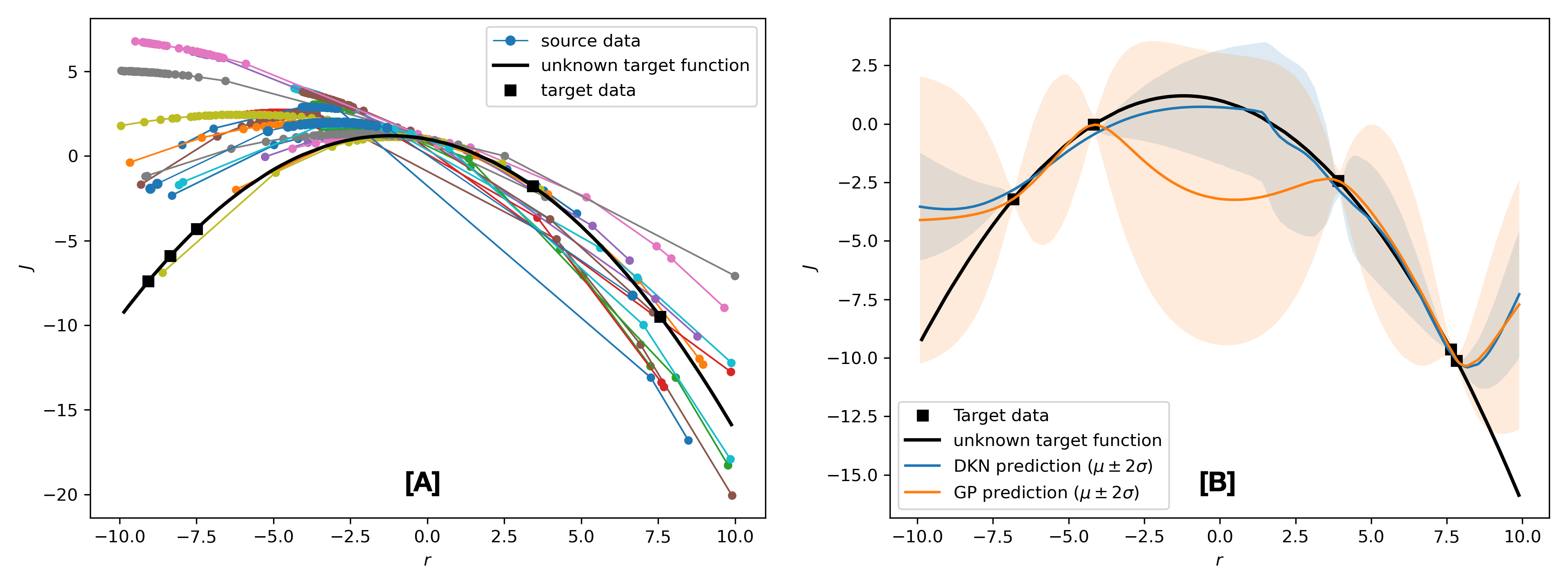
In order to generate the source dataset, we extract unique system parameters from using a 2D uniform random distribution. We evaluate the performance output for a given by forward simulating each system realized by sampling from for , which provides enough time for the transient response to fade. For each sampled system parameter, we solve the source optimization task of maximizing the performance function given in (9c) within iterations, which depends on and therefore has a variety of optimizers and optimal values. The source data collected is illustrated in Fig. 2[A] using colored circles joined by thin continuous lines. We observe that indeed the source performance functions are not identical to the target task performance function which is shown with the continuous thick black line. Our proposed approach is agnostic to the optimization strategy used for optimizing each source task; in fact, a mix of random search and BO are used for source task optimization and source data collection. The target task data is collected by evaluating the performance of the target system at randomly selected values.
Our DKN architecture involves a latent encoder with 100 neurons per hidden layer, with 4 hidden layers following the input layer. We select a latent dimension of 10, and the activation functions are rectified linear units (ReLUs). The latent output is passed to a GP with a scaled Matern-3/2 kernel as the covariance and a constant mean kernel. The entire pipeline is implemented using PyTorch [30] and GPyTorch [31]. The DKN is trained for 10000 iterations with the learning rate scheduled at: and for the first 2000 iterations, and and thereafter. We train using the Adam algorithm and fix the batch-size at 8. The weights corresponding to the highest log marginal likelihood was saved as and .
Fig. 2[B] illustrates the effectiveness of meta-learning for predicting the target performance function. With the same limited target data, the trained DKN generates a more accurate mean estimate of the true performance function, as compared to a GP trained for 1000 iterations with a squared-exponential kernel: see the blue (DKN) and orange (GP) continuous lines. Furthermore, it is encouraging that the uncertainty bands for the DKN are less pronounced than the GP in the areas that are most relevant for optimization.
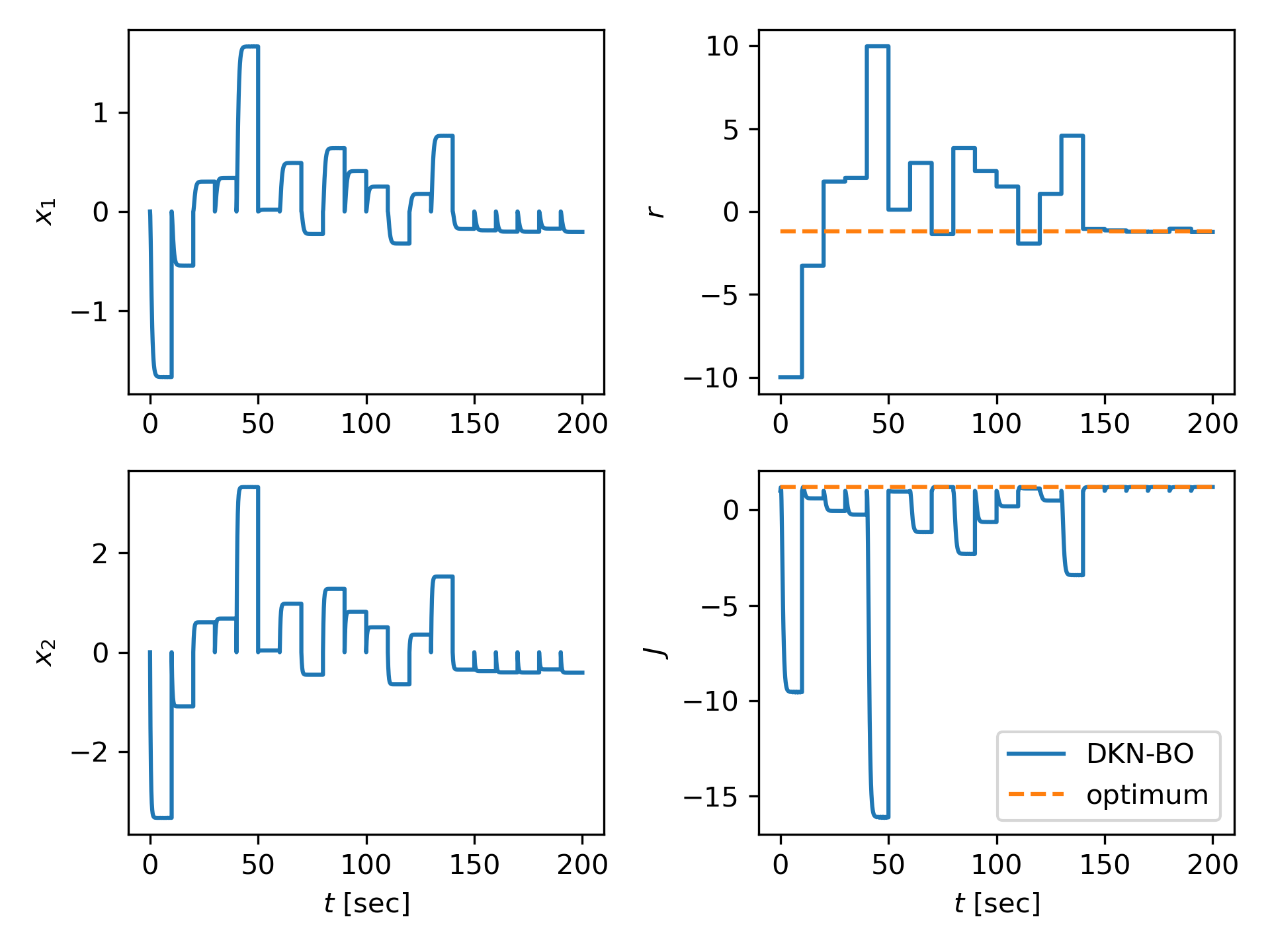
Fig. 3 demonstrates an instance of DKN-BO for optimizing control performance. We start the target system at the origin and simulate the system forward in time, collecting performance outputs every 10 s for value candidates generated by the DKN-BO procedure. The state variation and shows that we do not assume that we can reset the experiment each time a new candidate is selected, and the closed-loop performance is optimized in an online manner. The corresponding variation of the control parameter . The bottom right subplot, which shows the performance output, illustrates clearly that DKN-BO finds the optimal value within 100 s, which is comparable to the performance reported in [29], even though we do not have access to any model information and do not estimate .
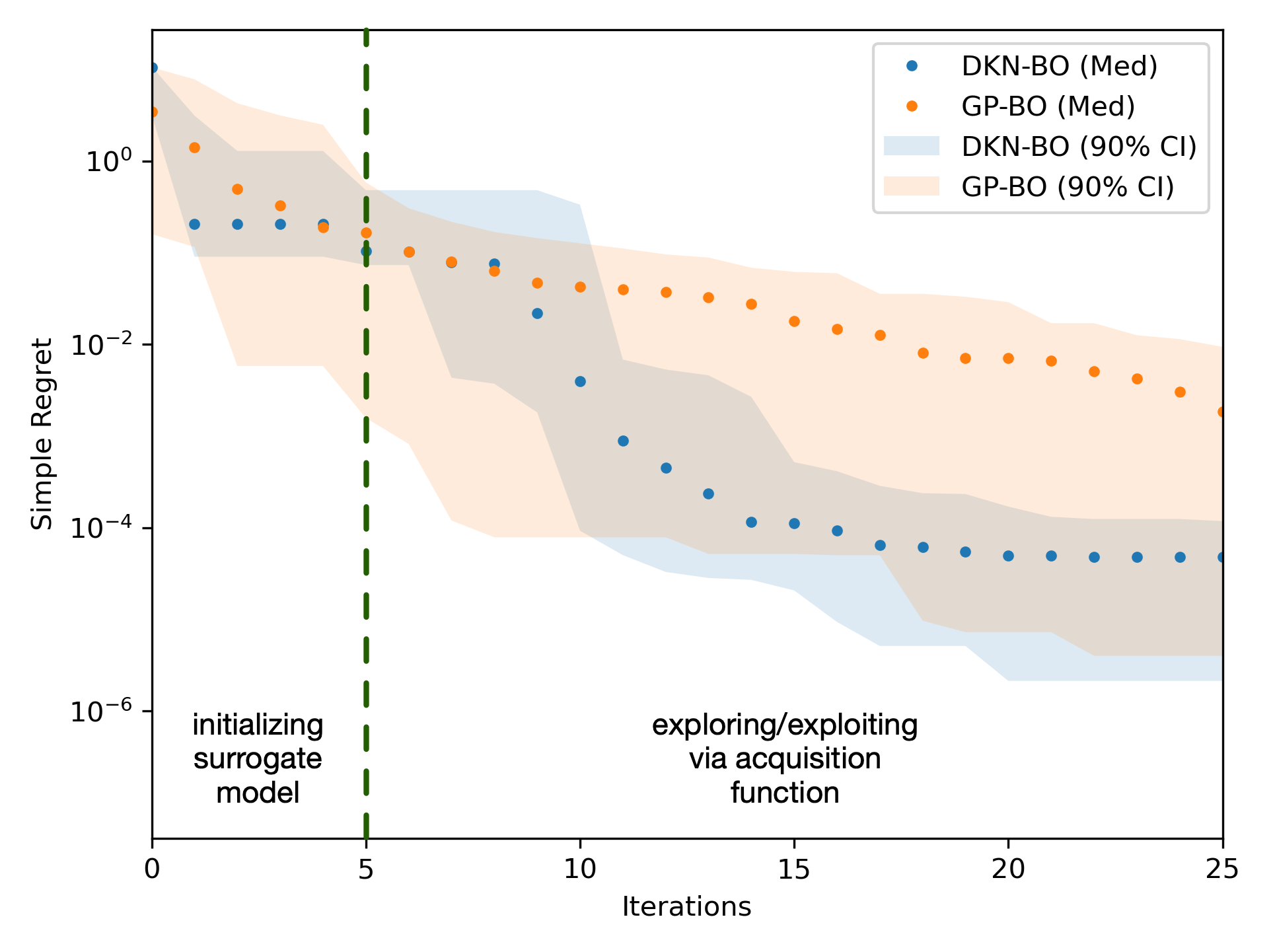
We also repeated our experiments 100 times with varying target datasets, and report the statistics of the simple regret decay in Fig. 4. We observe that DKN-BO performs well in a few-shot setting, and converges to a median regret that is two orders of magnitude below classical GP-BO within 10 iterations. Furthermore, the DKN-BO algorithm is robust to the target dataset as is evident from its tighter confidence intervals compared with GP-BO.
6 Conclusions
This paper provides a highly generalizable and computationally simple framework for leveraging prior data for optimizing unseen closed-loop performance optimization tasks, even if the prior data is not from the task to be optimized. This is done in a few-shot manner using meta-learned Bayesian optimization and deep kernel networks as surrogate models. The latent encoding of the DKN enables a task-independent representation of the controlled inputs to the closed-loop system, and the base kernel allows conditioning for task-specific predictions.
References
- [1] M. Neumann-Brosig, A. Marco, D. Schwarzmann, and S. Trimpe, “Data-efficient autotuning with bayesian optimization: An industrial control study,” IEEE Transactions on Control Systems Technology, vol. 28, no. 3, pp. 730–740, 2019.
- [2] Q. Lu, L. D. González, R. Kumar, and V. M. Zavala, “Bayesian optimization with reference models: A case study in MPC for HVAC central plants,” Computers & Chemical Engineering, vol. 154, p. 107491, 2021.
- [3] R. R. Duivenvoorden, F. Berkenkamp, N. Carion, A. Krause, and A. P. Schoellig, “Constrained Bayesian optimization with particle swarms for safe adaptive controller tuning,” IFAC-PapersOnLine, vol. 50, no. 1, pp. 11 800–11 807, 2017.
- [4] C. König, M. Khosravi, M. Maier, R. S. Smith, A. Rupenyan, and J. Lygeros, “Safety-aware cascade controller tuning using constrained Bayesian optimization,” arXiv preprint arXiv:2010.15211, 2020.
- [5] S. Bansal, R. Calandra, T. Xiao, S. Levine, and C. J. Tomlin, “Goal-driven dynamics learning via bayesian optimization,” in 2017 IEEE 56th Annu. Conf. on Decis. and Control (CDC). IEEE, 2017, pp. 5168–5173.
- [6] J. A. Paulson and A. Mesbah, “Data-driven scenario optimization for automated controller tuning with probabilistic performance guarantees,” IEEE Contr. Syst. Lett., vol. 5, no. 4, pp. 1477–1482, 2020.
- [7] A. Chakrabarty, C. Danielson, S. Bortoff, and C. Laughman, “Accelerating self-optimization control of refrigerant cycles with bayesian optimization and adaptive moment estimation,” Applied Thermal Engineering, 2021.
- [8] W. Xu, C. N. Jones, B. Svetozarevic, C. R. Laughman, and A. Chakrabarty, “VABO: Violation-aware bayesian optimization for closed-loop control performance optimization with unmodeled constraints,” in Proc. American Control Conference, 2022, pp. 1–6.
- [9] M. Khosravi, A. Eichler, N. Schmid, R. S. Smith, and P. Heer, “Controller tuning by Bayesian optimization an application to a heat pump,” in 2019 18th Eur. Control Conf. (ECC). IEEE, 2019, pp. 1467–1472.
- [10] A. Pal, L. Zhu, Y. Wang, and G. G. Zhu, “Multi-objective stochastic Bayesian optimization for iterative engine calibration,” in Proc. of the Amer. Control Conf. IEEE, 2020, pp. 4893–4898.
- [11] F. Berkenkamp, A. Krause, and A. P. Schoellig, “Bayesian optimization with safety constraints: safe and automatic parameter tuning in robotics,” Machine Learning, pp. 1–35, 2021.
- [12] R. Lam, M. Poloczek, P. Frazier, and K. E. Willcox, “Advances in bayesian optimization with applications in aerospace engineering,” in 2018 AIAA Non-Deterministic Approaches Conference, 2018, p. 1656.
- [13] J. Snoek, H. Larochelle, and R. P. Adams, “Practical Bayesian optimization of machine learning algorithms,” in Proc. NeurIPS, 2012, p. 2951–2959.
- [14] L. Xin, L. Ye, G. Chiu, and S. Sundaram, “Identifying the dynamics of a system by leveraging data from similar systems,” in Proc. of the 2022 American Control Conference (ACC), 2022, pp. 818–824.
- [15] C. Finn, P. Abbeel, and S. Levine, “Model-agnostic meta-learning for fast adaptation of deep networks,” in Proceedings of the 34th International Conference on Machine Learning, ser. Proceedings of Machine Learning Research, D. Precup and Y. W. Teh, Eds., vol. 70. PMLR, 06–11 Aug 2017, pp. 1126–1135.
- [16] A. Antoniou, H. Edwards, and A. Storkey, “How to train your MAML,” arXiv preprint arXiv:1810.09502, 2018.
- [17] M. Patacchiola, J. Turner, E. J. Crowley, M. F. O’Boyle, and A. J. Storkey, “Bayesian meta-learning for the few-shot setting via deep kernels,” in Proc. NeurIPS, 2020, pp. 16 108–16 118.
- [18] J. Yoon et al., “Bayesian model-agnostic meta-learning,” NeurIPS, vol. 31, 2018.
- [19] C. Finn, K. Xu, and S. Levine, “Probabilistic model-agnostic meta-learning,” in Proc. NeurIPS, 2018, pp. 9537–9548.
- [20] E. Arcari, A. Carron, and M. N. Zeilinger, “Meta learning MPC using finite-dimensional gaussian process approximations,” 2020. [Online]. Available: https://arxiv.org/abs/2008.05984
- [21] M. O’Connell, G. Shi, X. Shi, and S.-J. Chung, “Meta-learning-based robust adaptive flight control under uncertain wind conditions,” arXiv preprint arXiv:2103.01932, 2021.
- [22] S. M. Richards, N. Azizan, J.-J. Slotine, and M. Pavone, “Adaptive-control-oriented meta-learning for nonlinear systems,” arXiv preprint arXiv:2103.04490, 2021.
- [23] C. K. Williams and C. E. Rasmussen, Gaussian Processes For Machine Learning. MIT press Cambridge, MA, 2006, vol. 2, no. 3.
- [24] A. G. Wilson, Z. Hu, R. Salakhutdinov, and E. P. Xing, “Deep kernel learning,” in Artificial Intelligence and Statistics (AISTATS). PMLR, 2016, pp. 370–378.
- [25] J. Courts, J. Hendriks, A. Wills, T. B. Schön, and B. Ninness, “Variational state and parameter estimation,” IFAC-PapersOnLine, vol. 54, no. 7, pp. 732–737, 2021.
- [26] H. Chen, L. Zheng, R. Al Kontar, and G. Raskutti, “Stochastic gradient descent in correlated settings: A study on gaussian processes,” NeurIPS, vol. 33, pp. 2722–2733, 2020.
- [27] M. Wistuba and J. Grabocka, “Few-shot Bayesian optimization with deep kernel surrogates,” in Proc. ICLR, 2021.
- [28] M. Guay and T. Zhang, “Adaptive extremum seeking control of nonlinear dynamic systems with parametric uncertainties,” Automatica, vol. 39, no. 7, pp. 1283–1293, 2003.
- [29] D. Nesic, A. Mohammadi, and C. Manzie, “A framework for extremum seeking control of systems with parameter uncertainties,” IEEE Trans. Automatic Control, vol. 58, no. 2, pp. 435–448, 2012.
- [30] A. Paszke, S. Gross et al., “PyTorch: An Imperative Style, High-Performance Deep Learning Library,” pp. 8024–8035, 2019.
- [31] J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger, and A. G. Wilson, “GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration,” in Advances in Neural Information Processing Systems, 2018.