1
Optimizing Function Layout for Mobile Applications
Abstract.
Function layout, also referred to as function reordering or function placement, is one of the most effective profile-guided compiler optimizations. By reordering functions in a binary, compilers are able to greatly improve the performance of large-scale applications or reduce the compressed size of mobile applications. Although the technique has been studied in the context of large-scale binaries, no recent study has investigated the impact of function layout on mobile applications.
In this paper we develop the first principled solution for optimizing function layouts in the mobile space. To this end, we identify two important optimization goals, the compressed code size and the cold start-up time of a mobile application. Then we propose a formal model for the layout problem, whose objective closely matches the goals. Our novel algorithm to optimize the layout is inspired by the classic balanced graph partitioning problem. We carefully engineer and implement the algorithm in an open source compiler, LLVM. An extensive evaluation of the new method on large commercial mobile applications indicates up to compressed size reduction and up to start-up time improvement on top of the state-of-the-art approach.
1. Introduction
As mobile applications become an essential part of everyday life, the task of making them faster, smaller, and more reliable becomes urgently important. Profile-guided optimization (PGO) is a critical component in modern compilers for improving the performance and the size of applications, which in turn enables the development and delivery of new app features for mobile devices with limited storage and low memory. The technique, also known as feedback-driven optimization (FDO), leverages the program’s dynamic behavior to generate optimized applications. Currently PGO is a part of most commercial and open-source compilers for static languages; it is also used for dynamic languages, as a part of Just-In-Time (JIT) compilation.
Modern PGO has been successful in speeding up server workloads (Chen et al., 2016; Panchenko et al., 2019; He et al., 2022) by providing a double-digit percentage performance boost. This is achieved via a combination of multiple compiler optimizations which include function inlining, loop optimizations, and code layout. PGO relies on program execution profiles, such as the execution frequencies of basic blocks and function invocations, to guide compilers to optimize critical paths of a program more selectively and effectively. Typically, server-side PGO targets at improving CPU and cache utilization during the steady state of program execution, leading to higher server throughput. This poses a unique challenge for applying PGO for mobile applications which are largely I/O bound and do not have a well-defined steady-state performance due to their user-interactive nature (Lee et al., 2022a). Instead, app download speed and app launch time are critical to the success of mobile apps because they directly impact user experience, and therefore, user retention (Chabbi et al., 2021; Liu et al., 2022).
In this paper we revisit a classic PGO technique, function layout, and show how to successfully apply it in the context of mobile applications. We emphasize that most of the earlier compiler optimizations focus on a single objective, such as the performance or the size of a binary. However, function layout might impact multiple key metrics of a mobile application. We show how to place functions in a binary to simultaneously improve its (compressed) size and start-up performance. The former objective is directly related to the app download speed and has been extensively discussed in recent works on compiler optimizations for mobile applications (Liu et al., 2022; Lee et al., 2022b; Chabbi et al., 2021; Lee et al., 2022a; Rocha et al., 2022, 2020). The latter receives considerably less attention but nevertheless is of prime importance in the mobile space (Inc., 2022; Developers, 2022; Mansour, 2020; Inc., 2015).
Function layout, along with basic block reordering and inlining, is among the most impactful profile-guided compiler optimizations. The seminal work of Pettis and Hansen (Pettis and Hansen, 1990) introduces a heuristic for function placement that leads to a reduction in I-TLB (translation lookaside buffer) cache misses, which improves the steady-state performance of large-scale binaries. The follow up work of Ottoni and Maher (Ottoni and Maher, 2017) describes an improvement to the placement scheme by considering the performance of the processor instruction cache (I-cache). The two heuristics are implemented in the majority of modern compilers and binary optimizers (Panchenko et al., 2019; Lavaee et al., 2019; Ottoni and Maher, 2017; Propeller, 2020). However, these optimizations are not widely used in mobile development and the corresponding layout algorithms have not been thoroughly studied. To the best of our knowledge, the recent work of Lee, Hoag, and Tillmann (Lee et al., 2022a) is the only study describing a technique for function placement for native mobile applications. With this in mind, we provide the first comprehensive investigation of function layout algorithms in the context of mobile applications. Next in Section 1.1 we explain how function layout impacts the compressed app size, which eventually affects download speed. Then in Section 1.2 we describe how an optimized function placement can improve the start-up time. Finally, Section 1.3 highlights our main contributions, a unified optimization model to tackle these two seemingly unrelated objectives and a novel algorithm for the problem based on the recursive balanced graph partitioning.
1.1. Function Layout for App Download Speed
As mobile apps continue to grow rapidly, reducing the binary size is crucial for application developers (Lee et al., 2022a; Bhatia, 2021; Liu et al., 2022). Smaller apps can be downloaded faster, which directly impacts user experience (Reinhardt, 2016). For example, a recent study in (Chabbi et al., 2021) establishes a strong correlation between the app size and the user engagement. Furthermore, mobile app distribution platforms may impose size limitations for downloads that use cellular data (Chabbi et al., 2021). Indeed, in the Apple App Store, when an app’s size crosses a certain threshold, users will not get timely updates, which often include critical security improvements, until they are connected to a Wi-Fi network.
Mobile apps are distributed to users in a compressed form via the mobile app platforms. Typically, application developers do not have a direct control over the compression technique utilized by the platforms. However, the recent work of Lee, Hoag, and Tillmann (Lee et al., 2022a) observes that by modifying the content of a binary, one may improve its compressed size. In particular, co-locating “similar” functions in the binary improves the compression ratio achieved by popular compression algorithms such as ZSTD or LZFSE. A similar technique, co-locating functions based on their similarity, is utilized in Redex, a bytecode Android optimizer (Inc, 2021).
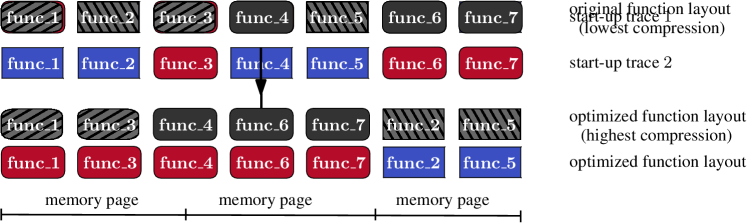
Why does function layout affect compression ratios? Most modern lossless compression tools rely on the Lempel-Ziv (LZ) scheme (Ziv and Lempel, 1977). Such algorithms try to identify long repeated sequences in the data and substitute them with pointers to their previous occurrences. If the pointer is represented in fewer bits than the actual data, then the substitution results in a compressed-size win. That is, the shorter the distance between the repeated sequences, the higher the compression ratio is. To make the computation effective, LZ-based algorithms search for common sequences inside a sliding window, which is typically much shorter than the actual data. Therefore, function layouts in which repeated instructions are grouped together, lead to smaller (compressed) mobile apps; see Figure 1 for an example. In Section 2 we describe an algorithmic framework for finding such layouts.
1.2. Function Layout for App Launch Time
Start-up time is one of the key metrics for mobile applications. Launching an app quickly is important to ensure users have a good first impression. Start-up delays have a direct impact on user engagement (Yan et al., 2012). A study in (Mansour, 2020) indicates that of users abandon an app after one use and of them give a poorly performing app three chances or fewer before uninstalling it.
Start-up time is the time between a user clicking on an application icon to the display of the first frame after rendering. There are several start-up scenarios: cold start, warm start, and hot start (Inc., 2022; Developers, 2022; Inc., 2015). Switching back and forth between different apps on a mobile leads to hot/warm start and typically does not incur significant delays. In contrast, starting an app from scratch or resuming it after a memory intensive process is referred to as cold start. Our main focus is on improving this cold start scenario, which is usually the key performance metric.
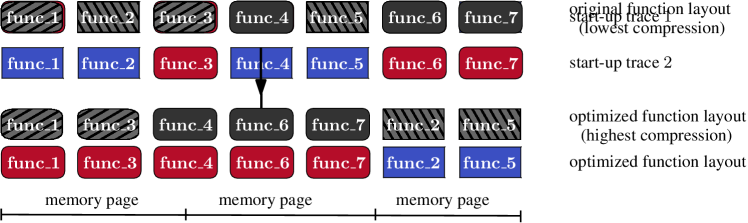
Unlike server workloads, where code layout algorithms optimize the cache utilization (Ottoni and Maher, 2017; Panchenko et al., 2019; Newell and Pupyrev, 2020), start-up performance is mostly dictated by memory page faults (Easton and Fagin, 1978). When an app is launched, its code has to be transferred from disk to the main memory before it can be executed. Function layout can affect performance because the transfer happens at the granularity of memory pages. As illustrated in Figure 2, interleaving cold functions that are never executed with hot ones results in more memory pages to fetch from disk. A tempting solution is to group together hot functions in the binary. Notice however that some mobile apps have a billion of daily active users who use the apps on a variety of devices and platforms. Thus, optimizing the layout for one usage scenario might result in sub-optimal performance for others. The main challenge is to produce a single function layout that optimizes the start-up performance across all use cases. This is accomplished by a novel optimization model, which we develop in Section 2.
1.3. Contributions
We model the problem of computing an optimized function layout for mobile apps as the balanced graph partitioning problem (Garey et al., 1974). The approach allows for a single algorithm that can improve both app start-up time (impacting user experience) and app size (impacting download speed). However, while the layout algorithm is the same for the objectives, it operates with different data collected while profiling the binary. For the sake of clarity, we call the optimizations Balanced Partitioning for Start-up Optimization (bps) and Balanced Partitioning for Compression Optimization (bpc). Though we emphasize that the underlying implementation, outlined in Algorithm 1, is identical.
The former optimization, bps, is applied for hot functions in the binary that are executed during app start-up. The latter optimization, bpc, is applied for all the remaining cold functions. In our experiments, we record around of functions being hot. That allows us to reorder most of the functions in a “compression-friendly” manner, while at the same time improving the overall start-up performance. Compared to the prior work (Lee et al., 2022a), we improve the compressed size by up to and the start-up time by up to , while speeding up the function layout phase by x for SocialApp, one of the largest mobile apps in the world. We summarize the contributions of the paper as follows.
-
•
We formally define the function layout problem in the context of mobile applications. To this end, we identify and formalize two optimization objectives, based on the application start-up time and the compressed size.
-
•
Next we present the Balanced Partitioning algorithm, which takes as input a bipartite graph between function and utility vertices, and outputs an order of the function vertices. We also show how to reduce the aforementioned objectives of bpc and bps to an instance for the balanced partitioning.
-
•
Finally, we extensively evaluate the compressed size, the start-up performance, and the build time of the new algorithms with two large commercial iOS applications, SocialApp and ChatApp. Furthermore, we experiment with app size on Android native binaries, AndroidNative.
The rest of the paper is organized as follows. Section 2 builds an optimization model for compression and start-up performance, respectively. Then Section 3 introduces the recursive balanced graph partitioning algorithm that is the basis to effectively solve the two optimization problems. Next, in Section 4, we describe our implementation of the technique in an open source compiler, LLVM. Section 5 shows an experimental evaluation with real-world mobile applications. We conclude the paper with a discussion of related works in Section 6 and propose possible future directions in Section 7.
2. Building an Optimization Model
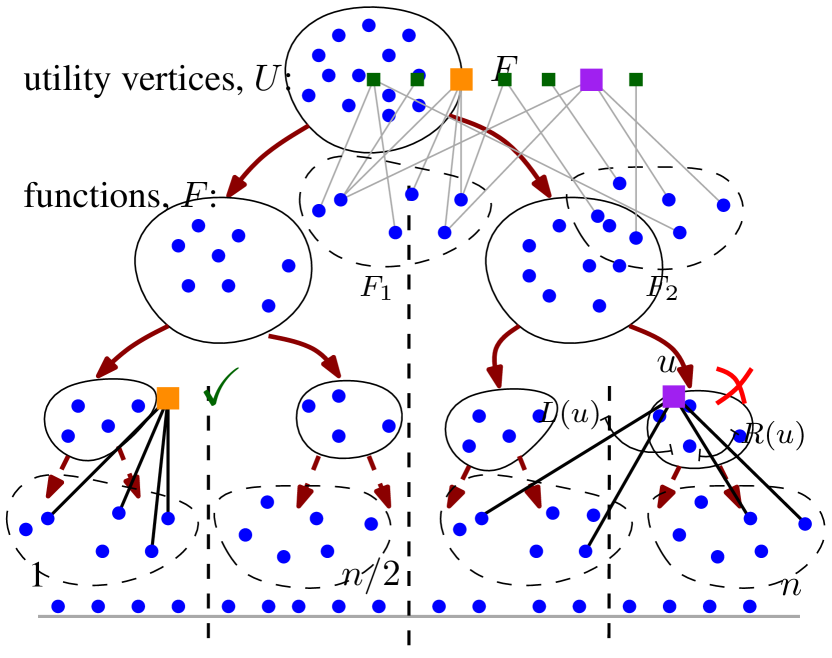
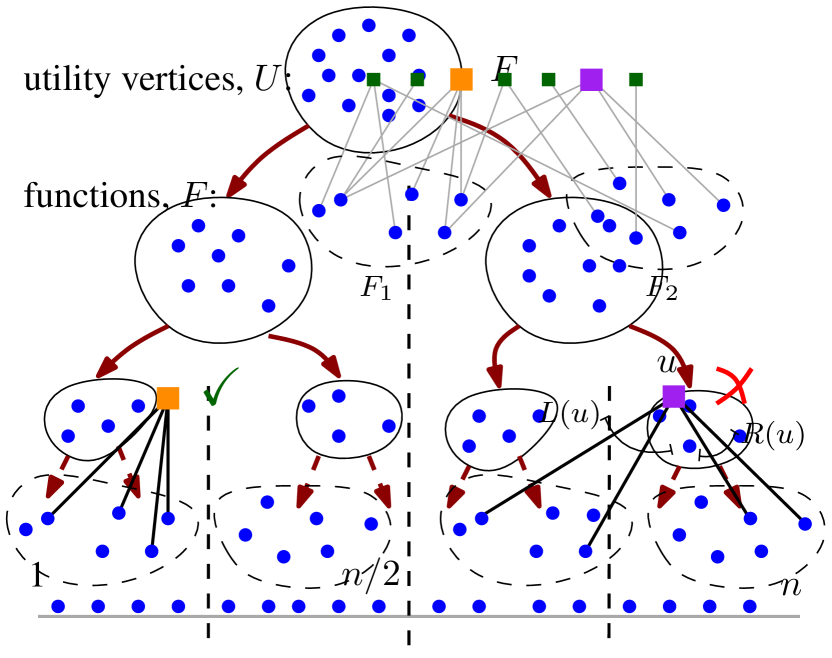
We model the function layout problem with a bipartite graph, denoted , where and are disjoint sets of vertices and are the edges between the sets. The set is a collection of all functions in a binary, and the goal is to find a permutation (also called an order or a layout) of . The set represents auxiliary utility vertices that are used to define an objective for optimization. Every utility vertex is adjacent with a subset of functions, so that for some integer . Intuitively, the goal of the layout algorithm is to place all functions so that are nearby in the resulting order, for each utility vertex . That is, the utility vertex encodes a locality preference for the corresponding functions. Next we formalize the intuition for each of the two objectives.
2.1. Compression
As explained in Section 1.1, the compression ratio of a Lempel-Ziv-based algorithm can be improved if similar functions are placed nearby in the binary. This observation is based on earlier theoretical studies (Raskhodnikova et al., 2013) and has been verified empirically (Ferragina and Manzini, 2010; Lin et al., 2014) in the context of lossless data compression. The works define (sometimes, implicitly) a proxy metric that correlates an order of functions with the compression achieved by an LZ scheme. Suppose we are given some data to compress, e.g., a sequence of bytes representing the instructions in a binary. Define a k-mer to be a contiguous substring in the data of length , which is a small constant. Let be the size of the sliding window utilized by the compression algorithm; typically, is much smaller than the length of the data. Then the compression ratio achieved by an LZ-based data compression algorithm is dictated by the number of distinct k-mers in the data within each sliding window of size . In other words, the compressed size of the data is minimized when each k-mer is present in as few windows of size as possible.
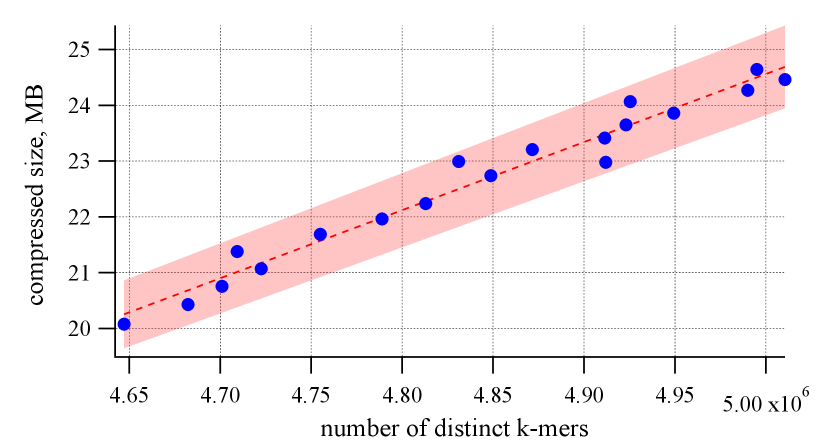
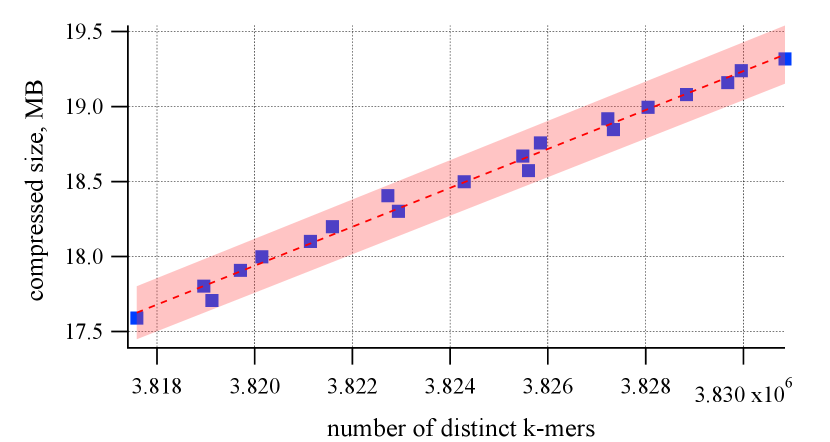
To verify the intuition, we computed and plotted the number of distinct -mers within KB-windows on a collection of functions from SocialApp and ChatApp; see Figure 3. To get one data point for the plot, we fixed a certain layout of functions in the binary and extracted its .text section to a string, by concatenating their instructions. Then for every (contiguous) substring of length , we count the number of distinct k-mers in the substring; this number is the proxy metric predicting the compressed size of the data. Next we apply a compression algorithm for the entire array and measure the compressed size. To get multiple points on Figure 3, we repeat the process by starting with a different function layout, which is produced from the original one by randomly permuting some of its functions. The results in Figure 3 indicate a high correlation between the actual compression ratio achieved on the data and the predicted value based on k-mers. We record a Pearson correlation coefficient of between the two quantities. In fact, the high correlation is observed for various values of (in our evaluation, ), different window sizes (KB KB), and various compression tools. In particular, we experimented with ZSTD (which combines a dictionary-matching stage with a fast entropy-coding stage), LZ4 (which belongs to the LZ77 family of byte-oriented compression schemes), and LZMA (a variant of a dictionary compression and as a part of the xz tool).
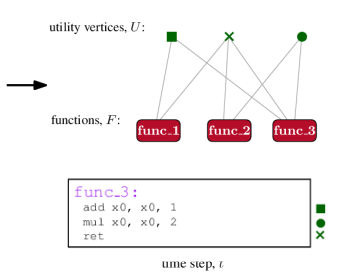
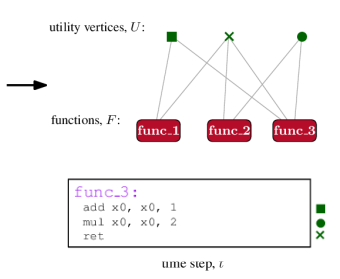
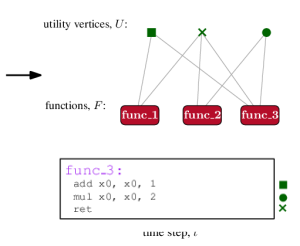
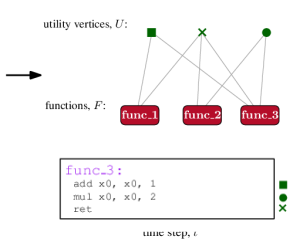
Given the high predictive power of the simple proxy metric, we suggest to layout functions in a binary so as to optimize the metric, as it can be easily extracted and computed from the data. To this end, we represent each function, , as a sequence of instructions. For every instruction in the binary, that occurs in at least two functions, we create a utility vertex . The bipartite graph, contains an edge if function contains instruction ; refer to Figure 4 for an illustration of the process. The goal is to order so that instructions appear in as few windows as possible. Equivalently, the goal is to co-locate functions that share many utility vertices, so that the compression algorithm is able to efficiently encode the corresponding instructions.
2.2. Start-up
In order to optimize the performance of the cold start, we develop the following simplified memory model. First, we assume that when a mobile application starts, none of its code is present in the main memory. Thus, the executed code needs to be fetched from the disk to the main memory. The disk-memory transfer happens at the granularity of memory pages, whose size is typically larger than the size of a function. Second, we assume that when a page is fetched, it is never evicted from the memory. That is, when a function is executed for the first time, its page should be in the memory; otherwise we get a page fault, which incurs a start-up delay. Therefore, our goal is to find a layout of functions that results in as few page faults as possible, for a typical start-up scenario.
In this model, the start-up performance is affected only by the first execution of a function; all subsequent executions do not result in page faults. Hence, we record, for each function , the timestamp when it was first executed, and collect the sequence of functions ordered by the timestamps. Such sequence of functions is called the function trace. The traces list the functions participating in the cold start and may differ from each other depending on the user or the usage scenario of the application. Next we assume that we have a representative collection of traces, .
Given an order of functions, we determine which memory page every function belongs to; to this end, we need the sizes of the functions and assume a certain size of a page. Then for every start-up trace, , and an index , we define to be the number of page faults during the execution of the first functions in . Similarly, for a set of traces , we define the evaluation curve as the average number of page faults for each , that is, .
To build an intuition, consider what happens when there is a single trace (or equivalently, when all traces are identical). Then the optimal layout is to use the order induced by , in which case the evaluation curve looks linear in . In contrast, a random permutation of functions results in fetching most pages early in the execution and the corresponding evaluation curve looks like a step function. We refer the reader to Figure 5(b) for a concrete example of how different layouts lead to different evaluation curves. In practice, we have a diverse set of traces, and the goal is to create a function order whose evaluation curve is as flat as possible.
We remark that although all traces have the same length, the prefix of each trace that corresponds to the startup part of that execution may differ in length due to device- and user-specific diverging execution paths. Therefore, instead of optimizing the value of for a particular value of , we try to minimize the area under the curve . To achieve this, we select a discrete set of threshold values , and and use the bipartite graph with utility vertices
and edge set
where is the index of function in . That way, the algorithm tries to find an order of in which the first positions of every occur, as much as possible, consecutively.
3. Recursive Balanced Graph Partitioning
Our algorithm for function layout is based on the recursive balanced graph partitioning scheme. Recall that the input is an undirected bipartite graph , where and are disjoint sets of functions and utilities, respectively, and are the edges between them; see Figure 6(a). The goal of the algorithm is to find a permutation of so that a certain objective is optimized.
For a high-level overview of our method, refer to Algorithm 1. It combines recursive graph bisection with a local search optimization on each step. Given an input graph with , we apply the bisection algorithm to obtain two disjoint sets of (approximately) equal cardinality, with and . We shall lay out on the set and lay out on the set . Thus, we have divided the problem into two problems of half the size, and we recursively compute orders for the two subgraphs induced by vertices and , adjacent utility vertices, and incident edges. Of course, when the graph contains only one function, the order is trivial; see Figure 6(b) for an overview of the approach.
Every bisection step of Algorithm 1 is a variant of the local search optimization; it is inspired by the popular Kernighan-Lin heuristic (Kernighan and Lin, 1970) for the graph bisection problem. Initially we arbitrarily split into two sets, and , and then apply a series of iterations that exchange pairs of vertices in and trying to improve a certain cost. To this end we compute, for every function , the move gain, that is, the difference of the cost after moving from its current set to another one. Then the vertices of () are sorted in the decreasing order of the gains to produce list (). Finally, we traverse the lists and in the order and exchange the pairs of vertices, if the sum of their move gains is positive. Note that unlike the classic graph bisection heuristic (Kernighan and Lin, 1970), we do not update move gains after every swap. The process is repeated until a convergence criterion is met (e.g., no swapped vertices) or the maximum number of iterations is reached. The final order of the functions is obtained by concatenating the two (recursively computed) orders for and .
Optimization objective
An important aspect of the algorithm is the objective to optimize at a bisection step. Our goal is to find a layout in which functions having many utility vertices in common are co-located in the order. We capture this goal with the following cost of a given partition of into and :
| (1) |
where and are the numbers of functions adjacent to utility vertex in parts and , respectively; see Figure 6(a). Observe that is the degree of vertex , and thus, it is independent of the split. The objective, which we try to minimize, is the summation of the individual contributions to the cost over the utilities. The contribution of one utility vertex, , is minimized when or , that is, when all functions of belong to the same part; in that case, the algorithm might be able to group the functions in the final order. In contrast, when , the cost takes its highest value, as the functions will likely be spread out in the order. Of course, it is easy to minimize the cost for one utility vertex (by placing its functions to one of the parts). However, minimizing for all utilities simultaneously is a challenging task, due to the constraint on the sizes of and .
There are multiple ways of defining the objective, , that satisfy the conditions above. After an extensive evaluation of various candidates, we identified the following objective:
| (2) |
which is inspired by the so-called uniform log-gap cost utilized in the context of index compression (Chierichetti et al., 2009; Dhulipala et al., 2016). We refer to Section 5.4 for an evaluation of alternatives and their impact on function layout.
It is straightforward to implement method from Algorithm 1 by traversing all the edges for and summing up the cost differences of moving to another set.
Computational complexity
In order to estimate the computational complexity of Algorithm 1 and predict its running time, denote and . Suppose that at each bisection step, we apply a constant number of refinement steps (referred to as the iteration limit in the pseudocode). There are levels of recursion, and we assume that every call of ReorderBP splits the graph into two equal-sized parts with vertices and edges. Each call of the graph bisection consists of computing move gains and sorting two arrays with elements. The former can be done in steps, while the latter takes steps. Therefore, the total number of steps is expressed as follows:
It is easy to verify that summing over all subproblems yields , which is the complexity of Algorithm 1. We complete the discussion by noticing that it is possible to reduce the bound to via a modified procedure for performing swaps (Mackenzie et al., 2022) but the strategy does not result in a runtime reduction on our datasets.
The next section describes important details of our implementation.
3.1. Algorithm Engineering
While implementing Algorithm 1 in an open source compiler, we developed a few modifications improving certain aspects of the technique. In particular, we implement the algorithm in parallel manner and limit the depth of the recursion in order to reduce the running time. Next we enhance the procedures for the initial split of functions into two parts and for the way to perform swaps between the parts, which is beneficial for the quality of the identified solutions. Finally, we propose a sampling technique to reduce the space requirements of the algorithm.
Improving the running time.
Due to the simplicity of the algorithm, it can be implemented to run in parallel. Notice that two subgraphs arising at the end of the bisection step are disjoint, and thus, the two recursive calls are independent and can be processed in parallel. To this end, we employ the fork-join computation model in which small enough graphs are processed sequentially, while larger graphs which occur on the first few levels of recursion are solved in a parallel manner.
To speed up the algorithm further, we limit the depth of the recursive tree by a specified constant ( in our implementation) and apply at most a constant number of local search iterations per split ( in our implementation). If we reach the lowest node in the recursive tree and still have unordered functions, which happens when , then we use the original relative order of the functions provided by the compiler.
Finally, we observe that the objective cost employed in the optimization requires repeated computation of expressions for integer arguments. To avoid calls to evaluate floating-point logarithms, we create a table with pre-computed values for , where the upper bound is chosen small enough to fit in the processor data cache. That way, we replaced the majority of the logarithm evaluations with a table lookup, saving approximately of the total runtime.
Optimizing the quality.
One ingredient of Algorithm 1 is how the two initial sets, and , are initialized. Arguably the initialization procedure might affect the quality of the final vertex order, since it serves as the starting point for the local search optimization. To initialize the bisection, we consider two alternatives. The simpler, outlined in the pseudocode, is to randomly split into two (approximately) equal-sized sets. A more involved strategy is to employ minwise hashing (Chierichetti et al., 2009; Dhulipala et al., 2016) to order the functions by similarity and then assign the first functions to and the last to . As discussed in Section 5.4, splitting the vertices randomly is our preferred option due to its simplicity.
Another interesting aspect of Algorithm 1 is the way functions exchanged between the two sets. Recall that we pair the functions in with functions in based on the computed move gains, which are positive values when a function should be moved to another set or negative when a function should stay in its current set. We observed that it is beneficial to skip some of the moves in the exchange process and keep the function in its current set. To this end, we introduce a fixed probability ( in our implementation) of skipping the move for a vertex, which otherwise would have been placed to a new set. Intuitively this adjustment prevents the optimization from becoming stuck at a local minimum that is worse than the global one. It is also helpful for avoiding redundant swapping cycles, which might occur in the algorithm; refer to (Wang and Suel, 2019; Mackenzie et al., 2022) for a detailed discussion of the problem in the context of graph reordering.
Reducing the space complexity.
One potential downside to our start-up function layout algorithm is the need to collect full traces during profiling. If too many executions are profiled, then the storage requirements may be too high to be practical. A natural way to address this issue is to cap the number of traces stored, say we only store traces, for a fixed integer . If the profiling process generates more than traces, we select a representative random sample of size . This can be done on the fly (without knowing a priori how many traces will be generated) using reservoir sampling (Vitter, 1985): When the th trace arrives, if we keep the trace, otherwise, with probability we ignore the trace, and with complementary probability we pick uniformly at random one of the traces that are currently in the sample and swap it out with the new trace. The process yields a sample of traces chosen uniformly at random from the stream of traces.
The parameter, , allows us to trade-off the space needed for profiling and the quality of the layout we ultimately produce (the more samples the better the layout). Figure 8(b) provides an empirical evaluation of this trade-off and suggests to be our default setting.
4. Implementation in LLVM
Both bpc and bps use profile data to guide function layout. Ideally, profile data should accurately represent common real-world scenarios. The current instrumentation in LLVM (Lattner and Adve, 2004) produces an instrumented binary with large size and performance overhead due to added instrumentation instructions, added metadata sections, and changes in optimization passes. On mobile devices, increased code size can lead to performance regressions that can change the behavior of the application. Profiles collected from these instrumented binaries might not accurately represent our target scenarios. To cope with this, the work of Machine IR Profile (MIP) (Lee et al., 2022a) focuses on small binary size and performance overhead for instrumented binaries. This is done in part by extracting instrumentation metadata from the binary and using it to post-process the profiles offline.
MIP collects profiles that are relevant for optimizing mobile apps. Similar to its upstream LLVM counterpart, MIP records function call counts which can be used to identify functions as either hot or cold. MIP also collects instrumentation data that is not found in upstream LLVM. Within each function, MIP can derive full boolean coverage data for each basic block. MIP has an optional mode, called return address sampling, which adds probes to callees to collect a sample of their callsites. This can be used to construct a dynamic call graph that includes dynamically dispatched calls like to Objective-C’s objc_msgSend function. Furthermore, MIP collects function timestamps by recording and incrementing a global timestamp for each function when it is called for the first time. We sort the functions by their initial call time to construct a function trace. To collect raw profiles at runtime, we run instrumented apps under normal usage, and dump raw profiles to the disk, which is uploaded to a database. These raw profiles are later merged offline into a single optimization profile.
4.1. Overview of the Build Pipeline
Figure 7 shows an overview of our build pipeline. We collect thousands of raw profile data files from various uses and periodically run offline post-processing to produce a single optimization profile. During post-processing, bps finds the optimized order of hot functions that were profiled, which includes start-up as well as non-start-up functions. Our apps are built with link-time optimization (LTO or ThinLTO). At the end of LTO, bpc orders cold functions for highly compressed binary size. These two orders of functions are concatenated and passed to the linker which finalizes the function layout in the binary. Both bps and bpc share the same underlying implementation.
Although we could run bps and bpc as one optimization pass, we have two separate passes for the following reasons: (i) Performing bps and bpc at the end of LTO would require carrying large amounts of function traces through the build pipeline; (ii) It is more convenient to simulate the expected page faults for bps offline using function traces; (iii) Likewise, we can evaluate bpc, in separate, for compression without considering profile data.
4.2. Hot Function Layout
As shown in Figure 7, we first merge the raw profiles into the optimization profile with instrumentation metadata during post-processing. For the block coverage and dynamic call graph data, we simply accumulate them into the optimization profile on the fly. However, in order to run bps, we retain function timestamps from each raw profile. We encode the sequence of indices (that is, function trace) to the functions that participate in the cold start-up, and append them to a separate section of the optimization profile.
The bps algorithm uses function traces with thresholds, described in Section 2.2, to set utility vertices, and produces an optimized order for start-up functions. Once bps is completed, the embedded function traces are no longer needed, and can be removed from the optimization profile. Third-party library functions, and outlined functions that appear later than instrumentation in the compilation pass, might not be instrumented. To order such functions, we first check if their call sites are profiled using block coverage data. If that is the case, they inherit the order of their first caller. For instance, if an uninstrumented outlined function, , is called from the profiled functions, and , and bps orders followed by , then we insert after ; this results in the layout .
4.3. Cold Function Layout
We run bpc without intermediate representation (IR), after optimization and code generation are finished, as shown in Figure 7. Although one could run the pass utilizing IR with (Full)LTO, our approach supports ThinLTO operating on subsets of modules in parallel. During code generation, each function publishes a set of hashes that represent its contents, which are meaningful across modules. We use one -bit stable hash (Lee et al., 2022a) per instruction by combining hashes of its opcode and operands. That way, every instruction is converted to a -mer, that is, a substring of length . While computing stable hashes, we omit hashes of pointers and instead utilize hashes of the contents of their targets. Unlike outliners that need to match sequences of instructions, we neither consider the order of hashes, nor the duplicates of hashes. We only track the set of unique stable hashes, per function, as the input to bpc.
Since hot functions are already ordered, we filter out those functions before running bpc. Notice that outliners may optimistically produce many identical functions (Lee et al., 2022a), which will be folded later by the linker. To efficiently model the deduplication, bpc groups functions that have identical sets of hashes, and runs with the set of unique functions that are cold.
As a result of bps and bpc, all functions are ordered. We directly pass these orders to the linker during the LTO pipeline, and the linker enforces the layout of functions. To avoid name conflicts for local symbols, our build pipeline uses unique naming for internal symbols. This way, we achieve a smaller compressed app for faster downloads, while launching the app faster.
5. Evaluation
We design our experiments to answer two primary questions: (i) How well does the new function layout impact real-world binaries in comparison with alternative techniques? (ii) How do various parameters of the algorithm contribute to the solution, and what are the best parameters? We also investigate the scalability of our algorithm.
5.1. Experimental Setup
We evaluated our approach on two commercial iOS applications and one commercial Android application; refer to Table 1 for basic properties of the apps. SocialApp is one of the largest mobile applications in the world. The app, whose total size is over MB, provides a variety of usage scenarios, which makes it an attractive target for compiler optimizations. ChatApp is a medium sized mobile app whose total size is over MB. AndroidNative consists of around shared natives binaries. Unlike the two iOS binaries that are built with ThinLTO, each Android native binary is relatively small, and hence, can be compiled with (Full)LTO without significant increase in the build time. Since there is no fully automated MIP pipeline for building AndroidNative, we use the app only to evaluate the compressed binary size.
| text size | binary size | total | hot | blocks per func. | language | build | |||
|---|---|---|---|---|---|---|---|---|---|
| (MB) | (MB) | func. | func. | p50 | p95 | p99 | mode | ||
| SocialApp | Obj-C/Swift | Oz+ThinLTO | |||||||
| ChatApp | Obj-C/C++ | Oz+ThinLTO | |||||||
| AndroidNative | N/A | C/C++ | Oz+LTO | ||||||
The experiments presented in this section were conducted on a Linux-based server with a dual-node 28-core 2.4 GHz Intel Xeon E5-2680 (Broadwell) having GB RAM. The algorithms are implemented on top of release_14 of LLVM.
5.2. Start-up Performance
Here we present the impact of function layout on start-up performance. The new algorithm, which we refer to as bps, is compared with the following alternatives:
-
•
baseline is the original ordering functions dictated by the compiler; the function layout follows the order of object files that are passed into the linker;
-
•
random is a result of randomly permuting the hot functions;
-
•
order-avg is a natural heuristic for ordering hot functions suggested in (Lee et al., 2022a) based on the average timestamp of a function during start-up computed across all traces.
To evaluate the impact results of function layout in a production environment, we switched between using the current order-avg algorithm and the new bps algorithm for two different release versions, release and release , and recorded the number of page faults during start-up. Table 2 presents the detailed results for the number of page faults on average and of millions of samples published in production. The experiment is designed this way, as in the production environment for iOS apps, we can ship only a single binary and we cannot regress the performance by utilizing less effective algorithms (e.g., baseline or random). We acknowledge that the improvements might come as a result of multiple optimizations, simultaneously shipped with bps. To account for this, we repeated the alternations three times in consecutive releases, and recorded the overall reduction in page faults. On average, bps reduced the number of major page faults by and for SocialApp and ChatApp, respectively. The improvement translates into (average) and (p99) reductions of the cold start-up time for SocialApp.
| average | p99 | ||
|---|---|---|---|
| SocialApp | |||
| order-avg | release | ||
| bps | release | ||
| ChatApp | |||
| order-avg | release | ||
| bps | release |
| Text | Binary | |
|---|---|---|
| SocialApp | ||
| random | ||
| order-avg | ||
| bps | ||
| ChatApp | ||
| random | ||
| order-avg | ||
| bps |
Table 3 shows a similar evaluation of the start-up performance with different function layouts on a particular device, , during the first s of the cold start-up. We repeat the experiment three times and calculated the mean number of page faults in (i) the .text segment and (ii) the entire binary, which additionally includes other data segments. Overall, bps reduces the total major page faults in the binary by and for SocialApp and ChatApp, respectively, while order-avg reduces them by and , respectively. As expected, random significantly increases the page faults, negatively impacting the start-up performance.
One interesting observation from Tables 2 and 3 is that function layout has a bigger impact on the start-up performance of ChatApp than that of SocialApp. Our explanation is that SocialApp consists of dozens of native binaries and four of them participate in the start-up execution, which causes extra page faults while dynamically loading the binaries due to rebase or rebind. In contrast, ChatApp consists of only a few native binaries and only one large binary is responsible for the start-up; thus, an optimized function layout can directly impact the performance.
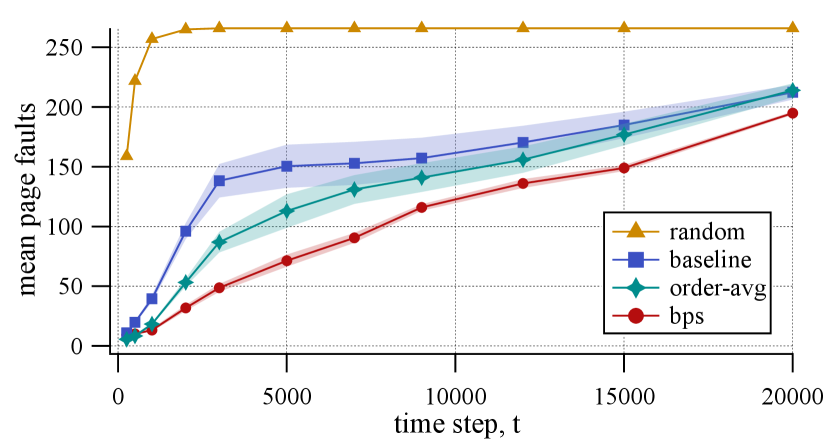
Next we investigate the start-up performance using a model developed in Section 2.2. Figure 8(a) illustrates the mean number of page faults simulated during start-up with up to K time steps, utilizing different function layout algorithms, on SocialApp. As expected, random immediately suffers from many page faults early in the execution, as the randomized placement of functions likely spans many pages. Interestingly, baseline outperforms random; this is likely due to the natural co-location of related functions in the source code. Then, order-avg improves the evaluation curve over baseline, and bps stretches the curve even closer to the linear line, further minimizing the expected number of page faults.
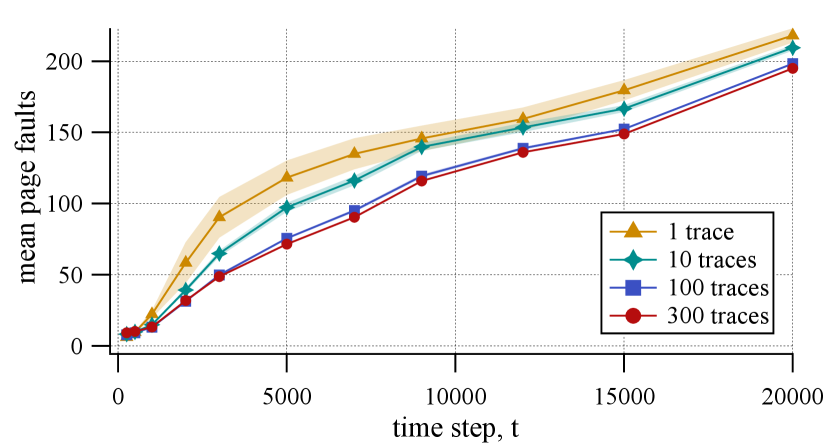
Figure 8(b) shows the average number of page faults for a different number of function traces on SocialApp. Ideally, we want to build a function layout utilizing as few traces as possible. In practice, the start-up scenarios are fairly consistent across different usages, and one can reduce the need of capturing all raw function traces. We observe that running bps with more than traces does not improve the page faults on our dataset. As described in Section 3.1, we use the value by default for bps to reduce the space complexity of post-processing.
5.3. Compressed Binary Size
We now present the results of size optimizations on the selected applications. In addition to the baseline and random function layout algorithms, we compare bpc with the following heuristic:
-
•
greedy is a greedy approach for ordering cold functions discussed in (Lee et al., 2022a). It is a procedure that iteratively builds an order by appending one function at a time. On each step, the most recently placed function is compared (based on the instructions) with not yet selected functions, and the one with the highest similarity score is appended to the order. To avoid an expensive -computation of the scores, a number of pruning rules is applied to reduce the set of candidates; we refer to (Lee et al., 2022a) for details.
Table 4 summarizes the app size reduction from each function layout algorithm, where the improvements are computed on top of baseline (that is, the original order of functions generated by the compiler). The compressed size reduction is measured in three modes: the size of the .text section of the binary directly impacted by our optimization, the size of the executables excluding resource files such as images and videos, and the total app size in a compressed package. We observe that bpc reduces the size of .text by and for SocialApp and ChatApp, respectively. Since this section is the largest in the binary (responsible for of the compressed ipa size), this translates into overall and improvements. At the same time, the impact of all the tested algorithm on the uncompressed size of a binary is minimal (within ), which is mainly due to differences in code alignment. We stress that while the absolute savings may feel insignificant, this is a result of applying a single compiler optimization on top of the heavily tuned state-of-the-art techniques; the gains are comparable to those reported by other recent works in the area (Lee et al., 2022a, b; Rocha et al., 2022; Damásio et al., 2021; Liu et al., 2022).
| Text | Executables | App Size | ||
| SocialApp | ||||
| random | ||||
| greedy | ||||
| bpc | ||||
| ChatApp | ||||
| random | ||||
| greedy | ||||
| bpc | ||||
| AndroidNative | ||||
| random | ||||
| greedy | ||||
| bpc |
An interesting observation is the behavior of random on the dataset, which worsen the compression ratios by around in comparison to the baseline layout. Again the explanation is that similar functions are naturally clustered in the source code. For example, functions within the same object file tend to have many local calls, which makes the corresponding call instructions good candidates for a compact LZ-based encoding. Yet bpc is able to significantly improve the instruction locality by reordering functions across different object files.
Additionally, we evaluate the compressed size reduction for AndroidNative. Notice that the total app size is measured on Android package kit (apk) which includes not only native binaries, but also Android Dex bytecode. Unlike the aforementioned two iOS apps, the .text size of the native binaries is only of the total app size. Therefore, the overall app compressed size win is smaller than for the .text or the executable sections. We observe that these compressed sizes for AndroidNative are more sensitive to different layouts. This is because AndroidNative is a traditional C/C++ binary, where the number of blocks per function is substantially larger than those of the iOS apps, as illustrated in Table 1. Function call instructions encode their call targets with relative offsets whose values differ for each call-site. Unlike the iOS apps written in Objective-C having many dynamic calls, AndroidNative has fewer call-sites, making it more compression-sensitive.
5.4. Further Analysis of Balanced Partitioning
The new Algorithm 1 has a number of parameters that can affect its quality and performance. In the following we discuss some of the parameters and explain our choice of their default values.
As discussed in Section 3, the central component of the algorithm is the objective to optimize at a bisection step, which we refer to as the cost of a partition the set of functions into two disjoint parts. Equation 1 provides a general form of the objective, where the summation is taken over the utility vertices. For a given utility vertex having functions adjacent in one part and functions adjacent in another part, can be an arbitrary objective that is minimized when or and maximized when . Besides to the uniform log-gap defined by Equation 2, we consider two alternatives. The first one is probabilistic fanout defined as follows:
where is a constant. The objective is motivated by partitioning graphs in the context of database sharding (Kabiljo et al., 2017), where represents the probability that a query to a database accesses a certain shard. The second utilized objective represents the absolute difference between and :
It is easy to verify that both objectives satisfy the requirements mentioned above.
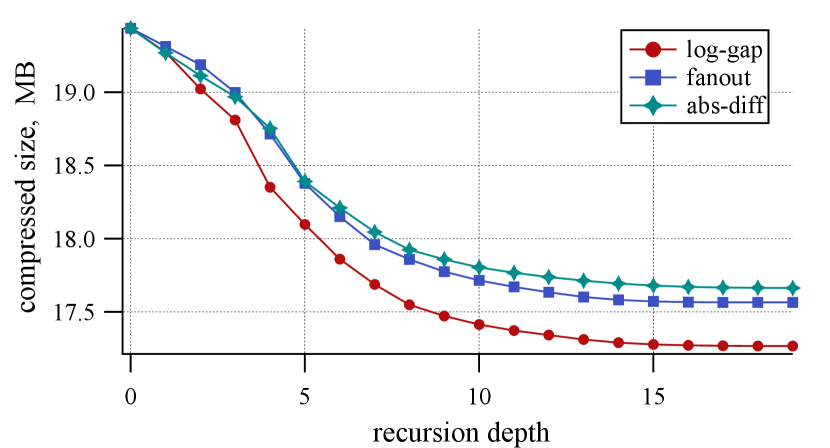
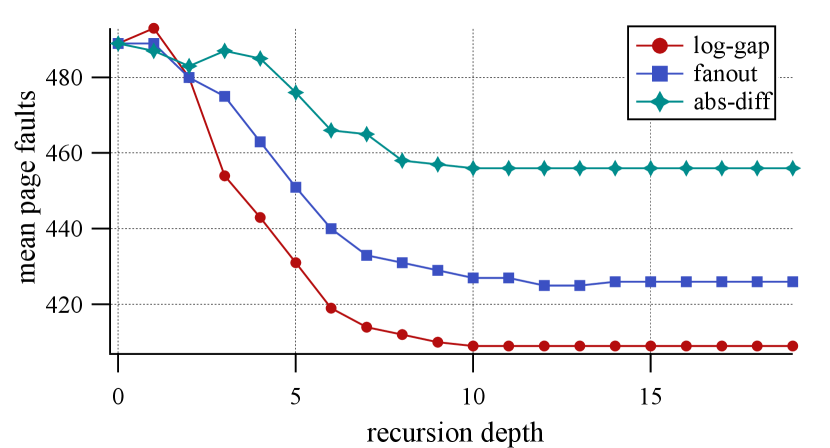
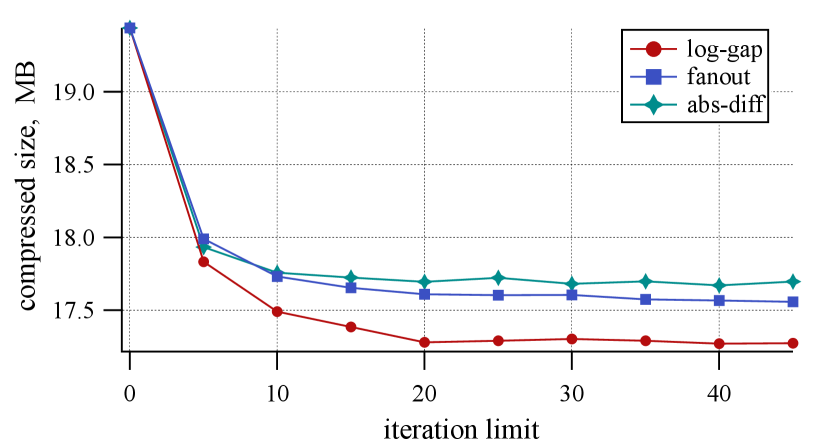
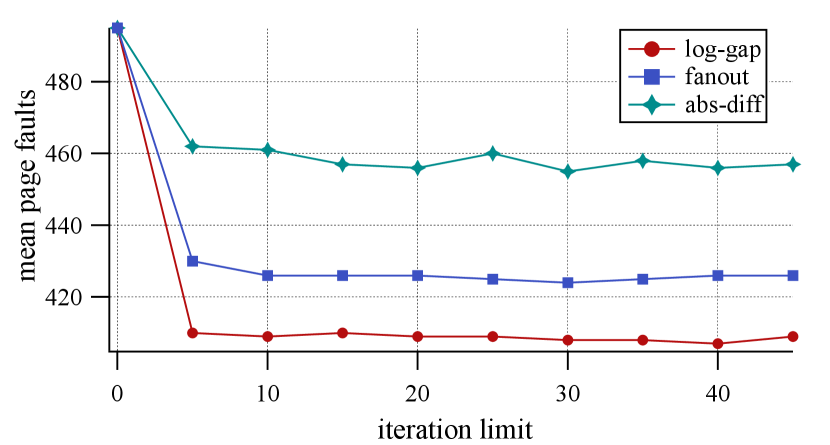
The plots on Figure 9 illustrate the impact of the optimization objective on the quality of resulting function layouts, that is, the corresponding compressed size and the (estimated) number of page faults during start-up. For the fanout objective, we utilize , as it typically results in the best outcomes in the evaluation. We observe that the uniform log-gap cost results in the smallest binaries, outperforming fanout and absolute difference by and , respectively. Similarly, this objective is the best choice for start-up optimization, where it yields fewer page faults by and on average, respectively. Thus, we consider the uniform log-gap as the preferred option for the optimization. However, function orders produced by the algorithm coupled with the other two objectives are still meaningfully better than alternatives investigated in Sections 5.2 and 5.3.
Next we experiment with two parameters affecting Algorithm 1: the number of refinement iterations and the maximum depth of the recursion. Figure 9 (top) illustrates the impact of the latter on the quality of the result evaluated on ChatApp. For every (that is, when the input graph is split into parts), we stop the algorithm and measure the quality of the order respecting the computed partition. It turns out that bisecting vertices is beneficial only when contains a few tens of vertices. Therefore, we limit the depth of the recursion by levels. To investigate the effect of the maximum number of refinement iterations, we apply the algorithm with various values in the range between and ; see Figure 9 (bottom). We observe an improvement of the quality up to iteration , which serves as the default limit in our implementation.
Finally, we explore the choice of the initial splitting strategy of into and in Algorithm 1. Arguably the initialization procedure might affect the quality of the final order, as it provides the starting point for the subsequent local search optimization. To verify the hypothesis, we implemented three initialization techniques that bisect a given graph: (i) a random splitting as outlined in the pseudocode, (ii) a similarity-based minwise hashing (Chierichetti et al., 2009; Dhulipala et al., 2016), and (iii) an input-based strategy that splits the functions based on their relative order in the compiler. In the experiments we found no consistent winner among the three options. Therefore, we recommend the simplest approach (i) in the implementation.
5.5. Build Time Analysis
We now discuss the impact of function layout on the build time of the applications. The time overhead by running bpc is minimal: it takes less than seconds on the larger SocialApp and close to second on the smaller ChatApp. In contrast, greedy results in a noticeable slowdown, increasing the overall build of SocialApp by around minutes, which accounts for more than of the total build time, which is around minutes.
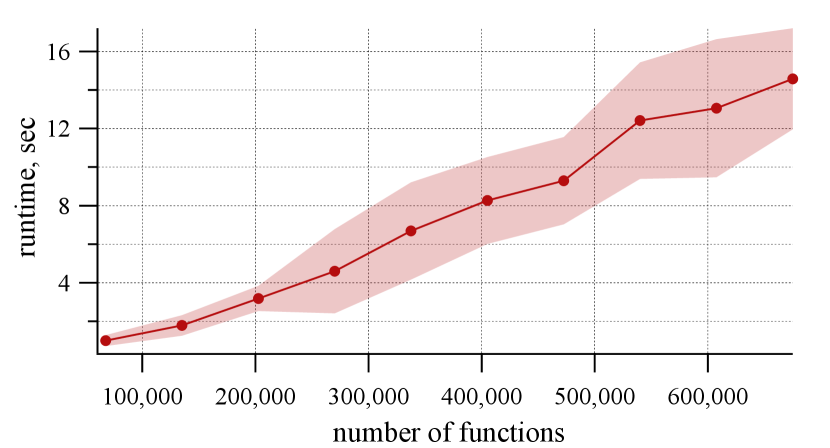
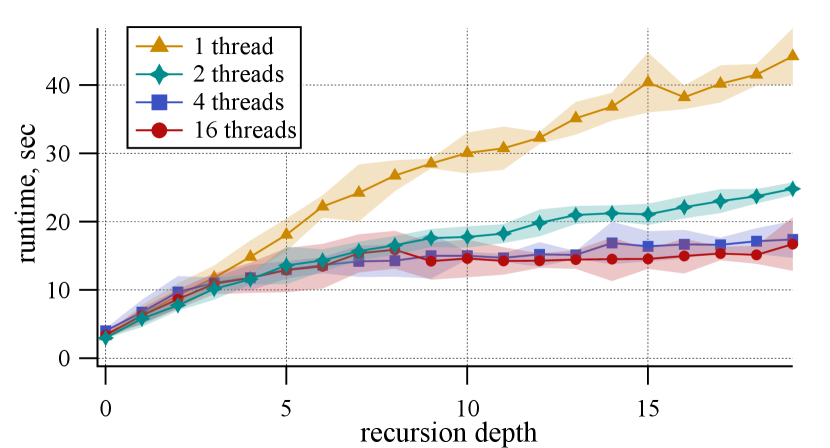
The worst-case time complexity of our implementation is upper bounded by , where is the total number of functions and is the number of function-utility edges. The estimation aligns with Figure 10(a), which plots the dependency of the runtime on the number of functions in the binary. We emphasize that the measurements are done in a multi-threaded environment in which distinct subgraphs (arising from the recursive computation) are processed in parallel. In order to assess the speed up of the parallelism, we limit the number of threads for the computation; see Figure 10(b). Observe that using two threads provides approximately x speedup, whereas four threads yields a x speedup in comparison with the single-threaded implementation. Increasing the number of threads beyond that does not yield measurable runtime improvements. However it is likely that for larger instances with more recursive subgraphs, utilizing multiple threads can be beneficial.
6. Related Work
There exists a rich literature on profile-guided compiler optimizations. Here we discuss previous works that are closely related to PGO in the mobile space, code layout techniques, and our algorithmic contributions.
PGO
Most compiler optimizations for mobile applications are aimed at reducing the code size. Such techniques include algorithms for function inlining and outlining (Lee et al., 2022b; Damásio et al., 2021), merging similar functions (Rocha et al., 2020, 2021), loop optimization (Rocha et al., 2022), unreachable code elimination, and many others. In addition, some works describe performance improvements for mobiles, by improving their responsiveness, memory management, and start-up time (Yan et al., 2012; Lee et al., 2022a). The optimizations can be applied at the compile time or link time (Liu et al., 2022). Post-link-time PGO has been successful for large data-center applications (Panchenko et al., 2019; Propeller, 2020). Our approach is complimentary to the mentioned works and can be applied in combination with the existing optimizations.
Code Layout
The work by Pettis and Hansen (Pettis and Hansen, 1990) is the basis for the majority of modern code reordering techniques for server workloads. The goal of their basic block reordering algorithm is to create chains of blocks that are frequently executed together in the order. Many variants of the technique have been suggested in the literature and implemented in various tools (Panchenko et al., 2019; Ottoni and Maher, 2017; Newell and Pupyrev, 2020; Propeller, 2020; Lavaee et al., 2019; Schwarz et al., 2001; Mestre et al., 2021). Alternative models have been studied in several papers (Kalamationos and Kaeli, 1998; Gloy and Smith, 1999; Lavaee and Ding, 2014), where a temporal-relation graph is taken into account. Temporal affinities between code instructions can also be utilized for reducing conflict cache misses (Hashemi et al., 1997).
Code reordering at the function-level is also initiated by Pettis and Hansen (Pettis and Hansen, 1990) whose algorithm is implemented in many compilers and binary optimization tools (Propeller, 2020; Panchenko et al., 2019). This approach greedily merges chains of functions and is designed to primarily reduce I-TLB misses. An improvement is proposed by Ottoni and Maher (Ottoni and Maher, 2017), who suggest to work with a directed call graph in order to reduce I-cache misses. As discussed in Section 1, the approaches are designed to improve the steady-state performance of server workloads and cannot be applied for mobile apps. The very recent work of Lee, Hoag, and Tillmann (Lee et al., 2022a) is the only study discussing heuristics for function layout in the mobile space; our novel algorithm significantly outperforms their heuristics.
Algorithms
Our model for function layout relies on the classic problem of balanced graph partitioning (Andreev and Räcke, 2006; Garey et al., 1974; Kernighan and Lin, 1970). There exists a rich literature on graph partitioning from both theoretical and practical points of view. We refer the reader to surveys by Bichot and Siarry (Bichot and Siarry, 2013) and by Buluç et al. (Buluç et al., 2016). The most closely related work to our study is on graph reordering (Dhulipala et al., 2016; Mackenzie et al., 2022), which utilizes recursive graph bisection for creating “compression-friendly” inverted indices. While on a high-level our algorithm shares many similarities with these works (Dhulipala et al., 2016; Mackenzie et al., 2022), the application area and the optimization objective discussed in the paper are different.
The general problem of how to optimize memory performance has been studied from the theoretical point of view. One classic stream of works deals with the problem of how to design cache eviction policies to minimize cache misses (Fiat et al., 1991; Sleator and Tarjan, 1985; Young, 2016). A more recent stream of works deals with the problem of computing a suitable data layout for a given cache eviction policy (Petrank and Rawitz, 2005; Lavaee, 2016; Chatterjee et al., 2019). Our setting for start-up optimization is closest to the latter stream; however, a major difference in our setting is the fact that the short-time horizon of the start-up means that page evictions do not play a significant role in our setup. Therefore, we cannot rely on previous methods.
7. Discussion
In this paper we designed, implemented, and evaluated the first function layout algorithm for mobile compiler optimizations. With the careful design of the algorithm, the implementation is fairly simple and scales to process largest instances within several seconds. We regularly apply the optimization for large commercial mobile applications, which results in significant start-up performance wins and app size reductions.
An important contribution of the work is a formal model for function layout optimizations. We believe that the model utilizing the bipartite graph with utility vertices is general enough and will be useful in various contexts. One particularly intriguing future direction is to design a joint optimization for hot and cold functions in the binary. In our current implementation, every function is either optimized for start-up or for size. However it might be possible to relax the constraint and design an approach in which the two objectives are unified. Our early experiments indicate up to size reduction when all functions are re-ordered with bpc, possibly at the cost of a worsen start-up time. Unifying the optimizations is a possible future work.
From a theoretical point of view, our work is related to a computationally hard problem of balanced graph partitioning (Andreev and Räcke, 2006). While the problem is hard in theory, real-world instances may obey certain characteristics, which may simplify the analysis of algorithms. For example, control-flow and call graphs arising from modern programming languages have constant treewidth, which is a standard notion to measure how close a graph is to a tree (Chatterjee et al., 2019; Mestre et al., 2021; Ahmadi et al., 2022). Many NP-hard optimization problems can be solved efficiently on graphs with a small treewidth, and therefore, exploring function layout algorithms parameterized by the treewidth is of interest.
Acknowledgements.
We would like to thank Nikolai Tillmann for fruitful discussions of the problem, and YongKang Zhu for helping with evaluating the approach on AndroidNative.References
- (1)
- Ahmadi et al. (2022) Ali Ahmadi, Majid Daliri, Amir Kafshdar Goharshady, and Andreas Pavlogiannis. 2022. Efficient approximations for cache-conscious data placement. In PLDI ’22: 43rd ACM SIGPLAN International Conference on Programming Language Design and Implementation, Ranjit Jhala and Isil Dillig (Eds.). ACM, San Diego, CA, USA, 857–871. https://doi.org/10.1145/3519939.3523436
- Andreev and Räcke (2006) Konstantin Andreev and Harald Räcke. 2006. Balanced graph partitioning. Theory of Computing Systems 39, 6 (2006), 929–939. https://doi.org/10.1007/s00224-006-1350-7
- Bhatia (2021) Sapan Bhatia. 2021. Superpack: Pushing the limits of compression in Facebook’s mobile apps. https://engineering.fb.com/2021/09/13/core-data/superpack/
- Bichot and Siarry (2013) Charles-Edmond Bichot and Patrick Siarry. 2013. Graph Partitioning. John Wiley & Sons. https://doi.org/10.1002/9781118601181
- Buluç et al. (2016) Aydin Buluç, Henning Meyerhenke, Ilya Safro, Peter Sanders, and Christian Schulz. 2016. Recent Advances in Graph Partitioning. In Algorithm Engineering - Selected Results and Surveys. Springer, Cham, 117–158. https://doi.org/10.1007/978-3-319-49487-6_4
- Chabbi et al. (2021) Milind Chabbi, Jin Lin, and Raj Barik. 2021. An Experience with Code-Size Optimization for Production iOS Mobile Applications. In International Symposium on Code Generation and Optimization, Jae W. Lee, Mary Lou Soffa, and Ayal Zaks (Eds.). IEEE, Seoul, South Korea, 363–377. https://doi.org/10.1109/CGO51591.2021.9370306
- Chatterjee et al. (2019) Krishnendu Chatterjee, Amir Kafshdar Goharshady, Nastaran Okati, and Andreas Pavlogiannis. 2019. Efficient parameterized algorithms for data packing. Proceedings of the ACM on Programming Languages 3, POPL (2019), 1–28. https://doi.org/10.1145/3290366
- Chen et al. (2016) Dehao Chen, Tipp Moseley, and David Xinliang Li. 2016. AutoFDO: Automatic feedback-directed optimization for warehouse-scale applications. In International Symposium on Code Generation and Optimization. ACM, New York, NY, USA, 12–23. https://doi.org/10.1145/2854038.2854044
- Chierichetti et al. (2009) Flavio Chierichetti, Ravi Kumar, Silvio Lattanzi, Michael Mitzenmacher, Alessandro Panconesi, and Prabhakar Raghavan. 2009. On compressing social networks. In Knowledge Discovery and Data Mining. ACM, Paris, France, 219–228. https://doi.org/10.1145/1557019.1557049
- Damásio et al. (2021) Thaís Damásio, Vinícius Pacheco, Fabrício Goes, Fernando Pereira, and Rodrigo Rocha. 2021. Inlining for code size reduction. In 25th Brazilian Symposium on Programming Languages. ACM, Joinville, Brazil, 17–24. https://doi.org/10.1145/3475061.3475081
- Developers (2022) Google Developers. 2022. App Startup Time. https://developer.android.com/topic/performance/vitals/launch-time
- Dhulipala et al. (2016) Laxman Dhulipala, Igor Kabiljo, Brian Karrer, Giuseppe Ottaviano, Sergey Pupyrev, and Alon Shalita. 2016. Compressing Graphs and Indexes with Recursive Graph Bisection. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD’16). ACM, New York, NY, USA, 1535–1544. https://doi.org/10.1145/2939672.2939862
- Easton and Fagin (1978) Malcolm C Easton and Ronald Fagin. 1978. Cold-start vs. warm-start miss ratios. Commun. ACM 21, 10 (1978), 866–872.
- Ferragina and Manzini (2010) Paolo Ferragina and Giovanni Manzini. 2010. On compressing the textual web. In Proceedings of the third ACM international conference on Web Search and Data Mining. ACM, New York, NY, USA, 391–400. https://doi.org/10.1145/1718487.1718536
- Fiat et al. (1991) Amos Fiat, Richard M Karp, Michael Luby, Lyle A McGeoch, Daniel D Sleator, and Neal E Young. 1991. Competitive paging algorithms. Journal of Algorithms 12, 4 (1991), 685–699. https://doi.org/10.1016/0196-6774(91)90041-V
- Garey et al. (1974) Michael R Garey, David S Johnson, and Larry Stockmeyer. 1974. Some simplified NP-complete problems. In Proceedings of the sixth annual ACM Symposium on Theory of Computing. ACM, New York, NY, USA, 47–63. https://doi.org/10.1145/800119.803884
- Gloy and Smith (1999) Nikolas Gloy and Michael D Smith. 1999. Procedure placement using temporal-ordering information. Transactions on Programming Languages and Systems 21, 5 (1999), 977–1027.
- Hashemi et al. (1997) Amir H Hashemi, David R Kaeli, and Brad Calder. 1997. Efficient procedure mapping using cache line coloring. SIGPLAN Notices 32, 5 (1997), 171–182. https://doi.org/10.1145/258915.258931
- He et al. (2022) Wenlei He, Julián Mestre, Sergey Pupyrev, Lei Wang, and Hongtao Yu. 2022. Profile inference revisited. Proceedings of the ACM on Programming Languages 6, POPL (2022), 1–24. https://doi.org/10.1145/3498714
- Inc. (2022) Apple Inc. 2022. Reducing Your App’s Launch Time. https://developer.apple.com/documentation/xcode/reducing-your-app-s-launch-time
- Inc. (2015) Facebook Inc. 2015. Optimizing Facebook for iOS Start Time. https://engineering.fb.com/2015/11/20/ios/optimizing-facebook-for-ios-start-time
- Inc (2021) Facebook Inc. 2021. Redex: A bytecode optimizer for Android apps. https://fbredex.com
- Kabiljo et al. (2017) Igor Kabiljo, Brian Karrer, Mayank Pundir, Sergey Pupyrev, Alon Shalita, Yaroslav Akhremtsev, and Alessandro Presta. 2017. Social Hash Partitioner: A Scalable Distributed Hypergraph Partitioner. Proc. VLDB Endow. 10, 11 (2017), 1418–1429. https://doi.org/10.14778/3137628.3137650
- Kalamationos and Kaeli (1998) J Kalamationos and David R Kaeli. 1998. Temporal-based procedure reordering for improved instruction cache performance. In High-Performance Computer Architecture. IEEE Computer Society, Las Vegas, Nevada, USA, 244–253. https://doi.org/10.1109/HPCA.1998.650563
- Kernighan and Lin (1970) Brian W Kernighan and Shen Lin. 1970. An efficient heuristic procedure for partitioning graphs. Bell System Technical Journal 49, 2 (1970), 291–307.
- Lattner and Adve (2004) Chris Lattner and Vikram Adve. 2004. LLVM: A compilation framework for lifelong program analysis & transformation. In International Symposium on Code Generation and Optimization. IEEE Computer Society, San Jose, CA, USA, 75. https://doi.org/10.1109/CGO.2004.1281665
- Lavaee (2016) Rahman Lavaee. 2016. The hardness of data packing. In Proceedings of the 43rd SIGPLAN-SIGACT Symposium on Principles of Programming Languages. ACM, St. Petersburg, FL, USA, 232–242. https://doi.org/10.1145/2837614.2837669
- Lavaee et al. (2019) Rahman Lavaee, John Criswell, and Chen Ding. 2019. Codestitcher: inter-procedural basic block layout optimization. In Proceedings of the 28th International Conference on Compiler Construction, José Nelson Amaral and Milind Kulkarni (Eds.). ACM, Washington, DC, USA, 65–75. https://doi.org/10.1145/3302516.3307358
- Lavaee and Ding (2014) Rahman Lavaee and Chen Ding. 2014. ABC Optimizer: Affinity Based Code Layout Optimization. Technical Report. University of Rochester.
- Lee et al. (2022a) Kyungwoo Lee, Ellis Hoag, and Nikolai Tillmann. 2022a. Efficient profile-guided size optimization for native mobile applications. In ACM SIGPLAN International Conference on Compiler Construction. ACM, Seoul, South Korea, 243–253. https://doi.org/10.1145/3497776.3517764
- Lee et al. (2022b) Kyungwoo Lee, Manman Ren, and Shane Nay. 2022b. Scalable size inliner for mobile applications (WIP). In Proceedings of the 23rd ACM SIGPLAN/SIGBED International Conference on Languages, Compilers, and Tools for Embedded Systems. ACM, San Diego, CA, USA, 116–120. https://doi.org/10.1145/3519941.3535074
- Lin et al. (2014) Xing Lin, Guanlin Lu, Fred Douglis, Philip Shilane, and Grant Wallace. 2014. Migratory compression: Coarse-grained data reordering to improve compressibility. In USENIX Conference on File and Storage Technologies (FAST). USENIX, Santa Clara, CA, USA, 257–271.
- Liu et al. (2022) Gai Liu, Umar Farooq, Chengyan Zhao, Xia Liu, and Nian Sun. 2022. Linker Code Size Optimization for Native Mobile Applications. arXiv preprint arXiv:2210.07311 abs/2210.07311 (2022). https://doi.org/10.48550/arXiv.2210.07311
- Mackenzie et al. (2022) Joel Mackenzie, Matthias Petri, and Alistair Moffat. 2022. Tradeoff Options for Bipartite Graph Partitioning. IEEE Transactions on Knowledge and Data Engineering (2022), 1–15. https://doi.org/10.1109/TKDE.2022.3208902
- Mansour (2020) Nezar Mansour. 2020. Understanding Cold, Hot, and Warm App Launch Time. https://blog.instabug.com/understanding-cold-hot-and-warm-app-launch-time/
- Mestre et al. (2021) Julián Mestre, Sergey Pupyrev, and Seeun William Umboh. 2021. On the Extended TSP Problem. In 32nd International Symposium on Algorithms and Computation (LIPIcs, Vol. 212), Hee-Kap Ahn and Kunihiko Sadakane (Eds.). Schloss Dagstuhl - Leibniz-Zentrum für Informatik, Fukuoka, Japan, 42:1–42:14. https://doi.org/10.4230/LIPIcs.ISAAC.2021.42
- Newell and Pupyrev (2020) Andy Newell and Sergey Pupyrev. 2020. Improved Basic Block Reordering. IEEE Transactions in Computers 69, 12 (2020), 1784–1794. https://doi.org/10.1109/TC.2020.2982888
- Ottoni and Maher (2017) Guilherme Ottoni and Bertrand Maher. 2017. Optimizing Function Placement for Large-scale Data-center Applications. In International Symposium on Code Generation and Optimization. IEEE Press, Austin, USA, 233–244. https://doi.org/10.1109/CGO.2017.7863743
- Panchenko et al. (2019) Maksim Panchenko, Rafael Auler, Bill Nell, and Guilherme Ottoni. 2019. BOLT: a practical binary optimizer for data centers and beyond. In International Symposium on Code Generation and Optimization. IEEE, Washington, DC, USA, 2–14. https://doi.org/10.1109/CGO.2019.8661201
- Petrank and Rawitz (2005) Erez Petrank and Dror Rawitz. 2005. The hardness of cache conscious data placement. Nordic Journal of Computing 12, 3 (2005), 275–307.
- Pettis and Hansen (1990) Karl Pettis and Robert C Hansen. 1990. Profile guided code positioning. SIGPLAN Notices 25, 6 (1990), 16–27. https://doi.org/10.1145/989393.989433
- Propeller (2020) Propeller 2020. Propeller: Profile Guided Optimizing Large Scale LLVM-based Relinker. https://github.com/google/llvmpropeller.
- Raskhodnikova et al. (2013) Sofya Raskhodnikova, Dana Ron, Ronitt Rubinfeld, and Adam Smith. 2013. Sublinear algorithms for approximating string compressibility. Algorithmica 65, 3 (2013), 685–709. https://doi.org/10.1007/s00453-012-9618-6
- Reinhardt (2016) Peter Reinhardt. 2016. Effect of Mobile App Size on Downloads. https://segment.com/blog/mobile-app-size-effect-on-downloads/
- Rocha et al. (2022) Rodrigo CO Rocha, Pavlos Petoumenos, Björn Franke, Pramod Bhatotia, and Michael O’Boyle. 2022. Loop rolling for code size reduction. In IEEE/ACM International Symposium on Code Generation and Optimization (CGO), Jae W. Lee, Sebastian Hack, and Tatiana Shpeisman (Eds.). IEEE, Seoul, Republic of Korea, 217–229. https://doi.org/10.1109/CGO53902.2022.9741256
- Rocha et al. (2021) Rodrigo CO Rocha, Pavlos Petoumenos, Zheng Wang, Murray Cole, Kim Hazelwood, and Hugh Leather. 2021. HyFM: Function merging for free. In Proceedings of the 22nd ACM SIGPLAN/SIGBED International Conference on Languages, Compilers, and Tools for Embedded Systems, Jörg Henkel and Xu Liu (Eds.). ACM, Virtual Event, Canada, 110–121. https://doi.org/10.1145/3461648.3463852
- Rocha et al. (2020) Rodrigo CO Rocha, Pavlos Petoumenos, Zheng Wang, Murray Cole, and Hugh Leather. 2020. Effective function merging in the SSA form. In Proceedings of the 41st ACM SIGPLAN Conference on Programming Language Design and Implementation, Alastair F. Donaldson and Emina Torlak (Eds.). ACM, London, UK, 854–868. https://doi.org/10.1145/3385412.3386030
- Schwarz et al. (2001) Benjamin Schwarz, Saumya Debray, Gregory Andrews, and Matthew Legendre. 2001. PLTO: A link-time optimizer for the Intel IA-32 architecture. In Workshop on Binary Rewriting. 1–7.
- Sleator and Tarjan (1985) Daniel D Sleator and Robert E Tarjan. 1985. Amortized efficiency of list update and paging rules. Commun. ACM 28, 2 (1985), 202–208.
- Vitter (1985) Jeffrey Scott Vitter. 1985. Random Sampling with a Reservoir. ACM Trans. Math. Softw. 11, 1 (1985), 37–57. https://doi.org/10.1145/3147.3165
- Wang and Suel (2019) Qi Wang and Torsten Suel. 2019. Document reordering for faster intersection. Proceedings of the VLDB Endowment 12, 5 (2019), 475–487.
- Yan et al. (2012) Tingxin Yan, David Chu, Deepak Ganesan, Aman Kansal, and Jie Liu. 2012. Fast app launching for mobile devices using predictive user context. In Proceedings of the 10th international conference on Mobile systems, applications, and services. ACM, Ambleside, United Kingdom, 113–126. https://doi.org/10.1145/2307636.2307648
- Young (2016) Neal E. Young. 2016. Online Paging and Caching. In Encyclopedia of Algorithms. Springer New York, New York, NY, 1457–1461. https://doi.org/10.1007/978-1-4939-2864-4_267
- Ziv and Lempel (1977) Jacob Ziv and Abraham Lempel. 1977. A universal algorithm for sequential data compression. IEEE Transactions on information theory 23, 3 (1977), 337–343.