Optimizing Guided Traversal for Fast Learned Sparse Retrieval
Abstract.
Recent studies show that BM25-driven dynamic index skipping can greatly accelerate MaxScore-based document retrieval based on the learned sparse representation derived by DeepImpact. This paper investigates the effectiveness of such a traversal guidance strategy during top retrieval when using other models such as SPLADE and uniCOIL, and finds that unconstrained BM25-driven skipping could have a visible relevance degradation when the BM25 model is not well aligned with a learned weight model or when retrieval depth is small. This paper generalizes the previous work and optimizes the BM25 guided index traversal with a two-level pruning control scheme and model alignment for fast retrieval using a sparse representation. Although there can be a cost of increased latency, the proposed scheme is much faster than the original MaxScore method without BM25 guidance while retaining the relevance effectiveness. This paper analyzes the competitiveness of this two-level pruning scheme, and evaluates its tradeoff in ranking relevance and time efficiency when searching several test datasets.
1. Introduction
Document retrieval for searching a large dataset often uses a sparse representation of document feature vectors implemented as an inverted index which associating each search term with a list of documents containing such a term. Recently learned sparse representations have been developed to compute term weights using a neural model such as transformer based retriever (Dai and Callan, 2020; Bai et al., 2020; Formal et al., 2021b, a; Mallia et al., 2021; Lin and Ma, 2021) and deliver strong relevance results, together with document expansion (e.g. (Cheriton, 2019)). A downside is that top document retrieval latency using a learned sparse representation is much large than using the BM25 model as discussed in (Mallia et al., 2021; Mackenzie et al., 2021). In the traditional BM25-based document retrieval with additive ranking, a dynamic index pruning strategy based on top threshold is very effective by computing the rank score upper bound on the fly for each visited document during index traversal in order to skip low-scoring documents that are unable to appear in the final top list. Well known traversal algorithms with such dynamic pruning strategies include MaxScore (Turtle and Flood, 1995) and WAND (Broder et al., 2003), and their block-based versions Block-Max WAND (BMW) (Ding and Suel, 2011) and Block-Max MaxScore (BMM) (Chakrabarti et al., 2011; Dimopoulos et al., 2013).
Mallia et al. (Mallia et al., 2022) propose to use BM25 to guide traversal, called GT, for fast learned sparse retrieval because the distribution of learned weights results in less pruning opportunities and they conducted an evaluation with retrieval model DeepImpact (Mallia et al., 2021). One variation they propose is to compute the final rank scoring as a linear combination of the learned weights and BM25 weights, denoted as GTI. GT is a special case of GTI and this paper treats GTI as the main baseline. Since the BM25 weight for a document term pair may not exist in a learned sparse index, zero filling is used in Mallia et al. (Mallia et al., 2022) to align the BM25 and learned weight models. During our evaluation using GT for SPLADE v2 and its revision SPLADE++ (Formal et al., 2021a, 2022), we find that as retrieval depth decreases, BM25 driven skipping becomes too aggressive in dropping documents desired by top ranking based on learned term weights, which can cause a significant relevance degradation. In addition, there is still some room to further improve index alignment of GTI for more accurate BM25 driven pruning.
To address the above issues, we improve our earlier pruning study on dual guidance with combined BM25 and learned weights (Qiao et al., 2022). Our work generalizes GTI by constraining the pruning influence of BM25 and providing an alternative smoothing method to align the BM25 index with learned weights. In Section 4, we propose a two-level parameterized guidance scheme with index alignment, called 2GTI, to manage pruning decisions during MaxScore based traversal. We analyze some formal properties of 2GTI on its relevance behaviors and configuration conditions when 2GTI outperforms a two-stage top search algorithm for a query in relevance.
Section 5 and Appendix A present an evaluation of 2GTI with SPLADE++ (Formal et al., 2021b, a, 2022) and uniCOIL (Lin and Ma, 2021; Gao et al., 2021a) in addition to DeepImpact (Mallia et al., 2021) when using MaxScore on the MS MARCO datasets. This evaluation shows that when retrieval depth is small, or when the BM25 index is not well aligned with the underlying learned sparse representation, 2GTI can outperform GTI and retain relevance more effectively. In some cases, there is a tradeoff that 2GTI based retrieval may be slower than that of GTI while 2GTI is still much faster than the original MaxScore method without BM25 guidance. 2GTI is also effective for the BEIR datasets in terms of the zero-shot relevance and retrieval latency. In Appendix B, we have extended the use of 2GTI for a BMW-based algorithm such as VBMW (Mallia et al., 2017). We demonstrate that 2GTI with VBMW can be useful for a class of short queries and when is small.
2. Background and Related Work
The top- document retrieval problem identifies top ranked results in matching a query. A document representation uses a feature vector to capture the semantics of a document. If these vectors contain much more zeros than non-zero entries, then such a representation is considered sparse. For a large dataset, document retrieval often uses a simple additive formula as the first stage of search and it computes the rank score of each document as:
| (1) |
where is the set of all search terms, is a weight contribution of term in document , and is a document-independent or query-specific term weight. Assume that can be statically or dynamically scaled, this paper views for simplicity of presentation. An example of such formula is BM25 (Jones et al., 2000) which is widely used. For a sparse representation, a retrieval algorithm often uses an inverted index with a set of terms, and a document posting list of each term. A posting record in this list contains document ID and its weight for the corresponding term.
Threshold-based skipping. During the traversal of posting lists in document retrieval, the previous studies have advocated dynamic pruning strategies to skip low-scoring documents, which cannot appear on the final top- list (Broder et al., 2003; Strohman and Croft, 2007). To skip the scoring of a document, a pruning strategy computes the upper bound rank score of a candidate document , referred to as .
If where is the rank score threshold in the top final list, this document can be skipped. For example, WAND (Broder et al., 2003) uses the maximum term weights of documents of each posting list to determine the rank score upper bound of a pivot document while BMW (Ding and Suel, 2011) and its variants (e.g. (Mallia et al., 2017)) optimize WAND use block-based maximum weights to compute the score upper bounds. MaxScore (Turtle and Flood, 1995) uses term partitioning and the top- threshold to skip unnecessary index visitation and scoring computation. Previous work has also pursued a “rank-unsafe” skipping strategy by deliberately over-estimating the current top- threshold by a factor (Broder et al., 2003; Macdonald et al., 2012; Tonellotto et al., 2013; Crane et al., 2017).
Learned sparse representations. Earlier sparse representation studies are conducted in (Zamani et al., 2018), DeepCT (Dai and Callan, 2020), and SparTerm (Bai et al., 2020). Recent work on this subject includes SPLADE (Formal et al., 2021b, a, 2022), which learns token importance for document expansion with sparsity control. DeepImpact (Mallia et al., 2021) learns neural term weights on documents expanded by DocT5Query (Cheriton, 2019). Similarly, uniCOIL (Lin and Ma, 2021) extends the work of COIL (Gao et al., 2021a) for contextualized term weights. Document retrieval with term weights learned from a transformer has been found slow in (Mallia et al., 2022; Mackenzie et al., 2021). Mallia et al. (Mallia et al., 2022) state that the MaxScore retrieval algorithm does not efficiently exploit the DeepImpact scores. Mackenzie et al. (Mackenzie et al., 2021) view that the learned sparse term weights are “wacky” as they affect document skipping during retrieval thus they advocate ranking approximation with score-at-a-time traversal.
Our scheme uses a hybrid combination of BM25 and learned term weights, motivated by the previous work in composing lexical and neural ranking (Yang et al., 2022; Lin et al., 2021b; Gao et al., 2021b; Ma et al., 2021; Li et al., 2022). GTI adopts that for final ranking. A key difference in our work is that hybrid scoring is used for two-level pruning control and its formula can be different from final ranking. The multi-level hybrid scoring difference provides an opportunity for additional pruning and its quality control. Thus the outcome of 2GTI is not a simple linear ranking combination of BM25 and learned weights and two-level guided pruning yields a non-linear ensemble effect to improve time efficiency while retaining relevance. Our evaluation will include a relevance and efficiency comparison with MaxScore using a simple linear combination.
This paper mainly focuses on MaxScore because it has been shown more effective for relatively longer queries (Mallia et al., 2019a). We also consider VBMW (Mallia et al., 2017) because it is generally acknowledged to represent the state of the art (Mackenzie et al., 2021) for many cases, especially when is small and the query length is short (Mallia et al., 2019a).
3. Design Considerations
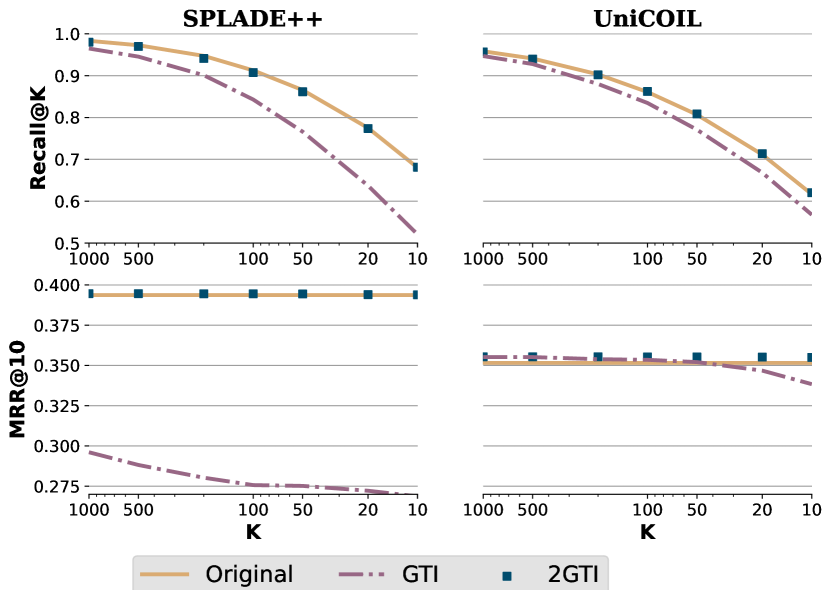
Figure 1 shows the performance of the original MaxScore retrieval algorithm without BM25 guidance, GTI, and the proposed 2GTI scheme in terms of MRR@10 and recall@k when varying top in searching MS MARCO passages on Dev query set. Here is the targeted number of top documents to retrieve and it is also called retrieval depth sometime in the literature. Section 5 has more detailed dataset and index information. For both SPLADE++ and uniCOIL, we build the BM25 model following (Mallia et al., 2022) to expand passages first using DocT5Query, and then use the BERT’s Word Piece tokenizer to tokenize the text, and align the token choices of BM25 with these learned models. From Figure 1, there are significant recall and MRR drops with GTI when varies from 1,000 to 10. There are two reasons contributing to the relevance drops.
-
(1)
When the number of top documents is relatively small, the relevance drops significantly. As is small, dynamically-updated top score threshold becomes closer to the maximum rank score of the best document. Fewer documents fall into top positions and more documents below the updated top score threshold would be removed earlier. Then the accuracy of skipping becomes more sensitive. The discrepancy of BM25 scoring and learned weight scoring can cause good candidates to be removed inappropriately by BM25 guided pruning, which can lead to a significant relevance drop for small .
-
(2)
The relevance drop for SPLADE++ with BM25 guided pruning is noticeably much more significant than uniCOIL. That can be related to the fact that SPLADE++ expands tokens of each document tokens differently and much more aggressively than uniCOIL. As a result, 98.6% of term document pairs in SPLADE++ index does not exist in the BM25 index even after docT5Query document expansion while this number is 1.4% for uniCOIL. Thus, BM25 guidance can become less accurate and improperly skip more good documents.
With the above consideration, our objective is to control the influence of BM25 weights in a constrained manner for safeguarding relevance prudently, and to develop better weight alignment when the BM25 index is not well aligned with the learned sparse index. In Figure 1, the recall@k number of 2GTI marked with blue squares is similar to that of the original method without BM25 guidance. Their MRR@10 numbers overlapped with each other, forming a nearly-flat lines, which indicates their MRR@10 numbers are similar even decreases. The following two sections present our solutions in addressing the above two issues respectively.
4. Two-level Guided Traversal
4.1. Two-level guidance for MaxScore
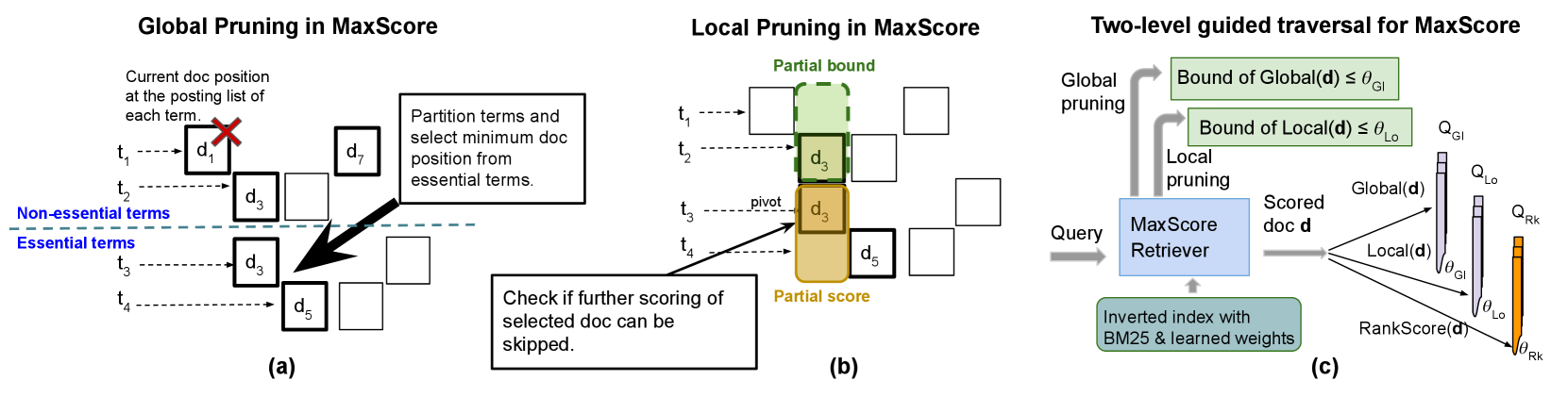
We assume the posting list of each term is sorted in an increasing order of document IDs in the list. The MaxScore algorithm (Turtle and Flood, 1995) can be viewed to conduct a sequence of traversal steps and at each traversal step, it conducts term partitioning and then examines if scoring of a selected document should be skipped. We differentiate pruning-oriented actions in two levels as follows.
-
•
Global level. MaxScore uses the maximum scores (upper bounds) of each term and the current known top threshold to partition terms into two lists at each index traversal step: the essential list and non-essential list. The documents that do not contain essential terms are impossible to appear in top results and thus can be eliminated. In the next step of index traversal, it will start with the minimum unvisited document ID only from the posting lists of essential terms. Thus index visitation is driven by moving such a minimum document ID pointer from the essential list.
We consider this level of pruning as global because it guides skipping of multiple documents and explores inter-document relationship implied by maximum term weights. Figure 2(a) depicts an example of global pruning flow in MaxScore with 4 terms and each posting list maintains a pointer to the current document being visited at a traversal step. The term partitioning identifies two essential terms and . The minimum document ID among the current document pointers in these essential terms is , and any document ID smaller than is skipped from further consideration during this traversal step. The current visitation pointer of the posting list of non-essential lists also moves to the smallest document ID equal to or bigger than .
-
•
Local level. Once a document is selected for possible full evaluation, the ranking score upper bound of this document can be estimated and gradually tightened using maximum weight contribution or the actual weight of each query term for this document. This incrementally refined score upper bound is compared against the dynamically updated top threshold, which provides another opportunity to fully or partially skip the evaluation of this document. We differentiate this level of skipping decision as local because this pruning is localized towards a specific document selected. Figure 2(b) illustrates an example of local pruning in MaxScore. is the document selected after term partitioning and the maximum or actual weights contributed from all posting lists for document are utilized for the local pruning decision.
Instead of directly using BM25 to guide pruning at the global and local levels, we propose to use a linear combination of BM25 weights and learned weights to guide skipping at each level as follows, which allows a parameterizable control of their influence.
-
•
We incrementally maintain three accumulated scores for each document , , and . is for global pruning, is for local pruning, and is for final ranking.
where , follows Expression 1 using BM25 weights, and follows Expression 1 using learned weights. The RankScore formula follows the GTI setting in (Mallia et al., 2022), and 2GTI with behaves like GTI. 2GTI with is the same as MaxScore retrieval and it uses learned neural weights only when .
-
•
With the above three scores for each evaluated document, we maintain three separate queues: , , for documents with the largest scores in terms of , , and respectively. The lowest-scoring document in each queue is removed separately without inter-queue coordination. These queues are maintained for different purposes: the first two queues regulate global and local pruning while the last queue is to produce the final top results. When a document based on local pruning is eliminated for further consideration, this document is not added to global and local queues and . But this document may have some partial score accumulated for its , and it is still added to in case this document with the partial score may qualify in the top results based on the latest value.
These three queues yield three dynamic top- thresholds , , and . They can be used for a pruning decision to avoid any further scoring effort to obtain or refine .
Revised MaxScore pruning control flow: Figure 2(c) illustrates the extra control flow added for the revised MaxScore algorithm. Let be the number of query terms. We define:
-
•
Given posting lists corresponding to query terms, each -th posting list contains a sequence of posting records and each record contains document ID , its BM25 weight and learned weight . Posting records are sorted in an increasing order of their document IDs.
-
•
An array of where is the maximum contribution of the learned weight to any document for -th term.
-
•
An array of where is the maximum contribution of the BM25 weight to any document for -th term.
-
•
search terms are presorted so that where .
Global pruning with term partitioning. For each query term , we find the largest integer from 1 to so that . All terms from to are considered as essential. If a document does not contain any essential term, the upper bound of . This document cannot appear in the final top list based on the global score. Then this document is skipped without appearing in any of the three queues.
Once the essential term list above the position is determined, let the next minimum document ID among the current position pointers in the posting lists of all essential terms be document . We also call it the document.
Local pruning. Next we check if the detailed scoring of the selected pivot document can be avoided fully or partially. Following an implementation in (Tonellotto et al., 2018), we describe this procedure with a modification to use hybrid scoring as follows and it repeats the following three steps with the initial value of term position as the position and decreases by 1 at each loop iteration.
-
•
Let be the sum of all term weights of document in the posting lists from position to after linear combination. Namely when -th posting list contains , and otherwise this value is 0.
As decreases, the term weight of pivot document is extracted from the posting list of -th term if available.
-
•
Let be the bound for partial local score of document in the posting lists of the first to -th query terms.
-
•
At any time during the above calculation, if
further rank scoring for document is skipped and this document will not appear in any of the three queues. Figure 2(b) depicts that the partial bound and partial score of for pivot document are computed to assist a pruning decision.
Complexity. 2GTI’s complexity is the same as MaxScore and GTI. The in-memory space cost includes the space to host the inverted index involved for this query and the three queues. The time complexity is proportional to the total number of posting records involved for a query multiplied by for queue updating.
A posting list may be divided and compressed in a block-wise manner and Block MaxScore can use 2GT similarly while a previous study (Mallia et al., 2019a) shows Block-Max MaxScore is actually slower than MaxScore under several compression schemes. We will discuss the use of 2GT in block-based BMW in Appendix B.
4.2. Relevance properties of 2GTI
2GTI ensembles BM25 and learned weights for pruning in addition to rank score composition, producing a top ranked list which can be different than additive ranking with learned weights or their linear combination of BM25 weights. Thus 2GTI is not rank-safe compared to any of such baselines. Two-level pruning is driven by different combination coefficients , , and configured in 2GTI and their value gap provides an opportunity for additional pruning while 2GTI tries to retain relevance effectiveness. Is there a relevance guarantee 2GTI can offer in case such pruning skips relevant documents erroneously sometimes? To address this question analytically, this subsection presents three properties regarding the relevance outcome and competitiveness of the 2GTI based retrieval.
Our analysis will use the following terms. Given query , let be a ranked list of all documents of the given dataset sorted in a descend order of their rank scores based on a linear combination of their BM25 weights and learned weights with coefficient , namely for document . Specifically, there are three ranked lists: , , and . 2GTI maintains 3 queues , , and with 3 dynamically updated top thresholds, , , . Let , , be the final top threshold of these 3 queues at the end of 2GTI. Namely it is the rank score of -th document in the corresponding queue. The following fact is true:
Proposition 1.
Assume the subset of top documents in each of ,, and is unique after arbitrarily swapping rank positions of documents with the same score. Then any document that appears in top- positions of , , and is in the top- outcome of 2GTI.
Proof.
For any document that appears in the top positions of all three ranked lists, , and
If document is eliminated by global pruning during 2GTI retrieval, and the -based rank score of both document and -th document in ranked list has to be . Then the subset of top documents in is not unique after arbitrarily swapping rank positions of documents with the same score, which is a contradiction.
With the same reason, we can argue that document cannot be eliminated by local pruning or rejected by when being added to during 2GTI retrieval. Then this document has to appear in the final outcome of 2GTI. ∎
The following two propositions analyze when 2GTI performs better in relevance than a two-stage search algorithm called which fetches top results from list , and then re-ranks using the scoring formula of .
Proposition 2.
Assume the subset of top documents in each of ,, and is unique after arbitrarily swapping rank positions of documents with the same score. If 2GTI is configured with or , the average -based rank score of the top documents produced by 2GTI is no less than that of two-stage algorithm .
Proof.
We let denote the top document subset in the outcome of . To prove this proposition, we compare the average -based rank score of documents in and that in at the end of 2GTI. Notice that for any document satisfying , it is in the top results of ranked list and this top subset is deterministic based on the assumption of this proposition. Then cannot be eliminated by global pruning in 2GTI.
Given any document satisfying and at the end of 2GTI, it is either eliminated by local pruning with threshold or by top thresholding of Queue with threshold . In the later case, . When is eliminated by local pruning, global pruning has to use a different formula because is not eliminated by global pruning, and then 2GTI has to be configured with instead of . In that case local pruning is identical to elimination with top threshold of . Then .
Since the size of both and is , . We can derive:
Thus
∎
Definition 1. For a dataset in which documents are only labeled relevant or irrelevant for any test query, we call ranked list outmatches if whenever orders a pair of relevant and irrelevant documents correctly for a query, also orders them correctly.
Proposition 3.
Assume documents in a dataset are only labeled as relevant or irrelevant for a test query. Given a query, when outmatches , which outmatches , 2GTI retrieves equal or more relevant documents in top- positions than two-stage algorithm .
Proof.
When 2GTI completes its retrieval for a query, we count the number of relevant documents in top positions of list , queue , and queue as , and , respectively. To show , we initialize them as 0 first and run the following loop to compute and iteratively. The loop index variable varies from , , until , and at each iteration we look at document at Position of , and document at Position of . Let and be their binary label by which value 1 means relevant and 0 means irrelevant.
-
•
If , we add to both and . Continue this loop.
-
•
Now . If , , we add to , and continue the loop. If , , there are two cases:
-
–
If is within top positions of current , we add to both and . Swap the positions of documents and in . Continue the loop.
-
–
If is not within top positions of , since is in the top of , it cannot be globally pruned and it will be evaluated by 2GTI for a possibility of entering . If is ranked before in list , and since outmatches , has to be ranked before in both and . That is a contradiction. If is ranked after in , we swap the positions of and in . Continue the loop.
-
–
The above process repeats and moves to a higher position until . When , with top-1 document in and top-1 in , the only possible cases are or and . Therefore, at the end of the above process, .
Similarly, we can verify that since outmatches . Therefore . The number of relevant documents up to position retrieved for 2GTI is while the number of relevant documents up to position retrieved for is . Thus this proposition is true. ∎
The above analysis indicates that the top documents agreed by three rankings , , and are always kept on the top by 2GTI, and a properly configured 2GTI algorithm could outperform a two-stage retrieval and re-ranking algorithm in relevance, especially when ranking outmatches and outmatches for a query. Since two-stage search with neural re-ranking conducted after BM25 retrieval is well adopted in the literature, this analysis provides useful insight into the “worst-case” relevance competitiveness of 2GTI with two-level pruning. GTI can be considered as a special case of 2GTI with when the same index is used, and the above three propositions are true for GTI. 2GTI provides more flexibility in pruning with quality control than GTI and Section 5 further evaluates their relevance difference.
4.3. Alignment of tokens and weights
The BM25 model is usually built on word-level tokenization on the original or expanded document sets and the popular expansion method uses DocT5Query with the same tokenization method. When a learned representation uses a different tokenization method such as BERT’s WordPiece based on subwords from BERT vocabulary, we need to align it with BM25 for a consistent term reference. For example, when using BM25 to guide the traversal of SPLADE index, the WordPiece tokenizer is used for a document expanded with DocT5Query before BM25 weighting is applied to each token. Once tokens are aligned, from the index point of view, the same token has two different posting lists based on BM25 weights and based on SPLADE. To merge them when postings do not align one-to-one, the missing weight is set to zero as proposed in (Mallia et al., 2022). We call this zero-filling alignment. As alternatives, we propose two more methods to fill missing weights with better weight smoothness.
-
•
One-filling alignment. We assign 1 as term frequency for a missing token in the BM25 model while this token appears in the learned token list of a document. The justification is that a zero weight is to be too abrupt when such a term is considered to be useful for a document based on a learned neural model. Having term frequency one means that this token is present in the document, even with the lowest value.
-
•
Scaled alignment. This alternative replaces the missing weights in the BM25 model based on a scaled learned score by using the ratio of mean values of non-zero weights in both models. For document ID that contains term , let its BM25 weight be and its learned weight be . Let be an adjusted BM25 weight. Set contains all posting records with nonzero BM25 weights. Set contains posting records with non-zero learned weights. Then is defined as:
5. Evaluations
| Index | Avg. Q Length | #Postings | Size | Merged |
|---|---|---|---|---|
| MS MARCO passages | ||||
| BM25-T5 | 4.5 (4.5) | 644M | 1.2G | - |
| DeepImpact | 4.2 (4.2) | 644M | 2.6G | 2.6G |
| BM25-T5-B | 6.6 (6.6) | 699M | 1.2G | - |
| UniCOIL | 6.6 (686.3) | 592M | 1.5G | 1.7G |
| SPLADE++ | 23.3 (867.6) | 2.62B | 5.6G | 8.3G |
| MS MARCO documents | ||||
| BM25-T5-B | 6.8 (7.0) | 3.39B | 5.4G | - |
| UniCOIL | 6.6 (685.0) | 3.04B | 7.0G | 8.3G |
Datasets and settings. Our evaluation uses the MS MARCO document and passage collections (Craswell et al., 2020; Campos et al., 2016), and 13 publicly available BEIR datasets (Thakur et al., 2021). The results for the BEIR datasets are described in Appendix A. For MS MARCO, the contents in the document collections are segmented during indexing and re-grouped after retrieval using “max-passage” strategy following (Lin et al., 2021a). There are 8.8M passages with an average length of 55 words, and 3.2M documents with an average length of 1131 words before segmentation. The Dev query set for passage and document ranking has 6980 and 5193 queries respectively with about one judgment label per query. Each of the passage/document ranking task of TREC Deep Learning (DL) 2019 and 2020 tracks provides 43 and 54 queries respectively with many judgment labels per query.
In producing an inverted index, all words use lower case letters. Following GT, we packed the learned score and the term frequency in the same integer. For DeepImpact, we adopt GT’s index111https://github.com/DI4IR/dual-score directly. The BM25-T5’s index is dumped from the DeepImpact index. Both BM25-T5 and DeepImpact are using natural words tokenization.
SPLADE and uniCOIL use the BERT’s Word Piece tokenizer. In order to align with them, the BM25-T5-B index reported in the following tables uses the same tokenizer as well. The impact scores of uniCOIL is obtained from Pyserini (Lin et al., 2021a) 222https://github.com/castorini/pyserini/blob/master/docs/experiments-unicoil.md. For SPLADE, in order to achieve the best performance, we retrained the model following the setup in SPLADE++ (Formal et al., 2022). We start from the pretrained model coCondenser (coCondenser, 2021) and distill using the sentenceBERT hard negatives 333https://huggingface.co/datasets/sentence-transformers/msmarco-hard-negatives from a cross-encoder teacher (MiniLM-L-6-v2, 2022) with MarginMSE loss. For FLOP regularization, we use 0.01 and 0.008 for query and documents respectively. We construct the inverted indexes, convert them to the PISA format, and compress them using SIMD-BP128 (Lemire and Boytsov, 2015) following (Mallia et al., 2019a, 2022).
| MS MARCO Dev | DL’19 | DL’20 | MS MARCO Dev | DL’19 | DL’20 | |||||||
| Method | MRR (Recall) | MRT () | nDCG (Recall) | MRT | nDCG (Recall) | MRT | MRR (Recall) | MRT () | nDCG (Recall) | MRT | nDCG (Recall) | MRT |
| SPLADE++, Passages. . For 2GTI-Accurate: ; for 2GTI-Fast: (), (). For GTI and 2GTI: . | ||||||||||||
| BM25-T5-B | 0.2611 (0.5179) | 1.7 (8.7) | 0.5931 (0.1556) | 0.8 | 0.5981 (0.2034) | 1.0 | 0.2611 (0.9361) | 9.2 (28.4) | 0.5931 (0.7608) | 6.4 | 0.5981 (0.7641) | 7.4 |
| SPLADE++-Org | 0.3937 (0.6801) | 121 (483) | 0.7304 (0.1776) | 135 | 0.7290 (0.2437) | 138 | 0.3937 (0.9832) | 278 (819) | 0.7304 (0.8286) | 317 | 0.7290 (0.8287) | 307 |
| -GT | 0.2720 (0.5246) | 121 (438) | 0.6379 (0.1677) | 130 | 0.6106 (0.2192) | 139 | 0.2973 (0.9648) | 336 (1048) | 0.6636 (0.8030) | 330 | 0.6605 (0.8072) | 344 |
| -GTI | 0.2687 (0.5209) | 118 (440) | 0.6352 (0.1669) | 131 | 0.6083 (0.2190) | 139 | 0.2961 (0.9648) | 332 (1059) | 0.6595 (0.8025) | 318 | 0.6587 (0.8066) | 333 |
| -2GTI-Accurate | 0.3939† (0.6812) | 31.1 (171) | 0.7401 (0.1846) | 31.9 | 0.7278 (0.2480) | 36.8 | 0.3946† (0.9799) | 109 (478) | 0.7394 (0.8209) | 123 | 0.7297 (0.8339) | 132 |
| -2GTI-Fast | 0.3934† (0.6792) | 22.7 (116) | 0.7380 (0.1837) | 23.5 | 0.7278 (0.2480) | 26.2 | 0.3937† (0.9662) | 43.1 (144) | 0.7394 (0.8218) | 42.1 | 0.7306 (0.8205) | 45.0 |
| UniCOIL, Passages. . For 2GTI-Accurate: ; for 2GTI-Fast: (), (). For GTI and 2GTI: . | ||||||||||||
| BM25-T5-B | 0.2611 (0.5179) | 1.7 (8.7) | 0.5931 (0.1556) | 0.8 | 0.5981 (0.2034) | 1.0 | 0.2611 (0.9361) | 9.2 (28.4) | 0.5931 (0.7608) | 6.4 | 0.5981 (0.7641) | 7.4 |
| UniCOIL-Org | 0.3516 (0.6168) | 10.5 (102) | 0.7027 (0.1761) | 10.4 | 0.6746 (0.2346) | 14.2 | 0.3516 (0.9582) | 35.3 (197) | 0.7027 (0.7822) | 38.6 | 0.6746 (0.7758) | 42.8 |
| -GT | 0.3347 (0.5639) | 2.1 (11.2) | 0.6990 (0.1770) | 1.7 | 0.6769 (0.2444) | 2.4 | 0.3514 (0.9458) | 10.6 (33.9) | 0.7028 (0.7857) | 10.3 | 0.6746 (0.7741) | 10.8 |
| -GTI | 0.3384 (0.5678) | 2.1 (11.2) | 0.6959 (0.1733) | 1.6 | 0.6739 (0.2422) | 2.4 | 0.3552 (0.9468) | 10.6 (33.2) | 0.7130 (0.7917) | 10.3 | 0.6899 (0.7857) | 10.8 |
| -2GTI-Accurate | 0.3550† (0.6205) | 3.3 (19.2) | 0.7135 (0.1769) | 2.4 | 0.6891 (0.2451) | 3.4 | 0.3554 (0.9566) | 16.9 (68.4) | 0.7130 (0.7904) | 15.5 | 0.6899 (0.7823) | 16.5 |
| -2GTI-Fast | 0.3548† (0.6193) | 2.6 (14.3) | 0.7135 (0.1769) | 1.9 | 0.6891 (0.2451) | 2.8 | 0.3552 (0.9468) | 10.6 (33.2) | 0.7129 (0.7917) | 10.3 | 0.6899 (0.7857) | 10.8 |
| UniCOIL, Documents. . For 2GTI-Accurate: ; for 2GTI-Fast: (), (). For GTI and 2GTI: . | ||||||||||||
| BM25-T5-B | 0.2716 (0.4749) | 2.7 (13.9) | 0.4246 (0.0741) | 3.6 | 0.4463 (0.1693) | 3.1 | 0.2950 (0.9197) | 12.4 (50.0) | 0.5594 (0.5690) | 15.0 | 0.5742 (0.7148) | 15.7 |
| UniCOIL-Org | 0.3313 (0.5638) | 26.0 (252) | 0.5477 (0.0880) | 28.1 | 0.4996 (0.1920) | 27.3 | 0.3530 (0.9426) | 71.0 (447) | 0.6415 (0.5864) | 79.2 | 0.6059 (0.7502) | 86.0 |
| -GT | 0.3280 (0.5455) | 6.8 (36.2) | 0.5199 (0.0779) | 6.2 | 0.4903 (0.1871) | 7.1 | 0.3530 (0.9361) | 20.9 (73.8) | 0.6445 (0.5842) | 21.6 | 0.6059 (0.7444) | 22.7 |
| -GTI | 0.3334 (0.5531) | 6.9 (36.6) | 0.5223 (0.0781) | 6.1 | 0.4905 (0.1857) | 7.2 | 0.3639 (0.9368) | 20.6 (72.9) | 0.6581 (0.5920) | 21.7 | 0.6156 (0.7445) | 22.6 |
| -2GTI-Accurate | 0.3423† (0.5710) | 10.2 (56.4) | 0.5486 (0.0852) | 8.9 | 0.4998 (0.1886) | 10.5 | 0.3644 (0.9422) | 33.2 (149) | 0.6581 (0.5932) | 32.8 | 0.6156 (0.7477) | 37.4 |
| -2GTI-Fast | 0.3418† (0.5663) | 7.4 (40.4) | 0.5453 (0.0847) | 6.5 | 0.4997 (0.1845) | 8.2 | 0.3639 (0.9368) | 20.6 (73.0) | 0.6581 (0.5920) | 21.7 | 0.6156 (0.7445) | 22.5 |
| DeepImpact, Passages. . For 2GTI-Accurate: ; for 2GTI-Fast: (), (). For GTI and 2GTI: . | ||||||||||||
| BM25-T5 | 0.2723 (0.5319) | 0.7 (4.7) | 0.6283 (0.1611) | 0.3 | 0.6321 (0.2218) | 0.5 | 0.2723 (0.9348) | 4.9 (21.3) | 0.6283 (0.7704) | 4.6 | 0.6321 (0.7598) | 5.6 |
| DeepImpact-Org | 0.3276 (0.5844) | 9.4 (73.3) | 0.6964 (0.1698) | 4.9 | 0.6524 (0.2035) | 7.8 | 0.3276 (0.9474) | 23.8 (97.0) | 0.6964 (0.7623) | 25.5 | 0.6524 (0.7534) | 38.9 |
| -GT | 0.3276 (0.5805) | 0.7 (4.7) | 0.6997 (0.1698) | 0.3 | 0.6682 (0.2194) | 0.5 | 0.3276 (0.9454) | 5.1 (21.1) | 0.6964 (0.7745) | 4.9 | 0.6527 (0.7574) | 5.8 |
| -GTI | 0.3375 (0.5866) | 0.7 (4.7) | 0.6953(0.1690) | 0.3 | 0.6846 (0.2372) | 0.5 | 0.3413 (0.9455) | 5.2 (21.7) | 0.7072 (0.7871) | 4.7 | 0.6854 (0.7745) | 5.7 |
| -2GTI-Accurate | 0.3405† (0.5987) | 1.1 (8.1) | 0.7065 (0.1703) | 0.7 | 0.6850 (0.2361) | 1.2 | 0.3414 (0.9469) | 7.4 (33.0) | 0.7072 (0.7875) | 7.8 | 0.6854 (0.7778) | 9.1 |
| -2GTI-Fast | 0.3395† (0.5934) | 0.7 (5.1) | 0.7045 (0.1693) | 0.4 | 0.6882 (0.2371) | 0.6 | 0.3413 (0.9455) | 5.2 (21.7) | 0.7072 (0.7871) | 4.7 | 0.6854 (0.7745) | 5.7 |
Table 1 shows the dataset and index characteristics of the different weighting models on the MS MARCO Dev dataset. Following (Mackenzie et al., 2021), we assume that a query can be pre-processed with a ”pseudo-document” trick that assigns custom weights to query terms in uniCOIL and SPLADE. Therefore, there may be token repetition in each query to reflect token weighting. Column 1 is the mean query length in tokens without or with counting duplicates. Column 3 is the inverted index size while the last column is the size after merging BM25 and learned weights in the index.
The C++ implementation of 2GTI with the modified MaxScore and VBMW algorithms are embedded in PISA (Mallia et al., 2019b), and the code will be released in https://github.com/Qiaoyf96/2GTI. Our evaluation using this implementation runs as a single thread on a Linux server with Intel i5-8259U 2.3GHz and 32GB memory. Weights are chosen by sampling queries from the MS MARCO training dataset.
Metrics. For MS MARCO Dev set, we report the relevance in terms of mean reciprocal rank (MRR@10 on passages and MRR@100 on documents), following the official leader-board standard. We also report the recall@k ratio which is the percentage of relevant-labeled results appeared in the final top- results. For TREC DL test sets, we report normalized discounted cumulative gain (nDCG@10) (Järvelin and Kekäläinen, 2002). The above reporting follows the common practice of the previous work (e.g. (Mallia et al., 2021; Gao et al., 2021a, b; Formal et al., 2021a)).
Before timing queries, all compressed posting lists and metadata for tested queries are pre-loaded into memory, following the same assumption in (Khattab et al., 2020; Mallia et al., 2017). Retrieval mean response times (MRT) are reported in milliseconds. The 99th percentile time () is reported within parentheses in the tables below, corresponding to the time occurring in the 99th percentile denoted as tail latency in (Mackenzie et al., 2018).
Statistical significance. For the reported numbers on MS MARCO passage and document Dev sets in the rest of this section, we have performed a pairwise t-test on relevance difference between 2GTI and a GTI baseline, and between 2GTI and the original learned sparse retrieval without BM25 guidance. No statistically significant degradation has been observed at the 95% confidence level. We have also performed a pairwise t-test comparing the reported relevance numbers of 2GTI and GTI and mark ‘†’ in the evaluation tables if there is a statistically significant improvement by 2GTI over GTI at the 95% confidence level. We do not perform a t-test on DL’19 and DL’20 query sets as the number of queries in these sets is small.
Overall results with MS MACRO. Table 2 lists a comparison of 2GTI with the baseline using three sparse representations for retrieval on MS MARCO and TREC DL datasets. 2GTI uses scaled filling alignment as default while GTI uses zero filling as specified in (Mallia et al., 2022). The value is chosen the same for GTI and 2GTI for each representation, which is the best for most of cases. The “accurate” configuration denotes the one that reaches the highest relevance score. The “fast” configuration denotes the one that reaches a relevance score within 1% of the accurate configuration while being much more faster.
2GTI vs. GTI in SPLADE++. Table 2 shows 2GTI with default scaled filling significantly outperforms GTI with default zero filling for SPLADE++, where BM25 index is not well aligned. “SPLADE++-Org” denotes the original MaxScore retrieval performance using SPLADE++ model trained by ourselves and its MRR@10 number is higher than what has been reported in (Formal et al., 2022). When , GT is slightly better than GTI, and with the fast configuration, MRR@10 of 2GTI is 32.4% higher than that of GT while 2GTI is 7.8x faster than GT for the Dev set. The significant increase in nDCG@10 and decrease in the MRT are also observed in DL’19 and DL’20. When , there is also a large relevance increase and time reduction from GTI or GT to 2GTI for all three test sets. For example, the relevance is 46.4% or 44.6% higher and the mean latency is 5.2x or 5.3x faster for the Dev set.
Compared to the original MaxScore method, 2GTI has about the same relevance score for both and while having much smaller latency. For example, 6.5x reduction (278ms vs. 43.1ms) for the Dev passage set when and 5.3x reduction when (121ms vs 22.7ms) with the 2GTI-fast configuration.
2GTI vs. GTI in DeepImpact and uniCOIL. As shown in Table 2, GTI (or GT) performs very well for in both DeepImpact and uniCOIL in speeding up retrieval while maintaining a relevance similar as the original retrieval. The two-level differentiation for dynamic index pruning does not improve relevance or shorten retrieval time. This can be explained as BM25-T5 index is well aligned with the DeepImpact index and with the uniCOIL index. Also because of this reason, filling to address index alignment is not needed with no improvement in these two cases.
When decreases from 1,000 to 10, as shown in Figure 1 discussed in Section 3, the recall ratio starts to drop, and relevance effectiveness degrades. When as shown in Table 2, DeepImpact-2GTI-fast can increase MRR@10 from 0.3375 by GTI to 0.3395 for the Dev set and deliver slightly higher MRR@10 or nDCG@10 scores than GTI in DL’19 and DL’19 sets. For uniCOIL, 2GTI-fast increases MRR@10 from 0.3384 by GTI to 0.3548 for the Dev set and increases nDCG@10 from 0.6959 to 0.7135 for DL’19. There is also a modest relevance increase for DL’20 passages with and a similar trend is observed for the document retrieval task. The price paid for 2GTI is its retrieval latency increase while its latency is still much smaller than the original retrieval time.
Design options with weight alignment and threshold over-estimation. Table 3 examines the impact of weight alignment and a design alternative based on threshold over-estimation for MS MARCO passage Dev set using SPLADE++ when . In the top portion of this table, threshold over-estimation by a factor of (1.1, 1.3, and 1.5) is used in the original retrieval algorithm without BM25 guidance, and these factor choices are similar as ones in (Macdonald et al., 2012; Tonellotto et al., 2013; Crane et al., 2017). That essentially sets , , and while multiplying and by the above factor in 2GTI. The result shows that even threshold over-estimation can reduce the retrieval time, relevance reduction is significant, meaning that the aggressive threshold used causes incorrect dropping of some desired documents.
The second portion of Table 3 examines the impact of different weight filling methods described in Section 4.3 for alignment when they are applied to GTI and 2GTI, respectively. In both cases, scaled filling marked as “/s” is most effective while one-filling marked as “/1” outperforms zero-filling marked as “/0” also. The MRT of 2GTI/s becomes 10.5x smaller than 2GTI/0 while there is no negative impact to its MRR@10. The MRT of GTI/s is about 13.0x smaller than GTI/0 while there is a large MRR@10 number increase.
| SPLADE++. | MRR@10 | Recall@10 | MRT | |
| Threshold over-estimation | ||||
| Original | 0.3937 | 0.6801 | 121 | 483 |
| - | 0.3690 | 0.5707 | 107 | 457 |
| - | 0.3210 | 0.4393 | 95.0 | 420 |
| - | 0.2825 | 0.3670 | 88.2 | 393 |
| Weight alignment for GTI ( | ||||
| GTI/0 | 0.2687 | 0.5209 | 118 | 440 |
| GTI/1 | 0.3036 | 0.5544 | 26.7 | 114 |
| GTI/s | 0.3468 | 0.5774 | 9.1 | 36.1 |
| Weight alignment for 2GTI-Accurate () | ||||
| 2GTI/0 | 0.3933 | 0.6799 | 328 | 1262 |
| 2GTI/1 | 0.3933 | 0.6818 | 89.3 | 393 |
| 2GTI/s | 0.3939 | 0.6812 | 31.1 | 171 |
A validation on 2GTI’s properties. To corroborate the competitiveness analysis in Section 4.2, Table 4 gives MRR@10 scores and retrieval times in milliseconds of the algorithms with different configurations on the Dev set of MS MARCO passages with and SPLADE++ weights. The result shows that the listed configurations of 2GTI have a higher MRR@10 number than 2-stage search , and 2GTI with that behaves as GTI. MRR@10 of ranking with a simple linear combination of BM25 and learned weights is only slightly higher than 2GTI, but it is much slower.
| MRR@10 | Recall@10 | MRT | ||
|---|---|---|---|---|
| (BM25 retri. SPLADE++ rerank) | 0.3461 | 0.5179 | - | - |
| GTI/s (, ) | 0.3468 | 0.5774 | 9.1 | 36.1 |
| 2GTI/s (, ) | 0.3939 | 0.6812 | 29.8 | 165 |
| 2GTI/s-Accurate (=1, =0, =0.05) | 0.3939 | 0.6812 | 31.1 | 171 |
| 2GTI/s-Fast (, ) | 0.3934 | 0.6792 | 22.7 | 116 |
| Linear comb. () | 0.3946 | 0.6805 | 120 | 477 |
| BT-SPLADE-L | MRR@10 | Recall@10 | MRT | |
|---|---|---|---|---|
| Original MaxScore | 0.3799 | 0.6626 | 17.4 | 59.4 |
| 2GTI/s (=1, =0.3, =0.05) | 0.3772 | 0.6584 | 8.0 | 27.5 |
| GTI/s (, ) | 0.3284 | 0.5520 | 6.6 | 24.9 |
Sensitivity on weight distribution. We have distorted the SPLADE++ weight distribution in several ways to examine the sensitivity of 2GTI and found that 2GTI is still effective. For example, we apply a square root function to the neural weight of every token in MS MARCO passages, the relevance score of both original retrieval and 2GTI drops to 0.356 MRR@10 due to weight distortion, while 2GTI is 5.0x faster than the original MaxScore when .
Efficient SPLADE model. Table 5 shows the application of 2GTI in a recently published efficient SPLADE model (Lassance and Clinchant, 2022) which has made several improvements in retrieval speed. We have used the released checkpoint of this efficient model called BT-SPLADE-L, which has a weaker MRR@10 score, but significantly faster than our trained SPLADE baseline reported in Table 2. When used with this new SPLADE model, 2GTI/s-Fast version results in a 2.2x retrieval time speedup over MaxScore. Its MRR@10 is higher than GTI/s and has less than 1% degradation compared to the original MaxScore.
6. Concluding Remarks
The contribution of this paper is a two-level parameterized guidance scheme with index alignment to optimize retrieval traversal with a learned sparse representation. Our formal analysis shows that a properly configured 2GTI algorithm including GTI can outperform a two-stage retrieval and re-ranking algorithm in relevance.
Our evaluation shows that the proposed 2GTI scheme can make the BM25 pruning guidance more accurate to retain the relevance. For MaxScore with SPLADE++ on MS MARCO passages, 2GTI can lift relevance by up-to 32.4% and is 7.8x faster than GTI when , and by up-to 46.4% more accurate and 5.2x faster when . In all evaluated cases, 2GTI is much faster than the original retrieval without BM25 guidance. For example, up-to 6.5x faster than MaxScore on SPLADE++ when . We have also observed similar performance patterns on BEIR datasets when comparing 2GTI with GTI and the original MaxScore using SPLADE++ learned weights. Compared to other options such as threshold underestimation to reduce the influence of BM25 weights, the two-level control is more accurate in maintaining the strong relevance with a much lower time cost. While our study is mainly centered with MaxScore-based retrieval, 2GTI can be used for VBMW and our evaluation shows that VBMW-2GTI can be a preferred choice for a class of short queries without stop words when is small.
Acknowledgments. We thank Wentai Xie, Xiyue Wang, Tianbo Xiong, and anonymous referees for their valuable comments and/or help. This work is supported in part by NSF IIS-2225942 and has used the computing resource of the XSEDE and ACCESS programs supported by NSF. Any opinions, findings, conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the NSF.
Appendix A Additional Evaluation Results
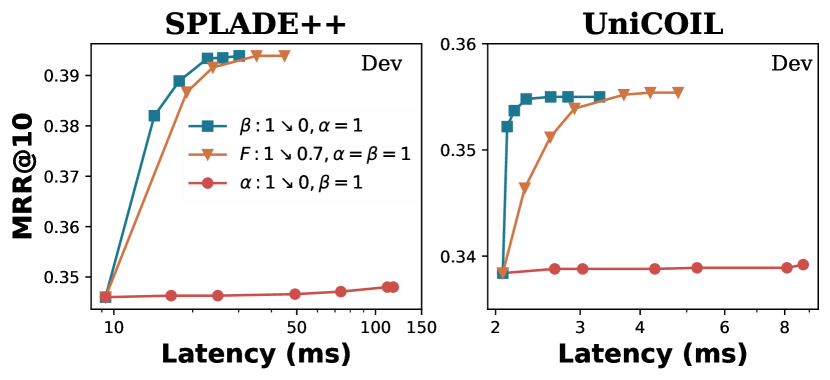
Impact of and adjustment on 2GTI. Figure 3 examines the impact of adjusting parameters and on global and local pruning for the MS MARCO Dev passage test set when in controlling the influence of BM25 weights for SPLADE++ (left) and uniCOIL (right). The axis corresponds to the latency increase while axis corresponds to the MRR@10 or nDCG@10 increase. The results for MS MARCO DL’19, and DL’20 are similar.
The red curve connected with dots fixes and varies from 1 at the left end to 0 at the right end. As decreases from 1 to 0, the latency increases because BM25 influences diminish at the global pruning level and fewer documents are skipped. The relevance for this curve is relatively flat in general and lower than that of the blue curve, representing the global level BM25 guidance reduces time significantly, while having less impact on the relevance.
The blue curve connected with squares fixes at the global level and varies from 1 at the left bottom end to 0 at the right top end. Decreasing value is positive in general for relevance towards some point as BM25 influence decreases gradually at the local level and after such a point, the relevance gain becomes much smaller or negative. For example, after in the blue curve in SPLADE++ becomes 0.3 for the Dev set, its additional decrease does not lift MRR@10 visibly anymore while the latency continues to increase, which indicates the relevance benefit has reached the peak at that point. Our experience with the tested datasets is that the parameter setting for 2GTI can reach a relevance peak typically when is close to 1 and varies between 0.3 and 1.
Note that even the above result advocates that is close to 1, and still have different values to be more effective for the tested data, reflecting the usefulness of two-level pruning control.
Threshold under-estimation. In Figure 3, the brown curve connected with triangles fixes and under-estimates the skipping threshold by a factor of at the local and global levels. That behaves like GTI coupled with scaled weight filling as a special case of 2GTI. varies from 1 at the left bottom end to 0.7 at the right top end of this brown curve. As decreases, the skipping threshold becomes very loose and there is less chance that desired documents are skipped. Then retrieval relevance can improve while retrieval time can increase substantially. Comparing with the blue curve that adjusts , retrieval takes a much longer time in the brown curve to reach the peak relevance, as shown in this figure, and the brown curve is generally placed on the right side of the blue curve. For example on the Dev set with uniCOIL, the brown curve with threshold under-estimation reaches the best relevance at mean latency 3.7ms while the blue curve with adjustment reaches the same peak at mean latency 2.3ms, which is 1.6x faster.
Zero-shot performance on the BEIR datasets. We evaluate the zero-shot ranking effectiveness and response time of 2GTI using the 13 search and semantic relatedness datasets from the BEIR collection. Our training of SPLADE++ model is only based on MS MARCO data without using any BEIR data. Table 6 lists the nDCG@10 scores of original MaxScore on SPLADE++, 2GTI/s-Fast (=1, =0.3, =0.05) and GTI (==1, =0.05). The retrieval depth is and . This table also reports mean response time of retrieval in milliseconds. The SPLADE++ model trained by ourself has an average nDCG@10 score 0.500 close to 0.507 reported in the SPLADE++ paper (Formal et al., 2022). The original MaxScore’s nDCG@10 score does not change when and .
.
| Original MaxScore | 2GTI/s-Fast | GTI/s | ||||
| Dataset | nDCG | MRT | nDCG | MRT | nDCG | MRT |
| =10 | ||||||
| DBPedia | 0.447 | 99.0 | 0.449 | 34.5 | 0.306 | 10.6 |
| FiQA | 0.355 | 5.1 | 0.354 | 3.4 | 0.256 | 0.8 |
| NQ | 0.551 | 72.9 | 0.551 | 28.6 | 0.524 | 7.3 |
| HotpotQA | 0.681 | 453 | 0.681 | 191 | 0.549 | 46.8 |
| NFCorpus | 0.351 | 0.3 | 0.347 | 0.2 | 0.327 | 0.1 |
| T-COVID | 0.705 | 15.9 | 0.707 | 9.9 | 0.569 | 2.6 |
| Touche-2020 | 0.291 | 8.7 | 0.291 | 3.2 | 0.237 | 1.3 |
| ArguAna | 0.446 | 8.8 | 0.448 | 4.0 | 0.454 | 4.0 |
| C-FEVER | 0.234 | 635 | 0.231 | 355 | 0.196 | 241 |
| FEVER | 0.781 | 1028 | 0.771 | 655 | 0.590 | 160 |
| Quora | 0.817 | 21.5 | 0.817 | 6.7 | 0.763 | 1.7 |
| SCIDOCS | 0.155 | 3.7 | 0.155 | 2.1 | 0.140 | 1.2 |
| SciFact | 0.682 | 3.2 | 0.680 | 2.9 | 0.680 | 1.7 |
| Average | 0.500 | - | 0.499 | 2.0x | 0.430 | 6.1x |
| =1000 | ||||||
| Average | 0.500 | - | 0.501 | 2.5x | 0.496 | 2.7x |
When , 2GTI has almost identical nDCG@10 scores as the original MaxScore while 2GTI is on average 2.0x faster than MaxScore for these BEIR datasets. When GTI runs on the same index data, its average nDCG@10 score is 0.43 MRR@10 and it is faster than 2GTI with an average 6.1x speedup over the original MaxScore for these datasets. Two-level pruning in 2GTI can preserve relevance better than GTI and this is consistent with what we have observed for searching MS MARCO passages.
When , the guided traversal algorithms have a better chance to retain relevance. 2GTI has a slightly higher average relevance of 0.501 MRR@10 than that with and it is about 2.5x faster on average than the original MaxScore. For GTI running on the same index with the same alignment, the average MRR@10 is 0.496 whil average speedup 2.7x over MaxScore. Its relevance score is close to that of 2GTI as BM25-driven pruning under a large value can still keep a good recall ratio.
Appendix B Two-level guidance for BMW
Two-level guidance can be adopted to control index traversal of a BMW based algorithm such as VBMW as well because we can also view that such an algorithm conducts a sequence of index traversal steps, and can differentiate its index pruning of each traversal step at the global inter-document and local intra-document levels. We use the same symbol notations as in the previous subsection, assuming the posting lists are sorted by an increasing order of their document IDs. We still keep a position pointer in each posting list of search terms to track the current document ID being handled for each term , incrementally accumulate three scores , , and for each document visited, and maintain three separate score-sorted queues , , and .
-
•
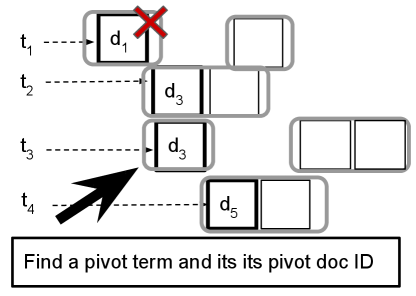
Pruning at the global inter-document level with pivot identification. BMW (Ding and Suel, 2011) keeps a sorted search term list in each traversal step so that with . The pivot position that partitions these current document pointers is the smallest integer called such that This inequality means that any document ID where does not qualify for being in the final top list based on score . Then with the above pivot detection, for , the current visitation pointer of the -th posting list moves to the closest block that contains a document ID equal to or bigger than .
Figure 4 illustrates an example of global pruning in BMW with 4 terms and each posting list maintains a pointer to the current document being visited at a traversal step. Documents in each posting list are covered by a curved rectangle, representing these lists are stored and compressed in a block-wise manner. In the figure, the pivot identification at one traversal step locates document , and document IDs smaller than are skipped for any further consideration in this traversal step.
-
•
Local pruning. Let be the corresponding pivot document in pivot term . In Figure 4, pivot term and . A traversal procedure is executed to check if detailed scoring of document can be avoided fully or partially and this procedure can be similar as the one in the revised MaxScore algorithm described earlier. As each posting list is packaged in a block manner in BMW, let and be the BM25 and learned block maximum weights of the block in the -th posting list that contains , respectively, and they are 0 if no such a block exists in this list. The upper bound of can be tightened using the block-wise maximum weight instead of the list-wise maximum weight contributed by each term as: When decompressing the needed block of a posting list, the block-max contribution from the corresponding term in the above expression can be replaced by the actual BM25 and learned weights for document . Then the upper bound of is further tightened, which can be directly compared with after every downward adjustment.
| Dataset | Method | |||
|---|---|---|---|---|
| Dev | MaxScore-2GTI | 0.355†, 2.6 (14.3) | 0.355†, 3.4 (18.4) | 0.355, 5.5 (26.0) |
| VBMW-2GTI | 0.353†, 4.3 (30.6) | 0.354†, 5.2 (35.6) | 0.355, 8.6 (51.6) | |
| VBMW-GTI | 0.339, 2.4 (14.2) | 0.347, 3.0 (17.2) | 0.353, 5.4 (27.1) | |
| DL’19 | MaxScore-2GTI | 0.714, 1.9 (12.9) | 0.713, 2.3 (14.2) | 0.713, 4.3 (18.6) |
| VBMW-2GTI | 0.708, 2.0 (20.0) | 0.708, 3.7 (23.2) | 0.710, 6.6 (33.1) | |
| VBMW-GTI | 0.694, 1.7 (9.0) | 0.700, 2.2 (11.7) | 0.710, 4.3 (17.9) | |
| DL’20 | MaxScore-2GTI | 0.689, 2.8 (12.1) | 0.689, 3.3 (13.0) | 0.689, 5.3 (22.2) |
| VBMW-2GTI | 0.683, 3.9 (18.4) | 0.686, 4.9 (22.6) | 0.686, 8.4 (46.8) | |
| VBMW-GTI | 0.676, 2.3 (10.5) | 0.680, 2.9 (13.7) | 0.685, 5.3 (24.8) |
Evaluations on effectiveness of 2GTI on VBMW. We choose uniCOIL to study the usefulness of VBMW-2GTI in searching the MS MARCO Dev set. SPLADE++ is not chosen because the test queries are long on average and MaxScore is faster than VBMW for such queries. Table 7 reports the performance for VBMW-2GTI, VBMW-GTI, and MaxScore-2GTI for passage retrieval with uniCOIL when varying . Each entry has a report format of where is MRR@10 for Dev or NDCG@10 for DL’19 and DL’20. is the MRT in ms, and is the latency in ms. 2GTI uses the fast setting with , . For both 2GTI and GTI, . The result shows 2GTI provides a positive boost in relevance for VBMW compared to GTI when is 10 and 20. For , the relevance difference is negligible. MaxScore-2GTI is still faster than VBMW-2GTI on average for all tested queries while their relevance difference is small. we examine below if VBMW-2GTI can be useful for a subset of queries.
Table 8 reports the relevance and time of these three algorithms in the passage Dev set for queries subdivided based on their lengths and if a query contains a stop word or not. That is for uniCOIL with , , , and . Each entry has the same report format as in Table 7. The result shows that VBMW-2GTI is much faster than MaxScore-2GTI for short queries () that do not contain stop words and VBMW-2GTI has an edge in relevance over VBMW-GTI while being very close to MaxScore-2GTI for this class of queries. The above result suggests that a fusion method can do well by switching the algorithm choice based on query characteristics and VBMW-2GTI can be used for a class of queries.
| QLength | 4-5 | 6-7 | ||
|---|---|---|---|---|
| # Q w/ SW | 113 | 1720 | 2175 | 2030 |
| MaxScore-2GTI | 0.286, 1.6 (12.2) | 0.376, 1.7 (8.9) | 0.347, 2.4 (11.5) | 0.315, 4.3 (20.9) |
| VBMW-2GTI | 0.289, 2.1 (15.2) | 0.373, 2.2 (12.5) | 0.346, 3.4 (16.1) | 0.313, 8.5 (50.8) |
| VBMW-GTI | 0.257, 1.1 (6.1) | 0.346, 1.4 (6.8) | 0.334, 2.6 (12.2) | 0.307, 7.4 (43.9) |
| # Q w/o SW | 327 | 445 | 130 | 40 |
| MaxScore-2GTI | 0.397, 1.3 (9.0) | 0.430, 1.9 (9.4) | 0.439, 3.7 (12.1) | 0.558, 5.4 (15.9) |
| VBMW-2GTI | 0.399, 0.9 (4.0) | 0.430, 1.6 (6.3) | 0.438, 3.6 (12.7) | 0.565, 5.6 (23.3) |
| VBMW-GTI | 0.385, 0.7 (3.4) | 0.420, 1.3 (5.1) | 0.433, 2.6 (9.9) | 0.560, 4.1 (12.9) |
References
- (1)
- Bai et al. (2020) Yang Bai, Xiaoguang Li, Gang Wang, Chao liang Zhang, Lifeng Shang, Jun Xu, Zhaowei Wang, Fangshan Wang, and Qun Liu. 2020. SparTerm: Learning Term-based Sparse Representation for Fast Text Retrieval. ArXiv abs/2010.00768 (2020).
- Broder et al. (2003) Andrei Z. Broder, David Carmel, Michael Herscovici, Aya Soffer, and Jason Zien. 2003. Efficient Query Evaluation Using a Two-level Retrieval Process. In Proc. of the 12th ACM International Conference on Information and Knowledge Management. 426–434.
- Campos et al. (2016) Daniel Fernando Campos, Tri Nguyen, Mir Rosenberg, Xia Song, Jianfeng Gao, Saurabh Tiwary, Rangan Majumder, Li Deng, and Bhaskar Mitra. 2016. MS MARCO: A Human Generated MAchine Reading COmprehension Dataset. ArXiv abs/1611.09268 (2016).
- Chakrabarti et al. (2011) Kaushik Chakrabarti, Surajit Chaudhuri, and Venkatesh Ganti. 2011. Interval-based pruning for top-k processing over compressed lists. 2011 IEEE 27th International Conference on Data Engineering (2011), 709–720.
- Cheriton (2019) David R. Cheriton. 2019. From doc2query to docTTTTTquery.
- coCondenser (2021) coCondenser. 2021. https://huggingface.co/Luyu/co-condenser-marco. (2021).
- Crane et al. (2017) Matt Crane, J. Shane Culpepper, Jimmy Lin, Joel Mackenzie, and Andrew Trotman. 2017. A Comparison of Document-at-a-Time and Score-at-a-Time Query Evaluation. In Proceedings of the Tenth ACM International Conference on Web Search and Data Mining (Cambridge, United Kingdom) (WSDM ’17). ACM, New York, NY, USA, 201–210.
- Craswell et al. (2020) Nick Craswell, Bhaskar Mitra, Emine Yilmaz, Daniel Fernando Campos, and Ellen M. Voorhees. 2020. Overview of the TREC 2020 Deep Learning Track. ArXiv abs/2102.07662 (2020).
- Dai and Callan (2020) Zhuyun Dai and Jamie Callan. 2020. Context-Aware Term Weighting For First Stage Passage Retrieval. Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval (2020).
- Dimopoulos et al. (2013) Constantinos Dimopoulos, Sergey Nepomnyachiy, and Torsten Suel. 2013. Optimizing top-k document retrieval strategies for block-max indexes. In WSDM ’13.
- Ding and Suel (2011) Shuai Ding and Torsten Suel. 2011. Faster Top-k Document Retrieval Using Block-Max Indexes. In Proc. of the 34th International ACM SIGIR Conference on Research and Development in Information Retrieval. 993–1002.
- Formal et al. (2021a) Thibault Formal, C. Lassance, Benjamin Piwowarski, and Stéphane Clinchant. 2021a. SPLADE v2: Sparse Lexical and Expansion Model for Information Retrieval. ArXiv abs/2109.10086 (2021).
- Formal et al. (2022) Thibault Formal, Carlos Lassance, Benjamin Piwowarski, and Stéphane Clinchant. 2022. From Distillation to Hard Negative Sampling: Making Sparse Neural IR Models More Effective. Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval (2022).
- Formal et al. (2021b) Thibault Formal, Benjamin Piwowarski, and Stéphane Clinchant. 2021b. SPLADE: Sparse Lexical and Expansion Model for First Stage Ranking. Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval (2021).
- Gao et al. (2021a) Luyu Gao, Zhuyun Dai, and Jamie Callan. 2021a. COIL: Revisit Exact Lexical Match in Information Retrieval with Contextualized Inverted List. NAACL (2021).
- Gao et al. (2021b) Luyu Gao, Zhuyun Dai, Tongfei Chen, Zhen Fan, Benjamin Van Durme, and Jamie Callan. 2021b. Complementing Lexical Retrieval with Semantic Residual Embedding. arXiv:2004.13969 [cs.IR]
- Järvelin and Kekäläinen (2002) Kalervo Järvelin and Jaana Kekäläinen. 2002. Cumulated gain-based evaluation of IR techniques. ACM Transactions on Information Systems (TOIS) 20, 4 (2002), 422–446.
- Jones et al. (2000) Karen Spärck Jones, Steve Walker, and Stephen E. Robertson. 2000. A probabilistic model of information retrieval: development and comparative experiments. In Information Processing and Management. 779–840.
- Khattab et al. (2020) Omar Khattab, Mohammad Hammoud, and Tamer Elsayed. 2020. Finding the best of both worlds: Faster and more robust top-k document retrieval. In Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval. 1031–1040.
- Lassance and Clinchant (2022) Carlos Lassance and Stéphane Clinchant. 2022. An efficiency study for SPLADE models. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2220–2226.
- Lemire and Boytsov (2015) Daniel Lemire and Leonid Boytsov. 2015. Decoding billions of integers per second through vectorization. Softw. Pract. Exp. 45, 1 (2015), 1–29.
- Li et al. (2022) Hang Li, Shuai Wang, Shengyao Zhuang, Ahmed Mourad, Xueguang Ma, Jimmy Lin, and G. Zuccon. 2022. To Interpolate or not to Interpolate: PRF, Dense and Sparse Retrievers. SIGIR (2022).
- Lin et al. (2021a) Jimmy Lin, Xueguang Ma, Sheng-Chieh Lin, Jheng-Hong Yang, Ronak Pradeep, and Rodrigo Nogueira. 2021a. Pyserini: A Python Toolkit for Reproducible Information Retrieval Research with Sparse and Dense Representations. In Proceedings of the 44th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR 2021). 2356–2362.
- Lin and Ma (2021) Jimmy J. Lin and Xueguang Ma. 2021. A Few Brief Notes on DeepImpact, COIL, and a Conceptual Framework for Information Retrieval Techniques. ArXiv abs/2106.14807 (2021).
- Lin et al. (2021b) Sheng-Chieh Lin, Jheng-Hong Yang, and Jimmy J. Lin. 2021b. In-Batch Negatives for Knowledge Distillation with Tightly-Coupled Teachers for Dense Retrieval. In REPL4NLP.
- Ma et al. (2021) Xueguang Ma, Kai Sun, Ronak Pradeep, and Jimmy Lin. 2021. A Replication Study of Dense Passage Retriever. arXiv:2104.05740 [cs.CL]
- Macdonald et al. (2012) Craig Macdonald, Nicola Tonellotto, and Iadh Ounis. 2012. Effect of Dynamic Pruning Safety on Learning to Rank Effectiveness. In Proceedings of the 35th International ACM SIGIR Conference on Research and Development in Information Retrieval (Portland, Oregon, USA) (SIGIR ’12). Association for Computing Machinery, New York, NY, USA, 1051–1052.
- Mackenzie et al. (2018) Joel Mackenzie, J. Shane Culpepper, Roi Blanco, Matt Crane, Charles L. A. Clarke, and Jimmy Lin. 2018. Query Driven Algorithm Selection in Early Stage Retrieval. In Proc. of the 11th ACM International Conference on Web Search and Data Mining. 396–404.
- Mackenzie et al. (2021) Joel Mackenzie, Andrew Trotman, and Jimmy Lin. 2021. Wacky Weights in Learned Sparse Representations and the Revenge of Score-at-a-Time Query Evaluation. arXiv:2110.11540 [cs.IR]
- Mallia et al. (2021) Antonio Mallia, Omar Khattab, Torsten Suel, and Nicola Tonellotto. 2021. Learning passage impacts for inverted indexes. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. 1723–1727.
- Mallia et al. (2022) Antonio Mallia, Joel Mackenzie, Torsten Suel, and Nicola Tonellotto. 2022. Faster Learned Sparse Retrieval with Guided Traversal. In Proceedings of the 45th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR 2022). 1901–1905.
- Mallia et al. (2017) Antonio Mallia, Giuseppe Ottaviano, Elia Porciani, Nicola Tonellotto, and Rossano Venturini. 2017. Faster BlockMax WAND with Variable-sized Blocks. In Proc. of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval. 625–634.
- Mallia et al. (2019b) Antonio Mallia, Michal Siedlaczek, Joel Mackenzie, and Torsten Suel. 2019b. PISA: Performant indexes and search for academia. Proceedings of the Open-Source IR Replicability Challenge (2019).
- Mallia et al. (2019a) Antonio Mallia, Michal Siedlaczek, and Torsten Suel. 2019a. An Experimental Study of Index Compression and DAAT Query Processing Methods. In Proc. of 41st European Conference on IR Research, ECIR’ 2019. 353–368.
- MiniLM-L-6-v2 (2022) MiniLM-L-6-v2. 2022. https://huggingface.co/cross-encoder/ms-marco-MiniLM-L-6-v2. (2022).
- Qiao et al. (2022) Yifan Qiao, Yingrui Yang, Haixin Lin, Tianbo Xiong, Xiyue Wang, and Tao Yang. 2022. Dual Skipping Guidance for Document Retrieval with Learned Sparse Representations. ArXiv abs/2204.11154 (April 2022).
- Strohman and Croft (2007) Trevor Strohman and W. Bruce Croft. 2007. Efficient document retrieval in main memory. In Proc. of the 30th International ACM SIGIR Conference on Research and Development in Information Retrieval. 175–182.
- Thakur et al. (2021) Nandan Thakur, Nils Reimers, Andreas Rücklé, Abhishek Srivastava, and Iryna Gurevych. 2021. BEIR: A Heterogeneous Benchmark for Zero-shot Evaluation of Information Retrieval Models. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 2). https://openreview.net/forum?id=wCu6T5xFjeJ
- Tonellotto et al. (2013) Nicola Tonellotto, Craig Macdonald, and Iadh Ounis. 2013. Efficient and Effective Retrieval Using Selective Pruning. In Proc. of the Sixth ACM International Conference on Web Search and Data Mining (WSDM ’13). ACM, 63–72.
- Tonellotto et al. (2018) Nicola Tonellotto, Craig Macdonald, Iadh Ounis, et al. 2018. Efficient query processing for scalable web search. Foundations and Trends® in Information Retrieval 12, 4-5 (2018), 319–500.
- Turtle and Flood (1995) Howard Turtle and James Flood. 1995. Query Evaluation: Strategies and Optimizations. Information Processing & Management 31, 6 (1995), 831–850.
- Yang et al. (2022) Yingrui Yang, Yifan Qiao, Jinjin Shao, Xifeng Yan, and Tao Yang. 2022. Lightweight Composite Re-Ranking for Efficient Keyword Search with BERT. WSDM (2022).
- Zamani et al. (2018) Hamed Zamani, Mostafa Dehghani, William Bruce Croft, Erik G. Learned-Miller, and J. Kamps. 2018. From Neural Re-Ranking to Neural Ranking: Learning a Sparse Representation for Inverted Indexing. Proceedings of the 27th ACM International Conference on Information and Knowledge Management (2018).