Optimizing the random search of a finite-lived target by a Lévy flight

Random search processes are ubiquitous in nature, such as animals searching for food [1, 2], rescue operations looking for survivors after a shipwreck [3, 4] or even searches for a lost object like a key or a wallet. In typical search models, one considers the targets to be “immortal”, i.e., they do not disappear after a certain time. During the last decades, several models of random search of infinitely lived targets have been studied. The most popular among them is the search by a random walker, either diffusive or performing Lévy flights where the jumps are long-ranged. Several strategies have been incorporated to make the search by a random walker optimal. Lévy walks with certain exponent values can maximize the capture rate by a forager of dispersed resources [5, 6, 7, 8, 9, 10, 11, 12]. Another well known strategy is the intermittent search process where short range and long range moves alternate to locate a single target [13, 14]. A popular model that has received much attention in recent years is a resetting random walker, where the walker goes back to its starting point with a finite probability after every step and restarts the search process [15, 16, 17, 18, 19, 20, 21, 22]. In this case, it turns out that the mean time to find an infinitely lived target can be minimized by choosing an optimal resetting probability [15, 16, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 21]. This fact has also been verified in recent experiments in optical traps [33, 34, 35].

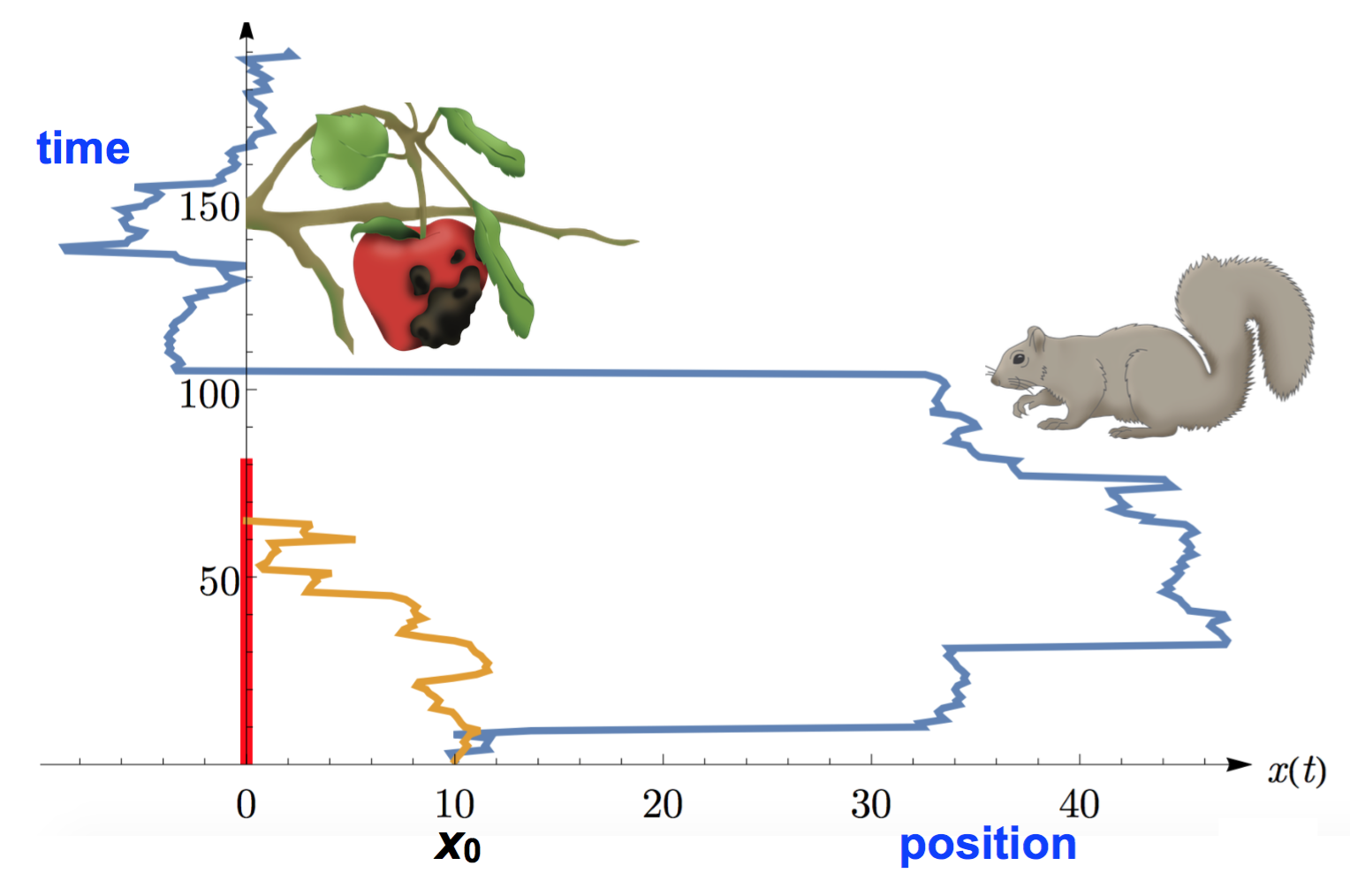
However, there are many instances where the target has a finite but random lifetime. For instance, ripe fruits in a tree rot in a few days. The lifetime of a fruit is typically random since it depends on the nature of the tree and the weather [36]. Similarly, after a shipwreck, a survivor can last in the water only a finite amount of time, which is random as it depends on the general health of the person and sea conditions [37]. Inside a cell, target sites along the DNA are often blocked for long periods of time, which gives a limited random time to the transcription factors to bind to them [38, 39, 40]. In many examples, the searcher has to capture the target before it disappears or dies. Alternatively, in a dual view, one can consider the target as permanent and the walker with a strong time constraint, as an aerial rescue vehicle having a limited flight time [41]. The termination of the search at a random time also appears in the context of foraging theory, where a searcher abandons a patch at any time with a certain give up probability [42]. For a mortal searcher performing a lattice random walk [43] or Brownian motion [44], the capture probability and conditional mean first-passage time cannot be optimized, or only with an infinite diffusion coefficient. If a resetting mechanism is further implemented, though, a non-zero resetting rate can be optimal provided the mortality rate is not too high [45, 46].

A general question then is: is there any way to optimize the search success for a non-permanent target with a random lifetime? A natural generalization of the Brownian case is to investigate the search by a Lévy flight with a Lévy exponent $0<\mu<2$. One can then ask whether there is an optimal value of $\mu$ that minimizes the conditional search time or, alternatively, maximizes the capture probability of the mortal target. In this Letter, we address this problem for a one-dimensional Lévy flight (see Fig. 1). In our model, the target is fixed at the origin and its lifetime $n$ is distributed geometrically via $p(n)=(1-a)\,a^{n}$ where $0<a<1$, i.e., at each discrete step, the target dies with probability $1-a$ and keeps alive with the complementary probability $a$. We assume that the Lévy searcher starts from $x_{0}>0$ and subsequently evolves in discrete time via

$$x_{n}=x_{n-1}+\eta_{n}$$

(1)

where $\eta_{n}$’s are independent and identically distributed jump variables, each distributed via the probability distribution function $f(\eta)$, which we assume to be symmetric and continuous with a power-law tail $\propto 1/|\eta|^{1+\mu}$ where $\mu\in(0,2)$. Note that both parameters $x_{0}$ and $a$ are given numbers and the searcher has no control in optimizing with respect to them. Thus the only parameter that the searcher has in her disposal to optimize is $\mu$, since it is associated with her motion. The search is successful only if the walker crosses the origin for the first time (takes $x_{n}<0$) while the target is still alive. We characterize the search success by two different observables: (i) the capture probability of the target and (ii) the conditional mean first-passage time (CMFPT), i.e., the mean search time conditioned to finding the target alive. We find that, for fixed $x_{0}$ and $a$, these two quantities can be optimized by varying the Lévy index $\mu$. The two optimal parameters $\mu_{cap}^{\star}(x_{0},a)$ and $\mu_{FP}^{\star}(x_{0},a)$ exhibit very rich phase diagrams in the $(x_{0},a)$ plane.

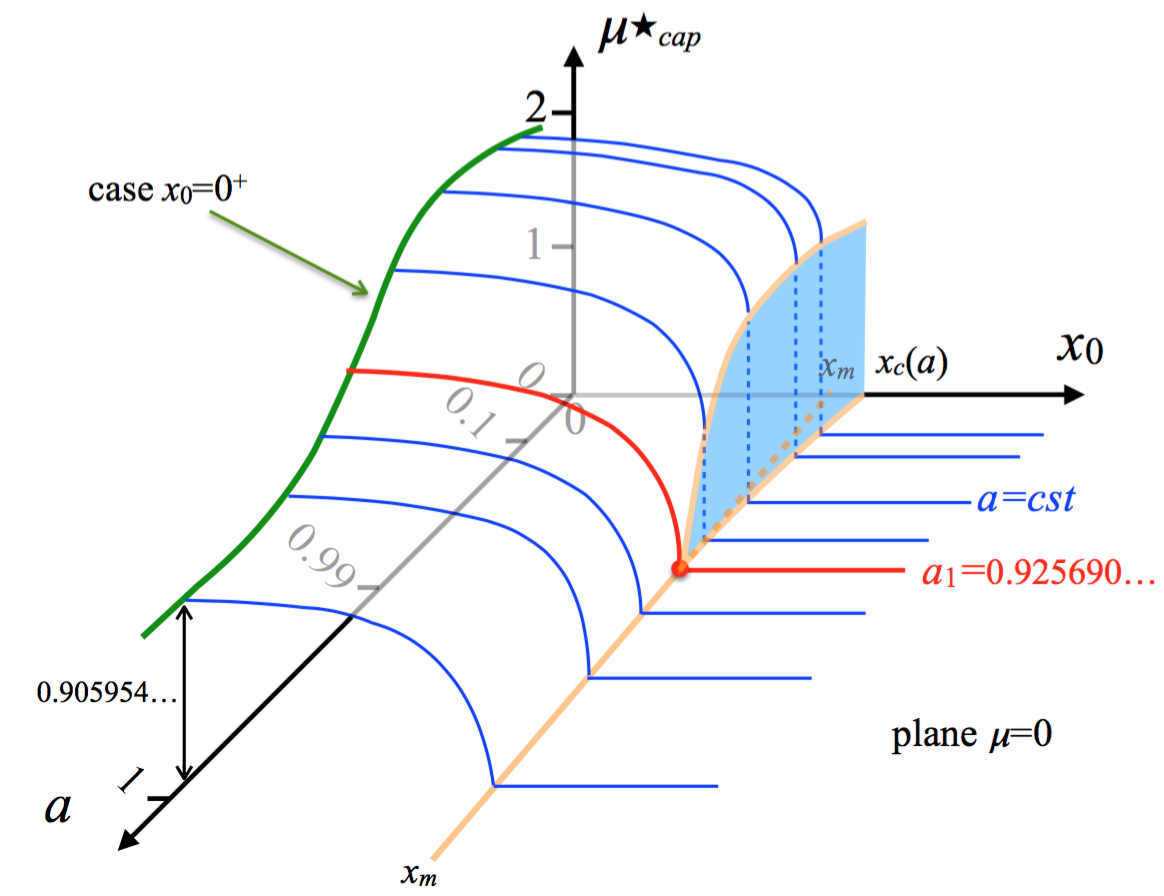
Our results, obtained analytically and numerically, are summarized schematically in Fig. 2 for the capture probability. For any fixed $a<a_{1}=2\,e\,(\sqrt{15}-2)/11=0.925690\ldots$, the index $\mu^{\star}_{cap}(x_{0},a)$ decreases monotonically as a function of $x_{0}$, and jumps to zero abruptly at a critical value $x_{0}=x_{c}(a)$. This signals a first-order transition. In contrast, for any $a>a_{1}$, $\mu^{\star}_{cap}(x_{0},a)$ again decreases with $x_{0}$ but vanishes continuously at $x_{c}(a)$, signaling a second-order transition. In the case $a>a_{1}$, the critical value $x_{c}(a)$ freezes to a constant value $x_{c}(a)=x_{m}=0.561459\ldots$. Thus $(x_{m},a_{1})$, shown by a red dot in Fig. 2, is a tricritical point that sits at the junction of a $1^{\rm st}$ and $2^{\rm nd}$-order transition. The green line $x_{0}\to 0$ is obtained analytically in the Supplemental Material [47]. A qualitatively similar diagram can be drawn for $\mu^{\star}_{FP}(x_{0},a)$, with a tricritical point at a slightly larger value $a_{2}=0.973989\ldots$ [47].

Both observables, the capture probability and the CMFPT, can be related to one fundamental quantity $Q_{\mu}(x_{0},n)$ associated with the random walk, denoting the probability that a Lévy walker with index $\mu$, starting at $x_{0}\geq 0$, does not cross $0$ up to step $n$ [48, 49, 50, 51, 52, 53, 54, 55, 56, 57]. Consequently, $Q_{\mu}(x_{0},n-1)-Q_{\mu}(x_{0},n)$ is the probability that the Lévy flight crosses the origin for the first time at the $n$-th step, with $Q_{\mu}(x_{0},n=0)=1$. Thus for the target to be captured at the $n$-th step, it has to remain alive at least up to step $n-1$, which occurs with probability $a^{n-1}$. Therefore the capture probability $C_{\mu}(x_{0},a)$, defined as the probability that the searcher starting at $x_{0}$ finds the target before the latter becomes inactive, is given by $C_{\mu}(x_{0},a)=\sum_{n=1}^{\infty}a^{n-1}\left[Q_{\mu}(x_{0},n-1)-Q_{\mu}(x_{0},n)\right]$. This sum can be rewritten as

$$C_{\mu}(x_{0},a)=\frac{1-(1-a)\widetilde{Q}_{\mu}(x_{0},s=a)}{a},$$

(2)

where $\widetilde{Q}_{\mu}(x_{0},s)\equiv\sum_{n=0}^{\infty}s^{n}Q_{\mu}(x_{0},n)$ is the generating function of $Q_{\mu}(x_{0},n)$. Similarly, the CMFPT $T_{\mu}(x_{0},a)$, the mean time taken by the successful trajectories to locate the target [44], can be expressed as $T_{\mu}(x_{0},a)=\sum_{n=1}^{\infty}na^{n-1}\left[Q_{\mu}(x_{0},n-1)-Q_{\mu}(x_{0},n)\right]/C_{\mu}(x_{0},a)$, where $C_{\mu}(x_{0},a)$ acts as a normalization factor. This can also be rewritten again in terms of the generating function of the survival probability

$$T_{\mu}(x_{0},a)=a\frac{\partial}{\partial a}\ln\left[1-(1-a)\widetilde{Q}_{\mu}(x_{0},s=a)\right].$$

(3)

Thus to analyze either $C_{\mu}(x_{0},a)$ or $T_{\mu}(x_{0},a)$, we need the generating function $\widetilde{Q}_{\mu}(x_{0},s)$ for Lévy flights. Unfortunately, there is no simple expression for $\widetilde{Q}_{\mu}(x_{0},s)$. However its Laplace transform with respect to $x_{0}$ is given by the exact Pollaczek-Spitzer formula [48, 50],

	$\displaystyle\int_{0}^{\infty}\widetilde{Q}_{\mu}(x_{0},s)\,e^{-\lambda x_{0}}dx_{0}=\frac{1}{\lambda\sqrt{1-s}}\varphi(\lambda,s)$		(4)
	$\displaystyle{\rm with}\quad\varphi(\lambda,s)=\exp\left[-\frac{\lambda}{\pi}\int_{0}^{\infty}\frac{\ln[1-s\hat{f}(k)]}{\lambda^{2}+k^{2}}dk\right]\,,\quad$		(5)

where $\hat{f}(k)=\int_{-\infty}^{\infty}f(\eta)\ e^{{\rm i}k\eta}d\eta$ is the Fourier transform of the step distribution. Here we will focus on Lévy stable jump distribution, with $\hat{f}(k)=e^{-|k|^{\mu}}$ with $0<\mu\leq 2$.

With an infinite-lived target ($a=1$), recall that $C_{\mu}=1$, owing to the recurrence property of $1d$ random walks, while $T_{\mu}=\infty$, independently of $x_{0}$ and $f(\eta)$ [58]. Hence, there is no option of optimizing them by varying $\mu$. However, for a finite-lived target where $a<1$, both quantities become nontrivial functions of $\mu$ and can be optimized by choosing $\mu$ appropriately with optimal values $\mu^{\star}_{cap}(x_{0},a)$ and $\mu^{\star}_{FP}(x_{0},a)$. One finds that, even for short-lived targets, $C_{\mu}$ at optimality can be larger than the maximal value $1/2$ that could be achieved by a naive ballistic strategy (see [47]).

In order to maximize the capture probability in Eq. (2) by varying $\mu$, for fixed $x_{0}$ and $a$, it turns out that we need to minimize $\widetilde{Q}_{\mu}(x_{0},s=a)$ with respect to $\mu$. We will study the exact relation in Eq. (4), both analytically in certain limits and numerically by inverting the Laplace transform in Eq. (4) using the Gaver-Stehfest method [59, 60], which we explain in [47].

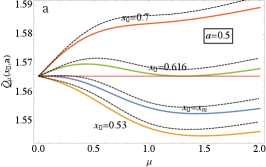
We start by plotting the numerically obtained $\widetilde{Q}_{\mu}(x_{0},a)$ as a function of $\mu$, for fixed $x_{0}$ and $a$. In Fig. 3a we show the data for $a=0.5$ and four different values of $x_{0}$. For small $x_{0}$, the curve has a single minimum at a nonzero value of $\mu^{\star}_{cap}(x_{0},a)$, while there is a local maximum at $\mu=0$. As $x_{0}$ increases to some value $x_{m}$, the derivative of $\widetilde{Q}_{\mu}(x_{0},a)$ with respect to $\mu$ at $\mu=0^{+}$ ¹¹1Here we consider the $\mu\to 0^{+}$ limit (and not strictly $\mu=0$). In the limit $\mu\to 0^{+}$ the jump distribution is normalizable but not when $\mu=0$ exactly. Hence we restrict only to the case $\mu\to 0^{+}$. vanishes, i.e., $\partial_{\mu}\widetilde{Q}_{\mu}(x_{m},a)\Big{|}_{\mu=0}=0\;.$ This value of $x_{m}$ can be determined analytically [see Eq. (7) below] and is given by $x_{m}=e^{-\gamma_{E}}=0.561459\ldots$, where $\gamma_{E}$ is the Euler constant. When $x_{0}$ slightly exceeds $x_{m}$, the curve has two minima: one at $\mu=0^{+}$ and one at $\mu=\mu^{\star}_{cap}(x_{0},a)$, but the value at $\mu=0^{+}$ is higher. This situation persists for $x_{m}<x_{0}<x_{c}(a)$. When $x_{0}$ exceeds $x_{c}(a)$, the local minimum at $\mu=0^{+}$ becomes the global one and $\mu^{\star}_{cap}(x_{0},a)$ drops to $0^{+}$, triggering a first-order transition. The point $x_{c}(a)$ is thus determined by

$$\left.\partial_{\mu}\widetilde{Q}_{\mu}(x_{c},a)\right|_{\mu^{\star}_{cap}(x_{c})}=0,\quad\left.\widetilde{Q}_{\mu}(x_{c},a)\right|_{\mu^{\star}_{cap}(x_{c})}=q_{0},$$

(6)

where $q_{0}\equiv\widetilde{Q}_{\mu=0}(x_{c},a)$. From Eq. (4), $q_{0}=1/\sqrt{(1-a)(1-ae^{-1})}$, independent of the position (see [47]). This scenario presented above for $a=0.5$ continues to hold up to $a=a_{1}\approx 0.926$.

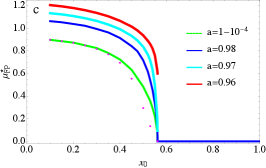
For $a>a_{1}$, a different scenario occurs as displayed in Fig. 3b where again $\widetilde{Q}_{\mu}(x_{0},a)$ is plotted as a function of $\mu$ for different values of $x_{0}$. In contrast to Fig. 3a, the curves always have a single minimum at $\mu=\mu^{\star}_{cap}(x_{0},a)$ that decreases continuously to $0^{+}$ as $x_{0}$ approaches a critical value $x_{c}(a)=x_{m}$, signaling a second-order phase transition. Thus the first and second-order phase transitions merge at $a=a_{1}$, making it a tricritical point. These numerical observations lead to the phase diagram presented in Fig. 2.

The CMFPT exhibits the same qualitative features as above, with a tricritical point now located at $a=a_{2}\approx 0.974...$ In Fig. 3c, we plot $\mu^{\star}_{FP}(x_{0},a)$ as a function of $x_{0}$ for four different values of $a$ close to $a_{2}$. The jump discontinuity at $x_{0}=x_{c}(a)$ is finite for $a<a_{2}$ while it vanishes for $a\geq a_{2}$, confirming indeed that $(x_{0}=x_{m},a=a_{2})$ is a tricritical point for $\mu^{\star}_{FP}(x_{0},a)$ in the $(x_{0},a)$ plane.

We show how $a_{1}$ and $a_{2}$ can be computed analytically using a standard Landau-like expansion well known in critical phenomena. There, by expanding the free energy in powers of the order parameter, the Landau theory gives access to the phase diagram close to a continuous critical/tricritical point. Here we follow the same spirit with $\mu$ playing the role of the “order parameter”. We then expand $\widetilde{Q}_{\mu}$ in powers of $\mu$ near $\mu=0^{+}$: $\widetilde{Q}_{\mu}(x_{0},a)=q_{0}+q_{1}\mu+q_{2}\mu^{2}/2!+q_{3}\mu^{3}/3!+q_{4}\mu^{4}/4!+\ldots$, where the dependence of the $q_{i}$’s on $x_{0}$ and $a$ is implicit. Depending on these parameters, the signs of $q_{i}$’s in this expansion may change, leading either to a first or second order transition and also to the possibility of a tricritical point. In the standard Landau’s theory with a positive order parameter it is enough to keep terms up to order $O(\mu^{3})$ and a tricritical point occurs when $q_{1}=q_{2}=0$ while $q_{3}>0$ [62] (see also [63] in the context of stochastic resetting). However, in our case, the dependence of $q_{i}$’s on $x_{0}$ and $a$ are such that this standard scenario is not realized and one needs to keep terms up to order $O(\mu^{4})$. From Eq. (4), we show that [47]

	$\displaystyle q_{1}=\frac{ae^{-1}}{2\sqrt{1-a}(1-ae^{-1})^{3/2}}(\ln x_{0}+\gamma_{E})$		(7)
	$\displaystyle q_{2}=\frac{3\sqrt{e}a^{2}}{4\sqrt{1-a}(e-a)^{5/2}}(\ln x_{0}+\gamma_{E})^{2}\;.$		(8)

For $x_{0}<x_{m}=e^{-\gamma_{E}}$, we have $q_{1}<0$ and $q_{2}>0$. In contrast, for $x_{0}>x_{m}$, we have both $q_{1},q_{2}>0$ and both of them vanish simultaneously at $x_{0}=x_{m}$, for any $a$. The tricritical point thus occurs when $q_{3}(x_{m},a)$ changes sign. We have [47]

$$q_{3}(x_{m},a)=\frac{a\sqrt{e}K}{8\sqrt{1-a}(e-a)^{7/2}}(11a^{2}+8ea-4e^{2})\;,$$

(9)

where $K=2\zeta(3)=2.40411...$. Thus $q_{3}(x_{m},a)<0$ for $a<a_{1}$ where $a_{1}=2e(\sqrt{15}-2)/11$ is the unique root of $11a^{2}+8ea-4e^{2}=0$ in $(0,1)$. At the transition point $x_{0}=x_{c}(a)$ and for $a<a_{1}$, since $q_{3}<0$, we need to keep terms up to order $O(\mu^{4})$ (assuming that $q_{4}>0$ in the Landau expansion). From Eqs. (6), the first-order jump discontinuity $\Delta(a)\equiv\mu_{cap}^{\star}(x_{c}(a),a)$ is given by [47]

$\displaystyle\Delta(a)=\frac{2}{3\,q_{4}}\left(2|q_{3}|+\sqrt{4q_{3}^{2}-9q_{2}q_{4}}\right)\Big{|}_{x_{0}=x_{c}(a)}\;,$

(10)

This discontinuity vanishes when $q_{3}\to 0$ and $q_{2}\to 0$ which occurs at the point $(x_{0}=x_{m},a=a_{1})$, indicating that this is a tricritical point. If $a>a_{1}$ then $q_{2}>0$ and $q_{3}>0$ : when $q_{1}$ changes sign (always at $x_{0}=x_{m}$), a $2^{\rm nd}$ order transition occurs. Hence $x_{c}(a)$ freezes to $x_{m}$ for $a>a_{1}$. A similar Landau-like expansion can be carried out exactly for the CMFPT, which leads to the same qualitative conclusions, with $a_{2}=0.973989\ldots$ [47].

As mentioned before, for a permanent target ($a=1$), there is no optimal strategy since the capture probability is $1$ and the CMFPT infinite, irrespective of $\mu$. However, surprisingly, for long-lived targets, there is a nontrivial optimal strategy characterized by the same $\mu_{cap}^{*}=\mu_{FP}^{*}$ for both observables. As $a\to 1$, Eqs. (4) and (3) imply $\widetilde{Q}_{\mu}(x_{0},a)\approx g_{\mu}(x_{0})/\sqrt{1-a}$ and $T_{\mu(x_{0},a)}\approx g_{\mu}(x_{0})/(2\sqrt{1-a}$), where $g_{\mu}(x_{0})$ is independent of $a$. Hence, both the capture probability and the CMFPT are optimized by minimizing $g_{\mu}(x_{0})$ with respect to $\mu$. Since the expression of $g_{\mu}(x_{0})$ is complicated, it is hard to obtain the full functional form of $\mu_{cap}^{*}=\mu_{FP}^{*}$ for all $x_{0}$. However, close to the transition point $x_{m}$, where $\mu_{cap}^{*}$ is expected to be small due to the continuous transition, $g_{\mu}$ directly follows from the small $\mu$ expansion of $Q_{\mu}$ above. Using Eqs. (7) and (9), we obtain exactly to leading order for small $(x_{m}-x_{0})/x_{m}$

$\displaystyle\mu_{cap}^{*}=\mu_{FP}^{\star}\approx A\left(\frac{x_{m}-x_{0}}{x_{m}}\right)^{1/2}\;,\;x_{0}<x_{m}\;,$

(11)

where $A=2(e-1)/\sqrt{\zeta(3)(11+8e-4e^{2})}=1.7549\ldots$ (see SM [47] for more details). This shows that the limit $a\to 1$ does allow an optimization with respect to $\mu$.

So far, we have analyzed the exact formula in Eq. (4) in the small $\mu$ limit. When $a\to 1$ and $x_{0}\to 0$, far from $x_{m}$, a small $x_{0}$ expansion in [47] gives $\mu^{\star}_{cap}\to 0.905954...$, as indicated in Fig. 2. But to obtain analytically the full curves in Figs. 3a and 3b, as a function of $\mu$ from Eq. (4) for any $(x_{0},a)$ is extremely hard. Yet, we have found a concavity approximation allowing a very accurate analytical estimate of $\widetilde{Q}_{\mu}(x_{0},a)$. Starting from the concavity of the logarithm, we approximate $\sum_{i}w_{i}\ln(r_{i})\approx\ln(\sum_{i}w_{i}r_{i})$ for any set of positive reals $r_{i}$ and normalized weights $\sum_{i}w_{i}=1$. With this, one can perform the inverse Laplace transform in Eq. (4) and deduce the general expression

$$\widetilde{Q}_{\mu,approx}(x_{0},s)=\frac{1}{\sqrt{1-s}}e^{-\frac{1}{\pi}\int_{0}^{\infty}\ln[1-s\hat{f}(k)]\frac{\sin(kx_{0})}{k}dk}\;,$$

(12)

where we have used the identity ${\cal L}^{-1}[k/(\lambda^{2}+k^{2})]=\sin(kx_{0})$ for $x_{0}>0$ (see also [47]). Eq. (12) is easy to evaluate numerically. Interestingly, the first two terms of its small $\mu$ expansion coincide with the exact expressions $q_{0}$ and $q_{1}$ above, as well as the first terms of its small $x_{0}$ expansion [47]. Consequently, Eq. (12) gives the correct slope-change point $x_{m}$ and also captures qualitatively the order of the transitions (see the dashed lines in Figs. 3a and 3b), along with the existence of a tricritical point.

We conclude with the remark that this problem of a finite-lived target is reminiscent of a Lévy flight subject to resetting with a probability $r$ to its initial position. The mean first-passage time (MFPT) to find a permanent target at the origin was computed for the resetting Lévy flight [56] where the walker has two parameters $\mu$ and $r$ that can be used to optimize the MFPT (see also [64] for a related problem). Indeed, the optimal pair $(\mu^{*},r^{*})$ was computed and found to undergo a first-order transition at a critical value of the initial distance $x_{0}$ from the target. This is rather different from our problem where the Lévy flight has only a single parameter $\mu$, which it can vary to optimize the MFPT. In our model, the walker has no control over the parameter $a$ associated with the lifetime of the target. Hence, here we optimize the search strategy by varying only $\mu$ for fixed $a$, which leads to a new phase diagram with a tricritical point.

In summary, we have studied a simple model of a Lévy flight of index $\mu$ in one-dimension searching for a finite-lived target at the origin with mean lifetime $1/(1-a)$. We have shown that the capture probability of the target can be maximized by choosing an optimal $\mu^{\star}_{cap}$ for fixed $a$ and $x_{0}$ (where $x_{0}$ denotes the initial distance from the target). The presence of a finite life-time leads to a very rich and nontrivial phase diagram for $\mu^{\star}_{cap}$ in the $(x_{0},a)$ plane. This work opens up many interesting possibilities for future works. For instance, it would be interesting to find the optimal strategy in higher dimensions, for multiple Lévy flights and for the case where the distribution of the target lifetime is non-exponential.

DB acknowledges support from the LPTMS at the Université Paris-Saclay (France) and from CONACYT (Mexico) grant Ciencia de Frontera 2019/10872. We thank Lya Naranjo for illustration support in Fig. 1.