1]University of North Texas, Denton, TX, 76203, USA 2]Santa Fe Institute, Santa Fe, NM, 87501, USA
Orthogonal-Ansatz VQE: Locating excited states without modifying a cost-function
Abstract
Most literature in the Variational Quantum Eigensolver (VQE) algorithm focuses on finding the ground state of a physical system, by minimizing a quantum-computed cost-function. When excited states are required, the cost-function is usually modified to include additional terms ensuring orthogonality with the ground state. This generally requires additional quantum circuit executions and measurements, increasing algorithmic complexity. Here we present a design strategy for the variational ansatz which enforces orthogonality in candidate excited states while still fully exploring the remaining subset of Hilbert space. The result is an excited-state VQE solver which trades increasing measurement complexity for increasing circuit complexity. The latter is anticipated to become preferable as quantum error mitigation and correction become more refined. We demonstrate our approach with three distinct ansatze, beginning with a simple single-body example, before generalizing to accommodate the full Hilbert space spanned by all qubits, and a constrained Hilbert space obeying particle number conservation.
[wires=4]
& \gate[wires=4]V_0
\qw\rstick[wires=4]
\qw \qw
\qw \qw
\qw \qw
[wires=4]
& \gate[wires=4]V_1(θ)
\gate[wires=4]V_0
\qw\rstick[wires=4]
\qw \qw \qw
\qw \qw \qw
\qw \qw \qw
Assumptions:
Guarantees:
1 Introduction
Quantum chemistry and materials science are anticipated to be among the first of applications transformed by quantum computing. Several promising algorithms have been developed over the past two decades for characterizing electronic states, including the Variational Quantum Eigensolver (VQE) [1, 2, 3], Quantum Phase Estimation [4, 5, 6], Quantum Subspace Expansion [7, 8, 9], Quantum Imaginary Time Evolution [10, 11], and many others. See [12] for a thorough review.
Variational algorithms like VQE are particularly popular today because their hybrid quantum-classical approach renders them compatible with the available qubit count, connectivity, decoherence, and gate fidelity, which pose severe engineering constraints on many other algorithms’ efficacy. In VQE, a parameterized quantum circuit is used to prepare an arbitrary trial state, whose energy is measured by estimating the expectation value of a molecule or material’s Hamiltonian operator . The parameters are then updated according to a classical optimization routine in an attempt to minimize the energy. Despite theoretical challenges in minimizing the potential energy surface of a chemical system [13, 14], many recent experiments have reported that VQE implemented on actual quantum hardware is capable of producing a high-quality estimate of the ground state.[15, 16, 17]
Many properties of interest require knowledge not only of the ground-state, but of excited states as well. Most strategies for locating excited states involve a modification of the system Hamiltonian, and therefore the cost-function to be measured on the quantum computer. For example, if one is interested in the lowest excited state above an energy , one may minimize the energy of a “folded” Hamiltonian , which will tend to quadratically increase the complexity of the cost-function.[18] More commonly, one attempts to find excited states iteratively, beginning from the ground state and working up one energy level at a time. One strategy is to directly subtract from the Hamiltonian the subspace spanned by the ground state [19], but we find this approach quickly leads to intractably complex cost-functions. This method is refined in Orthogonally-Constrained VQE (OC-VQE): one measures the energy of a trial state as usual, but adds to the cost-function an additional term obtained from a subsequent circuit measuring orthogonality with the ground state, which ensures the trial state will find its optimal value in the excited subspace.[20, 21, 18] As each excited state is located, every cost-function evaluation requires running additional circuits to guarantee each trial state optimizes to the correct subspace.
In this paper, we present Orthogonal-Ansatz VQE (OA-VQE), an alternative iterative eigensolver comparable to OC-VQE. In OA-VQE, trial-states are directly constrained to explore the excited subspace by modification of the parameterized quantum circuit rather than the cost-function. This has the immediate benefit of keeping the cost-function consistent for each excited state optimization - measurement complexity is determined only by the complexity of the Hamiltonian itself. Additionally, because the circuit must explore a smaller subspace each time a new excited state is located, the optimization step in OA-VQE becomes easier as the algorithm proceeds (albeit with a possibly longer circuit).
In Section 2, we describe the properties a parameterized quantum circuit family must have to be compatible with OA-VQE, and we summarize the algorithm. In Sections 3, 4, and 5, we present circuit families suitable for performing OA-VQE for various chemical systems and qubit mappings. In Section 6, we conclude by commenting on the limitations and potential of our algorithm.
2 Orthogonal-Ansatz VQE
Suppose the active space of our system of interest comprises the computational basis vectors , where . Our objective is to iteratively construct an alternate basis (such as an eigenbasis for some observable) with vectors guaranteeing orthogonality: .
Define the family of unitary operators with the following conditions:
| (1) | |||
| (2) | |||
| (3) |
Eq. 1 is the unitary constraint. Eq. 2 ensures that the th acts trivially on all basis vectors indexed before . Note that Eq. 2 implies must act trivially on the same vectors. Eq. 3 is redundant (it can be inferred from Eqs. 1 and 2) but instructive: it ensures that the th operating on the th basis vector results in a vector which spans only those basis vectors indexed on or after .
We now construct as:
| (4) |
The product is ordered such that acts directly on . In quantum computing parlance, the circuit implementing is applied to the state , and then each preceding circuit is applied, ending with the one implementing .
Consider the inner product for :
| (5) |
where equality is due to Eq. 1. Because of Eq. 2, the bra can be contracted to . Repeating this contraction, we are left with
| (6) |
Thus, the orthogonality of is guaranteed.
Now we will describe the Orthoganal-Ansatz Variational Quantum Eigensolver (OA-VQE) algorithm. We would like to find the eigenstates of a Hermitian operator acting on a given active space. We should construct a parameterized quantum circuit such that the ansatz thoroughly explores the entire active space, and variationally locate the parameters which minimize the expectation value . We identify the first of our orthogonalization operators . Next we should construct a new parameterized quantum circuit such that acts trivially on (Eq. 2), and thoroughly explores the span of every basis vector in the active space except (Eq. 3). A new ansatz is guaranteed from the arguments above to be orthogonal to the ground state; minimizing its expectation value therefore locates the first excited state. If circuits can be effectively parameterized to iteratively omit each basis vector, this protocol may be repeated to obtain as many eigenstates as desired, all without needing to alter the cost-function. As an additional benefit, one may expect each optimization to require fewer and fewer resources because subsequent eigenstates are located in a lower-dimensional space.
3 Single-Body Circuits
The eigendecomposition protocol described in Section 2 requires designing quantum circuits which thoroughly explore the Hilbert space spanned by certain basis vectors, while acting trivially on others. The next three sections present examples to illustrate how such circuits may be constructed for a specific problem. In the first example, we will briefly re-present a family of circuits used to solve the band-structure of a periodic system.
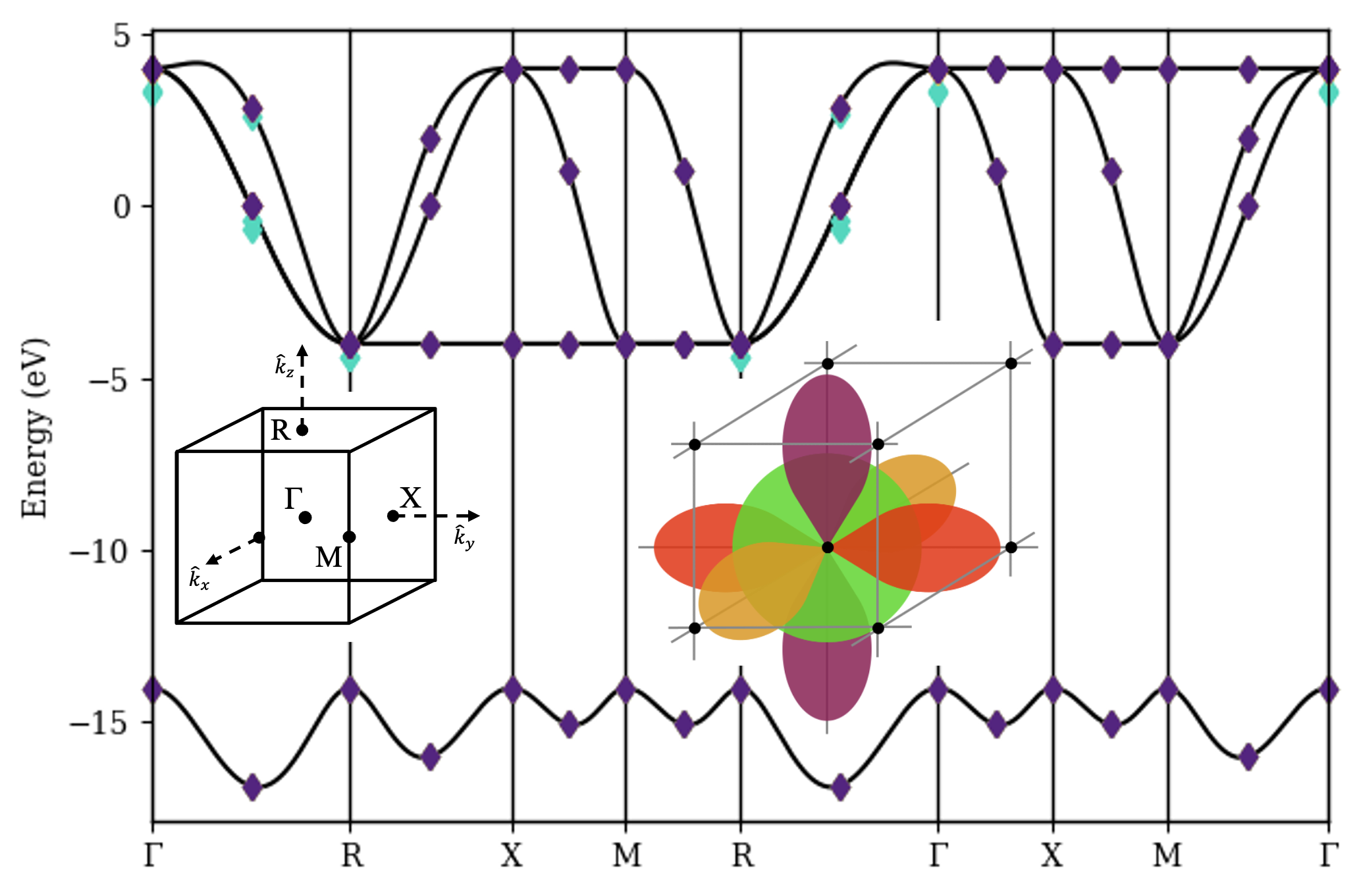
Band-structures are a tool for characterizing periodic materials under the single-body approximation, presuming all electrons in the material behave independently. Here we will use the reciprocal-orbital qubit mapping from [22], which assigns one qubit to each orbital included in the material’s unit cell. Since we consider only one electron, the active space consists only of those basis vectors with a Hamming weight of one. Considering a toy model for elemental polonium in a cubic lattice (Fig. 2(a)), we require four qubits; the basis vectors represent the reciprocal , , , and orbitals.
& \gate[wires=2]A_1
\gategroup[wires=4,steps=3,background,style=
,label style=
label position=below,
anchor=north,
yshift=-0.2cm
]
\qw \qw \qw
\lstick
\qw \gate[wires=2]A_2
\qw \qw
\lstick
\qw \qw \gate[wires=2]A_3
\qw
\lstick
\qw \qw \qw \qw
& \qw \qw \qw \gate[wires=2]A_1
\gategroup[wires=4,steps=3,background,style=
,label style=
label position=below,
anchor=north,
yshift=-0.2cm
]
\qw \qw \qw
\lstick
\gate[wires=2]A_4
\gategroup[wires=3,steps=2,background,style=
,label style=
label position=below,
anchor=north,
yshift=-0.2cm
]
\qw \qw \qw \gate[wires=2]A_2
\qw \qw
\lstick
\qw \gate[wires=2]A_5
\qw \qw \qw \gate[wires=2]A_3
\qw
\lstick
\qw \qw \qw \qw \qw \qw \qw
In order to construct a quantum circuit, we use the two-qubit gates presented in [23]. Each gate takes two independent angles , and rotates between the and , such that chaining each gate together as in Fig. 3(a) successfully spans the full active space. For excited states, cutting out individual basis vectors is as simple as cutting out qubits from the chain, as in Fig. 3(b). We have previously used this variational circuit design for band-structures under a different qubit mapping in [24].
4 Full Hilbert Space
In this section, we consider a case when the active space corresponds to the full Hilbert space accessible by all qubits. To ease the transition, we will continue to consider single-body band-structure calculations. Instead of the reciprocal-orbital qubit mapping used above, we will adopt a compact mapping which assigns each orbital to its own basis state, as was done for silicon in [19]. Considering the same toy model for elemental polonium as above, we require two qubits; the basis vectors represent the reciprocal , , , and orbitals.
To construct a suitable variational circuit, let us begin by writing down an arbitrary wavefunction spanning the basis states :
| (7) |
subject to the normalization constraint . Express the complex numbers in polar form as . We facilitate parameterization of this wave-function by adopting hyperspherical coordinates such that:
| (8) | ||||
| (9) |
Normalization is enforced by setting , and an arbitrary global phase is fixed by setting . This leaves free parameters for to span the full Hilbert space. Eliminating successive basis states for is accomplished simply by setting .
Now consider the following non-unitary operator:
| (10) |
It is clear that , and that satisfies the constraints in Eqs. 2 and 3. In order to satisfy Eq. 1 we must first construct the following Hermitian operator:
| (11) |
and unitary operator:
| (12) |
This construction is similar in form to the popular Unitary Coupled Cluster ansatz.[2, 21]
Implementing as a quantum circuit is equivalent to time-evolving a Hamiltonian operator , a well-studied problem in the quantum computing literature. The most straight-forward approach is Suzuki-Trotter decomposition [25], in which is approximated as the product , where and each factor is straightforward to implement as a quantum circuit (see Appendix A for a tutorial). Error in the approximation is reduced by increasing , leading to longer and longer circuits less suitable for noise-prone devices.
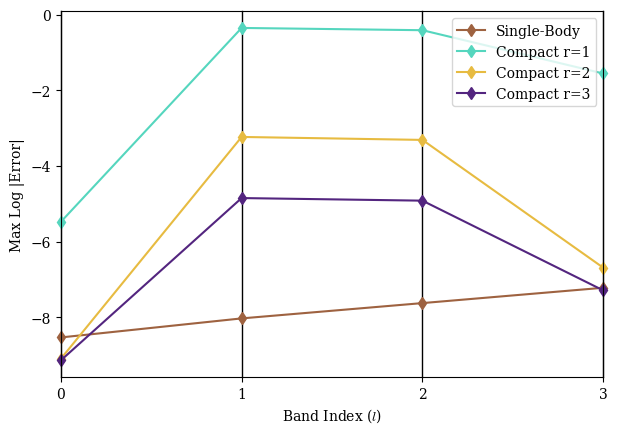
Fig. 2 demonstrates the success of band-structure calculations with self-orthogonalizing circuits on a noiseless quantum simulator.
All optimizations are carried out with the COBYLA algorithm implemented in the scipy Python package.
Results using the single-body circuits from Section 3 (four qubits) are virtually indistinguishable from the analytically obtained band-structure.
The compact basis enables the same calculation with exponentially fewer qubits (two qubits, in this case), but implementing the quantum circuit requires Trotterization, which introduces noticeable approximation error.
Nevertheless, we observe that the worst-case error falls off rapidly even for very small .
That said, implementing these circuits becomes much more difficult on a real quantum device vulnerable to qubit decoherence and gate infidelity.
One possible alternative would be to exploit the Linear Combination of Unitaries lemma [26, 27] for exponentially improved error scaling, at the cost of additional ancillary qubits.
5 Many-body Circuits
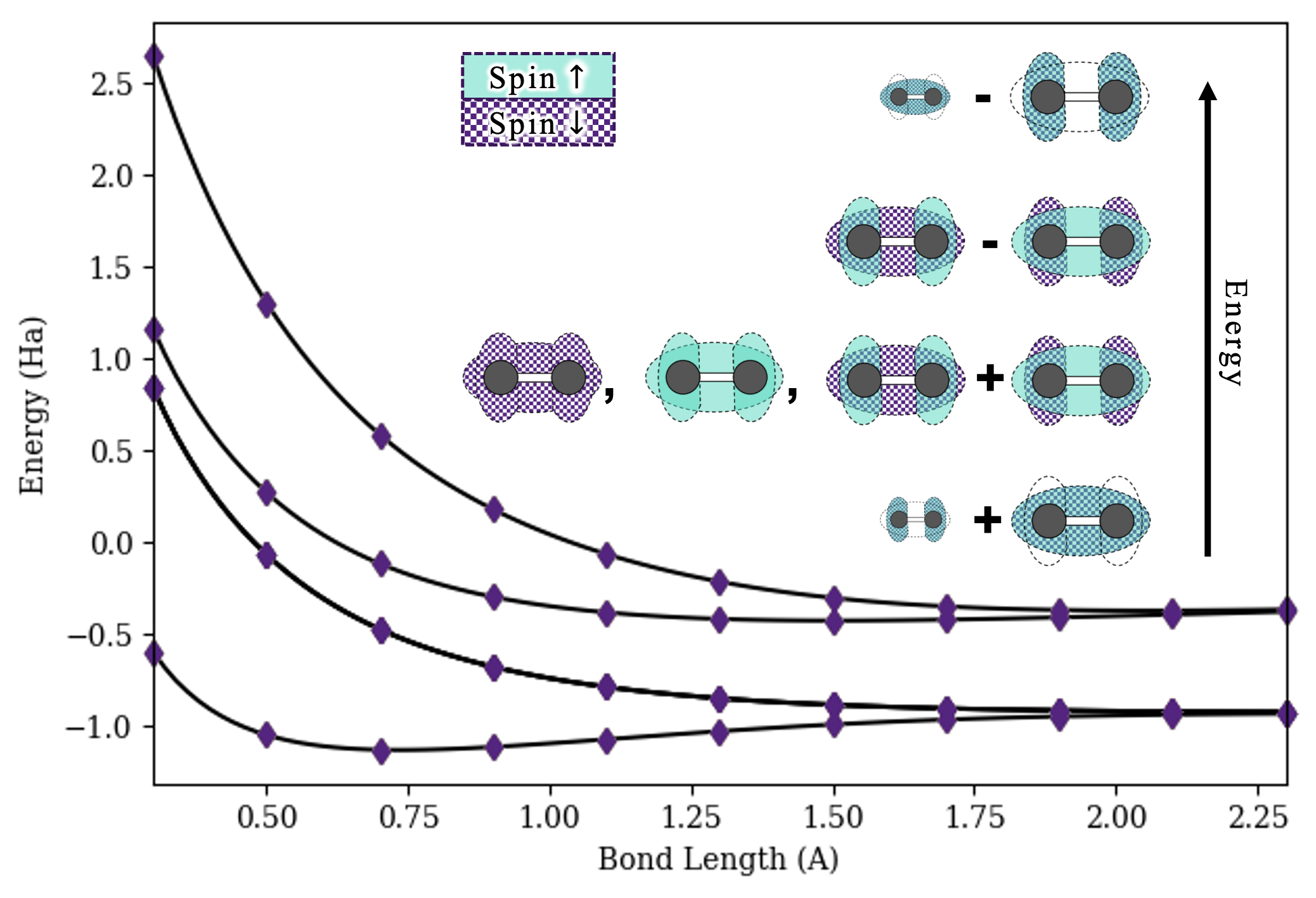
In this section, we consider a standard formulation in which the active space corresponds to all many-body states with fixed particle number. We again associate one qubit with each orbital, but we now adopt the Jordan-Wigner mapping [2, 28] to enforce fermionic anti-commutation relations. We shall consider the hydrogen molecule in a minimal basis (two atoms each contributing two spin-orbitals) with no symmetry reduction, so that we require four qubits. Our active space consists of the basis vectors , , , , , .
The self-orthogonalizing variational circuit and parameterization we adopt is essentially the same as in Section 4. The crucial difference is that we replace the ket with the state . Here is the vacuum state, indexes the vector in our active space (note that an order must be assigned to the vectors), and is shorthand for the normal-ordered product of creation operators which fill up the orbitals corresponding to the bits indicated in the basis vector. For example, if the basis vectors are ordered as in the previous paragraph, then , , and so on. These creation operators are then mapped onto qubit operators via the Jordan-Wigner mapping, and is implemented via Suzuki-Trotter decomposition or a comparable method as described above.
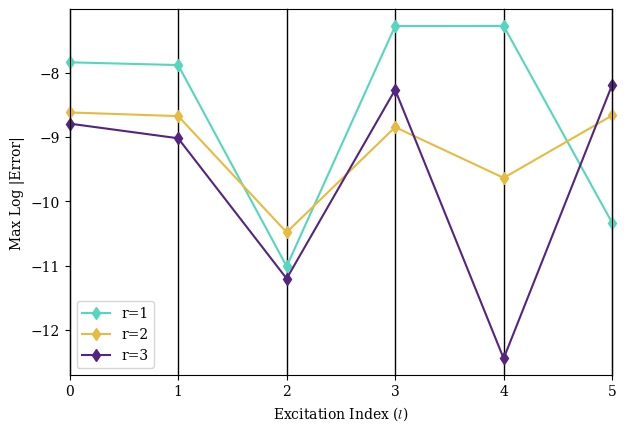
Fig. 4 gives the ground-state dissociation curve of the hydrogen molecule, in addition to the excited state energies for this basis.
Orbital integral calculations are made using the pyscf Python package [29] and the Jordan-Wigner mapping is carried out with the openfermion Python package.[30]
While we should not expect the minimal basis to yield extremely accurate calculations for excited states, we can observe the long-known fact that the first-excited state (triply-degenerate) lacks a minimum, illustrating the fact that electronic excitations in hydrogen gas tend to split the molecule apart.[31]
As observed in the compact single-body example in Fig. 2, the circuits require only very small Trotterization constants to be effective.
6 Conclusion
In this paper, we have formulated an Orthogonal-Ansatz Variational Quantum Eigensolver (OA-VQE) algorithm for iteratively locating excited states, using variational quantum circuits spanning only the subspace orthogonal to previously-located states. The main distinction of this approach as compared to Orthogonally-Constrained VQE (OC-VQE) is to leave the cost-function unchanged for all excited states, simplifying measurement complexity.
We have offered several families of self-orthogonalizing variational circuits, suitable for studying both single-body band structure calculations and many-body molecular spectroscopy. However, we emphasize that the circuit families presented in Sections 3-5 are by no means the only circuits consistent with the self-orthogonality constraints presented in Section 2. If other variational circuit families (eg. UCC, ADAPT, hardware-efficient ansatze, etc.) can be adapted to be consistent with Eqs. 1-3, they will be compatible with OA-VQE.
For example, the circuit families presented in Sections 4 and 5 have a similar form to Unitary Coupled Cluster (UCC) circuits. The “cluster operators” used in this paper are designed to robustly explore the entire Hilbert subspace orthogonal to previously located eigenstates. Meanwhile, the standard UCC cluster operator is formulated to preferentially explore the basis vectors most likely contributing to the ground state, for example by considering only single- and double-excitations (UCCSD) from the Hartree-Fock solution. Reconciling the UCCSD approximation with the self-orthogonality constraints presented here could lead to fewer terms in the Hermitian operator and thus more efficient implementations of as a quantum circuit.
The improved measurement complexity in OA-VQE is balanced by an increased circuit complexity required to guarantee orthogonality. In the short-term, this is a high price to pay due to relatively low coherence time and gate fidelity in present-day quantum computers. However, the relatively high cost of measuring and resetting qubits suggests that hybrid quantum-classical algorithms such as VQE may soon transition to favoring fewer, longer circuits. Moreover, not every circuit family will necessarily incur an asymptotic cost in circuit complexity: for example, the single-body circuits presented in Fig. 3 can overlap such that the circuit length is consistently . This emphasizes the importance of problem-specific quantum circuit design, rather than a one-size-fits-all approach, when developing algorithms for quantum chemistry and materials science.
7 Acknowledgments
We thank Marco Fornari, Itay Hen, and Rosa Di Felice for useful discussions. We acknowledge support from the US Department of Energy through the grant Q4Q: Quantum Computation for Quantum Prediction of Materials and Molecular Properties (DE-SC0019432).
Appendix A Suzuki-Trotter Circuits
This appendix is meant for readers unfamiliar with Hamiltonian simulation via Suzuki-Trotter simulation. We remind the reader that other methods of Hamiltonian simulation exist, such as in [26, 27], but we provide this tutorial so that the industrious reader may reproduce our procedure.
Our objective is to implement the unitary operator as a quantum circuit. We first map the Hamiltonian onto a sum of qubit operators:
| (13) |
Each is a “Pauli word”, consisting of one of the Pauli-spin operators , , , or the identity operator , acting on each of qubits.
The coefficients are determined by the particular qubit mapping.
In Section 4, we map projection operators directly onto Pauli words; we refer the reader to [24] for details.
In Section 5, we map a second-quantized Hamiltonian onto Pauli words using the Jordan-Wigner mapping; see [28] or documentation for the openfermion Python package [30] for details.
Next we take advantage of the second-order exponential product formula (also known as the first-order symmetrized product formula):
| (14) |
Higher-order formulae exist, but become needlessly complicated - see [25] for an excellent tutorial. Therefore, the following decomposition is sufficient:
| (15) |
If the coefficient in the exponential product formula is sufficiently small, the single-operator exponentials on the right-hand side are an adequate approximation of the complex operator exponential on the left. In order to guarantee the operator is sufficiently small, we introduce Trotterization:
| (16) |
Let ; then the error in the product formula scales with .
& \ctrl1
[-1em] \qw[-1em] \qw \qw \qw[-1em] \qw[-1em] \ctrl1
\qw
\targ
\ctrl1
\qw \qw \qw \ctrl1
\targ
\qw
\qw \targ
\ctrl1
\qw \ctrl1
\targ
\qw \qw
\qw \qw \targ
\gateR_z(θ)
\targ
\qw \qw \qw
& \gateH
\ctrl2
[-1em] \qw \qw \qw[-1em] \ctrl2
\gateH
\qw
\qw \qw \qw \qw \qw \qw \qw \qw
\gateHS^†
\targ
\ctrl1
\qw \ctrl1
\targ
\gateSH
\qw
\qw \qw \targ
\gateR_z(θ)
\targ
\qw \qw \qw
It now suffices to specify how to implement the factor as a quantum circuit. The circuit for is given in Fig. 5(a). To account for operators, one simply omits the CNOT gate on the corresponding qubit. To account for and operators, one must apply basis-rotation gates before and after: Fig. 5(b) illustrates the circuit for . See [28] for a more thorough explanation. The full operator is constructed by applying each one after the other.
References
- [1] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man Hong Yung, Xiao Qi Zhou, Peter J. Love, Alán Aspuru-Guzik, and Jeremy L. O’Brien. “A variational eigenvalue solver on a photonic quantum processor”. Nature Communications 5, 4213 (2014).
- [2] Jarrod R. McClean, Jonathan Romero, Ryan Babbush, and Alán Aspuru-Guzik. “The theory of variational hybrid quantum-classical algorithms”. New Journal of Physics 18, 23023 (2016). arXiv:1509.04279.
- [3] M. Cerezo, Andrew Arrasmith, Ryan Babbush, Simon C. Benjamin, Suguru Endo, Keisuke Fujii, Jarrod R. McClean, Kosuke Mitarai, Xiao Yuan, Lukasz Cincio, and Patrick J. Coles. “Variational quantum algorithms”. Nature Reviews Physics 3, 625–644 (2021). arXiv:2012.09265.
- [4] Daniel S. Abrams and Seth Lloyd. “Quantum algorithm providing exponential speed increase for finding eigenvalues and eigenvectors”. Physical Review Letters 83, 5162–5165 (1999). arXiv:9807070.
- [5] Alán Aspuru-Guzik, Anthony D. Dutoi, Peter J. Love, and Martin Head-Gordon. “Simulated quantum computation of molecular energies”. Science 309, 1704–1707 (2005).
- [6] Miroslav Dobšíček, Göran Johansson, Vitaly Shumeiko, and Göran Wendin. “Arbitrary accuracy iterative quantum phase estimation algorithm using a single ancillary qubit: A two-qubit benchmark”. Physical Review A - Atomic, Molecular, and Optical Physics76 (2007).
- [7] William J. Huggins, Joonho Lee, Unpil Baek, Bryan O’Gorman, and K. Birgitta Whaley. “A non-orthogonal variational quantum eigensolver”. New Journal of Physics 22, 073009 (2020).
- [8] Katherine Klymko, Carlos Mejuto-zaera, Stephen J Cotton, Filip Wudarski, Diptarka Hait, Jonathan Moussa, Wibe A De Jong, and Norm M Tubman. “Real time evolution for ultracompact Hamiltonian eigenstates on quantum hardware” (2021). arXiv:2103.08563v1.
- [9] David Zsolt Manrique, Irfan T. Khan, Kentaro Yamamoto, Vijja Wichitwechkarn, and David Muñoz Ramo. “Momentum-Space Unitary Coupled Cluster and Translational Quantum Subspace Expansion for Periodic Systems on Quantum Computers” (2020). arXiv:2008.08694.
- [10] Mario Motta, Chong Sun, Adrian T.K. Tan, Matthew J. O’Rourke, Erika Ye, Austin J. Minnich, Fernando G.S.L. Brandão, and Garnet Kin Lic Chan. “Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution”. Nature Physics 16, 205–210 (2020). arXiv:1901.07653.
- [11] Taichi Kosugi, Yusuke Nishiya, and Yu-ichiro Matsushita. “Probabilistic imaginary-time evolution by using forward and backward real-time evolution with a single ancilla: first-quantized eigensolver of quantum chemistry for ground states” (2021). arXiv:2111.12471.
- [12] Bela Bauer, Sergey Bravyi, Mario Motta, and Garnet Kin-Lic Chan. “Quantum Algorithms for Quantum Chemistry and Quantum Materials Science”. Chemical Reviews 120, 12685–12717 (2020). arXiv:2001.03685.
- [13] M. Cerezo, Akira Sone, Tyler Volkoff, Lukasz Cincio, and Patrick J. Coles. “Cost function dependent barren plateaus in shallow parametrized quantum circuits”. Nature Communications12 (2021). arXiv:2001.00550.
- [14] Lennart Bittel and Martin Kliesch. “Training Variational Quantum Algorithms Is NP-Hard”. Physical Review Letters 127, 120502 (2021).
- [15] Abhinav Kandala, Antonio Mezzacapo, Kristan Temme, Maika Takita, Markus Brink, Jerry M. Chow, and Jay M. Gambetta. “Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets”. Nature 549, 242–246 (2017). arXiv:1704.05018.
- [16] E. F. Dumitrescu, A. J. McCaskey, G. Hagen, G. R. Jansen, T. D. Morris, T. Papenbrock, R. C. Pooser, D. J. Dean, and P. Lougovski. “Cloud Quantum Computing of an Atomic Nucleus”. Physical Review Letters 120, 210501 (2018). arXiv:1801.03897.
- [17] Yunseong Nam, Jwo Sy Chen, Neal C. Pisenti, Kenneth Wright, Conor Delaney, Dmitri Maslov, Kenneth R. Brown, Stewart Allen, Jason M. Amini, Joel Apisdorf, Kristin M. Beck, Aleksey Blinov, Vandiver Chaplin, Mika Chmielewski, Coleman Collins, Shantanu Debnath, Andrew M. Ducore, Kai M. Hudek, Matthew Keesan, Sarah M. Kreikemeier, Jonathan Mizrahi, Phil Solomon, Mike Williams, Jaime David Wong-Campos, Christopher Monroe, and Jungsang Kim. “Ground-state energy estimation of the water molecule on a trapped ion quantum computer”. npj Quantum Information6 (2019). arXiv:1902.10171.
- [18] Oscar Higgott, Daochen Wang, and Stephen Brierley. “Variational quantum computation of excited states”. Quantum 3, 156 (2019). arXiv:1805.08138.
- [19] Frank T. Cerasoli, Kyle Sherbert, Jagoda Sławińska, and Marco Buongiorno Nardelli. “Quantum computation of silicon electronic band structure”. Physical Chemistry Chemical Physics 22, 21816–21822 (2020). arXiv:2006.03807.
- [20] Ilya G. Ryabinkin, Scott N. Genin, and Artur F. Izmaylov. “Constrained Variational Quantum Eigensolver: Quantum Computer Search Engine in the Fock Space”. Journal of Chemical Theory and Computation 15, 249–255 (2019). arXiv:1806.00461.
- [21] Joonho Lee, William J. Huggins, Martin Head-Gordon, and K. Birgitta Whaley. “Generalized Unitary Coupled Cluster Wave functions for Quantum Computation”. Journal of Chemical Theory and Computation 15, 311–324 (2019). arXiv:1810.02327.
- [22] Kyle Sherbert, Frank Cerasoli, and Marco Buongiorno Nardelli. “A systematic variational approach to band theory in a quantum computer”. RSC Adv. 11, 39438–39449 (2021). arXiv:2104.03409.
- [23] Bryan T. Gard, Linghua Zhu, George S. Barron, Nicholas J. Mayhall, Sophia E. Economou, and Edwin Barnes. “Efficient symmetry-preserving state preparation circuits for the variational quantum eigensolver algorithm”. npj Quantum Information6 (2020). arXiv:1904.10910.
- [24] Kyle Sherbert, Anooja Jayaraj, and Marco Buongiorno Nardelli. “Quantum algorithm for band structures with local tight-binding orbitals”. In Review (2022).
- [25] Naomichi Hatano and Masuo Suzuki. “Finding Exponential Product Formulas of Higher Orders”. In Arnab Das and Bikas K Chakrabarti, editors, Quantum Annealing and Other Optimization Methods. Pages 37–68. Springer Berlin Heidelberg (2005). arXiv:0506007.
- [26] Dominic W. Berry, Andrew M. Childs, Richard Cleve, Robin Kothari, and Rolando D. Somma. “Simulating hamiltonian dynamics with a truncated taylor series”. Physical Review Letters114 (2015). arXiv:1412.4687.
- [27] Amir Kalev and Itay Hen. “Quantum algorithm for simulating hamiltonian dynamics with an off-diagonal series expansion”. Quantum 5, 1–24 (2021). arXiv:2006.02539.
- [28] Jacob T. Seeley, Martin J. Richard, and Peter J. Love. “The Bravyi-Kitaev transformation for quantum computation of electronic structure”. Journal of Chemical Physics 137, 224109 (2012). arXiv:1208.5986.
- [29] Qiming Sun, Xing Zhang, Samragni Banerjee, Peng Bao, Marc Barbry, Nick S. Blunt, Nikolay A. Bogdanov, George H. Booth, Jia Chen, Zhi Hao Cui, Janus J. Eriksen, Yang Gao, Sheng Guo, Jan Hermann, Matthew R. Hermes, Kevin Koh, Peter Koval, Susi Lehtola, Zhendong Li, Junzi Liu, Narbe Mardirossian, James D. McClain, Mario Motta, Bastien Mussard, Hung Q. Pham, Artem Pulkin, Wirawan Purwanto, Paul J. Robinson, Enrico Ronca, Elvira R. Sayfutyarova, Maximilian Scheurer, Henry F. Schurkus, James E.T. Smith, Chong Sun, Shi Ning Sun, Shiv Upadhyay, Lucas K. Wagner, Xiao Wang, Alec White, James Daniel Whitfield, Mark J. Williamson, Sebastian Wouters, Jun Yang, Jason M. Yu, Tianyu Zhu, Timothy C. Berkelbach, Sandeep Sharma, Alexander Yu Sokolov, and Garnet Kin Lic Chan. “Recent developments in the P y SCF program package”. Journal of Chemical Physics153 (2020). arXiv:2002.12531.
- [30] Jarrod R. McClean, Nicholas C. Rubin, Kevin J. Sung, Ian D. Kivlichan, Xavier Bonet-Monroig, Yudong Cao, Chengyu Dai, E. Schuyler Fried, Craig Gidney, Brendan Gimby, Pranav Gokhale, Thomas Haner, Tarini Hardikar, Vojtěch Havlíček, Oscar Higgott, Cupjin Huang, Josh Izaac, Zhang Jiang, Xinle Liu, Sam Mcardle, Matthew Neeley, Thomas O’Brien, Bryan O’Gorman, Isil Ozfidan, Maxwell D. Radin, Jhonathan Romero, Nicolas P.D. Sawaya, Bruno Senjean, Kanav Setia, Sukin Sim, Damian S. Steiger, Mark Steudtner, Qiming Sun, Wei Sun, Daochen Wang, Fang Zhang, and Ryan Babbush. “OpenFermion: The electronic structure package for quantum computers”. Quantum Science and Technology5 (2020). arXiv:1710.07629.
- [31] R. Stephen Berry, Stuart A. Rice, and John Ross. “Physical Chemistry”. John Wiley & Sons, Inc. (1980).