Outliers Detection Is Not So Hard: Approximation Algorithms for Robust Clustering Problems Using Local Search Techniques
In this paper, we consider two types of robust models of the -median/-means problems: the outlier-version (-MedO/-MeaO) and the penalty-version (-MedP/-MeaP), in which we can mark some points as outliers and discard them. In -MedO/-MeaO, the number of outliers is bounded by a given integer. In -MedP/-MeaP, we do not bound the number of outliers, but each outlier will incur a penalty cost. We develop a new technique to analyze the approximation ratio of local search algorithms for these two problems by introducing an adapted cluster that can capture useful information about outliers in the local and the global optimal solution. For -MeaP, we improve the best known approximation ratio based on local search from to . For -MedP, we obtain the best known approximation ratio. For -MedO/-MeaO, there exists only two bi-criteria approximation algorithms based on local search. One violates the outlier constraint (the constraint on the number of outliers), while the other violates the cardinality constraint (the constraint on the number of clusters). We consider the former algorithm and improve its approximation ratios from to for -MedO, and from to for -MeaO.
1 Introduction
Using large data sets to make better decisions is becoming more important and routinely applied in Operations Research, Management Science, Biology, Computer Science, and Machine Learning (see e.g. Bernstein et al. 2019, Borgwardt and Happach 2019, Hochbaum and Liu 2018, Lu and Wedig 2013). Clustering large data is a fundamental problem in data analytics. Among many clustering types, center-based clustering is the most popular and widely used one. Center-based clustering problems include -median, -means, -center, facility location problems, and so on (see e.g. Ahmadian et al. 2017, Byrka et al. 2014, Lloyd 1982, Li 2013, Li et al. 2013, Ni et al. 2020). The -median and -means problems are the most basic and classic clustering problems. The goal of -median/means clustering is to find cluster centers such that the total (squared) distance from each input datum to the closest cluster center is minimized. Usually, one considers -median problems in arbitrary metrics while -means problems in the Euclidean space .
Both problems are NP-hard to approximate beyond with the lower bounds (Jain et al. 2003) and (Cohen-Addad and Karthik 2019) for -median and -means, respectively. There are many papers on designing efficient approximation algorithms. The best known approximations are (Byrka et al. 2014) and (Ahmadian et al. 2017) for -median and -means, respectively. If we restrict to a fixed-dimensional Euclidean space, the -median and -means problems have a PTAS (see Arora et al. 1998, Cohen-Addad et al. 2019, Friggstad et al. 2019b).
However, real-world data sets often contain outliers which may totally spoil -median/means clustering results. To overcome this problem, robust clustering techniques have been developed to avoid being affected by outliers. In general, there are two types of robust formulations: -median/means with outliers (-MedO/-MeaO) and -median/means with penalties (-MedP/-MeaP). We formally define these problems as follows.
Definition 1.1 (-Median Problem with Outliers/Penalties).
In the -median problem with outliers (-MedO), we are given a client set of points, a facility set of points, a metric space , and two positive integers and . The aim is to find a subset of cardinality at most , and an outlier set of cardinality at most such that the objective function is minimized. In the -median problem with penalties (-MedP), we have the same input except that the cardinality restrictions on the penalty set is replaced by a nonnegative penalty for each , and the objective function is to minimize .
Definition 1.2 (-Means Problem with Outliers/Penalties).
In the -means problem with outliers (-MeaO), we are given a data set in of points and two positive integers and . Let be the Euclidean distance of the points and . The aim is to find a cluster center set of cardinality at most , and an outlier set of cardinality at most such that the objective function is minimized. In the -means problem with penalties (-MeaP), we have the same input except that the cardinality restrictions on penalty set is instead of a nonnegative penalty for each , and the objective function is to minimize .
From the perspective of clustering, we can view a facility in the -median problem as a center, and view a client as a point. To avoid confusion, we use “center” and “point” for all problems we consider in this paper.
Basic versions of these problems have been widely studied, and many approximation algorithms based on many different techniques, including LP-rounding (see e.g. Charikar et al. 2002, Charikar and Li 2012, Li 2013), primal-dual (see e.g. Ahmadian et al. 2017, Jain and Vazirani 2001), dual-fitting (see e.g. Jain et al. 2003, Mahdian et al. 2006), local search (see e.g. Arya et al. 2004, Kanungo et al. 2004, Korupolu et al. 2000), Lagrangian relaxation (see e.g. Jain et al. 2003, Jain and Vazirani 2001), bi-point rounding (see e.g. Jain et al. 2003, Jain and Vazirani 2001), and pseudo-approximation (see e.g. Byrka et al. 2014, Li and Svensson 2016), have been developed and applied.
We now discuss the state-of-art approximation results for robust version of -median/-means. Chen (2008) has presented the first constant but very large approximation algorithm for -MedO via successive local search. Krishnaswamy et al. (2018) have obtained an iterative LP rounding framework yielding - and -approximation algorithms for -MedO and -MeaO, respectively. To the best of our knowledge, these are only two constant factor approximation results for -MedO and -MeaO.
The first constant -approximation for -MedP has been given by Charikar et al. (2001) using Lagrangian relaxation framework of Jain and Vazirani (2001). The best -approximation for -MedP has been obtained by Hajiaghayi et al. (2012), who called the problem the red-blue median problem. Three years later, Wang et al. (2015) have independently obtained the same factor approximation for -MedP and have further generalized it to a -approximation for the -facility location problem with linear penalties, which is a common generalization of facility location (in which there are facility opening costs and no cardinality constraint) and -MedP. Both of them use local search techniques. Zhang (2007) has obtained the approximation ratio for the -facility location problem (-FLP). The currently best ratio of for -FLP is due to Charikar and Li (2012). For the -median problem with uniform penalties, Wu et al. (2018) have adapted the pseudo-approximation technique of Li and Svensson (2016) and obtained a -approximation.
Zhang et al. (2019) have presented the first constant - approximation algorithm for -MeaP using local search. Feng et al. (2019) have improved this to a -approximation by combing Lagrangian relaxation with bipoint rounding. A summary of the up-to-date approximation results for -MedO/-MeaO and -MedP/-MeaP along with their ordinary versions is given in Table 1.
| Techniques and reference | -median | -MedO | -MedP | -means | -MeaO | -MeaP |
| LP rounding (Charikar et al. 2002) | ||||||
| Lagrangian relaxation (Jain and Vazirani 2001) | ||||||
| Lagrangian relaxation (Charikar et al. 2001) | ||||||
| Lagrangian relaxation (Jain et al. 2003) | ||||||
| Local search (Arya et al. 2004) | ||||||
| Local search (Kanungo et al. 2004) | ||||||
| Successive local search (Chen 2008) | constant | |||||
| Dependent LP rounding (Charikar and Li 2012) | ||||||
| Local search (Hajiaghayi et al. 2012) | ||||||
| Pseudo-approximation (Li and Svensson 2016) | ||||||
| Pseudo-approximation (Byrka et al. 2014) | ||||||
| Iterative LP rounding (Krishnaswamy et al. 2018) | ||||||
| Primal-dual (Ahmadian et al. 2017) | ||||||
| Local search (Zhang et al. 2019) | ||||||
| Bipoint rounding (Feng et al. 2019) |
The available literature suggests two observations concerning the approximation factor: i) -MedP/-MeaP seems more easy to approximate than -MedO/-MeaO. ii) The existence of outliers make the approximation of the corresponding robust clustering problems much harder than the ordinary clustering problems.
The best known approximation ratios for -MedO and -MeaO have been obtained by LP-rounding, but these algorithms are not strongly polynomial-time since they involve solving linear programs. Concerning time complexity, local search is better than LP-rounding, and this technique has been well applied to -median/-means and their penalty versions. Furthermore, the standard local search algorithm is also used for -median/-means with some special metrics such as the minor-free metric (Cohen-Addad et al. 2019) and the doubling metric (Friggstad et al. 2019b). These two papers show that the standard local search scheme yields a PTAS for the considered problems when the dimension is fixed. Their results hold in particular for the Euclidean metric, since both the minor-free metric and the doubling metric are extensions of the Euclidean metric.
Unfortunately, the standard local search algorithm for -MedO/-MeaO can not produce a feasible solution with a bounded approximation ratio (Friggstad et al. 2019a). So some research directions focus on bi-criteria approximation algorithms based on local search for these two problems. These algorithms have a bounded approximation ratio but violate either the -constraint or the outlier constraint by a bounded factor. Gupta et al. (2017) have developed a method for addressing outliers in a local search algorithm, yielding a bi-criteria -approximation algorithm ( as defined in Section 1.2) that violates the outlier constraint. Friggstad et al. (2019a) have provided - and -local search bi-criteria approximation algorithms for -MedO and -MeaO respectively.
We will consider the standard local search algorithm for -MedP/-MeaP, and the outlier-based local search algorithm by Gupta et al. (2017) for -MedO/-MeaO. Using our new technique, we will improve the approximation ratios for -MeaP, -MeaO and -MedO. For -MedP, we obtain the same approximation ratio which is the best one possible.
We list the related results about local search algorithms for -MedO/-MeaO and -MedP/-MeaP in Table 2.
| Reference | Problem | Ratio | # centers blowup | # outliers blowup |
| Arya et al. (2004) | -median | none | none | |
| Kanungo et al. (2004) | -means | none | none | |
| Chen (2008) | -MedO | constant | none | none |
| Hajiaghayi et al. (2012) | -MedP | none | none | |
| Zhang et al. (2019) | -MeaP | none | none | |
| Cohen-Addad et al. (2019) | -median/-means in minor-free metrics with fixed dimension | PTAS | none | none |
| Friggstad et al. (2019b) | -median/-means with fixed doubling dimension | PTAS | none | none |
| Friggstad et al. (2019a) | -MedO -MeaO | none none | ||
| Gupta et al. (2017) | -MedO -MeaO | none none | ||
| Our results | -MedP -MeaP -MedO -MedO -MeaO -MeaO | none none none none none none | none none |
1.1 Our techniques
We concentrate on -MedP and -MeaP to illustrate our techniques. The associated outlier versions are then easy generalizations.
In the standard local search algorithm, one starts from an arbitrary feasible solution. Operations such as add center, delete center, or swap centers, define the neighborhood of the currently feasible solution. One then searches for a local optimal solution in the whole neighborhood and takes it as the new current solution. This is iterated until the improvement becomes sufficiently small.
Similar to the previous analyses of local search algorithms for -median and -means, we want to find some valid inequalities by constructing swap operations in order to establish some “connections” between local and global optimal solutions. Integrating all these inequalities or connections carefully, we can bound cost of the local optimal solution by the global optimal cost.
In the analysis of -median (see Arya et al. 2004), these connections are given individually for each point (that is, each point yields an inequality that gives a bound of its cost after the constructed swap operation). We call this type of analysis an “individual form”.
Another analysis type is the “cluster form”, in which the connections between the local and global optimal solutions are revealed for some clusters containing several points. The cluster form analysis was first used for -means in Kanungo et al. (2004). In the work of Kanungo et al. (2004), the authors use the Centroid Lemma (introduced in Section 2.2) to obtain equality for each cluster in the optimal solution, and then deduce the approximation ratio by these equalities and the triangle inequality. They found that the cluster form analysis is tighter than the individual form. However, the same analysis does not apply to -MeaP due to the existence of outliers. Indeed, the clusters derived with equalities from the Centroid Lemma should contain no outliers in both the local and global optimal solutions, since they do not incur a cost for outliers.
To this end, we careful recognize and define an adapted cluster as a cluster that excludes outliers. In order to use the Centroid Lemma, we identify a new centroid for the adapted cluster and use the triangle inequality for the squared distances to identify the associated centroid of the global solution in the analysis. These new centroids can be found by a carefully defined mapping function.
Our cluster form analysis also applies to -MedP, although there is no result like the Centroid Lemma for this problem. In fact, we only need to denote the optimal center of the adapted cluster for -MedP (corresponding to the centroid in the analysis for -MeaP), and use its optimality to derive the inequality for the adapted cluster. During the entire process of the analysis, we do not compute the optimal center, so we do not need a result like the Centroid Lemma.
Our cluster form analysis establishes a bridge between local and global solutions for both robust and ordinary clusterings, and we obtain a clear and unified understanding of them. Furthermore, we believe that our technique can be generalized to other robust clustering problems such as the robust facility location and -center problems.
1.2 Our contributions
We use the standard local search algorithm for -MedP and -MeaP. Via a subtle cluster form analysis, we obtain the following result.
Theorem 1.3.
The standard local search algorithm yields - and -approximations for -MedP and -MeaP respectively.
Our analysis is different to that of Hajiaghayi et al. (2012) who have also obtained a local search -approximation for -MedP, and improve the previous local search -approximation (Zhang et al. 2019) and the primal-dual -approximation (Feng et al. 2019) for -MeaP. Moreover, our result indicates that the penalty-version of the clustering problems have the same approximation ratios as the ordinary version, when we adopt the local search technique followed with our cluster form analysis.
For -MedO and -MeaO, we use the outlier-based local search algorithm (based on Gupta et al. 2017).
The algorithm has a parameter for controlling the descending step-length of the cost in each iteration. This parameter is fixed in Gupta et al. (2017), while it is an input in our algorithm because both the approximation ratio and the number of outliers blowup are associated with the value of this parameter. This helps us to reveal a tradeoff between the approximation ratio and the outlier blowup. When selecting appropriate values for this parameter, we can obtain constant approximation ratios. In the following theorems, denotes the maximal distance between two points in the data set.
Theorem 1.4.
The outlier-based local search algorithm yields bicriteria - and -approximations for -MedO, and bicriteria - and -approximations for -MeaO, where and are the factors by which the outlier constraint is violated.
With the same outlier blowup, our ratios obtained with single-swap significantly improve the previous ratios and for the -MedO and -MeaO, respectively. The multi-swap version improves this even more, but with a larger outlier blowup.
These results strengthens our comprehension of robust clustering problems from a local search aspect. Furthermore, our cluster form analysis has a high potential to be applied in the robust version for FLP and -FLP, since the structures of these two problems are similar to -MedP, and the analyses for the connection cost and facility opening cost are seperated in the previous papers that study local search algorithms for FLP and -FLP (see Arya et al. 2004, Zhang 2007).
1.3 Outline of the paper
Section 2 presents the unified models and notations for -MedP/-MeaP and -MedO/-MeaO, and some useful technical lemmas. Section 3 then presents our standard local search algorithms for -MedP/-MeaP and our corresponding theoretical results. In Section 4, we develop our outlier-based local search algorithms for -MedO/-MeaO and present our corresponding theoretical results. The conclusions are given in Section 5. All technical proofs are given in the appendices.
2 Preliminaries
2.1 The models
We use the following notation for the problems studied in this paper (in addition to the notation introduced in the introduction). denotes the candidate center set, and denotes the connection cost between two points and . For -MedP and -MedO, we have and ; for -MeaP and -MeaO, we have and . Then, the penalty-version can be formulated as
and the outlier-version can be formulated as
Considering -MeaP and -MedP, we assume that is a set of centers. It is obvious that the optimal penalized point set with respect to is for -MedP and for -MeaP, implying that determines the corresponding clusters for all , where denotes the closest center in to , i.e., . Thus, we also call a feasible solution for -MedP and -MeaP.
Given a center set and a subset , we suppose that subject to . Let if , otherwise, . We simplify to . For -MedO and -MeaO, it is obvious that the optimal outlier set with respect to is , implying that the set can be seen as a feasible solution. We also use to denote a solution (not necessarily feasible) in which the center set is and the outlier set is for -MedO and -MeaO.
2.2 Some technical lemmas
Given a data subset and a point , we define . Let be a center point in that optimizes the objective of the -means/-median problem, i.e., . We remark that the notation () denotes an arbitrary element that minimizes (maximizes) the objective. From the well-known centroid lemma (Kanungo et al. 2004), we get for -means, where is the centroid of , that is defined as follows.
Definition 2.1 (Centroid).
Given a set , we call the point denoted by the centroid of .
Lemma 2.2 (Centroid Lemma (Kanungo et al. 2004)).
For any data subset and a point , we have .
So, the candidate center points of a -means problem are the centroid points for all subsets of . Note that the total amount of these candidate center points is . To cut down this exponential magnitude, Matoušek (2000) introduces the concept of approximate centroid set shown in the following definition.
Definition 2.3.
A set is an -approximate centroid set for if for any set , we have .
The following lemma shows the important observation that a polynomial size -approximate centroid set for can be found in polynomial time. In the remainder of this paper, we restrict that the candidate center set of -MeaP/-MeaO is the -approximate centroid set , by utilizing this observation.
Lemma 2.4 (Matoušek (2000)).
Given an -point set and a real number , an -approximate centroid set for , of size , can be computed in time .
For the -median problem, we do not need the approximate center set, since the candidate centers are in the finite set .
3 Local search approximation algorithms for -MedP and -MeaP
Let be a fixed integer. For any feasible solution , and with , we define the so-called multi-swap operation , such that all centers in are dropped from and all centers in are added to .
We further denote the connection cost of the point by , i.e., , and denote by , , and the following expressions ; ; , where is the optimal penalized point set with respect to .
Now we are ready to present our multi-swap local search algorithm.
Algorithm 1 The multi-swap local search algorithm: LS-Multi-Swap()
For -MedP, we run LS-Multi-Swap(); for -MeaP, we first call the algorithm of Makarychev et al. (2016) to construct an -approximate centroid set , then run LS-Multi-Swap(). The values of and will be determined in our analysis of the algorithm.
3.1 The analysis
Let be a global optimal solution with the penalized set . Similar to the feasible solution , we introduce the corresponding notations , , , , and .
We use the standard analysis for a local search algorithm, in which some swap operations between and are constructed, and then each point is reassigned to a center in the new solution. In the cluster form analysis, we try to bound the new cost for a set of points, rather than bounding the cost of each point individually and independently. To this end, we introduce the adapted cluster as follows.
With the adapted cluster, we set . We introduce a mapping and map each point to . We say that the center captures . Considering one of all constructed swap operations, we will reassign some points to a center determined by the mapping (for instance, reassign the point to . The details will be stated later).
Combining all swap operations, the sum of the costs of these points appears in the right hand side of the inequality which is derived from the local optimality of . For -MeaP, we can bound this sum by the connection costs of and , see Lemma 3.1. Note that all these points are not outliers in both and . This is the reason why we need to use the adapted cluster rather than the cluster which was used in the analysis for -means (Gupta et al. 2017).
In the proof of Lemma 3.1, we divide the set into some adapted clusters with respect to all , and apply the Centroid Lemma to each adapted cluster. Afterwards we bound the square of distances between a centroid of the adapted cluster and its mapped point . This explains why the domain of the mapping is the set of centroids of adapted clusters.
Lemma 3.1.
Let and be a local optimal solution and a global optimal solution of -MeaP, respectively. Then,
| (1) | |||||
Proof.
With the Cauchy-Schwarz inequality, we obtain
| (2) | |||||
Consider now , i.e., the image set of under . We list all elements of as where . For each , let and . Thus, is partitioned into . Noting that , we can enlarge each such that is a partition of with for each .
We will construct a swap operation between the points in and for each pair . Before doing this, we note that a center need not belong to the candidate center set for -MeaP. Thus, we introduce a center associated with each to ensure that the swap operation involved in can be implemented in Algorithm 3. For each , let . Combined with Definition 2.3, we have (see Zhang et al. 2019)
| (5) | |||||
The algorithm allows at most points to be swapped. To satisfy this condition, we consider the following two cases to construct swap operations (cf. Figure 1 for ).
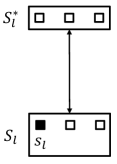
- Case 1
-
(cf. Figure 1(a)). For each with , we consider the pair . Let . W.l.o.g., we assume that . For -MedP, we consider the swap; for -MeaP, we consider the swap. Utilizing these swap operations, we obtain the following result.
Lemma 3.2.
If , then we have
(6) for -MedP, and
(7) for -MeaP.
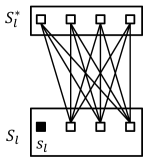
- Case 2
-
(cf. Figure 1(b)). For each with , we consider pairs with and . For -MedP, we consider the swap; for -MeaP, we consider the swap. Utilizing these swap operations, we obtain the following result.
Lemma 3.3.
For any and , we have
(8) for -MedP, and
(9) for -MeaP.
Lemma 3.2 shows a relationship between the sets and , while Lemma 3.3 shows a relationship between two points in and respectively. We remark that Lemma 3.3 holds for all pairs (no matter whether ). This is useful for the analysis of the algorithm for -MedO/-MeaO in Section 4.
Proof of Lemma 3.2.
We only prove it for -MeaP. The proof for -MedP is similar. After the operation swap, we penalize all points in for all , reassign each point to for all , and reassign each point to for all ( implies ). Since the operation swap does not improve the local optimal solution , we have
Combining this with and inequality (5) completes the proof. ∎
Proof of Lemma 3.3.
We again only prove it for -MeaP, and the proof for -MedP is again similar. Recall the definition of . W.l.o.g., we assume that . It follows from and that when . Since the operation swap does not improve the current solution , we have
This completes the proof. ∎
Combining Lemmas 3.2 and 3.3, we estimate the cost of for -MedP and -MeaP in the following two theorems respectively.
Theorem 3.4.
LS-Multi-Swap() for -MedP produces a local optimal solution satisfying .
Theorem 3.5.
Let be an -approximate centroid set for . LS-Multi-Swap( ) for -MeaP produces a local optimal solution satisfying .
Proof of Theorem 3.4..
Note that and for any and any . Summing the inequality (6) with weight and inequality (8) with weight over all constructed swap operations, we have
| (10) | |||||
The triangle inequality and the definition of imply that
| (11) | |||||
Combining inequalities (10) and (11), we obtain
| (12) | |||||
From the definitions of and , we get that
| (13) |
Finally, we complete the proof by combining inequalities (12)-(13) for . ∎
Proof of Theorem 3.5..
Similar to the proof of Theorem 3.4, we obtain by summing inequality (7) with weight and inequality (9) with weight over all constructed swap operations that
| (14) | |||||
Because of and Lemma 3.1, the RHS of (14) is not larger than
| (15) | |||||
The RHS of (15) is equal to
where
This implies that
which is equivalent to
Observe that
So, we have
| (16) |
Substituting into (16) completes the proof. ∎
We remark that Algorithm 3 can be adapted to a polynomial-time algorithm that only sacrifices in the approximation factor (see Arya et al. 2004). Combining this adaptation and Theorems 3.4-3.5, we obtain a -approximation algorithm for -MedP, and a -approximation algorithm for -MeaP, if and are sufficiently small.
4 Local search algorithm for -MedO/-MeaO
In this section, we focus on -MedO and -MeaO. We apply the technique for addressing outliers in a local search algorithm provided by Gupta et al. (2017) to -MedO and -MeaO, and use our new analysis to improve the approximation ratio.
4.1 The algorithm
Each iteration of the outlier-based multi-swap local search algorithm has a no-swap step and a swap step. Supposing that the current solution is , the no-swap step implements an “add outliers” operation that adds the points in (defined in Section 2.1) to , if this operation can reduce the cost by a given factor. Then, the swap step searches for a better solution by the multi-swap together with the “add outliers” operations. The algorithm terminates when both the no-swap and the swap step can not reduce the cost by the given factor.
Let denote the the cost of the solution . We give the formal description of the outlier-based local search algorithm in Algorithm 4.1. This algorithm has three parameters: is the number of points which are allowed to be swapped in a solution, and are used to control the descending step-length of the cost. The parameter is fixed as in the algorithm provided by Gupta et al. (2017), while it is an input in our algorithm, because the approximation ratio is associated with the value of this parameter.
The following proposition holds for this algorithm.
Proposition 4.1 (Gupta et al. 2017).
Let be the solution produced by LS-Multi-Swap-Outlier( ), and set if , otherwise, set . Then
-
(i)
,
-
(ii)
for any and .
Algorithm 2 The outlier-based local search algorithm: LS-Multi-Swap-Outlier()
For -MedO, we run LS-Multi-Swap-Outlier(). For -MeaO, we run LS-Multi-Swap-Outlier(), where is an -approximate centroid set for . The values of , , and will be determined in the analysis of the algorithm.
4.2 The analysis
The time complexity of Algorithm 4.1 is shown in the following theorem.
Theorem 4.2.
The running time of LS-Multi-Swap-Outlier() is .
Proof.
The proof is similar to that in Gupta et al. (2017). For the sake of completeness, we present it also here. W.l.o.g, we can assume that the optimal value of the problem is at least by scaling the distances, except for the trivial case that . Under this assumption, the cost of any solution is at most . The number of iterations is at most , since the cost is reduced to at most times the old cost in each iteration. The number of solutions searched by a swap operation is at most , since . This completes the proof. ∎
The algorithm may violates the outlier constraint in order to yield a bounded approximation ratio. We can also bound the number of outliers by a suitable factor, which is shown in the following result.
Theorem 4.3.
The number of outliers returned by LS-Multi-Swap-Outlier( ) is .
Proof.
From the proof of Theorem 4.2, we know that LS-Multi-Swap-Outlier( ) has at most iterations. In each iteration, the algorithm removes at most outliers. This completes the proof. ∎
Let be the solution returned by Algorithm 4.1, and be the global optimal solution. Similar to the penalty version, we use the same notations (except that the outlier version has not penalty cost) and adopt the same partition of and (). Similar to Lemmas 3.2 and 3.3, we obtain the following two results.
Lemma 4.4.
If , we have
| (17) | |||||
for -MedO, and
for -MeaO.
Proof.
We only prove it for -MeaO. The proof for -MedO is similar. We consider the swap. Since the swap step of the algorithm produces at most additional outliers in each iteration, and , we can let the points in be the additional outliers after the constructed swap operation. For the other points, it is obvious that we can apply the reassignments in the proof of Lemma 3.2 also here. Then, Proposition 4.1 yields
where the third inequality follows from (5).
∎
Lemma 4.5.
For any point and , we have
| (19) | |||||
for -MedO, and
| (20) | |||||
for -MeaO.
Next we will construct some swap operations for each pair , and then apply Lemmas 4.4 and 4.5 to these swaps. Similar to the analysis for the penalty version, we consider two cases according to the size of : and .
Note that the number of constructed swap operations will appear in the coefficient of after summing the inequalities in Lemmas 4.4 and 4.5. We want this number to be as small as possible, since it is proportional to the approximation ratio due to the later analysis. On the other hand, to obtain the entire cost of the solution , we need to swap all centers in at least once. Thus, for the case of , we consider the same swap operations in the analysis for the penalty version (we state it again in the following Case 1), since each center in is swapped exactly once.
For the case of , there are single-swap operations in the analysis for the penalty version. This makes the coefficient of the cost of small ( when ), but the number of swaps is large. In this section, we consider two methods to construct swap operations for this case, which are stated in Methods 1 and 2 in the following Case 2. Note that Method 2 is the same as that in Section 3.
- Case 1
-
(cf. Figure 1(a) for ). For each with , let and . We construct the swap for -MedO, and swap for -MeaO.
- Case 2.
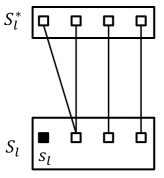
Combining these swap operations, we obtain the main results for Algorithm 4.1, which are shown in the following two theorems.
Theorem 4.6.
Let be the solution returned by LS-Multi-Swap-Outlier( ) for -MedO. If , then we have
| (21) |
If , then we have
| (22) |
Theorem 4.7.
Let be an -approximate centroid set for the data set , and be the solution returned by LS-Multi-Swap-Outlier() for -MeaO. If , then we have
| (23) |
where
If , then we have
| (24) |
where
Each of these two theorems gives two approximation ratios for Algorithm 4.1. The first one is obtained by Method 1, while the second one is obtained by Method 2.
Proof of Theorem 4.6..
We first prove inequality (21). For Case 2, we use Method 1 to construct swap operations. Note that each point in is swapped at most twice, and each point in is swapped once exactly, implying that the number of constructed swap operations is . Summing inequality (19) over these swaps and using Proposition 4.1, we obtain
| (25) | |||||
Using the definition of , we obtain
| (26) | |||||
Next we will prove the inequality (22). For Case 2, we use Method 2 to construct swap operations. Let and . Summing inequality (17) with weight 1 and inequality (19) with weight over all constructed swap operations, and observing that , we obtain
| (27) | |||||
Note that there are at most constructed swap operations. It follows from that
| (28) | |||||
Inequality (11) then yields the following upper bound for the RHS of (27).
| (29) | |||||
∎
Proof of Theorem 4.7..
We first use Method 1 for Case 2 to prove (23). Similar to the proof for -MedO, we have
| (30) | |||||
where the second inequality follows from Lemma 3.1 (this lemma still holds for the outlier version of -means), and the third inequality follows from (26).
When , it follows by factorization that inequality (30) is equivalent to
| (31) | |||||
where
Since the first term of the RHS of (31) is non-negative, we obtain
which gives (23).
Next we prove inequality (24). For Case 2, we use Method 2 to construct swap operations. Similar to the proof of Theorem 4.6, summing inequality (4.4) with weight 1 and inequality (20) with weight over all constructed swap operations implies that
| (32) | |||||
Because of Lemma 3.1, the RHS of (32) is bounded from above by
| (33) | |||||
Combining inequalities (26), (28), (32) and (33), we have
Using the factorization for this inequality and the condition in this theorem, we obtain the desired result.
∎
Consequently, we have the following corollaries that specify the tradeoff between the approximation ratio and the outlier blowup.
Corollary 4.8.
There exists a bi-criteria -, and a bi-criteria -approximation algorithm for -MedO.
Proof.
Corollary 4.9.
There exists a bi-criteria -, and a bi-criteria -approximation algorithm for -MeaO.
5 Conclusions
The previous analyses of local search algorithms for the robust -median/-means, use only the individual form, in which the constructed connections between the local and global optimal solutions are individual for each point. This has the disadvantage that the joint information about outliers remains hidden. In this paper, we develop a cluster form analysis and define the adapted cluster that captures the outlier information. We find that this new technique works better than the previous analysis methods of local search algorithms, since it improves the approximation ratios of local search algorithms for -MeaP, -MeaO and -MedO, and obtain the same ratio which is the best for -MedP.
We believe that our new technique will also work for the robust FLP, since the structure of FLP is similar to -median/-means. Also, our technique seems to be promising for the robust -center problem, even for any algorithm for robust clustering problems that is based on local search.
6 Acknowledgments
The first author is supported by the NSFC under Grant No. 12001039. The second author is supported by the Science Foundation of the Anhui Education Department under Grant No. KJ2019A0834. The third author is supported by the NSFC under Grant No. 11971349. The fourth and fifth authors are supported by the NSFC under Grant No. 11871081. The fourth author is also supported by Beijing Natural Science Foundation Project under Grant No. Z200002.
References
- Ahmadian et al. (2017) Ahmadian S, Norouzi-Fard A, Svensson O, Ward J (2017) Better guarantees for k-means and euclidean k-median by primal-dual algorithms. Proceedings of the 58th Annual Symposium on Foundations of Computer Science, 61–72 (IEEE).
- Arora et al. (1998) Arora S, Raghavan P, Rao S (1998) Approximation schemes for euclidean k-medians and related problems. Proceedings of the 30th Annual ACM Symposium on Theory of Computing, 106–113.
- Arya et al. (2004) Arya V, Garg N, Khandekar R, Meyerson A, Munagala K, Pandit V (2004) Local search heuristics for k-median and facility location problems. SIAM Journal on Computing 33(3):544–562.
- Bernstein et al. (2019) Bernstein F, Modaresi S, Sauré D (2019) A dynamic clustering approach to data-driven assortment personalization. Management Science 65(5):2095–2115.
- Borgwardt and Happach (2019) Borgwardt S, Happach F (2019) Good clusterings have large volume. Operations Research 67(1):215–231.
- Byrka et al. (2014) Byrka J, Pensyl T, Rybicki B, Srinivasan A, Trinh K (2017) An improved approximation for k-median, and positive correlation in budgeted optimization. ACM Transactions on Algorithms 13(2):23:1–23:31.
- Charikar et al. (2002) Charikar M, Guha S, Tardos É, Shmoys DB (2002) A constant-factor approximation algorithm for the k-median problem. Journal of Computer and System Sciencess 65(1):129–149.
- Charikar et al. (2001) Charikar M, Khuller S, Mount DM, Narasimhan G (2001) Algorithms for facility location problems with outliers. Proceedings of the 12th Annual ACM-SIAM Symposium on Discrete Algorithms, 642–651 (Society for Industrial and Applied Mathematics).
- Charikar and Li (2012) Charikar M, Li S (2012) A dependent lp-rounding approach for the k-median problem. International Colloquium on Automata, Languages, and Programming, 194–205 (Springer).
- Chen (2008) Chen K (2008) A constant factor approximation algorithm for k-median clustering with outliers. Proceedings of the 19th Annual ACM-SIAM Symposium on Discrete Algorithms, 826–835.
- Cohen-Addad and Karthik (2019) Cohen-Addad V, Karthik C (2019) Inapproximability of clustering in lp metrics. Proceedings of the 60th Annual Symposium on Foundations of Computer Science, 519–539 (IEEE).
- Cohen-Addad et al. (2019) Cohen-Addad V, Klein PN, Mathieu C (2019) Local search yields approximation schemes for k-means and k-median in euclidean and minor-free metrics. SIAM Journal on Computing 48(2):644–667.
- Feng et al. (2019) Feng Q, Zhang Z, Shi F, Wang J (2019) An improved approximation algorithm for the k-means problem with penalties. Proceedings of the 2nd Annual International Workshop on Frontiers in Algorithmics, 170–181 (Springer).
- Friggstad et al. (2019a) Friggstad Z, Khodamoradi K, Rezapour M, Salavatipour MR (2019a) Approximation schemes for clustering with outliers. ACM Transactions on Algorithms 15(2):1–26.
- Friggstad et al. (2019b) Friggstad Z, Rezapour M, Salavatipour MR (2019b) Local search yields a ptas for k-means in doubling metrics. SIAM Journal on Computing 48(2):452–480.
- Gupta et al. (2017) Gupta S, Kumar R, Lu K, Moseley B, Vassilvitskii S (2017) Local search methods for k-means with outliers. Proceedings of the 43rd International Conference on Very Large Data Bases 10(7):757–768.
- Hajiaghayi et al. (2012) Hajiaghayi M, Khandekar R, Kortsarz G (2012) Local search algorithms for the red-blue median problem. Algorithmica 63(4):795–814.
- Hochbaum and Liu (2018) Hochbaum DS, Liu S (2018) Adjacency-clustering and its application for yield prediction in integrated circuit manufacturing. Operations Research 66(6):1571–1585.
- Jain et al. (2003) Jain K, Mahdian M, Markakis E, Saberi A, Vazirani VV (2003) Greedy facility location algorithms analyzed using dual fitting with factor-revealing LP. Journal of the ACM 50(6):795–824.
- Jain and Vazirani (2001) Jain K, Vazirani VV (2001) Approximation algorithms for metric facility location and k-median problems using the primal-dual schema and lagrangian relaxation. Journal of the ACM 48(2):274–296.
- Kanungo et al. (2004) Kanungo T, Mount DM, Netanyahu NS, Piatko CD, Silverman R, Wu AY (2004) A local search approximation algorithm for k-means clustering. Computational Geometry 28(2-3):89–112.
- Korupolu et al. (2000) Korupolu MR, Plaxton CG, Rajaraman R (2000) Analysis of a local search heuristic for facility location problems. Journal of Algorithms 37(1):146–188.
- Krishnaswamy et al. (2018) Krishnaswamy R, Li S, Sandeep S (2018) Constant approximation for k-median and k-means with outliers via iterative rounding. Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing, 646–659.
- Li (2013) Li S (2013) A 1.488 approximation algorithm for the uncapacitated facility location problem. Information and Computation 222:45–58.
- Li and Svensson (2016) Li S, Svensson O (2016) Approximating k-median via pseudo-approximation. SIAM Journal on Computing 45(2):530–547.
- Li et al. (2013) Li Y, Shu J, Wang X, Xiu N, Xu D, Zhang J (2013) Approximation algorithms for integrated distribution network design problems. INFORMS Journal on Computing 25(3):572–584.
- Lloyd (1982) Lloyd S (1982) Least squares quantization in pcm. IEEE Transactions on Information Theory 28(2):129–137.
- Lu and Wedig (2013) Lu SF, Wedig GJ (2013) Clustering, agency costs and operating efficiency: Evidence from nursing home chains. Management Science 59(3):677–694.
- Mahdian et al. (2006) Mahdian M, Ye Y, Zhang J (2006) Approximation algorithms for metric facility location problems. SIAM Journal on Computing 36(2):411–432.
- Makarychev et al. (2016) Makarychev K, Makarychev Y, Sviridenko M, Ward J (2016) A bi-criteria approximation algorithm for k-means. Proceedings of the 19th International Workshop on Approximation Algorithms for Combinatorial Optimization Problems (APPROX), and the 20th International Workshop on Randomization and Computation (RANDOM), 14:1–14:20 (Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik).
- Matoušek (2000) Matoušek J (2000) On approximate geometric k-clustering. Discrete & Computational Geometry 24(1):61–84.
- Ni et al. (2020) Ni W, Shu J, Song M, Xu D, Zhang K (2020) A branch-and-price algorithm for facility location with general facility cost functions. INFORMS Journal on Computing URL http://dx.doi.org/10.1287/ijoc.2019.0921.
- Wang et al. (2015) Wang Y, Xu D, Du D, Wu C (2015) Local search algorithms for k-median and k-facility location problems with linear penalties. Proceedings of the 9th Annual International Conference on Combinatorial Optimization and Applications, 60–71 (Springer).
- Wu et al. (2018) Wu C, Du D, Xu D (2018) An approximation algorithm for the k-median problem with uniform penalties via pseudo-solution. Theoretical Computer Science 749:80–92.
- Zhang et al. (2019) Zhang D, Hao C, Wu C, Xu D, Zhang Z (2019) Local search approximation algorithms for the k-means problem with penalties. Journal of Combinatorial Optimization 37(2):439–453.
- Zhang (2007) Zhang P (2007) A new approximation algorithm for the k-facility location problem. Theoretical Computer Science 384(1):126–135.