PAC-Bayesian Generalization Bounds for
MultiLayer Perceptrons
Abstract
We study PAC-Bayesian generalization bounds for Multilayer Perceptrons (MLPs) with the cross entropy loss. Above all, we introduce probabilistic explanations for MLPs in two aspects: (i) MLPs formulate a family of Gibbs distributions, and (ii) minimizing the cross-entropy loss for MLPs is equivalent to Bayesian variational inference, which establish a solid probabilistic foundation for studying PAC-Bayesian bounds on MLPs. Furthermore, based on the Evidence Lower Bound (ELBO), we prove that MLPs with the cross entropy loss inherently guarantee PAC-Bayesian generalization bounds, and minimizing PAC-Bayesian generalization bounds for MLPs is equivalent to maximizing the ELBO. Finally, we validate the proposed PAC-Bayesian generalization bound on benchmark datasets.
1 Introduction
To explain why Deep Neural Networks (DNNs) with Stochastic Gradient Descent (SGD) optimization can achieve impressive generalization performance [15], a generalization bound should satisfy the five criteria: (i) small and non-vacuous [8, 39]; (ii) taking into account SGD optimization because DNNs not incorporate any explicit regularization [1, 13, 21]; (iii) showing the same architecture dependence as the generalization error, e.g., it should become smaller as the architecture of DNNs becomes complex [30, 33, 32]; (iv) showing the same sample size dependence as the generalization error, i.e., it should become smaller as the training sample size becomes larger [29, 30]; and (v) taking into account the statistical variations of samples and labels, especially random labels [38].
PAC-Bayesian theory provides a canonical probabilistic framework for studying generalization bounds [25, 26, 6, 11, 2, 28]. However, due to the extremely complicated architecture of DNNs, most existing works avoid directly formulating the prior distribution of the hypothesis expressed by DNNs and the posterior distribution given training samples through either relaxing the KL-divergence involved PAC-Bayesian theory [31, 39, 20] or approximating the distributions under some assumptions [19, 8, 23, 3], which make existing PAC-Bayesian generalization bounds difficult to satisfy the above criteria111We provide more discussions about PAC-Bayesian generalization bounds on DNNs in Appendix A. [29, 30]. Therefore, they cannot fully explain the generalization performance of DNNs.
In this paper, we study PAC-Bayesian generalization bounds on fully connected feedforward neural networks, namely MultiLayer Perceptrons (MLPs). Above all, we attempt to introduce explicitly probabilistic explanations for MLPs in three aspects: (i) we define a probability space for a fully connected layer based on Gibbs distribution [18, 9, 27]; (ii) we prove the entire architecture of MLPs corresponding to a family of Gibbs distributions; and (iii) we prove the equivalence between the cross entropy loss minimization and Bayesian variational inference [5, 14, 36]. In contrast to previous works using relaxation or approximation, the explicitly probabilistic explanations for MLPs establish a solid probabilistic foundation for studying PAC-Bayesian generalization bounds on MLPs.
Inspired by the previous work [10], we study PAC-Bayesian generalization bounds on MLPs from the perspective of Bayesian theory. Since minimizing the cross entropy loss of MLPs is equivalent to Bayesian variational inference, we prove that MLPs with the cross entropy loss inherently guarantee PAC-Bayesian generalization bounds based on the Evidence Lower Bound (ELBO) derived from Bayesian variational inference [5, 14]. To the best of our knowledge, this is the first time theoretically guaranteeing the PAC-Bayesian generalization performance for MLPs. Finally, we derive a novel PAC-Bayesian generalization bound and validate the bound on benchmark datasets.
2 PAC-Bayesian Theory
We assume that is a data generating distribution and is composed of i.i.d. samples generated from , i.e., . We define as a set of hypothesis and the loss function as , thus the empirical risk on the samples and the generalization error on the distribution are
| (1) |
The PAC-Bayesian theory establishes the connection between the probably approximately correct generalization bound and the expectation of the empirical risk , where denotes the posterior distribution of given .
Theorem 1:
PAC-Bayesian bounds on the generalization risk (Germain et al.[10]).
Given a distribution over , a hypothesis set , a loss function , a prior distribution over , a real number , and a real number , with probability at least over the samples , we have
| (2) |
We can extend it to arbitraray bounded loss, i.e., , where through defining and .
| (3) |
Formula 3 indicates that minimizing the generalization bound is equivalent to minimizing
| (4) |

To facilitate subsequent discussions, we define , , and as the random variables of the sample , the label , and the hypothesis , respectively. Therefore, and denote the prior distribution and the posterior distribution of , respectively. Based on Bayes’ rule, we can formulate the connection between and as
| (5) |
where is the likelihood of given and , and the evidence can be formulated as 222We only consider the discrete case, because we prove as a discrete random variable in the next section..
In the context of supervised classification based on MLPs, consists of finite labels, and 333For simplicity, . denotes the prior probability of belonging to class based on the expressed by MLPs. We define as the truly prior distribution of the true . Given and , is the truly posterior distribution with the one-hot format, i.e., , if ; otherwise . We aim to learn an optimal MLP from such that it approaches as close as possible. In this paper, we use the (Figure 1) for most theoretical derivations unless otherwise specified.
3 Probabilistic Explanations for Multilayer Perceptrons
In this section, we define the probability space for a fully connected layer, thereby deriving that the entire architecture of the MLP formulates a family of Gibbs distributions . Moreover, we prove that if is the cross entropy, minimizing can be explained as Bayesian variational inference, and it is equivalent to maximizing .
Definition 1:
the probability space for a fully connected layer.
Given a fully connected layer with neurons , where is an activation function, e.g, ReLU function, is the input of , and is the th linear filter with being the weight and being the bias, let inputting into be an experiment, we define the probability space as follows.
First, the sample space consists of possible outcomes , where . In terms of machine learning, a possible outcome defines a potential feature of . Since scalar values cannot describe the dependence within , we do not take into account for defining . Second, we define the event space as the -algebra. For example, if has linear filters and , thus indicates that none of outcomes, one of outcomes, or both outcomes could happen in the experiment. Third, we prove the probability measure as a Gibbs distribution to quantify the probability of possible outcomes occurring in .
| (6) |
where is the inner product, is the partition function only depending on , and the energy function equals the negative activation, i.e., . Notably, the higher activation indicates the lower energy , thus has the higher probability of occurring in . The detailed proofs and supportive simulations are presented in Appendix B444We recommend reading the supplementary file connecting the paper and the appendix together.
Based on for the fully connected layer , we can explicitly define the corresponding random variable . Specifically, since includes finite possible outcomes, should be a discrete measurable space and is a discrete random variable. For example, indicates the probability of the th outcome occurring in . Furthermore, the probability space of a fully connected layer enables us to derive probabilistic explanations for MLPs.
Theorem 2:
the corresponds to a family of Gibbs distributions
| (7) |
where is the energy function of given , and the partition function .
Proof: Definition 1 implies defining , thus would be fixed if not considering training. Therefore, is entirely determined by in the MLP, where denotes the random variable of , and the MLP forms a Markov chain . As a result, given a sample , the conditional distribution corresponding to the MLP can be derived as
| (8) |
The derivation is presented in Appendix C. The energy function implies that is entirely determined by the architecture of the MLP. In other words, the MLP formulates a family of Gibbs distributions .
Corollary 1:
Given the samples and the , if is the cross entropy, then minimizing is equivalent to maximizing .
| (9) |
where .
Proof: since the cross entropy , we have
| (10) |
Since is one-hot, namely that if , then , otherwise , we can simplify Equation (10) as
| (11) |
Therefore, minimizing is equivalent to maximizing the likelihood . In addition, based on Theorem 2 (Equation 7), we can extend as
| (12) |
Recall that sums up all the cases of , thus can be viewed as a constant with respect to .
Theorem 3:
given the samples and the , if is the cross entropy, then minimizing can be explained as Bayesian variational inference.
| (13) |
where and .
Proof: based on the property , we can derive as
| (14) |
Since is one-hot, namely that if , , otherwise , , thus we can simplify as
| (15) |
To keep consistent with the definition of variational inference, we reformulate as
| (16) |
where .
Though KL-divergence is asymmetric, i.e., , we show that converges to zero during minimizing , because is fixed and is the only variable. The proof for is presented in Appendix D. Moreover, since consists of i.i.d. samples and KL-divergence is additive for independent distributions, we can finally derive
| (17) |
As a result, minimizing with the cross entropy loss is equivalent to Bayesian variational inference. In summary, Theorem 3 provides a novel probabilistic explanation for MLPs from the perspective of Bayesian variational inference. Specifically, the MLP formulates a family of Gibbs distribution , and minimizing aims to search an optimal distribution , which is closest to the truly posterior distribution given .
4 PAC-Bayesian Bounds for Multilayer Perceptrons
In this section, we prove that MLPs with the cross entropy loss inherently guarantee PAC-Bayesian generalization bounds based on the ELBO derived from Bayesian variational inference. Moreover, we derive a novel PAC-Bayesian generalization bound for MLPs.
Theorem 4:
given the samples and the , if is the cross entropy, then minimizing inherently guarantees PAC-Bayesian generalization bounds for the MLP.
| (18) |
Proof: we only need prove Bayesian variational inference inducing PAC-Bayesian generalization bounds based on Theorem 3. Given the Bayesian variational inference (Equation 17), we have
| (19) |
Since is constant with respect to , we can derive the ELBO as
| (20) |
where , , , and . The detailed derivation of the ELBO is presented in Appendix E.
Since is the truly prior distribution of the true hypothesis , we have . Since infers the truly posterior distribution of , we have . Corollary 1 induces because we can express as . As a result, we derive
| (21) |
It implies that maximizing ELBO is equivalent to minimizing PAC-Bayesian generalization bounds, thus minimizing inherently guarantees PAC-Bayesian generalization bounds for the MLP.
Theorem 4 theoretically explains why MLPs can achieve great generalization performance without explicit regularization. More specifically, the ELBO indicates that minimizing makes MLPs not only to learn the likelihood but also to learn the prior knowledge via minimizing . In other words, minimizing inherently guarantees PAC-Bayesian generalization bounds for MLPs, even though they do not incorporate explicit regularization.
Corollary 2:
PAC-Bayesian generalization bounds for the MLP.
Given a distribution over , the samples , a probabilistic hypothesis set derived from the , the cross entropy loss 555The previous works prove PAC-Bayesian bounds being valid for unbounded loss functions [10, 2]., a real number , and a real number , with probability at least over the samples , we have
| (22) |
where , is the energy of given , and is the partition function.
Proof: the result is derived by two steps: (i) substituting in Equation 3 for the in Equation 20; and (ii) substituting for based on Equation 17 and 12.
Corollary 1 implies that when minimizing to zero, and the proposed PAC-Bayesian generalization bound would be entirely determined by the marginal likelihood , which is consistent with the theoretical connection between PAC-Bayesian theory and Bayesian inference proposed by Germain et al. [10].
Based on Corollary 2, we derive an applicable bound for examining the generalization of MLPs. Though is unknown, the i.i.d. assumption for induces being a constant as long as the number of different labels are equivalent. As a result, we have
| (23) |
Recall that sums up all the cases of , i.e., is a constant with respect to . In addition, we show that the functionality of is only to guarantee the validity of (Appendix F). Therefore, can be viewed as a constant for deriving PAC-Bayesian generalization bounds for MLPs, thus the bound can be further relaxed as
| (24) |
We use the above formula to approximate the generalization bound for subsequent experiments.
5 Experimental Results
In this section, we demonstrate the proposed PAC-Bayesian generalization bound on MLPs in four different cases: (i) different training algorithms, (ii) different architectures of MLPs, (iii) different sample sizes, and (iv) different labels, namely real labels and random labels.
All the experimental results are derived based on the classifying the MNIST dataset [17]. Since the dimension of a single MNIST image is , has input nodes. Since the MNIST dataset consists of different labels, has output nodes. All the activation functions are ReLU . Because of space limitation, we present more experimental results based on MLPs on other benchmark datasets in Appendix G.
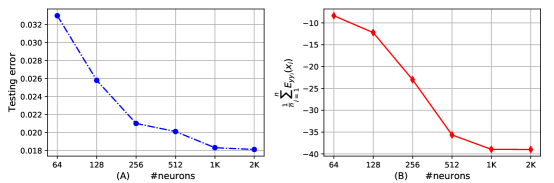
The bound can reflect the generalization of MLPs with different number of neurons [30].
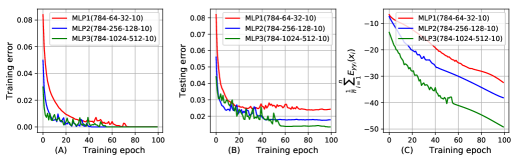
We design three MLPs (abbr. MLP1, MLP2, MLP3). They have the same architecture except the number of neurons in hidden layers, which are summarized in Figure 2. We use the same SGD optimization algorithm to train the three MLPs and all the three MLPs achieve zero training error. We visualize the training error, the testing error, and the bound in Figure 2, which shows that the bound has the same architecture dependence as the testing error. In other words, the MLP with the more number of neurons has the lower testing error and bound.
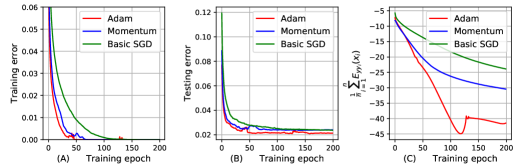
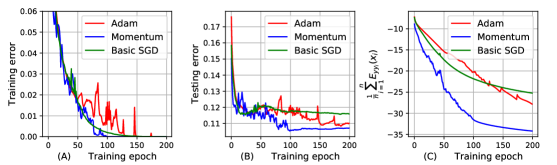
The bound can reflect the effect of SGD optimization on the generalization of MLPs [30].
We use three different training algorithms (the basic SGD [35], Momentum [34], and Adam [16]) to train MLP2 200 epochs, and visualize the training error, the testing error, and the generalization bound in Figure 3. We can observe that the bounds of MLP2 with different training algorithms is consistent with the corresponding testing errors of MLP2. For example, MLP2 with Adam training algorithm achieves the smallest testing error, thus the bound of MLP2 with Adam is also smaller than Momentum and the basic SGD.
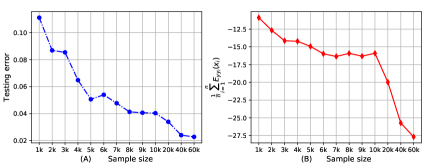
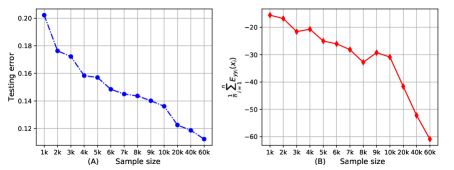
The bound can reflect the same sample size dependence as the testing error [29].
We create 13 different subsets of the MNIST dataset with different number of training samples, and train MLP2 to classify these samples until the training error becomes zero. Figure 4 shows the testing error and the bound with different sample sizes. The bound shows a general decreasing trend as the training sample size increases, which is consistent with the variation of the testing error.
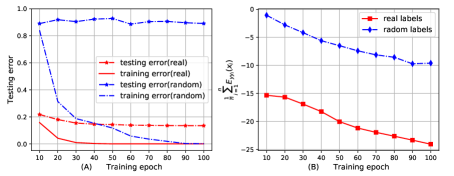
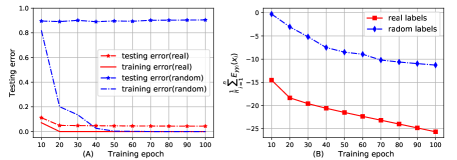
The bound can reflect the generalization performance of MLPs given random labels.
Zhang et al.[38] show that DNNs achieve low testing error when they are trained by random labels. We train MLP3 100 epochs to classify 10,000 samples of the MNIST dataset with random labels, and visualize the training error, the testing error and the bound in Figure 5.
We observe that the bound of MLP3 trained by random labels is higher than real labels, which is consistent with the testing error based on random labels is higher than real labels. In particular, we can theoretically explain why MLP3 trained by random labels has the higher testing error. Random labels imply that not depends on and , i.e., , thus the ELBO (Equation 20) can be reformulated as
| (25) |
As a result, minimizing equals minimizing , which is only one part of the PAC-Bayesian optimization (Equation 4). Therefore, MLPs with random labels cannot guarantee PAC-Bayesian generalization bounds.
6 Conclusions
In this work, we prove that MLPs with the cross entropy loss inherently guarantee PAC-Bayesian generalization bounds, and minimizing PAC-Bayesian generalization bounds for MLPs is equivalent to maximizing the ELBO. In addition, we derive a novel PAC-Bayesian generalization bound correctly explaining the generalization performance of MLPs. Extending the proposed PAC-Bayesian generalization bounds to general DNNs is promising for future work.
References
- [1] Zeyuan Allen-Zhu, Yuanzhi Li, and Yingyu Liang. Learning and generalization in overparameterized neural networks, going beyond two layers. In Advances in neural information processing systems, pages 6155–6166, 2019.
- [2] Pierre Alquier, James Ridgway, and Nicolas Chopin. On the properties of variational approximations of gibbs posteriors. The Journal of Machine Learning Research, 17(1):8374–8414, 2016.
- [3] Amiran Ambroladze, Emilio Parrado-Hernández, and John S Shawe-taylor. Tighter pac-bayes bounds. In Advances in neural information processing systems, pages 9–16, 2007.
- [4] Roberto Battiti. First and second order methods for learning: Between steepest descent and newton’s method. Neural Computation, 4:141–166, 1992.
- [5] David Blei, Alp Kucukelbir, and Jon MaAuliffe. Variational inference: A review for statisticians. Journal of Machine Learning Research, 112:859–877, 2017.
- [6] Olivier Catoni. Pac-bayesian supervised classification: the thermodynamics of statistical learning. arXiv preprint arXiv:0712.0248, 2007.
- [7] Pratik Chaudhari and Stefano Soatto. Stochastic gradient descent performs variational inference, converges to limit cycles for deep networks. In 2018 Information Theory and Applications Workshop (ITA), pages 1–10. IEEE, 2018.
- [8] Gintare Karolina Dziugaite and Daniel M Roy. Computing nonvacuous generalization bounds for deep (stochastic) neural networks with many more parameters than training data. arXiv preprint arXiv:1703.11008, 2017.
- [9] S. Geman and D. Geman. Stochastic relaxation, gibbs distributions, and the bayesian restoration of images. IEEE Transactions. on Pattern Analysis and Machine Intelligence, pages 721–741, June 1984.
- [10] Pascal Germain, Francis Bach, Alexandre Lacoste, and Simon Lacoste-Julien. Pac-bayesian theory meets bayesian inference. In Advances in Neural Information Processing Systems, pages 1884–1892, 2016.
- [11] Pascal Germain, Alexandre Lacasse, François Laviolette, and Mario Marchand. Pac-bayesian learning of linear classifiers. In Proceedings of the 26th Annual International Conference on Machine Learning, pages 353–360, 2009.
- [12] Geoffrey E Hinton. Training products of experts by minimizing contrastive divergence. Neural Computation, 14:1771–1800, 2002.
- [13] Elad Hoffer, Itay Hubara, and Daniel Soudry. Train longer, generalize better: closing the generalization gap in large batch training of neural networks. In Advances in Neural Information Processing Systems, pages 1731–1741, 2017.
- [14] Matthew D. Hoffman, David M. Blei, Chong Wang, and John Paisley. Stochastic variational inference. Journal of Machine Learning Research, 14:1303–1347, 2013.
- [15] Kenji Kawaguchi, Leslie Pack Kaelbling, and Yoshua Bengio. Generalization in deep learning. arXiv preprint arXiv:1710.05468, 2017.
- [16] Diederik P Kingma and Jimmy Ba. Adam: A method for stochastic optimization. arXiv preprint arXiv:1412.6980, 2014.
- [17] Y. LeCun, L. Bottou, and P. Haffner. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 11:2278–2324, 1998.
- [18] Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, and Fu Jie Huang. A tutorial on energy-based learning. MIT Press, 2006.
- [19] Gaël Letarte, Pascal Germain, Benjamin Guedj, and François Laviolette. Dichotomize and generalize: Pac-bayesian binary activated deep neural networks. In Advances in Neural Information Processing Systems, pages 6869–6879, 2019.
- [20] Guy Lever, François Laviolette, and John Shawe-Taylor. Tighter pac-bayes bounds through distribution-dependent priors. Theor. Comput. Sci., 473(Feb):4–28, 2013.
- [21] Yuanzhi Li and Yingyu Liang. Learning overparameterized neural networks via stochastic gradient descent on structured data. In Advances in Neural Information Processing Systems, pages 8157–8166, 2018.
- [22] Henry W Lin, Max Tegmark, and David Rolnick. Why does deep and cheap learning work so well? Journal of Statistical Physics, 168(6):1223–1247, 2017.
- [23] Ben London. A pac-bayesian analysis of randomized learning with application to stochastic gradient descent. In Advances in Neural Information Processing Systems, pages 2931–2940, 2017.
- [24] Stephan Mandt, Matthew D Hoffman, and David M Blei. Stochastic gradient descent as approximate bayesian inference. The Journal of Machine Learning Research, 18(1):4873–4907, 2017.
- [25] David A McAllester. Some pac-bayesian theorems. Machine Learning, 37(3):355–363, 1999.
- [26] David A McAllester. Pac-bayesian stochastic model selection. Machine Learning, 51(1):5–21, 2003.
- [27] Pankaj Mehta and David J. Schwab. An exact mapping between the variational renormalization group and deep learning. arXiv preprint arXiv:1410.3831, 2014.
- [28] Vaishnavh Nagarajan and J Zico Kolter. Deterministic pac-bayesian generalization bounds for deep networks via generalizing noise-resilience. arXiv preprint arXiv:1905.13344, 2019.
- [29] Vaishnavh Nagarajan and J Zico Kolter. Uniform convergence may be unable to explain generalization in deep learning. In Advances in Neural Information Processing Systems, pages 11611–11622, 2019.
- [30] Behnam Neyshabur, Srinadh Bhojanapalli, David McAllester, and Nathan Srebro. Exploring generalization in deep learning. In NeurIPS, 2017.
- [31] Behnam Neyshabur, Srinadh Bhojanapalli, and Nathan Srebro. A pac-bayesian approach to spectrally-normalized margin bounds for neural networks. arXiv preprint arXiv:1707.09564, 2017.
- [32] Behnam Neyshabur, Ryota Tomioka, and Nathan Srebro. In search of the real inductive bias: On the role of implicit regularization in deep learning. In ICLR, 2015.
- [33] Tomaso Poggio, Hrushikesh Mhaskar, Lorenzo Rosasco, Brando Miranda, and Qianli Liao. Why and when can deep-but not shallow-networks avoid the curse of dimensionality: a review. International Journal of Automation and Computing, 14(5):503–519, 2017.
- [34] Ning Qian. On the momentum term in gradient descent learning algorithms. Neural networks, 12(1):145–151, 1999.
- [35] David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams. Learning representations by back-propagating errors. Nature, 323:533–536, October 1986.
- [36] Martin J Wainwright and Michael I Jordan. Graphical models, exponential families, and variational inference. Foundations and Trends® in Machine Learning, 1(1-2):1–305, 2008.
- [37] Han Xiao, Kashif Rasul, and Roland Vollgraf. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. arXiv preprint arXiv:1708.07747, 2017.
- [38] Chiyuan Zhang, Samy Bengio, Moritz Hardt, Benjamin Recht, and Oriol Vinyals. Understanding deep learning requires rethinking generalization. In ICLR, 2016.
- [39] Wenda Zhou, Victor Veitch, Morgane Austern, Ryan P Adams, and Peter Orbanz. Non-vacuous generalization bounds at the imagenet scale: a pac-bayesian compression approach. arXiv preprint arXiv:1804.05862, 2018.
Appendix
A Related works about PAC-Bayesian generalization bounds on DNNs
In this appendix, we briefly discuss previous works using PAC-Bayesian theory to derive the generalization bound for neural networks, and explain what is the difference to the current paper.
To derive generalization bounds for neural networks based on PAC-Bayesian theory, it is prerequisite that obtaining the KL-divergence between the posterior distribution and the prior distribution of the hypothesis expressed by neural networks.
Behnam Neyshabur et al. [31]. This paper combines the perturbation bound and PAC-Bayesian theory to derive the generalization bound of neural networks. The authors approximate the KL-divergence involved PAC-Bayesian bounds by the perturbation bound based on the assumption that the prior distribution is Gaussian and the perturbation is Gaussian as well.
Wenda Zhou et al. [39]. In the context of compressing neural networks, this paper propose a generalization bound of neural networks through estimating the KL-divergence involved PAC-Bayesian bounds by the number of bits required to describe the hypothesis.
Gintare Karolina Dziugaite et al. [8]. To derive PAC-Bayesian generalization bounds for stochastic neural networks, this paper restricts the prior distribution and the posterior distribution as a family of multivariate normal distributions for simplifying the KL-divergence involved PAC-Bayesian bounds.
Letarte Gaël et al. [19]. This paper studies PAC-Bayesian generalization bounds for binary activated deep neural networks, which can be explained as a specific linear classifier, and the authors assume the prior distribution and the posterior distribution being Gaussian. As a result, PAC-Bayesian generalization bounds are determined by the summation of the Gaussian error function and the norm of the weights.
We can find that most existing works use relaxation or approximation to estimate the KL-divergence involved PAC-Bayesian bounds. However, the relaxation or approximation not only introduce estimation error of the generalization bound for neural networks but also make difficult to clearly explain why neural networks can achieve impressive generalization performance without explicit regularization. The limitation of existing PAC-Bayesian generalization bounds triggers a fundamental question:
Can we establish an explicit probabilistic representation for DNNs and
derive an explicit PAC-Bayesian generalization bound?
The current paper attempts to derive PAC-Bayesian generalization bounds for MLPs based on explicit probabilistic representations rather than approximation or relaxation. It is mainly inspired by the previous work [10], in which Germain et al. bridge Bayesian inference and PAC-Bayesian theory. They prove that minimizing the PAC-Bayesian generalization bound is equivalent to maximizing the Bayesian marginal likelihood if the loss function is the negative log-likelihood of the hypothesis. However, the paper only focuses on linear regression and model selection problem, and does not discuss how to use Bayesian inference to explain neural networks
The current paper is also inspired by the previous works [24, 7, 27, 22]. Mandt et al. provide novel explanations for SGD from the viewpoint of Bayesian inference, especially Bayesian variational inference [24, 7]. Mehta et al. demonstrate that the distribution of a hidden layer can be formulated as a Gibbs distribution in the Restricted Boltzmann Machine (RBM) [27, 22].
B The probability space for a fully connected layer

B.1 The proof of the probability space definition
We use the mathematical induction to prove the probability space for all the fully connected layers of the MLP in Figure 6. Above all, we define three probability space, i.e., , , and , for the three layers of the MLP, i.e., , , and , respectively. Subsequently, we first demonstrate that is a Gibbs distribution, and then we prove that and are Gibbs distributions based on and being Gibbs distributions, respectively.
Since the output layer is the softmax, each output node can be formulated as
| (26) |
where is the partition function and .
Comparing Equation 6 and 26, we can derive that forms a Gibbs distribution to measure the probability of occurring in , which is consistent with the definition of .
Based on the properties of the exponential function, namely and , we can reformulate as
| (27) |
where . Since are scalar, we can introduce a new partition function such that becomes a probability measure, thus we can reformulate as a Product of Expert (PoE) model [12]
| (28) |
where , especially each expert is defined as .
It is noteworthy that all the experts form a probability measure and establish an exact one-to-one correspondence to all the neurons in , thus the distribution of can be expressed as
| (29) |
Since , can be extended as
| (30) |
where is the partition function and . We can conclude that forms a Gibbs distribution to measure the probability of occurring in , which is consistent with the definition of .
Due to the non-linearity of , we cannot derive being a PoE model only based on the properties of exponential functions. Alternatively, the equivalence between the Stochastic Gradient Descent (SGD) and the first order approximation [4] indicates that can be approximated as
| (31) |
where and only depend on the activations in the previous training iteration, thus they can be regarded as constants and absorbed by and . The proof for the approximation in Appendix B.3.
Therefore, still can be modeled as a PoE model
| (32) |
where and the partition function is .
Similar to , we can derive the probability measure of as
| (33) |
where is the partition function and . We can conclude that forms a Gibbs distribution to measure the probability of occurring in , which is consistent with the definition of . Overall, we prove that the proposed probability space is valid for all the fully connected layers in the . Also note that we can easily extend the probability space to an arbitrary fully connected layer through properly changing the script.
B.2 The validation of the probability space definition
Setup.
We generate a synthetic dataset to validate the probability space for a fully connected layer. The dataset consists of 256 grayscale images and each image is sampled from the Gaussian distribution . To guarantee that the synthetic dataset has certain features that can be learned by MLPs, we sort each image in the primary or secondary diagonal direction by the ascending or descending order. As a result, the synthetic dataset has four features/classes, and the corresponding images are drawn in Figure 7.

There is an important reason why we generate the synthetic dataset. Since most benchmark dataset contains very complex features, we cannot explicitly explain the internal logic of MLPs. As a comparison, the synthetic dataset only has four simple features. Therefore, we can clearly demonstrate the proposed probability space for a fully connected layer by simply visualizing the weights of the layer.
To classify the synthetic dataset, we specify the MLP as follows: (i) since each synthetic image is , the input layer has nodes, (ii) two hidden layers and have and neurons, respectively, and (iii) the output layer has nodes. In addition, all the activation functions are chosen as ReLU unless otherwise specified.
Validation.
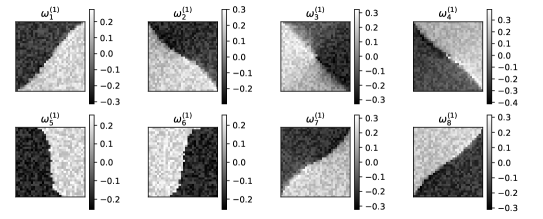
To demonstrate for all the fully connected layers in the , we only need to demonstrate for the first layer , because we derive for each layer in the back-forward direction based on the mathematical induction.
First, we demonstrate the sample space for . More specifically, we use the synthetic dataset to train the MLP 100 epochs (the training accuracy is ) and visualize the learned weights of the eight neurons in , i.e., in Figure 8 . We can find that can be regarded as a feature of the input. For example, describes a feature indicating the difference along the secondary diagonal direction, because it has low magnitude at top-left positions and high magnitude at bottom-right positions. In addition, is strongly related to Img0 in Figure 7, because the later has the same spatial feature. In the context of probability space, we define an experiment as inputting Img0 into , thus can be viewed as a possible outcome of the experiment. In addition, to keep consistent with the definition of outcome, we suppose and being mutually exclusive, because they have different weights at the same position, i.e., .
| 27.53 | 8.98 | -14.04 | 6.89 | 14.07 | -22.24 | 25.85 | -27.13 | |
| 27.53 | 8.98 | 0.0 | 6.89 | 14.07 | 0.0 | 25.85 | 0.0 | |
| 9.03e+11 | 7.94e+03 | 1.0 | 1.0 | 1.28e+06 | 1.0 | 1.68e+11 | 1.0 | |
| 0.843 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.157 | 0.0 | |
| -27.51 | -9.81 | 12.96 | -5.87 | -13.05 | 21.68 | -26.02 | 27.61 | |
| 0.0 | 0.0 | 12.96 | 0.0 | 0.0 | 21.68 | 0.0 | 27.61 | |
| 1.0 | 1.0 | 4.25e+05 | 1.0 | 1.0 | 2.60e+09 | 1.0 | 9.79e+11 | |
| 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.003 | 0.0 | 0.997 | |
| -2.69 | 26.28 | 24.64 | -28.39 | -20.44 | 12.23 | 10.13 | -6.84 | |
| 0.0 | 26.28 | 24.64 | 0.0 | 0.0 | 12.23 | 10.13 | 0.0 | |
| 1.0 | 2.58e+11 | 5.02e+10 | 1.0 | 1.0 | 2.04e+05 | 2.50e+04 | 1.0 | |
| 0.0 | 0.837 | 0.163 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 4.71 | -26.20 | -25.65 | 28.91 | 20.93 | -13.18 | -8.67 | 4.97 | |
| 4.71 | 0.0 | 0.0 | 28.91 | 20.93 | 0.0 | 0.0 | 4.97 | |
| 1.11e+02 | 1.0 | 1.0 | 3.59e+12 | 1.22e+09 | 1.0 | 1.0 | 1.44e+02 | |
| 0.0 | 0.0 | 0.0 | 1.0 | 0.0 | 0.0 | 0.0 | 0.0 |
-
•
and denote the linear output and the activation, respectively, where and .
Second, we demonstrate the Gibbs probability measure for . Based on Equation 33, we summarize given the four synthetic images (Figure 7) in Table 1, and find that correctly measures the probability of the outcomes occurring in the experiment based on the relation between and . For example, correctly describes the feature of Img0, thus it has the highest linear output and activation ( and ), thereby . As a comparison, since oppositely describes the feature of Img0, it has the lowest linear output and activation ( and ), thereby .
In summary, we demonstrate the probability space , for a fully connected layer based on the synthetic dataset. The learned weights of neurons generate a sample space consisting of multiple possible outcomes/features occurring in the input. The energy of each possible outcomes equals the negative activation of each neuron. The Gibbs function quantifies the probability of outcomes occurring in the input.
B.3 The equivalence between SGD and the first order approximation
If an arbitrary function is differentiable at point and its differential is represented by the Jacobian matrix , the first order approximation of near the point can be formulated as
| (34) |
where is a quantity that approaches zero much faster than approaches zero.
Based on the first order approximation [4], the activations in and in the can be expressed as follows:
| (35) |
where are the activations of the second hidden layer based on the parameters of learned in the th iteration, i.e., , given the activations of the first hidden layer, i.e., . In addition, the definitions of , , and are the same as .
Since has neurons and each neuron has parameters, namely , the dimension of is equal to and can be expressed as
| (36) |
where . Substituting for in Equation 35, we derive
| (37) |
If we only consider a single neuron, e.g., , we define and , thus . As a result, for a single neuron, Equation 37 can be expressed as
| (38) |
Equation 38 indicates that can be reformulated as two components: approximation and bias. Since is only related to and , it can be regarded as a constant with respect to . The bias component also does not contain any parameters in the th training iteration.
In summary, can be reformulated as
| (39) |
where and . Similarly, the activations in the first hidden layer also can be formulated as the approximation. To validate the approximation, we only need prove approaching zero, which can be guaranteed by SGD.
Given the and the empirical risk , SGD aims to optimize the parameters of the MLP through minimizing [35].
| (40) |
where denotes the Jacobian matrix of with respect to at the th iteration, and denotes the learning rate. Since the functions of all the layers are differentiable, the Jacobian matrix of with respect to the parameters of the th hidden layer, i.e., , can be expressed as
| (41) |
where denote the parameters of the th layer. Equation 40 and 41 indicate that can be learned as
| (42) |
Table 2 summarizes SGD training procedure for the MLP shown in Figure 6.
SGD minimizing indicates converging to zero, thereby converging to zero.
| Layer | Gradients | Parameters | Activations | |||
|---|---|---|---|---|---|---|
| — | — | — |
-
•
The up-arrow and down-arrow indicate the order of gradients and parameters(activations) update, respectively.
C The derivation of the marginal distribution
Since the entire architecture of the in Figure 6 corresponds to a joint distribution , the marginal distribution can be formulated as
| (43) |
Based on the definition of the Gibbs probability measure (Equation 6), we have
| (44) |
where and , i.e., .
Similarly, we have
| (45) |
where , and , i.e., . Therefore, we have
| (46) |
Since is a constant with respect to , we have
| (47) |
In addition, , thus we have
| (48) |
Therefore, we can simplify as
| (49) |
Similarly, since and is also a constant with respect to , we can derive
| (50) |
In addition, since , we can extend as
| (51) |
Since , we can further extend as
| (52) |
Overall, we prove that is also a Gibbs distribution and it can be expressed as
| (53) |
where is the energy function of given and the partition function .
D approachs
This appendix demonstrates because during minimizing .
Recall , the property of cross entropy, i.e., , allows us to derive
| (54) |
where denotes the entropy of . Since is one-hot, namely that if , then , otherwise , we have
| (55) |
Therefore, we can simplify as
| (56) |
induces . To guarantee is a valid value, we relax as
| (57) |
where is a small positive value. As a result, we have
| (58) |
Corollary 1 indicates that minimizing is equivalent to maximizing . Since , maximizing makes to approach 1. As a result, , , and approach 0. In addition, we have . In summary, converges to 0 when minimizing .
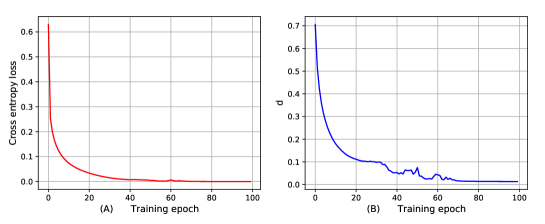
Moreover, we train the MLP1 designed in Section 5 on the MNIST dataset and visualize the variation of the cross entropy loss and during 100 epochs in Figure 9. We can observe that shows a similar decreasing trend as the cross entropy loss and converges to zero when the cross entropy loss approaches zero. Since converges to zero, during minimizing .
E The derivation of the ELBO from Bayesian variational inference
Given the samples , the , and the cross entropy loss , recall the corresponding Bayesian variational inference (Equation 17) as
| (59) |
Since , we have
| (60) |
Since is constant with respect to , we have
| (61) |
Since , we have
| (62) |
Since , we have
| (63) |
Finally, we can derive the ELBO as
| (64) |
where , , , and .
Again, since is constant with respect to , minimizing is equivalent to maximizing the ELBO.
F The variations of and during minimizing
In this appendix, we show the variation of and during minimizing , and prove that is not helpful to decrease the generalization bound because is a constant with respect to .
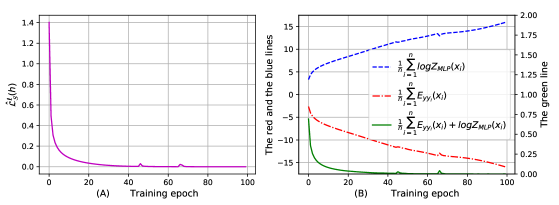
We train MLP1 designed in Section 5 on the MNIST dataset and visualize the variations of , , and their summation during minimizing in Figure 10. We can observe that is increasing and is decreasing. Notably, their summation has the same decreasing trend as and quickly converges to zero, which indicates
| (65) |
Recall that sums up all the cases of . As a result, is a constant with respect to . In other words, the functionality of is only to guarantee the validity of , thus it can be viewed as a constant for deriving the generalization bound.
As a result, the PAC-Bayesian generalization bound (Equation 22) can be relaxed as
| (66) |
G Experiments on MLPs with the Fashion-MNIST dataset
This appendix validates the PAC-Bayesian generalization bound for MLPs on the Fashion-MNIST dataset [37].
The bound can reflect the generalization of MLPs with different number of neurons.
We train the with different number of neurons on the Fashion-MNIST dataset, and visualize the testing error and the bound in Figure 11. We can observe that the MLP achieves lower testing error as the number of neurons increases, and the variation of the bound is consistent with that of testing error.
The bound can reflect the effect of SGD optimization on the generalization of MLPs.
We specify the to classify the Fashion-MNIST dataset. The MLP has 512 neurons in and 256 neurons in . All the activation functions are ReLU . Since the dimension of a single Fashion-MNIST image is , has input nodes. Since the Fashion-MNIST dataset consists of different labels, has output nodes. We still use three different training algorithms (the basic SGD, Momentum, and Adam) to train the MLP 200 epochs, and visualize the training error, the testing error, and the generalization bound in Figure 12.
We can observe that the bounds of the MLP with different training algorithms is consistent with the corresponding testing errors of the MLP. In contrast to Adam achieving the lowest testing error for classifying the MNIST dataset (Figure 3), Momentum achieves the lowest testing error for classifying the Fashion-MNIST dataset. Figure 12 shows the bound of the MLP with Momentum is also smaller than Adam and the basic SGD.
The bound can reflect the same sample size dependence as the testing error.
Similar to the experiment in Section 5, we also create 13 different subsets of the Fashion-MNIST dataset with different number of training samples, and train the MLP2 designed in Section 5 on the 13 subsets. Figure 13 shows the testing error and the bound with different sample sizes. Similar to Figure 4, the bound shows a general decreasing trend as the training sample size increases, which is consistent with the variation of the testing error.
The bounds can reflect the generalization performance of MLPs given random labels.
We train the MLP3 designed in Section 5 100 epochs to classify 10,000 samples of the Fashion-MNIST dataset with random labels, and visualize the training error, the testing error and the bound in Figure 14.
We observe that the bound of MLP3 trained by random labels is higher than real labels, which is consistent with the testing error based on random labels is higher than real labels.