Pair Density Waves and Supercurrent Diode Effect in Altermagnets
Abstract
Metallic altermagnets are unusual collinear magnets that feature zero net magnetization with momentum-dependent spin splitting. Here, we show that this spin splitting can induce pair density wave states even in the absence of external magnetic fields. Focusing on BCS-type attractive interactions, we find the stabilization of symmetrically distinct pair density wave states depending on the chemical potential. These states include Fulde-Ferrell and Fulde-Ferrell* states, both of which break inversion symmetry. We investigate the supercurrent properties and discover non-reciprocal supercurrents for both the Fulde-Ferrell and Fulde-Ferrell* states with distinct spatial dependencies. We propose that the supercurrent diode effect can serve as an experimental tool for distinguishing between different pair density waves in metallic altermagnets and discuss the relation to material candidates.
Introduction.— Collinear magnets are commonly thought to display either ferromagnetic or antiferromagnetic order [1, 2]. Ferromagnets (FM) break time-reversal symmetry with a net magnetic moment leading to spin split electronic bands. On the other hand, traditional antiferromagnets (AFM) show zero net magnetization and are symmetric under the time reversal, which flips the spin, followed by a lattice translation, resulting in Kramer’s spin degenerate bands in momentum space. However, recent investigations have challenged this binary classification, proposing a new subtype of collinear magnetism termed altermagnets (AM), which are characterized by momentum-dependent spin split bands with zero net magnetization [3, 4, 5, 6, 7, 8]. In AM the symmetry that connects the magnetic sublattices with opposite spins are non-trivial rotations [9], for example a fourfold rotation leads to -wave AM on the square lattice [10, 11, 12].
The interplay between magnetism and superconductivity can lead to qualitatively new phenomena, for example a change of pairing symmetry [13, 14], and has been a central focus in condensed matter physics research [15, 16]. The the spin splitting of electronic bands in FM impedes the formation of conventional -wave spin-singlet superconductivity as the formation of Cooper pairs is energetically suppressed. However, an alternative is to stabilize Cooper pairs with a finite center of mass momentum, as proposed to be realizeable in FM/superconductor junctions [17, 18, 19]. Here, we study the effect of the unique momentum-dependent spin splitting of AM on superconductivity. Theoretical investigations have focused on cases where superconductivity is induced solely through the proximity effect within AM/superconductor junctions [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30]. Nevertheless, the understanding of bulk superconductivity in AM has been limited [31, 32, 33, 34, 35, 36, 37], despite the presence of superconductivity in AM materials, which include RuO2 thin films with strain [38, 39] and possibly hole-doped La2CuO4 [5, 15].

In this work, we explore the bulk superconductivity arising from a conventional BCS-type attractive interaction between electrons in -wave AM metals. We find the emergence of pair density wave (PDW) states even in the absence of an external magnetic field or charge density wave instabilities. Deriving the Ginzburg–Landau theory from a microscopic model, we find the stabilization of inversion symmetry-breaking PDW states like Fulde–Ferrell (FF) and Fulde–Ferrell* (FF*) states. Further investigation into supercurrent properties reveals non-reciprocal supercurrents in the FF state along the direction and in the FF* state along and directions. In a related context, a recent work studied the symmetry properties of possible supercurrent diode effects, e.g. non-reciprocal critical supercurrents [40, 41, 42, 43, 44, 45], in altermagnetic superconductors and related heterostructures [46]. Here we derive the effective Ginzburg-Landau theory and show that non-reciprocal supercurrents may appear for intrinsic inversion-symmetry breaking bulk superconducting states of AM.
Model of a AM metal.— We focus on a two-dimensional -wave AM metal [6, 5] with a low-energy Hamiltonian expanded near the point as
| (1) |
with the two-component spinor and the Pauli matrices act on spin space. The first term describes the kinetic energy, while and denote the strength of AM splitting and the chemical potential, respectively. The AM breaks the time-reversal symmetry and the fourfold rotational symmetry about axis, which is characterized by anisotropic spin splitting vanishing along and axes, thus forming a -wave magnet. However, the system still preserves a magnetic fourfold rotational symmetry such that . As a result, the net magnetization of the system must be zero although the two bands become spin split. The band structure looks similar to those of RuO2 and KRu4O8 [5, 47]. Throughout this study, we fix meV.
There are diverse microscopic mechanism of superconducting pairing and in the following we focus on a basic effective BCS-type attractive interaction, most commonly treated for phonon-mediated pairing. The resulting effective interaction is written in momentum space as
| (2) |
Here, is the strength of onsite interactions and the attraction holds only near the Fermi level within regions bounded by the Debye frequency as illustrated in Fig. 1. Such interactions typically lead to the condensation of spin-singlet -wave states with the order parameter . Alternatively, sought-after spin-singlet -wave PDW states with the order parameter carrying a finite center of mass momentum can potentially be realized. Below, we focus on such -wave states ignoring the long-range interactions that can induce spin-singlet -wave or spin-triplet -wave states [35, 48, 37, 49] (see Sec. III of the Supplementary Material for details).
PDW in AM.— The phase diagram of superconducting states can be obtained by minimizing the Ginzburg–Landau free energy. The PDW order parameter can be conveniently written as
| (3) |
with corresponding wavevectors . Here, and are connected through the magnetic fourfold rotation such that . The free energy is constructed by imposing gauge, translational, inversion, and magnetic fourfold rotational symmetries and is written as [50]
| (4) | |||||
The quadratic and quartic coefficients can be explicitly calculated starting from the microscopic Hamiltonian given in Eq. (1) by integrating out the electronic degrees of freedom [51, 52, 53, 54, 55, 56] (see Sec. I of the Supplementary Material for details). Depending on the coefficients, the free energy stabilizes the state or different types of PDW states. First, the free energy stabilizes the PDW states if the minimum of is located at , i.e., . The wavevector determines the center of mass momentum that the Cooper pair carries in the ground state. Second, the system selects one of the symmetrically distinct PDW states depending on the quartic coefficients. In Table. 1, we list all possible PDW states which include inversion-breaking ones: the FF and FF* state. For these, the system may display a non-reciprocal superconducting current, since the time-reversal symmetry is broken by the AM and the inversion symmetry is spontaneously broken by the superconducting PDW. It is also worthwhile to note that the free energy contains a symmetry where two additional symmetries come from translation invariance along the and directions. As a result, the PDW states can induce fractional vortices except for the FF state as pointed out in Ref. 50.
| State | Stability [50] | Inversion | Diode direction | |
| Fulde–Ferrell | , | X | ||
| (FF) | ||||
| Fulde–Ferrell* | X | |||
| (FF*) | ||||
| Uni-directional | O | none | ||
| (UD) | ||||
| Bi-directional-I | , | O | none | |
| (BD-I) | ||||
| Bi-directional-II | , | O | none | |
| (BD-II) |
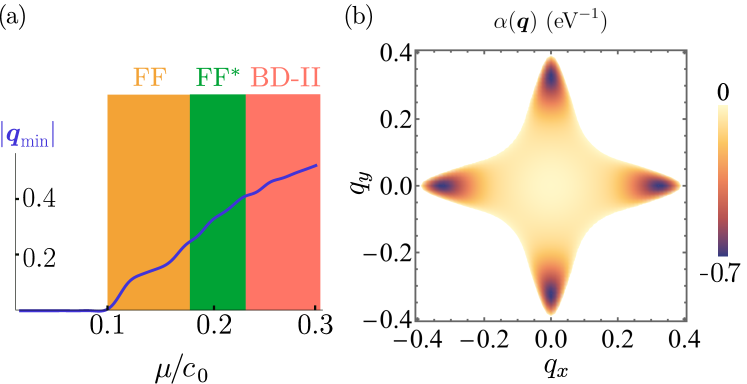
To investigate whether the system stabilizes PDW and which ones, we calculate the coefficients of the free energy, and . We obtain the phase diagram for varying as shown in Fig. 2(a). When , the minimum of is located at and the system selects the state. The system starts to stabilize the PDW state when . Within such a regime, the ordering wavevector is finite, , and gradually increases as increases, reflecting the size of the normal Fermi surface as shown in Fig. 2(a). In Fig. 2(b), we plot with which clearly shows that and the ordering wavevectors lie on the and axes and are fourfold degenerate. The degeneracy originates from the magnetic fourfold rotational symmetry.
When , the quartic coefficients satisfy the following relations given in Table. 1: , , and . Within such a regime, the system selects the FF state with the order parameter which spontaneously breaks the inversion symmetry. Here we highlight that the realization of the FF state in AM does not require an external magnetic field unlike the original proposal given in Ref. 57 and Rashba spin-orbit coupled systems [58, 59, 60]. At the same time, the inversion symmetry of the system is spontaneously broken by the superconducting state, unlike the Rashba systems where the inversion is broken by the spin-orbit coupling.
For , the system stabilizes the FF* state with which also breaks the inversion symmetry. Unlike the FF state, the order parameter of the FF* state has two phase parameters, and . As a result, the system can have a half-quantum vortex as a defect though careful comparison between the energy of the conventional vortex and the half-quantum vortex will be needed [50]. When , the system selects the so-called BD-II state with which preserves the inversion symmetry.
Diode effect in PDW.— In the following, we consider the supercurrent diode effect as a tool to distinguish the different forms of PDW states. Near the superconducting phase transition temperature, the formation of the PDW states can be described phenomenologically by a Ginzburg–Landau functional , with the free energy density which can be spatially homogeneous given by
Here, is the covariant derivative. The supercurrent can be derived from Eq. (LABEL:eq:free_real) by standard means [61, 62, 63, 64], by varying the free energy concerning the vector potential and subsequently enforcing , yielding the following result (see Sec. II of the Supplementary Material for details):
Here, we included contributions from the fourth order derivatives as they are crucial for ensuring the stability of the ground state [62, 63].
For the FF state with and , the supercurrent is given by
| (7) |
For the FF* state with , , and , the supercurrent is written as
| (8) |
For both cases, the supercurrent vanishes at and . We want to emphasize that the FF* state can induce a non-reciprocal supercurrent concurrently in both the and directions unlike the FF state, which can induce the non-reciprocal current only in the direction. Other PDW states, which include UD, BD-I, and BD-II states, cannot induce the non-reciprocal current, since they preserve the inversion symmetry.
In equilibrium , where is the free energy given in Eq. (4), leading to for the FF state and for the FF* state. At the same time, which does not contain linear nor cubic terms unlike the Rashba systems with external magnetic field considered in Ref. 40 and Ref. 42. Then one can rewrite the supercurrent as
| (9) |
for the FF state and
| (10) |
for the FF* state. We note that the supercurrent formula in Eq. (9) has the same form as the one given in Ref. 40 for the FF state in Rashba spin-orbit coupled systems.
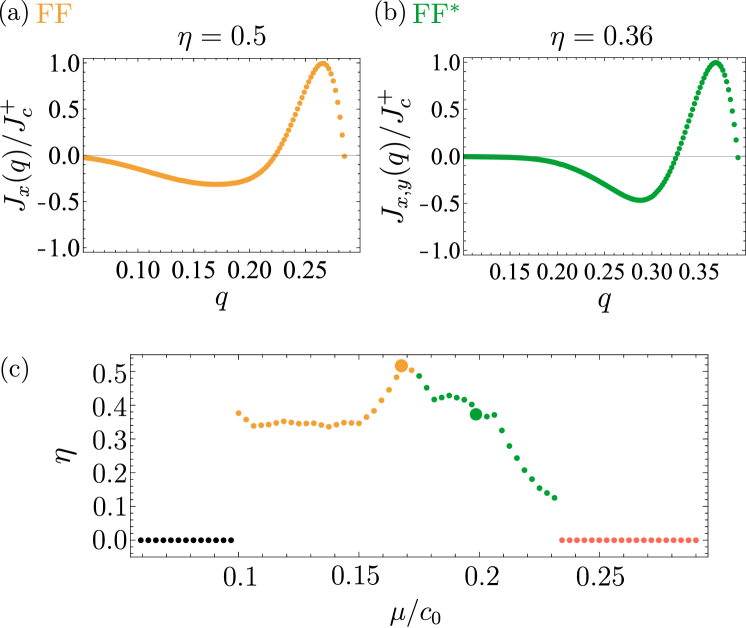
In Fig. 3(a), we plot the supercurrent along direction for the FF state stabilized for , using Eq. (9). It shows the nonreciprocity of the critical current; the maximum and the minimum are different around the , where the supercurrent vanishes. Using Eq. (10), we also plot the current relation for , where the system stabilizes the FF* state, in Fig. 3(b). Unlike the FF state, the FF* state induces the non-reciprocal current in both the and directions.
The non-reciprocal nature of the supercurrent can be conveniently quantified by a diode coefficient [40] which is defined as
| (11) |
In Fig. 3(c), we plot the coefficient as a function of . When , the system selects the state preserving the inversion symmetry with vanishing . For , one of the inversion breaking states, i.e., FF state and FF* state, is stabilized and becomes finite. When , becomes zero again, since the system stabilizes the BD-II state and preserves the inversion symmetry. Overall, the supercurrent diode effect can be utilized to detect different types of PDW states in future experiments.
Summary and outlook.— We have studied bulk superconductivity in a two-dimensional metallic system with -wave AM spin splitting in momentum space. We focused on the emergence of superconductivity driven by onsite attractive interactions analyzed through a microscopically derived Ginzburg–Landau theory. We find that symmetrically distinct PDW states can be stabilized as a function of varying chemical potential , including the inversion-breaking FF and FF* states. We then investigated the supercurrent properties and found a non-zero non-reciprocity; i.e. the FF state induces a non-reciprocal supercurrent in one direction, while the FF* state can induce it in two orthogonal directions.
There have been many theoretical proposals for realizing superconductivity of different types in AM [35, 36]. In the future it would worthwhile to explore PDW formation with different pairing symmetries and potential topological properties, for example with spin-triplet pairing or in the presence of Rashba spin-orbit coupling [33]. Beyond collinear AM other real space non-collinear spin textures might show similar effects [65].
Recent research has identified several promising material candidates for studying the interplay between altermagnetism and superconductivity. RuO2 thin films, which exhibit d-wave altermagnetic characteristics with momentum-dependent spin splitting and zero net magnetization, demonstrate superconductivity under strain [38, 39]. Hole-doped La2CuO4, known for high-temperature superconductivity, offers a rich context for exploring PDW states and the supercurrent diode effect [66]. While other metallic altermagnets, such as KRu4O8 [5], MnTe [67], and CrSb [68], have not yet shown superconductivity, they could be tuned via pressure or proximity effects. These materials, supported by microscopic theoretical modelling, provide exciting opportunities for experimental realisation of non-reciprocal effects of superconductivity.
Acknowledgements.— We thank P. Rao, J. Habel, M. J. Park, V. Leeb, R.-X. Zhang, and L. Šmejkal for insightful discussions related to this work. We acknoweldge M. Scheurer, I. Eremin, R. Fernandes, and D. Agterberg for comments on the manuscript. We especially thank D. Agterberg for pointing out an earlier flaw in the derivation of Eq. (7). G.B.S. is funded by the European Research Council (ERC) under the European Unions Horizon 2020 research and innovation program (grant agreement No. 771537). J. K. acknowledges support from the Imperial-TUM flagship partnership. The research is part of the Munich Quantum Valley, which is supported by the Bavarian state government with funds from the Hightech Agenda Bayern Plus. G.B.S was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) (RS-2024-00453943).
I Supplementary Material
I.1 I. Ginzburg-Landau free energy and one-loop expansion
In this section, we compute the quadratic and quartic coefficients in the Ginzburg-Landau free energy and see how the symmetrically distinct pair density waves (PDW) states are stabilized. We first introduce the free electron and hole propagator
| (S1) |
where is the Matsubara frequency with being the temperature. The non-interacting Hamiltonian given in the main text is written as
| (S2) |
where and denote the strength of the altermagnetism and the chemical potential respectively. The Ginzburg-Landau free energy for the PDW states in our system, which respects gauge, translational, inversion, and magnetic fourfold rotational symmetries, is written as
| (S3) |
where
| (S4) |
Here, The PDW order parameter is written as with the corresponding wavevectors . Ref. 50, 16, 66 provided an identical free energy for a system with the fourfold rotational symmetry of a square lattice. For later simplicity, we rewrite it as
| (S5) |
The quadratic coefficient in Eq. (S5) is given as [51, 52]
| (S6) |
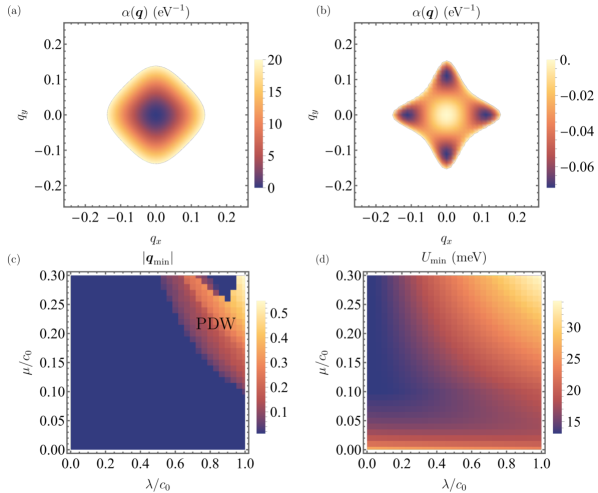
Here, the sum over is done near the Fermi level within regions bounded by the Debye frequency . In this work, we set meV, meV, and K. We plot for , , and meV using Eq. (S6) in Fig. S1(a). The minimum is located at . In Fig. S1(b), we plot for , , and meV. The minimum is located at and the system selects the PDW state, which carries the finite center of mass momentum. We also obtain the phase diagram as shown in Fig. S1(c), which indicates the emergence of PDW states in the presence of band splitting caused by the altermagnetism. In Fig. S1(d), we plot , absolute value of the second term in Eq. (S6). It corresponds to minimum strength of attractive interaction, , required to stabilize the superconducting state.
The quartic coefficients in Eq. (S5) are written as
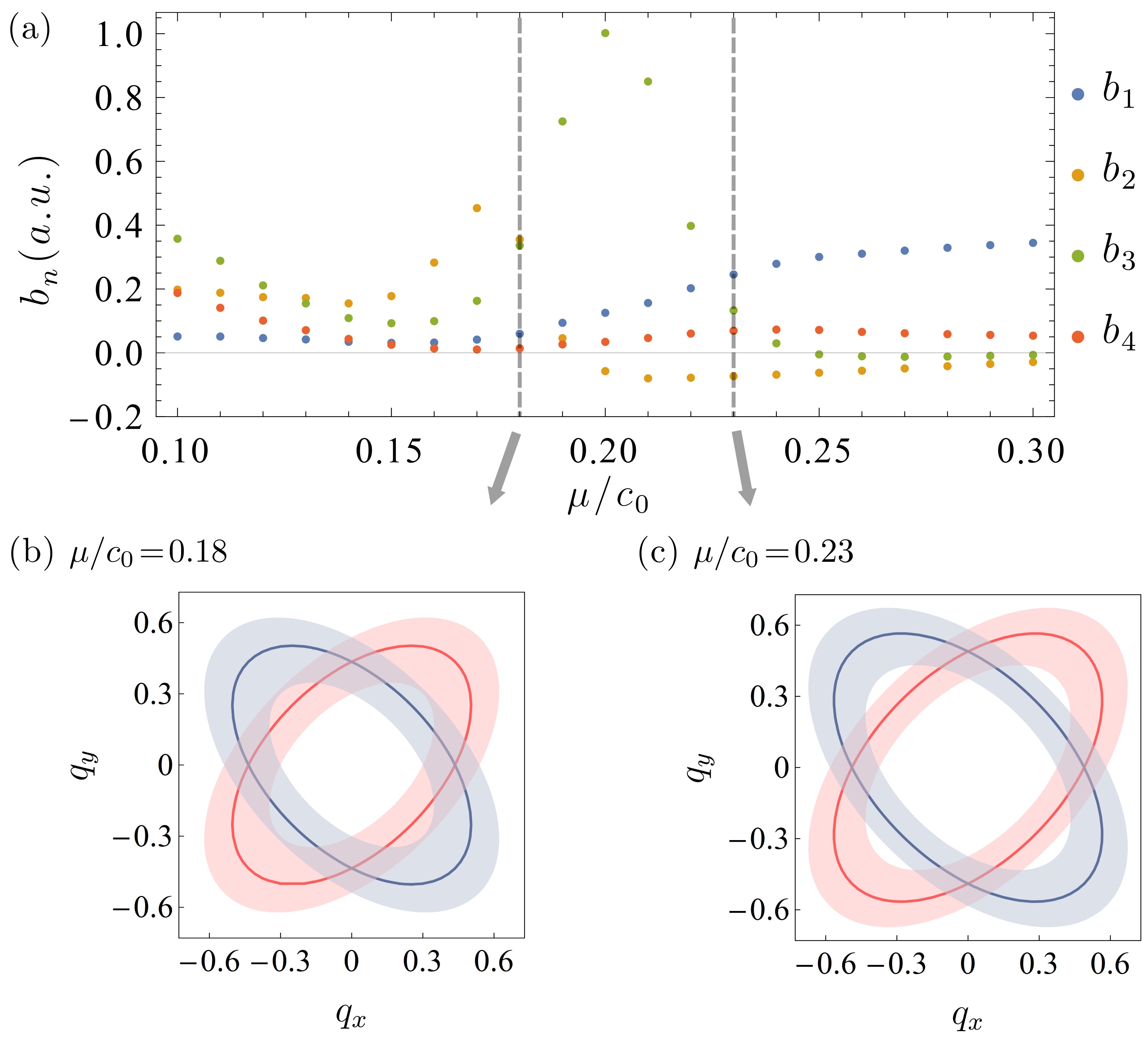
where the symmetry factor 4 is coming from the cyclic permutation of the trace. Utilizing Eq. (LABEL:eq:s_quartic), we plot the quartic coefficients in Fig. S2(a) for while varying , corresponding precisely to the parameter regime outlined in the main text. Depending on the value of the coefficients, the system stabilizes symmetrically distinct PDW states.
I.2 II. The diode effect in inversion breaking states
Here we formulate the supercurrent in PDW states starting from the Ginzburg-Landau functional. The free energy density in real space is written as
| (S8) |
where is the covariant derivative and is the external magnetic field. To minimize with respect to , we make the substitution in Eq. (S8) and collect the linear terms in :
| (S10) | |||||
where we have used in Eq. (LABEL:eq:s_free_1) and Gauss’s theorem in Eq. (S10). Here, includes terms up to first order in , and includes terms up to third order in . Below, we use the London gauge, where in the interior of the bulk superconductor, and discard such terms. At the minimum, the coefficient of the linear terms in must vanish. Then we obtain
With the Ampere’s law we find
| (S12) |
I.3 III. Leading pairing instability: -wave versus -wave
In the main text, we focus on the case where -wave pairing dominates over other symmetry channels. In this section, we investigate whether this dominance persists when the -wave component of the attractive interaction is present, and explore how the leading pairing symmetry changes depending on the relative interaction strengths.
We consider a general spin-singlet pairing interaction of the form
| (S13) |
where denotes the attractive interaction strength in the pairing channel labeled by , and is the corresponding form factor. We focus on the spin-singlet -wave and -wave channels, with form factors given by
| (S14) | ||||
| (S15) | ||||
| (S16) |
Below, we set for simplicity. The order parameter in each pairing channel is defined as the expectation value of the Cooper pair field:
| (S17) |
where is the center-of-mass momentum of the pair, and is the complex amplitude of the spin-singlet PDW state in the -wave channel.
To determine the leading pairing instability, we follow the one-loop expansion method described in Section I of the Supplemental Material. In particular, the quadratic coefficient for each pairing channel is computed using
| (S18) |
where the Matsubara frequency sum and momentum integral are performed near the Fermi surface within an energy window set by the Debye cutoff . For each point in the plane, we evaluate and and identify the pairing channel with the lowest value of at its global minimum . Figure S3(a) shows the result for meV and meV. In this case, the -wave channel remains dominant across the entire parameter range. This regime, where , corresponds to the situation considered in the main text. In contrast, when is increased to meV, as shown in Fig. S3(b), the -wave channel becomes the leading instability in a broad region of the phase diagram.
These results show that the leading pairing symmetry depends sensitively on the relative strength of the attractive interactions in the -wave and -wave channels. Even within the spin-singlet sector, sufficiently strong anisotropic attraction can favor a -wave order parameter over the -wave state as proposed in Refs. 35, 37.
References
- White et al. [1983] R. M. White, R. M. White, and B. Bayne, Quantum theory of magnetism, Vol. 1 (Springer, 1983).
- Fazekas [1999] P. Fazekas, Lecture notes on electron correlation and magnetism, Vol. 5 (World scientific, 1999).
- Yuan et al. [2020] L.-D. Yuan, Z. Wang, J.-W. Luo, E. I. Rashba, and A. Zunger, Giant momentum-dependent spin splitting in centrosymmetric low-z antiferromagnets, Physical Review B 102, 014422 (2020).
- Šmejkal et al. [2020] L. Šmejkal, R. González-Hernández, T. Jungwirth, and J. Sinova, Crystal time-reversal symmetry breaking and spontaneous hall effect in collinear antiferromagnets, Science advances 6, eaaz8809 (2020).
- Šmejkal et al. [2022a] L. Šmejkal, J. Sinova, and T. Jungwirth, Beyond conventional ferromagnetism and antiferromagnetism: A phase with nonrelativistic spin and crystal rotation symmetry, Physical Review X 12, 031042 (2022a).
- Šmejkal et al. [2022b] L. Šmejkal, J. Sinova, and T. Jungwirth, Emerging research landscape of altermagnetism, Physical Review X 12, 040501 (2022b).
- Feng et al. [2022] Z. Feng, X. Zhou, L. Šmejkal, L. Wu, Z. Zhu, H. Guo, R. González-Hernández, X. Wang, H. Yan, P. Qin, et al., An anomalous hall effect in altermagnetic ruthenium dioxide, Nature Electronics 5, 735 (2022).
- Steward et al. [2023] C. R. Steward, R. M. Fernandes, and J. Schmalian, Dynamic paramagnon-polarons in altermagnets, Physical Review B 108, 144418 (2023).
- Fernandes et al. [2024] R. M. Fernandes, V. S. de Carvalho, T. Birol, and R. G. Pereira, Topological transition from nodal to nodeless zeeman splitting in altermagnets, Phys. Rev. B 109, 024404 (2024).
- Leeb et al. [2024] V. Leeb, A. Mook, L. Šmejkal, and J. Knolle, Spontaneous formation of altermagnetism from orbital ordering, Physical Review Letters 132, 236701 (2024).
- Das et al. [2024] P. Das, V. Leeb, J. Knolle, and M. Knap, Realizing altermagnetism in fermi-hubbard models with ultracold atoms, Physical Review Letters 132, 263402 (2024).
- Rao et al. [2024] P. Rao, A. Mook, and J. Knolle, Tunable band topology and optical conductivity in altermagnets, Physical Review B 110, 024425 (2024).
- Bergeret et al. [2005] F. Bergeret, A. F. Volkov, and K. B. Efetov, Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures, Reviews of modern physics 77, 1321 (2005).
- Scalapino [2012] D. J. Scalapino, A common thread: The pairing interaction for unconventional superconductors, Reviews of Modern Physics 84, 1383 (2012).
- Dai et al. [2012] P. Dai, J. Hu, and E. Dagotto, Magnetism and its microscopic origin in iron-based high-temperature superconductors, Nature Physics 8, 709 (2012).
- Fradkin et al. [2015] E. Fradkin, S. A. Kivelson, and J. M. Tranquada, Colloquium: Theory of intertwined orders in high temperature superconductors, Reviews of Modern Physics 87, 457 (2015).
- Demler et al. [1997] E. A. Demler, G. Arnold, and M. Beasley, Superconducting proximity effects in magnetic metals, Physical Review B 55, 15174 (1997).
- Ryazanov et al. [2001] V. Ryazanov, V. Oboznov, A. Y. Rusanov, A. Veretennikov, A. A. Golubov, and J. Aarts, Coupling of two superconductors through a ferromagnet: Evidence for a junction, Physical review letters 86, 2427 (2001).
- Kontos et al. [2002] T. Kontos, M. Aprili, J. Lesueur, F. Genêt, B. Stephanidis, and R. Boursier, Josephson junction through a thin ferromagnetic layer: negative coupling, Physical review letters 89, 137007 (2002).
- Ouassou et al. [2023] J. A. Ouassou, A. Brataas, and J. Linder, dc josephson effect in altermagnets, Physical Review Letters 131, 076003 (2023).
- Beenakker and Vakhtel [2023] C. Beenakker and T. Vakhtel, Phase-shifted andreev levels in an altermagnet josephson junction, Physical Review B 108, 075425 (2023).
- Papaj [2023] M. Papaj, Andreev reflection at the altermagnet-superconductor interface, Phys. Rev. B 108, L060508 (2023).
- Zhang et al. [2024] S.-B. Zhang, L.-H. Hu, and T. Neupert, Finite-momentum cooper pairing in proximitized altermagnets, Nature Communications 15, 1801 (2024).
- Wei et al. [2024] M. Wei, L. Xiang, F. Xu, L. Zhang, G. Tang, and J. Wang, Gapless superconducting state and mirage gap in altermagnets, Physical Review B 109, L201404 (2024).
- Giil and Linder [2024] H. G. Giil and J. Linder, Superconductor-altermagnet memory functionality without stray fields, Physical Review B 109, 134511 (2024).
- Sun et al. [2023] C. Sun, A. Brataas, and J. Linder, Andreev reflection in altermagnets, Physical Review B 108, 054511 (2023).
- Ghorashi et al. [2024] S. A. A. Ghorashi, T. L. Hughes, and J. Cano, Altermagnetic routes to majorana modes in zero net magnetization, Physical Review Letters 133, 106601 (2024).
- Li and Liu [2023] Y.-X. Li and C.-C. Liu, Majorana corner modes and tunable patterns in an altermagnet heterostructure, Physical Review B 108, 205410 (2023).
- Maeda et al. [2024] K. Maeda, B. Lu, K. Yada, and Y. Tanaka, Theory of tunneling spectroscopy in unconventional p-wave magnet-superconductor hybrid structures, Journal of the Physical Society of Japan 93, 114703 (2024).
- Lu et al. [2024] B. Lu, K. Maeda, H. Ito, K. Yada, and Y. Tanaka, josephson junction induced by altermagnetism, Physical Review Letters 133, 226002 (2024).
- Brekke et al. [2023] B. Brekke, A. Brataas, and A. Sudbø, Two-dimensional altermagnets: Superconductivity in a minimal microscopic model, Physical Review B 108, 224421 (2023).
- Mæland et al. [2024] K. Mæland, B. Brekke, and A. Sudbø, Many-body effects on superconductivity mediated by double-magnon processes in altermagnets, Physical Review B 109, 134515 (2024).
- Zhu et al. [2023] D. Zhu, Z.-Y. Zhuang, Z. Wu, and Z. Yan, Topological superconductivity in two-dimensional altermagnetic metals, Phys. Rev. B 108, 184505 (2023).
- Sumita et al. [2023] S. Sumita, M. Naka, and H. Seo, Fulde-ferrell-larkin-ovchinnikov state induced by antiferromagnetic order in -type organic conductors, Physical Review Research 5, 043171 (2023).
- Chakraborty and Black-Schaffer [2024a] D. Chakraborty and A. M. Black-Schaffer, Zero-field finite-momentum and field-induced superconductivity in altermagnets, Physical Review B 110, L060508 (2024a).
- Bose et al. [2024] A. Bose, S. Vadnais, and A. Paramekanti, Altermagnetism and superconductivity in a multiorbital t-j model, Physical Review B 110, 205120 (2024).
- Hong et al. [2025] S. Hong, M. J. Park, and K.-M. Kim, Unconventional p-wave and finite-momentum superconductivity induced by altermagnetism through the formation of bogoliubov fermi surface, Physical Review B 111, 054501 (2025).
- Uchida et al. [2020] M. Uchida, T. Nomoto, M. Musashi, R. Arita, and M. Kawasaki, Superconductivity in uniquely strained ruo 2 films, Physical Review Letters 125, 147001 (2020).
- Ruf et al. [2021] J. P. Ruf, H. Paik, N. J. Schreiber, H. P. Nair, L. Miao, J. K. Kawasaki, J. N. Nelson, B. D. Faeth, Y. Lee, B. H. Goodge, et al., Strain-stabilized superconductivity, Nature Communications 12, 59 (2021).
- Yuan and Fu [2022] N. F. Yuan and L. Fu, Supercurrent diode effect and finite-momentum superconductors, Proceedings of the National Academy of Sciences 119, e2119548119 (2022).
- He et al. [2022] J. J. He, Y. Tanaka, and N. Nagaosa, A phenomenological theory of superconductor diodes, New Journal of Physics 24, 053014 (2022).
- Daido et al. [2022] A. Daido, Y. Ikeda, and Y. Yanase, Intrinsic superconducting diode effect, Physical Review Letters 128, 037001 (2022).
- Scammell et al. [2022] H. D. Scammell, J. Li, and M. S. Scheurer, Theory of zero-field superconducting diode effect in twisted trilayer graphene, 2D Materials 9, 025027 (2022).
- Lu et al. [2023] B. Lu, S. Ikegaya, P. Burset, Y. Tanaka, and N. Nagaosa, Tunable josephson diode effect on the surface of topological insulators, Physical Review Letters 131, 096001 (2023).
- Cayao et al. [2024] J. Cayao, N. Nagaosa, and Y. Tanaka, Enhancing the josephson diode effect with majorana bound states, Physical Review B 109, L081405 (2024).
- Banerjee and Scheurer [2024] S. Banerjee and M. S. Scheurer, Altermagnetic superconducting diode effect, Physical Review B 110, 024503 (2024).
- González-Hernández et al. [2021] R. González-Hernández, L. Šmejkal, K. Vỳbornỳ, Y. Yahagi, J. Sinova, T. Jungwirth, and J. Železnỳ, Efficient electrical spin splitter based on nonrelativistic collinear antiferromagnetism, Physical Review Letters 126, 127701 (2021).
- Chakraborty and Black-Schaffer [2024b] D. Chakraborty and A. M. Black-Schaffer, Constraints on superconducting pairing in altermagnets, arXiv preprint arXiv:2408.03999 (2024b).
- de Carvalho and Freire [2024] V. S. de Carvalho and H. Freire, Unconventional superconductivity in altermagnets with spin-orbit coupling, Physical Review B 110, L220503 (2024).
- Agterberg and Tsunetsugu [2008] D. Agterberg and H. Tsunetsugu, Dislocations and vortices in pair-density-wave superconductors, Nature Physics 4, 639 (2008).
- Radzihovsky [2011] L. Radzihovsky, Fluctuations and phase transitions in larkin-ovchinnikov liquid-crystal states of a population-imbalanced resonant fermi gas, Physical Review A 84, 023611 (2011).
- Soto-Garrido and Fradkin [2014] R. Soto-Garrido and E. Fradkin, Pair-density-wave superconducting states and electronic liquid-crystal phases, Physical Review B 89, 165126 (2014).
- Liu [2017] C.-X. Liu, Unconventional superconductivity in bilayer transition metal dichalcogenides, Physical review letters 118, 087001 (2017).
- Hu et al. [2019] L.-H. Hu, C.-X. Liu, and F.-C. Zhang, Topological larkin-ovchinnikov phase and majorana zero mode chain in bilayer superconducting topological insulator films, Communications Physics 2, 25 (2019).
- Sim et al. [2020] G. Sim, A. Mishra, M. J. Park, Y. B. Kim, G. Y. Cho, and S. Lee, Multipolar superconductivity in luttinger semimetals, Physical Review Research 2, 023416 (2020).
- Sim et al. [2022] G. Sim, M. J. Park, and S. Lee, Topological triplet-superconductivity in spin-1 semimetal, Communications Physics 5, 220 (2022).
- Fulde and Ferrell [1964] P. Fulde and R. A. Ferrell, Superconductivity in a strong spin-exchange field, Physical Review 135, A550 (1964).
- Agterberg and Kaur [2007] D. Agterberg and R. Kaur, Magnetic-field-induced helical and stripe phases in rashba superconductors, Physical Review B 75, 064511 (2007).
- Dimitrova and Feigel’Man [2007] O. Dimitrova and M. Feigel’Man, Theory of a two-dimensional superconductor with broken inversion symmetry, Physical Review B 76, 014522 (2007).
- Agterberg [2012] D. Agterberg, Magnetoelectric effects, helical phases, and fflo phases, Non-Centrosymmetric Superconductors: Introduction and Overview , 155 (2012).
- Kopnin [2001] N. B. Kopnin, Theory of nonequilibrium superconductivity, Vol. 110 (Oxford University Press, 2001).
- Samokhin and Truong [2017] K. Samokhin and B. Truong, Current-carrying states in fulde-ferrell-larkin-ovchinnikov superconductors, Physical Review B 96, 214501 (2017).
- Samokhin and Truong [2019] K. Samokhin and B. Truong, Fulde-ferrell-larkin-ovchinnikov superconductors near a surface, Physical Review B 99, 014503 (2019).
- Yerin et al. [2023] Y. Yerin, S.-L. Drechsler, M. Cuoco, and C. Petrillo, Multiple-q current states in a multicomponent superconducting channel, Journal of Physics: Condensed Matter 35, 505601 (2023).
- Lee et al. [2024] S. H. Lee, Y. Qian, and B.-J. Yang, Fermi surface spin texture and topological superconductivity in spin-orbit free noncollinear antiferromagnets, Physical Review Letters 132, 196602 (2024).
- Agterberg et al. [2020] D. F. Agterberg, J. S. Davis, S. D. Edkins, E. Fradkin, D. J. Van Harlingen, S. A. Kivelson, P. A. Lee, L. Radzihovsky, J. M. Tranquada, and Y. Wang, The physics of pair-density waves: Cuprate superconductors and beyond, Annual Review of Condensed Matter Physics 11, 231 (2020).
- Krempaskỳ et al. [2024] J. Krempaskỳ, L. Šmejkal, S. D’Souza, M. Hajlaoui, G. Springholz, K. Uhlířová, F. Alarab, P. Constantinou, V. Strocov, D. Usanov, et al., Altermagnetic lifting of kramers spin degeneracy, Nature 626, 517 (2024).
- Reimers et al. [2024] S. Reimers, L. Odenbreit, L. Šmejkal, V. N. Strocov, P. Constantinou, A. B. Hellenes, R. Jaeschke Ubiergo, W. H. Campos, V. K. Bharadwaj, A. Chakraborty, et al., Direct observation of altermagnetic band splitting in crsb thin films, Nature Communications 15, 2116 (2024).