Department of Information and Computing Sciences, Utrecht University, the NetherlandsH.L.Bodlaender@uu.nlhttps://orcid.org/0000-0002-9297-3330 Department of Information and Computing Sciences, Utrecht University, the Netherlands and Mathematical Institute, Utrecht University, the NetherlandsM.vanderWegen@uu.nlhttps://orcid.org/0000-0003-0899-6925 \ccsdescComputing methodologies Planning and scheduling \ccsdescTheory of computation Fixed parameter tractability \ccsdescTheory of computation Parameterized complexity and exact algorithms \CopyrightHans L. Bodlaender and Marieke van der Wegen
Acknowledgements.
We would like to thank Sukanya Pandey for helpful discussions. \hideLIPIcsParameterized Complexity of Scheduling Chains of Jobs with Delays
Abstract
In this paper, we consider the parameterized complexity of the following scheduling problem. We must schedule a number of jobs on machines, where each job has unit length, and the graph of precedence constraints consists of a set of chains. Each precedence constraint is labelled with an integer that denotes the exact (or minimum) delay between the jobs. We study different cases; delays can be given in unary and in binary, and the case that we have a single machine is discussed separately. We consider the complexity of this problem parameterized by the number of chains, and by the thickness of the instance, which is the maximum number of chains whose intervals between release date and deadline overlap.
We show that this scheduling problem with exact delays in unary is -hard for all , when parameterized by the thickness, even when we have a single machine (). When parameterized by the number of chains, this problem is -complete when we have a single or a constant number of machines, and -complete when the number of machines is a variable. The problem with minimum delays, given in unary, parameterized by the number of chains (and as a simple corollary, also when parameterized by the thickness) is -hard for a single or a constant number of machines, and -hard when the number of machines is variable.
With a dynamic programming algorithm, one can show membership in XP for exact and minimum delays in unary, for any number of machines, when parameterized by thickness or number of chains. For a single machine, with exact delays in binary, parameterized by the number of chains, membership in XP can be shown with branching and solving a system of difference constraints. For all other cases for delays in binary, membership in XP is open.
keywords:
Scheduling, parameterized complexity1 Introduction
In this paper, we study a problem in the field of parameterized complexity of scheduling problems. Here, we look at scheduling jobs with precedence constraints with exact or minimum delays, and assume that jobs have unit length. We study one of the simplest types of precedence constraint graphs: we assume that the precedences form a collection of disjoint chains. Chains have a release date and deadline. It is not hard to see (by a simple reduction from 3-Partition) that this problem is NP-hard, even when all delays are 0. In this paper, we study the parameterized complexity of the problem, and look at two different parameters: the number of chains, and the thickness of the instance — that is, the maximum number of chains that have overlapping intervals from release time to deadline. We look at different variants: a constraint gives an exact bound or a lower bound on the delay between successive jobs; we can have one, a constant, or a variable number of machines, and the delays can be given in unary or binary notation. If delays are given in unary, then each of the studied variants belongs to XP, and is hard for (or classes higher in the -hierarchy.) For one variation (see below), we also show membership in XP when delays are given in binary. We call the studied problems Chain Scheduling with Exact Delays and Chain Scheduling with Minimum Delays, for details see Section 2.
1.1 Related literature.
Looking at variants of scheduling problems with special attention to parameters (like the number of available machines) is a common approach in the rich field of study of scheduling problems. Studying such parameterizations using techniques and terminology from the field of parameterized algorithms and complexity was pioneered in 1995 [3], but recently receives growing attention, e.g. [2, 10, 12].
The scheduling of chains of jobs (without delays) was studied by Woeginger [14] and Bruckner [4], who gave respectively a 2-approximation algorithm, and a linear time algorithm for two machines. General precedence graphs with delays between jobs was studied already in 1992 by Wikum et al. [13]; this was followed by a large body of literature, studying different variations and approaches, including theoretical and experimental studies.
1.2 A different interpretation
The problem we studied can also be interpreted as another type of scheduling problem. Now, we let each chain represent one job: this job only occasionally needs to use the machine (or some specific resource) — at the other time steps, the job is running but does not need a resource. E.g., if we have a chain with delays 2 and 3, then, we can interpret this as a job that needs a resource at its first, fourth, and eighth time step. The variant with minimum delays now has as interpretation that we allow pre-emption, i.e., jobs can be halted at some time steps and resumed later.
1.3 Our results
| parameter | exact delays | minimum delays | |
|---|---|---|---|
| Single machine | thickness | -hard for all | -hard |
| chains | -complete | -hard | |
| Constant number | thickness | -hard for all | -hard |
| of machines | chains | -complete | -hard |
| Variable number | thickness | -hard for all | -hard |
| of machines | chains | -complete | -hard |
In this paper, we give a number of hardness results, which are summarized in Table 1. All variants are already hard when the (exact or minimum) delays are given in unary. We also give the following algorithmic results:
-
•
With a dynamic programming algorithm, one can show that the Chain Scheduling with Exact Delays and Chain Scheduling with Minimum Delays belong to XP, when delays are given in unary, and parameterized by either thickness or number of chains, for any number of machines.
-
•
Combining branching with solving a set of difference constraints shows XP-membership of Chain Scheduling with Exact Delays when parameterized by number of chains, for the case of one machines, when delays are given in binary.
For all other cases, the membership in XP when delays are given in binary is open.
1.4 Organization of this paper
In Section 2, we give a number of preliminary definitions. Section 3 gives hardness proofs for Chain Scheduling with Exact Delays when parameterized by the thickness. The complexity of Chain Scheduling with Exact Delays parameterized by the number of chains is established in Section 4; a relatively simple modification then gives hardness for the corresponding problems with minimum delays. Section 5 gives our algorithmic results (membership in XP). Some conclusions are given in Section 6.
2 Preliminaries
We first describe the problems we study in more details. We have a number of identical machines . In the paper, we study separately the cases that we have a single machine (), the number of machines is some fixed constant, or the number of machines is variable.
On these machines, we must schedule jobs. Each job has unit length. On the set of jobs, we have a collection of precedence constraints. Each precedence constraint is an ordered pair of jobs : it tells that job cannot be started before job is completed. We say that is a direct predecessor of , and is a predecessor of if there is a directed path from to in the graph formed by the precedence constraints; then is a successor of .
The precedence constraints have associated with them a delay, denoted : each delay is a non-negative integer. We study two variations of the problem: exact delays and minimum delays. If we consider exact (resp. minimum) delays, then if constraint has delay then job must be started exactly (resp. at least) time steps after job was finished. That is: when job starts at time , then job starts at time exactly (resp. at least) . (Note that jobs run directly after each other, only if the delay is .) It is allowed to schedule a job on a different machine than its predecessor — thus, we do not need to specify on what machine a job is running, but only ensure that at each time step, the number of scheduled jobs is at most the number of available machines.
In this paper, we consider the case that the graph of the precedence constraints consists of a set of chains. I.e., each job has at most one direct predecessor and at most one direct successor. Chains are the maximal sets of jobs that are predecessors or successors of each other.
Each chain has a release date and a deadline . We have that the first job in the chain cannot start before time and the last job in the chain should be completed at or before time .
In this paper, we consider the following two parameterizations of the problem. The first is the number of chains, denoted by . The second is the thickness, denoted by , defined as follows. We say that two chains overlap, when their intervals have a non-empty intersection. We define the thickness to be the maximum size of a collection of chains that mutually overlap. That is, for any time , there are at most chains for which we have that and .
Chain Scheduling with Exact Delays is the problem where we are given as input the set of jobs with chains of precedence constraints, delays for each precedence constraint, release dates and deadlines of chains, and number of machines, and ask whether there exists a schedule that fulfills all the demands: at each time step, the number of jobs scheduled is at most the number of machines; jobs in a chain are not scheduled before the release date or after the deadline, and for each precedence constraint the delay between and is exactly .
As said, we study several variants of this problem: delays can be given in unary or binary, the number of machines can be 1, fixed or variable, and we can parameterize by the number of chains or by thickness. If we require that the stated delays are lower bounds, we obtain the Chain Scheduling with Minimum Delays problem: here, when we have a precedence contraint with delay , we must have that job starts at least time steps after job is finished.
For the -hardness proofs, we use reductions from the following version of the Satisfiability problem. A Boolean formula is said to be -normalized, if it is the conjunction of the disjunction of the conjunction of …of literals, with alternations of AND’s and OR’s.
The following parameterized problem was considered by Downey and Fellows [6].
Weighted -Normalized Satisfiability
Given: A -normalized Boolean formula and a positive integer .
Parameter:
Question: Can be satisfied by setting exactly variables to true?
3 Parameterization by thickness
In this section, we look at the Chain Scheduling with Exact Delays problem, when parameterized by the thickness . We will show, for several variations, that the problem is hard for the class , for all integers .
3.1 Parallel machines
We consider the version with parallel machines, where is part of the input. The delays are assumed to be exact.
We will give a reduction from Weighted -Normalized Satisfiablity. Assume we have a -normalized Boolean formula and integer . Let be the number of ‘levels’ of disjunction. We assume the variables of to be .
We make an instance of the Chain Scheduling with Exact Delays problem, with machines and thickness .
An element of the formula is either a literal, or a disjunction or conjunction of smaller elements. We will first assign to each element a size , and then to each element an integer interval. To each element, we associate an interval size; the interval size of formula is denoted by .
The interval size of a literal (i.e., a formula of the form or ) is . The interval size of a conjunction is the sum of the size of the terms, i.e., . For each disjunction of terms, its size is times the maximum size of its terms: define , and then .
To each element of we assign an integer interval with . We will do this top-down: first we assign an interval to , then we define a subinterval for every term of , etc.
To , we assign the interval . To elements of a conjunction and disjunction, we assign subintervals of the intervals assigned to the conjunction of disjunction, in such a way that these intervals have the same nesting as the elements in the formula.
Consider an element that is the conjunction . Then assign the interval ; the interval , etc. I.e., is assigned the interval .
Suppose element is the disjunction . The construction is similar to that of conjunctions, but now we assign each term the same length interval and keep unused intervals between the terms. Recall that . Assign to the interval .
Note the nesting of intervals, and that we assigned to each element an interval equal to its size. Also note that we can compute all intervals and sizes in polynomial time.
We now can describe the jobs, precedence constraints and release dates and deadlines.
For each , , we start a chain . Each of those chains start with a job and then a delay of . The first job of the chain is released at time 0. We will add jobs and specify delays between jobs in the chain such that the total processing time including the delay times is . Set the deadline of those chains to , so that the first job can start at times .
These chains reflect the variables that are set to true; more precisely, when the first job of one of the chains starts at a time , then this corresponds to setting to true. We call these the true variable chains.
To prevent two chains selecting the same variable, we add chains, each with jobs with delay , release date and deadline . We call those chains fill chains. Those chains have to be scheduled from time until time . This implies that at each time at most one other job can be schedules, thus at most one true variable chain starts. Hence, the true variable chains select exactly variable to be set to true.
We will now extend the true variable chains. Consider the interval from left to right.
-
•
For each timestep that we encounter that is not part of an interval that corresponds to a literal, we add a delay of at the end of the chain.
-
•
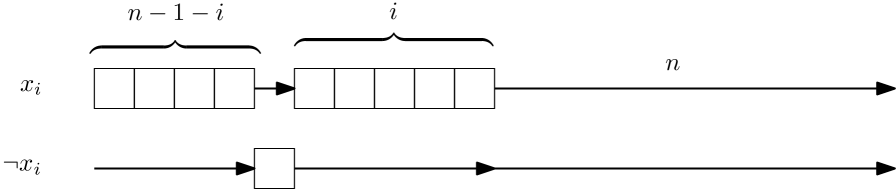
For each interval that corresponds to a positive literal , we add the following gadget to the chain: jobs with delay , then a delay of , then jobs with delay and then a delay of . (See Figure 1.) Notice that no job is scheduled from until if the chain starts at time , and there is a job scheduled at this time otherwise.
-
•
For each element of that is a negative literal , we make the following gadget: a delay of , a job, then a delay of , and then a delay of . (See Figure 1.) Notice that a job is scheduled from until if the chain starts at time , and there is no job scheduled at this time otherwise.
Add one job at the end of the chain. Notice that the total processing time of those chains is indeed .
To check whether variables are true, we add some chains that consist of a single job. We call those chains variable check chains.
-
•
For each element of that consists of a single positive literal (i.e., is of the form ), we make a chain with one job, that is released at time and has deadline .
-
•
For element of that consists of a single negative literal (i.e., is of the form ), we make a chains with one job, release date and deadline .
The intuition behind this construction is as follows: suppose that we have machines. For each element of that is of the form , there is one job scheduled from until . So for at least one of the true variable chains, we need that no job of this chain to be scheduled from until . This means that one of the true variable chains starts at time . For each element of that is of the form , there are job scheduled from until . So for none of the true variable chains we can schedule a job of this chain from until . This means that none of the true variable chains starts at time . The other machines take care of the disjunctions.
For each element of that is a disjunction, we make one chain. This chain has jobs with delay . The chain will be released at time and has deadline . We call those chains disjunction chains. Notice that for every element of that is a literal, there are exactly disjunction chains that overlap the interval , that is, there are exactly disjunction chains with release time at most and deadline at least .
We now have specified all jobs and the machines they run on. Note that the thickness of this construction is .
Claim 1.
If is satisfiable by setting exactly variables to true, then the Chain Scheduling with Exact Delays scheduling problem has a solution.
Proof 3.1.
Suppose is satisfiable by making variables true. For each , with , we let one true variable chain start at time .
First we introduce a notion satisfying, intuitively, this will be the elements that make true. We define this top-down. First we call satisfying. For each element of :
-
•
If is satisfying and is a conjunction , then all terms are satisfying.
-
•
If is satisfying and is a disjunction , then at least one is satisfied, say . We say that is satisfying, and the other term with are not satisfying.
-
•
If is not satisfying, all its terms are not satisfying.
For each element of that is a disjunction , consider the disjunction chain associated with this element. If is not satisfying, then start this chain arbitrarily, say at its release time. If is satisfying, let be its term that is satisfying. Now, start this chain at time , where is again the maximum interval size of the terms .
Now we will verify that is a feasible schedule, that is, that we never use more than machines.
First consider a time step from to , with . At this time step there are jobs of fill chains scheduled. Since the variables are different, the true variable chains start at different times. Hence, there is at most one job of a true variable chain scheduled at . Thus, there are at most jobs scheduled at time .
Consider a time step from to with , such that for all elements of that are literals. Notice that at those times no jobs of fill chains and variable check chains are scheduled. There are at most jobs of true variable chains scheduled at time step , since there are only true variable chains. And there are at most jobs of disjunction chains scheduled, since there are levels of disjunction. It follows that there are at most jobs scheduled at time step .
Consider a time step from to with , such that for an element of that is a literal. We distinguish three cases.
Suppose that is satisfying, and is a positive literal . Then we know that there are machines used for the disjunction chains. Besides, there is one machine used for the variable check chains. Since we know that is satisfying, is true. Thus one of the true variable chains starts at time . So this chain has no job scheduled from until . So at most true variable chains have a job scheduled from until . In total there are at most machines used.
Suppose that is satisfying, and is a negative literal, say . Then we know that there are machines used for the disjunction chains. There are machines used for the variable check chains. Since we know that is satisfying, is false. Thus none of the true variable chains starts at time . Hence, no true variable chain has a job scheduled from until . In total there are at most machines used from until .
Suppose that is not satisfying. Let be the last satisfying element on the path from to . The disjunction chain that corresponds to has no job that is scheduled form until . Hence, there are at most machines used for the disjunction chains from time until . It follows that there are machines for the true variable chains and the variable check chains. Since all true variable chains start at different times, those chains together have jobs that can be scheduled from until . We conclude that we used at most machines from time until .
Claim 2.
Suppose the Chain Scheduling with Exact Delays scheduling problem has a solution, then can be satisfied by setting exactly variables to true.
Proof 3.2.
For each true variable chain, if it starts at time , then set to true. All other variables are set to false, i.e, is true, if and only if there is a true variable chain that starts at time .
Note that all variable chains must start at different times, and they must start at times . If two of these start at the same time , then both have a job scheduled from until , but there are fill chains that have a job scheduled from until as well, which is a contradiction with the total number of machines. Thus, we have set exactly variables to true.
We claim that this setting makes true. We define elements of to be demonstrated in the following way, recursively. We say that is demonstrated.
-
•
If a conjunction is demonstrated, then all its terms are demonstrated.
-
•
If a disjunction is demonstrated, then we consider the corresponding disjunction chain . If for every time step in a job of is scheduled, we say that is demonstrated.
After this top-down definition of demonstrated elements, we will now inductively show bottom-up that demonstrated elements are satisfied by the setting of variables described above.
Consider a demonstrated element that is a literal. By the definition of demonstrated, of the disjunction chains have a job scheduled at each time step of . Consider the time step from until . We know that machines process a job of a disjunction chain at this time step, so at most machines process jobs of true variable chains and variable check chains.
Suppose that is a positive literal, say . Notice that one machine processes a check variable chain from until . So at most machines process a job of a true variable chain. Hence there must be at least one true variable chain that does not have a job scheduled at this time. By construction of the true variable chains, such a chain must start at time ; and thus we set to true, i.e., our setting satisfies the formula consisting of the single positive literal .
If is a negative literal , machines are processing check variable chains from until ; thus no true variable chain can have a job scheduled at this step. By construction of the true variable chains, this implies that no true variable chain starts at time , and thus is set to false. Hence, is satisfied.
Now consider a demonstrated element and assume, by induction, that for all its terms holds: if is demonstrated, then is true.
Suppose that that is a conjunction. All its terms are demonstrated, and by the induction hypothesis, all its terms are true. Thus the conjunction is also true.
Suppose that is a disjunction. Since the corresponding disjunction chain has length , there is at least one such that for every time step in a job of is scheduled. By definition, this is demonstrated. By induction, is true, and thus is true.
We conclude that is satisfied.
We now have shown:
Theorem 3.3.
The Chain Scheduling with Exact Delays problem, parameterized by the thickness , is -complete for all .
3.2 Single machine
Again, assume the delays are exact. We now show that the problem stays hard when there is only one machine.
Theorem 3.4.
The Chain Scheduling with Exact Delays problem, parameterized by the thickness , is -complete for all , when only machine is available.
Let be the thickness of the original instance. The main idea of the transformation is to replace each time step on machines by time steps on a single machine. Every chain will be assigned a number and its jobs will be scheduled at times , this will make sure that at every timestep only one job is scheduled. For every interval , we will have chains that have one job; this ensures that at at most time steps of the interval a job of a regular chain is scheduled. We now proceed with the formal description.
We transform from the case with machines (Theorem 3.3). Suppose we have an instance with machines. For every interval , we add additional chains, with a single job, release date and deadline . We call those chains extra.
We copy the chains from the given instance, except that:
-
•
If a chain has release date , then it now has release date .
-
•
If a chain has deadline , then it now has deadline .
-
•
Every delay is replaced by a delay .
We call these chains regular.
Claim 3.
Suppose we have a solution for the transformed instance with one machine. Then we have a solution for the original instance with machines.
Proof 3.5.
For each regular chain, let it start at time , when its transformed instance starts at time . This implies that for every job in the chain it will start at time , when its transformed instance starts at time . We know that for each time interval , steps are used for extra jobs, so time steps are available for jobs of regular chains. Thus, at every time step in the original instance, at most jobs are scheduled.
Claim 4.
Suppose we have a solution for the original instance with machines. Then we have a solution for the transformed instance with machine.
Proof 3.6.
We start with assigning a number to every chain such that for every time step all the chains that overlap this time step have different number. We denote this assignment by . We can do this as follows: go through time , and every time a chain is released, assign a number that is currently unused, if a deadline passes, the number of the corresponding chain becomes available again. We can do this with numbers, since by definition for every timestep there are at most chains that overlap this timestep.
For every regular chain , let start at time , where is the starting time of the corresponding original chain. Then chains of thickness number only have jobs starting at times with . For every time , all jobs that are scheduled to start at time in the original instance, will now be scheduled in the interval in the transformed instance. Those jobs are in different chains and those chains are assigned different numbers. Thus those jobs are scheduled at different times in the tranformed instance.
In the original instance, at each time at most chains have a job scheduled to start at , so, in the transformed instance, for each interval , at most regular chains have a job scheduled in this interval. Thus, we can schedule the extra chains in this time interval at the time steps where no job of a regular chain is scheduled.
3.3 Constant number of parallel machines
We can easily transform the single machine instance to an instance with a constant number of parallel machines. Let be the maximum deadline of all chains. Introduce new chains with jobs each and delays. The new machines will be processing those new chains, while the original machine processes the original chains. We conclude the following result.
Theorem 3.7.
The Chain Scheduling with Exact Delays problem with a fixed number of machines, parameterized by the thickness , is -complete for all .
3.4 Minimum delays
The proof above seems not to modifiable to the Chain Scheduling with Minimum Delays problem. In Section 4.4, we show that Chain Scheduling with Minimum Delays, parameterized by the number of chains is -hard when , and -hard when the number of machines is variable. As the thickness is at most the number of chains, it follows that Chain Scheduling with Minimum Delays, parameterized by the thickness is -hard for one machine, and -hard for a variable number of machines. Membership in or is open, however.
4 Parameterization by the number of chains
We now give the complexity results when we use the number of chains as parameter. In Sections 4.1, 4.2, and 4.3, we consider Chain Scheduling with Exact Delays, with the number of machines respectively 1, a constant, or variable. In Section 4.4, we consider Chain Scheduling with Exact Delays.
4.1 Single machine
In this section, we consider the variant where the number of chains is a parameter, and at each step in time, there is one machine available. We assume that the delays are exact.
Theorem 4.1.
The Chain Scheduling with Exact Delays problem, parameterized by the number of chains is -complete, when there is one machine.
Theorem 4.1 is proven by two transformations: from and to Independent Set with standard parameterization.
Lemma 4.2.
The Chain Scheduling with Exact Delays problem with one machine, parameterized by the number of chains , is -hard.
Proof 4.3.
A set of integers is said to be a Golomb ruler if all differences of two elements are unique, that is, for with and .
Erdös and Turán [9] gave the following explicit construction of a Golumb ruler. Let be a prime number. Then the set is a Golomb ruler with elements. We can build a Golumb ruler of size in time: with help of the Sieve of Eratosthenes, we find a prime number between and (such a number always exist, by the classic postulate of Bertrand (see [1]), and then follow the Erdös-Turán-construction with this value of , and take the first elements of this set. Notice that the elements in this set are smaller than .
Suppose we have an input of independent set and . Assume and let be the number of edges. First, build a Golumb ruler of size . Denote the elements by . Notice that . Write .
We will construct an instance of Chain Scheduling with Exact Delays. We will make chains. We call one chain the start time forcing chain, the other chains are the vertex selection chains.
The start time forcing chain has release date , deadline and total execution time (including delays) . I.e., it must start at time 1. The chain will have a job starting at every time in except the times .
The vertex selection chains have release date . They have deadline and total execution time , where . So, they can start at times . The vertex selection chains start with a job and then a delay of . Note that as a result of this, in order not to conflict with the start time forcing chain, they have to start at an element of .
Now, for each edge , and each ordered pair of vertex selection chains with we dedicate an interval of time steps. More precisely, we have intervals for . And to each interval we assign a unique label where and . In the interval we will check whether the chains and did not select the edge , that is, whether does not start at or does not start at .
We will now extend the vertex selection chains. Consider the interval from left to right. For each interval that we encounter, we extend the vertex selection chains as follows.
-
•
For each chain , with , , add a delay of .
-
•
Add the following gadget to the chain : a delay of , a job, and then a delay if .
-
•
Add the following gadget to the chain : a delay of , a job, and then a delay if .
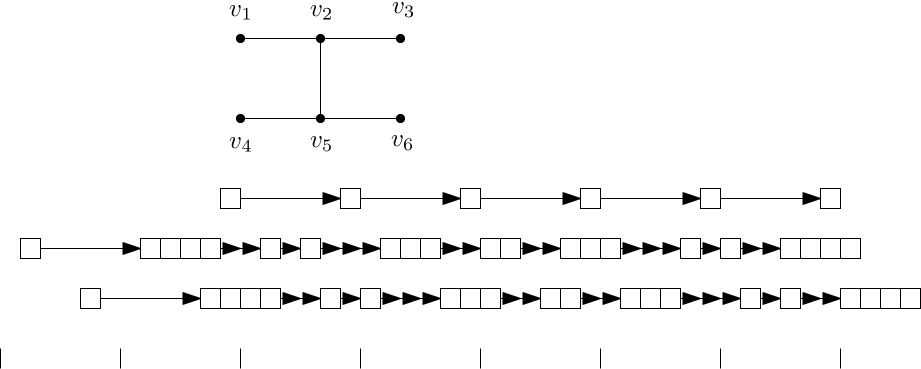
Add one job at the end of all chains. See Figures 2, 3 and 4 for an example of the construction and a feasible schedule.


We claim that there is a feasible schedule, if and only if has an independent set of size at least .
Claim 5.
If has an independent set of size at least , then there is a feasible schedule.
Suppose form an independent set in . Let the vertex selection chain start at times for .
Notice that for the first time steps, at most one resource is used. The same holds for the last time steps. We show that this is a feasible scheduling by contradiction. Suppose that there are two resources needed at some time step , and that is in the interval for checking whether the chains and do not select the edge . Write . Notice that job of in the interval starts at time . And the job of in the interval starts at time . Thus . Equivalently, . Since is a Golomb ruler, it follows that either and or and .
In the first case, and , we see that and . But there is no edge , since and are in an independent set. This yields a contradiction.
In the second case, and , we see that , but this yields a contradiction with the fact that the vertices of the independent set are distinct.
We conclude that this schedule always uses at most one machine.
Claim 6.
If there is a feasible schedule, then has an independent set of size at least .
Suppose that there is a feasible schedule. Notice that the time of the first step of a vertex selection chains must be an element of , otherwise the job conflicts with the start time forcing chain. Now, set . Notice that , as otherwise two vertex selection chains start at the same time, and conflict with each other for their first job.
We prove that is an independent set by contradiction. Suppose that there exists an edge , with . Let be the chain that starts at and the chain that starts at . Now consider the interval , and write . By the construction of the chains, it follows that starts its job of the interval at time . The job of in the interval starts at time as well. This yields a contradiction. We conclude that is an independent set. This shows that the Chain Scheduling with Exact Delays problem with a single machine, parametrized by the number of chains, is -hard.
Lemma 4.4.
The Chain Scheduling with Exact Delays problem with one machine, parameterized by the number of chains is in .
Proof 4.5.
We show that the problem belongs to by a transformation to Independent Set. Suppose we are given an instance of the Chain Scheduling with Exact Delays problem with a single machine. We now build a graph as follows: for each chain and each possible starting time of this chain, we take one vertex . We now add edges as follows: each pair of vertices that represent the same chain with different starting times is adjacent (i.e., for each chain, its vertices form a clique). For each pair of vertices , , , we add an edge if and only if starting chain on time and starting chain on time will cause that there is a time step where a job of both chains is scheduled.
It is not hard to see that the given instance of the Chain Scheduling with Exact Delays problem has a solution, if and only if the constructed graph has an independent set of size at least (with the number of chains). Indeed, if there is an independent set of size at least , then for every chain there is a vertex in the independent set, since for every chain we can have at most one vertex in an independent set. Scheduling chain at time gives a feasible schedule. On the other hand, if we have a feasible schedule, then the set is an independent set of size .
4.2 Constant number of parallel machines
If we assume that there are machines, but is considered to be a constant (i.e., not a fixed parameter; is part of the problem description), then the problem is -complete.
Theorem 4.6.
The Chain Scheduling with Exact Delays problem with machines, parameterized by the number of chains, is -complete.
Hardness follows easily from the case that : add chains with maximum length that consist of jobs with 0 delay.
Membership follows by formulating the problem as a Weighted CNF-SAT problem, i.e., giving a CNF-SAT formula that has a solution with at most (parameter) variables true, if and only if the scheduling problem has a solution.
We have a variable for each chain and each time that it can start, say .
We have a number of clauses that force that each chains starts at some time: for each chain , we have clause , ranging over all starting times of chain . We call those clauses chain clauses. This forces that each chain has one of its variables to be true.
The parameter is set to the number of chains. It follows that for each chain, exactly one of its variables is true.
Then, we have clauses that check that we never use more than machines. For each time , look at the set
For each subset of of these variables, we take a clause . We call those clauses the time clauses.
Claim 7.
Suppose there is a solution for the Weighted CNF-SAT instance, then the Chain Scheduling with Exact Delays scheduling problem has a solution.
Proof 4.7.
Let be a solution for the CNF-SAT instance. The chain clauses garantee that for every chain there is at least one variable true. Since equals the number of chains, we have that for every chain there is exactly one variable true. Let chain start at time for all .
We show that this is a feasible schedule by contradiction. Suppose that at time more than jobs are scheduled to start. Let be the set of chains that those jobs are in. Let be a subset of size . Then the time clause is not satisfied. This yields a contradiction.
Claim 8.
If there exists a solution for the scheduling problem, then we have a solution for the Weighted CNF-SAT instance.
Proof 4.8.
Suppose we have a feasible schedule. For each chain set the variable to true, where is the starting time of in the schedule. Notice that there are exactly variables set to true.
For every chain we set one variable to true, so the chain clauses are satisfied.
For every time , at most jobs start at . Consider the set . At most variables in this set are set to true. So, for every subset of variables, there is at least one variable false. Hence, the clause is satisfied.
4.3 Variable number of parallel machines
In this section, we show that Chain Scheduling with Exact Delays problem with machines, where is part of the input, is -complete.
Theorem 4.9.
The Chain Scheduling with Exact Delays problems with a variable number of machines, parameterized by the number of chains , is -complete.
We prove this by reductions from and to Dominating Set problems.
Lemma 4.10.
The Chain Scheduling with Exact Delays problems with a variable number of machines, parameterized by the number of chains , is -hard.
Proof 4.11.
Let , be an instance of Dominating Set. Assume that . We will make an instance of the scheduling problem with machines and chains.
The first chain will have release date and deadline . It will consist of jobs, with delay between each pair of consecutive jobs. Notice that this chain has to start at time . We will call this chain the check chain.
The other chains will be identical, we call them the vertex selection chains. They have release date and deadline . They will have total execution time , so they can start at times . Start each chain with a job and then a delay of .
Consider the interval from left to right. For each integer with , add the following to the vertex selection chains:
-
•
a delay of if ,
-
•
a delay of is ,
-
•
a job otherwise.
Notice that for each interval , we made a gadget the represents the adjacencies of vertex : there is no job at time of the execution of the chain if or for . See Figure 5.
Claim 9.
If has a dominating set of size at most , then there is a feasible schedule.
Let be a dominating set. Let the vertex selection chains start at times , , , . We will show that this is a feasible schedule.
Notice that at each time that is not of the form at most jobs are scheduled to start, since the check chain has no job starting at this time.
Now consider the time , for some . The check chain has a job scheduled to start at this time. We will show that there is a vertex selection chain that has no job starting at this time. Let be the vertex that dominates . Then we know that or . So the vertex selection chains have a delay of starting at time of their execution time. Let be the chain that starts at time . It follows that has a delay of starting at time .
Claim 10.
If there is a feasible schedule, then has a dominating set of size at most .
Let be the starting times of the vertex selection chains in a feasible schedule. Consider the set . We will show that this is a dominating set.
Let be a vertex. Consider the time . Notice that a job of the check chain is scheduled to start at this time, so one of the vertex selection chains has no job starting at this time. Let be the starting time of the chain . It follows that has no job at time of its execution time. Hence or . We conclude that is dominated. We conclude that the Chain Scheduling with Exact Delays problem with a variable number of machines is -hard, when parametrized by the number of chains.
Lemma 4.12.
The Chain Scheduling with Exact Delays problems with a variable number of machines, parameterized by the number of chains , is in .
Proof 4.13.
We use a reduction to Threshold Dominating Set. In the Threshold Dominating Set problem, we are given a graph and integers and , and ask for a set of at most vertices, such that each vertex in is dominated at least times.
Downey and Fellows [8] showed that Threshold Dominating Set, parameterized by and is -complete.
Suppose we have an instance of the Chain Scheduling with Exact Delays scheduling problem with machines and chains. Let the largest deadline in this instance. We will distinguish three cases: , , and . If , any schedule is feasible, so we reduce to a trivial dominating set instance.
Suppose that . We will construct an instance of Threshold Dominating Set where we look for a set of vertices that dominates each vertex at least once.
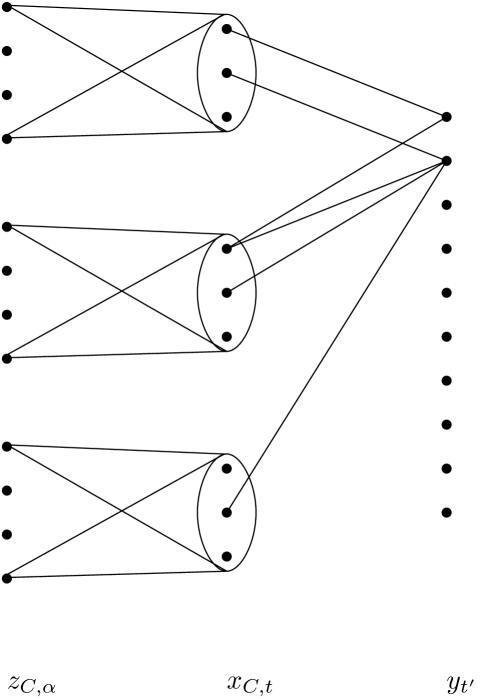
We construct a graph with three types of vertices:
-
•
For each chain and each time step , we have vertex if and only if it is possible to start chain at time (i.e., is not before the release date of and plus the execution time of is at most the deadline of ).
-
•
We have an independent set with for each time , with , a vertex .
-
•
For each chain we have vertices , with .
We have the following edges:
-
•
For each chain , the set of vertices of the form forms a clique.
-
•
There is an edge between to , if and only if starting chain at time makes that no job of starts at time .
-
•
Each vertex is adjacent to all vertices of the form .
See Figure 6.
Claim 11.
If contains a threshold dominating set of size at most that dominates every vertex at least once, then there is a feasible schedule.
Let be a threshold dominating set with , such that each vertex is dominated at least once.
We will show that consists of vertices of the form , one for each chain .
Consider a chain . Notice that there are vertices , so does not contain all of them. Let be such that . Since is dominated by , at least one vertex of the form is contained in . Since we have chains and has size , it follows that for every chain , contains exactly one vertex of the form and no vertex of the form . Moreover, does not contain vertices of the form .
Make a schedule as follows: for every chain , start this chain at time , for such that . Consider a time . Since vertex is dominated by a vertex , we know that there is an edge from to . By the construction of , it follows that chain has no job starting at time . It follows that at most jobs start at time . We conclude that this is a feasible schedule.
Claim 12.
If there is a feasible schedule, then has a threshold dominating set of size at most that dominates every vertex at least once.
Consider the set , that contains for every chain the vertex , where is the starting time of in the schedule.
It is clear that all vertices of the form and are dominated. Now consider a vertex . Since we have a feasible schedule, there is at least one chain that does not have a job starting at time . It follows that is dominated by the corresponding vertex .
Consider the last case .
We will construct an instance of Threshold Dominating Set where we look for a set of vertices that dominates each vertex at least times.
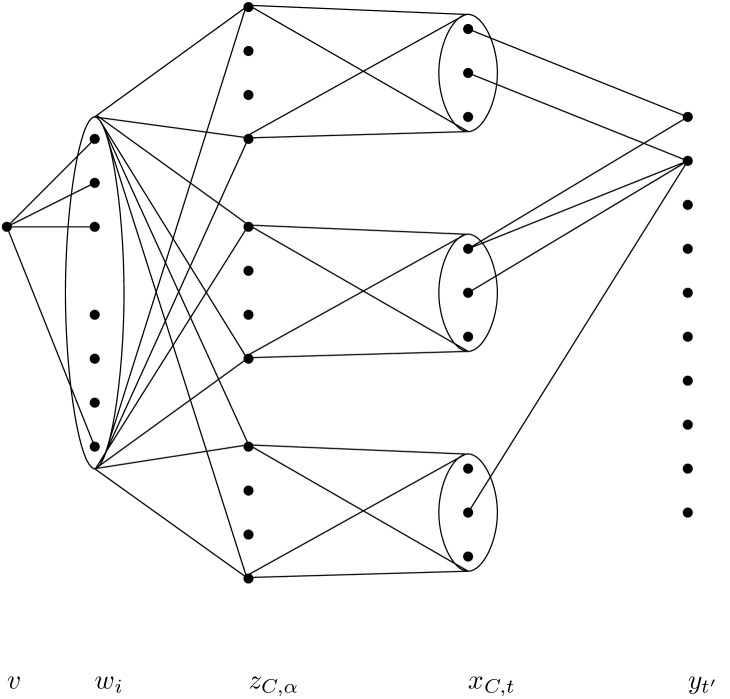
We construct a graph with five types of vertices, this graph will be similar to the graph in the previous case.
-
•
For each chain and each time step , we have vertex if and only if it is possible to start chain at time (i.e., is not before the release date of and plus the execution time of is at most the deadline of ).
-
•
We have an independent set with for each time , with , a vertex .
-
•
For each chain we have vertices , with .
-
•
We have a clique of vertices , .
-
•
We have a vertex .
We have the following edges:
-
•
For each chain , the set of vertices of the form forms a clique.
-
•
There is an edge between to , if and only if starting chain at time makes that no job of starts at time .
-
•
Each vertex is adjacent to all vertices of the form .
-
•
As written above, the vertices form a clique.
-
•
There is an edge for every .
-
•
Each vertex is adjacent to all vertices of the form .
-
•
Each vertex is adjacent to all vertices of the form .
See Figure 7.
Claim 13.
If has a threshold dominating set of size at most that dominates every vertex at least times, then there is a feasible schedule.
Suppose that a threshold dominating set with , such that each vertex is dominated at least times.
First, notice that, as has degree , needs to contain and all its neighbours, i.e., all vertices of the form . It follows that contains at most other vertices.
As in the proof of Claim 11, it follows that contains exactly one vertex of the form for every chain .
Again as in the proof of Claim 11, we make a schedule by starting every chain at the time for which . Now consider a time . We know that is dominated at least times. It follows that there are chains that have no job starting at time . We conclude that at most chains have a job starting at time , hence we use at most machines.
Claim 14.
If there is a feasible schedule, then has a threshold dominating set of size at most that dominates every vertex at least times.
Consider the set that contains , all vertices and for every chain the vertex , where is the starting time of is the schedule.
It is clear that and every vertex is dominated at least times. Notice that every vertex is dominated by every vertex , and by one vertex , so is dominated at least times. The same holds for all vertices .
Now consider a vertex . We know that at most chains start a job at time . Hence, at least chains do not start a job at time . We conclude that is dominated at least times.
We conclude that the Chain Scheduling with Exact Delays problem parametrized by the number of chains is in .
4.4 Minimum delays
With a simple modification, the hardness proofs for exact delays in unary can be modified to hardness proofs for minimum delays (still in unary). The modification consists of taking a number of copies of the instance, as described below.
Suppose we have an instance for Chain Scheduling with Minimum Delays with exact delays with chains and machines. The th chain has jobs , with precedence constraints , release date and deadline .
We define the minimum duration of a chain to be . Thus, when the first job of is executed at a time , then the last job is executed at time or later, and thus the minimum duration denotes the minimum number of time steps from the first till the last execution of a job in the chain.
Set to be the maximum deadline of all chains.
We now build an instance for Chain Scheduling with Minimum Delays. The intuition behind the construction is the following: we build identical copies of the original instance after each other. Each is executed in its own slot of consecutive time steps, in the same way as a solution of the original instance. If we have a solution of the new instance, then one of the copies has no preemption, i.e., must have delays equal to the minimum, and this gives a solution of the original instance.
For each chain from the original instance, we make a new chain in the new instance. This chain has jobs with and . We have precedence constraints () whose minimum delay equals the exact delay for the original jobs . The last job of the th copy precedes the first job of the st copy: we have a precedence constraint , for . We set the minimum delay for this precedence in such a way that the minimum execution time between a job and its next copy equals : the precedence constraint goes with a minimum delay of . The release date of the the new chain equals and the deadline equals .
Claim 15.
The instance of the Chain Scheduling with Exact Delays problem has a solution, if and only if the instance of the Chain Scheduling with Minimum Delays problem has a solution.
Proof 4.14.
Suppose we have a solution of the Chain Scheduling with Exact Delays problem with exact delays, where jobs are executed at time . Now, schedule for the instance with minimum delays, jobs on time .
One can easily verify that this schedule fulfills the constraints. Note that all delays equal the minimum delays.
Now, suppose we have a solution of the Chain Scheduling with Minimum Delays problem with minimum delays. Note that the total execution time of a chain is at least : the total execution time from a job till is constructed to be at least , for . The total number of time steps from the release time till the deadline is . Thus, the total slack in a chain, i.e., the sum of the differences between the scheduled delay time and the stated minimum delay, cannot be larger than . Notice that this is at most .
Say copy is tainted when there is at least one job for some and where the delay from to is larger than the stated minimum delay. As each chain has at most jobs of this type, we can have at most tainted copies.
Thus, there is a copy that is not tainted. From the times that the jobs of copy are scheduled, we build a solution.
Notice that the first job is scheduled at the earliest at time and that is scheduled at least time steps after . So is scheduled at the earliest at time . Analogously, we find that is scheduled before . Hence, every job is scheduled between and . Suppose that job is scheduled to start at time , then schedule the corresponding job to start at time . Notice that this is a feasible schedule, and that the exact delays are satisfied since the copy is not tainted.
Theorem 4.15.
The Chain Scheduling with Minimum Delays problem with one machine, parameterized by the number of chains , is -hard.
Theorem 4.16.
The Chain Scheduling with Minimum Delays problem with machines, parametrized by the number of chains, is -hard.
Theorem 4.17.
The Chain Scheduling with Minimum Delays problems with a variable number of machines, parameterized by the number of chains , is -hard.
Since the tickness is upper bounded by the number of chains, the same results follow when parametrized by the tickness.
5 XP algorithms
In this section, we give two positive results. First, we show membership in XP for all studied variants, when delays are given in unary, with a relatively straightforward dynamic programming algorithm. Then, in the case of one machine, we show that Scheduling with Exact Delays is in XP, when parameterized by the number of chains, even when delays are given in binary.
Lemma 5.1.
Given an instance of Chain Scheduling with Exact Delays or Chain Scheduling with Minimum Delays, one can build in polynomial time an equivalent instance, where all release dates and deadlines of chains are nonnegative integers, bounded by , where is the number of chains, the number of jobs, and the maximum delay between two successive jobs in a chain. In addition, for each chain , we have .
Proof 5.2.
We first look at Chain Scheduling with Minimum Delays. Consider the following operations. If we have a pair of successive jobs and in a chain with minimum delay , if job is scheduled to start at time , job is scheduled to start at time , and there is a time with , and less than jobs are starting at time (with the number of machines), then we obtain a valid schedule when we reschedule job at and do not change the time for any other job. If the first job in a chain is scheduled at time , and there is a time step with , then we obtain a valid schedule when we reschedule this first job at time and no not change the time for any other job. Call a schedule left-adjusted when these steps are not possible. If there is a valid schedule, then there is also a valid left-adjusted schedule: just take any valid schedule, and perform the steps above while possible.
In a left-adjusted schedule, for each chain , there is a job (of this or another chain) starting at time , and we cannot have an interval with successive time steps between and the scheduled time of the last job in the chain without any job (of any chain) scheduled. Thus, the last job of a chain is scheduled to start at time or earlier. This shows that we obtain an equivalent instance if we set for all chains the deadline to . Since , we obtain an equivalent instance if we set all deadlines to .
In the case of Chain Scheduling with Exact Delays, valid schedules are trivially left-adjusted, so setting deadlines to again gives an equivalent instance.
Now, consider the interval graph where each chain is a vertex, with edges between vertices if the chains overlap, here, the intervals associated with chain vertices are the intervals . We consider the different connected components of this interval graph. Take the component that contains the chain with minimum release date, and call this . For each chain in the component, subtract from its release date and deadline. We obtain an equivalent instance, with at least one release date equal to 0. We say that this first component is handled.
We now handle the other components, one by one as follows. Set to be the maximum deadline of all chains in handled components. Take, among all components that are not yet handled, the one with minimum release date of a chain in it. Say this minimum release date is . Subtract from all chains in the component from the release date and deadline. Thus, the earliest release date in the component is now . It is easy to see that this gives an equivalent schedule.
The algorithm thus consists of two steps: first, we set deadlines to , and then we handle the components. Now, order the chains by release date: . Notice that . Since , it follows that the maximum deadline is at most .
Theorem 5.3.
Chain Scheduling with Exact Delays and Chain Scheduling with Minimum Delays belong to XP, when delays are given in unary, and parameterized by the number of chains or thickness, for any number of machines.
Proof 5.4.
As the thickness is never larger than the number of chains, it suffices to give the result for the thickness.
The first step is to build the equivalent instance with deadlines and release dates in unary, and for all chains , as in Lemma 5.1.
We give now the dynamic programming algorithm; there are only small differences between the algorithms for Chain Scheduling with Exact Delays and Chain Scheduling with Minimum Delays.
The algorithm uses the notion of a state. A state consists of a time step , and for each chain with , we have a bool started. If , then the state also contains a job and a time . (The intuition is as follows: is the last job of chain that is scheduled at or before time ; is scheduled at time . If no job of is scheduled at or before time , then started is false.)
We say a state is possible, when there is a schedule with the following properties:
-
•
The schedule assigns a time to all jobs in a chain whose deadline is before , and for all chains with and started is true, a time is assigned to all jobs in the chain from the first job up to job — i.e., we do not assign times for jobs preceded by .
-
•
Jobs are scheduled at time , for all chains with and started is true.
-
•
The schedule respects the conditions on (minimum or exact) delays, and number of machines.
The dynamic programming algorithm now consists of computing for each time step , in order of increasing , the set of possible states for time . Let be the maximum over all chains of . Note that the number of states at time is bounded by : each of the at most chains with , we either have started false, or select one of the (at most ) jobs in the chain, and one of the (at most ) timesteps in . So, for fixed , the number of states is polynomial in the input size.
It is not hard to see, that given a set of all possible states at time , we can compute in polynomial time the set of all possible states at time . (The details are somewhat tedious: for all possible states at time , consider all decisions of the form where for each machine we decide if we schedule a job on this machines, and if so, what job. For each of these, check whether delay and deadline conditions are still fulfilled; if so, add this to the possible states for time . The check is different for exact or minimum delays; apart from that, these variants are handled in the same way.)
Continue computing this set for the time step that equals the maximum deadline minus . If it has a possible state, then this state reflects a schedule where all jobs are scheduled, and we decide positively; otherwise, no valid schedule exists.
Theorem 5.5.
Chain Scheduling with Exact Delays with , parameterized by the number of chains, with delays in binary belongs to XP.
Proof 5.6.
Suppose we have chains . Suppose chain has jobs , , , , with directly preceding ; we write the exact delay of this constraint as . Write . Note that has to be scheduled exactly time after starts.
For each chain , we take a variable that denotes the time that the first job of is scheduled.
Claim 16.
Variables give a valid schedule, if and only if the following constraints are fulfilled.
-
1.
For each , .
-
2.
For each , .
-
3.
For each and with , and each , with , , we have .
Proof 5.7.
Suppose we have a valid schedule where chain starts at time . As the first job in a chain does not start before the release date, we have . As the last job of the chain starts at time , we have . If the third condition would not hold for a 4-tuple , , , , then both the th job of chain and the th job of would be scheduled at time ; this gives a conflict as we have only one machine.
The other direction is (also) simple: the first condition ensures that chains do not start before the release date; the second that they finish before the deadline, and the third that no two jobs are scheduled at the same time.
The first step of the algorithm is to compute for each pair , with a set . Note that each of these sets has size , or more precisely, is at most the product of the sizes of the two chains. Now, sort each set .
Suppose with . Condition 3 of Claim 16 for the pair , can be expressed as
Our algorithm now branches on these possibilities. For each of the pairs of chains, we have branches, which gives a total of subproblems.
Each of these subproblems asks to solve a set of inequalities. These inequalities are of the form or (Condition 1 of Claim 16) or (Condition 2 of Claim 16), for some integers . As we work with integers and look for integer solutions, we reformulate constraints of the form as . We now have a system of linear inequalities which can be solved in polynomial time with text book (shortest paths) methods, see e.g., [5, Section 24.4]. If at least one of the subproblems has a solution, then this solution gives starting times for the chains that gives a valid schedule; otherwise, there is no valid schedule.
We have branches, each taking polynomial time, and this gives a running time of .
6 Conclusions
In this paper, we have shown a number of results on the parameterized complexity of Chain Scheduling with Exact Delays and Chain Scheduling with Minimum Delays. In a few cases, we obtained -completeness or -completeness; in the other cases, we only showed hardness results, often together with XP-membership. We expect that the problems, parameterized by the thickness do not belong to — for the same ‘compositionality’ reason as why one can believe that Graph Bandwidth does not belong to : see the discussion in [11, Section 4]. The machinery to prove such results currently is not available, but we conjecture that also the variants with minimum delays inhibit some form of compositionality and do not belong to .
We end this paper with mentioning some open problems. In this paper, we proved for the case that delays are given in binary, for only one of the cases membership in XP. What is the complexity of the other cases when delays are given in binary? Also, an interesting question is to study the variant where we have maximum delays, with all of its subcases.
References
- [1] Martin Aigner and Günter M. Ziegler. Bertrand’s postulate. In Proofs from THE BOOK, pages 7–12. Springer, 2001. doi:10.1007/978-3-662-04315-8_2.
- [2] S. Bessy and R. Giroudeau. Parameterized complexity of a coupled-task scheduling problem. Journal of Scheduling, 22(3):305–313, 2019. doi:10.1007/s10951-018-0581-1.
- [3] Hans L. Bodlaender and Michael R. Fellows. -hardness of precedence constrained -processor scheduling. Oper. Res. Lett., 18(2):93–97, 1995. doi:10.1016/0167-6377(95)00031-9.
- [4] Peter Brucker, Johann Hurink, and Wieslaw Kubiak. Scheduling identical jobs with chain precedence constraints on two uniform machines. Mathematical Methods of Operations Research, 49:211––219, 1999. doi:10.1007/PL00020913.
- [5] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, 3rd Edition. MIT Press, 2009. URL: http://mitpress.mit.edu/books/introduction-algorithms.
- [6] Rodney G. Downey and Michael R. Fellows. Fixed-parameter tractability and completeness I: Basic results. SIAM Journal on Computing, 24:873–921, 1995. doi:10.1137/S0097539792228228.
- [7] Rodney G. Downey and Michael R. Fellows. Fixed-parameter tractability and completeness II: On completeness for . Theoretical Computer Science, 141(1-2):109–131, 1995. doi:10.1016/0304-3975(94)00097-3.
- [8] Rodney G. Downey and Michael R. Fellows. Threshold dominating sets and an improved characterization of . Theoretical Computer Science, 209(1-2):123–140, 1998. doi:10.1016/S0304-3975(97)00101-1.
- [9] P. Erdös and P. Turán. On a problem of Sidon in additive number theory, and on some related problems. Journal of the London Mathematical Society, s1-16(4):212–215, 1941. doi:10.1112/jlms/s1-16.4.212.
- [10] Michael R. Fellows and Catherine McCartin. On the parametric complexity of schedules to minimize tardy tasks. Theoretical Computer Science, 298(2):317–324, 2003. doi:10.1016/S0304-3975(02)00811-3.
- [11] Michael R. Fellows and Frances A. Rosamond. Collaborating with Hans: Some remaining wonderments. In Fedor V. Fomin, Stefan Kratsch, and Erik Jan van Leeuwen, editors, Treewidth, Kernels, and Algorithms — Essays Dedicated to Hans L. Bodlaender on the Occasion of His 60th Birthday, volume 12160 of Lecture Notes in Computer Science, pages 7–17. Springer, 2020. doi:10.1007/978-3-030-42071-0\_2.
- [12] Matthias Mnich and Andreas Wiese. Scheduling and fixed-parameter tractability. Mathematical Programming, 154(1):533–562, 2015. doi:10.1007/s10107-014-0830-9.
- [13] Erick D. Wikum, Donna C. Llewellyn, and George L. Nemhauser. One-machine generalized precedence constrained scheduling problems. Operations Research Letters, 16(2):87–99, 1994. doi:10.1016/0167-6377(94)90064-7.
- [14] Gerhard J. Woeginger. A comment on scheduling on uniform machines under chain-type precedence constraints. Operations Research Letters, 26(3):107–109, 2000. doi:10.1016/S0167-6377(99)00076-0.