Parametrization of the Driven Betatron Oscillation

The tune of an AC dipole $\nu_{\text{acd}}$ is defined as the ratio between the frequencies of the AC dipole $f_{\text{acd}}$ and the beam revolution $f_{\text{rev}}$: $\nu_{\text{acd}}=f_{\text{acd}}/f_{\text{rev}}$. In the following, for any tunes, only their fractional parts are considered. For instance, if $f_{\text{acd}}/f_{\text{rev}}$ is larger than one, $\nu_{\text{acd}}$ means the fractional part of $f_{\text{acd}}/f_{\text{rev}}$. Since the beam sees an AC dipole only once per revolution, the tune of an AC dipole $\nu_{\text{acd}}$ and $1-\nu_{\text{acd}}$ are equivalent (cf. Nyquist sampling theorem). Hence, under the influence of an oscillating dipole field a beam is driven by a pair of driving terms at $\nu_{\text{acd}}$ and $1-\nu_{\text{acd}}$. Obviously, the driving term closer to the machine tune $\nu$ ($0<\nu<1$) has bigger effects on a beam. In the following, the driving term closer to $\nu$ is called the primary and the other is called the secondary. A symbol $\nu_{d}$ is used for the primary driving tune:

For example, the frequencies of the AC dipole and beam revolution in the Tevatron are $f_{\text{acd}}\simeq 20.5$ kHz and $f_{\text{rev}}\simeq 47.7$ kHz, respectively, and hence the tune of the AC dipole is $\nu_{\text{acd}}=20.5/47.7\simeq 0.43$. Since the machine tune of the Tevatron is $\nu\simeq 0.58$, $1-\nu_{\text{acd}}\simeq 0.57$ is the primary driving tune and $\nu_{\text{acd}}\simeq 0.43$ is secondary in this case (Table 1).

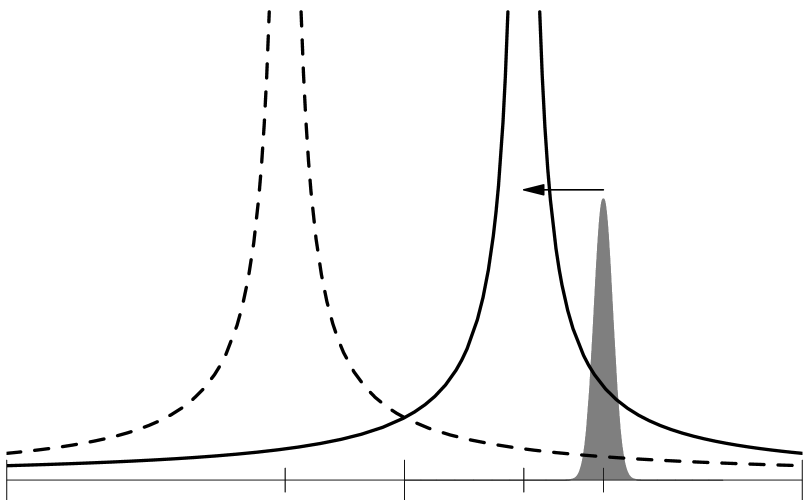
The distance from the primary driving term to the machine tune $\delta_{d}\equiv\nu_{d}-\nu$ is an important parameter of the driven betatron oscillation. As seen later, the secondary driving term generates a difference between the free and driven oscillations and affects linear optics measurements. Ideally, if the beam is driven very close to the machine tune $\nu$ ($\delta_{d}\to 0$), the influence of the primary driving term becomes dominant and the secondary driving term can be ignored. In reality, however, the finite tune spread of the beam causes beam losses if $|\delta_{d}|$ is too small and there is always a lower limit for $|\delta_{d}|$ (Fig 2). AC dipoles are currently used in the Tevatron and RHIC and planned for the LHC. In these synchrotrons, the lower limit of $|\delta_{d}|$ is about 0.01 to prevent beam losses.

When the amplitude of the field is constant, the position of the driven beam $x_{d}$ is given by peggs ; tomas

where $C$ is the circumference of a ring, ${\Delta}s$ $(0\leq{\Delta}s<C)$ is the longitudinal position measured from the location of the AC dipole, $\theta_{\text{acd}}$ is the maximum kick angle of the AC dipole, $\beta_{\text{acd}}$ is the amplitude function at the location of the AC dipole, $\psi$ is the phase advance of the free oscillation measured from the location of the AC dipole, and $\chi_{\text{acd}}$ is the initial phase of the AC dipole. The two terms in Eq 2 are completely symmetric and represent the influences of the two driving terms ¹¹1Eq 2 is assuming the amplitude of the AC dipole field is adiabatically ramped up to a constant value. The exact expression of $x_{d}$ includes transient modes which are inversely proportional to the ramp up time and oscillate with the machine tune $\nu$. If the ramp up is slow enough, all of these modes are very small and decohere before the end of the ramp up. Hence these ignored modes do not affect the motion of the beam centroid but they may affect the beam size tomas .. To quantify the effect of the secondary driving term, it is useful to define a parameter which describes the ratio between the primary (larger) and secondary (smaller) modes in Eq 2:

When $|\delta_{d}|=0.01$, $|\lambda_{d}|\simeq 0.06$ for the Tevatron with $\nu\simeq 0.58$ and $|\lambda_{d}|\simeq 0.03$ for the RHIC and LHC with $\nu\simeq 0.3$ and $0.7$ (Table 1). This is the effect of the secondary driving term on the amplitude of the driven oscillation. When the machine tune is closer to the half-integer, the two driving terms are closer to each other and the influence of the secondary driving term gets larger. This is why $|\lambda_{d}|$ of the Tevatron is larger than that of the RHIC and LHC.

Eq 2 can be written in the following compact form which includes the influences of both driving terms:

Here, $A_{d}$ is a quantity with dimensions of $(\text{length})^{1/2}$:

$\beta_{d}$ is a newly defined amplitude function of the driven oscillation which satisfies

$\psi_{d}$ is a newly defined phase advance of the driven oscillation measured from the location of the AC dipole:

and the sign in front of $\chi_{\text{acd}}$ is positive when $\nu_{d}=\nu_{\text{acd}}$ and negative when $\nu_{d}=1-\nu_{\text{acd}}$. Hence, the driven oscillation can be parametrized in the same form as the free oscillation even when the influences of the both driving terms are included. Since $A_{d}$ is a constant of motion, the difference between the free and driven oscillations comes from the amplitude function $\beta_{d}$ and phase advance $\psi_{d}$. As discussed previously, in the limit, $\nu_{d}\to\nu$, the primary driving term becomes dominant and the secondary driving term can be ignored. In this limit $\lambda_{d}\to 0$ and $\beta_{d}$ and $\psi_{d}$ converge to $\beta$ and $\psi$.

If the lesser mode in Eq 2 is ignored, the oscillation phase has an apparent jump of $2\pi\delta_{d}$ at the location of the AC dipole. However, if the influences of both driving terms are properly included as Eq 4, the phase advance is smooth at the location of the AC dipole. A relation between the phase advances of free and driven oscillations, $\psi$ and $\psi_{d}$, is given by

For the free oscillation, the phase advance in a single revolution is $\psi(s+C)-\psi(s)=2\pi\nu$ (mod $2\pi$). In the equation above, $\psi_{d}=2\pi\nu_{d}$ when $\psi=2\pi\nu$. Hence, the phase advance in a single revolution is $2\pi\nu_{d}$ for the driven motion.

If a synchrotron has a gradient error, its machine tune $\nu$ and amplitude function $\beta$ change books . Suppose a synchrotron has a gradient error with the strength $q_{\text{err}}=B^{\prime}\ell/(B\rho)$ at the longitudinal position $s=0$. Then, the equation of motion is given by

where the prime denotes the derivative with the longitudinal coordinate $s$, $k$ is the spring constant, and $\delta$ is the Dirac’s delta function.

By comparing the single turn transfer matrices with and without the gradient error, the new tune $\nu_{q}$ and amplitude function $\beta_{q}$ satisfy the following two equations books :

where $\beta_{\text{err}}$ is the amplitude function at the gradient error and $\psi$ is the phase advance measured from the gradient error. By substituting the first equation into the second, the ratio between the new and original amplitude functions $\beta_{q}/\beta$ is given by

Here, $\lambda_{q}$ is a parameter similar to $\lambda_{d}$ in Eq 3:

where $\delta_{q}$ is the tune shift by a gradient error $\delta_{q}\equiv\nu_{q}-\nu$. When the gradient error $q_{\text{err}}$ is small, the new and original amplitude functions satisfy

This quantity behaves like a standing wave in a synchrotron and is called the $\beta$-beat (or sometimes $\beta$-wave). The amplitude of the $\beta$-beat is $2|\lambda_{q}|$.

As seen in Eqs 6 and 12, the relation between $\beta_{d}$ and $\delta_{d}$ for an oscillating dipole field is the same as the relation between $\beta_{q}$ and $\delta_{q}$ for a gradient error. The following argument gives insight why an oscillating dipole field changes the observed phase space motion as like a gradient error.

When the oscillation amplitude of the AC dipole field is constant, the Hill’s equation of motion is given by

The right-hand-side describes the kicks by the AC dipole located at $s=0$. The summation runs over the time period when the oscillation amplitude of the AC dipole field is constant and the sign in front of the initial phase $\chi_{\text{acd}}$ is the same convention as Eq 4. Eq 4 is the particular solution of this inhomogeneous Hill’s equation when the oscillation amplitude of the AC dipole field is adiabatically ramped to a constant amplitude. Since the phase of the driven oscillation $\psi_{d}$ increases by $2\pi\nu_{d}$ (mod $2\pi$) in one revolution, the position of the driven oscillation at the location of the AC dipole $s=Cn$ is given by

Notice the phases of the driven oscillation $x_{d}$ and the kicks by the AC dipole in Eq 15 are both $2\pi{\nu_{d}}n\pm\chi_{\text{acd}}$ at the location of the AC dipole. Hence, when the beam passes the AC dipole, its magnetic field is proportional to the position of the driven oscillation $x_{d}$ like a quadrupole magnet. This is the physical reason why an oscillating dipole field changes the amplitude function like a gradient error. The phases of the driven oscillation and the AC dipole are synchronized like this only when the oscillation amplitude of the AC dipole field is constant after the adiabatic ramp up. Since $x_{d}$ is the solution of Eq 15, it formally satisfies the following equation

Here, Eq 16 is used to change the right-hand-side and $q_{\text{acd}}$ is a constant given by

Eq 17 is exactly the same as the Hill’s equation with a gradient error, Eq 9. By comparing Eqs 9, 10, 18, and 17, it is trivial that the relation between $\beta_{d}$ and $\delta_{d}$ is the same as the relation between $\beta_{q}$ and $\delta_{q}$.

As discussed in the previous two sections, for the driven motion, the observed amplitude function $\beta_{d}$ differs from the actual $\beta$ as if there is a gradient error. Hence, $\beta_{d}$ is beating relative to $\beta$ and the beating amplitude is about $2|\lambda_{d}|$ from Eq 14. Remember the effect of the secondary driving term on the beam motion is the order of $\lambda_{d}$. Since the amplitude function is proportional to the square of the position, its effect on the amplitude function is of the order of $2|\lambda_{d}|$. Since the minimum difference between the primary driving tune and machine tune $|\delta_{d}|$ is about 0.01 for the Tevatron, RHIC, and LHC, the beating amplitude of $\beta_{d}$ relative to $\beta$ is 12-13% for the Tevatron and 6-7% for the RHIC and LHC (Table 1).

When turn-by-turn beam positions at all BPMs are given for the free oscillation, the relative $\beta$-function can be determined by simply comparing the square of the oscillation amplitude at each BPM. If the same analysis is applied to the turn-by-turn data of the driven oscillation, what is calculated is $\beta_{d}$ instead of $\beta$. If the difference between $\beta_{d}$ and $\beta$ is simply ignored and $\beta$ is determined in this way, the error may be as large as $2|\lambda_{d}|$. Furthermore, since the beating of $\beta_{d}$ cannot be distinguished from the real $\beta$-beat caused by gradient errors, the real $\beta$-beat cannot be measured in this way without depending on a machine model.

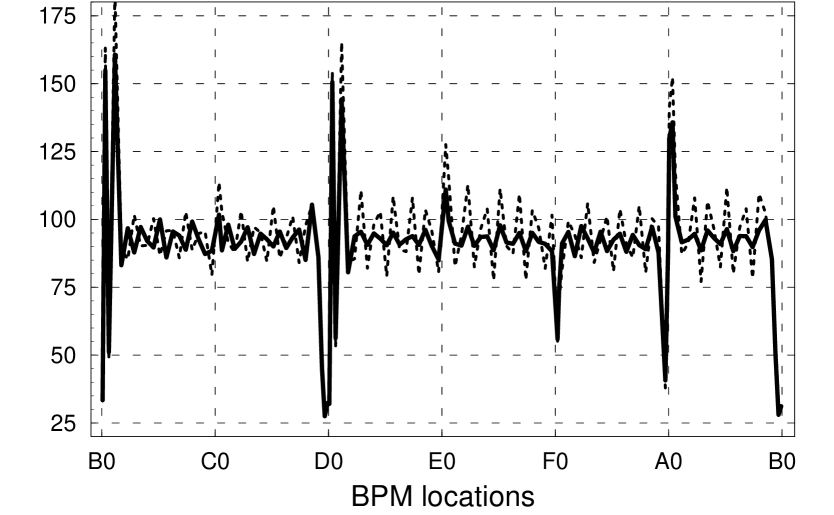
To calculate the true $\beta$-function from turn-by-turn data of the driven oscillation without depending on a machine model, multiple sets of data are necessary pacopt . Fig 3 shows amplitude functions of the free and driven oscillations, $\beta$ and $\beta_{d}(\delta_{d}=-0.01)$. They are both measured from data of the driven oscillation. Multiple data sets are used to calculate $\beta$ as described in pacopt and $\beta_{d}$ is calculated by comparing the square of the amplitude at each BPM. As expected, $\beta_{d}$ is showing the beating of 10-15% relative to $\beta$.

The previous section discussed the global behavior of $\beta_{d}$ compared to $\beta$. This section considers how $\beta_{d}$ changes depending on $\delta_{d}$ at one location of a synchrotron. From Eq 6, the relation between $\beta_{d}$ and $\beta$ becomes nonlinear when $\lambda_{d}$ is large or the phase term $\cos(2\psi-2\pi\nu)$ is close to zero. Since the difference between $\beta$ and $\beta_{d}$ has a considerable impact on the linear optics measurement, it is important to understand the properties of Eq 6 over wide ranges of parameters. Fig 4 shows the numerical calculations of $\beta_{d}/\beta$ based on Eq 6. The two plots are for two different machine tunes: $\nu=0.58$ like the Tevatron and $\nu=0.3$ like the RHIC and LHC. Since $\lambda_{d}$ is almost twice as large for the same $\delta_{d}$ when $\nu=0.58$ compared to $\nu=0.3$, the nonlinearity grows much faster with $\delta_{d}$ in the Tevatron. It is also seen in the left plot that the nonlinearity becomes larger when $|\cos(2\psi-2\pi\nu)|$ gets closer to zero. Such a nonlinear relation between $\beta_{d}$ and $\delta_{d}$ can be actually seen for the driven oscillation excited in the Tevatron. An example is shown in the next section.

The previous section discussed the amplitude function of the driven motion $\beta_{d}$. Parameters corresponding to the other Courant-Snyder parameters $\alpha$ and $\gamma$ can be also defined as for the free oscillation:

The explicit forms of these parameters are given by

and

When $\beta_{d}$, $\alpha_{d}$, $\gamma_{d}$, and $A_{d}$ are defined this way, they satisfy the Courant-Snyder invariance:

Hence, the turn-by-turn position and angle of the driven oscillation also form an ellipse on the phase space, like the free oscillation. Since not only $A_{d}$ but also the Courant-Snyder-like parameters $\beta_{d}$, $\alpha_{d}$, and $\gamma_{d}$ depend on the difference between the primary driving tune and the machine tune $\delta_{d}$, both the area and shape of the phase space ellipse changes with $\delta_{d}$ for the driven oscillation. In two collision straight sections of the Tevatron, B0 and D0, there are pairs of BPMs with no magnetic element in-between. The beam travels along straight lines between these pairs and, hence, both position and angle can be directly measured at these locations. Fig 5 shows the measured phase ellipses of the driven oscillations by using a pair of such BPMs. The frequency of the AC dipole was changed to adjust $\delta_{d}$ to $\pm 0.04$ and $\pm 0.02$, while the kick angle of the AC dipole $\theta_{\text{acd}}$ was kept the same. As expected, the shape of the phase space ellipse changes with $\delta_{d}$. Since $\delta_{d}$ dependence of $\beta_{d}$, $\alpha_{d}$, and $\gamma_{d}$ comes from the secondary driving term, the rotation of the phase space ellipse is its qualitative evidence.

By fitting Eq (23) to an ellipse in Fig 5, its area ${\pi}A_{d}^{2}$ and the parameters $\beta_{d}$, $\alpha_{d}$, and $\gamma_{d}$ can be determined. Fig 6 shows $\beta_{d}$ determined from the fits to ellipses in Fig 5 (and three more). The curve in the figure is the fit of Eq 6 to the data with parameters $\beta$ and $\psi$. The model of Eq 6 is fitting well to the data even though the nonlinearity is strong in the relation between $\beta_{d}$ and $\delta_{d}$ at the location. The $\beta$-function at the location can be calculated as one of the fit parameters. In the figure it is the value of $\beta_{d}$ when $\delta_{d}=0$.

When the secondary driving term is negligible, by ignoring the smaller term of Eq 2 or taking the limit of $\lambda_{d}\to 0$ in Eqs 4, 5, and 6, the amplitude of the driven oscillation can be approximated by

In this case, the amplitude of the driven oscillation depends on the primary driving tune $\nu_{d}$ only through $|\sin(\pi\delta_{d})|$ (remember $\delta_{d}=\nu_{d}-\nu$) and is symmetric around the machine tune $\nu$. From Eqs 4, 5, and 6, the amplitude including the effect of the secondary driving term $a_{d}(s;\delta_{d})$ is given by

Now, the amplitude depends on $\nu_{d}$ through the factor $[1+\lambda_{d}^{2}-2\lambda_{d}\cos(2\psi(s)-2\pi\nu)]^{1/2}$ as well. To the first order in $\delta_{d}$, the amplitude is approximated by

Hence, the secondary driving term makes the $\nu_{d}$ dependence of the amplitude asymmetric around the machine tune $\nu$. The magnitude of this asymmetry at each location is determined by the factor $\cos(2\psi-2\pi\nu)$.

Fig 7 shows the relation between the amplitude of the driven oscillation and $\nu_{d}$ at three BPM locations in the Tevatron. In the measurements, only the frequency of the AC dipole was changed while its kick angle $\theta_{\text{acd}}$ was kept the same. The dashed and solid lines represent the fits of Eq 24 and Eq 25 to the data. The fit parameters are $\theta_{\text{acd}}[\beta_{\text{acd}}\beta]^{1/2}$ and $\nu$ for Eq 24 and $\theta_{\text{acd}}[\beta_{\text{acd}}\beta]^{1/2}$, $\nu$, and $\psi$ for Eq 25 ²²2The ring-wide $\beta$-function can be determined from the fit up to a constant $\theta_{\text{acd}}\sqrt{\beta_{\text{acd}}}$. The constant is determined from the analysis using a pair of BPMs in the collision straight sections. See pacopt for details. The phase advance $\psi$ can be determined for the fit, too.. At two locations where $|\cos(2\psi-2\pi\nu)|$ is close to one, the asymmetry around the machine tune ($\nu\simeq 0.5785$) is large and the result of the fits without the secondary driving term (Eq 24) is not well matched.

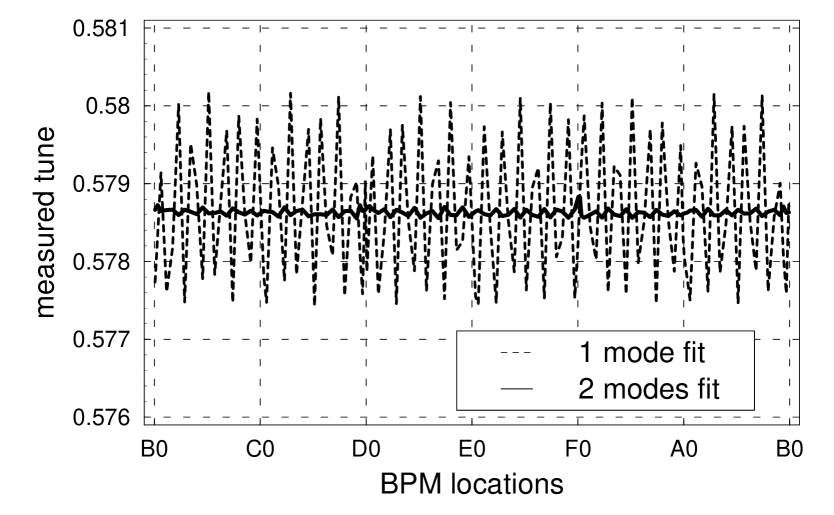
Although the existence of a secondary driven term effect is clear in Fig 7, there is better evidence that Eq 25 fits the data better than 24. From the fits in Fig 7, the machine tune $\nu$ can be determined at each BPM location. Fig 8 shows machine tunes determined at all BPM locations from the fits of the amplitude versus $\nu_{d}$. The dashed and solid lines represent machine tunes from the fits of Eqs 24 and 25. Since the machine tune $\nu$ is a global parameter of a synchrotron, the variation of the measured machine tune over BPMs shows the inaccuracy of the measurement. From the figure, it is clear the model including the secondary driving fits to the data much better. This also shows the importance of the secondary driving term in the driven oscillation.