Parsimonious and Efficient Likelihood Composition by Gibbs Sampling
Abstract
The traditional maximum likelihood estimator (MLE) is often of limited use in complex high-dimensional data due to the intractability of the underlying likelihood function. Maximum composite likelihood estimation (McLE) avoids full likelihood specification by combining a number of partial likelihood objects depending on small data subsets, thus enabling inference for complex data. A fundamental difficulty in making the McLE approach practicable is the selection from numerous candidate likelihood objects for constructing the composite likelihood function. In this paper, we propose a flexible Gibbs sampling scheme for optimal selection of sub-likelihood components. The sampled composite likelihood functions are shown to converge to the one maximally informative on the unknown parameters in equilibrium, since sub-likelihood objects are chosen with probability depending on the variance of the corresponding McLE. A penalized version of our method generates sparse likelihoods with a relatively small number of components when the data complexity is intense. Our algorithms are illustrated through numerical examples on simulated data as well as real genotype SNP data from a case-control study.
Keywords: Composite likelihood estimation, Gibbs sampling, Jackknife, Efficiency, Model Selection
1 Introduction
While maximum likelihood estimation plays a central role in statistical inference, today its application is challenged in a number of fields where modern technologies allow scientists to collect data in unprecedented size and complexity. These fields include genetics, biology, environmental research, meteorology and physics, to name a few. Two main issues arise when attempting to apply traditional maximum likelihood to high-dimensional or complex data. The first concerns modelling and model selection, since high-dimensional data typically imply complex models for which the full likelihood function is difficult, or impossible, to specify. The second relates to computing, when the full likelihood function is available but it is just too complex to be evaluated.
The above limitations of traditional maximum likelihood have motivated the development of composite likelihood methods, which avoid the issues from full likelihood maximization by combining a set of low-dimensional likelihood objects. ? was an early proponent of composite likelihood estimation in the context of data with spatial dependence; ? developed composite likelihood inference in its generality and systematically studied its properties. Over the years, composite likelihood methods have proved useful in a range of complex applications, including models for geostatistics, spatial extremes and statistical genetics. See ? for a comprehensive survey of composite likelihood theory and applications.
Let be a random vector with pdf (or pmf) , where , , is the unknown parameter. From independent observations , one typically computes the maximum likelihood estimator (MLE), , by maximizing the likelihood function . Now suppose that complications in the -dimensional pdf (pmf) make it difficult to specify (or compute) as the data dimension grows, but it is relatively easy to specify (or compute) one-, two-,…, dimensional distributions up to some order for some functions of . One can then follow ? to estimate by the maximum composite likelihood estimator (McLE), which maximizes the composite likelihood function:
| (1) |
where each is a user-specified partial likelihood (or sub-likelihood) depending on marginal or conditional events on variables. For example, can be defined using a marginal event (marginal composite likelihood), pairs of variables such as (pairwise likelihood), or conditional events like (conditional composite likelihood). For simplicity, we assume that is common to all sub-likelihood components, so that any factorization based on a subset of , yields a valid objective function.
Although the composite likelihood approach provides a flexible framework with a sound theory for making inference about in situations involving multivariate data, there exist at least two challenges hindering the efficiency improvement and feasible computing of McLE in applications. The first challenge lies with selecting the right sub-likelihood components for constructing an informative composite likelihood function. The current practice of keeping all plausible factors in (1) is not well justified in terms of efficiency relative to MLE, since inclusion of redundant factors can deteriorate dramatically the variance of the corresponding composite likelihood estimator (e.g., see ?). A better strategy would be to choose a subset of likelihood components which are maximally informative on , and drop noisy or redundant components to the maximum extent. However, little work is found in the literature in regard to optimal selection of sub-likelihood components. The second challenge lies with the computational complexity involved in the maximization of , which can go quickly out of reach as (and ) increases. Particularly, note that computing involves operations, where is the number of operations for each sub-likelihood component. The computational burden is exacerbated when is relatively large and the different sub-likelihood factors do not depend on distinct elements of . One would like to see this computing complexity be alleviated to a manageable level by applying parsimonious likelihood composition in the presence of high (or ultra-high) dimensional data.
Motivated by the aforementioned challenges, in this paper we propose a new class of stochastic selection algorithms for optimal likelihood composition. Our method uses Gibbs sampler, a specific Markov Chain Monte Carlo (MCMC) sampling scheme to generate informative – yet parsimonious – solutions. The resulting estimates will converge to the one maximally informative on the target parameter as the underlying Markov chain reaches equilibrium. This is because sub-likelihood components generated in the algorithms are drawn according to probabilities determined by a criterion minimizing the McLE’s variance or its consistent approximation. Theory of unbiased estimating equations prescribes McLE’s asymptotic variance as an optimality criterion, i.e., the -optimality criterion, see ?, but such an ideal objective has scarce practical utility due to the mathematical complexity and computational cost involved in evaluating the numerous covariance terms implied by the asymptotic variance expression (?). To address this issue, we replace the asymptotic variance by a rather inexpensive jackknife variance estimator computed by a one-step Newton-Raphson iteration. Such a replacement is shown to work very well based on our numerical study.
Another advantage of our approach is that proper use of the Gibbs sampler can generate sparse composition rules, i.e., composite likelihoods involving a relatively small number of informative sub-likelihood components. Note that the model space implied by the set of all available sub-likelihood components can be large, even when is moderate. For example, if , we have possible composition rules based on pair-wise likelihood components alone. To cope with such a high-dimensionality, we combine Gibbs sampling with a composite likelihood stochastic stability mechanism. Analogously to the stochastic stability selection proposed by ? in the context of high-dimensional model selection, our approach selects a small but sufficient number of informative likelihood components through the control of the error rates of false discoveries.
The paper is organized as follows: In Section 2, we outline the main framework and basic concepts related to composite likelihood estimation. We also describe the -optimality criterion and introduce its jackknife approximation. In Section 3, we describe our core algorithm for simultaneous likelihood estimation and selection. In Section 4, we discuss an extension of our algorithm by incorporating the ideas of model complexity penalty and stochastic stability selection. This leads to a second algorithm for parsimonious likelihoods composition for high-dimensional data. In Section 5, we illustrate our methods through numerical examples involving simulated data and real genetic single nucleotide polymorphism (SNP) data from a breast cancer case-control study. Section 6 concludes the paper with final remarks.
2 Sparse Composite Likelihood Functions
2.1 Binary Likelihood Composition
Let be a set of marginal or conditional sample sub-spaces associated with probability density functions (pdfs) . See ? for interpretation and examples of . Given independent -dimensional observations , , , we define the composite log-likelihood function:
| (2) |
where , and is the partial log-likelihood
| (3) |
Each partial likelihood object (sub-likelihood) is allowed to be selected or not, depending on whether is or . We aim to approximate the unknown complete log-likelihood function by selecting a few – yet the most informative – sub-likelihood objects from the available objects, where is allowed to be larger than and . Given the composition rule , the maximum composite likelihood estimator (McLE), denoted by , is defined by the solution of the following system of estimating equations:
| (4) |
where , , , are unbiased partial scores functions. Under standard regularity conditions on the sub-likelihoods (?), with asymptotic variance given by the matrix
| (5) |
where
is the sensitivity matrix for the th component, and .
The main approach followed here is to minimize, in some sense, the asymptotic variance, . To this end, theory of unbiased estimating equations suggests that both matrices and should be considered in order to achieve this goal (e.g., see ?). On one hand, note that measures the covariance between the composite likelihood score and the MLE score . To see this, differentiate both sides in and obtain This shows that adding sub-likelihood components is desirable, since it increases the covariance with the full likelihood. On the other hand, including too many correlated sub-likelihoods components inflates the variance through the covariance terms in .
2.2 Fixed-Sample Optimality and its Jackknife Approximation
The objective of minimizing the asymptotic variance is still undefined since in (5) is a positive semidefinite matrix. Therefore, we consider the following one-dimensional objective function
| (6) |
The minimizer, , of the ideal objective (6) corresponds to the -optimal solution (fixed-sample optimality) (e.g., see ?, Chapter 2). Clearly, such a program still lacks practical relevance, since (6) depends on the unknown parameter . Therefore, should be replaced by some sample-based estimate, say .
One option is to use the following consistent estimates of and in (6):
| (7) |
where the estimator is the McLE. Although this strategy works in simple models when is relatively large and is small, the estimator is knowingly unstable when is small compared to (?). Another issue with this approach in high-dimensional datasets is that the number of operations required to compute (or ) increases quadratically in .
To reduce the computational burden and avoid numerical instabilities, we estimate by the following one-step jackknife criterion:
| (8) |
where the pseudo-value is a composite likelihood estimator based on a sample without observation , and . Alternatively, one could use the delete- jackknife estimate where observations at the time are deleted to compute the pseudo-values. The delete- version is computationally cheaper than delete- jackknife and therefore should be preferred when the sample size, , is moderate or large. Other approaches – including bootstrap – should be considered depending on the model set up. For example, block re-sampling techniques such as the block-bootstrap (see ? and subsequent papers) are viable options for spatial data and time series.
When the sub-likelihood scores are in closed form, the pseudo-values can be efficiently approximated by the following one-step Newton-Raphson iteration:
| (9) |
where is any root- consistent estimator of . Note that does not need to coincide with the McLE, , so a computationally cheap initial estimator – based only on a few small sub-likelihoods subset – may be considered. Remarkably, the number of operations required in the Newton-Raphson iteration (9) grows linearly in the number of sub-likelihood components, so that the one-step jackknife objective has computational complexity comparable to a single evaluation of the composite likelihood function (4). Large sample properties of jackknife estimator of McLE’s asympotic variance can be derived under regularity conditions on and analogous to those described in ?. Then, for the one-step jackknife using the root- consistent starting point , we have uniformly on . Moreover, the estimator is asymptotically equivalent to the classic jackknife estimator.
3 Parameter estimation and likelihood composition
3.1 Likelihood Composition via Gibbs Sampling
When computing the McLE of , our objective is to find an optimal binary vector to estimate where is the ideal objective function defined in (6). Typically, the population quantity cannot be directly assessed, so we replace with the sample-based jacknife estimate described in Section 2 and aim at finding
This task, however, is computationally infeasible through enumerating the space if is even moderately large. For example, for composite likelihoods defined based on all pairs of variables , (pairwise likelihood), contains elements when .
To overcome this enumeration complexity, we carry out a random search method based on Gibbs sampling. We regard the weight vector as a random vector following the joint probability mass function (pmf)
| (10) |
where is the normalizing constant. The above distribution depends on the tuning parameter , which controls the extent to which we emphasize larger probabilities (and reduce smaller probabilities) on . Then is also the mode of , meaning that will have the highest probability to appear, and will be more likely to appear earlier rather than later, if a random sequence of is to be generated from .
Therefore, estimating can be readily done based on the random sequence generated from . But generating a random sample from directly is difficult because contains an intractable normalizing constant . Instead, we will generate a Markov chain using the product of all univariate conditional pmf’s with respect to as the transitional kernel. The stationary distribution of such a Markov chain can be proved to be (?, Chapter 10). Hence, the part of this Markov chain after reaching equilibrium can be regarded as a random sample from for most purposes. The MCMC method just described is in fact the so-called Gibbs sampling method. The key factor for the Gibbs sampling to work is all the univariate conditional probability distributions of the target distribution can be relatively easily simulated.
Let us write ; , if , and otherwise; and . Then it is easy to see that the conditional pmf of given , , is
| (11) |
where , . Note that is simply a Bernoulli pmf and so it is easily generated. For each binary vector , is computed using the one-step jackknife estimator described in Section 2. Therefore, the probability mass function is well defined for any . On the other hand, we have shown that the Gibbs sampling can be used to generate a Markov chain from , from which we can find a consistent estimator for the mode if is unique. Consequently, the universally maximum composite log-likelihood estimator of can be approximated by the McLE, .
Note that the mode is not necessarily unique. In this case one can still consider consistent estimation for but in the following meaning. We know is the minimum and always unique according to its definition. Thus can be consistently and uniquely estimated based on the Markov chain of induced from the Markov chain of generated from when the length of the Markov chain goes to infinity. Therefore, any estimator such that becomes consistent with can be regarded as a consistent estimator of . Consequently, the McLE for each such is still the universally McLE but not necessarily unique. From a practitioner’s view point there is no need to identify all consistent estimators of and all universally McLE of . Finding out one such or a tight superset of it would be a sufficient advance in parsimonious and efficient likelihood composition.
3.2 Algorithm 1: MCMC Composite Likelihood Selection (MCMC-CLS)
The above discussion motivates the steps of our core Gibbs sampling algorithm for simultaneous composite likelihood estimation and selection. Let be given and fixed.
-
0.
For , choose an initial binary vector of weights and compute the one-step jackknife estimator . E.g. randomly set 5 elements of to 1 and the rest to 0.
-
1.
For each for a given , obtain by repeating to for each sequentially.
-
1.1.
Compute, if not available yet, , .
-
1.2.
Compute the conditional pmf of given :
(12) where . Note this is a Bernoulli pmf.
-
1.3.
Generate a random number from the Bernoulli pmf obtained in , and denote the result as .
-
1.4.
Set . Also compute and record .
-
1.1.
-
2.
Compute and regard it as the estimate of . Alternatively, column-combine generated in Step into an matrix ; then compute row averages of , say , and set where , if , and if , where is some constant larger than .
-
3.
Finally, compute (or ) and (or ).
Firstly, note that Gibbs sampling has been used in various contexts in the literature of model selection. ? used a similar strategy to generate the distribution of the variable indicators in Bayesian linear regression. ? used Gibbs sampler for selecting robust linear regression models. ? used the Gibbs sampler for selecting generalized linear regression models. ? and ? used Gibbs sampling for selection in the context of time series models. However, to our knowledge this is the first work proposing a general-purpose Gibbs sampler for construction of composite likelihoods.
Secondly, the sequence is a Markov chain, which requires an initial vector and a burn-in period to be in equilibrium. Values of do not affect the eventual attainment of equilibrium so can be arbitrarily chosen. From a computational point of view most components of should be set to 0 to reduce computing load. For example, we can randomly set all but 5 of the components to 0. To assess whether the chain has reached equilibrium, we suggest the control-chart method discussed in ?. For the random variable , we have the following probability inequality for any given :
This inequality can be used to find an upper control limit for . For example, by setting , an at least upper control limit for can be estimated as where , and are the minimum, sample mean and sample variance based on the first observations, , , where typically we set . We then count the number of observations passing the upper control limit in the remaining sample . If more than 10% of the points are above the control limit, then at a significance level not more than 90% there is statistical evidence against equilibrium. Upper control limits of different levels for can be similarly calculated and interpreted by choosing different values of .
Thirdly, computed in Step 2 is simply a sample mode of based on its definition in (10). Hence, by the Ergodic Theorem for stationary Markov chain, is a strongly consistent estimator of under minimal regularity conditions. With similar arguments is a strongly consistent estimator of the success probability involved in the marginal distribution of induced from . Hence, it is not difficult to see that the resultant estimator should satisfy without requiring to be very large. Propositions 1 and 2 in ? provide an exposition of this property. Therefore, the estimator captures all informative sub-likelihood components with high probability.
Finally, the tuning constant adjusts the mixing behavior of the chain, which has important consequences on the exploration/exploitation trade-off on the search space . If is too small, the algorithm produces solutions approaching the global optimal value slowly; if is large, then the algorithm finds local optima and may not reach . The former behavior corresponds to a rapidly mixing chain, while the latter occurs when the chain is mixing too slowly. In the composite likelihood selection setting, the main hurdle is the computational cost, so should be set according to the available computing capacity, after running some graphical or numerical diagnostics (e.g., see ?). We choose to use in our empirical study, which does not seem to create adverse effects.
4 An extension for high-dimensional data
4.1 Sparsity-enforcing penalization
Without additional modifications, Algorithm 1 ignores the likelihood complexity, since solutions with many sub-likelihoods have in principle the same chance to occur as those with fewer components. To discourage selection of overly complex likelihoods, we augment the Gibbs distribution (10) as follows:
| (13) |
where
| (14) |
is the jackknifed variance objective defined in Section 2, is the normalization constant, and is a complexity penalty enforcing sparse solutions when is large. Maximization of is interpreted as a maximum a posteriori estimation for , where the probability distribution proportional to is regarded as a prior pmf over . In this paper, we use the penalty term of form , since it corresponds to well-established model-selection criteria. For example, choices , and correspond to the AIC, BIC and HQC criteria, respectively (e.g., see ?). Other penalties could be considered as well depending on the model structure and available prior information; however, these are not shown to be crucial based on our empirical study so will not be explored in this paper.
4.2 Composite Likelihood Stability Selection
To find the optimal solution , one could compute a sequence of optimal values and then take . There are, however, various issues in this approach: first, the globally optimal value might not be a member of the set , since the mode of is not necessarily the composite likelihood solution which minimizes . Second, even if is in such a set, determining is typically challenging. To address the above issues, we employ the idea of stability selection, introduced by ? in the context of variable selection for linear models. Given an arbitrary value for , stochastic stability exploits the variability of random samples generated from by the Gibbs procedure, say and choses all the partial likelihoods that occur in a large fraction of generated samples. For a given , we define the set of stable likelihoods by the vector , with elements
| (15) |
so we regard as stable those sub-likelihoods selected more frequently and disregard sub-likelihood items with low selection probabilities. Following ?, we choose the tuning constant using the following bound on the expected number of false selections, :
| (16) |
where is average number of selected sub-likelihood components. In multiple testing, the quantity is sometimes called the per-comparison error rate (PCER). By increasing , only few likelihood components are selected, so that we reduce the expected number of falsely selected variables. We choose the threshold by fixing the PCER at some desired value (e.g., ), and then choose corresponding to the desired error rate. The unknown quantity in our setting can be estimated by the average number of sub-likelihood components over Gibbs samples.
4.3 Algorithm 2: MCMC Composite Likelihood with Stability Selection (MCMC-CLS2)
The preceding discussions lead to Algorithm 2 which is essentially the same as Algorithm 1 with two exceptions: (i) we replace in Algorithm 1 by the augmented objective function defined in (14); (ii) Steps 2 in Algorithm 1 is replaced by the following stability selection step.
-
.
Column-combine generated in Step into an matrix . Compute the row averages of , denoted as , i.e. , . Then set where if and if , , where and is a nominal level for per-comparison error rate (e.g., 0.05 or 0.1).
The estimated threshold is obtained from (16) by plugging-in , the sample average of the numbers of selected sub-likelihood components in Gibbs samples.
5 Numerical Examples
5.1 Normal Variables with Common Location
Let , where the parameter of interest is the common location . We study the scenario where many components bring redundant information on by considering covariance matrix with elements , for all , and off-diagonal elements if , for some , while elsewhere.
We consider one-wise score composite likelihood estimator solving , where . It is easy to find the composite likelihood estimator is where . For this simple model, the jackknife criterion can be easily computed in closed form. The pseudo-values are , and the average of pseudo-values is . It can be shown that
up to a constant not depending on . It can also be shown that -criterion has the following expression
| (17) |
depending on the unknown parameter . This suggests that including too many correlated (redundant) components (with ) damages McLE’s variance as increases. Particularly, setting , for all , implies , while choosing only uncorrelated sub-likelihoods ( if , and elsewhere), gives .
In Table 1, we show Monte Carlo simulation results from runs of Algorithm 1 (MCMC-CLS1) using the two approaches described in Section 3.2: one consists of choosing the best weights vector (CLS1 min); the other uses thresholding, i.e. selects elements when the weights are selected with a sufficiently large frequency (CLS1 thres.). In the same table we also report results on the Algorithm 2 (MCMC-CLS2) based on the stochastic stability selection approach. Our algorithms are compared with the estimator including all one-wise sub-likelihood components (No selection) and the optimal maximum likelihood estimator (MLE). We compute the MLE of in two ways: either based on using the known value or based on using the sample covariance . Note that the latter is not available when . Note our algorithms are designed to obtain simultaneous estimation and dimension reduction in the presence of limited information (i.e. or ) where the optimal weights are difficult to estimate from the data. Stochastic selection with and was carried out for samples of and observations from a model with correlated components, with . To compare the methods we computed Monte Carlo estimates of the variance () and squared bias () of . Table 2 further reports the average number of selected likelihood components (no. comp).
For all considered data dimensions, our selection methods outperform the all one-wise likelihood (AOW or No selection) estimator and show relatively small losses in terms of mean squared error () compared to the MLEs. The gains in terms of variance reduction are particularly evident for larger data dimensions (e.g., see ). At the same time, our method tends to select mostly uncorrelated sub-likelihoods, while discarding the redundant components which do not contribute useful information on .
| No selection | CLS1 (min) | CLS1 (thresh.) | CLS2 | MLE (known ) | MLE (unknown ) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 0.50 | 80.26 | 7.19 | 79.18 | 0.04 | 81.36 | 0.00 | 87.55 | 0.01 | 52.52 | 0.04 | NA | NA | |
| 0.90 | 115.06 | 10.31 | 96.97 | 0.05 | 114.82 | 0.08 | 114.90 | 0.02 | 62.28 | 0.04 | NA | NA | |||
| 30 | 0.50 | 80.08 | 7.18 | 60.61 | 1.60 | 54.06 | 1.18 | 52.16 | 0.74 | 26.22 | 0.03 | NA | NA | ||
| 0.90 | 103.50 | 9.28 | 61.27 | 0.01 | 44.14 | 0.01 | 44.68 | 0.00 | 24.93 | 0.02 | NA | NA | |||
| 25 | 10 | 0.50 | 17.14 | 8.28 | 15.27 | 0.18 | 17.45 | 0.06 | 17.73 | 0.06 | 12.01 | 0.03 | 20.99 | 0.03 | |
| 0.90 | 19.89 | 1.78 | 14.75 | 0.07 | 18.65 | 0.03 | 19.08 | 0.02 | 13.02 | 0.02 | 21.64 | 0.04 | |||
| 30 | 0.50 | 11.87 | 1.06 | 7.38 | 0.12 | 6.14 | 0.00 | 6.07 | 0.00 | 4.86 | 0.00 | NA | NA | ||
| 0.90 | 24.51 | 2.20 | 11.59 | 0.02 | 6.69 | 0.00 | 6.75 | 0.00 | 5.73 | 0.01 | NA | NA | |||
| 100 | 10 | 0.50 | 4.14 | 0.37 | 3.09 | 0.02 | 3.55 | 0.03 | 4.24 | 0.09 | 2.56 | 0.02 | 2.79 | 0.02 | |
| 0.90 | 6.18 | 0.55 | 3.25 | 0.00 | 4.58 | 0.00 | 4.58 | 0.00 | 3.12 | 0.00 | 3.37 | 0.00 | |||
| 30 | 0.50 | 3.40 | 0.30 | 1.79 | 0.00 | 1.60 | 0.00 | 1.60 | 0.00 | 1.20 | 0.00 | 1.69 | 0.00 | ||
| 0.90 | 5.54 | 0.50 | 2.60 | 0.01 | 1.68 | 0.01 | 1.68 | 0.01 | 1.41 | 0.01 | 2.03 | 0.01 | |||
| No selection | CLS1 (min) | CLS1 (thres.) | CLS2 | |||
|---|---|---|---|---|---|---|
| 5 | 10 | 0.50 | 10 | 3.77 | 3.92 | 3.72 |
| 0.90 | 10 | 3.28 | 2.58 | 2.36 | ||
| 30 | 0.50 | 30 | 13.94 | 11.01 | 10.84 | |
| 0.90 | 30 | 12.04 | 6.53 | 6.43 | ||
| 25 | 10 | 0.50 | 10 | 4.30 | 3.58 | 3.26 |
| 0.90 | 10 | 3.27 | 2.04 | 2.00 | ||
| 30 | 0.50 | 30 | 12.81 | 7.70 | 7.48 | |
| 0.90 | 30 | 11.96 | 5.98 | 5.98 | ||
| 100 | 10 | 0.50 | 10 | 4.28 | 2.56 | 2.31 |
| 0.90 | 10 | 3.17 | 2.00 | 2.00 | ||
| 30 | 0.50 | 30 | 12.22 | 6.08 | 6.05 | |
| 0.90 | 30 | 11.94 | 6.00 | 6.00 |
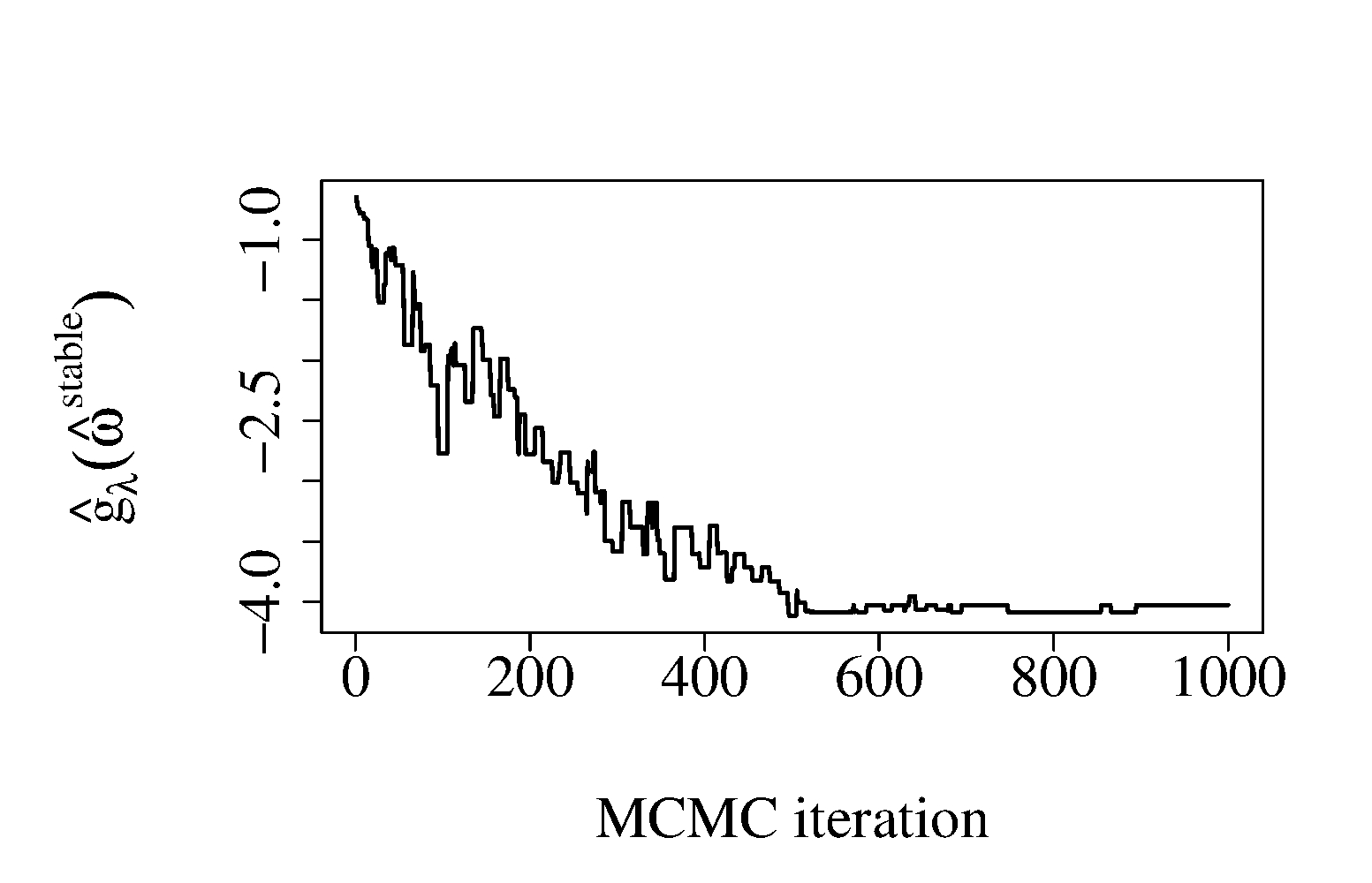
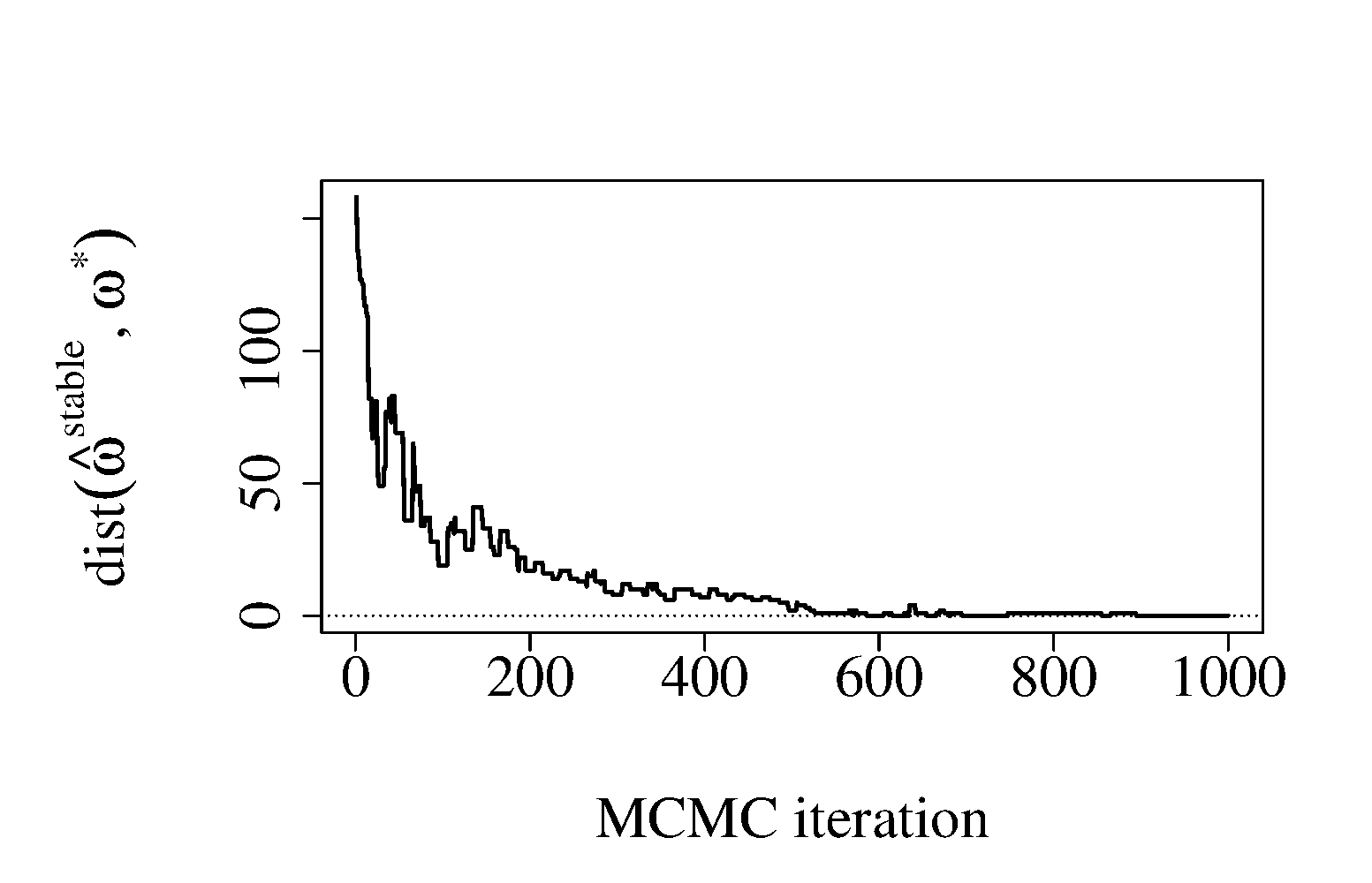
Next, we illustrate the selection procedure based on MCMC-CLS2 (Algorithm 2). We draw a random sample of observations from the model described above with , , and . This corresponds to 200 strongly redundant variables and 50 independent variables. We applied Algorithm 2 with and (corresponding to the AIC penalty). In Figure 1 (b), we show the relative frequencies of the components, , , in MCMC iterations. As expected, the uncorrelated sub-likelihood components (components 201–250) are sampled much more frequently than the redundant ones (components 1–200). Figure 1 (c) shows the objective function (up to a constant) evaluated at the best solution computed from past MCMC samples (). Figure 1 (d) shows the Hamming distance, , between the current selected rule, and true optimal value, . Overall, our algorithm quickly approaches the optimal solution and the final selection has 94.0% asymptotic relative efficiency (ARE) compared to MLE. When no stochastic selection is applied and all 250 sub-likelihood components are included, the relative efficiency is only 13%. As far as computing time is concerned, our non-optimized R implementations of the MCMC-CLS1 and MCMC-CLS2 algorithms for the above example takes, respectively 4.25 and 1.87 seconds per MCMC iteration, respectively. The computing time was measured on a laptop computer with Intel ®Core i7-2620M CPU 2.70GHz.
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
5.2 Exchangeable Normal Variables with Unknown Correlation
Let , where and is the unknown parameter of interest. The marginal univariate sub-likelihoods do not contain information on , so we consider pairwise sub-likelihoods
| (18) |
where and . Given , we estimate by solving the composite score equation by Newton-Raphson iterations where each pairwise score
| (19) |
is a cubic function of . It is well known that the composite likelihood estimation can lead to poor results for this model. ? carries out asymptotic variance calculations, showing that efficiency losses compared to MLE occur whenever , with more pronounced efficiency losses for near . Particularly, if (exactly one pair), ; if , ARE=1 if approaches or . The next simulation results show that in finite samples composite likelihood selection is advantageous even in such a challenging situation.
Since closed-form pairwise score expressions are available for this model, we use the objective function based on the one-step jackknife with pseudo-values computed as in Equation (9). In Table 3, we present results from Monte Carlo runs of the MCMC-CLS algorithm applied to the model with dimensions, which correspond to sub-likelihoods, respectively. We compute Monte Carlo estimates for the finite-sample relative efficiency , where denotes the Monte Carlo estimate of the finite-sample variance is the estimator selected by the MCMC-CLS algorithm, while is the all pairwise (APW) estimator obtained by including all available pairs (thus indicates that our stochastic selection outperforms no selection). We show values of around , since they correspond to the largest asymptotic efficiency losses of pairwise likelihood compared to MLE (see ?, Figure 1). In all considered cases, our stochastic selection method improves the efficiency of the estimator based on all pairwise components; at the same time, our composite likelihoods employ a much smaller number of components. For example, when the efficiency improvements range from 8% to 39%, using only about half of the available components.
| 10 | 28 | 45 | 10 | 28 | 45 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1.27(0.03) | 1.11(0.01) | 1.07(0.01) | 1.15(0.01) | 1.12(0.01) | 1.06(0.01) | ||||
| No. comp. | 5.83(0.09) | 13.70(0.16) | 21.12(0.22) | 7.30(0.08) | 13.82(0.16) | 21.45(0.22) | |||
| 1.36(0.02) | 1.14(0.01) | 1.06(0.01) | 1.19(0.01) | 1.11(0.01) | 1.06(0.01) | ||||
| No. comp. | 5.51(0.08) | 13.32(0.07) | 20.96(0.22) | 7.01(0.07) | 13.64(0.18) | 21.23(0.22) | |||
| 1.39(0.02) | 1.17(0.01) | 1.10(0.01) | 1.38(0.02) | 1.14(0.01) | 1.08(0.01) | ||||
| No. comp. | 5.80(0.08) | 12.60(0.16) | 20.99(0.20) | 5.39(0.08) | 13.27(0.15) | 21.45(0.21) | |||
5.3 Real Data Analysis: Australian Breast Cancer Family Study
In this section, we apply the MCMC-CLS algorithm to a real genetic dataset of women with breast cancer obtained from the Australian Breast Cancer Family Study (ABCFS) (?) and control subjects from the Australian Mammographic Density Twins and Sisters Study (?). All women were genotyped using a Human610-Quad beadchip array. The final data set that we used consisted of a subset of 20 single nucleotide polymorphisms (SNPs) corresponding to genes encoding a candidate susceptibility pathway, which is motivated by biological considerations. After recommended data cleaning and quality control procedures (e.g., checks for SNP missingness, duplicate relatedness, population outliers (?)), the final data consisted of observations ( cases and controls).
To detect group effects due to cancer, we consider an extension of the latent multivariate Gaussian model first introduced by ?. Let , , be independent observations of a multivariate categorical variable measured on subjects. Each variable can take values or , representing the copy number of one of the alleles of SNP of subject . The binary variable or represents disease status of the th subject (0 = control and 1 = disease). We assume a latent random -vector , where is a conditional mean vector with elements and is the correlation matrix. Our main interest is on the unknown mean parameter , which is common to all the SNP variables and represents the main effect due to disease. We assume , , and , where and are SNP-specific thresholds. The above model reflects the ordinal nature of genotypes and assumes absence of the Hardy-Weinberg equilibrium (HWE) (allele frequencies and genotypes in a population are constant from generation to generation). If the HWE holds the parameters and are not needed, since we have the additional constraint .
Let and define intervals to be , and , corresponding to and , respectively. The full log-likelihood function is
where is the pdf of the -variate normal density function with mean and correlation matrix . Clearly, the full log-likelihood function is intractable when is moderate or large, due to the multivariate integral in the likelihood expression. Note that for the marginal latent components, we have , so and can be estimated by minimizing the one-wise composite log-likelihood
| (20) | ||||
| (21) |
where denotes the normal pdf with mean and unit variance. We focus on using the one-wise composite log-likelihood in this section, except when is to be estimated where we use pairwise composite log-likelihood. Differently from the expression in ?, the disease group effect is common to multiple sub-likelihood components; also, we allow for the inclusion/exclusion of particular sub-likelihood components (corresponding to SNPs) by selecting .
| (a) | (b) |
 |
 |
| (c) | (d) |
 |
 |
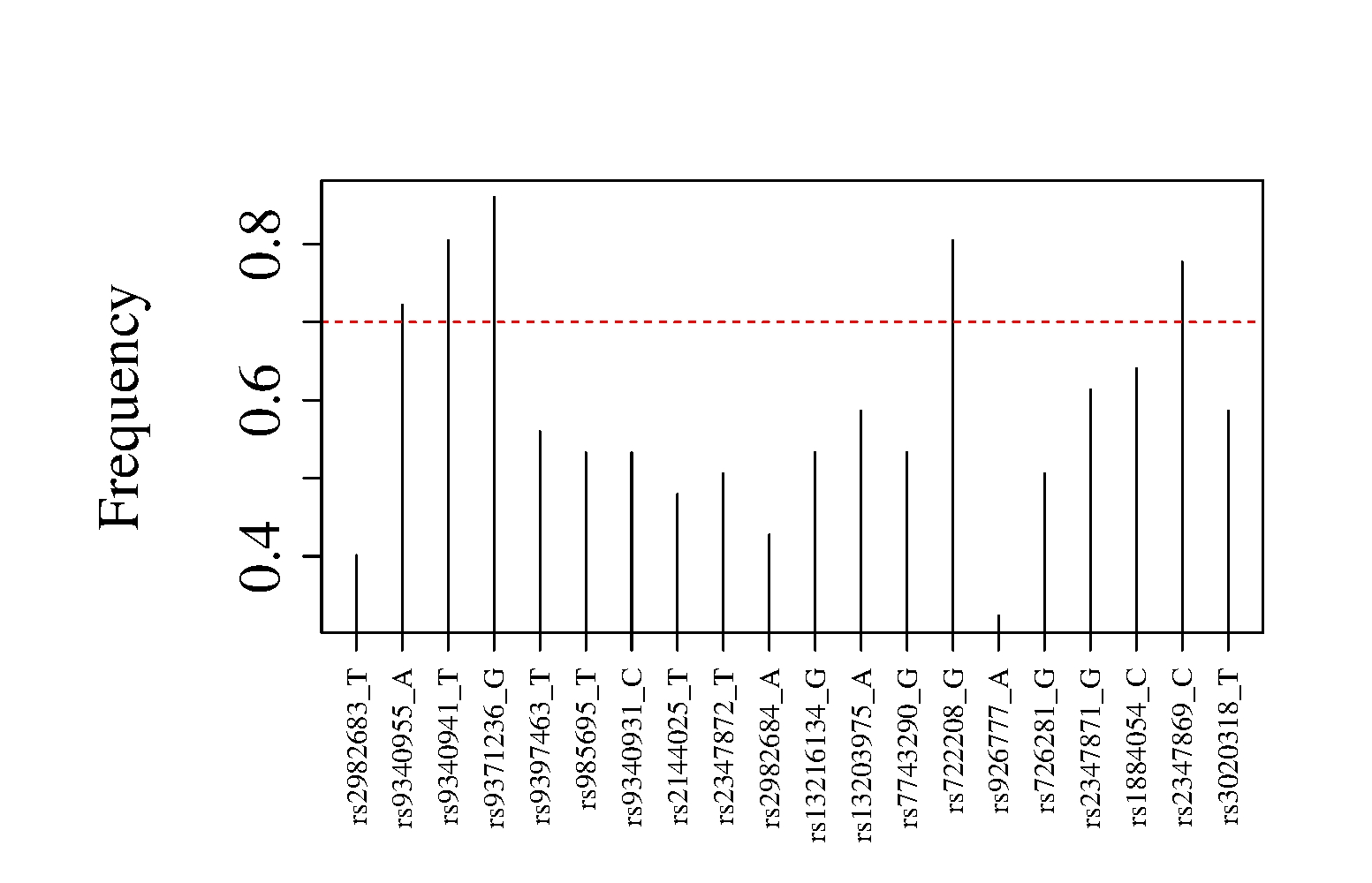
We estimated the optimal composition rule based on Gibbs samples from Algorithm 1, where the objective function was estimated by delete-10 jackknife. We selected five marginal likelihoods (SNPs) occurring with at least frequency in 250 runs of the Gibbs sampler (see Figure 2 (a)). In Figure 2 (b), we show the trajectory of the objective function evaluated at the current optimal solution (optimal solutions are computed from past samples using a threshold). The estimated variance tends to sway toward the minimum as more composition rules are drawn by our Gibbs sampler. This behavior is in agreement with preliminary simulation results carried out on this model (not presented here) as well as the examples presented in Sections 5.1 and 5.2.
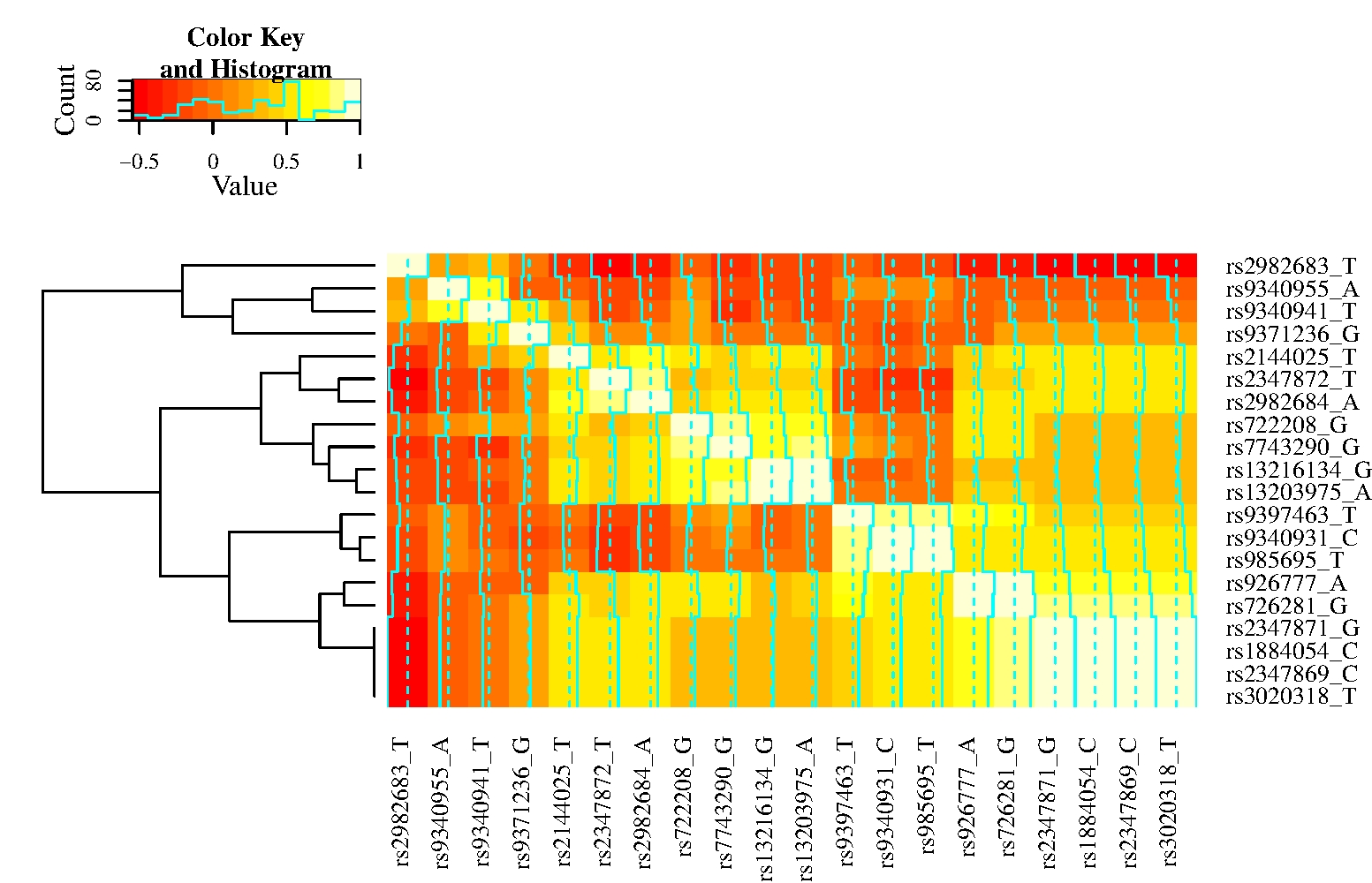
Figure 2 (c) shows the empirical distribution of parameter estimates, , based on sampled vectors , . The vertical dashed line corresponds to the selected parameter estimate , which is located near the mode of the empirical distribution. Particularly, the selected McLE is and the corresponding delete-10 jackknife standard error is . The McLE based on using all 20 target SNPs is with the delete-10 jackknife standard error . Our estimator gives a substantial accuracy improvement, supporting the conclusion of a difference between case and control groups (i.e., ) with higher confidence. Finally, in Figure 2 (d), we show estimates for the correlation matrix for the target SNPs, based on the pairwise composite likelihood described in ?.
6 Final remarks
Composite likelihood estimation is a rapidly-growing need for a number of fields, due to the astonishing growth of data complexity and the limitations of traditional maximum likelihood estimation in this context. The Gibbs sampling protocol proposed in this paper addresses an important unresolved issue by providing a tool to automatically select the most useful sub-likelihoods from a pool of feasible components. Our numerical results on simulated and real data show that the composition rules generated by our MCMC approach are useful to improve the variance of traditional McLE estimators, typically obtained by using all sub-likelihood components available. Another advantage deriving from our method is the possibility to generate sparse composition rules, since our Gibbs sampler selects only a (relatively small) subset of informative sub-likelihoods while discarding non-informative or redundant components.
In the present paper, likelihood sparsity derives naturally from the discrete nature of our MCMC approach based on binary composition rules with . On the other hand, the development of sparsity-enforcing likelihood selection methods suited to real-valued weights would be valuable as well and could result in more efficient composition rules. For example, ? discuss the optimality of composite likelihood estimating functions involving both positive and negative real-valued weights. Actually, the row averages computed in Step 2 of Algorithm 1 can also be used to replace in defined by (2), providing a composite log-likelihood with between-0-and-1 weights. It would be of interest to see how well this form of composite log-likelihood gets on in regard to the efficiency. This, however, was not pursued in this paper and is left for future exploration. Finally, the penalized version of the objective function described in Section 4 enforces sparse likelihood functions, which is necessary in situations where the model complexity is relatively large compared to the sample size. Thus developing a thorough theoretical understanding on the effect of the penalty on the selection as would be very valuable for improved selection algorithm in high-dimensions.
REFERENCES
- [2] [] Besag, J. (1974), “Spatial interaction and the statistical analysis of lattice systems,” Journal of the Royal Statistical Society. Series B (Methodological), pp. 192–236.
- [4] [] Brooks, S., Friel, N., and King, R. (2003), “Classical model selection via simulated annealing,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 65(2), 503–520.
- [6] [] Claeskens, G., and Hjort, N. L. (2008), Model selection and model averaging, Vol. 330 Cambridge University Press Cambridge.
- [8] [] Cox, D. R., and Reid, N. (2004), “A note on pseudolikelihood constructed from marginal densities,” Biometrika, 91(3), 729–737.
- [10] [] Dite, G. S., Jenkins, M. A., Southey, M. C., Hocking, J. S., Giles, G. G., McCredie, M. R., Venter, D. J., and Hopper, J. L. (2003), “Familial risks, early-onset breast cancer, and BRCA1 and BRCA2 germline mutations,” Journal of the National Cancer Institute, 95(6), 448–457.
- [12] [] George, E. I., and McCulloch, R. E. (1993), “Variable selection via Gibbs sampling,” Journal of the American Statistical Association, 88(423), 881–889.
- [14] [] Hall, P., Horowitz, J. L., and Jing, B.-Y. (1995), “On blocking rules for the bootstrap with dependent data,” Biometrika, 82(3), 561–574.
- [16] [] Han, F., and Pan, W. (2012), “A Composite Likelihood Approach to Latent Multivariate Gaussian Modeling of SNP Data with Application to Genetic Association Testing,” Biometrics, 68(1), 307–315.
- [18] [] Heyde, C. C. (1997), Quasi-likelihood and its application: a general approach to optimal parameter estimation. Springer.
- [20] [] Lindsay, B. G. (1988), “Composite likelihood methods,” Contemporary Mathematics, 80, 221–239.
- [22] [] Lindsay, B. G., Yi, G. Y., and Sun, J. (2011), “Issues and Strategies in the Selection of Composite Likelihoods,” Statistica Sinica, 21(1), 71–105.
- [24] [] Meinshausen, N., and Bühlmann, P. (2010), “Stability selection,” Journal of the Royal Statistical Society: Series B (Statistical Methodology), 72(4), 417–473.
- [26] [] Odefrey, F., Stone, J., Gurrin, L. C., Byrnes, G. B., Apicella, C., Dite, G. S., Cawson, J. N., Giles, G. G., Treloar, S. A., English, D. R. et al. (2010), “Common genetic variants associated with breast cancer and mammographic density measures that predict disease,” Cancer research, 70(4), 1449–1458.
- [28] [] Qian, G. (1999), “Computations and analysis in robust regression model selection using stochastic complexity,” Computational Statistics, 14, 293–314.
- [30] [] Qian, G., and Field, C. (2002), “Using MCMC for logistic regression model selection involving large number of candidate models,” in Monte Carlo and Quasi-Monte Carlo Methods 2000 Springer, pp. 460–474.
- [32] [] Qian, G., and Zhao, X. (2007), “On time series model selection involving many candidate ARMA models,” Computational Statistics & Data Analysis, 51(12), 6180–6196.
- [34] [] Robert, C. P., and Casella, G. (2004), Monte Carlo statistical methods, Vol. 319 Citeseer.
- [36] [] Shao, J. (1992), “One-step jackknife for M-estimators computed using Newton’s method,” Annals of the Institute of Statistical Mathematics, 44(4), 687–701.
- [38] [] Varin, C., Reid, N., and Firth, D. (2011), “An Overview of Composite Likelihood Methods,” Statistica Sinica, 21, 5–42.
- [40] [] Weale, M. E. (2010), “Quality control for genome-wide association studies,” in Genetic Variation Springer, pp. 341–372.
- [41]