Particle acceleration in self-driven turbulent reconnection
Abstract
The theoretical prediction that magnetic reconnection spontaneously drives turbulence has been supported by magnetohydrodynamic (MHD) and kinetic simulations. While reconnection with externally driven turbulence is accepted as an effective mechanism for particle acceleration, the acceleration during the reconnection with self-driven turbulence is studied for the first time in this work. By using high-resolution 3D MHD simulations of reconnection with self-generated turbulence, we inject test particles into the reconnection layer to study their acceleration process. We find that the energy gain of the particles takes place when they bounce back and forth between converging turbulent magnetic fields. The particles can be efficiently accelerated in self-driven turbulent reconnection with the energy increase by about 3 orders of magnitude in the range of the box size. The acceleration proceeds when the particle gyroradii become larger than the thickness of the reconnection layer. We find that the acceleration in the direction perpendicular to the local magnetic field dominates over that in the parallel direction. The energy spectrum of accelerated particles is time-dependent with a slope that evolves toward -2.5. Our findings can have important implications for particle acceleration in high-energy astrophysical environments.
I Introduction
Almost all observed high-energy astrophysical processes indicate the existence of high-energy cosmic ray particles (e.g., Longair, 2011; Lhaaso Collaboration et al., 2021), the origin of which is one of the most important but unsolved problems in space physics and astrophysics. From a theoretical perspective, theories of three classical acceleration mechanisms, including stochastic acceleration (second-order Fermi), diffusive shock acceleration (first-order Fermi), and magnetic reconnection acceleration, have been developed to understand the observational phenomena in the solar wind and various astrophysical environments (see reviews by, e.g., Lazarian et al., 2020; Marcowith et al., 2020; Liu and Jokipii, 2021). The essence of a particle’s acceleration is the interaction between (turbulent) magnetic fields and particles, such as gyroresonant interaction and transit time damping (Kulsrud and Pearce, 1969; Schlickeiser, 2002; Yan and Lazarian, 2004; Xu and Lazarian, 2018; Zhdankin, 2022), mirror interaction (Lazarian and Xu, 2021) and other non-resonant interactions (Brunetti and Lazarian, 2016; Xu and Zhang, 2017; Comisso and Sironi, 2022; Bresci et al., 2022; Huang and Bhattacharjee, 2012), gradient drift and curvature drift in non-uniform magnetic fields (Caprioli and Spitkovsky, 2014; Marcowith et al., 2020; Guo et al., 2021). This work focuses on the magnetic reconnection acceleration of particles in the presence of turbulence that has been actively studied in recent years (e.g., Lazarian and Vishniac, 1999, hereafter LV99) and (de Gouveia dal Pino and Lazarian, 2005; Kowal et al., 2009; Beresnyak and Li, 2016; Li et al., 2019; Chitta and Lazarian, 2020; Jafari et al., 2021; Kadowaki et al., 2021; Zhang et al., 2021a, b; Xu and Lazarian, 2023).
The theoretical studies of magnetic reconnection date back to the 1950s (Sweet, 1958; Parker, 1957; Petschek, 1964), with intensive efforts devoted to explaining the reconnection rates indicated by observations (see Lazarian et al., 2020, for a recent review). Appealing to the ubiquitous turbulence as a trigger and regulator of the reconnection process, LV99 proposed a 3D turbulent reconnection model describing a fast reconnection process with a reconnection rate independent of micro-plasma effects. The fast reconnection of turbulent magnetic fields can lead to a more efficient transfer of magnetic energy to the kinetic energy of the fluid. These predictions have been confirmed by both non-relativistic (Kowal et al., 2009, 2017, 2020) and relativistic (Takamoto et al., 2015) MHD turbulence simulations. The LV99 model makes the modern MHD turbulence theory (Goldreich and Sridhar, 1995, hereafter GS95) self-consistent and predicts the rate of magnetic field diffusion in space that is consistent with simulations (Lazarian et al., 2004; Beresnyak, 2013). Very importantly, turbulent reconnection predicts that the classical magnetic flux-freezing theorem (Alfvén, 1942) is violated in turbulent fluids (Eyink, 2011).
Various astrophysical implications of the LV99 reconnection are reviewed in (Lazarian et al., 2020), including anomalous cosmic rays (Lazarian and Opher, 2009), nonlinear turbulent dynamo (Xu and Lazarian, 2016), (first) star formation (Stacy et al., 2022), gamma-ray bursts (Lazarian et al., 2003; Zhang and Yan, 2011; Lazarian et al., 2019), microquasars (de Gouveia dal Pino and Lazarian, 2005, henceforth GL05), active galactic nuclei (AGNs: Kadowaki et al., 2015; Khiali and de Gouveia Dal Pino, 2016) and radio galaxies (Brunetti and Lazarian, 2016). By studying emissions from accelerated particles, one can get insight into the processes of turbulent reconnection.
Earlier studies on reconnection acceleration mostly focus on 2D reconnection models. Drake et al. (2006) considered the 2D reconnection and reported that the first-order Fermi acceleration can happen in this case. In the restricted 2D configuration, particles are trapped within contracting magnetic islands, i.e., plasmoids, which can arise from the plasma tearing instability when a long narrow current sheet is prescribed (see Loureiro et al., 2007). The trapping of particles within the islands limits the acceleration efficiency in 2D reconnection. Moreover, 2D magnetic islands are not tenable and susceptible to turbulence (given a sufficiently large system size) in 3D, where 3D open-ended loops are expected. As shown by MHD and kinetic simulations (e.g., Cargill et al., 2012; Li et al., 2019; Vlahos et al., 2019; Zhang et al., 2021a, b), 3D reconnection acceleration is more efficient than their 2D counterpart. In analogy to the classical diffusive shock acceleration (first-order Fermi), where particles are confined in the vicinity of a shock, GL05 first proposed that a first-order Fermi process operates within the 3D turbulent reconnection region. Particles are confined in the converging magnetic fluxes of opposite polarity (e.g., see Fig. 1 in Nowak et al., 2021) and bounce back and forth between the reconnection-driven inflows. A more rigorous study on turbulent reconnection acceleration is recently carried out by (Xu and Lazarian, 2023). They found an efficient acceleration in the presence of reconnection-driven turbulence and non-universal particle energy spectral indices depending on the reconnection rate. We note that, unlike the shock acceleration, fluid compressibility (Drury, 2012) is not necessary for reconnection acceleration to happen. The testing of the GL05 picture was performed by (Kowal et al., 2011) using 3D turbulent reconnection simulations (Kowal et al., 2009). (Kowal et al., 2011) provided the first numerical demonstration of the volume-filling reconnection that happens in the 3D case. They further showed that the reconnection acceleration is efficient in the presence of turbulence.
The injection mechanism of turbulence varies in different astrophysical environments, but in general, it can be divided into externally driven turbulence and spontaneously driven one. For instance, supernova explosions (Norman and Ferrara, 1996; Ferrière, 2001), merger events and AGN feedback (Chandran, 2005; Subramanian et al., 2006; Enßlin and Vogt, 2006) and baroclinic forcing behind shock waves (Inoue et al., 2013; Hu et al., 2022; Dhawalikar et al., 2022) are frequently also quoted by the sources of turbulence. In addition, various instabilities such as magnetorotational instability in accretion disks (Balbus and Hawley, 1998) and kink instability of twisted flux tubes in the solar corona (Gerrard and Hood, 2003) can also excite turbulence. Particularly, turbulence can be driven by magnetic reconnection itself as suggested in LV99 and (Lazarian and Vishniac, 2009). Numerical studies on reconnection-driven turbulence are very challenging because they require high resolution and a long computational time to reach a steady state. Attempts including (Beresnyak, 2017) for incompressible medium, and (Oishi et al., 2015) and (Huang and Bhattacharjee, 2016) for compressible medium demonstrate the generation of turbulence by reconnection.
The dynamical evolution and statistical properties of reconnection-driven turbulence (initiated by stochastic noise) were studied by Kowal et al. (2017). They found that the reconnection produces a Kolmogorov-like spectrum of velocity fluctuations with the anisotropic scaling following the relation predicted in GS95, where and are the parallel and perpendicular scales of a turbulent eddy with respect to the local magnetic field.111The notion “local” means that the scaling of turbulent eddies is measured with respect to the local magnetic field in the direct vicinity of these eddies, rather than with respect to the global mean magnetic field. This notion was absent in the original GS95 treatment, but introduced later in LV99 and Cho and Vishniac (2000). The actual notion of eddies in strong Alfvénic turbulence is based on the LV99 finding that the turbulent reconnection takes place over just one turnover of eddies.
Furthermore, Kowal et al. (2020) found that the Kelvin-Helmholtz instability dominates over the tearing instability for the generation of turbulence in the 3D reconnection layer, while the tearing instability is only important at the initial stage of the reconnection. In the absence of external driving, the reconnection-driven turbulence in 3D enables fast reconnection.
Our goal is to numerically study particle acceleration in 3D magnetic reconnection with reconnection-driven turbulence, which has not been numerically investigated. By performing high-resolution MHD simulations, we will examine the effect of reconnection-driven turbulence on reconnection acceleration and acceleration efficiency. In Section II, we describe the numerical methods for reconnection simulations with reconnection-driven turbulence and test particle simulations. Section III presents our numerical results for reconnection acceleration. Finally, we provide a discussion in Section IV and a summary in Section V.
II Simulation Methods
II.1 Reconnection simulations with reconnection-driven turbulence
A high-order shock-capturing Godunov-type code AMUN222https://bitbucket.org/amunteam/amun-code/ is adopted to solve a set of equations for isothermal compressible magnetohydrodynamics
| (1) | |||
| (2) | |||
| (3) | |||
| (4) |
where is the plasma density, v the fluid velocity, B the magnetic field, the isothermal sound speed, the viscosity coefficient, and the identity matrix. With Ohm’s law, the electric field can be written as
| (5) |
where is the current density and is the Ohmic resistivity coefficient. In addition, an isothermal equation of state is used to supplement the above equations. The MHD equations (1)-(4) were integrated numerically using 3th-order 4-stage Strong Stability Preserving Runge-Kutta method (Gottlieb et al., 2011), 7th-order Compact Monotonicity Preserving interpolation (Suresh and Huynh, 1997) to reconstruct the Riemann states, and the HLLD Riemann solver (Mignone, 2007).
Our numerical simulations are performed in a 3D domain with physical dimensions of , , and (), fixing the domain center at the origin of Cartesian coordinates. We consider periodic boundary conditions along the and axes and an open one along the axis. Uniform initial density is set to be in the upstream region, and within the current sheet, its value increases to make the total pressure uniform in the entire domain. The initial antiparallel magnetic field with the strength of is set along the axis, with a single discontinuity of the -component of the magnetic field placed in the middle of the box on the - plane, and the guide field strength of along the axis.333This work is limited to a single guide field strength. Note that recent kinetic scale simulations have claimed that the guide field plays a critical role in the reconnection acceleration of particles (Dahlin et al., 2015; Li et al., 2017; Arnold et al., 2021). However, MHD-scale turbulent reconnection simulations claimed that the contribution of the guide field does not change the dynamics of magnetic reconnection and its reconnection rate (Beresnyak, 2012, 2017). More confirmation is needed. These settings result in the dimensionless fluid velocity and the simulation time units to be and , respectively. Since the AMUN code runs with the normalized magnetic field multiplied by a factor , Alfvén velocity using the code units is . Furthermore, the initial random velocity field with an amplitude of at the fixed wavenumber of is represented by Fourier modes of random phases and directions, being limited in the spatial region within the distance of from the initial magnetic field discontinuity (see Kowal et al., 2017, for more details). Besides, the isothermal sound speed is set to be , resulting in a plasma parameter of . To control the effects of numerical diffusion, we set the viscosity and resistivity coefficients to be . We terminate our simulation at the time of , the snapshot of which is adopted to explore test particle acceleration.
II.2 Test particle simulations
The equation of motion for a charged particle is given by
| (6) |
where is the Lorentz factor of relativistic particle, and is the speed of light. The symbols u, , and are the particle velocity, mass, and electric charge, respectively. We focus on the acceleration processes resulting from the motional electric field , ignoring the possible acceleration from resistivity effects of the electric field, i.e., the last term in Equation (5). It has been demonstrated that the Fermi-type acceleration by the motional electric field dominates over the acceleration by non-ideal electric fields (Guo et al., 2019). In our study, we make sure that the resistivity effects of the electric field do not enter, as could also be from numerical resistivity. Therefore, Equation (6) is further rewritten as
| (7) |
With this equation, we integrate particle trajectories using the 8th order embedded Dormand-Prince method (Hairer et al., 2008) with an adaptive time step based on an error estimator.444In terms of the precision of long-term integration, we explore different methods for integrating particle trajectories such as a simple functional iteration, the implicit Gauss-Legendre method, and the explicit Runge-Kutta method. After taking into the numerical accuracy and calculation time account, we choose the 8th-order explicit Runge-Kutta method by Dorman & Prince with step control and dense output, using a very small precise control parameter of to ensure high-precision numerical output. This method has a higher accuracy than the classic 4th-order explicit Runge-Kutta method and has also been used in recent publications (Kowal and Falceta-Gonçalves, 2021; Zhang and Xiang, 2021) The local values of the plasma velocity v and magnetic field B at each step of the integration were obtained by cubic interpolation with the discontinuity detector based on a total variation diminishing limiter.
In our simulations, for our results not to be limited to a particular astrophysical system, all physical quantities are normalized to be dimensionless, and the results are applicable to studying the acceleration of relativistic particles in the nonrelativistic reconnection process. We consider the relativistic test particles with their speed close to the light speed that is larger than the Alfvén speed by several orders of magnitude. Therefore, we have , where is the velocity of turbulent magnetic reconnection. Since for a nonrelativistic reconnection process, the reconnection timescale is longer than the Alfvén wave crossing time (), which is much longer than the crossing time of a relativistic particle, we adopt a single snapshot from our reconnection simulation to perform the test particle simulations. In practice, with 10,000 protons as test particles that are injected instantly into a snapshot at , we integrate the evolution equation of particles over 0.1 in units of .555As in all numerical experiments, an optimal number of particles should be used. Our results presented below will not be changed with the number of particles if this number exceeds 5,000. Moreover, we find that after , the particle acceleration from one snapshot provides a representative result for all snapshots.
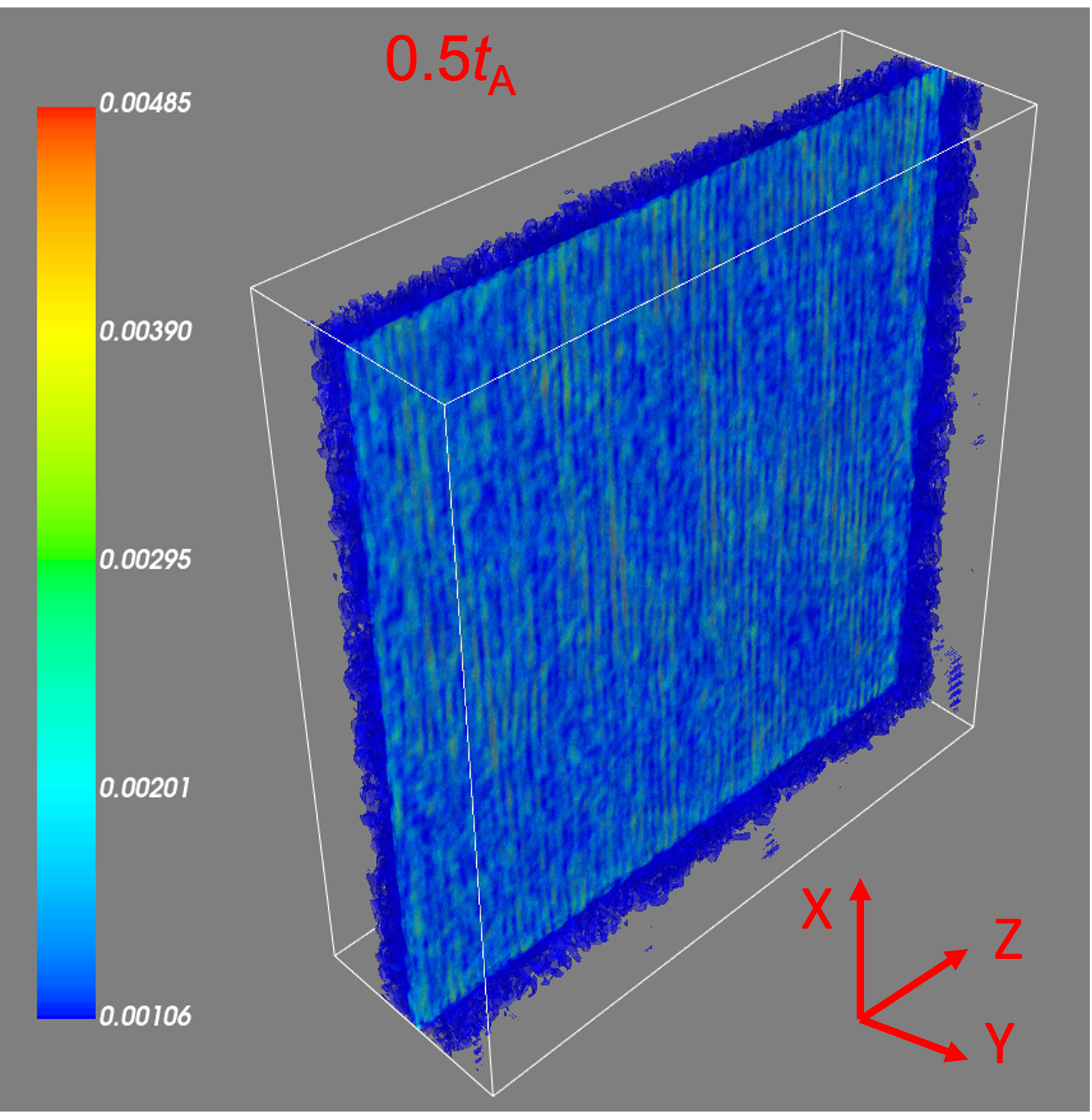
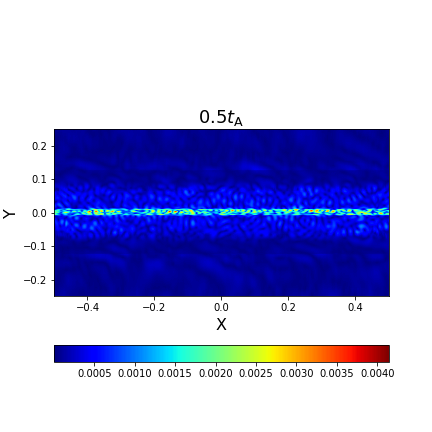
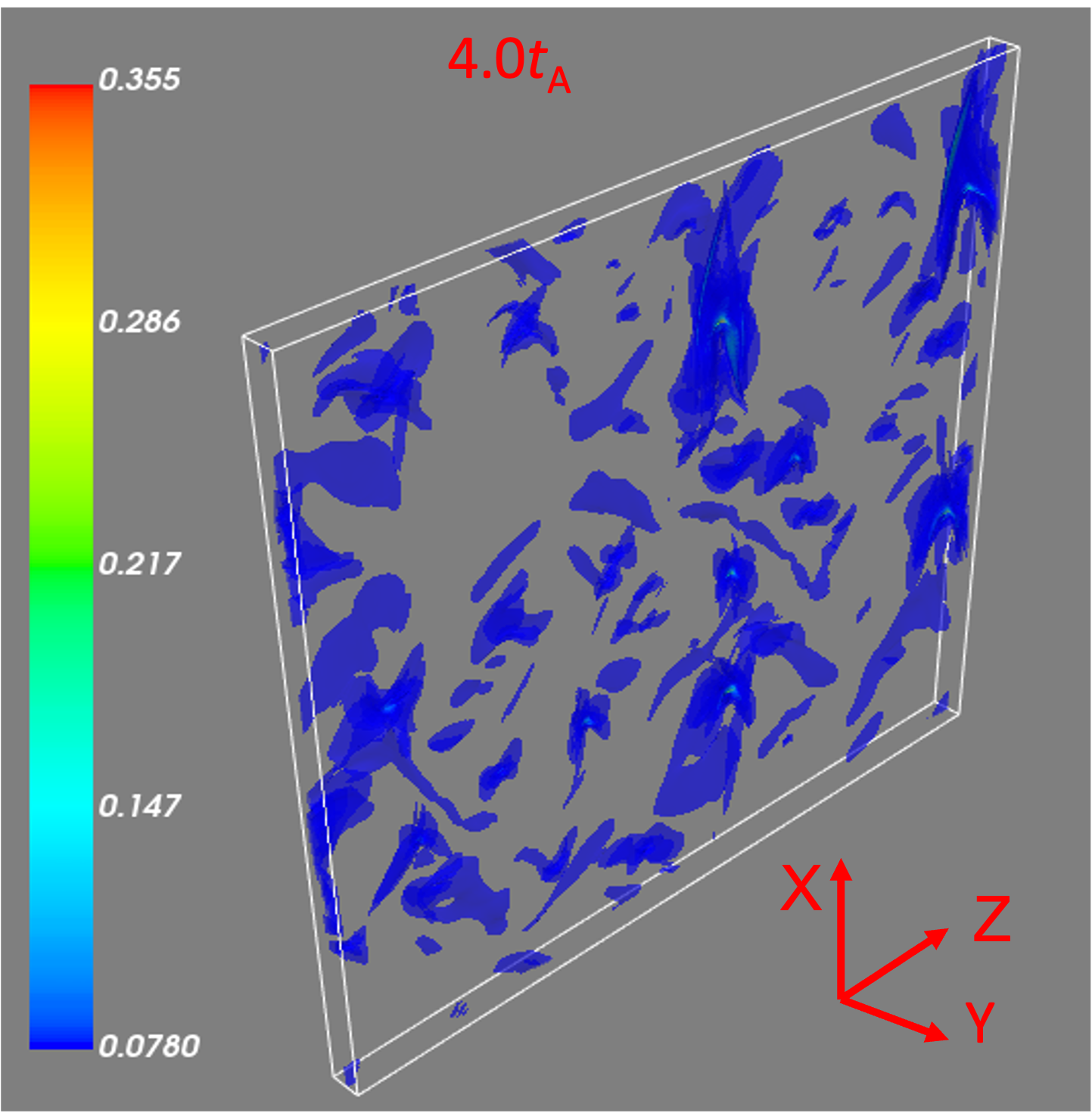
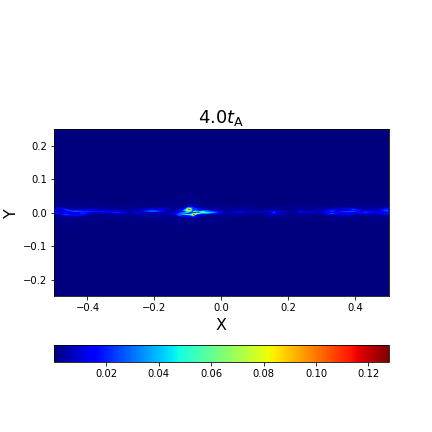
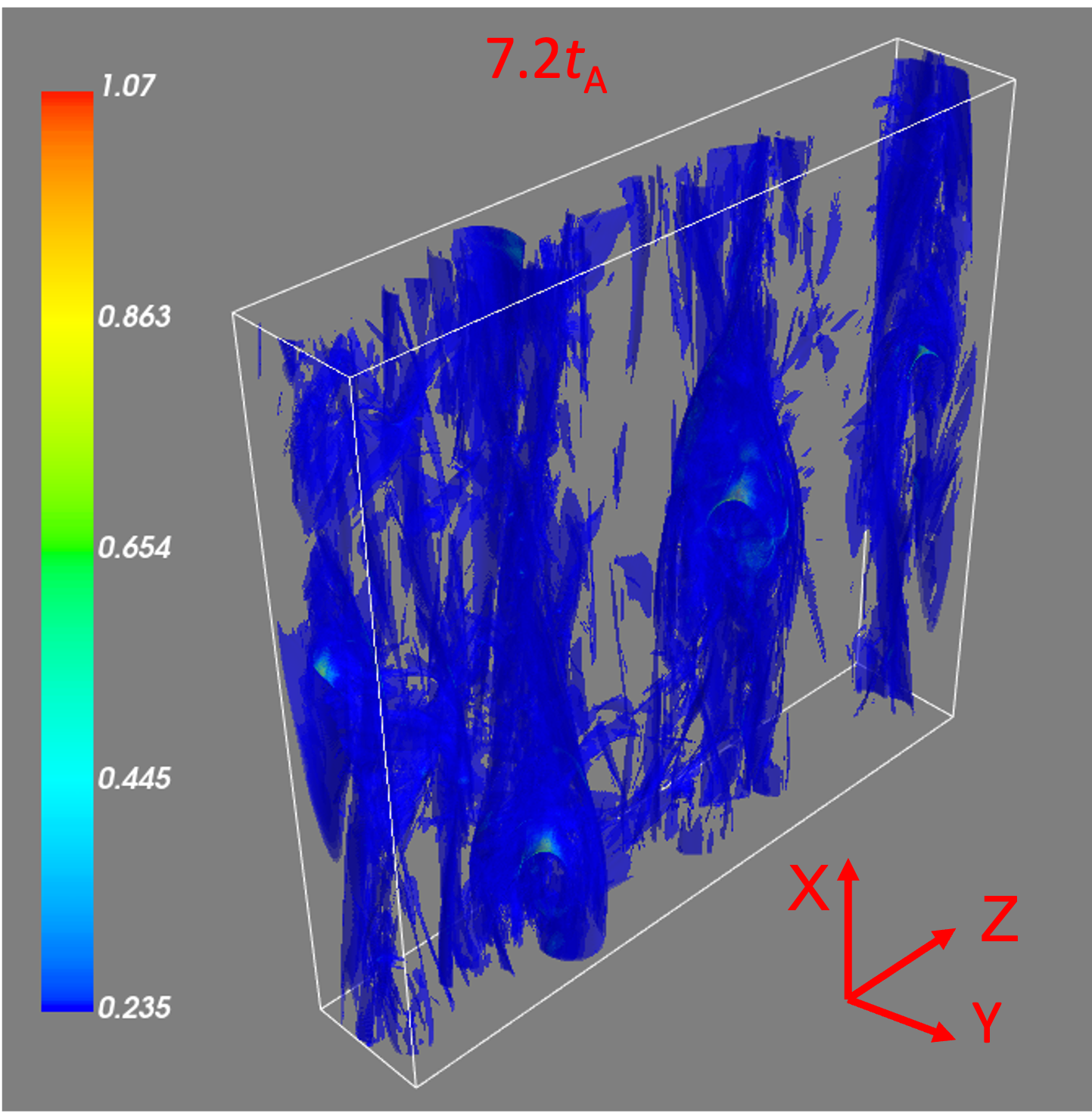
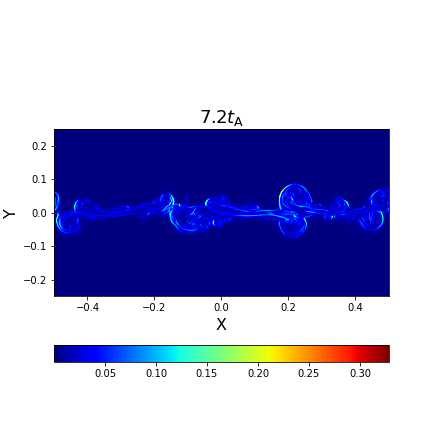
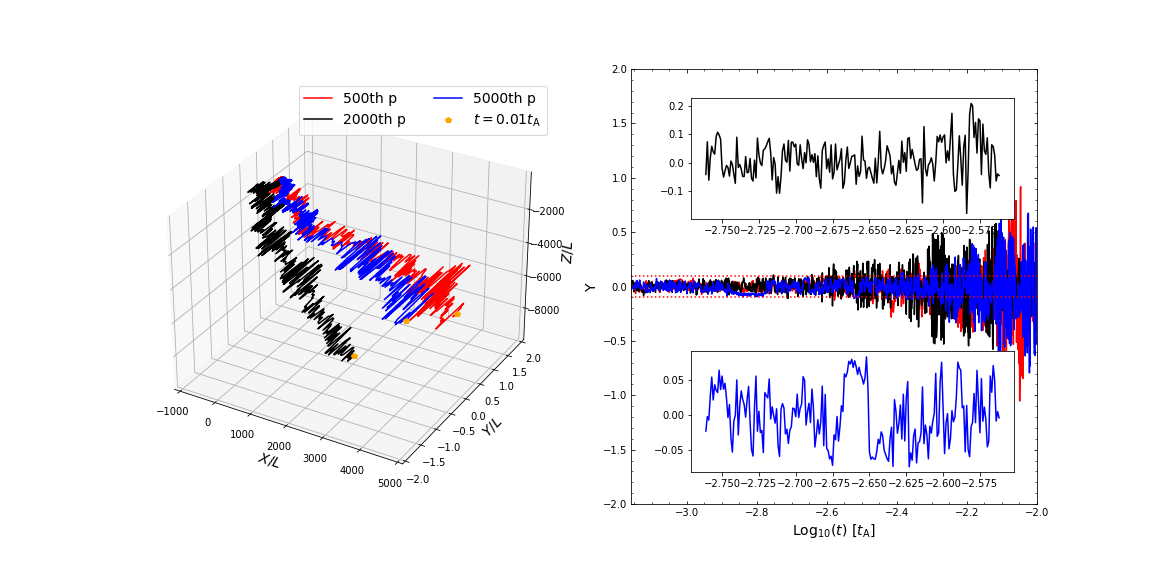
III Reconnection acceleration with reconnection-driven turbulence
III.1 Structures of turbulent reconnection layer
Before studying the acceleration of the test particles, we in this subsection first explore the evolution of the current sheet structure. With a high-resolution simulation of , we explore how the current sheet evolves during the spontaneously driven turbulent reconnection process. At the selected three snapshots 0.5, 4.0 and 7.2 , we present 3D distributions of the current density (see left column of Figure 1) and 2D slices of current density on the - plane at (see the right column of Figure 1). Here, the current density is obtained by . As seen, the current density with a noise-like structure is evenly distributed in a sheet-like plate at the early stage of evolution (). It then begins to form high current density clumps at (not shown in the paper). When the system evolves to , we see a very inhomogeneous distribution of the current density. This is probably because the initial stochastic noise triggers various MHD instabilities (e.g., Kelvin-Helmholtz and tearing instabilities) that make the current sheet fragment. As the system evolves further, the current sheet begins to thicken and forms a significant magnetic flux rope with a multi-scale complex structure at (not shown). With the periodic conditions set along the outflow directions, outflows do not leave the system, which leads to a continuous accumulation of energy. At later times, the reconnection layer is slowly eating through the undisturbed fluid, and reconnection-driven turbulence is fueled by the free energy of the oppositely directed magnetic fields. This will cause the current sheet to slowly widen and increase the volume of the reconnection layer with a lower growth rate. The detailed statistical analysis of the reconnection simulation demonstrates that MHD turbulence with Kolmogorov turbulent energy spectrum and scale-dependent turbulence anisotropy (GS95, LV99) is well developed at . Therefore, we stop our simulation at .
With a similar setup, Kowal et al. (2017) discussed the boundary effect on reconnection (see also Beresnyak (2017) for periodic conditions in the three directions). Recently, our reconnection-driven turbulence simulation by MHD-PIC considered a reflective boundary in the direction perpendicular to the current sheet and found that a reflective boundary makes larger-scale reconnection structures (Liang et al., 2023). Nevertheless, the problem of periodic boundary conditions will be further investigated and quantified in future work. As shown in Figure 1, we observe that the evolution of stochastic reconnection leads to the formation of thickening regions in the current density. This broadened reconnection layer over the range provides a favorable place for the rapid acceleration of particles. The acceleration efficiency of particles in reconnection strongly depends on the reconnection rate, i.e., the inflow speed driven by reconnection (Xu and Lazarian, 2023), which can be measured as the growth speed of the current layer width, i.e., at (see Beresnyak, 2017; Kowal et al., 2017, for more details). Although the width of the reconnection layer increases constantly, the reconnection rate almost remains its stable value, which is similar to the results in Kowal et al. (2017) and Beresnyak (2017).
III.2 Reconnection acceleration
III.2.1 Trajectory analysis of particles
With 3D data cubes taken from the above-mentioned reconnection simulation at the final snapshot of , we perform test particle simulations to study the acceleration of particles that interact with reconnecting turbulent magnetic fields. As an example, the left panel of Figure 2 presents the trajectories of three test particles with the almost same initial location inside the reconnection layer. As shown in this panel, the particles are confined in the vicinity of the reconnection region () to gain their kinetic energy by repeatedly bouncing back and forth off the inflows.
The right panel of Figure 2 further illustrates the motions of particles in the direction of the axis (along the inflow directions) as a function of time, in which we also show two zoomed-in parts to illustrate the more details. The boundaries of the reconnection layer are indicated by the horizontal dotted lines. It can be seen that with the increase of particle energy, the acceleration proceeds with the particle moving beyond the reconnection layer after .
III.2.2 Particle acceleration processes
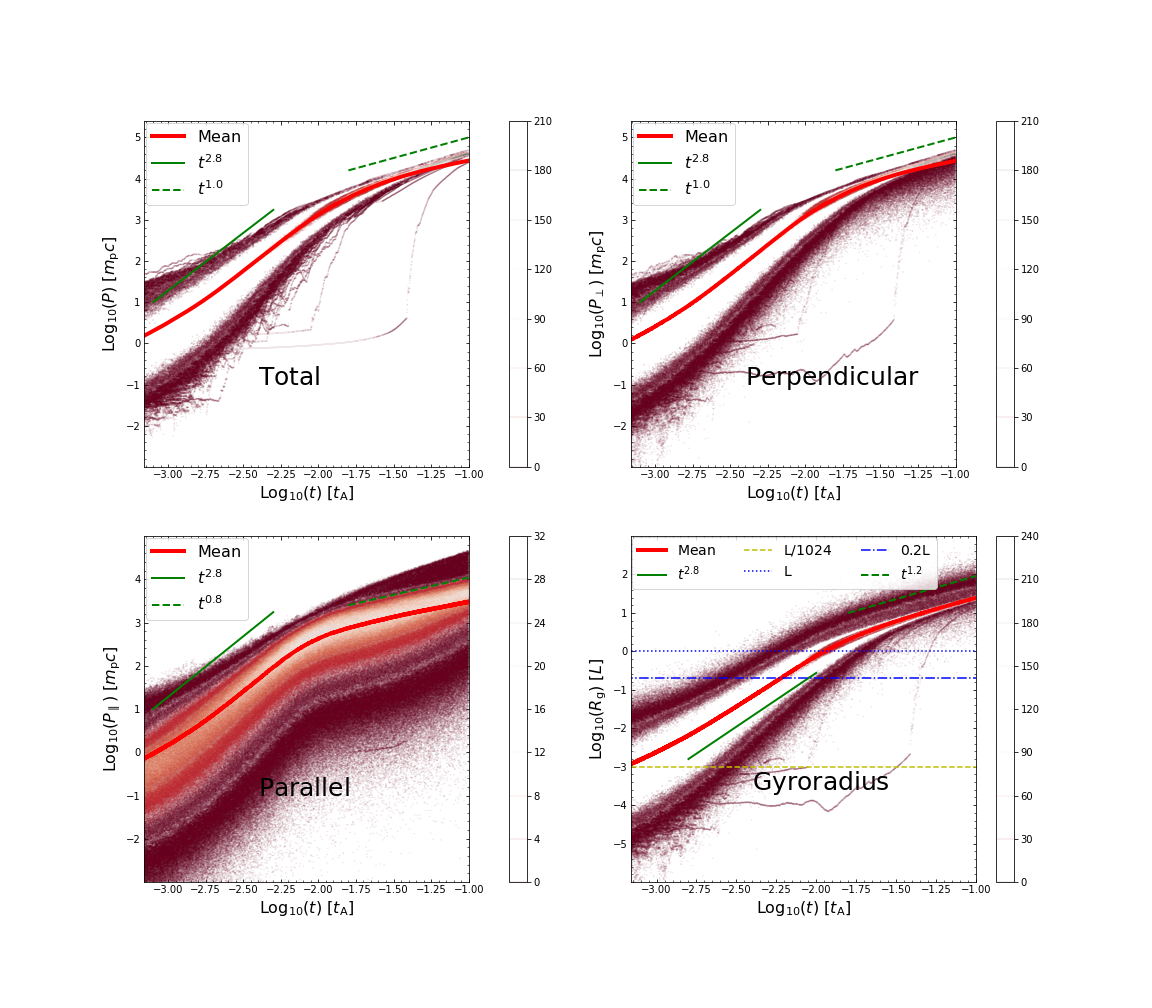
When particles are confined within and near the reconnection layer, they are accelerated with continuous energy gain. As an example, Figure 3 shows the total (left upper), perpendicular (right upper), and parallel (left lower) momentum of a test particle (normalized by , where is the proton mass) as a function of its location in the direction. The perpendicular and parallel components of momentum are measured with respect to the local magnetic field. The acceleration during turbulent reconnection leads to an energy increase of about 3 orders of magnitude in a zig-zag manner. The inset is a zoom-in to clearly show that the particle gains energy via bouncing back and forth crossing the reconnection layer many times. As argued in Xu and Lazarian (2023), the kinetic energy of the reconnection-driven inflows is transferred to particles via their repeated head-on collisions. The lower right panel shows the distributions of the gyroradius of the particle, , where is the particle perpendicular momentum. With the increase of particle energy, generally increases with time. Its large fluctuations are mainly caused by both the large fluctuations of the magnetic fields (mainly and components) and velocities in the reconnection region.
The total , perpendicular and parallel momentum, and gyroradius of all 10,000 test particles as a function of the time are shown in Figure 4, where the red thick solid lines represent the mean values and the color scales indicate their distribution. In the right lower panel, the horizontal dotted and dashed lines indicate the box scale in the and directions, and the grid size of , respectively, while the blue dash-dotted line indicates the approximate thickness of the reconnection layer. As shown, the momentum and gyroradius of particles all increase with time, roughly following , with the energy increase by about 3 orders of magnitude in the range of box size. The increase of both parallel and perpendicular momentum of particles is consistent with the theoretical expectation in Xu and Lazarian (2023) and previous simulations (e.g., Kowal et al., 2011; del Valle et al., 2016). When the gyroradius of particles is greater than the box size, we see a shallower power law of approximately () due to our periodic boundary conditions. During this stage, the gain of energy is due to a much slower drift acceleration caused by gradients of large-scale magnetic fields in the perpendicular direction (see the right upper panel). The presence of a guide field allows the particles to slightly accelerate in the parallel direction as well (see the left lower panel for ).
As shown in Figures 3 and 4, during the exponential growth phase with the power law of , the gyroradius of the accelerated particles becomes comparable to the size of the box. To confine the particles around the reconnection layer, the Larmor radius of particles should be smaller than the box size , where the maximum energy can be estimated by . However, due to the setting of periodic boundary conditions, the particles can be continuously accelerated with a lower acceleration efficiency (with ) after . We would like to stress that the energy increase by three orders of magnitude seen in the simulation is limited by the box size, corresponding to three orders of magnitude of the particle gyroradius, beyond which the energy increase is due to the consideration of periodic boundary conditions.
Our simulations show that particles with both smaller and larger than the thickness of the reconnection layer () can be accelerated. In the former case, particles bounce back and forth within the reconnection layer, while in the latter case, particles gyrate around the reconnection layer. Theoretical models for turbulent reconnection acceleration in these two different cases can be found in de Gouveia dal Pino and Lazarian (2005); Lazarian et al. (2012); Xu and Lazarian (2023) (see also Figure 2). The numerical demonstration has been carried out by MHD simulations for the former case Kowal et al. (2011); Kowal et al. (2012a); del Valle et al. (2016) and by kinetic simulations for the latter case Zhang et al. (2021b, a). Here, we clearly see both cases in a self-driven reconnection for the first time (to our knowledge).
III.2.3 Spectral energy distribution of accelerated particles
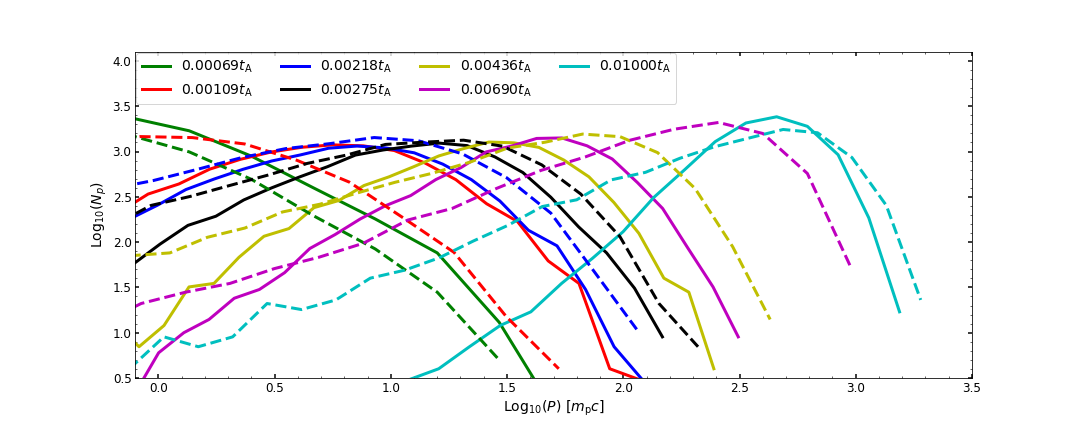
Spectral energy distributions of accelerated particles are plotted in Figure 5 at the integration time , , , , , , and , which correspond to the acceleration processes within and around the reconnection layer. The upper panel of this figure shows the spectra of momentum components perpendicular and parallel to the local magnetic field by the solid and dashed lines, respectively. Note that the particles are injected with an initial Gaussian distribution of energies, which are decomposed into perpendicular and parallel components. With increasing integration time, as a result of reconnection acceleration, particle energy spectra shift to higher and higher energies. Spectral continuously broadening is not very clear as we use instant injection. As seen, the acceleration in the perpendicular direction dominates an increase of particle energy only at an early time before about . Most time, the acceleration in the parallel direction dominates the energy increase.
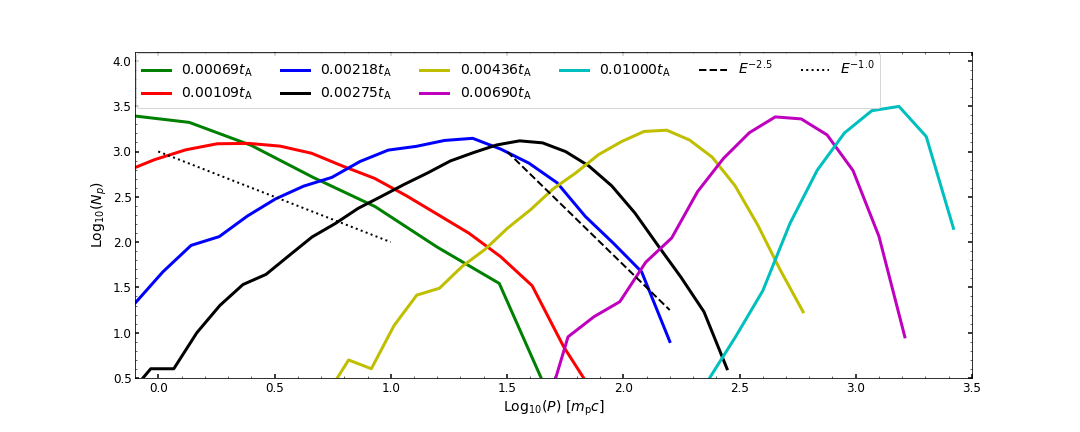
The lower panel of Figure 5 presents the time evolution of the spectrum of total particle momentum. Most time the total energy spectrum follows that of the perpendicular energy. The energy distribution of accelerated particles exhibits a non-thermal tail which is estimated as a power-law distribution of , where the spectral index evolves from approximately 1.0 to 2.5. The slope 2.5 is consistent with the theoretical expectation in Xu and Lazarian (2023) for nonrelativistic reconnection acceleration with a weak guide field (see also de Gouveia dal Pino and Lazarian, 2005). Here, we do not consider the escape of particles from the box in our simulations. This setup is applicable to the case when the escape from the entire system happens much slower than the acceleration. Indeed, we observe that during our simulation, particles are mainly confined in and around the reconnection layer (see Figure 2). So the escape from the entire system is relatively slow. As we do not continuously inject new particles at low energies, with the acceleration of the bulk population, the minimum energy and the peak of the energy distribution both move to higher and higher energies with the increase of simulation time. During the exponential growth process of that we are interested in, the energy particles can reach is limited by our box size. As a result, it is difficult to see an extended power-law tail of the accelerated particles. During the early time of the particle simulation, a power-law shape can be seen over approximately one order of magnitude in energies.
As here we deal with the acceleration process with spatial inhomogeneity (see Figure 1). The “escape” can happen locally from a region with a higher level of turbulence and higher reconnection efficiency (and thus higher acceleration efficiency) to a region with a lower level of turbulence and lower reconnection efficiency (and thus lower acceleration efficiency). This local “escape” may affect the measured spectral shape. We note that the local “escape” can be time-dependent with the increase of particle gyroradius from a value much smaller than the largest thickness of the reconnection layer to a value larger than it.
The particle energy spectra we obtained are similar to those obtained in other particle-in-cell (PIC) and MHD simulations (e.g., Cerutti et al., 2013; Guo et al., 2014; Kowal et al., 2012b; Medina-Torrejón et al., 2021; Pezzi et al., 2022). The non-thermal power-law tail cannot further extend to higher energies. In realistic astrophysical systems with a limited size, e.g., in the black hole X-ray binary jets, the direct solution of the Fokker Planck equation controlling electron evolution also predicts a non-thermal tail with non-extending power-law features Zhang et al. (2018). In the former case considered here, the smallest energy of particles increases with time. As a result, we see that in the late stage of particle acceleration, the spectral distribution of particles becomes narrower as shown in Figure 5.
IV Discussion
In the framework of the externally driven turbulent reconnection, Kowal et al. (2012b) demonstrated that charged particles trapped within the reconnection layer experience many head-on collisions with contracting magnetic fields which significantly enhances the acceleration rate. Differently, our present numerical work is an attempt to explore the properties of particle acceleration with self-driven turbulent reconnection. It is noted that in the framework of the externally driven turbulent reconnection, particle energy spectral distributions presented in del Valle et al. (2016) are similar to our current analysis. Although the understanding of CR acceleration in various MHD turbulence settings has been discussed by different authors (Lehe et al., 2009; Lynn et al., 2013; Guo et al., 2014, 2019; Ergun et al., 2020; Guo et al., 2021; Zhang et al., 2021a; Zhang and Xiang, 2021; Isliker et al., 2022), the acceleration by self-driven turbulent reconnection is an insufficiently studied subject.
Tearing reconnection has been considered an alternative mechanism for the fast magnetic reconnection process. The particle acceleration in magnetic islands (ropes) has been extensively studied using 2D PIC simulations of collisionless electron-ion or electron-positron plasmas (e.g., Zenitani and Hoshino, 2001; Drake et al., 2006, 2010; Lyubarsky and Liverts, 2008; Clausen-Brown and Lyutikov, 2012; Cerutti et al., 2013; Li et al., 2015), and also using 3D PIC simulations (e.g., Sironi and Spitkovsky, 2014; Cerutti et al., 2014; Guo et al., 2014; Zhang et al., 2021a; Nathanail et al., 2022). It should be pointed out that these studies can only probe particle acceleration at the kinetic scales of the plasma, i.e., a few hundredths of the skin depth. The current difficulty in achieving sufficiently large length scales is the reason why the 3D PIC simulations do not observe turbulent flow behavior in the reconnection layer (Lazarian et al., 2020). On the other hand, some turbulence-related processes, such as flux-freezing violation (Eyink, 2011) and Richardson dispersion (Richardson, 1926; Eyink et al., 2013) that follow turbulent reconnection theory (LV99), can not be explained in the framework of the tearing reconnection. The numerical results of the turbulent reconnection provided in Kowal et al. (2020) demonstrate that the tearing mode plays a role only at the early stage of reconnection. As the reconnection layer evolves in time, the tearing instability is suppressed and the Kelvin–Helmholtz instability plays the dominant role in driving turbulence and initiating the turbulent reconnection.
Compared with Kowal et al. (2017) in the case of externally driven turbulent reconnection, we find that in the present reconnection-driven turbulence, the phase of exponential acceleration with an index of shown in Figure 4 is similar to the earlier low-resolution simulations with index approximately . This exponential acceleration process is related to the largest thickness of the reconnection layer of . The turbulence driven by the reconnection in this paper has very different injection properties compared to that of Kowal et al. (2017). The former happens at a large scale by an external force, and the latter due to the action of the reconnection itself has a different injection caused by the associated instabilities from the initial small-scale perturbations.
As turbulence regulates the reconnection rate, the reconnection rate with externally-driven turbulence and reconnection-driven turbulence can be very different Kowal et al. (2017). The efficiency of reconnection acceleration associated with the motional electric field induced by inflows depends on the reconnection rate Xu and Lazarian (2023). Therefore, we expect that the acceleration efficiency has dependent on the turbulence-driving mechanism in reconnection. Despite those differences, we find that the overall acceleration process is very similar in terms of energy growth. As a result, reconnection-driven turbulence can effectively accelerate particles.
We have explored whether particle acceleration takes place rather than studied the evolution of the spectrum with the evolution of the turbulent reconnection layer. For this purpose, the snapshot of the simulations is reasonable. Note that the frozen-box approximation in 2D MHD simulation has been claimed to lead to a super-Fermi acceleration Majeski and Ji (2023). In the case of a 3D simulation, whether there is an artificial super-Fermi acceleration requires specialized research in the future. As for reconnection acceleration, it would be more desirable to self-consistently explore the acceleration of particles together with the co-evolution of fluids, as done by e.g., Lehe et al. (2009) and Lynn et al. (2013) for particle acceleration in MHD turbulence. In general, the PIC and MHD simulations are complementary for studying particle accelerations. The obvious advantage of MHD simulations is that they can simulate turbulent reconnection on macroscopic scales which is challenging with the PIC.
V Summary
We have numerically studied for the first time particle acceleration in the magnetic reconnection with reconnection-driven turbulence.666Around the same time, Liang et al. (2023) used an MHD-PIC method to simulate reconnection-driven turbulence and turbulent reconnection acceleration of particles. They found that particles can be efficiently accelerated in reconnection-driven turbulence. Our research confirmed the theoretical picture proposed by de Gouveia dal Pino and Lazarian (2005) and further developed and quantified in Xu and Lazarian (2023) that the particles can be efficiently accelerated within the turbulent reconnection layer via bouncing back and forth between converging magnetic fields. The current numerical study with high-resolution simulations on reconnection acceleration with self-driven turbulence extends earlier numerical studies with low resolution and externally driven turbulence Kowal et al. (2011); Kowal et al. (2012b); del Valle et al. (2016).
The main results are summarized as follows:
-
•
The self-driven turbulence is important not only for enabling the fast turbulent reconnection but also for enabling the particle acceleration in the turbulence-broadened reconnection layer, with the energy gain coming from the kinetic energy of the reconnection-driven inflows. Therefore, the acceleration efficiency is expected to strongly depend on the reconnection rate.
-
•
We found that the acceleration in the direction perpendicular to the local magnetic fields dominates that in the parallel direction, which is consistent with the theoretical expectation in Xu and Lazarian (2023). The particle energy increases with time by about 3 orders of magnitude in the range of the box size and approximately follows the scaling of before . Given periodic boundary conditions, the particle energy can be increased constantly with the increase of simulation time and approximately follows the scaling of .
-
•
We demonstrate the reconnection acceleration of particles with their gyroradii both smaller and larger than the thickness of the reconnection layer. The latter case was first theoretically predicted by Lazarian et al. (2012).
-
•
The energy spectra of the accelerated particles present the non-thermal power-law tail, , with evolving from to . The upper limit slope is consistent with the theoretical expectation in Xu and Lazarian (2023) for nonrelativistic reconnection acceleration with a weak guide field.
Our current study demonstrated efficient particle acceleration in self-driven turbulent reconnection. It has important implications on a wide range of astrophysical problems, including reconnection acceleration in e.g., accretion discs, jets, and the origin of high-energy cosmic rays.
VI Acknowledgements
We thank the anonymous referee for valuable comments that significantly improved the quality of the paper. J.F.Z. acknowledges the support from the National Natural Science Foundation of China (grants No. 11973035), the Hunan Province Innovation Platform and Talent Plan–HuXiang Youth Talent Project (No. 2020RC3045), and the Hunan Natural Science Foundation for Distinguished Young Scholars (No. 2023JJ10039). G.K. thanks for support from the São Paulo Research Foundation, FAPESP (grants 2013/10559-5 and 2019/03301-8). A.L. thanks the support of NSF AST 1816234 and NASA TCAN 144AAG1967 and NASA AAH7546 grants.
References
- Longair (2011) M. S. Longair, High Energy Astrophysics (2011).
- Lhaaso Collaboration et al. (2021) Lhaaso Collaboration, Z. Cao, F. Aharonian, Q. An, Axikegu, L. X. Bai, Y. X. Bai, Y. W. Bao, D. Bastieri, X. J. Bi, et al., Science 373, 425 (2021), eprint 2111.06545.
- Lazarian et al. (2020) A. Lazarian, G. L. Eyink, A. Jafari, G. Kowal, H. Li, S. Xu, and E. T. Vishniac, Physics of Plasmas 27, 012305 (2020), eprint 2001.00868.
- Marcowith et al. (2020) A. Marcowith, G. Ferrand, M. Grech, Z. Meliani, I. Plotnikov, and R. Walder, Living Reviews in Computational Astrophysics 6, 1 (2020), eprint 2002.09411.
- Liu and Jokipii (2021) S. Liu and J. R. Jokipii, Frontiers in Astronomy and Space Sciences 8, 100 (2021).
- Kulsrud and Pearce (1969) R. Kulsrud and W. P. Pearce, Astrophys. J. 156, 445 (1969).
- Schlickeiser (2002) R. Schlickeiser, Cosmic Ray Astrophysics (2002).
- Yan and Lazarian (2004) H. Yan and A. Lazarian, Astrophys. J. 614, 757 (2004), eprint astro-ph/0408172.
- Xu and Lazarian (2018) S. Xu and A. Lazarian, Astrophys. J. 868, 36 (2018), eprint 1810.07726.
- Zhdankin (2022) V. Zhdankin, Journal of Plasma Physics 88, 175880303 (2022), eprint 2203.13054.
- Lazarian and Xu (2021) A. Lazarian and S. Xu, Astrophys. J. 923, 53 (2021), eprint 2106.08362.
- Brunetti and Lazarian (2016) G. Brunetti and A. Lazarian, Mon. Not. R. Astron. Soc. 458, 2584 (2016), eprint 1603.00458.
- Xu and Zhang (2017) S. Xu and B. Zhang, Astrophys. J. Lett. 846, L28 (2017), eprint 1708.08029.
- Comisso and Sironi (2022) L. Comisso and L. Sironi, Astrophys. J. Lett. 936, L27 (2022), eprint 2209.04475.
- Bresci et al. (2022) V. Bresci, M. Lemoine, L. Gremillet, L. Comisso, L. Sironi, and C. Demidem, Phys. Rev. D 106, 023028 (2022), eprint 2206.08380.
- Huang and Bhattacharjee (2012) Y.-M. Huang and A. Bhattacharjee, Phys. Rev. Lett. 109, 265002 (2012), eprint 1211.6708.
- Caprioli and Spitkovsky (2014) D. Caprioli and A. Spitkovsky, Astrophys. J. 794, 47 (2014), eprint 1407.2261.
- Guo et al. (2021) F. Guo, J. Giacalone, and L. Zhao, Frontiers in Astronomy and Space Sciences 8, 27 (2021), eprint 2102.06054.
- Lazarian and Vishniac (1999) A. Lazarian and E. T. Vishniac, Astrophys. J. 517, 700 (1999), eprint astro-ph/9811037.
- de Gouveia dal Pino and Lazarian (2005) E. M. de Gouveia dal Pino and A. Lazarian, Astron. & Astrophys. 441, 845 (2005).
- Kowal et al. (2009) G. Kowal, A. Lazarian, E. T. Vishniac, and K. Otmianowska-Mazur, Astrophys. J. 700, 63 (2009), eprint 0903.2052.
- Beresnyak and Li (2016) A. Beresnyak and H. Li, Astrophys. J. 819, 90 (2016), eprint 1406.6690.
- Li et al. (2019) X. Li, F. Guo, H. Li, A. Stanier, and P. Kilian, Astrophys. J. 884, 118 (2019), eprint 1909.01911.
- Chitta and Lazarian (2020) L. P. Chitta and A. Lazarian, Astrophys. J. Lett. 890, L2 (2020), eprint 2001.08595.
- Jafari et al. (2021) A. Jafari, E. T. Vishniac, and S. Xu, Astrophys. J. 906, 109 (2021), eprint 2004.06186.
- Kadowaki et al. (2021) L. H. S. Kadowaki, E. M. de Gouveia Dal Pino, T. E. Medina-Torrejón, Y. Mizuno, and P. Kushwaha, Astrophys. J. 912, 109 (2021), eprint 2011.03634.
- Zhang et al. (2021a) Q. Zhang, F. Guo, W. Daughton, H. Li, and X. Li, Phys. Rev. Lett. 127, 185101 (2021a), eprint 2105.04521.
- Zhang et al. (2021b) H. Zhang, L. Sironi, and D. Giannios, Astrophys. J. 922, 261 (2021b), eprint 2105.00009.
- Xu and Lazarian (2023) S. Xu and A. Lazarian, Astrophys. J. 942, 21 (2023), eprint 2211.08444.
- Sweet (1958) P. A. Sweet, Symposium - International Astronomical Union 6, 123 (1958).
- Parker (1957) E. N. Parker, JGR 62, 509 (1957).
- Petschek (1964) H. E. Petschek, NASA Special Publication 50, 425 (1964).
- Kowal et al. (2017) G. Kowal, D. A. Falceta-Gonçalves, A. Lazarian, and E. T. Vishniac, Astrophys. J. 838, 91 (2017), eprint 1611.03914.
- Kowal et al. (2020) G. Kowal, D. A. Falceta-Gonçalves, A. Lazarian, and E. T. Vishniac, Astrophys. J. 892, 50 (2020), eprint 1909.09179.
- Takamoto et al. (2015) M. Takamoto, T. Inoue, and A. Lazarian, Astrophys. J. 815, 16 (2015), eprint 1509.07703.
- Goldreich and Sridhar (1995) P. Goldreich and S. Sridhar, Astrophys. J. 438, 763 (1995).
- Lazarian et al. (2004) A. Lazarian, E. T. Vishniac, and J. Cho, Astrophys. J. 603, 180 (2004), eprint physics/0311051.
- Beresnyak (2013) A. Beresnyak, ArXiv e-prints (2013), eprint 1301.7424.
- Alfvén (1942) H. Alfvén, Nature (London) 150, 405 (1942).
- Eyink (2011) G. L. Eyink, Phys. Rev. E 83, 056405 (2011), eprint 1008.4959.
- Lazarian and Opher (2009) A. Lazarian and M. Opher, Astrophys. J. 703, 8 (2009), eprint 0905.1120.
- Xu and Lazarian (2016) S. Xu and A. Lazarian, Astrophys. J. 833, 215 (2016), eprint 1608.05161.
- Stacy et al. (2022) A. Stacy, C. F. McKee, A. T. Lee, R. I. Klein, and P. S. Li, Mon. Not. R. Astron. Soc. 511, 5042 (2022), eprint 2201.02225.
- Lazarian et al. (2003) A. Lazarian, V. Petrosian, H. Yan, and J. Cho, arXiv e-prints astro-ph/0301181 (2003), eprint astro-ph/0301181.
- Zhang and Yan (2011) B. Zhang and H. Yan, Astrophys. J. 726, 90 (2011), eprint 1011.1197.
- Lazarian et al. (2019) A. Lazarian, B. Zhang, and S. Xu, Astrophys. J. 882, 184 (2019), eprint 1801.04061.
- Kadowaki et al. (2015) L. H. S. Kadowaki, E. M. de Gouveia Dal Pino, and C. B. Singh, Astrophys. J. 802, 113 (2015), eprint 1410.3454.
- Khiali and de Gouveia Dal Pino (2016) B. Khiali and E. M. de Gouveia Dal Pino, Mon. Not. R. Astron. Soc. 455, 838 (2016), eprint 1506.01063.
- Drake et al. (2006) J. F. Drake, M. Swisdak, H. Che, and M. A. Shay, Nature (London) 443, 553 (2006).
- Loureiro et al. (2007) N. F. Loureiro, A. A. Schekochihin, and S. C. Cowley, Physics of Plasmas 14, 100703 (2007), eprint astro-ph/0703631.
- Cargill et al. (2012) P. J. Cargill, L. Vlahos, G. Baumann, J. F. Drake, and Å. Nordlund, Space Science Reviews 173, 223 (2012).
- Vlahos et al. (2019) L. Vlahos, A. Anastasiadis, A. Papaioannou, A. Kouloumvakos, and H. Isliker, Philosophical Transactions of the Royal Society of London Series A 377, 20180095 (2019), eprint 1903.08200.
- Nowak et al. (2021) N. Nowak, G. Kowal, and D. A. Falceta-Gonçalves, Physics of Plasmas 28, 062310 (2021), eprint 2104.11732.
- Drury (2012) L. O. Drury, Mon. Not. R. Astron. Soc. 422, 2474 (2012), eprint 1201.6612.
- Kowal et al. (2011) G. Kowal, E. M. de Gouveia Dal Pino, and A. Lazarian, Astrophys. J. 735, 102 (2011), eprint 1103.2984.
- Norman and Ferrara (1996) C. A. Norman and A. Ferrara, Astrophys. J. 467, 280 (1996), eprint astro-ph/9602146.
- Ferrière (2001) K. M. Ferrière, Reviews of Modern Physics 73, 1031 (2001), eprint astro-ph/0106359.
- Chandran (2005) B. D. G. Chandran, Astrophys. J. 632, 809 (2005), eprint astro-ph/0506096.
- Subramanian et al. (2006) K. Subramanian, A. Shukurov, and N. E. L. Haugen, Mon. Not. R. Astron. Soc. 366, 1437 (2006), eprint astro-ph/0505144.
- Enßlin and Vogt (2006) T. A. Enßlin and C. Vogt, Astron. & Astrophys. 453, 447 (2006), eprint astro-ph/0505517.
- Inoue et al. (2013) T. Inoue, J. Shimoda, Y. Ohira, and R. Yamazaki, Astrophys. J. Lett. 772, L20 (2013), eprint 1305.4656.
- Hu et al. (2022) Y. Hu, S. Xu, J. M. Stone, and A. Lazarian, Astrophys. J. 941, 133 (2022), eprint 2207.06941.
- Dhawalikar et al. (2022) S. Dhawalikar, C. Federrath, S. Davidovits, R. Teyssier, S. R. Nagel, B. A. Remington, and D. C. Collins, Mon. Not. R. Astron. Soc. 514, 1782 (2022), eprint 2205.14417.
- Balbus and Hawley (1998) S. A. Balbus and J. F. Hawley, Reviews of Modern Physics 70, 1 (1998).
- Gerrard and Hood (2003) C. L. Gerrard and A. W. Hood, SoPh 214, 151 (2003).
- Lazarian and Vishniac (2009) A. Lazarian and E. T. Vishniac, in Magnetic Fields in the Universe II: From Laboratory and Stars to the Primordial Universe, edited by A. Esquivel, J. Franco, G. García-Segura, E. M. de Gouveia Dal Pino, A. Lazarian, S. Lizano, and A. Raga (2009), vol. 36 of Revista Mexicana de Astronomia y Astrofisica Conference Series, pp. 81–88, eprint 0812.2019.
- Beresnyak (2017) A. Beresnyak, Astrophys. J. 834, 47 (2017), eprint 1301.7424.
- Oishi et al. (2015) J. S. Oishi, M.-M. Mac Low, D. C. Collins, and M. Tamura, Astrophys. J. Lett. 806, L12 (2015), eprint 1505.04653.
- Huang and Bhattacharjee (2016) Y.-M. Huang and A. Bhattacharjee, Astrophys. J. 818, 20 (2016), eprint 1512.01520.
- Cho and Vishniac (2000) J. Cho and E. T. Vishniac, Astrophys. J. 539, 273 (2000), eprint astro-ph/0003403.
- Gottlieb et al. (2011) S. Gottlieb, D. Ketcheson, and C.-W. Shu, Strong Stability Preserving Runge-Kutta and Multistep Time Discretizations (WORLD SCIENTIFIC, 2011), eprint https://www.worldscientific.com/doi/pdf/10.1142/7498, URL https://www.worldscientific.com/doi/abs/10.1142/7498.
- Suresh and Huynh (1997) A. Suresh and H. T. Huynh, Journal of Computational Physics 136, 83 (1997).
- Mignone (2007) A. Mignone, Journal of Computational Physics 225, 1427 (2007), eprint astro-ph/0701798.
- Dahlin et al. (2015) J. T. Dahlin, J. F. Drake, and M. Swisdak, Physics of Plasmas 22, 100704 (2015), eprint 1503.02218.
- Li et al. (2017) X. Li, F. Guo, H. Li, and G. Li, Astrophys. J. 843, 21 (2017).
- Arnold et al. (2021) H. Arnold, J. F. Drake, M. Swisdak, F. Guo, J. T. Dahlin, B. Chen, G. Fleishman, L. Glesener, E. Kontar, T. Phan, et al., Phys. Rev. Lett. 126, 135101 (2021), eprint 2011.01147.
- Beresnyak (2012) A. Beresnyak, Phys. Rev. Lett. 108, 035002 (2012), eprint 1109.4644.
- Guo et al. (2019) F. Guo, X. Li, W. Daughton, P. Kilian, H. Li, Y.-H. Liu, W. Yan, and D. Ma, Astrophys. J. Lett. 879, L23 (2019), eprint 1901.08308.
- Hairer et al. (2008) E. Hairer, S. Nørsett, and G. Wanner, Solving Ordinary Differential Equations I: Nonstiff Problems, Springer Series in Computational Mathematics (Springer Berlin Heidelberg, 2008), ISBN 9783540566700.
- Kowal and Falceta-Gonçalves (2021) G. Kowal and D. A. Falceta-Gonçalves, Frontiers in Astronomy and Space Sciences 8, 75 (2021), eprint 2104.13821.
- Zhang and Xiang (2021) J.-F. Zhang and F.-Y. Xiang, Astrophys. J. 922, 209 (2021), eprint 2109.11357.
- Liang et al. (2023) S.-M. Liang, J.-F. Zhang, N.-N. Gao, and H.-P. Xiao, Astrophys. J. 952, 93 (2023), eprint 2306.03418.
- del Valle et al. (2016) M. V. del Valle, E. M. de Gouveia Dal Pino, and G. Kowal, Mon. Not. R. Astron. Soc. 463, 4331 (2016), eprint 1609.08598.
- Lazarian et al. (2012) A. Lazarian, G. Kowal, E. de Gouveia Dal Pino, and E. T. Vishniac, in Multi-scale Dynamical Processes in Space and Astrophysical Plasmas (2012), vol. 33 of Astrophysics and Space Science Proceedings, p. 11, eprint 1205.3795.
- Kowal et al. (2012a) G. Kowal, A. Lazarian, E. T. Vishniac, and K. Otmianowska-Mazur, Nonlinear Processes in Geophysics 19, 297 (2012a), eprint 1203.2971.
- Cerutti et al. (2013) B. Cerutti, G. R. Werner, D. A. Uzdensky, and M. C. Begelman, Astrophys. J. 770, 147 (2013), eprint 1302.6247.
- Guo et al. (2014) F. Guo, H. Li, W. Daughton, and Y.-H. Liu, Phys. Rev. Lett. 113, 155005 (2014), eprint 1405.4040.
- Kowal et al. (2012b) G. Kowal, E. M. de Gouveia Dal Pino, and A. Lazarian, Phys. Rev. Lett. 108, 241102 (2012b), eprint 1202.5256.
- Medina-Torrejón et al. (2021) T. E. Medina-Torrejón, E. M. de Gouveia Dal Pino, L. H. S. Kadowaki, G. Kowal, C. B. Singh, and Y. Mizuno, Astrophys. J. 908, 193 (2021), eprint 2009.08516.
- Pezzi et al. (2022) O. Pezzi, P. Blasi, and W. H. Matthaeus, Astrophys. J. 928, 25 (2022), eprint 2112.09555.
- Zhang et al. (2018) J.-F. Zhang, Z.-R. Li, F.-Y. Xiang, and J.-F. Lu, Mon. Not. R. Astron. Soc. 473, 3211 (2018), eprint 1710.00583.
- Lehe et al. (2009) R. Lehe, I. J. Parrish, and E. Quataert, Astrophys. J. 707, 404 (2009), eprint 0908.4078.
- Lynn et al. (2013) J. W. Lynn, E. Quataert, B. D. G. Chandran, and I. J. Parrish, Astrophys. J. 777, 128 (2013), eprint 1307.0021.
- Ergun et al. (2020) R. E. Ergun, N. Ahmadi, L. Kromyda, S. J. Schwartz, A. Chasapis, S. Hoilijoki, F. D. Wilder, P. A. Cassak, J. E. Stawarz, K. A. Goodrich, et al., Astrophys. J. 898, 153 (2020).
- Isliker et al. (2022) H. Isliker, A. Cathey, M. Hoelzl, S. Pamela, and L. Vlahos, arXiv e-prints arXiv:2208.03362 (2022), eprint 2208.03362.
- Zenitani and Hoshino (2001) S. Zenitani and M. Hoshino, Astrophys. J. Lett. 562, L63 (2001), eprint 1402.7139.
- Drake et al. (2010) J. F. Drake, M. Opher, M. Swisdak, and J. N. Chamoun, Astrophys. J. 709, 963 (2010), eprint 0911.3098.
- Lyubarsky and Liverts (2008) Y. Lyubarsky and M. Liverts, Astrophys. J. 682, 1436 (2008), eprint 0805.0085.
- Clausen-Brown and Lyutikov (2012) E. Clausen-Brown and M. Lyutikov, Mon. Not. R. Astron. Soc. 426, 1374 (2012), eprint 1205.5094.
- Li et al. (2015) X. Li, F. Guo, H. Li, and G. Li, Astrophys. J. Lett. 811, L24 (2015), eprint 1505.02166.
- Sironi and Spitkovsky (2014) L. Sironi and A. Spitkovsky, Astrophys. J. Lett. 783, L21 (2014), eprint 1401.5471.
- Cerutti et al. (2014) B. Cerutti, G. R. Werner, D. A. Uzdensky, and M. C. Begelman, Astrophys. J. 782, 104 (2014), eprint 1311.2605.
- Nathanail et al. (2022) A. Nathanail, V. Mpisketzis, O. Porth, C. M. Fromm, and L. Rezzolla, Mon. Not. R. Astron. Soc. 513, 4267 (2022), eprint 2111.03689.
- Richardson (1926) L. F. Richardson, Proceedings of the Royal Society of London Series A 110, 709 (1926).
- Eyink et al. (2013) G. Eyink, E. Vishniac, C. Lalescu, H. Aluie, K. Kanov, K. Bürger, R. Burns, C. Meneveau, and A. Szalay, Nature (London) 497, 466 (2013).
- Majeski and Ji (2023) S. Majeski and H. Ji, Physics of Plasmas 30, 042106 (2023), eprint 2210.06533.