Particle interactions and lattice dynamics: Scenarios for efficient bidirectional stochastic transport?
Abstract
Intracellular transport processes driven by molecular motors can be described by stochastic lattice models of self-driven particles. Here we focus on bidirectional transport models excluding the exchange of particles on the same track. We explore the possibility to have efficient transport in these systems. One possibility would be to have appropriate interactions between the various motors’ species, so as to form lanes. However, we show that the lane formation mechanism based on modified attachment/detachment rates as it was proposed previously is not necessarily connected to an efficient transport state and is suppressed when the diffusivity of unbound particles is finite. We propose another interaction mechanism based on obstacle avoidance that allows to have lane formation for limited diffusion. Besides, we had shown in a separate paper that the dynamics of the lattice itself could be a key ingredient for the efficiency of bidirectional transport. Here we show that lattice dynamics and interactions can both contribute in a cooperative way to the efficiency of transport. In particular, lattice dynamics can decrease the interaction threshold beyond which lanes form. Lattice dynamics may also enhance the transport capacity of the system even when lane formation is suppressed.
pacs:
87.10.Hk, 87.10.Mn, 05.60.Cd, 87.10.Wd1 Introduction
Many biological processes depend on efficient transport on the microscopic scale. Biological cells contain a large number of microscopic machines that are for example able to maintain the exchange of nutrients between the cell and the surrounding medium. Another important issue is the transport of cargos between the cell center and the membrane [1]. In this context, transport driven by molecular motors is of particular importance: Molecular motors are specialized proteins that are able to perform a directed motion along actin filaments and microtubules, i.e., filaments that are part of the cytoskeleton [2].
Several aspects of motor driven biological transport have been modeled recently [3, 4, 5, 6, 7, 8, 9] with variants of the so-called asymmetric exclusion process (ASEP) [10, 11]. The use of this type of models has been motivated since the molecular motors move stepwise (hence the relevance of a model defined on a discrete lattice) and interact via mutual exclusion. But in addition to this, molecular motors can attach and detach from the filament. This property of molecular motors led to extensions of the ASEP [3, 4, 8] which successfully describe the unidirectional motion of in vitro motor assays [12].
In the case of bidirectional systems of molecular motors, the theoretical understanding is so far incomplete. It has been shown that simple extensions of the unidirectional models are not able to describe efficient bidirectional transport if the filament is embedded in a small volume and the diffusivity of unbound particles is limited [13]. This situation could for example be relevant for motor-driven transport in axons. The question that naturally arises is the following: What are the minimal ingredients that must be added to the existing unidirectional models in order to describe bidirectional transport of stochastic interacting particles?
In this article, we consider different kinds of particle-particle interactions which may lead to lane formation, i.e., the self-organized separation of particles moving in opposite directions. This is in contrast to models for bidirectional transport with predefined lanes for each direction (e.g., [14]). We shall discuss their ability to generate efficient bidirectional transport. A first mechanism which has formerly been proposed by Klumpp and Lipowsky [15] takes into account the experimentally observed preferential adsorption of motors to a filament if the neighboring site is occupied by a motor of the same type [16, 17, 18]. In [15], they have observed lane formation above a critical value of the coupling parameter. We complete their results and present a more extensive study of the model. We show that the properties of the model depend strongly on the kind of diffusion reservoir that is considered around the filaments. In particular we have shown that lane formation is hindered if diffusion occurs in a confined environment. In a second part, as an alternative mechanism, we introduce particle-particle interactions that induce lane changes if oppositely moving particles are encountered. This mechanism does allow to have lane formation in a confined environment.
Eventually, we also consider that the filament itself can undergo some dynamical process, motivated by the experimentally observed continuous reorganization of the microtubule network. We shall consider a much simplified version of the filament dynamics, as this was done in [19]. There, we had shown that a dynamic lattice may enhance the transport efficiency of bidirectional stochastic transport. Here, we shall study the influence of lattice dynamics in the presence of particle-particle interactions and show that both mechanisms can cooperate to obtain efficient transport.
Our work is organized as follows: After introducing some general definitions and summarizing some previously obtained results (next section), we shall consider two types of interactions: first, we investigate the model introduced by Klumpp and Lipowsky [15] considering the preferential binding of particles (section 3). In section 4, we discuss the effect of another type of interaction, namely a dynamic particle-particle interaction on the filament inducing lane changes. As mentioned above, for both types of interactions, we apply different kinds of particle reservoirs: we shall consider grand-canonical and canonical particle reservoirs and also the effect of a finite diffusivity of unbound particles. We shall also systematically discuss the impact of a dynamic lattice on lane formation and transport capacity of the systems. In the final section, we compare the different approaches and discuss their relevance for axonal transport.
2 General definitions
2.1 Model definition
The models which are discussed in this article are variants of the totally asymmetric simple exclusion process (TASEP) with two species of particles. The two species have opposite ‘charges’ resulting in opposite moving directions on a one-dimensional lattice with regular spacing. The one-dimensional lattice represents the microtubule, or more precisely, one of the filaments that compose the microtubule, and thus it will be referred to as a filament in the remaining of the paper.
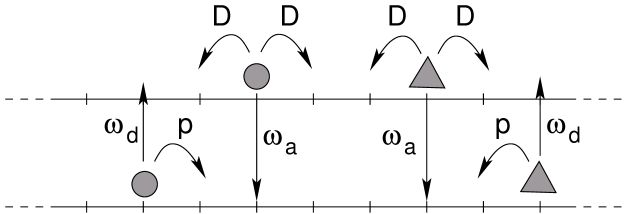
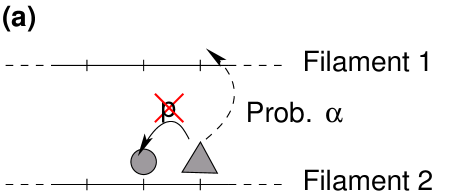
Particles hop with rate along the filament in the direction determined by their charge which we will refer to as positive or negative depending on the preferential moving direction (see figure 1). We additionally consider attachment and detachment of particles to and from the lattice as first proposed in [3]. Particles detach from the lattice with rate to a reservoir. The adsorption of a particle from the reservoir onto a site of the lattice occurs at rate . We examine different kinds of reservoirs which are specified below in the corresponding sections. They have in common that particles in the reservoir diffuse freely without any interactions between particles. On the filament, all particles interact via hard-core exclusion and positional exchanges of oppositely charged particles are excluded in contrast to the model considered in [20]. A stepping or attachment move is therefore rejected if the target site is already occupied by another particle.
As standard set of parameters for the particle dynamics, we will use , and . This choice of parameters corresponds to processive motion (i.e., motors are attached on the filament long enough so that directed motion contributes significantly to the overall motion), a basic feature of the molecular motors contributing to long-range transport, as conventional kinesin or cytoplasmic dynein [1].
As there are several parallel microtubules in axons, each of them made of several protofilaments, we could a priori consider a large number of parallel filaments. However, in order to keep the model simple, we shall consider only one filament except when the mechanism under study requires to have at least two filaments in parallel.
Particle densities are denoted by and defined as the number of particles divided by the system length. The index refers to the particle species. Densities and particle numbers are therefore related through and we choose the total density to be equal to throughout the paper. Note that and can be greater than one as they take into account the total number of particles (including those in the reservoir which is assumed to have an infinite capacity in this paper), divided by the number of filament sites. The quantities , denote the densities of bound particles on the filament and , the densities of particles in the reservoir.

2.2 Reservoirs
When motors detach from the microtubule, they undergo diffusive motion in the surrounding cytoplasm - a region of the cell that will be referred to as the reservoir. Depending on the geometry of the reservoir, the diffusive motion can have various characteristics. We shall define three types of reservoirs below.
2.2.1 Grand-canonical reservoir
If the surroundings of the filament is an open space, motors can diffuse very far from the filament, and thus, most of the time, motors that attach to the filament have completely lost the memory of their previous detachment point. Hence there is no need to keep track of spatial positions of the diffusing motors.
Actually, the grand-canonical reservoir will be modeled by a single number, representing the density of motors in the reservoir, which is assumed to be constant and (in this paper) equal to . Attachment to empty sites on the filament occurs at rate .
This type of reservoir is relevant if the filament is embedded in a large volume and the number of attached motors is small compared to the number of motors in solution. This is the case for many in vitro experiments.
2.2.2 Canonical reservoir
An infinite diffusion rate in the surroundings of the lattice is also considered in the canonical reservoir, and thus particles in the reservoir do not have any spatial coordinate and can attach to any empty site along the lattice.
However, in the canonical setup, we consider that the total number of particles in the system is finite. This implies, with our definition of the density, that is fixed. Again, attachment occurs at rate .
This type of reservoir is relevant if the filament is embedded in a large volume and the number of motors attached to the filament is of the same order as the number of motors in solution. This situation can also be encountered in in vitro experiments.
2.2.3 Finite diffusion
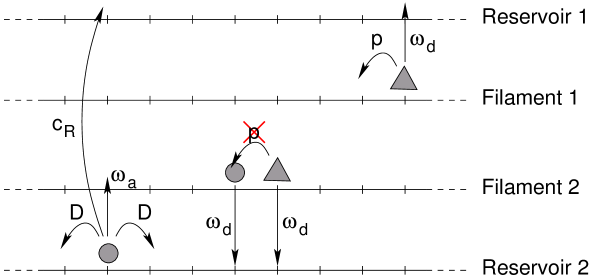
Actually, the axon is a rather crowded environment111 The importance of confinement in the axon was for example illustrated by the simulations in [22] which reproduce the experimental results of H. Erez et al [23] for transected axons. , where the size of the transported objects is of the same order as the distance between the microtubules [24, 25], and the previous reservoirs are not relevant to model the diffusive motion episodes. In order to study the effects of confinement, we shall introduce a reservoir with a memory effect: there must be a correlation between the locations where a motor detaches, and where it attaches again on the microtubule.
In order to do so, the model is extended by a second lane which represents the reservoir (see figure 2). Particles in the reservoir symmetrically hop to both neighboring sites with rate without any interaction between particles. Note that this one-dimensional reservoir actually represents a three-dimensional region around the microtubule, which allows for several particles at the same longitudinal position. Only the longitudinal diffusion, along the microtubule, is modelled explicitly. The transversal dimensions of the three-dimensional diffusion reservoir, which are not represented explicitly, can be tuned by taking a larger or weaker effective attachment rate (see [26] for an example). The larger the diffusive region is (in the direction transverse to the microtubule), the weaker the effective attachment rate is. Thus, under strong confinement, diffusion in the transverse direction should be more limited, the attachment rate in the model will be larger, and the memory effect will increase.
2.3 Lattice dynamics
2.3.1 Definition
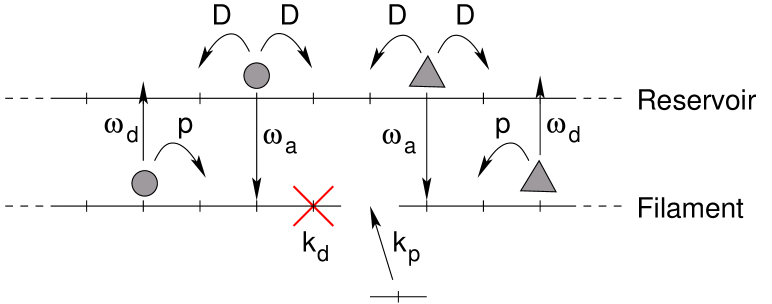
In this paper, we shall also consider that the underlying lattice itself can evolve dynamically. We shall consider the same type of lattice dynamics as in [19]: a site of the lattice is randomly eliminated at rate and recreated at rate (see figure 3). The indices refer to the processes of microtubule de-/polymerization, although the dynamics we consider here have little in common with realistic dynamics and must rather be considered as a minimal model. A particle cannot bind to an eliminated site and immediately detaches from the lattice if it steps onto an eliminated site or is bound to a site which is being eliminated. We fix the polymerization rate equal to in order to reduce the number of free parameters (we saw indeed in [19] that transport features were more sensitive to than to ).
2.3.2 Summary of previous results - impact of the lattice dynamics
It has been shown that bidirectional transport models in which the particle species interact only via an exclusion interaction generically exhibit macroscopic clustering at any finite density [13]. This large cluster controls the current in the system and therefore limits the total transport capacity. In particular, for large systems, the current vanishes.
Considering the case of bidirectional transport on dynamical lattices, it has been shown that lattice dynamics can induce a transition from the clustered phase to a homogenous phase in which the particles are distributed over the whole system [19]. The homogenous states are density-dependent so that a finite (non-vanishing) current of particles is present even in very large systems, which would not be the case on a static lattice. The transition takes place because the lattice dynamics breaks up forming clusters and thus limits the reachable maximum cluster sizes. At a given strength of the lattice dynamics, the nascent clusters are dissolved more quickly than they can form and the system appears homogenous. The transition depends mostly on the rate at which binding sites disappear suggesting that the finite lifetime of individual binding sites is crucial for the observed transition.
In order to support this point of view, it has been verified that this effect is not simply due to the cutting of the filament into several segments of different lengths, by considering a static lattice with the same density of individual holes. In that case, the phase transition is not observed, thus indicating that the cluster dissolution is really an effect of the dynamics of the lattice.
Though this scenario was inspired by the fact that microtubules are themselves evolving through the so-called dynamic instability, i.e., events of polymerization and depolymerization, the dynamics of the filament as we have defined it in [19] or in section 2.3.1 do not aim at being realistic, but rather are the simplest kind of lattice dynamics that could be considered in order to illustrate the aforementioned mechanism.
3 Interactions through modified attachment/detachment rates
3.1 Model definition
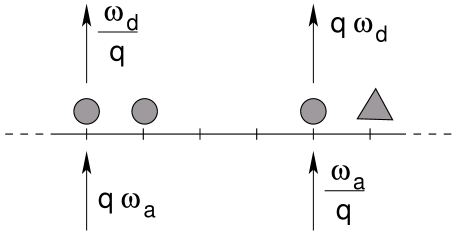
Decoration experiments with kinesin on microtubules [16, 17, 18] showed that kinesins attach on the microtubule preferentially in the vicinity of similar motors. This motivates the assumption of a general attractive interaction between molecular motors of the same species. This experimental fact was first considered by Klumpp and Lipowsky [15] in a modification of the above-presented basic model by consideration of detachment and attachment rates that depend on the next neighbor in the stepping direction of the particle: If the next site in moving direction is occupied by a particle of the same species, the detachment rate is lowered by a factor whereas the attachment to that site is enhanced by a factor . If the next site is occupied by a particle of the opposite species, the detachment is enhanced by a factor and attachment is lowered by a factor (see figure 4). In all other cases, the rates remain unchanged. In the remaining, we shall call the strength of the interaction, as the modified attachment and detachment rates are supposed to be due to attractive/repulsive interactions between similar/different motor species.
We shall now study the consequences of having these modified attachment/detachment rates on the efficiency of transport, as an extension of the results presented in [15]. In particular, several types of reservoirs will be considered and shown to have a strong influence on transport properties.
In a first stage, we shall study the influence of these modified attachment/detachment rates on a static lattice, i.e., the lattice dynamics defined in section 2.3.1 will not be considered.
3.2 Static lattice
3.2.1 Infinite diffusion rate
In [15], it has been shown that for a grand-canonical setup, lane formation is observed if the particles’ attachment/detachment rates are modified according to figure 4 on a static lattice. In this section, we briefly present some new results obtained in the same frame, in order to discuss the efficiency of the lane formation mechanism.
Grand-canonical reservoir
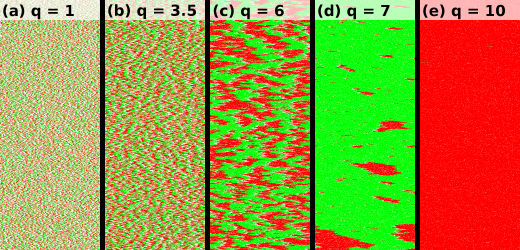
As already shown in [15], lane formation occurs in the grand-canonical setup if the interaction strength exceeds a critical value . This effect is illustrated in the space-time plots in figure 5. With increasing interaction strength, the typical size of the jams in the system increases, until one particle species completely takes over the system at so that all particles move in the same direction.
The transition manifests itself by a dramatic increase of the magnetization as shown in [15]. Here, we define the magnetization slightly differently, since we normalize the difference in the densities of the two particle species with the total density of particles on the filament . This quantity takes the value one for completely demixed subsystems, i.e., in the case of lane formation and is zero for equal numbers of particles of both species on the filament (see figure 6(a)). For or , we will refer to unpolarized or polarized states, respectively, as is known from systems with magnetization. The currents of the two species along the filament exhibit a bifurcation at the transition: while one species dominates the filament and moves in a TASEP-like fashion, the excluded species does not participate in transport at all for (see figure 6(b)). In a real system, there are several filaments, so that, above the transition, some of them conduct transport in one direction while others conduct transport in the other direction.
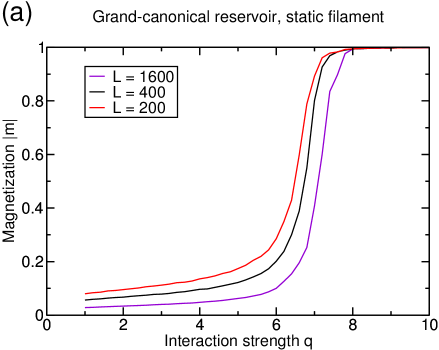
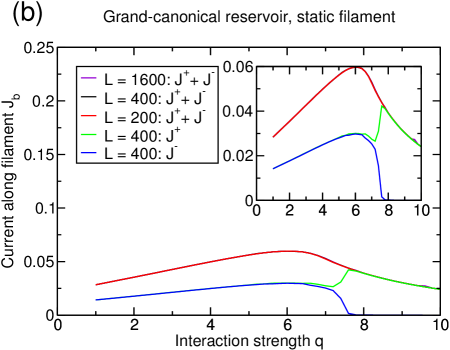
Two remarks can be made from the data shown in figure 6(b). First, the current does not exhibit strong finite-size effects, although the magnetization does. In particular, the critical interaction strength above which lane formation occurs depends on the system size and increases for larger systems. In [15], numerical evidence was given that has a finite value in the limit of infinite system sizes which is supported by the mean field treatment of the system in the same paper. However, one has to be cautious before claiming that there is true symmetry breaking in the thermodynamic limit. Indeed, a subtlety has been exemplified in the case of another bidirectional transport model, the AHR model [20], for which numerical evidence for a phase transition had been found. Actually, a very careful analysis [21] of the AHR model has shown that the correlation length can grow up to , and then remain finite, so that there is no true symmetry breaking. So, although the data presented in [15] seem to be rather convincing, there might be a subtlety which cannot be addressed by a numerical treatment.
Second, although the difference in current between the two species is very large above the transition, indicating that lane formation has occurred, the transition does not influence the total current of the system as it is continuous. For the choice of parameters considered here, the maximum of the total current is actually located before the onset of lane separation. This can be seen by the sum of the currents (black and red line in figure 6(b)) which corresponds to the current of a single species in a system with two filaments, of which each is dominated by a different species. It is to note that the relative position of the onset of lane formation with respect to the maximum of the total current varies with the reservoir density such that the onset of lane formation might also occur for lower interaction strengths than the maximum in the current. The interesting feature is that, above the transition for high values of , the current actually decreases although the encounters of oppositely moving particles are less frequent. This decrease is instead caused by the filament being overcrowded, as can be seen in figure 5. The density on the filament is close to one and although all particles move in the same direction, most of the attempted steps are rejected because of the lack of vacancies. The stronger the interactions between particles, the more the situation worsens. Consequently, the current continues to decrease for increasing interactions strengths, since the particles have an ever-increasing affinity to the filament and the number of vacancies thus decreases with increasing .
Canonical reservoir
Considering that actually, the number of motors in the system may not be infinite, we fix the total number of positive (negative) particles () and observe the consequences of using a canonical reservoir instead of a grand-canonical one on the transport properties.
Besides, we consider here more than only one track on which particles can walk. In this scenario, choosing more than one filament becomes important since lane formation would be hindered otherwise. In a system with a single filament, the species which is excluded from the filament becomes dominant in the reservoir and therefore tends to suppress lane formation. Putting two (or more generally any pair number of) filaments in a system resolves this issue. This is an appropriate approach as in the biological situation, one typically has several filaments in parallel. In the following, we shall consider the case of two filaments only.
Note that for multilane unidirectional systems, strong correlations between the lanes were found, both for strong and weak coupling [27, 28]. Thus, simulating only one lane turns out to be representative for the whole system. This is in contrast to the bidirectional case considered here, for which lane formation may require to consider more than one filament.
The behavior of the system is qualitatively different for densities and since in the latter case, there are not enough particles to fill both filaments completely with a single particle species each. The results are illustrated in figure 7. For the magnetization, it is interesting to see that the transition still takes place, even at very low total particle densities. The fewer particles are present in the system, the higher the interaction between particles has to be in order to induce polarization. For , there are exactly as many particles of one species in the system as there are sites on a single filament and lane formation is extremely stable in this case since there are enough particles to mediate the interaction at best but not too many to avoid that particles frequently attach to the “wrong” filament on which the species is not dominant. For densities , the latter effect is not avoided anymore as the reservoir cannot be emptied. There are always many particles of both species in the reservoir which interfere with the existing lanes such that the transition to the polarized state is hindered.
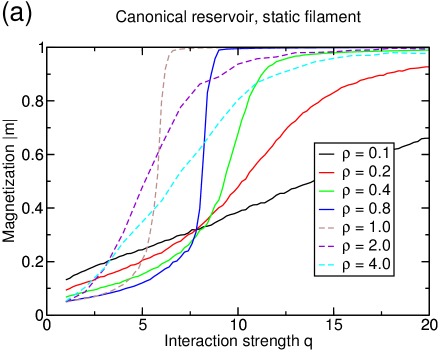
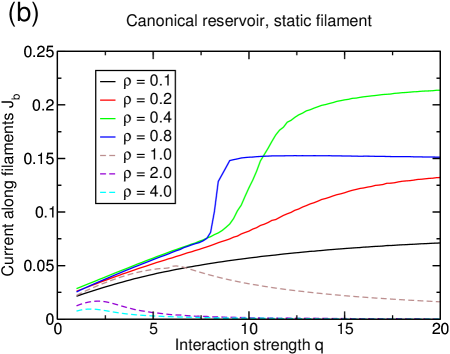
The current also reflects these two regimes: For , the current increases monotonously with increasing interaction strength. At the polarization transition, the current jumps toward a value very close to the current of the one-species TASEP, which is the upper-bound for the flux on the filament (see figure 8). For densities , the behavior is distinctively different as the curves for the current have much more similarity with those found in the grand-canonical setup and decrease with further increasing interaction.
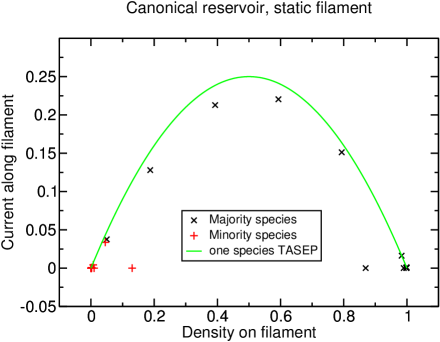
On the basis of these observations, we are able to draw an approximative phase diagram (figure 9). The system was considered to be phase separated at magnetization , where a distinction is made between two different phase-separated regimes depending on the current at infinite interaction strength as explained above. In terms of the transport capacity, only “phase-separated I” can be considered to be an efficient state, as the current in “phase-separated II” does not reach very high values due to the overcrowding of the filament as discussed above.
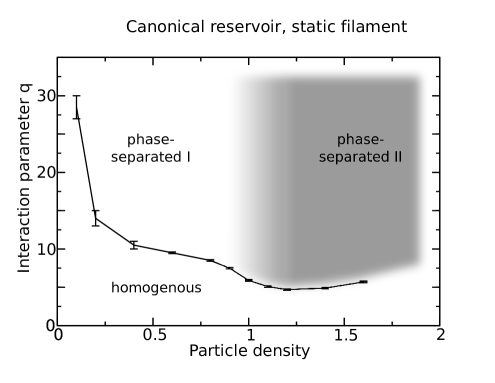
In total, we can draw the conclusion that for low densities, the dominating effect of the interaction is to induce lane formation which leads to very good values of the current but necessitates strong particle-particle interactions. For intermediate total densities (greater than one) or a grand-canonical reservoir, lane formation is not efficient as it occurs at densities on the filament that are so high that they mostly prevent particles from moving.
3.2.2 Finite diffusion rate
In order to study the effect of confinement, we consider now a reservoir such as the one defined in section 2.2.3. Actually, we consider two identical subsystems (see figure 10) for the same reasons as explained above. Particles can hop from one reservoir to the other while conserving their longitudinal position at rate . This corresponds to diffusion in transverse direction. We choose the diffusion in both directions along the reservoir lattices to be equal to the attachment rate, i.e., . The two filament lattices are not directly coupled in this model, an assumption that facilitates lane formation for this setup.
Without the modified attachment/detachment rates defined in section 3.1, this model has been shown to generically form a single big cluster which contains almost all of the particles in the system [13]. The existence of this big cluster is a clear indicator for an inefficient state since it blocks most of the transport. Furthermore, the cluster formation depends on the number of particles rather than density so that systems form larger and more stable clusters with increasing system size although the total density of particles is constant. As a consequence, the current vanishes in the thermodynamic limit.
If modified attachment/detachment rates are included, we see that the finite diffusion in the reservoir inhibits even partial demixing of the particles into the different subsystems (see figure 11(a)). Although lane formation is suppressed by the limited diffusion, the current (figure 11(b)) is enhanced by the interaction, though a single big cluster is still present in the system. The increase in the current is caused by the reduced time blocked particles spend in front of each other and the fact that, in low density regions, particles of a given species are more likely to have nearest neighbors of the same species.
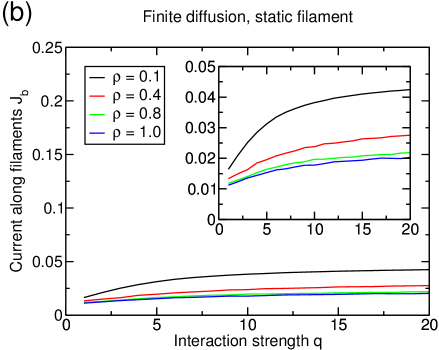
3.3 Dynamic lattice
In this section, we are interested in the impact that a dynamic lattice has, first, on the lane formation mechanism that exists at least in the case of infinite diffusion, and, second, on the overall transport efficiency. We shall consider for the filament the simplified dynamic lattice defined in section 2.3.1. We again discriminate between reservoirs with infinite and finite diffusion rates.
3.3.1 Infinite diffusion rate
Eliminating lattice sites reduces the effectivity of the particle-particle interaction since it is next-neighbor and does not reach across holes in the filament. As a consequence, the transition is shifted to higher values of with increasing depolymerization rate as can be seen in figure 12(a). For a very dynamic lattice, there seems to be no transition toward lane formation at all. This effect is partly due to the fact that lattice dynamics cuts the filament in shorter segments on which lane formation is less stable, as has been verified by comparison with a static lattice with the same density of holes. However, the effect observed here is stronger if the lattice additionally is dynamic.
However, although lane formation is hindered by the lattice dynamics, it positively affects the current of the system (figure 12(b)). By pushing particles to the reservoir when a lattice site is eliminated, the lattice dynamics keeps the density on the filament low enough so that particles have enough space in front of them to move. Thus, extreme densities that were strongly limiting the current in the case of a static lattice (see section 3.2.1) are avoided here.
The results shown in figure 12 are obtained for the grand-canonical reservoir but are qualitatively the same for a canonical setup at high densities. For densities , the current on the static lattice is already close to optimal (see section 3.2.1) and so there is little space for improvement. Actually, the lattice dynamics corrupts these states by shifting the transition to higher values of and making the phase separation less stable.
3.3.2 Finite diffusion rate
In the model with finite diffusion rates in the reservoir, there is no lane formation on the static lattice and the same remains true if a lattice dynamics at any strength is added. But as has already been reported in [19], a dynamic lattice is capable of dramatically increasing the current along the lattice and reaching an efficient state by dissolving large clusters. This effect is obviously also present in this system and the strength of the additional interaction only has very little impact on the current on the dynamic lattice.
The increase of current due to the modified attachment/detachment rates on the dynamic lattice is of the same order as the one observed on the static lattice (figure 11) and represents only a small fraction of the increase due to lattice dynamics: In a system of density and length , the maximum current increase caused by the lattice dynamics is almost ten-fold, whereas the modified attachment/detachment rates do not even double the current in the system.
3.4 Summary
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/88db96e3-d2b1-4b9c-b6e8-7ba05651c62e/x16.png)
An overview of the results of this section with its multiple scenarios is shown in table 1 with the color of the cell indicating if lane formation is possible.
In summary, particle-particle interactions which modify the attachment and detachment rates of particles depending on the occupation of the neighboring sites can lead to lane formation for reservoirs with an infinite diffusion rate only. In this case, although the number of encounters of particles of different species is reduced, the throughput of particles is extremely low in systems with a large number of particles. This is due to overcrowding of the lattice caused by the strong attractive interactions in lane-separated systems.
On the other hand, we have observed that efficient transport through lane formation can be obtained if the total particle density is limited to low enough values. However, in order to be in this optimal regime, the interaction strength should be large enough. There is no direct experimental measurement of the interaction strength that would allow to decide whether real systems are in this efficient regime. Crude estimates for can be made from the decoration experiments with kinesin, and would give [18] or [17], thus values that would be too low to trigger lane formation. However, this is certainly not a definite statement, as the interaction terms could have a different form than the one of figure 4, and further experimental measurements (in particular involving two types of motors) should be performed to refine the prediction. It should be noted that due to the dynamics of microtubules in real systems, the interaction strength needed to obtain separated lanes may be shifted to higher values, as we have found that it is the case here for a much simplified lattice dynamics. More generally, the fact that the lane formation mechanism is dependent on an infinite diffusivity around the transport lattice is a major drawback for the relevance of this type of interaction for the axon, which is a rather crowded environment. Thus, though an efficient regime was evidenced by our simulations for the canonical reservoir, we are not able to decide yet whether it is relevant for real systems, and thus it is worth to explore alternative scenarios (as will be done in the next sections).
In the absence of the aforementioned particle-particle interaction, the lattice dynamics was shown to improve the current along the filament for all three types of reservoirs. With the interaction presented here, it has a positive effect whenever current is hindered by a (possibly local) high density. The lattice dynamics dominate the behavior of the system in the sense that the lane formation disappears for strong lattice dynamics whereas for strong particle-particle interactions, the effect of the lattice dynamics remains visible.
4 Side-stepping in front of obstacles
The interaction presented in the previous section was able to induce lane formation and efficient transport only in the case of infinite diffusion in the reservoir. By contrast, in this section, we propose another type of particle interaction that is capable of inducing lane formation even for finite diffusion rates in the reservoir. As a consequence, only the reservoir with a finite diffusion rate will be treated here.
4.1 Model definition
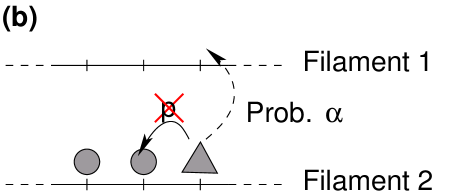
Particles obey to the same hopping rules as depicted in figure 10, i.e., they hop into a preferential direction along the filaments and hop with equal rates in both directions in the reservoirs. In order to keep the model simple, we consider again only two filaments and the two associated reservoirs. Exchanges between reservoirs or reservoir and filament occur with the same rates as before (see fig. 10). The particles still interact via hard-core exclusion on the filament but instead of modifying attachment and detachment, we consider the following interaction between particles: If a particle’s step along the filament is rejected because the target site is occupied by a particle of the opposite species, the particle switches to the other filament with probability provided the site at the same longitudinal position is empty on the other filament (see figure 13(a)). We shall refer to this interaction as the “single obstacle” interaction in the following.
So far, there is no experimental data showing a similar behavior of molecular motors. However, the only known experiments on interactions between molecular motors are the decoration experiments for kinesins addressed in section 3 which was shown to be rather questionable as a cause for possible lane formation. Here, the idea is that opposed motors push against each other and thus could exert a force which might induce lane changes. This effect might be even more pronounced if one thinks of the relatively large cargos carried by the molecular motors.
We shall also consider a variant of this interaction where the particle may only switch from one filament to the other with probability if it encounters two particles of the opposite species on the two next sites in stepping direction (see figure 13(b)). This mechanism will be referred to as the “two obstacles” interaction.
4.2 Static lattice
4.2.1 “Single obstacle” interaction
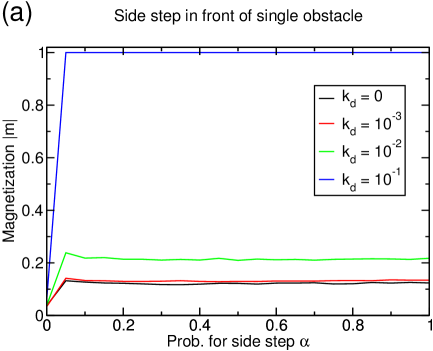
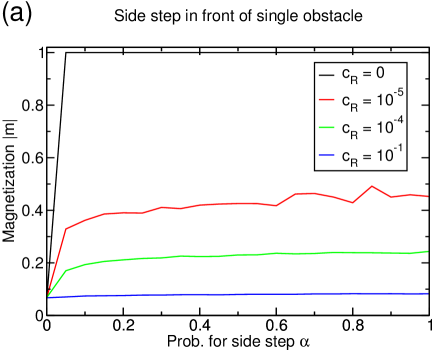
On a static lattice, changing lanes in front of a single particle of opposite species does not lead to dramatic effects. In particular, no lane formation is observed although the absolute magnetization of the filament slightly increases. This effect competes with the reservoir exchange rate which tends to mix the system and destroys any phase separation between the two subsystems. At , no effect of the additional particle-particle interaction is visible at any probability .
Nevertheless, there is a small effect for decoupled reservoirs at . The increase of the magnetization is stronger the fewer particles we have in the system, but even for densities as low as , the magnetization does not exceed . It is noteworthy that at the system size considered here, there is no important clustering at this low density. In a clustered system with higher particle density, absolute increases in magnetization are almost negligible: For , the magnetization passes from at to at .
Alike, the current does not improve much with this side-stepping interaction. The clustered systems remain clustered and exhibit a maximal gain of their current of while starting from an extremely low value being caused by the existence of the large cluster.
4.2.2 “Two obstacles” interaction
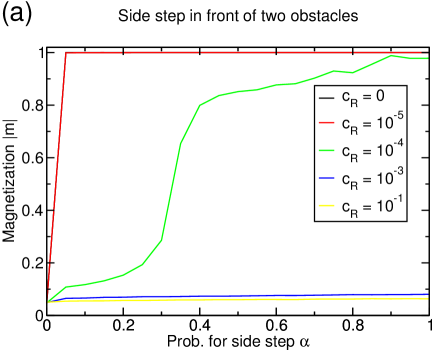
If we consider a stronger condition for filament changes as shown in figure 13(b), lane formation is obtained much more easily compared to the single obstacle model (section 4.2.1) and occurs at any density with decoupled reservoirs, i.e., . The current of particles along each filament is consequently very high and close to the optimal value found in a one-species TASEP. The interaction is asymmetric in the sense that a single particle changes the filament if opposed to two particles of opposite charge while the single particle cannot induce any lane change on the two particles. As a consequence, a particle species which is only slightly dominant on one filament can push more and more particles from the minority species to the other filament. Ultimately, complete lane formation is observed.
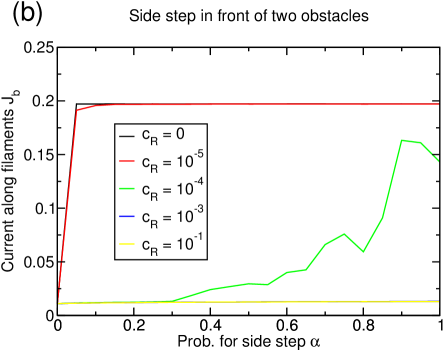
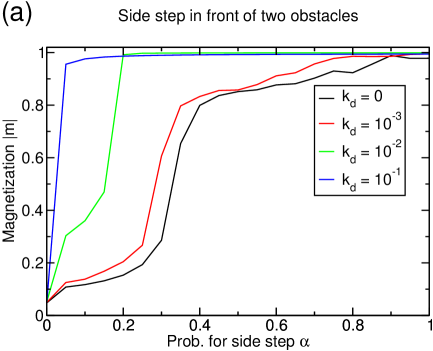
As discussed in the last section, the lane formation competes with the mixing through the reservoirs. If the reservoir coupling is increased, the magnetization is lowered at some point and lane formation disappears (figure 14(a)). The onset of remixing the separated lanes occurs at lower couplings for higher densities as in these cases, more particles are continuously transported to reservoir belonging to the ‘wrong’ filament. For , the system is completely mixed at any density.
The current increases by one order of magnitude if lane formation occurs (figure 14(b)) and is very close to the optimal value in the one-species TASEP.
4.3 Dynamic lattice
4.3.1 “Single obstacle” interaction
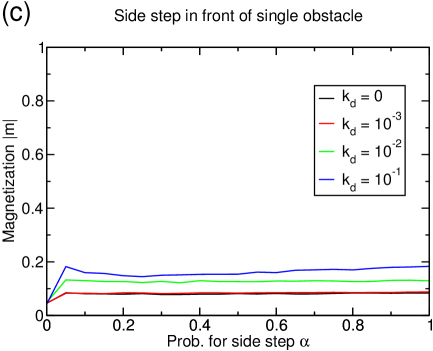
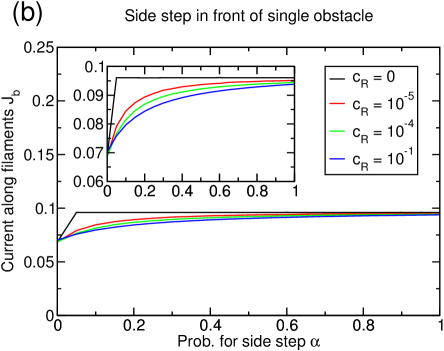
If the possibility to perform filament changes is combined with lattice dynamics, the system’s tendency toward lane formation is increased (see figure 15(a)). A system of density reaches complete lane formation at . However, at this value of the depolymerization rate , the basic model without filament changes does not exhibit a large cluster anymore, but is in a homogenous state with very small structures, and thus has already improved transport properties only due to lattice dynamics.
The enhanced lane formation can be understood in the following way: In order to form lanes, filament changes of particles are necessary which can only occur if particles of different species meet. Consequently, more lane changes are induced if there are more interfaces between positive and negative particles. In a clustered system, almost all the particles are accumulated in the cluster so that there are only very few interfaces. The lattice dynamics, though, inhibits the formation of large clusters and instead distributes the particles more homogeneously over the whole system leading to many very small clusters. This effectively increases the number of interfaces between positive and negative particles and thus favors lane changes and lane formation. The effect which has been mentioned in section 3.3.1 that holes in the lattice decrease the effectivity of a particle-particle interaction because the interaction is only next-neighbor seems to be overcompensated by the increase in interfaces due to the dissolution of the big cluster.
The strength of the lattice dynamics that is needed to form lanes depends on the particle density, e.g., a system of density does not exhibit complete lane formation at any lattice dynamics (see figure 15(c)) while a system of density forms lanes at much lower lattice dynamics (not shown).
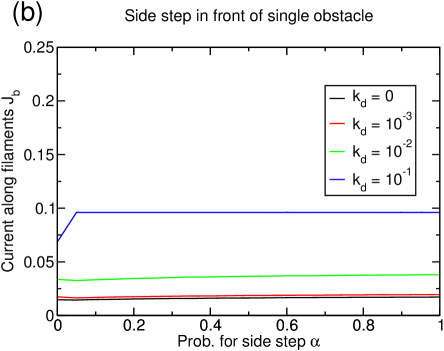
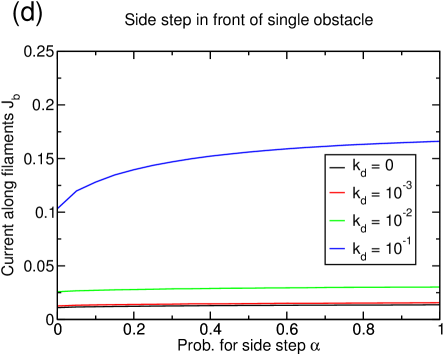
Again, the current is more strongly (and positively) affected by the lattice dynamics than by the additional particle-particle interaction as can be seen in figure 15(b) and (d): The higher the lattice dynamics, the higher the overall position of the current curves. In particular, for the completely lane separated system at for , the current increases by due to the lane formation, but more than quadruples because of the lattice dynamics (figure 15(b)). This impression is strengthened by the observation that similar gains due to the dynamic lattice are obtained even if no lane formation occurs (figure 15(d)). The values of the current for are remarkable since they are rather close to the maximum current of that would be found in a one-species TASEP, although encounters between particles of different species are still frequent in our model even at important lattice dynamics.
These results have so far been obtained at decoupled reservoirs . The influence of the reservoir coupling is shown in figure 16 for a dynamic lattice. Already an extremely small reservoir coupling destroys the lane formation (figure 16(a)). If diffusion in longitudinal and transverse direction are equal, i.e., , the lane formation effect disappears almost completely. However, the current is only marginally affected (figure 16(b)) and reaches almost identical values for all reservoir couplings at . This once more confirms that the lattice dynamics is dominant in determining the transport capacity of the system.
4.3.2 “Two obstacles” interaction
As for the the “single obstacle” interaction, the lattice dynamics also improve the lane formation mechanism by increasing the number of interfaces between oppositely moving particles for the “two obstacles” interaction (figure 17(a)). The influence of the lattice dynamics and the competition with the reservoir coupling on the magnetization and therefore on the lane formation remains qualitatively unchanged compared to section 4.3.1.
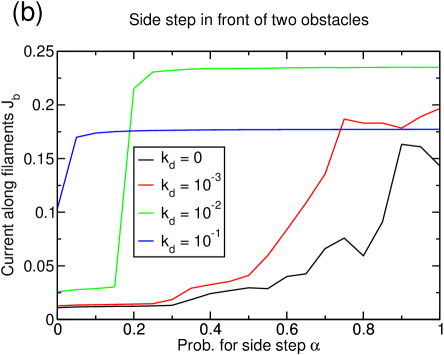
There is nevertheless an interesting difference for the value of the current in the systems with lane formation: For the most dynamic lattices , the current in the separated system can sometimes be lower than in de-mixed or even mixed systems at lower lattice dynamics (blue and green lines in figure 17(b)). In these cases, the lattice dynamics actually inhibit any further improvement of the current by eliminating too many sites of the filament along which no transport can happen. This effect is the more pronounced, the lower the density of particles is.
4.4 Summary
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/88db96e3-d2b1-4b9c-b6e8-7ba05651c62e/x29.png)
The most important results of this section are summarized in table 2.
The proposed interaction between particles which eventually induces filament changes of the particles has been shown to lead to lane formation under special conditions. In general, three factors determine the possibility of lane formation: 1. A higher particle density decreases the tendency to form separate lanes for both species (in contrast to what was observed for the modified attachment/detachment rates of section 3). 2. The reservoir coupling suppresses lane formation by mixing partially phase-separated subsystems (already true for the modified attachment/detachment rates of section 3). This mixing is very efficient as the rates needed to inhibit lane formation are several orders of magnitude smaller than all the other rates in the system. 3. Lattice dynamics promotes lane formation by increasing the number of contacts between positive and negative particles through a redistribution of the particles on several filament segments. We therefore have two effects leading to higher currents, one of which (lattice dynamics) improves the other (lane formation).
Considering the current, lane-separated states can obviously be considered as efficient transport states. They have a high throughput of particles and because of the absence of large structures, no finite-size effects are present, so that we have a density-dependent state. This property is necessary to have finite current in very long systems. However, we have shown that the effect of lattice dynamics on the current has a much larger amplitude than the one due to the side stepping mechanism.
5 Discussion
In the present article, we presented two different types of particle-particle interactions in a quasi one-dimensional lattice gas with oppositely moving particle species. Both types of interactions lead to lane formation under certain conditions. We explored the robustness of these lane-separated states and their transport capacity. An efficient transport state was supposed to be characterized by a system size-independent (= density-dependent) state, with a finite current that compares to the current in a one-species TASEP serving as a benchmark.
The first type of interaction which was considered by Klumpp and Lipowsky [15] affects the affinity to the filament in the vicinity of other particles. The lane-separated states that are found (only for infinite reservoir diffusion) exhibit a density-dependent current but many of these states also have extremely high densities on the filament so that the actual current of bound particles is rather low compared to an optimal regime. This is in particular the case for open systems (grand-canonical reservoir), or for closed systems with high enough densities (canonical reservoir). The conclusion is that lane formation does not necessarily imply efficient transport although this can be the case. Lower densities with a canonical reservoir do lead to very efficient states which compare well to the one-species TASEP.
Lane formation with this type of interaction (leading to modified attachment/detachment rates) was only possible for an infinite diffusion rate in the reservoir. With regard to an application of these concepts to real transport processes as intracellular transport, this is a very strong assumption. The interior of a cell is very crowded and considering the typical sizes of vesicles and organelles, diffusion should be very limited. In the case of finite diffusion, no lane formation is observed and the interaction plays a minor role in improving the current, compared to the much more positive impact of lattice dynamics.
In the second type of interaction that has been considered in this paper, particles hop to the neighboring filament when they meet an oppositely charged motor. Although this model is in principle able to exhibit lane formation at finite longitudinal diffusion, the lane-separated state is extremely sensitive to diffusion between reservoirs, i.e., diffusion in the transverse direction. This is in sharp contrast to the first interaction model which actually needed infinite diffusion rates to exhibit lane formation. The difference comes from the nature of the particle-particle interaction. Any de-mixing in the first scenario has to be carried out via particle exchanges with the reservoir whereas in the second scenario, particles directly switch from one filament to the other and do not need the reservoir to form lanes. From a biological point of view, the strong limitation of transversal diffusion required for the scenario based on side-stepping could be realized if the axon is compartmentalized such that diffusing particles cannot reach easily other filaments than the ones in their direct neighborhood.
Furthermore, based on the experimental observation that microtubule-based transport in axons takes place on dynamic microtubules, we have considered that the underlying lattice itself can undergo some dynamics, through the much simplified random polymerization/depolymerization of filament units. As, from a general point of view, the consequences of a lattice dynamics on transport properties are not known, we chose to concentrate on a simplified lattice dynamics, to study generic effects, rather than going directly into the full complexity of the biological system.
We had already shown in [19] how such a lattice dynamics can drive the system from a size-dependent state with inefficient transport, to a density-dependent state with efficient transport. In the present paper, we have studied again what would be the influence of a dynamic lattice on the transport efficiency, but now in the presence of interactions. In almost all cases (i.e., for almost all types of reservoirs and particle interactions), we found that lattice dynamics improves the efficiency of transport. Actually, we found only one case in which the lattice dynamics does not improve the current in the system: if the system forms lanes at low enough density , with infinite diffusion rate in the reservoir, then lattice dynamics worsens a state which is already close to optimal transport. However, an infinite diffusion rate in the reservoir is not expected to be relevant for transport in real cells, and besides, there is no experimental evidence yet that the motor-motor interaction strength is sufficient to reach this state. In all the other cases, the benefits from lattice dynamics as described in [19] were still valid also when combined with particle-particle interactions.
More precisely, the lattice dynamics modifies the lane formation mechanism for both types of interaction scenarios. In the first scenario, while lane formation is shifted to stronger interactions, lattice dynamics still improve the transport in the system by lowering the density on the filament in the inefficiently crowded states. The second lane formation mechanism through side-stepping is enhanced by the lattice dynamics as it relies on direct contacts between particles of opposite species which are increased by the dissolution of clusters. Then lattice dynamics on the one hand lowers the interaction strength required to form lanes, and on the other hand improves the current in lane separated states.
For both types of interactions, the same effects are already present on a static lattice with a sufficient density of holes, due to an effective limitation of the system size. But our results indicate that the effects are enhanced when the lattice undergoes some dynamics (at equal hole density).
In total, lane formation appears difficult to achieve in bidirectional systems as considered here, because the fact that the run length along the filament is finite (due to processivity or lattice dynamics) actively works against any sorting of particles onto different filaments. Lane formation can be achieved only for special combinations of parameters or characteristics of the system. It is an open question to know whether biological parameters for axonal transport are or are not in this regime. Several types of molecular motors which participate in intracellular transport have been studied experimentally, but results are obtained mostly for in vitro experiments, while it is not obvious that dynamical parameters are the same in an in vivo environment. Besides, some motors (as dyneins) are more difficult to study, and we are lacking data. There are almost no experimental results about interactions between different types of motors. It cannot be excluded that other interactions between motors than those considered here lead to lane formation mechanisms which are less sensitive to system parameters. There is an urgent need for more data on particle-particle interactions which could possibly be acquired by statistical exploitation of in vitro experiments involving many motors.
As mentioned above, the lattice dynamics were intentionally kept simple in this paper. We found that such lattice dynamics produce transport enhancement through cluster dissolution, and in [19], we found that it was robust for several types of simple lattice dynamics. Still, in further studies, we plan to apply our approach to more biologically relevant dynamics, but there is still a need of experimental observations about the precise dynamics of the microtubule network.
Anyhow, for the interactions considered in this paper, we found that for finite diffusion the lattice dynamics always has a positive effect on transport, whether lane formation is present or not. Thus in the context of axonal transport, lattice dynamics and motor-motor interactions should not be considered as competing mechanisms, but rather as two complementary processes that can contribute in a cooperative way to the efficiency of bidirectional transport. Only further experimental informations can allow to quantify the contribution of the various ingredients. However, in view of our results, we suggest that the microtubule dynamics could play an important role in the regulation of bidirectional transport, whether in combination with motor-motor interactions or not.
Bibliography
References
- [1] B. Alberts, A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. Molecular Biology of the Cell. Taylor and Francis, 4 edition, 2002.
- [2] M. Schliwa and G. Woehlke. Molecular motors. Nature, 422:759, 2003.
- [3] R. Lipowsky, S. Klumpp, and T. M. Nieuwenhuizen. Random walks of cytoskeletal motors in open and closed compartments. Phys. Rev. Lett., 87:108101, 2001.
- [4] A. Parmeggiani, T. Franosch, and E. Frey. Phase coexistence in driven one-dimensional transport. Phys. Rev. Lett., 90:086601, 2003.
- [5] S. Klumpp, and R. Lipowsky, Traffic of Molecular Motors through Tube-Like Compartments Journal of Statistical Physics, 113: 233, 2003.
- [6] M. R. Evans, R. Juhász, and L. Santen. Shock formation in an exclusion process with creation and annihilation. Phys. Rev. E, 68:026117, 2003.
- [7] R. Juhasz, and L. Santen Dynamics of an exclusion process with creation and annihilation J. Phys. A, 37: 3933, 2004.
- [8] A. Parmeggiani, T. Franosch, and E. Frey. Totally asymmetric simple exclusion process with Langmuir kinetics. Phys. Rev. E, 70:046101, 2004.
- [9] J. Tailleur, M. R. Evans, and Y. Kafri. Nonequilibrium phase transitions in the extraction of membrane tubes by molecular motors. Phys. Rev. Lett., 102:118109, 2009.
- [10] J. Krug. Boundary-induced phase transitions in driven diffusive systems. Phys. Rev. Lett., 67, 1882, 1991.
- [11] B. Derrida. An exactly soluble non-equilibrium system: The asymmetric simple exclusion process. Phys. Rep., 301, 65, 1998.
- [12] K. Nishinari, Y. Okada, A. Schadschneider, and D. Chowdhury. Intracellular transport of single-headed molecular motors kif1a. Phys. Rev. Lett., 95:118101, 2005.
- [13] M. Ebbinghaus and L. Santen. A model for bidirectional traffic of cytoskeletal motors. J. Stat. Mech., P03030, 2009.
- [14] R. Juhasz. Weakly coupled, antiparallel, totally asymmetric simple exclusion processes. Phys. Rev. E, 76:021117, 2007.
- [15] S. Klumpp and R. Lipowsky. Phase transitions in systems with two species of molecular motors. Europhys. Letters, 66:90–96, 2004.
- [16] A. Vilfan, E. Frey, F. Schwabl, M. Thormählen, Y.-H. Song, and E. Mandelkow. Dynamics and cooperativity of microtubule decoration by the motor protein kinesin. J. Mol. Biol., 312:1011, 2001.
- [17] W.H. Roos, O. Campàs, F. Montel, G. Woehlke, J.P. Spatz, P. Bassereau, and G. Cappello Dynamic kinesin-1 clustering on microtubules due to mutually attractive interactions. Phys. Biol., 5:046004, 2008.
- [18] E. Muto, H. Sakai, and K. Kaseda. Long-range cooperative binding of kinesin to a microtubule in the presence of atp. J. Cell Biol., 168:691, 2005.
- [19] M. Ebbinghaus, C. Appert-Rolland, and L. Santen. Bidirectional transport on a dynamic lattice. Phys. Rev. E, 82:040901(R), 2010.
- [20] P.F. Arndt, T. Heinzel, V. Rittenberg Spontaneous breaking of translational invariance in one-dimensional stationary states on a ring. J. Phys. A, 31: L45, 1998.
- [21] N. Rajewsky, T. Sasamoto, and E. R. Speer. Spatial particle condensation for an exclusion process on a ring. Physica A, 279:123–142, 2000.
- [22] P. Greulich, and L. Santen. Boundary-induced orientation of dynamic filament networks and vesicle agglomerations. arXiv:1106.5733, 2011.
- [23] H. Erez, G. Malkinson, M. Prager-Khoutorsky, C.I. De Zeeuw, C.C. Hoogenraad, and M.E. Spira. Formation of microtubule-based traps controls the sorting and concentration of vesicles to restricted sites of regenerating neurons after axotomy. J. Cell Biol., 176:497, 2007.
- [24] O.A. Shemesh and M.E. Spira. Hallmark cellular pathology of Alzheimer’s disease induced by mutant human tau expression in cultured Aplysia neurons. Acta Neuropathologica, 120:209, 2010.
- [25] J. Chen, Y. Kanai, N.J. Cowan, and N. Hirokawa Projection domains of MAP2 and tau determine spacings between microtubules in dendrites and axons. Nature, 360:674, 1992.
- [26] M. Ebbinghaus, C. Appert-Rolland, and L. Santen. Bidirectional traffic on microtubules. To appear in Lecture Notes in Computer Science, Springer (Proceedings of the ACRI2010 conference, 21-24 Sept. 2010).
- [27] T. Reichenbach and E. Frey and T. Franosch. Exclusion Processes with Internal States. Phys. Rev. Lett., 97:050603, 2006.
- [28] C. Schiffmann and C. Appert-Rolland and L. Santen. Shock Dynamics of two-lane driven lattice gases. J. Stat. Mech., P06002, 2010.