Pattern Alternating Maximization Algorithm for Missing Data in “Large P, Small N” Problems

Nicolas Städler The Netherlands Cancer Institute, 1066 CX Amsterdam, The Netherlands. Daniel J. Stekhoven Seminar für Statistik, ETH Zürich, CH-8092 Zürich, Switzerland. Peter Bühlmann Seminar für Statistik, ETH Zürich, CH-8092 Zürich, Switzerland.

Abstract

We propose a new and computationally efficient algorithm for maximizing the observed log-likelihood for a multivariate normal data matrix with missing values. We show that our procedure based on iteratively regressing the missing on the observed variables, generalizes the standard EM algorithm by alternating between different complete data spaces and performing the E-Step incrementally. In this non-standard setup we prove numerical convergence to a stationary point of the observed log-likelihood.

For high-dimensional data, where the number of variables may greatly exceed sample size, we add a Lasso penalty in the regression part of our algorithm and perform coordinate descent approximations. This leads to a computationally very attractive technique with sparse regression coefficients for missing data imputation. Simulations and results on four microarray datasets show that the new method often outperforms other imputation techniques as k-nearest neighbors imputation, nuclear norm minimization or a penalized likelihood approach with an $\ell_{1}$ -penalty on the inverse covariance matrix.

Keywords Missing data, observed likelihood, (partial) E- and M-Step, Lasso, penalized variational free energy

1 Introduction and Motivation

Missing data imputation for large datasets is an essential pre-processing step in complex data applications. A well-known example are microarray datasets which contain the expression values of thousands of genes from a series of experiments. Missing values are inherent to such datasets. They occur for diverse reasons, e.g. insufficient resolution, image corruption, dust or scratches on the slides. Apart from microarrays, much attention has been recently given to the so-called matrix completion problem. Most prominent in this context is the “Netflix” movie rating dataset with rows corresponding to customers and columns representing their movie rating and the customers have seen/rated only a small fraction of all possible movies. The goal is to estimate the ratings for unseen movies. Filling in missing values in gene expression data is a inherently different problem from dealing with missings in the context of matrix completion. For example the Netflix dataset involves a huge number of customers (480’000) and movies (17’000) with about 98% of the ratings missing. In big contrast, microarrays have the typical “large p, small n” form where the number of different genes $p$ is in the ten thousands and the number of experimental conditions $n$ is in the hundreds. Usually only a small fraction of the expression values are missing. In this paper, we propose a new and computationally efficient EM-type algorithm for missing value imputation in the high-dimensional multivariate normal model where the number of variables $p$ can greatly exceed the number of independent samples $n$ . Our motivating examples are microarray datasets with $p$ different genes (variables) and $n$ different experimental conditions (samples). The Gaussian assumption in our model is used for computation of the likelihood but empirical findings suggest that the method is useful for many continuous data matrices.

There is a growing literature of missing value imputation methods. For microarray data, examples are k-nearest neighbors imputation and singular value decomposition imputation (Troyanskaya et al., 2001), imputation based on Bayesian principal component analysis (Oba et al., 2003) or the local least squares imputation from Kim et al. (2006). For a review and a discussion on microarray data imputation see Aittokallio (2010). In the context of the so-called matrix completion problem, where the goal is to recover a low-rank matrix from an incomplete set of entries, it has been shown in a series of fascinating papers that one can recover the missing data entries by solving a convex optimization problem, namely, nuclear-norm minimization subject to data constraints (Candès and Recht, 2009; Candès and Tao, 2010; Keshavan et al., 2010). Efficient convex algorithms for the matrix completion problem were proposed by Cai et al. (2010) and Mazumder et al. (2010). If the missing data problem does not arise from a near low rank matrix scenario, there is substantial room to improve upon the convex matrix completion algorithms. We will empirically demonstrate this point for some microarray high-throughput biological data.

Here, we address the missing data problem through a likelihood approach (Little and Rubin, 1987; Schafer, 1997). We model the correlation between different variables in the data by using the Multivariate Normal Model (MVN) $\mathcal{N}(\mu,\Sigma)$ with a p-dimensional covariance matrix $\Sigma$ . Recently, in the high-dimensional setup with $p\gg n$ , Städler and Bühlmann (2012) proposed to maximize the penalized observed log-likelihood with an $\ell_{1}$ -penalty on the inverse covariance matrix. They called their method MissGLasso, as an extension of the GLasso (Friedman et al., 2008) for missing data. A similar approach, in the context of so-called transposable models, is given by Allen and Tibshirani (2010).

The MissGLasso uses an EM algorithm for optimization of the penalized observed log-likelihood. Roughly, the algorithm can be summarized as follows. In the E-Step, for each sample, the regression coefficients of the missing against the observed variables are computed from the current estimated covariance matrix $\hat{\Sigma}$ . In the following M-Step, the missing values are imputed by linear regressions and $\hat{\Sigma}$ is re-estimated by performing a GLasso on completed data. There are two main drawbacks of this algorithm in a high-dimensional context. First, the E-Step is rather complex as it involves (for each sample) inversion and multiplication of large matrices in order to compute the regression coefficients. Secondly, a sparse inverse covariance does not imply sparse regression coefficients while we believe that in high-dimensions, sparse regression coefficients would enhance imputations.

Our new algorithm, MissPALasso (Missingness Pattern Alternating Lasso algorithm) in this paper, generalizes the E-Step in order to resolve the disadvantages of MissGLasso. In particular, inversion of a matrix (in order to compute the regression coefficients) will be replaced by a simple soft-thresholding operator. In addition, the regression coefficients will be sparse, which leads to a new sparsity concept for missing data estimation.

In order to motivate MissPALasso, we develop first the Missingness Pattern Alternating maximization algorithm (MissPA) for optimizing the (unpenalized) observed log-likelihood. MissPA generalizes the E- and M-Step of the standard EM originally proposed by Dempster et al. (1977) by alternating between different complete data spaces and performing the E-Step incrementally. Such a generalization does not fit into any of the existing methodologies which extend the standard EM. However, by exploiting the special structure of our procedure and applying standard properties of the Kullback-Leibler divergence, we prove convergence to a stationary point of the observed log-likelihood.

The further organization of the paper is as follows: Section 2 introduces the setup and the useful notion of missingness patterns. In Section 3 we develop our algorithms: MissPA is presented in Section 3.2 and MissPALasso then follows in Section 3.3 as an adapted version for high-dimensional data with $p\gg n$ . Section 4 compares performance of MissPALasso with other imputation methods on simulated and real data and reports on computational efficiency. Finally, in Section 5, we present some mathematical theory which describes the numerical properties of the Missingness Pattern Alternating maximization algorithm.

2 Setup

We assume $X=(X_{1},\ldots,X_{p})\sim\mathcal{N}(\mu,\Sigma)$ has a p-variate normal distribution with mean $\mu$ and covariance $\Sigma$ . In order to simplify the notation we set without loss of generality $\mu=0$ : for $\mu\neq 0$ , some of the formulae involve the parameter $\mu$ and an intercept column of $(1,\ldots,1)$ in the design matrices but conceptually, we can proceed as for the case with $\mu=0$ . We then write $\mathbf{X}=(\mathbf{X}_{\mathrm{obs}},\mathbf{X}_{\mathrm{mis}})$ , where $\mathbf{X}$ represents an i.i.d. random sample of size $n$ , $\mathbf{X}_{\mathrm{obs}}$ denotes the set of observed values, and $\mathbf{X}_{\mathrm{mis}}$ the missing data.

Missingness Patterns and Different Parametrizations

For our purpose it will be convenient to group rows of the matrix $\mathbf{X}$ according to their missingness patterns (Schafer, 1997). We index the unique missingness patterns that actually appear in our data by $k=1,\ldots,s$ . Furthermore, with $o_{k}\subset\{1,\ldots,p\}$ and $m_{k}=\{1,\ldots,p\}\setminus o_{k}$ we denote the set of observed variables and the set of missing variables, respectively. $\mathcal{I}_{k}$ is the index set of the samples (row numbers) which belong to pattern $k$ , whereas $\mathcal{I}^{c}_{k}=\{1,\ldots,n\}\setminus\mathcal{I}_{k}$ stands for the row numbers which do not belong to that pattern. By convention, samples with all variables observed do not belong to a missingness pattern.

Consider a partition $X=(X_{o_{k}},X_{m_{k}})$ of a single Gaussian random vector. It is well known that $X_{m_{k}}|X_{o_{k}}$ follows a linear regression on $X_{o_{k}}$ with regression coefficients $B_{m_{k}|o_{k}}$ and covariance $\Sigma_{m_{k}|o_{k}}$ given by

	$\displaystyle B_{m_{k}\|o_{k}}$	$\displaystyle=$	$\displaystyle\Sigma_{m_{k},o_{k}}\Sigma_{o_{k}}^{-1},$		(2.1)
	$\displaystyle\Sigma_{m_{k}\|o_{k}}$	$\displaystyle=$	$\displaystyle\Sigma_{m_{k}}-\Sigma_{m_{k},o_{k}}\Sigma_{o_{k}}^{-1}\Sigma_{o_{k},m_{k}}.$

Consequently, we can write the density $p(x;\Sigma)$ of $X$ as

\displaystyle p(x;\Sigma)=p(x_{m_{k}}|x_{o_{k}};B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})p(x_{o_{k}};\Sigma_{o_{k}}),

i.e., the density can be characterized by either the parameter $\Sigma$ or $(\Sigma_{o_{k}},B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})$ . With the transformation (2.1) we can switch between both parametrizations.

Observed Log-Likelihood and Maximum Likelihood Estimation (MLE)

A systematic approach to estimate the parameter of interest $\Sigma$ from $\mathbf{X}_{\mathrm{obs}}$ maximizes the observed log-likelihood $\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})$ given by

\displaystyle\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})=\sum_{i\notin\bigcup_{k}\mathcal{I}_{k}}\log p(x_{i};\Sigma)+\sum_{k=1}^{s}\sum_{i\in\mathcal{I}_{k}}\log p(x_{i,o_{k}};\Sigma_{o_{k}}).

(2.2)

Inference for $\Sigma$ can be based on the observed log-likelihood (2.2) if the underlying missing data mechanism is ignorable. The missing data mechanism is said to be ignorable if the probability that an observation is missing may depend on $\mathbf{X}_{\mathrm{obs}}$ but not on $\mathbf{X}_{\mathrm{mis}}$ (Missing at Random) and if the parameters of the data model and the parameters of the missingness mechanism are distinct. For a precise definition see Little and Rubin (1987).

Explicit maximization of $\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})$ is only possible for special missing data patterns. Most prominent are examples with a so-called monotone missing data pattern (Little and Rubin, 1987; Schafer, 1997), where $X_{1}$ is more observed than $X_{2}$ , which is more observed than $X_{3}$ , and so on. In this case, the observed log-likelihood factorizes and explicit maximization is achieved by performing several regressions. For a general pattern of missing data, the standard EM algorithm is often used for optimization of (2.2). See Schafer (1997) for a detailed description of the algorithm. In the next section we present an alternative method for maximizing the observed log-likelihood. We will argue that this new algorithm is computationally more efficient than the standard EM.

3 Pattern Alternating Missing Data Estimation and
$\ell_{1}$ -Regularization

For each missingness pattern, indexed by $k=1,\ldots,s$ , we introduce some further notation:

	$\displaystyle\mathbf{X}^{k}=(x_{i,j})\quad\textrm{with}\quad i\in\mathcal{I}_{k}\quad j=1,\ldots,p$
	$\displaystyle\mathbf{X}^{-k}=(x_{i,j})\quad\textrm{with}\quad i\in\mathcal{I}_{k}^{c}\quad j=1,\ldots,p.$

Thus, $\mathbf{X}^{k}$ is the $|\mathcal{I}_{k}|\times p$ submatrix of $\mathbf{X}$ with rows belonging to the $k$ th pattern. Similarly, $\mathbf{X}^{-k}$ is the $|\mathcal{I}_{k}^{c}|\times p$ matrix with rows not belonging to the $k$ th pattern. In the same way we define $\mathbf{X}^{k}_{o_{k}},\mathbf{X}^{k}_{m_{k}},\mathbf{X}^{-k}_{o_{k}}$ and $\mathbf{X}^{-k}_{m_{k}}$ . For example, $\mathbf{X}^{k}_{o_{k}}$ is defined as the $|\mathcal{I}_{k}|\times|o_{k}|$ matrix with

\mathbf{X}^{k}_{o_{k}}=(x_{i,j})\quad\textrm{with}\quad i\in\mathcal{I}_{k},\quad j\in o_{k}.

3.1 MLE for Data with a Single Missingness Pattern

Assume that the data matrix $\mathbf{X}$ has only one single missingness pattern, denoted by $s$ . This is the most simple example of a monotone pattern. The observed log-likelihood factorizes according to:

	$\displaystyle\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})=\sum_{i\in\mathcal{I}_{s}}\log p(x_{i,o_{s}};\Sigma_{o_{s}})+\sum_{i\in\mathcal{I}_{s}^{c}}\log p(x_{i};\Sigma)$
	$\displaystyle=\sum_{i=1}^{n}\log p(x_{i,o_{s}};\Sigma_{o_{s}})+\sum_{i\in\mathcal{I}_{s}^{c}}\log p(x_{i,m_{s}}\|x_{i,o_{s}};B_{m_{s}\|o_{s}},\Sigma_{m_{s}\|o_{s}}).$		(3.3)

The left and right part in Equation (3.1) can be maximized separately. The first part is maximized by the sample covariance of the observed variables based on all samples, whereas the second part is maximized by a regression of the missing against observed variables based on only the fully observed samples. In formulae:

\displaystyle\hat{\Sigma}_{o_{s}}={}^{t}\mathbf{X}_{o_{s}}\mathbf{X}_{o_{s}}/n,

(3.4)

and

	$\displaystyle\hat{B}_{m_{s}\|o_{s}}={}^{t}\mathbf{X}^{-s}_{m_{s}}\mathbf{X}^{-s}_{o_{s}}({}^{t}\mathbf{X}^{-s}_{o_{s}}\mathbf{X}^{-s}_{o_{s}})^{-1},$
	$\displaystyle\hat{\Sigma}_{m_{s}\|o_{s}}={}^{t}\!(\mathbf{X}^{-s}_{m_{s}}-\mathbf{X}^{-s}_{o_{s}}\,{}^{t}\!\hat{B}_{m_{s}\|o_{s}})(\mathbf{X}^{-s}_{m_{s}}-\mathbf{X}^{-s}_{o_{s}}\,{}^{t}\!\hat{B}_{m_{s}\|o_{s}})/\|\mathcal{I}_{s}^{c}\|.$		(3.5)

Having these estimates at hand, it is easy to impute the missing data:

\hat{x}_{i,m_{s}}=\hat{B}_{m_{s}|o_{s}}{}^{t}\!x_{i,o_{s}}\;\textrm{for all}\;i\in\mathcal{I}_{s},\quad\textrm{or, in matrix notation,}\quad\hat{\mathbf{X}}^{s}_{m_{s}}=\mathbf{X}^{s}_{o_{s}}\,{}^{t}\!\hat{B}_{m_{s}|o_{s}}.

It is important to note, that, if interested in imputation, only the regression part of the MLE is needed and the estimate $\hat{\Sigma}_{o_{s}}$ in (3.4) is superfluous.

3.2 MLE for General Missing Data Pattern

We turn now to the general case, where we have more than one missingness pattern, indexed by $k=1,\ldots,s$ . The general idea of the new algorithm is as follows. Assume we have some initial imputations for all missing values. Our goal is to improve on these imputations. For this purpose, we iterate as follows:

•

Keep all imputations except those of the $1$ st missingness pattern fixed and compute the single pattern MLE (for the first pattern) as explained in Section 3.1. In particular, compute the regression coefficients of the missing $1$ st pattern against all other variables (treated as “observed”) based on all samples which do not belong to the $1$ st pattern.
•

Use the resulting estimates (regression coefficients) to impute the missing values from only the $1$ st pattern.

Next, turn to the $2$ nd pattern and repeat the above steps. In this way we continue cycling through the different patterns until convergence.

We now describe the Missingness Pattern Alternating maximization algorithm (MissPA) which makes the above idea precise. Let $T={}^{t}\mathbf{X}\mathbf{X}$ be the sufficient statistic in the multivariate normal model. Furthermore, denote by $T^{k}={}^{t}\!(\mathbf{X}^{k})\mathbf{X}^{k}$ , $T^{-k}={}^{t}\!(\mathbf{X}^{-k})\mathbf{X}^{-k}=\sum_{l\neq k}T^{l}$ . Let $\mathcal{T}$ and $\mathcal{T}^{k}\,(k=1,\ldots,s)$ be some initial guess of $T$ and $T^{k}\,(k=1,\ldots,s)$ , for example, using zero imputation. Our algorithm proceeds as follows.


Algorithm 1: MissPA

(1)	$\mathcal{T}$ , $\mathcal{T}^{k}$ : initial guess of $T$ and $T^{k}$ $(k=1,\ldots,s)$ .
(2)	For $k=1,\ldots,s$ do:
	M-Step: Compute the MLE $\hat{B}_{m_{k}\|o_{k}},$ and $\hat{\Sigma}_{m_{k}\|o_{k}}$ , based on $\mathcal{T}^{-k}=\mathcal{T}-\mathcal{T}^{k}$ :
	$\hat{B}_{m_{k}\|o_{k}}=\mathcal{T}^{-k}_{m_{k},o_{k}}(\mathcal{T}^{-k}_{o_{k},o_{k}})^{-1},$
	$\hat{\Sigma}_{m_{k}\|o_{k}}=\left(\mathcal{T}^{-k}_{m_{k},m_{k}}-\mathcal{T}^{-k}_{m_{k},o_{k}}(\mathcal{T}^{-k}_{o_{k},o_{k}})^{-1}\mathcal{T}^{-k}_{o_{k},m_{k}}\right)/\|\mathcal{I}_{k}^{c}\|.$
	Partial E-Step:
	Set $\mathcal{T}^{l}=\mathcal{T}^{l}$ for all $l\neq k$ (this takes no time),
	Set $\mathcal{T}^{k}=\mathbb{E}[T^{k}\|\mathbf{X}^{k}_{o_{k}},\hat{B}_{m_{k}\|o_{k}},\hat{\Sigma}_{m_{k}\|o_{k}}],$
	Update $\mathcal{T}=\mathcal{T}^{-k}+\mathcal{T}^{k}$ .
(3)	Repeat step (2) until some convergence criterion is met.
(4)	Compute the final maximum likelihood estimator $\hat{\Sigma}$ via:
	$\hat{\Sigma}_{o_{s}}=\mathcal{T}_{o_{s},o_{s}}/n$ , $\hat{\Sigma}_{m_{s},o_{s}}=\hat{B}_{m_{s}\|o_{s}}\hat{\Sigma}_{o_{s}}$ and $\hat{\Sigma}_{m_{s}}=\hat{\Sigma}_{m_{s}\|o_{s}}+\hat{B}_{m_{s}\|o_{s}}\hat{\Sigma}_{o_{s},m_{s}}$ .

Note, that we refer to the maximization step as M-Step and to the imputation step as partial E-Step. The word partial refers to the fact that the expectation is only performed with respect to samples belonging to the current pattern. The partial E-Step of our algorithm takes the following simple form:

	$\displaystyle\mathcal{T}^{k}_{o_{k},m_{k}}={}^{t}\!(\mathbf{X}_{o_{k}}^{k})\hat{\mathbf{X}}_{m_{k}}^{k},$
	$\displaystyle\mathcal{T}^{k}_{m_{k},m_{k}}={}^{t}\!(\hat{\mathbf{X}}_{m_{k}}^{k})\hat{\mathbf{X}}_{m_{k}}^{k}+\|\mathcal{I}_{k}\|\hat{\Sigma}_{m_{k}\|o_{k}},$

where $\hat{\mathbf{X}}^{k}_{m_{k}}=\mathbb{E}[\mathbf{X}^{k}_{m_{k}}|\mathbf{X}^{k}_{o_{k}},\hat{B}_{m_{k}|o_{k}},\hat{\Sigma}_{m_{k}|o_{k}}]=\mathbf{X}^{k}_{o_{k}}{}^{t}\!\hat{B}_{m_{k}|o_{k}}$ .

Our algorithm does not require an evaluation of $\hat{\Sigma}_{o_{k}}$ in the M-Step, as it is not used in the following partial E-Step. But, if we are interested in the observed log-likelihood or the maximum likelihood estimator $\hat{\Sigma}$ at convergence, we compute $\hat{\Sigma}_{o_{s}}$ (at convergence), use it together with $\hat{B}_{m_{s}|o_{s}}$ and $\hat{\Sigma}_{m_{s}|o_{s}}$ to get $\hat{\Sigma}$ via the transformations (2.1) as explained in step (4).

MissPA is computationally more efficient than the standard EM for missing data: one cycle through all patterns ( $k=1,\ldots,s$ ) takes about the same time as one iteration of the standard EM. But our algorithm makes more progress since the information from the partial E-Step is utilized immediately to perform the next M-Step. We will demonstrate empirically the gain of computational efficiency in Section 4.2. The new MissPA generalizes the standard EM in two ways. Firstly, MissPA alternates between different complete data spaces in the sense of Fessler and Hero (1994). Secondly, the E-Step is performed incrementally (Neal and Hinton, 1998). In Section 5 we will expand on these generalizations and we will provide an appropriate framework which allows analyzing the convergence properties of MissPA.

Finally, a small modification of MissPA, namely replacing in Algorithm 1 the M-Step by

M-Step2: Compute the MLE $\hat{B}_{m_{k}|o_{k}},$ and $\hat{\Sigma}_{m_{k}|o_{k}}$ , based on $\mathcal{T}$ :
$\hat{B}_{m_{k}|o_{k}}=\mathcal{T}_{m_{k},o_{k}}(\mathcal{T}_{o_{k},o_{k}})^{-1}$
$\hat{\Sigma}_{m_{k}|o_{k}}=\left(\mathcal{T}_{m_{k},m_{k}}-\mathcal{T}_{m_{k},o_{k}}(\mathcal{T}_{o_{k},o_{k}})^{-1}\mathcal{T}_{o_{k},m_{k}}\right)/n,$

results in an alternative algorithm. We show in Section 5 that Algorithm 1 with M-Step2 is equivalent to an incremental EM in the sense of Neal and Hinton (1998).

3.3 High-Dimensionality and Lasso Penalty

The M-Step of Algorithm 1 is basically a multivariate regression of the missing ( $X_{m_{k}}$ ) against the observed variables ( $X_{o_{k}}$ ). In a high-dimensional framework with $p\gg n$ the number of observed variables $|o_{k}|$ will be large and therefore some regularization is necessary. The main idea is, in order to regularize, to replace the regressions with a Lasso (Tibshirani, 1996). We give now the details.

Estimation of $B_{m_{k}|o_{k}}$ :

The estimation of the multivariate regression coefficients in the M-Step2 can be expressed as $|m_{k}|$ separate minimization problems of the form

\displaystyle\hat{B}_{j|o_{k}}=\mathop{\arg\min}\limits_{\beta}-\mathcal{T}_{j,o_{k}}\beta+{}^{t}\!\beta\mathcal{T}_{o_{k},o_{k}}\beta/2,

where $j\in m_{k}$ . Here, $\hat{B}_{j|o_{k}}$ denotes the $j$ th row vector of the $(|m_{k}|\times|o_{k}|)$ -matrix $\hat{B}_{m_{k}|o_{k}}$ and represents the regression of variable $j$ against the variables from $o_{k}$ .

Consider now the objective function

\displaystyle-\mathcal{T}_{j,o_{k}}\beta+{}^{t}\!\beta\mathcal{T}_{o_{k},o_{k}}\beta/2+\lambda\|\beta\|_{1},

(3.6)

with an additional Lasso penalty. Instead of minimizing (3.6) with respect to $\beta$ (for all $j\in m_{k}$ ), it is computationally much more efficient to improve it coordinate-wise only from the old parameters (computed in the last cycle through all patterns). For that purpose, let $B_{m_{k}|o_{k}}^{(r)}$ be the regression coefficients for pattern $k$ in cycle $r$ and $B_{j|o_{k}}^{(r)}$ its $j$ th row vector. In cycle $r+1$ we compute $B_{j|o_{k}}^{(r+1)}$ by minimizing (3.6) with respect to each of the components of $\beta$ , holding the other components fixed at their current value. Closed-form updates have the form:

\displaystyle B_{j|l}^{(r+1)}=\frac{\mathop{Soft}\big{(}\mathcal{T}_{l,l}B_{j|l}^{(r)}-S_{l},\lambda\big{)}}{\mathcal{T}_{l,l}},\qquad\textrm{for all $l\in o_{k}$,}

(3.7)

where

•

$B_{j|l}^{(r+1)}$ is the $l$ th component of $B_{j|o_{k}}^{(r+1)}$ equal to the element $(j,l)$ of matrix $B_{m_{k}|o_{k}}^{(r+1)}$ .

•

$S_{l}$ , the gradient of $-\mathcal{T}_{j,o_{k}}\beta+{}^{t}\!\beta\mathcal{T}_{o_{k},o_{k}}\beta/2$ with respect to $\beta_{l}$ , which equals

\displaystyle S_{l}=-\mathcal{T}_{j,l}+\sum_{\begin{subarray}{c}v<l\\ v\in o_{k}\end{subarray}}\mathcal{T}_{l,v}B_{j|v}^{(r+1)}+\mathcal{T}_{l,l}B_{j|l}^{(r)}+\sum_{\begin{subarray}{c}v>l\\ v\in o_{k}\end{subarray}}\mathcal{T}_{l,v}B_{j|v}^{(r)}.

(3.8)

•

$\mathop{Soft}(z,\lambda)=\left\{\begin{array}[]{ll}z-\lambda&\textrm{if}\;z>\lambda\\ z+\lambda&\textrm{if}\;z<-\lambda\\ 0&\textrm{if}\;\left|z\right|\leq\lambda\end{array}\right.$ , is the standard soft-thresholding operator.

In a sparse setup the soft-thresholding update (3.7) can be evaluated very quickly as $l$ varies and often coefficients which are zero remain zero after thresholding. See also the naive- or covariance update idea of Friedman et al. (2010) for efficient computation of (3.7) and (3.8).

Estimation of $\Sigma_{m_{k}|o_{k}}$ :

We update the residual covariance matrix as:

\displaystyle\Sigma_{m_{k}|o_{k}}^{(r+1)}=\Big{(}\mathcal{T}_{m_{k},m_{k}}-\mathcal{T}_{m_{k},o_{k}}{}^{t}\!B_{m_{k}|o_{k}}^{(r+1)}-B_{m_{k}|o_{k}}^{(r+1)}\mathcal{T}_{o_{k},m_{k}}+B_{m_{k}|o_{k}}^{(r+1)}\mathcal{T}_{o_{k},o_{k}}{}^{t}\!B_{m_{k}|o_{k}}^{(r+1)}\Big{)}/n.

(3.9)

Formula (3.9) can be viewed as a generalized version of Equation (3.5), when multiplying out the matrix product in (3.5) and taking expectations.

Our regularized algorithm, the MissPALasso, is summarized in Table 1. Note, that we update the sufficient statistic in the partial E-Step according to $\mathcal{T}=\gamma\mathcal{T}+\mathcal{T}^{k}$ where $\gamma=1-|\mathcal{I}_{k}|/n$ . This update, motivated by Nowlan (1991), calculates $\mathcal{T}$ as an exponentially decaying average of recently-visited data points. It prevents MissPALasso from storing $\mathcal{T}^{k}$ for all $k=1,\ldots,s$ which gets especially cumbersome for large $p$ ’s. As we are mainly interested in estimating the missing values, we will output the data matrix with missing values imputed by the regression coefficients $\hat{B}_{m_{k}|o_{k}}$ ( $k=1,\ldots,s$ ) as indicated in step (4) of Table 1. MissPALasso provides not only the imputed data matrix $\hat{\mathbf{X}}$ but also $\hat{\mathcal{T}}$ , the completed version of the sufficient statistic ${}^{t}\!\mathbf{X}\mathbf{X}$ . The latter can be very useful if MissPALasso is used as a pre-processing step followed by a learning method which is expressible in terms of the sufficient statistic. Examples include regularized regression (e.g., Lasso), discriminant analysis, or estimation of directed acyclic graphs with the PC-algorithm (Spirtes et al., 2000).

By construction, the regression estimates $\hat{B}_{m_{k}|o_{k}}$ are sparse, due to the employed $\ell_{1}$ -penalty, and therefore, imputation of missing values $\hat{\mathbf{X}}^{k}_{m_{k}}=\mathbf{X}^{k}_{o_{k}}\,{}^{t}\!\hat{B}_{m_{k}|o_{k}}$ is based on sparse regressions. This is in sharp contrast to the MissGLasso approach (see Section 4.1) which places sparsity on $\Sigma^{-1}$ . But this does not imply that regressions of variables in $m_{k}$ on variables in $o_{k}$ are sparse since the inverse of sub-matrices of a sparse $\Sigma^{-1}$ are not sparse in general. MissPALasso employs another type of sparsity and this seems to be the main reason for its better statistical performance than MissGLasso.

Remark 3.1.

In practice, we propose to compute MissPALasso for a decreasing sequence of values for $\lambda$ , using each solution as a warm start for the next problem with smaller $\lambda$ . This pathwise strategy is computationally very attractive and our algorithm converges (for each $\lambda$ ) after a few cycles.


Algorithm 2: MissPALasso

(1)	Set $r=0$ and start with initial guess for $\mathcal{T}$ and $B_{m_{k}\|o_{k}}^{(0)}$ ( $k=1,\ldots,s$ ).
(2)	In cycle $r+1$ ; for $k=1,\ldots,s$ do:
	Penalized M-Step2:
	For all $j\in m_{k}$ , compute $B_{j\|o_{k}}^{(r+1)}$ by improving $-\mathcal{T}_{j,o_{k}}\beta+{}^{t}\!\beta\mathcal{T}_{o_{k},o_{k}}\beta/2+\lambda\\|\beta\\|_{1}$
	in a coordinate-wise manner from $B_{j\|o_{k}}^{(r)}$ .
	Set $\Sigma_{m_{k}\|o_{k}}^{(r+1)}\!=\Big{(}\mathcal{T}_{m_{k},m_{k}}\!-\mathcal{T}_{m_{k},o_{k}}{}^{t}\!B_{m_{k}\|o_{k}}^{(r+1)}\!-B_{m_{k}\|o_{k}}^{(r+1)}\mathcal{T}_{o_{k},m_{k}}\!+B_{m_{k}\|o_{k}}^{(r+1)}\mathcal{T}_{o_{k},o_{k}}{}^{t}\!B_{m_{k}\|o_{k}}^{(r+1)}\Big{)}/n.$
	Partial E-Step:
	Set $\mathcal{T}^{k}=\mathbb{E}[T^{k}\|\mathbf{X}^{k}_{o_{k}},B_{m_{k}\|o_{k}}^{(r+1)},\Sigma^{(r+1)}_{m_{k}\|o_{k}}],$
	Update $\mathcal{T}=\gamma\mathcal{T}+\mathcal{T}^{k}$ where $\gamma=1-\|\mathcal{I}_{k}\|/n$ .
	Increase: $r\leftarrow r+1.$
(3)	Repeat step (2) until some convergence criterion is met.
(4)	Output the imputed data matrix $\hat{\mathbf{X}}$ , with missing values estimated by:
	$\hat{\mathbf{X}}^{k}_{m_{k}}=\mathbf{X}^{k}_{o_{k}}\,{}^{t}\!\hat{B}_{m_{k}\|o_{k}}$ , $k=1,\ldots,s$ .

Table 1: MissPALasso. In the

k

th M-Step of cycle

r+1

, instead of a multivariate Lasso regression, a coordinate descent approximation of the corresponding Lasso problem is performed. Regression coefficients

B^{(r)}_{m_{k}|o_{k}}

k=1,\ldots,s

, are stored in sparse matrix format.

4 Numerical Experiments

4.1 Performance of MissPALasso

In this section we will explore the performance of MissPALasso developed in Section 3.3. We compare our new method with alternative ways of imputing missing values in high-dimensional data. We consider the following methods:

•

KnnImpute: Impute the missing values by the K-nearest neighbors imputation method introduced by Troyanskaya et al. (2001).
•

SoftImpute: The soft imputation algorithm is proposed by Mazumder et al. (2010) in order to solve the matrix completion problem. They propose to approximate the incomplete data matrix $\mathbf{X}$ by a complete (low-rank) matrix $\mathbf{Z}$ minimizing

$\frac{1}{2}\sum_{(i,j)\in\Omega}(z_{ij}-x_{ij})^{2}+\lambda\|\mathbf{Z}\|_{*}.$

Here, $\Omega$ denotes the indices of observed entries and $\|\mathbf{Z}\|_{*}$ is the nuclear norm, or the sum of the singular values. The missing values of $\mathbf{X}$ are imputed by the corresponding values of $\mathbf{Z}$ .
•

MissGLasso: Compute $\hat{\Sigma}$ by minimizing $-\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})+\lambda\|\Sigma^{-1}\|_{1},$ where $\|\Sigma^{-1}\|_{1}$ is the entrywise $\ell_{1}$ -norm. Then, use this estimate to impute the missing values by conditional mean imputation. MissGLasso is described in Städler and Bühlmann (2012).
•

MissPALasso: This is the method introduced in Section 3.3.

To assess the performances of the methods we use the normalized root mean squared error (Oba et al., 2003) which is defined by

NRMSE

\displaystyle=

\displaystyle\sqrt{\frac{\textbf{mean}\left((\mathbf{X}^{\mathrm{true}}-\hat{\mathbf{X}})^{2}\right)}{\textbf{var}\left(\mathbf{X}^{\mathrm{true}}\right)}}.

Here, $\mathbf{X}^{\mathrm{true}}$ is the original data matrix (before deleting values) and $\hat{\mathbf{X}}$ is the imputed matrix. With mean and var we abbreviate the empirical mean and variance, calculated over only the missing entries.

All methods involve one tuning parameter. In KnnImpute we have to choose the number $K$ of nearest neighbors, while SoftImpute, MissGLasso and MissPALasso involve a regularization parameter which is always denoted by $\lambda$ . In all of our experiments we choose the tuning parameters to obtain optimal performance in terms of NRMSE.

4.1.1 Simulation Study

We consider both high- and a low-dimensional MVN models with $\sim\mathcal{N}_{p}(0,\Sigma)$ where

•

Model 1: $p=50$ and $500$ ;
$\Sigma$ : block diagonal with $p/2$ blocks of the form $\bigl{(}\begin{smallmatrix}1&0.9\\ 0.9&1\end{smallmatrix}\bigr{)}.$
•

Model 2: $p=100$ and 1000;
$\Sigma$ : two blocks $\textrm{B}_{1}$ , $\textrm{B}_{2}$ each of size $\frac{p}{2}\times\frac{p}{2}$ with $\textrm{B}_{1}=\textrm{I}_{\frac{p}{2}}$ and $(\textrm{B}_{2})_{j,j^{\prime}}=0.9^{|j-j^{\prime}|}$ .
•

Model 3: $p=55$ and 496;
$\Sigma$ : block diagonal with $b=1,\ldots,10$ for $p=55$ and $b=1,\ldots,31$ for $p=496$ (increasing) blocks $\textrm{B}_{b}$ of the size $b\times b$ , with $(\textrm{B}_{b})_{j,j^{\prime}}=0.9$ $(j\neq j^{\prime})$ and $(\textrm{B}_{b})_{j,j}=1$ .
•

Model 4: $p=100$ and 500;
$\Sigma_{j,j^{\prime}}=0.9^{|j-j^{\prime}|}$ for $j,j^{\prime}=1,\ldots,p.$

For all four settings we perform 50 independent simulation runs. In each run we generate $n=50$ i.i.d. samples from the model. We then delete randomly $5\%,10\%$ and $15\%$ of the values in the data matrix, apply an imputation method and compute the NRMSE. The results of the different imputation methods (tuning parameters such that NRMSE is minimal) are reported in Table 2 for the low-dimensional models and Table 3 for the high-dimensional models. MissPALasso is very competitive in all setups. SoftImpute works rather poorly, perhaps because the resulting data matrices are not well approximable by low-rank matrices. KnnImpute works very well in model 1 and model 4. Model 1, where each variable is highly correlated with its neighboring variable, represents an example which fits well into the KnnImpute framework. However, in model 2 and model 3, KnnImpute performs rather poorly. The reason is that with an inhomogeneous covariance matrix, as in model 2 and 3, the optimal number of nearest neighbors is varying among the different blocks, and a single parameter $K$ is too restrictive. For example in model 2, a variable from the first block is not correlated to any other variable, whereas a variable from the second block is correlated to other variables. Except for the low-dimensional model 3 MissGLasso is inferior to MissPALasso. Furthermore, MissPALasso strongly outperforms MissGLasso with respect to computation time (see Figure 4 in Section 4.2). Interestingly, all methods exhibit a quite large NRMSE in the high-dimensional model 3. They seem to have problems coping with the complex covariance structure in higher dimensions. If we look at the same model but with $p=105$ the NRMSE for 5% missing values is: 0.85 for KnnImpute, 0.86 for SoftImpute, 0.77 for MissGLasso and 0.77 for MissPALasso. This indicates an increase in NRMSE according to the size of $p$ . Arguably, we consider here only multivariate normal models which are ideal, from a distributional point of view, for MissGLasso and our MissPALasso. The more interesting case will be with real data (all from genomics) where model assumptions never hold exactly.

		KnnImpute	SoftImpute	MissGLasso	MissPALasso
Model 1	5%	0.4874 (0.0068)	0.7139 (0.0051)	0.5391 (0.0079)	0.5014 (0.0070)
p=50	10%	0.5227 (0.0051)	0.7447 (0.0038)	0.5866 (0.0057)	0.5392 (0.0055)
	15%	0.5577 (0.0052)	0.7813 (0.0037)	0.6316 (0.0048)	0.5761 (0.0047)
Model 2	5%	0.8395 (0.0101)	0.8301 (0.0076)	0.7960 (0.0082)	0.7786 (0.0075)
p=100	10%	0.8572 (0.0070)	0.8424 (0.0063)	0.8022 (0.0071)	0.7828 (0.0066)
	15%	0.8708 (0.0062)	0.8514 (0.0053)	0.8082 (0.0058)	0.7900 (0.0054)
Model 3	5%	0.4391 (0.0061)	0.4724 (0.0050)	0.3976 (0.0056)	0.4112 (0.0058)
p=55	10%	0.4543 (0.0057)	0.4856 (0.0042)	0.4069 (0.0047)	0.4155 (0.0047)
	15%	0.4624 (0.0054)	0.4986 (0.0036)	0.4131 (0.0043)	0.4182 (0.0044)
Model 4	5%	0.3505 (0.0037)	0.5515 (0.0039)	0.3829 (0.0035)	0.3666 (0.0031)
p=100	10%	0.3717 (0.0033)	0.5623 (0.0033)	0.3936 (0.0027)	0.3724 (0.0026)
	15%	0.3935 (0.0032)	0.5800 (0.0031)	0.4075 (0.0026)	0.3827 (0.0026)

Table 2: Average (SE) NRMSE of KnnImpute, SoftImpute, MissGLasso and MissPALasso with different degrees of missingness in the low-dimensional models.

		KnnImpute	SoftImpute	MissGLasso	MissPALasso
Model 1	5%	0.4913 (0.0027)	0.9838 (0.0006)	0.6705 (0.0036)	0.5301 (0.0024)
p=500	10%	0.5335 (0.0020)	0.9851 (0.0005)	0.7613 (0.0031)	0.5779 (0.0019)
	15%	0.5681 (0.0016)	0.9870 (0.0004)	0.7781 (0.0013)	0.6200 (0.0015)
Model 2	5%	0.8356 (0.0020)	0.9518 (0.0009)	0.8018 (0.0012)	0.7958 (0.0017)
p=1000	10%	0.8376 (0.0016)	0.9537 (0.0007)	0.8061 (0.0002)	0.7990 (0.0013)
	15%	0.8405 (0.0014)	0.9562 (0.0006)	0.8494 (0.0080)	0.8035 (0.0011)
Model 3	5%	1.0018 (0.0009)	0.9943 (0.0005)	0.9722 (0.0013)	0.9663 (0.0010)
p=496	10%	1.0028 (0.0007)	0.9948 (0.0004)	0.9776 (0.0010)	0.9680 (0.0007)
	15%	1.0036 (0.0006)	0.9948 (0.0003)	0.9834 (0.0010)	0.9691 (0.0007)
Model 4	5%	0.3487 (0.0016)	0.7839 (0.0020)	0.4075 (0.0016)	0.4011 (0.0016)
p=500	10%	0.3721 (0.0014)	0.7929 (0.0015)	0.4211 (0.0012)	0.4139 (0.0013)
	15%	0.3960 (0.0011)	0.8045 (0.0014)	0.4369 (0.0012)	0.4292 (0.0014)

Table 3: Average (SE) NRMSE of KnnImpute, SoftImpute, MissGLasso and MissPALasso with different degrees of missingness in the high-dimensional models.

4.1.2 Real Data Examples

We consider the following four publicly available datasets:

•

Isoprenoid gene network in Arabidopsis thaliana: The number of genes in the network is $p=39$ . The number of observations (gene expression profiles), corresponding to different experimental conditions, is $n=118$ . More details about the data can be found in Wille et al. (2004).
•

Colon cancer: In this dataset, expression levels of 40 tumor and 22 normal colon tissues ( $n=62$ ) for $p=2000$ human genes are measured. For more information see Alon et al. (1999).
•

Lymphoma: This dataset, presented in Alizadeh et al. (2000), contains gene expression levels of 42 samples of diffuse large B-cell lymphoma, 9 observations of follicular lymphoma, and 11 cases of chronic lymphocytic leukemia. The total sample size is $n=62$ and $p=1332$ complete measured expression profiles are documented.
•

Yeast cell-cycle: The dataset, described in Spellman et al. (1998), monitors expressions of 6178 genes. The data consists of four parts, which are relevant to alpha factor ( $18$ samples), elutriation ( $14$ samples), cdc15 ( $24$ samples), and cdc28 ( $17$ samples). The total sample size is $n=73$ . We use the $p=573$ complete profiles in our study.

For all datasets we standardize the columns (genes) to zero mean and variance one. In order to compare the performance of the different imputation methods we randomly delete values to obtain an overall missing rate of $5\%$ , $10\%$ and $15\%$ . Table 4 shows the results for 50 simulation runs, where in each run another random set of values is deleted.

		KnnImpute	SoftImpute	MissGLasso	MissPALasso
Arabidopsis	5%	0.7732 (0.0086)	0.7076 (0.0065)	0.7107 (0.0076)	0.7029 (0.0077)
n=118	10%	0.7723 (0.0073)	0.7222 (0.0052)	0.7237 (0.0064)	0.7158 (0.0060)
p=39	15%	0.7918 (0.0050)	0.7369 (0.0041)	0.7415 (0.0053)	0.7337 (0.0050)
Colon cancer	5%	0.4884 (0.0011)	0.4921 (0.0011)	-	0.4490 (0.0011)
n=62	10%	0.4948 (0.0008)	0.4973 (0.0006)	-	0.4510 (0.0006)
p=2000	15%	0.5015 (0.0007)	0.5067 (0.0006)	-	0.4562 (0.0007)
Lymphoma	5%	0.7357 (0.0014)	0.6969 (0.0008)	-	0.6247 (0.0012)
n=62	10%	0.7418 (0.0009)	0.7100 (0.0006)	-	0.6384 (0.0009)
p=1332	15%	0.7480 (0.0007)	0.7192 (0.0005)	-	0.6525 (0.0008)
Yeast cell-cycle	5%	0.8083 (0.0018)	0.6969 (0.0012)	-	0.6582 (0.0016)
n=73	10%	0.8156 (0.0011)	0.7265 (0.0010)	-	0.7057 (0.0013)
p=573	15%	0.8240 (0.0009)	0.7488 (0.0007)	-	0.7499 (0.0011)

Table 4: Average (SE) NRMSE of KnnImpute, SoftImpute, MissGLasso and MissPALasso for different real datasets from genomics. The R implementation of MissGLasso is not able to handle real datasets of such high dimensionality.

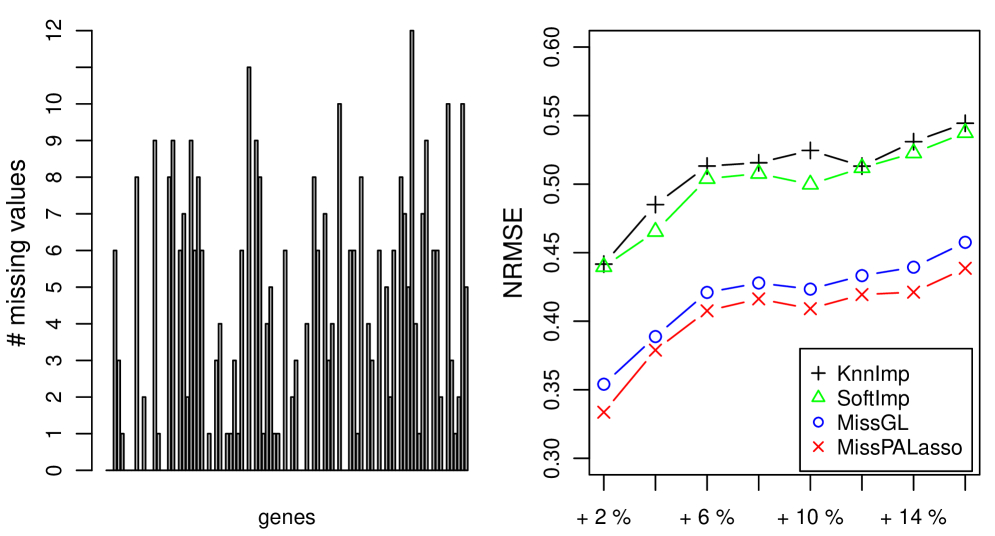
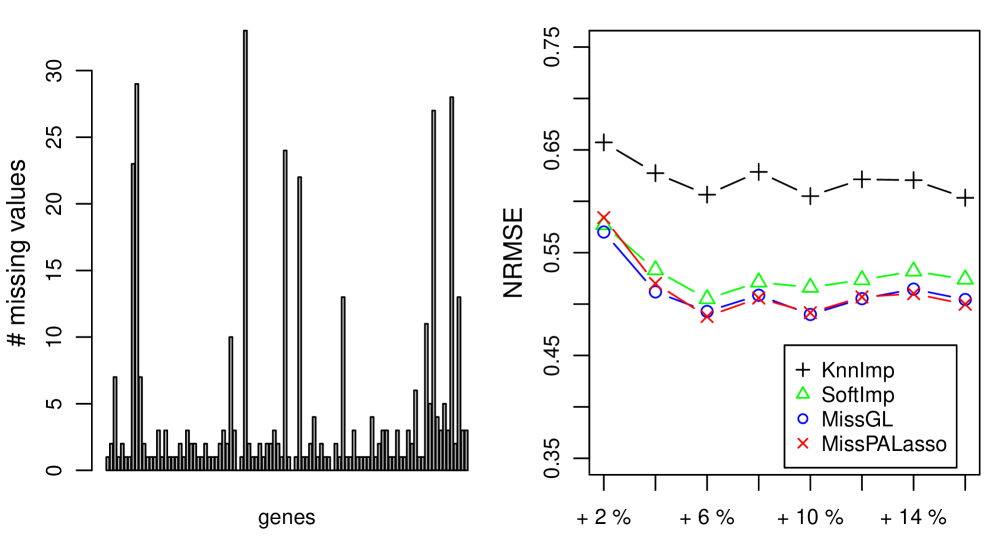
MissPALasso exhibits in all setups the lowest averaged NRMSE. MissGLasso performs nearly as well as MissPALasso on the Arabidopsis data. However, its R implementation cannot cope with large values of $p$ . If we would restrict our analysis to the 100 variables exhibiting the most variance we would see that MissGLasso performs slightly less than MissPALasso (results not included). Compared to KnnImpute, SoftImpute works well for all datasets. Interestingly, KnnImpute performs for all datasets much inferior to MissPALasso. In light of the simulation results of Section 4.1.1, a reason for the poor performance could be that KnnImpute has difficulties with the inhomogeneous correlation structure between different genes which is plausible to be present in real datasets.

To investigate the effect of already missing values on the imputation performance of the compared methods we use the original lymphoma and yeast cell-cycle datasets which already have “real” missing values. We only consider the 100 most variable genes in these datasets to be able to compare all four methods with each other. From the left panel of Figures 1 and 2 we can read off how many values are missing for each of the 100 variables. In the right panel of Figures 1 and 2 we show how well the different methods are able to estimate $2\%,4\%,6\%\ldots,16\%$ of additionally deleted entries.

Refer to caption — Figure 1: Lymphoma dataset. Left panel: Barplots which count the number of missing values for each of the 100 genes. Right panel: NRMSE for KnnImpute, SoftImpute, MissGLasso and MissPALasso if we introduce additional $2\%,4\%,6\%,\ldots,16\%$ missings.

4.2 Computational Efficiency

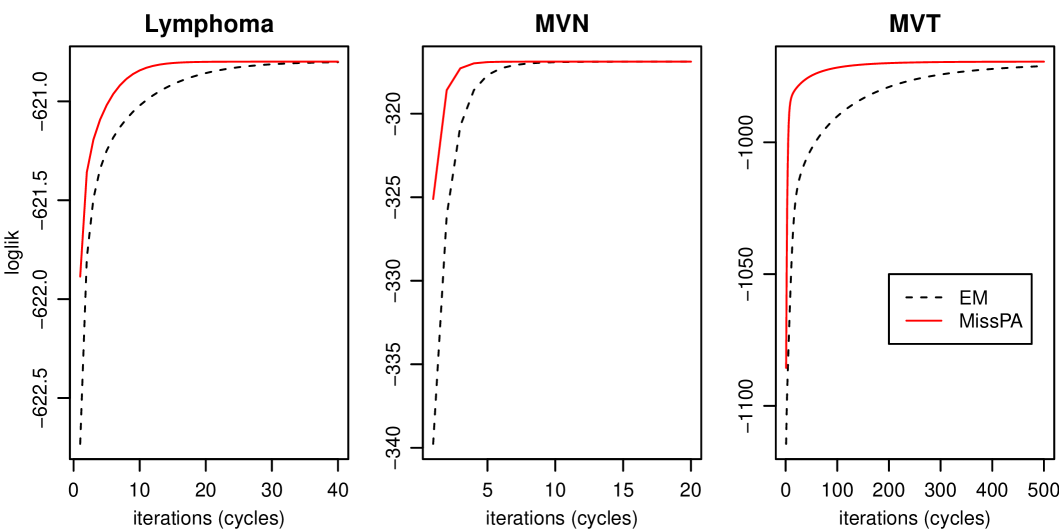
We first compare the computational efficiency of MissPA with the standard EM described for example in Schafer (1997). The reason why our algorithm takes less time to converge is because of the more frequent updating of the latent distribution in the M-Steps. A key attribute of MissPA is that the computational cost of one cycle through all patterns is the same as the cost of a single E-Step of the standard EM which requires computation of the regression parameters from $\hat{\Sigma}$ obtained in the previous M-Step. This is a big contrast to the incremental EM, mostly applied to finite mixtures (Thiesson et al., 2001; Ng and McLachlan, 2003), where there is a trade-off between the additional computation time per cycle, or “scan” in the language of Ng and McLachlan (2003), and the fewer number of “scans” required because of the more frequent updating after each partial E-Step. The speed of convergence of the standard EM and MissPA for three datasets are shown in Figure 3, in which the log-likelihood is plotted as a function of the number of iterations (cycles). The left panel corresponds to the subset of the lymphoma dataset when only the ten genes with highest missing rate are used. This results in a $62\times 10$ data matrix with $22.85\%$ missing values. For the middle panel we draw a random sample of size $62\times 10$ from $\mathcal{N}_{10}(0,\Sigma)$ , $\Sigma_{j,j^{\prime}}=0.9^{|j-j^{\prime}|}$ , and delete the same entries which are missing in the reduced lymphoma data. For the right panel we draw from the multivariate t-model with degrees of freedom equal to one and again with the same values deleted. As can be seen, MissPA converges after fewer cycles. A very extreme example is obtained with the multivariate t-model where the standard EM reaches the log-likelihood level of MissPA about 400 iterations later. We note here, that the result in the right panel highly depends on the realized random sample. With other realizations, we get less and more extreme results than the one shown in Figure 3.

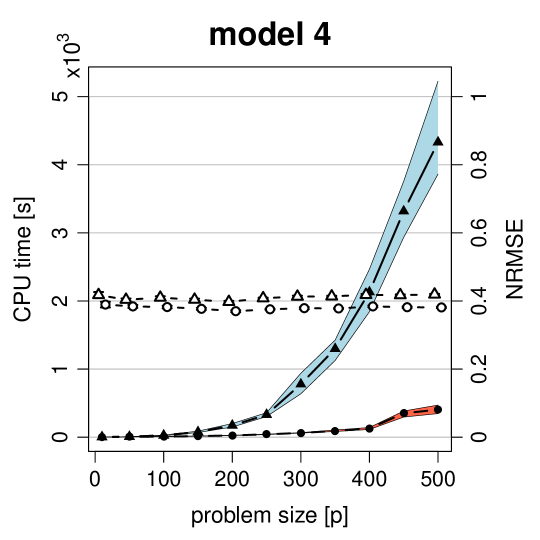
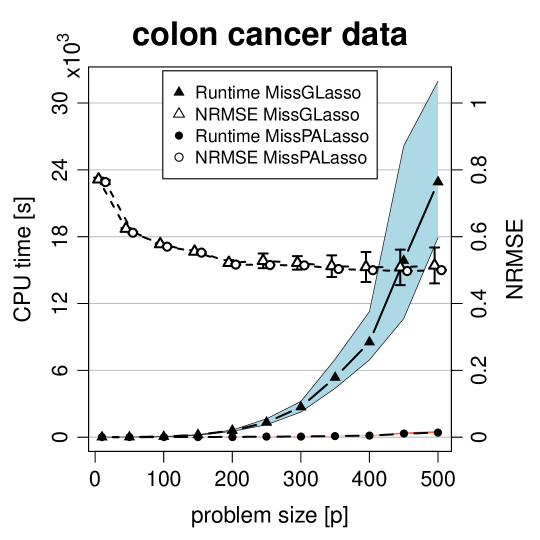
We end this section by illustrating the computational timings of MissPALasso and MissGLasso implemented with the statistical computing language R. We consider two settings. Firstly, model 4 of Section 4.1.1 with $n=50$ and a growing number of variables $p$ ranging from 10 to 500. Secondly, the colon cancer dataset from Section 4.1.2 with $n=62$ and also a growing number of variables where we sorted the variables according to the empirical variance. For each $p$ we delete $10\%$ of the data, run MissPALasso and MissGLasso ten times on a decreasing grid (on the log-scale) of $\lambda$ values with thirty grid points. For a fixed $\lambda$ we stop the algorithm if the relative change in imputation satisfies,

\displaystyle\frac{\|\hat{\mathbf{X}}^{(r+1)}-\hat{\mathbf{X}}^{(r)}\|^{2}}{\|\hat{\mathbf{X}}^{(r+1)}\|^{2}}\leq 10^{-5}.

In Figure 4 the CPU times in seconds are plotted for various values of $p$ in the two settings. As shown, with MissPALasso we are typically able to solve a problem of size $p=100$ in about 9 seconds and a problem of size $p=500$ in about 400 seconds. For MissGLasso these times are highly increased to 27 and 4300 seconds respectively. Furthermore, we can see that MissPALasso has much smaller variability in runtimes. The graphical Lasso algorithm (Friedman et al., 2008) and therefore MissGLasso have computational complexity $\mathcal{O}(p^{3})$ , whereas the complexity of MissPALasso is considerably smaller. We note that the matrix inversion in the M-Step of MissPA is replaced by soft-thresholding in MissPALasso. In sparse settings soft-thresholding as well as matrix multiplications can be evaluated very quickly as the regression coefficients $B_{m_{k}|o_{k}}$ contain many zeros. The exact complexity of MissPALasso depends on the fraction of missing values and also on the sparsity of the problem.

5 Theory

A key characteristic of our MissPA (Algorithm 1 in Section 3.2) is that the E-Step is only performed on those samples belonging to a single pattern. We already mentioned the close connection to the incremental EM introduced by Neal and Hinton (1998). In fact, if the density of $\mathbf{X}^{k}$ , $k\in\{1,\ldots,s\}$ , is denoted by $\mathrm{P}_{\Sigma}(\mathbf{X}^{k})=\prod_{i\in\mathcal{I}_{k}}p(x_{i};\Sigma)$ then the negative variational free energy (Neal and Hinton, 1998; Jordan et al., 1999) equals

\displaystyle\mathcal{F}[\Sigma\|\Psi_{1},\ldots,\Psi_{s}]

\displaystyle=

\displaystyle\sum_{k=1}^{s}\big{(}\mathbb{E}_{\Psi_{k}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{k})|\mathbf{X}^{k}_{o_{k}}]+\mathcal{H}_{k}[\Psi_{k}]\big{)}.

(5.10)

Here, $\Psi_{k}=\left(B_{k,m_{k}|o_{k}},\Sigma_{k,m_{k}|o_{k}}\right)$ denotes the regression parameter of the latent distribution

\displaystyle\mathrm{P}_{\Psi_{k}}(\mathbf{X}^{k}_{m_{k}}|\mathbf{X}^{k}_{o_{k}})

\displaystyle=

\displaystyle\prod_{i\in\mathcal{I}_{k}}p(x_{i,m_{k}}|x_{i,o_{k}};B_{k,m_{k}|o_{k}},\Sigma_{k,m_{k}|o_{k}})

and $\mathcal{H}_{k}[\Psi_{k}]=-\mathbb{E}_{\Psi_{k}}[\log\mathrm{P}_{\Psi_{k}}(\mathbf{X}_{m_{k}}^{k}|\mathbf{X}_{o_{k}}^{k})|\mathbf{X}^{k}_{o_{k}}]$ is the entropy. An iterative procedure alternating between maximization of $\mathcal{F}$ with respect to $\Sigma$

	$\displaystyle\hat{\Sigma}$	$\displaystyle=$	$\displaystyle\mathop{\arg\max}\limits_{\Sigma}\mathcal{F}[\Sigma\\|\Psi_{1},\ldots,\Psi_{s}]$
		$\displaystyle=$	$\displaystyle\frac{1}{n}\sum_{k=1}^{s}\mathbb{E}_{\Psi_{k}}[^{t}\mathbf{X}^{k}\mathbf{X}^{k}\|\mathbf{X}^{k}_{o_{k}}]=:\frac{1}{n}\mathcal{T},$

and maximizing $\mathcal{F}$ with respect to $\Psi_{k}$

$\displaystyle(\hat{B}_{k,m_{k}\|o_{k}},\hat{\Sigma}_{k,m_{k}\|o_{k}})$	$\displaystyle=$	$\displaystyle\mathop{\arg\max}\limits_{\Psi_{k}}\mathcal{F}[\hat{\Sigma}\\|\Psi_{1},\ldots,\Psi_{s}]$
	$\displaystyle=$	$\displaystyle\mathop{\arg\max}\limits_{\Psi_{k}}\mathbb{E}_{\Psi_{{k}}}[\log\mathrm{P}_{\hat{\Sigma}}(\mathbf{X}^{k})\|\mathbf{X}^{k}_{o_{k}}]+\mathcal{H}_{k}[\Psi_{k}]$
	$\displaystyle=$	$\displaystyle\left(\mathcal{T}_{m_{k},o_{k}}\mathcal{T}_{o_{k},o_{k}}^{-1},\frac{1}{n}(\mathcal{T}_{m_{k},m_{k}}-\mathcal{T}_{m_{k},o_{k}}\mathcal{T}_{o_{k},o_{k}}^{-1}\mathcal{T}_{o_{k},m_{k}})\right)$

is equivalent to our Algorithm 1 with $\mathcal{T}^{-k}$ replaced by $\mathcal{T}$ (see M-Step2 in Section 3.2). Alternating maximization of (5.10) is a GAM procedure in the sense of Gunawardana and Byrne (2005). Within their framework convergence to a stationary point of the observed log-likelihood can be shown.

Unfortunately, the MissPA algorithm does not quite fit into the GAM formulation. As already mentioned MissPA extends the standard EM also in another way namely by using for each pattern a different complete data space (for each pattern $k$ only those samples are augmented which do not belong to pattern $k$ ). MissPA is related to the SAGE algorithm (Fessler and Hero, 1994) as follows: Consider the parameter of interest $\Sigma$ in the parameterization $\theta=\left(\Sigma_{o_{k}},B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}}\right)$ introduced in Section 2, equation (2.1). From

\mathrm{P}_{\theta}(\mathbf{X}_{\rm obs},\mathbf{X}^{-k})=\mathrm{P}_{\theta}(\mathbf{X}_{\rm obs}|\mathbf{X}^{-k})\mathrm{P}_{\theta}(\mathbf{X}^{-k})

and from observing that $\mathrm{P}_{\theta}(\mathbf{X}_{\rm obs}|\mathbf{X}^{-k})=\mathrm{P}_{\Sigma_{o_{k}}}(\mathbf{X}_{o_{k}})$ we conclude that $\mathbf{X}^{-k}$ is an admissible hidden-data space with respect to $(B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})$ in the sense of Fessler and Hero (1994). The M-Step of MissPA then maximizes a conditional expectation of the log-likelihood $\log\mathrm{P}_{\theta}(\mathbf{X}^{-k})$ with respect to $(B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})$ . Different from a SAGE algorithm is the conditional distribution involved in the expectation. Our algorithm updates after each M-Step only the conditional distribution for a single pattern. As a consequence, we do not need to compute estimates for $\Sigma_{o_{k}}$ .

In summary, the MissPA algorithm has similarities with a GAM and a SAGE procedure. However, neither the SAGE nor the GAM framework fit our proposed MissPA. In the next section we provide theory which justifies alternating between complete data spaces and incrementally performing the E-Step. In particular, we prove convergence to a stationary point of the observed log-likelihood.

5.1 Convergence Theory for the MissPA Algorithm

Pattern-Depending Lower Bounds

Denote the density of $\mathbf{X}^{k}$ , $k\in\{1,\ldots,s\}$ , by $\mathrm{P}_{\Sigma}(\mathbf{X}^{k})=\prod_{i\in\mathcal{I}_{k}}p(x_{i};\Sigma)$ and define for $k,l\in\{1,\ldots,s\}$

	$\displaystyle\mathrm{P}_{\Sigma}(\mathbf{X}^{l}_{o_{k}})$	$\displaystyle=$	$\displaystyle\prod_{i\in\mathcal{I}_{l}}p(x_{i,o_{k}};\Sigma_{o_{k}})\quad\textrm{and}$
	$\displaystyle\mathrm{P}_{\Sigma}(\mathbf{X}^{l}_{m_{k}}\|\mathbf{X}^{l}_{o_{k}})$	$\displaystyle=$	$\displaystyle\prod_{i\in\mathcal{I}_{l}}p(x_{i,m_{k}}\|x_{i,o_{k}};B_{m_{k}\|o_{k}},\Sigma_{m_{k}\|o_{k}}).$

Set $\{\Sigma_{l}\}_{l\neq k}=(\Sigma_{1},\ldots,\Sigma_{k-1},\Sigma_{k+1},\ldots,\Sigma_{s})$ and consider for $k=1,\ldots,s$

\displaystyle\mathcal{F}_{k}[\Sigma_{k}||\{\Sigma_{l}\}_{l\neq k}]

\displaystyle=

\displaystyle\log\mathrm{P}_{\Sigma_{k}}(\mathbf{X}^{k}_{o_{k}})+\sum_{l\neq k}\big{(}\mathbb{E}_{\Sigma_{l}}[\log\mathrm{P}_{\Sigma_{k}}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\Sigma_{l}]\big{)}.

Here $\mathcal{H}_{l}[\tilde{\Sigma}]=-\mathbb{E}_{\tilde{\Sigma}}[\log\mathrm{P}_{\tilde{\Sigma}}(\mathbf{X}_{m_{l}}^{l}|\mathbf{X}_{o_{l}}^{l})|\mathbf{X}^{l}_{o_{l}}]$ denotes the entropy. Note that $\mathcal{F}_{k}$ is defined for fixed observed data $\mathbf{X}_{\mathrm{obs}}$ . The subscript $k$ highlights the dependence on the pattern $k$ . Furthermore, for fixed $\mathbf{X}_{\mathrm{obs}}$ and fixed $k$ , $\mathcal{F}_{k}$ is a function in the parameters $(\Sigma_{1},\ldots,\Sigma_{s})$ . As a further tool we write the Kullback-Leibler divergence in the following form:

\displaystyle\mathcal{D}_{l}[\tilde{\Sigma}||\Sigma]=\mathbb{E}_{\tilde{\Sigma}}[-\log\big{(}\mathrm{P}_{\Sigma}(\mathbf{X}^{l}_{m_{l}}|\mathbf{X}^{l}_{o_{l}})/\mathrm{P}_{\tilde{\Sigma}}(\mathbf{X}^{l}_{m_{l}}|\mathbf{X}^{l}_{o_{l}})\big{)}|\mathbf{X}^{l}_{o_{l}}].

(5.11)

An important property of the Kullback-Leibler divergence is its non-negativity:

	$\displaystyle\mathcal{D}_{l}[\tilde{\Sigma}\|\|\Sigma]\geq 0,\quad\textrm{with equality if and only if}$
	$\displaystyle\mathrm{P}_{\tilde{\Sigma}}(\mathbf{X}^{l}_{m_{l}}\|\mathbf{X}^{l}_{o_{l}})=\mathrm{P}_{\Sigma}(\mathbf{X}^{l}_{m_{l}}\|\mathbf{X}^{l}_{o_{l}}).$

A simple calculation shows that

\displaystyle\mathbb{E}_{\tilde{\Sigma}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\tilde{\Sigma}]=-\mathcal{D}_{l}[\tilde{\Sigma}||\Sigma]+\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l}_{o_{l}})

(5.12)

and $\mathcal{F}_{k}[\Sigma_{k}||\{\Sigma_{l}\}_{l\neq k}]$ can be written as

\displaystyle\mathcal{F}_{k}[\Sigma_{k}||\{\Sigma_{l}\}_{l\neq k}]

\displaystyle=

\displaystyle\ell(\Sigma_{k};\mathbf{X}_{\mathrm{obs}})-\sum_{l\neq k}\mathcal{D}_{l}[\Sigma_{l}||\Sigma_{k}].

(5.13)

In particular, for fixed values of $\{\Sigma_{l}\}_{l\neq k}$ , $\mathcal{F}_{k}[\,\cdot\,||\{\Sigma_{l}\}_{l\neq k}]$ lower bounds the observed log-likelihood $\ell(\,\cdot\,;\mathbf{X}_{\mathrm{obs}})$ due to the non-negativity of the Kullback-Leibler divergence.

Optimization Transfer to Pattern-Depending Lower Bounds

We give now an alternative description of the MissPA algorithm. In cycle $r+1$ through all patterns, generate $(\Sigma_{1}^{r+1},\ldots,\Sigma_{s}^{r+1})$ given $(\Sigma_{1}^{r},\ldots,\Sigma_{s}^{r})$ according to

\displaystyle\Sigma_{k}^{r+1}=\mathop{\arg\max}\limits_{\Sigma}\mathcal{F}_{k}[\Sigma||\mathrm{Z}_{k}^{r+1}],\quad k=1,\ldots,s,

(5.14)

with $\mathrm{Z}_{k}^{r+1}=(\Sigma_{1}^{r+1},\ldots,\Sigma_{k-1}^{r+1},\Sigma_{k+1}^{r},\ldots,\Sigma_{s}^{r}).$

We have

	$\displaystyle\mathcal{F}_{k}[\Sigma\|\|\mathrm{Z}_{k}^{r+1}]$	$\displaystyle=$	$\displaystyle\log\mathrm{P}_{\Sigma}(\mathbf{X}^{k}_{o_{k}})+\sum_{l<k}\left(\mathbb{E}_{\Sigma_{l}^{r+1}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})\|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\Sigma_{l}^{r+1}]\right)$
			$\displaystyle+\sum_{l>k}\left(\mathbb{E}_{\Sigma_{l}^{r}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})\|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\Sigma_{l}^{r}]\right).$

The entropy terms do not depend on the optimization parameter $\Sigma$ , therefore,

\displaystyle\mathcal{F}_{k}[\Sigma||\mathrm{Z}_{k}^{r+1}]

\displaystyle=\textrm{const}+\log\mathrm{P}_{\Sigma}(\mathbf{X}^{k}_{o_{k}})+\sum_{l<k}\mathbb{E}_{\Sigma_{l}^{r+1}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}]+\sum_{l>k}\mathbb{E}_{\Sigma_{l}^{r}}[\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}].

Using the factorization $\log\mathrm{P}_{\Sigma}(\mathbf{X}^{l})=\log\mathrm{P}(\mathbf{X}_{o_{k}}^{l};\Sigma_{o_{k}})+\log\mathrm{P}(\mathbf{X}_{m_{k}}^{l}|\mathbf{X}_{o_{k}}^{l};B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})$ (for all $l\neq k$ ), and separate maximization with respect to $\Sigma_{o_{k}}$ and $(B_{m_{k}|o_{k}},\Sigma_{m_{k}|o_{k}})$ we end up with the expressions from the M-Step of MissPA. Summarizing the above, we have recovered the M-Step as a maximization of $\mathcal{F}_{k}[\Sigma||\mathrm{Z}_{k}^{r+1}]$ which is a lower bound of the observed log-likelihood. Or in the language of Lange et al. (2000), optimization of $\ell(\,\cdot\,;\mathbf{X}_{\mathrm{obs}})$ is transferred to the surrogate objective $\mathcal{F}_{k}[\,\cdot\,||\mathrm{Z}_{k}^{r+1}]$ .

There is still an important piece missing: In M-Step $k$ of cycle $r+1$ we are maximizing $\mathcal{F}_{k}[\;\cdot\;||\mathrm{Z}_{k}^{r+1}]$ whereas in the following M-Step ( $k+1$ ) we optimize $\mathcal{F}_{k+1}[\;\cdot\;||\mathrm{Z}_{k+1}^{r+1}]$ . In order for the algorithm to make progress, it is essential that $\mathcal{F}_{k+1}[\;\cdot\;||\mathrm{Z}_{k+1}^{r+1}]$ attains higher values than its predecessor $\mathcal{F}_{k}[\;\cdot\;||\mathrm{Z}_{k}^{r+1}]$ . In this sense the following proposition is crucial.

Proposition 5.1.

For $r=0,1,2,\ldots$ we have that

	$\displaystyle\mathcal{F}_{s}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{s}^{r}]\leq\mathcal{F}_{1}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{1}^{r+1}],\quad\textrm{and}$
	$\displaystyle\mathcal{F}_{k}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k}^{r+1}]\leq\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]\quad\textrm{for $k=1,\ldots,s-1$}.$

Proof. We have,

\mathcal{F}_{k}[\Sigma_{k}^{r+1}||\mathrm{Z}_{k}^{r+1}]=\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{k}_{o_{k}})+\mathbb{E}_{\Sigma_{k+1}^{r}}[\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{k+1})|\mathbf{X}_{o_{k+1}}^{k+1}]+\mathcal{H}_{k+1}[\Sigma_{k+1}^{r}]+\textrm{rest}

and

\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}||\mathrm{Z}_{k+1}^{r+1}]=\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{k+1}_{o_{k+1}})+\mathbb{E}_{\Sigma_{k}^{r+1}}[\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{k})|\mathbf{X}_{o_{k}}^{k}]+\mathcal{H}_{k}[\Sigma_{k}^{r+1}]+\textrm{rest}

where

\textrm{rest}=\sum_{l<k}\big{(}\mathbb{E}_{\Sigma_{l}^{r+1}}[\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\Sigma_{l}^{r+1}]\big{)}+\sum_{l>k+1}\big{(}\mathbb{E}_{\Sigma_{l}^{r}}[\log\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{l})|\mathbf{X}^{l}_{o_{l}}]+\mathcal{H}_{l}[\Sigma_{l}^{r}]\big{)}.

Furthermore, using (5.12) and noting that $\mathcal{D}_{k}[\Sigma_{k}^{r+1}||\Sigma_{k}^{r+1}]=0$ , we obtain

	$\displaystyle\mathcal{F}_{k}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k}^{r+1}]-\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]$	$\displaystyle=\mathcal{D}_{k}[\Sigma_{k}^{r+1}\|\|\Sigma_{k}^{r+1}]-\mathcal{D}_{k+1}[\Sigma_{k+1}^{r}\|\|\Sigma_{k}^{r+1}]$
		$\displaystyle=-\mathcal{D}_{k+1}[\Sigma_{k+1}^{r}\|\|\Sigma_{k}^{r+1}]\leq 0.$

Note that equality holds if and only if $\mathrm{P}_{\Sigma_{k}^{r+1}}(\mathbf{X}^{k+1}_{m_{k+1}}|\mathbf{X}^{k+1}_{o_{k+1}})=\mathrm{P}_{\Sigma_{k+1}^{r}}(\mathbf{X}^{k+1}_{m_{k+1}}|\mathbf{X}^{k+1}_{o_{k+1}})$ . $\Box$

In light of Proposition 5.1 it is clear that (5.14) generates a monotonely increasing sequence of the form:

	$\displaystyle\mathcal{F}_{s}[\Sigma_{s}^{0}\|\|\mathrm{Z}_{s}^{0}]\leq\mathcal{F}_{1}[\Sigma_{s}^{0}\|\|\mathrm{Z}_{1}^{1}]\leq\mathcal{F}_{1}[\Sigma_{1}^{1}\|\|\mathrm{Z}_{1}^{1}]\leq\mathcal{F}_{2}[\Sigma_{1}^{1}\|\|\mathrm{Z}_{2}^{1}]\leq\mathcal{F}_{2}[\Sigma_{2}^{1}\|\|\mathrm{Z}_{2}^{1}]\leq\cdots$
	$\displaystyle\cdots\leq\mathcal{F}_{k}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k}^{r+1}]\leq\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]\leq\mathcal{F}_{k+1}[\Sigma_{k+1}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]\leq\cdots$

For example, we can deduce that $\{\mathcal{F}_{s}[\Sigma_{s}^{r}||\mathrm{Z}_{s}^{r}]\}_{r=0,1,2,\ldots}$ is a monotone increasing sequence in $r$ .

Convergence to Stationary Points

Ideally we would like to show that a limit point of the sequence generated by the MissPA algorithm is a global maximum of $\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})$ . Unfortunately, this is too ambitious because for general missing data patterns the observed log-likelihood is a non-concave function with several local maxima. Thus, the most we can expect is that our algorithm converges to a stationary point. This is ensured by the following theorem which is proved in the Appendix.

Theorem 5.1.

Assume that $\mathcal{K}=\{(\Sigma_{1},\ldots,\Sigma_{s}):\mathcal{F}_{s}[\Sigma_{s}||\Sigma_{1},\ldots,\Sigma_{s-1}]\geq\mathcal{F}_{s}[\Sigma_{s}^{0}||\mathrm{Z}_{s}^{0}]\}$ is compact. Then every limit point $\bar{\Sigma}_{s}$ of $\{\Sigma_{s}^{r}\}_{r=0,1,2,\ldots}$ is a stationary point of $\ell(\;\cdot\;;\mathbf{X}_{\mathrm{obs}})$ .

6 Discussion and Extensions

We have presented the novel Missingness Pattern Alternating maximization algorithm (MissPA) for maximizing the observed log-likelihood for a multivariate normal data matrix with missing values. Simplified, our algorithm iteratively cycles through the different missingness patterns, performs multivariate regressions of the missing on the observed variables and uses these regression coefficients for partial imputation of the missing values. We argued theoretically and gave numerical examples showing that our procedure is computationally more efficient than the standard EM algorithm. Furthermore, we analyze the numerical properties using non-standard arguments and prove that solutions of our algorithm converge to stationary points of the observed log-likelihood.

In a high-dimensional setup with $p\gg n$ the regression interpretation opens up the door to do regularization by replacing least squares regressions with Lasso analogues. Our proposed algorithm, the MissPALasso, performs a coordinate descent approximation of the corresponding Lasso problem in order to gain speed. On simulated and four real datasets (all from genomics) we demonstrate that MissPALasso outperforms other imputation techniques such as k-nearest neighbors imputation, nuclear norm minimization or a penalized likelihood approach with an $\ell_{1}$ -penalty on the inverse covariance matrix.

Even though MissPALasso performs well on simulated and real data it is a “heuristic” motivated by the previously developed MissPA and by the wish to have sparse regression coefficients for imputation. It is unclear which objective function is optimized by MissPALasso. The comments of two referees on this point made us thinking of another way of imposing sparsity in the regression coefficients: Consider a penalized variational free energy

\displaystyle-\mathcal{F}[\Sigma\|\Psi_{1},\ldots,\Psi_{s}]+\sum_{k=1}^{s}\mathrm{Pen}_{\lambda}(\Psi_{k}),

(6.15)

with $\mathcal{F}[\Sigma\|\Psi_{1},\ldots,\Psi_{s}]$ defined in equation (5.10) and $\mathrm{Pen}_{\lambda}(\Psi_{k})=\lambda\|B_{k,m_{k}|o_{k}}\|_{1}$ . A small calculation shows that alternating minimization of (6.15) with respect to $\Sigma$ and $\Psi_{k}$ leads to an algorithm which is similar but different from MissPALasso. In fact, minimizing (6.15) with respect to $\Sigma_{k,m_{k}|o_{k}}$ and $B_{k,m_{k}|o_{k}}$ gives $\hat{\Sigma}_{k,m_{k}|o_{k}}=\Sigma_{m_{k}|o_{k}}$ and $\hat{B}_{k,m_{k}|o_{k}}$ satisfies the subgradient equation

0=\left(\Omega_{m_{k},m_{k}}\hat{B}_{k,m_{k}|o_{k}}-\Omega_{m_{k},o_{k}}\right)^{t}\!\mathbf{X}_{o_{k}}^{k}\mathbf{X}_{o_{k}}^{k}+\lambda\Gamma(\hat{B}_{k,m_{k}|o_{k}}),

where $\Gamma(x)$ is the subgradient of $|x|$ , applied componentwise to the elements of a matrix and $\Omega=\Sigma^{-1}$ . The formulation (6.15) looks very compelling and can motivate new algorithms for missing data imputation. For example in the context of the Netflix problem where the fraction of the missing values and the number of customers is huge one might impose constraints on the parameters $\Sigma_{k,m_{k}|o_{k}}$ and employ a stochastic gradient descent optimization strategy to solve (6.15).

Appendix A Proof of Theorem 5.1

Proof. First, note that the sequence $\{(\Sigma_{1}^{r},\ldots,\Sigma_{s}^{r})\}_{r=0,1,2,\ldots}$ lies in the compact set $\mathcal{K}$ . Now, let $\Sigma_{s}^{r_{j}}$ be a subsequence converging to $\bar{\Sigma}_{s}$ as $j\rightarrow\infty$ . By invoking compactness, we can assume w.l.o.g (by restricting to a subsequence) that $(\Sigma_{1}^{r_{j}},\ldots,\Sigma_{s}^{r_{j}})\rightarrow(\bar{\Sigma}_{1},\ldots,\bar{\Sigma}_{s})$ .

As a direct consequence of the monotonicity of the sequence $\{\mathcal{F}_{s}[\Sigma_{s}^{r}||\mathrm{Z}_{s}^{r}]\}_{r=0,1,2,\ldots}$ we obtain

\lim_{r}\mathcal{F}_{s}[\Sigma_{s}^{r}||\mathrm{Z}_{s}^{r}]=\mathcal{F}_{s}[\bar{\Sigma}_{s}||\bar{\Sigma}_{1},\ldots,\bar{\Sigma}_{s-1}]\equiv\bar{\mathcal{F}}.

From (5.14) and Proposition 5.1, for $k=1,\ldots,s-1$ and $r=0,1,2,\ldots,$ the following “sandwich”-formulae hold:

	$\displaystyle\mathcal{F}_{s}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{s}^{r}]\leq\mathcal{F}_{1}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{1}^{r+1}]\leq\mathcal{F}_{1}[\Sigma_{1}^{r+1}\|\|\mathrm{Z}_{1}^{r+1}]\leq\mathcal{F}_{s}[\Sigma_{s}^{r+1}\|\|\mathrm{Z}_{s}^{r+1}],$
	$\displaystyle\mathcal{F}_{s}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{s}^{r}]\leq\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]\leq\mathcal{F}_{k+1}[\Sigma_{k+1}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]\leq\mathcal{F}_{s}[\Sigma_{s}^{r+1}\|\|\mathrm{Z}_{s}^{r+1}].$

As a consequence we have for $k=1,\ldots,s-1$

	$\displaystyle\lim_{r}\mathcal{F}_{1}[\Sigma_{s}^{r}\|\|\mathrm{Z}_{1}^{r+1}]=\lim_{r}\mathcal{F}_{1}[\Sigma_{1}^{r+1}\|\|\mathrm{Z}_{1}^{r+1}]=\bar{\mathcal{F}}\quad\textrm{and}$		(A.16)
	$\displaystyle\lim_{r}\mathcal{F}_{k+1}[\Sigma_{k}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]=\lim_{r}\mathcal{F}_{k+1}[\Sigma_{k+1}^{r+1}\|\|\mathrm{Z}_{k+1}^{r+1}]=\bar{\mathcal{F}}.$		(A.17)

Now consider the sequence $(\Sigma_{1}^{r_{j}+1},\ldots,\Sigma_{s}^{r_{j}+1})$ . By compactness of $\mathcal{K}$ this sequence converges w.l.o.g to some $(\Sigma^{*}_{1},\ldots,\Sigma^{*}_{s})$ . We now show by induction that

\bar{\Sigma}_{s}=\Sigma^{*}_{1}=\ldots=\Sigma^{*}_{s}.

From the $1$ st M-Step of cycle $r_{j}+1$ we have

\mathcal{F}_{1}[\Sigma_{1}^{r_{j}+1}||\mathrm{Z}_{1}^{r_{j}+1}]\geq\mathcal{F}_{1}[\Sigma||\mathrm{Z}_{1}^{r_{j}+1}]\quad\textrm{for all}\quad\Sigma.

Taking the limit $j\rightarrow\infty$ we get:

\mathcal{F}_{1}[\Sigma^{*}_{1}||\{\bar{\Sigma}_{l}\}_{l>1}]\geq\mathcal{F}_{1}[\Sigma|\{\bar{\Sigma}_{l}\}_{l>1}]\quad\textrm{for all}\quad\Sigma.

In particular, $\Sigma^{*}_{1}$ is the (unique) maximizer of $\mathcal{F}_{1}[\,\cdot\,||\{\bar{\Sigma}_{l}\}_{l>1}]$ . Assuming $\Sigma^{*}_{1}\neq\bar{\Sigma}_{s}$ would imply

\mathcal{F}_{1}[\Sigma^{*}_{1}||\{\bar{\Sigma}_{l}\}_{l>1}]>\mathcal{F}_{1}[\bar{\Sigma}_{s}||\{\bar{\Sigma}_{l}\}_{l>1}].

But this contradicts $\mathcal{F}_{1}[\Sigma^{*}_{1}||\{\bar{\Sigma}_{l}\}_{l>1}]=\mathcal{F}_{1}[\bar{\Sigma}_{s}||\{\bar{\Sigma}_{l}\}_{l>1}]=\bar{\mathcal{F}}$ , which holds by (A.16). Therefore we obtain $\Sigma_{1}^{*}=\bar{\Sigma}_{s}$ .

Assume that we have proven $\Sigma^{*}_{1}=\ldots=\Sigma^{*}_{k}=\bar{\Sigma}_{s}$ . We will show that $\Sigma_{k+1}^{*}=\bar{\Sigma}_{s}$ . From the k+1st M-Step in cycle $r_{j}+1$ :

\mathcal{F}_{k+1}[\Sigma_{k+1}^{r_{j}+1}||\mathrm{Z}_{k+1}^{r_{j}+1}]\geq\mathcal{F}_{k+1}[\Sigma||\mathrm{Z}_{k+1}^{r_{j}+1}]\quad\textrm{for all}\quad\Sigma.

Taking the limit for $j\rightarrow\infty$ , we conclude that $\Sigma^{*}_{k+1}$ is the (unique) maximizer of

\mathcal{F}_{k+1}[\,\cdot\,||\{\Sigma^{*}_{l}\}_{l<k+1},\{\bar{\Sigma}_{l}\}_{l>k+1}].

From (A.17),

\mathcal{F}_{k+1}[\Sigma^{*}_{k+1}||\{\Sigma^{*}_{l}\}_{l<k+1},\{\bar{\Sigma}_{l}\}_{l>k+1}]=\mathcal{F}_{k+1}[\Sigma^{*}_{k}||\{\Sigma^{*}_{l}\}_{l<k+1},\{\bar{\Sigma}_{l}\}_{l>k+1}]=\bar{\mathcal{F}},

and therefore $\Sigma^{*}_{k+1}$ must be equal to $\Sigma^{*}_{k}$ . By induction we have $\Sigma^{*}_{k}=\bar{\Sigma}_{s}$ and so we proved that $\Sigma^{*}_{k+1}=\bar{\Sigma}_{s}$ holds.

Finally, we show stationarity of $\bar{\Sigma}_{s}$ . Invoking (5.13) we can write

\mathcal{F}_{s}[\Sigma||\bar{\Sigma}_{s},\ldots,\bar{\Sigma}_{s}]=\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})-\sum_{l=1}^{s-1}\mathcal{D}_{l}[\bar{\Sigma}_{s}||\Sigma].

Note that

\frac{\partial}{\partial\Sigma}\mathcal{D}_{l}[\bar{\Sigma}_{s}||\Sigma]\bigg{|}_{\bar{\Sigma}_{s}}=0.

Furthermore, as $\Sigma_{s}^{r_{j}+1}$ maximizes $\mathcal{F}_{s}[\Sigma||\Sigma_{1}^{r_{j}+1},\ldots,\Sigma_{s-1}^{r_{j}+1}]$ , we get in the limit as $j\rightarrow\infty$

\frac{\partial}{\partial\Sigma}\mathcal{F}_{s}[\Sigma|\bar{\Sigma}_{s},\ldots,\bar{\Sigma}_{s}]\bigg{|}_{\bar{\Sigma}_{s}}=\frac{\partial}{\partial\Sigma}\mathcal{F}_{s}[\Sigma||\Sigma^{*}_{1},\ldots,\Sigma^{*}_{s-1}]\bigg{|}_{\Sigma^{*}_{s}}=0.

Therefore, we conclude that $\frac{\partial}{\partial\Sigma}\ell(\Sigma;\mathbf{X}_{\mathrm{obs}})\Big{|}_{\bar{\Sigma}_{s}}=0$ . $\Box$

References

Aittokallio (2010) Aittokallio, T. (2010) Dealing with missing values in large-scale studies: microarray data imputation and beyond. Briefings in Bioinformatics, 11, 253–264.
Alizadeh et al. (2000) Alizadeh, A., Eisen, M., Davis, R., Ma, C., Lossos, I., Rosenwald, A., Boldrick, J., Sabet, H., Tran, T., Yu, X., Powell, J., Yang, L., Marti, G., Moore, T., Hudson, J., Lu, L., Lewis, D., Tibshirani, R., Sherlock, G., Chan, W., Greiner, T., Weisenburger, D., Armitage, J., Warnke, R., Levy, R., Wilson, W., Grever, M. R., Byrd, J., Botstein, D., Brown, P. and Staudt, L. (2000) Distinct types of diffuse large b-cell lymphoma identified by gene expression profiling. Nature, 403, 503–511.
Allen and Tibshirani (2010) Allen, G. and Tibshirani, R. (2010) Transposable regularized covariance models with an application to missing data imputation. Annals of Applied Statistics, 4, 764–790.
Alon et al. (1999) Alon, U., Barkai, N., Notterman, D., Gishdagger, K., Ybarradagger, S., Mackdagger, D. and Levine, A. (1999) Broad patterns of gene expression revealed by clustering analysis of tumor and normal colon tissues probed by oligonucleotide arrays. Proceedings of the National Academy of Sciences of the United States of America, 96, 6745–6750.
Cai et al. (2010) Cai, J.-F., Candès, E. and Shen, Z. (2010) A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 20, 1956–1982.
Candès and Recht (2009) Candès, E. and Recht, B. (2009) Exact matrix completion via convex optimization. Foundations of Computational Mathematics, 9, 717–772.
Candès and Tao (2010) Candès, E. and Tao, T. (2010) The power of convex relaxation: Near-optimal matrix completion. IEEE Transactions on Information Theory, 56.
Dempster et al. (1977) Dempster, A., Laird, N. and Rubin, D. (1977) Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B, 39, 1–38.
Fessler and Hero (1994) Fessler, J. and Hero, A. (1994) Space-alternating generalized Expectation-Maximization algorithm. IEEE Transactions on Signal Processing, 42, 2664–2677.
Friedman et al. (2008) Friedman, J., Hastie, T. and Tibshirani, R. (2008) Sparse inverse covariance estimation with the graphical Lasso. Biostatistics, 9, 432–441.
Friedman et al. (2010) Friedman, J., Hastie, T. and Tibshirani, R. (2010) Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33, 1–22.
Gunawardana and Byrne (2005) Gunawardana, A. and Byrne, W. (2005) Convergence theorems for generalized alternating minimization procedures. Journal of Machine Learning Research, 6, 2049–2073.
Jordan et al. (1999) Jordan, M., Ghahramani, Z., Jaakkola, T. and Saul, L. (1999) An introduction to variational methods for graphical models. Machine Learning, 37, 183–233.
Keshavan et al. (2010) Keshavan, R., Oh, S. and Montanari, A. (2010) Matrix completion from a few entries. IEEE Transactions on Information Theory, 56.
Kim et al. (2006) Kim, H., Golub, G. and Park, H. (2006) Missing value estimation for DNA microarray gene expression data: local least squares imputation. Bioinformatics, 22, 1410–1411.
Lange et al. (2000) Lange, K., Hunter, D. and Yang, I. (2000) Optimization transfer using surrogate objective functions. Journal of Computational and Graphical Statistics, 9, 1–20.
Little and Rubin (1987) Little, R. and Rubin, D. (1987) Statistical Analysis with Missing Data. Series in Probability and Mathematical Statistics, Wiley.
Mazumder et al. (2010) Mazumder, R., Hastie, T. and Tibshirani, R. (2010) Spectral regularization algorithms for learning large incomplete matrices. Journal of Machine Learning Research, 99, 2287–2322.
Neal and Hinton (1998) Neal, R. and Hinton, G. (1998) A view of the EM algorithm that justifies incremental, sparse, and other variants. In Learning in Graphical Models, 355–368. Kluwer Academic Publishers.
Ng and McLachlan (2003) Ng, S. and McLachlan, G. (2003) On the choice of the number of blocks with the incremental EM algorithm for the fitting of normal mixtures. Statistics and Computing, 13, 45–55.
Nowlan (1991) Nowlan, S. (1991) Soft Competitive Adaptation: Neural Network Learning Algorithms based on Fitting Statistical Mixtures. Ph.D. thesis, School of Computer Science, Carnegie Mellon University, Pittsburgh.
Oba et al. (2003) Oba, S., Sato, M.-A., Takemasa, I., Monden, M., Matsubara, K.-I. and Ishii, S. (2003) A Bayesian missing value estimation method for gene expression profile data. Bioinformatics, 19, 2088–2096.
Schafer (1997) Schafer, J. (1997) Analysis of Incomplete Multivariate Data. Monographs on Statistics and Applied Probability 72, Chapman and Hall.
Spellman et al. (1998) Spellman, P., Sherlock, G., Zhang, M., Iyer, V., Anders, K., Eisen, M., Brown, P., Botstein, D. and Futcher, B. (1998) Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Molecular Biology of the Cell, 9, 3273–97.
Spirtes et al. (2000) Spirtes, P., Glymour, C. and Scheines, R. (2000) Causation, Prediction, and Search. The MIT Press, 2nd edition.
Städler and Bühlmann (2012) Städler, N. and Bühlmann, P. (2012) Missing values: sparse inverse covariance estimation and an extension to sparse regression. Statistics and Computing, 22, 219–235.
Thiesson et al. (2001) Thiesson, B., Meek, C. and Heckerman, D. (2001) Accelerating EM for large databases. Machine Learning, 45, 279–299.
Tibshirani (1996) Tibshirani, R. (1996) Regression shrinkage and selection via the Lasso. Journal of the Royal Statistical Society, Series B, 58, 267–288.
Troyanskaya et al. (2001) Troyanskaya, O., Cantor, M., Sherlock, G., Brown, P., Hastie, T., Tibshirani, R., Botstein, D. and Altman, R. (2001) Missing value estimation methods for DNA microarrays. Bioinformatics, 17, 520–525.
Wille et al. (2004) Wille, A., Zimmermann, P., Vranova, E., Fürholz, A., Laule, O., Bleuler, S., Hennig, L., Prelic, A., von Rohr, P., Thiele, L., Zitzler, E., Gruissem, W. and Bühlmann, P. (2004) Sparse graphical Gaussian modeling of the isoprenoid gene network in arabidopsis thaliana. Genome Biology, 5.