PAUSE: Low-Latency and Privacy-Aware Active User Selection for Federated Learning
Abstract
\Acfl enables multiple edge devices to collaboratively train a machine learning model without the need to share potentially private data. Federated learning proceeds through iterative exchanges of model updates, which pose two key challenges: (i) the accumulation of privacy leakage over time and (ii) communication latency. These two limitations are typically addressed separately—(i) via perturbed updates to enhance privacy and (ii) user selection to mitigate latency—both at the expense of accuracy. In this work, we propose a method that jointly addresses the accumulation of privacy leakage and communication latency via active user selection, aiming to improve the trade-off among privacy, latency, and model performance. To achieve this, we construct a reward function that accounts for these three objectives. Building on this reward, we propose a MAB-based algorithm, termed Privacy-aware Active User SElection (PAUSE) – which dynamically selects a subset of users each round while ensuring bounded overall privacy leakage. We establish a theoretical analysis, systematically showing that the reward growth rate of PAUSE follows that of the best-known rate in MAB literature. To address the complexity overhead of active user selection, we propose a simulated annealing-based relaxation of PAUSE and analyze its ability to approximate the reward-maximizing policy under reduced complexity. We numerically validate the privacy leakage, associated improved latency, and accuracy gains of our methods for the federated training in various scenarios.
Index Terms:
Federated Learning; Communication latency; Privacy; Multi-Armed Bandit; Simulated Annealing.I Introduction
The effectiveness of deep learning models heavily depends on the availability of large amounts of data. In real-world scenarios, data is often gathered by edge devices such as mobile phones, medical devices, sensors, and vehicles. Because these data often contain sensitive information, there is a pressing need to utilize them for training deep neural networks without compromising user privacy. A popular framework to enable training DNNs without requiring data centralization is that of federated learning (FL) [2]. In FL, each participating device locally trains its model in parallel, and a central server periodically aggregates these local models into a global one [3].
The distributed operation of FL, and particularly the fact that learning is carried out using multiple remote users in parallel, induces several challenges that are not present in traditional centralized learning [4, 5]. A key challenge stems from the fact that FL involves repeated exchanges of highly-parameterized models between the orchestrating server and numerous users. This often entails significant communication latency which– in turn– impacts convergence, complexity, and scalability [6]. Communication latency can be tackled by model compression [7, 8, 9, 10], and via over-the-air aggregation in settings where the users share a common wireless channel [11, 12, 13]. A complementary approach for balancing communication latency, which is key for scaling FL over massive networks, is user selection [14, 15, 16]. User selection limits the number of users participating in each round, traditionally employing pre-defined policies [17, 18, 19, 20], with more recent schemes exploring active user selection based on MAB framework [21, 22, 23, 24]. The latter adapts the policy based on, e.g., learning progress and communication delay.
Another prominent challenge of FL is associated with one of its core motivators–privacy preservation. While FL does not involve data sharing, it does not necessarily preserve data privacy, as model inversion attacks were shown to unveil private information and even reconstruct the data from model updates [25, 26, 27, 28]. The common framework for analyzing privacy leakage in FL is based on local differential privacy (LDP) [29]. LDP mechanisms limit privacy leakage in a given FL round, typically by employing privacy preserving noise (PPN) [30, 31, 32], that can also be unified with model compression [33, 34]. However, this results in having the amount of leaked privacy grow with the number of learning rounds [35], degrading performance by restricting the number of learning rounds and necessitating dominant PPN. Existing approaches to avoid accumulation of privacy leakage consider it as a separate task to tackling latency and scalability, often by focusing on a fixed pre-defined number of rounds [36], or by relying on an additional trusted coordinator unit [37, 38, 39], thus deviating from how FL typically operates. This motivates unifying privacy enhancement and user selection, as means to jointly tackle privacy accumulation and latency in FL.
In this work we propose a novel framework for private and scalable multi-round FL with low latency via active user selection. Our proposed method, coined PAUSE, is based on a generic per-round privacy budget, designed to avoid leakage surpassing a pre-defined limit for any number of FL rounds. This operation results in users inducing more PPN each time they participate. The budget is accounted for in formulating a dedicated reward function for active user selection that balances privacy, communication, and generalization. Based on the reward, we propose a MAB-based policy that prioritizes users with lesser PPN, balanced with grouping users of similar expected communication latency and exploring new users for enhancing generalization. We provide an analysis of PAUSE, rigorously proving that its regret growth rate obeys the desirable growth in MAB theory [40, 41, 42].
The direct application of PAUSE involves a brute search of a combinatorial nature, whose complexity grows dramatically with the number of users. To circumvent this excessive complexity and enhance scalability, we propose a reduced complexity implementation of PAUSE based on simulated annealing (SA) [43], coined SA-PAUSE. We analyze the computational complexity of SA-PAUSE, quantifying its reduction compared to direct PAUSE, and rigorously characterize conditions for it to achieve the same performance as costly brute search. We evaluate PAUSE in learning of different scenarios with varying DNNs, datasets, privacy budgets, and data distributions. Our experimental studies systematically show that by fusing privacy enhancement and user selection, PAUSE enables accurate and rapid learning, approaching the performance of FL without such constraints and notably outperforming alternative approaches that do not account for leakage accumulation. We also show that SA-PAUSE approaches the performance of direct PAUSE in both privacy leakage, model accuracy, and latency, while supporting scalable implementations on large FL networks.
The rest of this paper is organized as follows. We review some necessary preliminaries and formulate the problem in Section II. PAUSE is introduced and analyzed in Section III, while its reduced complexity, SA-PAUSE, is detailed in Section IV. Numerical simulations are reported in Section V, and Section VI provides concluding remarks.
Notation: Throughout this paper, we use boldface lower-case letters for vectors, e.g., . The stochastic expectation, probability operator, indicator function, and norm are denoted by , , , and , respectively. For a set , we write as its cardinality.
II System Model and Preliminaries
This section reviews the necessary background for deriving PAUSE. We start by recalling the FL setup and basics in LDP in Subsections II-A-II-B, respectively. Then, we formulate the active user selection problem in Subsection II-C.
II-A Preliminaries: Federated Learning
II-A1 Objective
The FL setup involves the collaborative training of a machine learning model , carried out by remote users and orchestrated by a server. Let the set of users be indexed by , and let denote the private dataset of user , which cannot be shared with the server. Define as the empirical risk of a model evaluated on . The goal is to determine the optimal parameter vector that minimizes the overall loss across all users, that is
| (1) |
II-A2 Learning Procedure
FL operates over multiple iterations divided into rounds [4]. At FL round , the server selects a set of participating users , and sends the current model to them. Each participating user of index then trains using its local data using, e.g., multiple iterations of mini-batch stochastic gradient descent (SGD) [44], into the updated .
The model update obtained by the th user, denoted , is shared with the server, which aggregates the local updates into a global model update. The aggregation rule commonly employed by the central server in FL is that of federated averaging (FedAvg) [2], in which the global model is obtained as
| (2) |
where . The updated global model is again distributed to the users and the learning procedure continues.
II-A3 Communication Model
Communication between the users and the server is associated with some varying latency [4]. We model this delay via the random variable , representing the total latency in the th round between the server and the th user. Accordingly, the communication latency of the whole round, denoted as , is determined by the user with the highest latency
| (3) |
The communication latency varies over time (due to fading [6]) and between users (due to system heterogeneity [45]). As the latter is device specific, we model as being drawn in an i.i.d. manner from a device specific distribution [21], denoted . We further assume the users differ in their expected latencies, . We denote the minimal difference between these terms as , and assume that there is a minimal latency corresponding to, e.g., the minimal delay. Mathematically, this implies that there exists some such that with probability one.
II-B Preliminaries: Local Differential Privacy
One of the main motivations for FL is the need to preserve the privacy of the users’ data. Nonetheless, the concealment of the dataset of the th user, , in favor of sharing the model updates trained using , was shown to be potentially leaky [25, 26, 27, 28]. Therefore, to satisfy the privacy requirements of FL, initiated privacy mechanisms are necessary.
In FL, privacy is commonly quantified in terms of LDP [46, 47], as this metric assumes an untrusted server by the users.
Definition 1 (-LDP [48]).
A randomized mechanism satisfies -LDP if for any pairs of input values in the domain of and for any possible output in it, it holds that
| (4) |
In Definition 1, a smaller means stronger privacy protection. A common mechanism to achieve -LDP is the Laplace mechanism (LM). Let be the Laplace distribution with location and scale . The LM is defined as:
Theorem 1 (LM [49]).
Given any function where is a domain of datasets, the LM defined as :
| (5) |
is -LDP. In (5), , i.e., they obey an i.i.d. zero-mean Laplace distribution with scale , where .
LDP mechanisms, such as LM, guarantee -LDP for a given query of in (4). In FL, this amounts for a single model update. As FL involves multiple rounds, one has to account for the accumulated leakage, given by the composition theorem:
Theorem 2 (Composition [48]).
Let be an -LDP mechanism on input , and is the sequential composition of , then satisfies -LDP.
Theorem 2 indicates that the privacy leakage of each user in FL is accumulated as the training proceeds.
II-C Problem Formulation
Our goal is to design a privacy leakage policy alongside privacy-aware user selection. Formally, we aim to set for every round an algorithm that selects users, while setting the privacy leakage budget . These policies should account for the following considerations:
III Privacy-Aware Active User Selection
This section introduces PAUSE. We first formulate its time-varying privacy budget policy and associated reward in Subsection III-A. The resulting user selection algorithm is detailed in Subsection III-B, with its regret growth analyzed in Subsection III-C. We conclude with a discussion in Subsection III-D.
III-A Reward and Privacy Policy
The formulation of PAUSE relies on two main components: a prefixed round-varying privacy budget; and a reward holistically accounting for privacy, latency, and generalization. The privacy policy is designed to ensure that C3 is preserved regardless of the number of iterations each user participated in. Accordingly, we define a sequence with , satisfying:
| (6) |
for finite. Using the sequence , the privacy budget of any user at the th time it participates in training the model is set to , and achieved using, e.g., LM. This guarantees that C3 holds. One candidate setting, which is also used in our experiments, sets . This guarantees achieving asymptotic leakage of by the limit of a geometric column. for which (6) holds when .
The reward guides the active user selection procedure and utilizes two terms. The first is the privacy reward, which accounts for the fact that our privacy policy has users introduce more dominant PPN each time they participate. The privacy reward assigned to the th user at round is
| (7) |
where is the number of rounds the th user has been selected up to and including the th round, i.e., . The privacy reward (7) yields higher values to users who have participated in fewer rounds.
The second term is the generalization reward, designed to meet C1. It assigns higher values for users whose data have been underutilized compared to the relative size of their data from the whole available data, . We adopt the generalization reward proposed in [23], which was shown to account for both i.i.d. balanced data and non-i.i.d. imbalanced data cases, and rewards the th user in an -sized group at round via the function
| (8) |
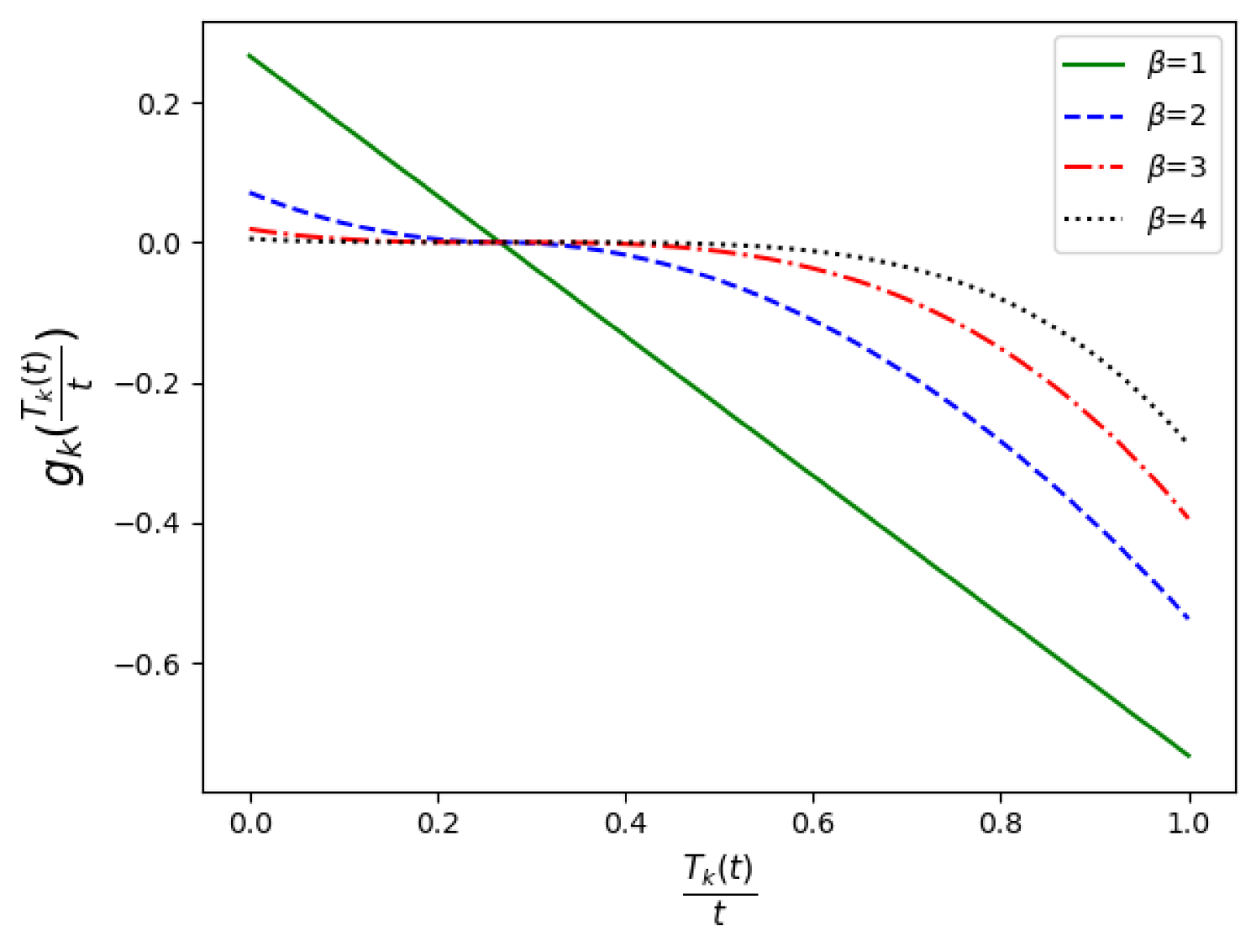
In (8), is a hyper-parameter that adjusts the fuzziness of the function, i.e., higher yields lower absolute value where the other parameters are fixed. Fig. 1 describes as a function of , and illustrates the effect of different values as means of balancing the reward assigned to users that participated much (high ).
Our proposed reward encompasses the above terms, grading the selection of a group of users of size at round as
| (9) |
The reward in (9) is composed of three additive terms which correspond to C2, C1 and C3, respectively, with and being hyper-parameters balancing these considerations. At this point we can make two remarks regarding the reward (9):
-
1.
Both and penalize repeated selection of the same users. However, each rewards differently, based on generalization and privacy considerations. The former accounts for the relative dataset sizes of the users, while the latter doesn’t. In the case of homogeneous data, where for all , , both and play a similar role. However, they differ significantly in the non-i.i.d case.
-
2.
The value of the first term is determined solely by the slowest user. This non-linearity, combined with the two other terms, directs the algorithm we derive from this reward to select a group of users with similar latency in a given round.
III-B PAUSE Algorithm
Here, we present PAUSE, which is a combinatorical -based [42] algorithm based on the reward (9). To derive PAUSE, we seek a policy such that is maximized over . To maximize the given term, as is customary in MAB settings, we aim to minimize the regret, defined as the loss of the algorithm compared to an algorithm composed by a Genie that has prior knowledge of the expectations of the random variables, i.e., of .
We define the Genie’s algorithm as selecting
| (10) |
where
The Genie policy (10) attempts to maximize the expectation of the reward (9) in each round, by replacing the order of the expectation and the operator. As the reward is history-dependent, the Genie’s policy is history-dependent as well.
We use the Genie policy to derive PAUSE, denoted , as an upper confidence bound (ucb)-type algorithm [41]. Accordingly, PAUSE estimates the unknown expectations with their empirical means, computed using the latency measured in previous rounds via
| (11) |
Note that (11) can be efficiently updated in a recursive manner, as
| (12) |
PAUSE uses (11) to compute the ucb terms for each user at the end of the th round [41], via
| (13) |
The ucb term in (13) is designed to tackle C2. Its formulation encapsulates the inherent exploration vs. exploitation trade-off in MAB problems, boosting exploitation of the fastest users in expectation using , while encouraging to explore other users in its second term. The resulting user selection rule at round is
| (14) |
The overall active user selection procedure is summarized as Algorithm 1. The chosen users send their noisy local model updates to the server which updates the global model by (2) and sends it back to all the users in . At the end of every round, we update the users’ reward terms for the next round, in which and change their values only for participating users . Note that, by the formulation of Algorithm 1, it holds that when is an integer divisor of , then in the first rounds, the server chooses every user exactly once due to the initial conditions.
Initial model parameters
III-C Regret Analysis
To evaluate PAUSE, we next analyze its regret, which for a policy is defined as the expectation of the reward gap between the given policy and the Genie’s policy:
| (15) |
We define the maximal reward gap for any policy as . This quantity is bounded as stated the following lemma:
We bound the regret of PAUSE in the following theorem:
Theorem 3.
The regret of PAUSE holds
| (17) |
Proof.
The proof is given in Appendix -A. ∎
III-D Discussion
PAUSE is particularly designed to facilitate privacy and communication constrained FL. It leverages MAB-based active user selection to dynamically cope with privacy leakage accumulation, without restricting the overall number of FL rounds as in [36, 20, 24]. PAUSE is theoretically shown to achieve best-known regret growth and it demonstrated promising results in our experiments as detailed in Section V.
The formulation of PAUSE in Algorithm 1 focuses on the server operation, requiring the users only to send their updates with the proper PPN. As such, it can be naturally combined with existing methods for alleviating latency and privacy via update encoding [4]. Moreover, the statement of Algorithm 1 complies with any privacy policy imposed, while adhering to the constraints C1-C3. This inherent adaptability makes it an agile solution across diverse policy frameworks.
A core challenge associated with applying PAUSE stems from the fact that (14) involves a brute search over options. Such computation is expected to become infeasible at large networks, i.e., as grows; making it incompatible with consideration C4. This complexity can be alleviated by approximating the brute search with low-complexity policies based on (14), as we do in the sequel.
IV SA-PAUSE
In this section we alleviate the computational burden associated with the brute search operation of PAUSE. The resulting algorithm, termed SA-PAUSE, is based on SA principles, as detailed in Subsection IV-A. We analyze SA-PAUSE, rigorously identifying conditions for which it coincides with PAUSE and characterize its time complexity in Subsection IV-B.
IV-A Simulated Annealing Algorithm
To ease the computational efficiency of the search procedure in (14), we construct a graph structure where the set of vertices comprises all possible subsets of users in . For each vertex (i.e., set of users) , we denote its neighboring set as . Two vertices are designated as neighbors, when they satisfy the following requirements:
-
R1
The intersection of the vertices contains exactly elements, i.e., the sets of users and differ in a single user, thus .
-
R2
One of the users which appears in only a single set minimizes one of the terms of the selection rule (14) in its designated group. i.e., one of the sets is an active neighbor of the other. Mathematically, we say that is an active neighbor of (and is a passive neighbor of ) if the distinct node in , i.e., , holds
The above graph construction is inherently undirected due to the symmetric nature of the neighbor relationships.
To formalize our optimization objective, we define the energy of each vertex as the quantity we seek to maximize in PAUSE’s search (14). Specifically, for any vertex , define
| (18) |
To identify a vertex exhibiting maximal energy, we introduce an optimized SA-based algorithm [43], which iteratively inspects vertices (i.e., candidate user sets) in the graph. The resulting procedure, detailed in Algorithm 2, is comprised of two stages taking place on FL round : initilalziaiton and iterative search.
Initialization: Following established SA methodology, we maintain an auxiliary temperature sequence, whose th entry is defined as , where parameter exceeds the maximum energy differential between any pair of vertices in the graph. Thus, one must first set the value of .
Accordingly, the initialization phase at round involves sorting all users according to their respective , , and values into three distinct lists. These three sorted lists are used first to determine an appropriate value for . For each list , we denote and as the sets containing the users with minimal and maximal values, respectively. The parameter is then established as follows, where represents a small positive constant:
| (19) |
Iterative Search: The algorithm’s iterative phase updates an inspected vertex, moving at iteration from the previously inspected into an updated . This necessitates the identification of . We decompose this task into the discovery of active and passive neighbors as specified in R2, utilizing the previously constructed sorted lists:
-
N1
Active Neighbor Identification - To determine the active neighbors in iteration , we examine each sorted list (, , and ) to identify the user with the minimal value within . An active neighbor is generated by substituting any of these minimal-value users with a user not present in . This procedure yields at most active neighbors of .
-
N2
Passive Neighbor Identification - For passive neighbors, we establish that a vertex qualifies as a passive neighbor of if it can be constructed through one of two mechanisms, illustrated using the sorted list. Let denote the user with minimal in and represent the user with the second-minimal value. is a passive neighbor of if it is obtained by either:
-
(a)
Replace any user in except with a user whose value is lower than ’s (positioned before in the sorted list).
-
(b)
Replace with a user whose value is lower than ’s (positioned before in the sorted list).
-
(a)
Once the neighbors set is formulated, the algorithm inspects a random neighbor . This set is inspected in the following iteration if it improves in terms of the energy (18) (for which it is also saved as the best set explored so far), or alternatively it is randomly selected with probability . The resulting procedure is summarized as Algorithm 2.
Sort the users along , , and , in three different lists.
IV-B Theoretical Analysis
Optimality: The SA search of SA-PAUSE, detailed in Algorithm 2, replaces searching over all possible user selections with exploration over a graph. To show its validity, we first prove that it indeed finds the reward-maximizing set of users, as done in PAUSE. Since in general there may be more than one set of users that maximizes the reward (or equivalently, the energy (18)), we use to denote the set of vertices exhibiting maximal energy in the graph. The ability of Algorithm 2 to recover the same users set as brute search via (14) (or one that is equivalent in terms of reward) is stated in the following theorem:
Theorem 4.
For Algorithm 2, it holds that:
| (20) |
Proof.
The proof is given in Appendix -B. ∎
Theorem 4 shows that Algorithm 2 is guaranteed to recover the reward-maximizing users set in the horizon of infinite number of iterations. While the SA algorithm operates over a finite number of iterations, and Theorem 4 applies as , the carefully designed cooling temperature sequence and algorithmic structure ensure robust practical performance of SA algorithms [50, 51]. This efficacy is empirically validated in Section V.
Time-Complexity: Having shown that Algorithm 2 can approach the users set recovered via PAUSE, we next show that it satisfies its core motivation, i.e., carry out this computation with reduced complexity, and thus supports scalability. While inherently the number of selected users is smaller than the overall number of users , and often , we accommodate in our analysis computationally intensive settings where is allowed to grow with , but in the order of .
On each FL round , the initialization phase requires operations due to the list sorting procedures. During each iteration , locating ’s users’ indices in the sorted lists can be accomplished in operations through pointer manipulation. The identification of exhibits complexity , as each neighbor can be found in constant time. While the number of active neighbors is bounded by , the quantity of passive neighbors varies across users and iterations. Given that each passive neighbor of corresponds to that node being an active neighbor of , and considering the bounded number of active neighbors per user, a balanced graph typically exhibits approximately passive neighbors per user. Specifically, in the average case where each user in has passive neighbors, the complexity order of Algorithm 2 is .
For comparative purposes, consider a simplified SA variant (termed Vanilla-SA) where the neighboring criterion is reduced to only the first condition in R1 (i.e., nodes are neighbors if they share exactly users). This algorithm closely resembles Algorithm 2, but eliminates list sorting and determines by exhaustively replacing each user in with each user in . In this case, by setting to be an upper bound on (16), e.g., we satisfy the conditions for Theorem 4 as well, ensuring asymptotic convergence. However, this approach results in , producing a densely connected graph that impedes search efficiency and invariably yields complexity. Table I presents a comprehensive comparison of time complexities across different scenarios.
| Best | Average | Worst | |
|---|---|---|---|
| Brute force search 14 | |||
| Vanilla-SA | |||
| Algorithm 2 | |||
Summary: Combining the optimality analysis in Theorem 4 with the complexity characterization in Table I indicates that the integration of Algorithm 2 to approximate PAUSE’s search (14) into SA-PAUSE enables the application of PAUSE to large-scale networks, meeting C4. The theoretical convergence guarantees, coupled with its practical efficiency, make it a robust solution for approximating PAUSE and thus still adhering for considerations C1-C3. The empirical validation of these theoretical results is presented comprehensively in the following section.
V Numerical Study
V-A Experimental Setup
Here, we numerically evaluate PAUSE in FL111The source code used in our experimental study, including all the hyper-parameters, is available online at https://github.com/oritalp/PAUSE/tree/production. We consider the training of a DNN for image classification based on MNIST and CIFAR-10. The trained model is comprised of a convolutional neural network (CNN) with three hidden layers. These layers are followed by a fully-connected network (FC) with two hidden layers for CIFAR-10, and a three-layer FC with 32 neurons at its widest layer for MNIST.
We examine our approach in both small and large network settings with varying privacy budgets. In the former, the data is divided between users, and of them being chosen at each round, while the latter corresponds to and users. The communication latency obeys a normal distribution for every . The users are equally divided into two groups: fast users, who had lower communication latency expectations, and slower users. For each configuration, we test our approach both in i.i.d and non-i.i.d data distributions. In the imbalnaced case, the data quantities are sampled from a Dirichlet distribution with parameter , where each user exhibits a dominant label comprising approximately a quarter of the data.
As PAUSE becomes computationally infeasible in the large network case, it is only tested on small networks, while SA-PAUSE is being tested in both scenarios. These algorithms are compared with the following benchmarks:
-
•
Random, uniformly sampling users without replacements [44], solely in the i.i.d balanced case.
-
•
FedAvg with privacy and FedAvg w.o. privacy, choosing all users, with and without privacy, respectively.
-
•
Fastest in expectation, using only the same pre-known five fastest users in expectation at each round.
-
•
The clustered sampling selection algorithm proposed in [20].
V-B Small Network with i.i.d. Data
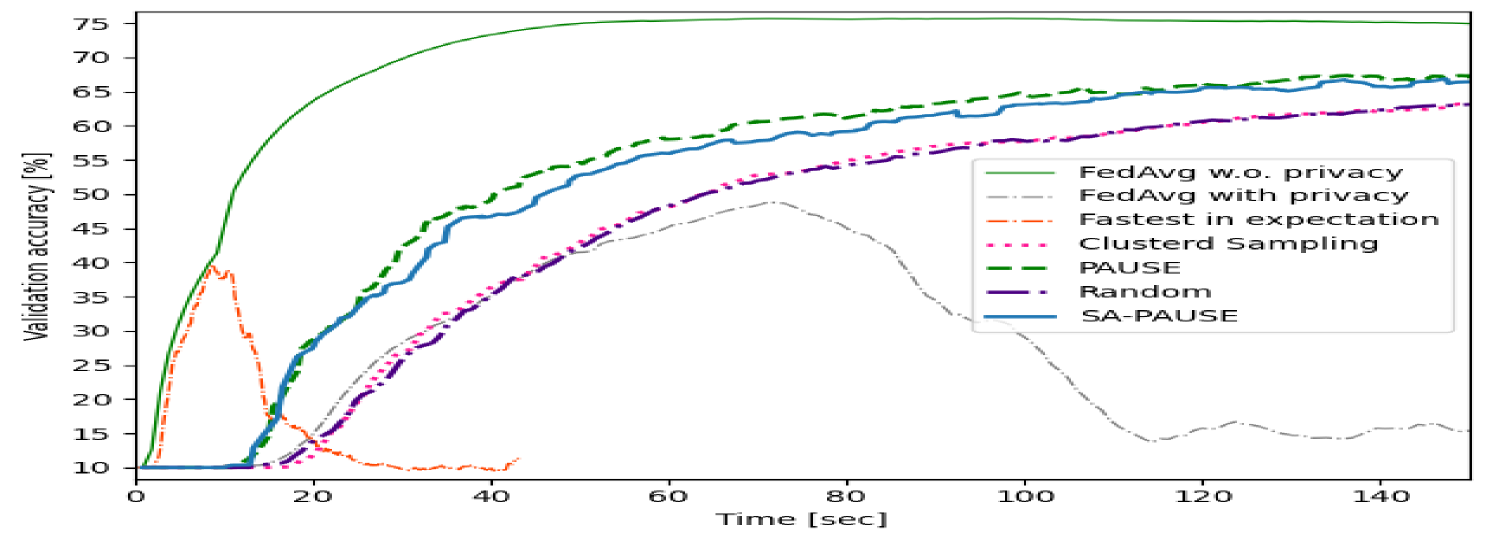
Our first study trains the mentioned CNN with an overall privacy budget of for image classification using the CIFAR-10 dataset. The resulting FL accuracy versus communication latency are illustrated in Fig. 2. The error curves were smoothened with an averaging window of size to attenuate the fluctuations. As expected, due to privacy leakage accumulation, the more rounds a user participates in, the noisier its updates are. This is evident in Fig. 2, where choosing all users quickly results in ineffective updates. PAUSE consistently achieves both accurate learning and rapid convergence. Further observing this figure indicates SA-PAUSE successfully approximates PAUSE’s brute-force search as well.
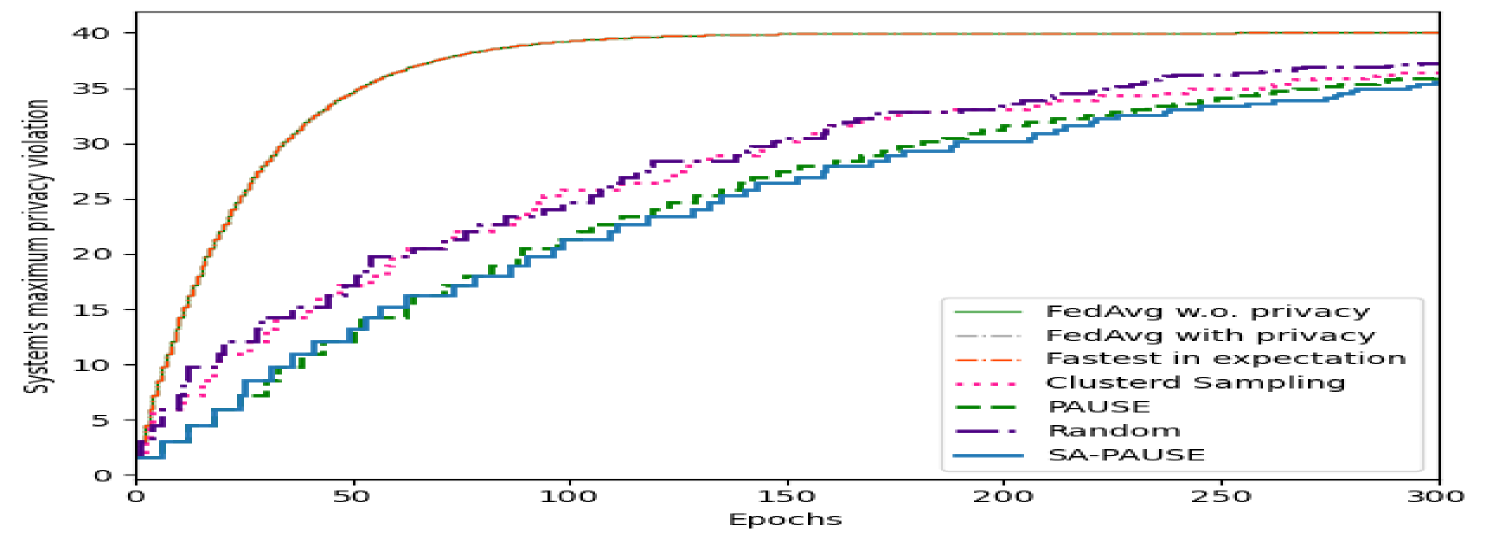
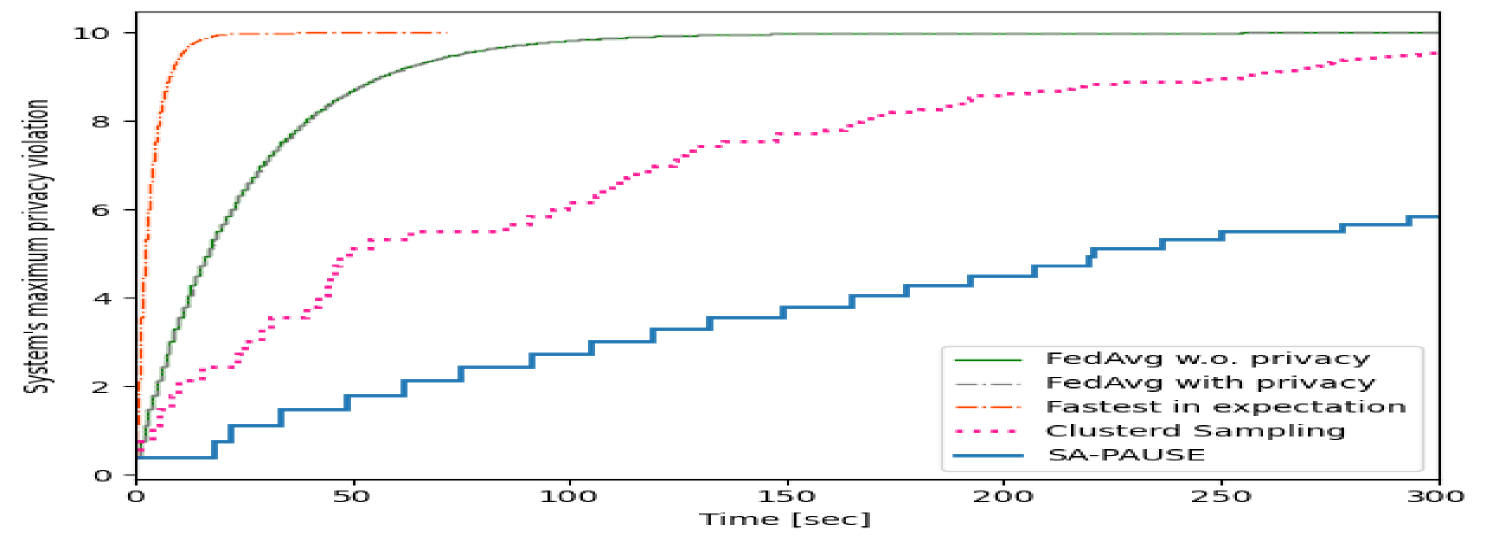
PAUSE’s ability to mitigate privacy accumulation is showcased in Fig. 3. There, we report the overall leakage as it evolves over epochs. Fig. 3 reveals that the privacy violation at each given epoch using PAUSE is lower compared to the random and the clustered sampling methods, adding to its improved accuracy and latency noted in Fig. 2. Note FedAvg with privacy and fastest in expectation methods’ maximum privacy violation coincide as in every epoch it’s raised by an .
V-C Small Network with non-i.i.d. Data
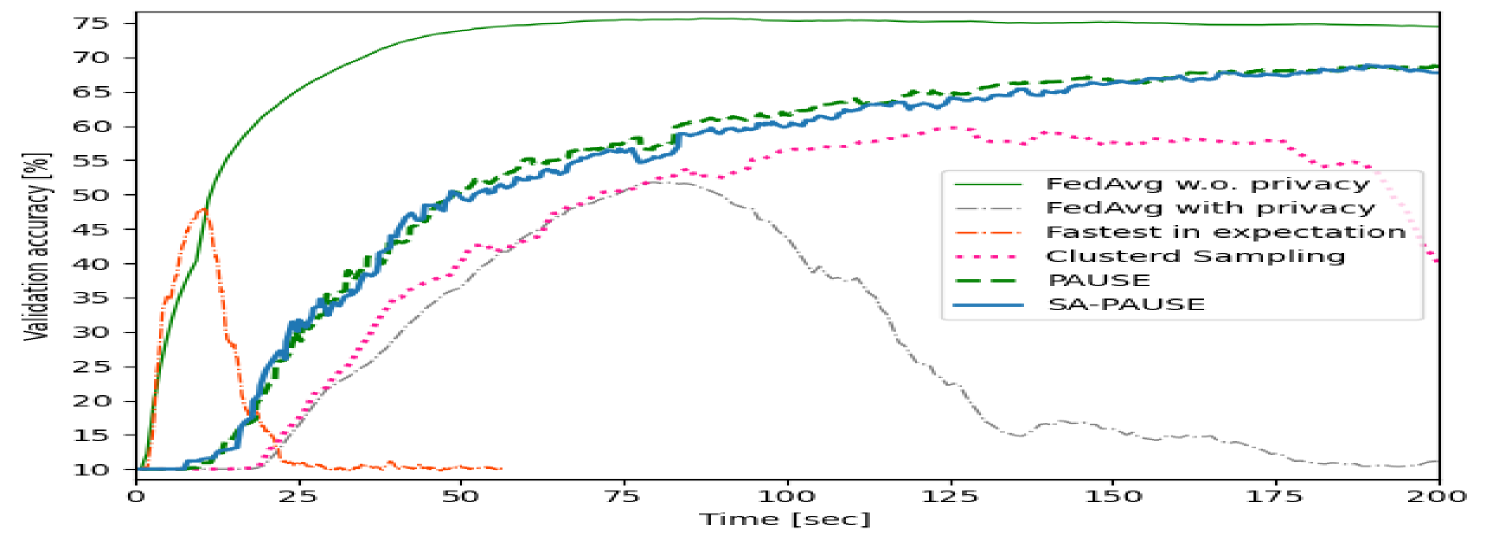
Subsequently, we train the same DNN with CIFAR-10 in the non-i.i.d case as described previously with an overall privacy budget of . As opposed to the balanced data test, this setting necessitates balancing between users with varying quantities of data, which might contribute differently to the learning process. The data quantities were sampled from a Dirichlet distribution with parameter . Analyzing the validation accuracy versus communication latency in Fig. 4 indicates the superiority of our algorithms also in this case in terms of accuracy and latency. Fig. 5 depicts the maximum privacy violation of the system, this time, versus the communication latency, and facilitates this statement by demonstrating both PAUSE and its approximation’s ability to maintain privacy better though performing more sever-clients iterations in any given time.
V-D Large Networks
We proceed to consider the large network settings. Here, we train two models: one for MNIST with i.i.d. data distribution, and on for CIFAR-10 with data distributed non-i.i.d. For these scenarios, we implemented two modifications. First, to accelerate the convergence of the SA procedure in Algorithm 2 under a reasonable amount of iterations, we modulate the temperature coefficient as in [52, 53]. This is accomplished by dividing the temperature coefficient by a constant , i.e., the temperature in the th iteration becomes [52, 53]. Second, to enhance exploitation [54, 55], we amplified the empirical mean in 13 by another constant, .
The overall privacy budgets for the MNIST and CIFAR-10 evaluations are set to and , respectively. In the former, the data quantities were sampled from a Dirichlet distribution with parameter . Both cases exhibited consistent trends with the small networks tests, systematically demonstrating SA-PAUSE’s robustness across diverse privacy budgets, datasets, and network scales.
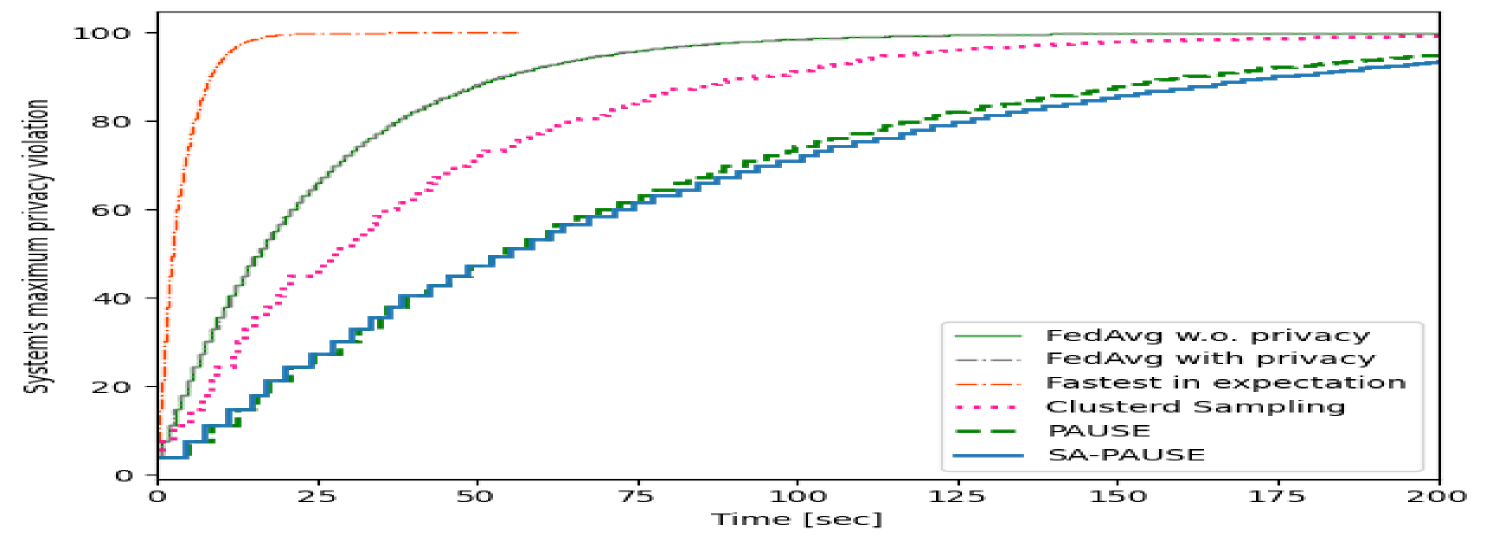
As before, the validation accuracy versus communication latency graphs are presented in Fig. 6 and Fig. 8, while the maximum overall privacy leakage versus time graphs are depicted in 7 and Fig. 9. These results systematically demonstrate the ability of our proposed SA-PAUSE to facilitate rapid learning over large networks with balanced and limited privacy leakage.
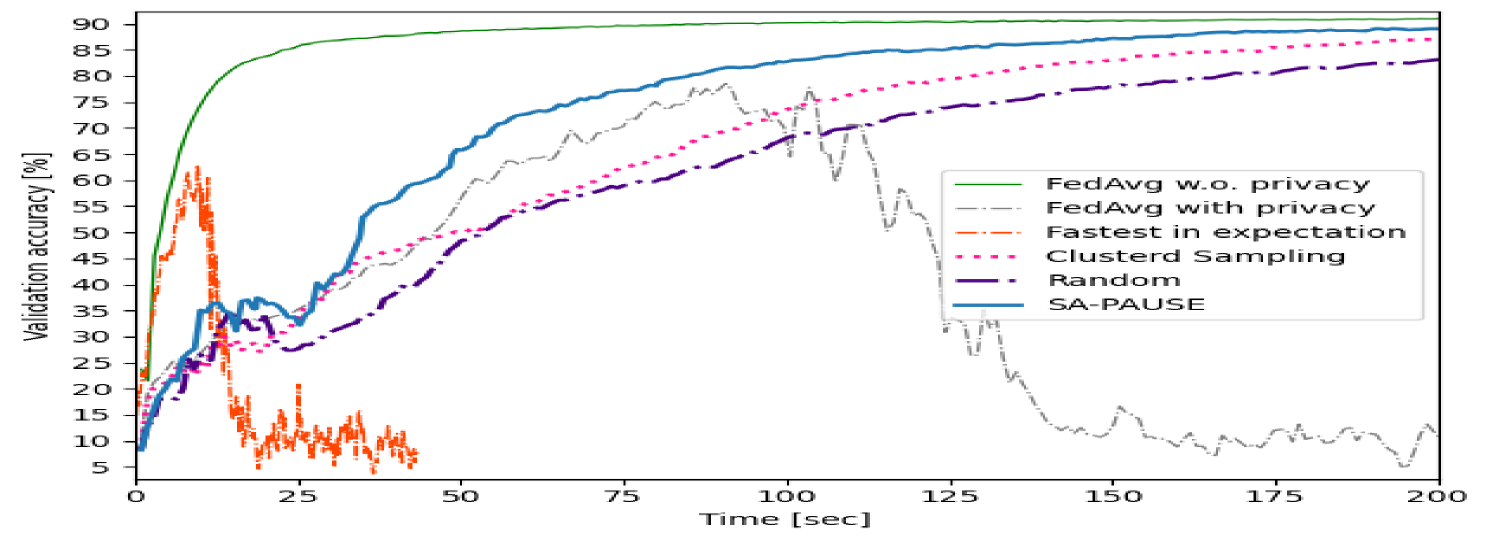
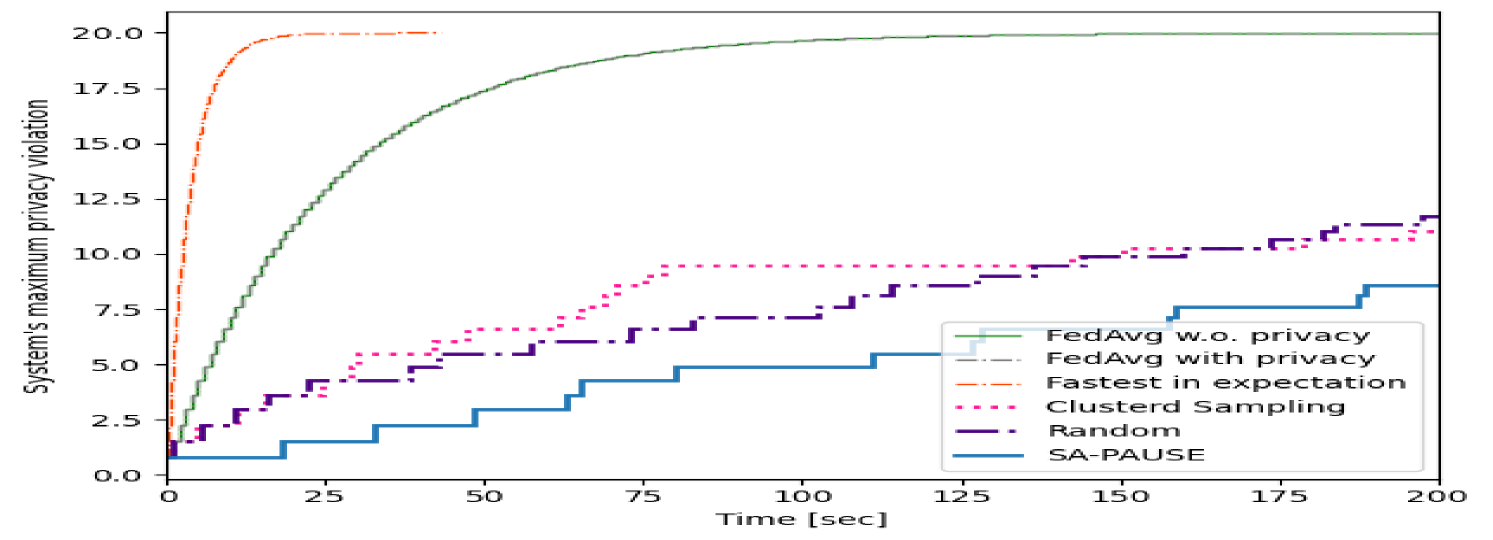
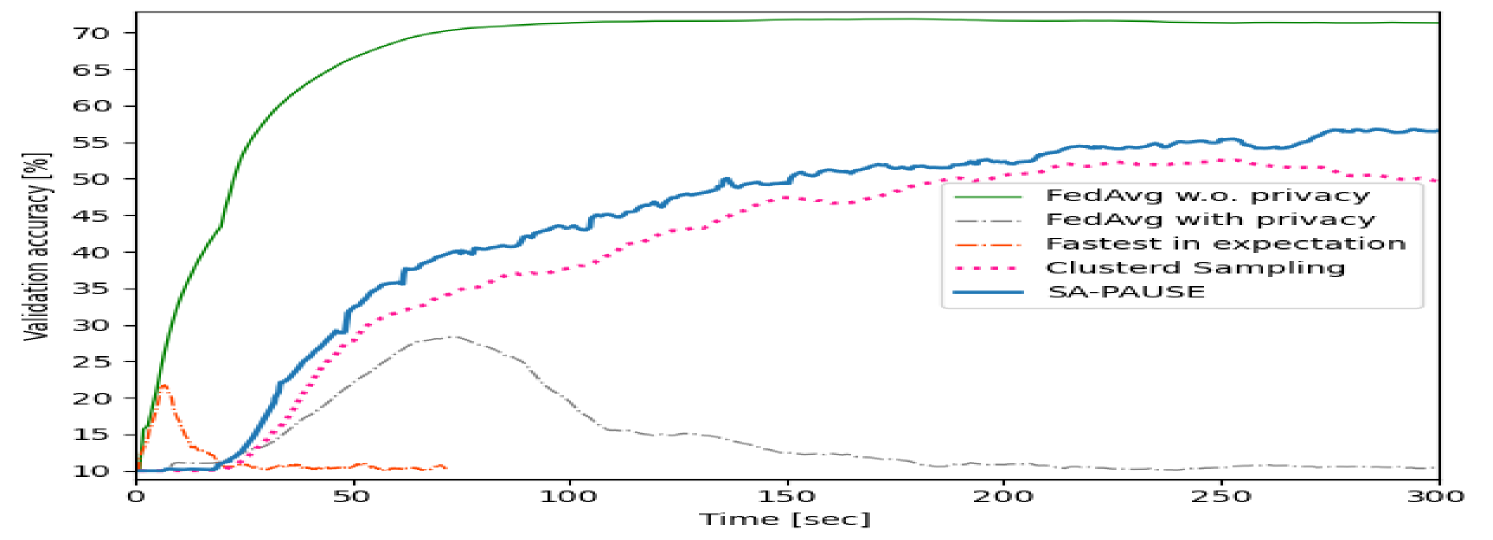
VI Conclusion
We proposed PAUSE, an active and dynamic user selection algorithm under fixed privacy constraints. This algorithm balances three FL aspects: accuracy of the trained model, communication latency, and system’s privacy. We showed that under common assumptions ,PAUSE’s regret achieves a logarithmic order with time. To address complexity and scalability, we developed SA-PAUSE, which integrates a SA algorithm with theoretical guarantees to approximate PAUSE’s brute-force search in feasible running time. We numerically demonstrated SA-PAUSE’s ability to approximate PAUSE’s search and its superiority over alternative approaches in diverse experimental scenarios.
-A Proof of Theorem 3
In the following, define . The regret can be bounded following the definition of as
| (-A.1) |
We introduce another indicator function for every along with its cumulative sum, denoted:
Let . In every round where , the counter is incremented for only a single user in , while for the remaining users . Thus, it holds that . Substituting this into (-A.1), we obtain that
| (-A.2) |
In the remainder, we focus on bounding for every . After that, we substitute the derived upper bound into (-A.2). To that aim, let and fix some whose value is determined later). We note that:
| (-A.3) |
where arises from considering the cases and its complementary state.
PAUSE’s policy (14) implies that in every iteration:
| (-A.4) |
Since this happens with probability one, we can incorporate it into the mentioned inequality (-A.3):
We now denote the users chosen in the th iteration by the PAUSE algorithm and by the Genie as: and , respectively. For every , the indicator function in the sum is equal to 1 only if the th user is chosen the least at the beginning of the th iteration, i.e., for every . The intersection of with implies . Therefore, this intersection of events implies that for every . Using this result, we can further bound every event in the indicator functions in the upper bound of :
Using the fact that for any finite set of events of size , it holds that , , and that the expectation of an indicator function is the probability of the internal event occurring, we have that
| (-A.5) |
In the following steps we focus on bounding the terms in the double sum. To that aim, we define the following:
| (-A.6) |
Using these notations and writing , we state the following lemma:
Lemma -A.1.
The event (-A.4) implies at least one of the next three events occurs:
-
1.
;
-
2.
;
-
3.
.
Proof.
Applying the union bound and the relationship between the events shown in Lemma -A.1 implies:
| (-A.8) |
We obtained three probability terms – , , and . we will start with bounding the first two using Hoeffding’s inequality [56]. Term will be bounded right after in a different manner. We’ll demonstrate how the first term is bounded; the second one is done similarly by replacing with :
| (-A.9) |
where is the latency of the user at the th round it participated. This, results in the following inequalities:
To bound we define another two definitions:
| (-A.10) |
Using the law of total probability to divide into 2 parts:
We denote the former term as and the latter as :
| (-A.11a) | ||||
| (-A.11b) | ||||
In the following we show that for a range of values of , which so far was arbitrarily chosen, is equal to . Recalling the definitions of (-A.6) and (-A.10), we know . plugging this relation into probability of contained events in , and upper bounding by omitting the intersection in , yields:
where the last two equalities derive from reorganizing the event and recalling the definitions of and , respectively. We now show this event exists in probability 0, and then the latest bound implies is equal to as well. We observe the mentioned event while recalling that by the relevant indexes in the summation in (-A.5):
| (-A.12) |
Next, we observe an enhanced version of the Genie that is rewarded by an additive term of in every round that . Recalling we observe solely cases where this statement occurs, the LHS is directly larger than . Thus, to secure non-existence of this event we may set any value fulfilling . Recalling , we reorganize this condition into:
| (-A.13) |
Moreover, this enhanced version adds another term of to the regret, as noted later in the proof closure.
Recall that we initially aimed to upper bound the probability of the event (-A.7) by splitting it into three events using the union bound (-A.8). We then showed and are bounded, and divided into 2 parts - and . By setting an appropriate value of (-A.13), we demonstrated can be shown to be equal to 0. The last step is to upper bound which is done similarly.
We start by recalling the definition of (-A.11) and then bound it by a containing event:
| (-A.14) |
The last equality arises from the definitions of (-A.6) and (-A.10), and definition (13). We now prove a lemma regarding this event, which its probability upper bounds :
Lemma -A.2.
The following event implies at least one of the next three events occur:
| (-A.15) |
-
1.
-
2.
-
3.
Proof.
We prove by contradiction, as , thus proving the lemma ∎
Combining the lemma, the union bound an the upper bound we found in (-A.14) yields:
We already showed in (-A.9) that the first term is bounded by . Repeating the same steps for instead of we can show that this value also bounds the second term. Furthermore, we now show that the event in the third term occurs with probability 0 when setting an appropriate value of . Observing the mentioned event:
| (-A.16) |
Similar to (-A.13), and recalling , by demanding we assure this event occurs with probability 0. As this is the same range as in (-A.13) we set to be the lowest integer in this range, i.e., .
Finally, as we showed: . plugging the bounds on , , and into (-A.8) we obtain:
Substituting this bound along with the chosen value of into the result we obtained at the beginning of the proof (-A.5) we obtain:
To conclude the theorem’s statement, we set this result back into (-A.2) while recalling the added regret from the Genie empowerment, obtaining
concluding the proof of the theorem.
-B Proof of Theorem 4
To prove the theorem we introduce essential terminology and definitions. We define reachability as follows: Given two nodes and and energy level , node is considered reachable from if there exists a path connecting them that traverses only nodes with energy greater than or equal to . Building upon this definition, a graph exhibits Weak Reversibility if, for any energy level and nodes and , is reachable from at height if and only if is reachable from at height .
Following [43], to prove that Theorem 4 holds, one has to show that the following requirements hold:
We prove the three mentioned conditions are satisfied to conclude the theorem. Requirements R1 and R2 follow from the formulation of SA-PAUSE. Specifically, weak reversibility (R1) stems directly from the definition and the undirected graph property, while the temperature sequence condition R2 is satisfied as we set to be as mentioned in (19).
To prove that R3 holds, by definition, we need to show there is a path with positive probability between any two nodes . Since the graph is undirected it is sufficient to show a path from to . In Algorithm 3, we present an implicit algorithm yielding a series of nodes . within this sequence, consecutive nodes are neighbors, i.e., the algorithm yields a path with positive probability from to .
;
This algorithm possesses a crucial characteristic; the conditional statement evaluates to true until it transitions to false, and from that moment on, it remains False to the end. Thus, the algorithm can be partitioned into two phases, the iterations before the statement becomes false, and the rest. We denote the iteration the condition becomes false as .
First, observe that when , is an active neighbor of , whereas during all subsequent iterations, the former is a passive neighbor of the latter. This proves the transitions occur in a positive probability in the first place.
Next, we prove the algorithm’s correctness and termination. Let the minimum value in . For every , if , then it is added to in an iteration . this is guaranteed because if such incorporation had not occurred by the th iteration, the conditional statement would remain satisfied, contradicting the definition of . The rest of the users, i.e., every such that , will be added during the second phase.
Notice the algorithm avoids cyclical additions and subtractions, as during the second phase, users from who are already present in for all are preserved when constructing . Instead, a user not belonging to is eliminated. Throughout this exposition, we have established that the algorithm terminates, and every user is eventually incorporated into the evolving set without subsequent elimination. This completes our verification of the algorithm’s correctness, and the proof as a whole.
References
- [1] O. Peleg, N. Lang, S. Rini, N. Shlezinger, and K. Cohen, “PAUSE: Privacy-aware active user selection for federated learning,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2025.
- [2] B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. y Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Artificial Intelligence and Statistics. PMLR, 2017, pp. 1273–1282.
- [3] P. Kairouz et al., “Advances and open problems in federated learning,” Foundations and trends® in machine learning, vol. 14, no. 1–2, pp. 1–210, 2021.
- [4] T. Gafni, N. Shlezinger, K. Cohen, Y. C. Eldar, and H. V. Poor, “Federated learning: A signal processing perspective,” IEEE Signal Process. Mag., vol. 39, no. 3, pp. 14–41, 2022.
- [5] T. Li, A. K. Sahu, A. Talwalkar, and V. Smith, “Federated learning: Challenges, methods, and future directions,” IEEE Signal Process. Mag., vol. 37, no. 3, pp. 50–60, 2020.
- [6] M. Chen, N. Shlezinger, H. V. Poor, Y. C. Eldar, and S. Cui, “Communication-efficient federated learning,” Proceedings of the National Academy of Sciences, vol. 118, no. 17, 2021.
- [7] D. Alistarh, T. Hoefler, M. Johansson, N. Konstantinov, S. Khirirat, and C. Renggli, “The convergence of sparsified gradient methods,” Advances in Neural Information Processing Systems, vol. 31, 2018.
- [8] P. Han, S. Wang, and K. K. Leung, “Adaptive gradient sparsification for efficient federated learning: An online learning approach,” in IEEE International Conference on Distributed Computing Systems (ICDCS), 2020, pp. 300–310.
- [9] A. Reisizadeh, A. Mokhtari, H. Hassani, A. Jadbabaie, and R. Pedarsani, “Fedpaq: A communication-efficient federated learning method with periodic averaging and quantization,” in International Conference on Artificial Intelligence and Statistics. PMLR, 2020, pp. 2021–2031.
- [10] N. Shlezinger, M. Chen, Y. C. Eldar, H. V. Poor, and S. Cui, “UVeQFed: Universal vector quantization for federated learning,” IEEE Trans. Signal Process., vol. 69, pp. 500–514, 2020.
- [11] M. M. Amiri and D. Gündüz, “Machine learning at the wireless edge: Distributed stochastic gradient descent over-the-air,” IEEE Trans. Signal Process., vol. 68, pp. 2155–2169, 2020.
- [12] T. Sery and K. Cohen, “On analog gradient descent learning over multiple access fading channels,” IEEE Trans. Signal Process., vol. 68, pp. 2897–2911, 2020.
- [13] K. Yang, T. Jiang, Y. Shi, and Z. Ding, “Federated learning via over-the-air computation,” IEEE Trans. Wireless Commun., vol. 19, no. 3, pp. 2022–2035, 2020.
- [14] S. Mayhoub and T. M. Shami, “A review of client selection methods in federated learning,” Archives of Computational Methods in Engineering, vol. 31, no. 2, pp. 1129–1152, 2024.
- [15] J. Li, T. Chen, and S. Teng, “A comprehensive survey on client selection strategies in federated learning,” Computer Networks, p. 110663, 2024.
- [16] L. Fu, H. Zhang, G. Gao, M. Zhang, and X. Liu, “Client selection in federated learning: Principles, challenges, and opportunities,” IEEE Internet Things J., vol. 10, no. 24, pp. 21 811–21 819, 2023.
- [17] J. Xu and H. Wang, “Client selection and bandwidth allocation in wireless federated learning networks: A long-term perspective,” IEEE Trans. Wireless Commun., vol. 20, no. 2, pp. 1188–1200, 2020.
- [18] S. AbdulRahman, H. Tout, A. Mourad, and C. Talhi, “FedMCCS: Multicriteria client selection model for optimal iot federated learning,” IEEE Internet Things J., vol. 8, no. 6, pp. 4723–4735, 2020.
- [19] E. Rizk, S. Vlaski, and A. H. Sayed, “Federated learning under importance sampling,” IEEE Trans. Signal Process., vol. 70, pp. 5381–5396, 2022.
- [20] Y. Fraboni, R. Vidal, L. Kameni, and M. Lorenzi, “Clustered sampling: Low-variance and improved representativity for clients selection in federated learning,” in International Conference on Machine Learning. PMLR, 2021, pp. 3407–3416.
- [21] W. Xia, T. Q. Quek, K. Guo, W. Wen, H. H. Yang, and H. Zhu, “Multi-armed bandit-based client scheduling for federated learning,” IEEE Trans. Wireless Commun., vol. 19, no. 11, pp. 7108–7123, 2020.
- [22] B. Xu, W. Xia, J. Zhang, T. Q. Quek, and H. Zhu, “Online client scheduling for fast federated learning,” IEEE Wireless Commun. Lett., vol. 10, no. 7, pp. 1434–1438, 2021.
- [23] D. Ben-Ami, K. Cohen, and Q. Zhao, “Client selection for generalization in accelerated federated learning: A multi-armed bandit approach,” IEEE Access, 2025.
- [24] Y. Chen, W. Xu, X. Wu, M. Zhang, and B. Luo, “Personalized local differentially private federated learning with adaptive client sampling,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2024, pp. 6600–6604.
- [25] L. Zhu and S. Han, “Deep leakage from gradients,” in Federated learning. Springer, 2020, pp. 17–31.
- [26] B. Zhao, K. R. Mopuri, and H. Bilen, “iDLG: Improved deep leakage from gradients,” arXiv preprint arXiv:2001.02610, 2020.
- [27] Y. Huang, S. Gupta, Z. Song, K. Li, and S. Arora, “Evaluating gradient inversion attacks and defenses in federated learning,” Advances in Neural Information Processing Systems, vol. 34, 2021.
- [28] H. Yin, A. Mallya, A. Vahdat, J. M. Alvarez, J. Kautz, and P. Molchanov, “See through gradients: Image batch recovery via gradinversion,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2021, pp. 16 337–16 346.
- [29] M. Kim, O. Günlü, and R. F. Schaefer, “Federated learning with local differential privacy: Trade-offs between privacy, utility, and communication,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021, pp. 2650–2654.
- [30] K. Wei et al., “Federated learning with differential privacy: Algorithms and performance analysis,” IEEE Trans. Inf. Forensics Security, vol. 15, pp. 3454–3469, 2020.
- [31] L. Lyu, “DP-SIGNSGD: When efficiency meets privacy and robustness,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021, pp. 3070–3074.
- [32] A. Lowy and M. Razaviyayn, “Private federated learning without a trusted server: Optimal algorithms for convex losses,” in International Conference on Learning Representations, 2023.
- [33] N. Lang, E. Sofer, T. Shaked, and N. Shlezinger, “Joint privacy enhancement and quantization in federated learning,” IEEE Trans. Signal Process., vol. 71, pp. 295–310, 2023.
- [34] N. Lang, N. Shlezinger, R. G. D’Oliveira, and S. E. Rouayheb, “Compressed private aggregation for scalable and robust federated learning over massive networks,” arXiv preprint arXiv:2308.00540, 2023.
- [35] C. Dwork, G. N. Rothblum, and S. Vadhan, “Boosting and differential privacy,” in IEEE Annual Symposium on Foundations of Computer Science, 2010, pp. 51–60.
- [36] J. Zhang, D. Fay, and M. Johansson, “Dynamic privacy allocation for locally differentially private federated learning with composite objectives,” in IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2024, pp. 9461–9465.
- [37] L. Sun, J. Qian, X. Chen, and P. S. Yu, “LDP-FL: Practical private aggregation in federated learning with local differential privacy,” in International Joint Conference on Artificial Intelligence, 2021.
- [38] A. Cheu, A. Smith, J. Ullman, D. Zeber, and M. Zhilyaev, “Distributed differential privacy via shuffling,” in Advances in Cryptology–EUROCRYPT 2019: 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Darmstadt, Germany, May 19–23, 2019, Proceedings, Part I 38. Springer, 2019, pp. 375–403.
- [39] B. Balle, J. Bell, A. Gascón, and K. Nissim, “The privacy blanket of the shuffle model,” in Advances in Cryptology–CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18–22, 2019, Proceedings, Part II 39. Springer, 2019, pp. 638–667.
- [40] Q. Zhao, Multi-armed bandits: Theory and applications to online learning in networks. Springer Nature, 2022.
- [41] P. Auer, N. Cesa-Bianchi, and P. Fischer, “Finite-time analysis of the multiarmed bandit problem,” Machine learning, vol. 47, pp. 235–256, 2002.
- [42] W. Chen, Y. Wang, and Y. Yuan, “Combinatorial multi-armed bandit: General framework and applications,” in International conference on machine learning. PMLR, 2013, pp. 151–159.
- [43] B. Hajek, “Cooling schedules for optimal annealing,” Mathematics of operations research, vol. 13, no. 2, pp. 311–329, 1988.
- [44] X. Li, K. Huang, W. Yang, S. Wang, and Z. Zhang, “On the convergence of FedAvg on non-iid data,” in International Conference on Learning Representations, 2019.
- [45] N. Lang, A. Cohen, and N. Shlezinger, “Stragglers-aware low-latency synchronous federated learning via layer-wise model updates,” IEEE Trans. on Commun., 2024, early access.
- [46] S. P. Kasiviswanathan, H. K. Lee, K. Nissim, S. Raskhodnikova, and A. Smith, “What can we learn privately?” SIAM Journal on Computing, vol. 40, no. 3, pp. 793–826, 2011.
- [47] Y. Wang, Y. Tong, and D. Shi, “Federated latent dirichlet allocation: A local differential privacy based framework,” in Proceedings of the AAAI Conference on Artificial Intelligence, vol. 34, no. 04, 2020, pp. 6283–6290.
- [48] T. Wang, X. Zhang, J. Feng, and X. Yang, “A comprehensive survey on local differential privacy toward data statistics and analysis,” Sensors, vol. 20, no. 24, p. 7030, 2020.
- [49] C. Dwork, F. McSherry, K. Nissim, and A. Smith, “Calibrating noise to sensitivity in private data analysis,” Journal of Privacy and Confidentiality, vol. 7, no. 3, pp. 17–51, 2016.
- [50] D. Henderson, S. H. Jacobson, and A. W. Johnson, “The theory and practice of simulated annealing,” Handbook of metaheuristics, pp. 287–319, 2003.
- [51] S. Ledesma, G. Aviña, and R. Sanchez, “Practical considerations for simulated annealing implementation,” Simulated annealing, vol. 20, pp. 401–420, 2008.
- [52] W. Ben-Ameur, “Computing the initial temperature of simulated annealing,” Computational optimization and applications, vol. 29, pp. 369–385, 2004.
- [53] I. Bezáková, D. Štefankovič, V. V. Vazirani, and E. Vigoda, “Accelerating simulated annealing for the permanent and combinatorial counting problems,” SIAM Journal on Computing, vol. 37, no. 5, pp. 1429–1454, 2008.
- [54] H. Wu, X. Guo, and X. Liu, “Adaptive exploration-exploitation tradeoff for opportunistic bandits,” in International Conference on Machine Learning. PMLR, 2018, pp. 5306–5314.
- [55] M. M. Drugan, A. Nowé, and B. Manderick, “Pareto upper confidence bounds algorithms: an empirical study,” in IEEE Symposium on Adaptive Dynamic Programming and Reinforcement Learning (ADPRL), 2014.
- [56] W. Hoeffding, “Probability inequalities for sums of bounded random variables,” The collected works of Wassily Hoeffding, pp. 409–426, 1994.