PEARL: Plausibly Deniable Flash Translation Layer using WOM coding
Abstract
When adversaries are powerful enough to coerce users to reveal encryption keys, encryption alone becomes insufficient for data protection. Plausible deniability (PD) mechanisms resolve this by enabling users to hide the mere existence of sensitive data, often by providing plausible “cover texts” or “public data volumes” hosted on the same device.
Unfortunately, with the increasing prevalence of (NAND) flash as a high-performance cost-effective storage medium, PD becomes even more challenging in the presence of realistic adversaries who can usually access a device at multiple points in time (“multi-snapshot”). This is because read/write operations to flash do not result in intuitive corresponding changes to the underlying device state.
The problem is further compounded by the fact that this behavior is mostly proprietary. For example, in a majority of commercially-available flash devices, an issued delete or overwrite operation from the upper layers almost certainly won’t result in an actual immediate erase of the underlying flash cells.
To address these challenges, we designed a new class of write-once memory (WOM) codes to store hidden bits in the same physical locations as other public bits. This is made possible by the inherent nature of NAND flash and the possibility of issuing multiple writes to target cells that have not previous been written to in existing pages.
We designed PEARL, a general-purpose Flash Translation Layer (FTL) that allows users to plausibly deniably store hidden data in NAND flash devices. We implemented and evaluated PEARL on a widely used simulator FlashSim[32]. PEARL performs well on real-world workloads, comparably to non-PD baselines. PEARL is the first system that achieves strong plausible deniability for NAND flash devices, secure against realistic multi-snapshot adversaries.
I Introduction
As computers permeate aspects of daily life, individual users, government officials, and organizations store increasing amounts of sensitive and private data on personal computers and mobile devices. While convenient, the ubiquitousness of computing devices that move data with individuals poses increasing threats to privacy. There have been a number of high-profile cases where a laptop or device with sensitive data is lost or stolen, leading to disclosure of sensitive information [15, 33, 38, 39, 49]. Thus, protecting sensitive data is essential, as one can never anticipate when a device may fall into the wrong hands.
To ensure sensitive data confidentiality, full disk encryption (FDE) is widely used. However, considering adversaries who are empowered by law or otherwise to request encryption keys [3, 31, 48, 42, 43], the FDE alone may not be enough as it would be defeated by coercion of users into submitting the key or password to reveal confidential data.
Plausible deniability (PD) is a key security property that helps to protect sensitive data against the mentioned powerful adversaries. PD by definition makes it possible to claim that “some information is not in possession [of the user] or some transactions have not taken place” [36]. In the context of secure storage, PD refers to the ability of a user to plausibly deny the existence of stored data even when an adversary has access to the storage medium. It supplements the capability of encryption to protect sensitive data from powerful adversaries.
PD assurances are sometimes a matter of life and death [41]. This has been demonstrated by numerous cases where information had to be transferred through checkpoints manned by hostile adversaries. One typical and prominent example involves the human rights group Network for Human Rights Documentation - Burma (ND-Burma). A large amount of data on human rights violations by the Burmese government was carried out of the country on mobile devices by ND-Burma activists, under threat of exposure at checkpoints and border crossings [6]. Similarly, in 2012, a videographer smuggled evidence of human rights violations out of Syria by hiding a micro-SD card in a wound [37], again risking his life.
Several PD storage mechanisms were proposed [36, 3, 40, 5, 7, 8, 9] for both file system and block device layers. However, a strong assumption underpins all these existing solutions, mostly deriving from traditional magnetic media, namely a high level of transactional commitment from the underlying storage medium. Specifically, write and erase operations are assumed to be honored when issued.
Needless to say, storage media such as NAND flash is wrapped in logic that prevents this to be the case. For example, most Flash Translation Layer (FTL) algorithms will likely prevent overwrites to touch underlying physical pages when issued and instead remap data elsewhere, only to later return and garbage collect such erased data if and when needed. This immediately breaks existing PD mechanisms built upon the assumption that the underlying device honors write/erase operations when requested. Stale data persisted on the underlying device (e.g., yet to be garbage collected pages) out of control of the PD logic then enables adversaries to easily infer the existence and most often location of hidden data [24].
New media requires new PD logic. Further, arguably, this logic needs to be placed closer to the physical layer to securely handle the PD requirements while also providing life-cycle and efficiency-related elements such as wear leveling and encoding optimizations.
NAND flash, arguably the most popular flash technology in modern production, stores data in an array of cells, each requiring a special ERASE operation before a write. Due to several addressing and packaging optimization reasons, almost always ERASE can only be performed at block level (containing many cells). As a result, even simple updates to data require a more complex set of steps which is implemented usually in an intermediary Flash Translation Layer (FTL) sitting between e.g., a file system and the underlying flash device. The FTL makes an excellent candidate [24] for implementing protection functionality including PD logic.
Two existing have considered PD tailored for NAND flash: DEFY [41], and DEFTL [24]. Unfortunately, neither is secure against practical adversaries which are almost always multi-snapshot [9]. Crossing a border twice, checking in airline luggage, living under an oppressive government with physical access to devices, leaving devices in untrusted places subject to “hotel maid” attacks, all these are instances of multi-snapshot opportunities for an adversary. Naturally, the security of a PD system should not break down completely (under reasonable user behavior) and should be resilient to such realistic externalities (hotel maids, border guards, airline checked luggage etc). Further, DEFY is compromised in the presence of capacity exhausting attacks [24].
PEARL introduces the first PD scheme that achieves security against multi-snapshot adversaries on NAND flash devices. This is made possible by re-purposing a new class of write-once memory (WOM) codes to naturally combine both public and hidden data together in one physical page, and managing the pages considering the nature of flash memory. PEARL is implemented as a general purpose FTL that, in addition to taking all necessary flash management duties, enables deniability of the existence of hidden data. It guarantees that the resulting state of a device with both public and hidden data is indistinguishable from a public-data only state. A number of key insights ground the design as follows.
First, PEARL operates at a much finer encoding granularity compared with previous PD schemes. Existing work [24, 41] store public and hidden data in different physical pages or even different flash blocks. These systems require plausible reasons to explain away the existence of written pages containing hidden data (e.g. masquerading as “random” or “free” data). This problem is compounded by the nature of NAND flash and the realistic adversaries with multi-snapshot access. Hidden data may end up being relocated even in the absence of hidden updates, and adversaries can observe implausible modifications (e.g., to “free” space containing hidden data). In contrast, PEARL uses the second write stage of a specially-designed WOM code to encode hidden data in a public cover. This makes such plausible reasons inherent – all pages contain public data by design.
Second, PEARL as an FTL smartly manages the mapping from both public and hidden data to physical pages and handles NAND-specific operations such as garbage collections considering the special nature of flash memory. As a result, all physical layer changes can be plausibly explained by public data requests only, thus preventing multi-snapshot adversaries from detecting the existence of hidden data by comparing snapshots and analyzing physical activities on flash.
We evaluated PEARL using a widely used simulator FlashSim [32]. The experimental results show PEARL is practically fast. It performs comparably to the non-PD baseline on real-world workloads.
II Related Work
PD storage systems are designed to protect users against powerful adversaries (e.g., corrupt government officials) who can coerce users to give up the encryption key(s). Generally speaking, a PD storage system allows the user to only reveal the key used to encrypt (non-sensitive) public data while claiming that no other data exists on the device.
Steganographic file systems [3, 36, 40, 41] were firstly proposed to provide plausibly-deniable storage. They allowed users to store both sensitive (hidden) files and non-sensitive (public) files inside one file system and hide the existence of hidden files from adversaries. To defend against single-snapshot adversaries, Anderson et al. [3] explored the idea of steganographic file systems and proposed two ideas for hiding data. Later McDonald et al. [36] implemented StegFS for Linux on the basis of the solution proposed in [3]. Pang et al. [40] improved on the previous constructions by avoiding hash collisions and provided more efficient storage. In addition to these steganographic file systems against single-snapshot adversaries, Han et al. [17] designed a multi-user steganographic file system (DRSteg) on shared storage. However, their solution does not scale well to practical scenarios as they attribute deniability to joint ownership of sensitive data. Gasti et al. [12] proposed a deniable shared file system (DenFS) specifically for cloud storage. Its security depends on processing data temporarily on a client machine, and it is not straightforward to deploy DenFS for local storage.
On the other hand, disk encryption tools [1, 20, 45, 5, 7, 8, 9] were designed to support PD at block device level. They worked by often storing both hidden and public “volumes” on the same device while preventing adversaries to gain information about how many volumes the device actually contains. Truecrypt [1], Rubberhose [20] and Mobiflage [45] provided deniability against only single-snapshot adversaries. Blass et al. [5] implemented HIVE, the first PD solution against multi-snapshot adversaries at device level, using a write-only Oblivious RAM (ORAM) for mapping data from logical volumes to underlying devices and hiding access patterns for hidden data within requests to public data. Later Chakraborti et al. [7] proposed DataLair with a more efficient write-only ORAM and improved the system performance. Chang et al. [8] proposed MobiCeal specifically for mobile devices. The idea is to use a dummy write mechanism to obfuscate writes to a hidden volume. Unfortunately the paper suffers from deniability compromises: the space occupied by dummy writes would be reclaimed while the space occupied by the hidden data would remain intact, thus enabling an attacker to detect the static hidden data. Chen et al. [9] introduced PD-DM, a locality-preserving PD solution that eliminated the randomness introduced by ORAM-based solutions and improved the system throughput especially on hard disk.
The above solutions required that the underlying devices honor write/erase operations atomically. Unfortunately in the case of flash this is simply not the case. Old data can linger on the device for years and attackers can easily unscrew the flash cover and read the FLASH chips directly with cheap off the shelf readers. Others have noted this too [24] – PD systems incorporating deniability in the upper layers (file system layer or block device layer) very often suffer from deniability compromises in the lower layers (flash memory). And unfortunately even systems such as Mobiflage and MobiCeal specifically designed for mobile devices do not address this essential vulnerability.
Special PD solutions are designed for NAND flash storage devices as well, considering its significant distinctive natures. DEFY [41] is a log structured file system for NAND flash devices that offers PD with a newly proposed secure deletion technology. It is based on WhisperYAFFS [47], a log structured file system which provides full disk encryption for flash devices. However, as claimed in [24], DEFY will be compromised by making several attempts to exhaust the writing capacity. DEFTL [24] instead incorporates deniability to the Flash Translation Layer (FTL) of flash-based block devices. Yet, it is against single-snapshot adversaries.
III NAND Flash
NAND flash is a non-volatile solid-state storage medium. It is becoming increasingly popular due to its low power consumption and shock resistance now. Unlike the traditional magnetic storage disk that stores data by magnetizing the ferromagnetic material on a disk, NAND flash stores data using only electronic circuits (floating-gates). Thus, NAND flash has its own characteristics [14]: 1) NAND flash supports efficient random accesses. 2) Read and write/program operations are performed in page units while erase operations are based on block units (usually larger than the page size by 64 or more times). 3) In addition to a data area, a page in NAND flash also contains a small spare OOB area which may be used for storing a variety of information such as the Error Correction Code (ECC) bytes, the logical page number and the page state. 4) An erase operation is required before writing in NAND flash. A floating-gate is charged during writing while only an erase can remove the charge from the gate. 5) NAND flash can withstand only a finite number of program-erase cycles (P/E cycles).
III-A Flash Translation Layer (FTL)
To use NAND flash devices, we need either a file system specifically for raw NAND flash or a Flash Translation Layer (FTL) between the file system and the raw flash device. Some of the example NAND flash file systems that have been added to Linux kernel are UBIFS [2] and F2FS [34]. On the other hand, the FTL is an intermediate software layer between the host application (e.g. file systems) and NAND flash. It accepts logical requests from host and maps the logical addresses (LBAs) to physical addresses of the NAND flash.
In addition to the logical-to-physical address mapping, a FTL is also responsible for some other necessary flash management duties such as wear leveling, garbage collection and so on. Wear leveling aims to smoothly distribute erases among blocks in the flash so that the blocks all reach their P/E cycle limit at the same time. Garbage collection is designed to efficiently reclaim pages that are no longer needed (i.e. invalid) in the device. Remembering that these pages cannot be simply erased at your leisure as they may be in blocks that still contain active data (i.e. valid). Instead, the FTL do the page recycle following these three steps: 1) adaptively select a victim block to be erased; 2) transparently move active data elsewhere; 3) erase the victim block.
According to how the logical-to-physical address mapping is performed, FTL schemes can be categorized into three groups: page-level FTLs, block-level FTLs and hybrid FTLs. The page-level FTL maps any logical page from the host to a physical page in the flash while the block-level FTL maps a whole logical block (containing multiple logical pages) to a physical block in flash. The hybrid FTL combines the page-level and block-level FTL by logically partitioning flash blocks into data blocks and log blocks. Data blocks are mapped with the block-level mapping while the log blocks are mapped using the page-level mapping scheme. Updates are written to log blocks, after which merge operations may happen to combine the active pages in data blocks and log blocks together as new data blocks. PEARL deploys a page-level FTL based on DFTL[16].
III-B Demand-based FTL (DFTL)
DFTL is an efficient page-level FTL that avoids the inefficiency of hybrid FTLs and reduces the SRAM requirement for the page-level mapping. The page-level mapping table is stored in the flash memory and only a small amount of active mapping entries are cached in SRAM. A data structure called Global Translation Directory (GTD) is used to keep track of the whole mapping table scattered over the flash device. Figure 1 shows the organization of DFTL.
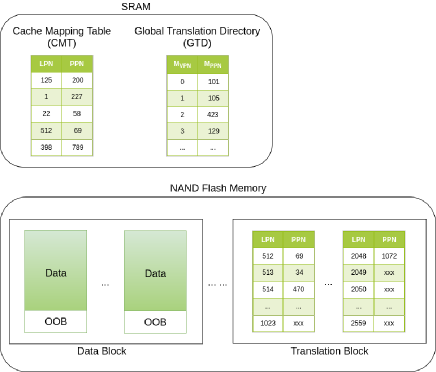
Logical-to-physical address translation
The address translation in DFTL is related to three data structures: the page-level mapping table, the Global Translation Directory (GTD) and the Cached Mapping Table (CMT). As shown in Figure 1, the page-level mapping table is packed into pages (named as translation pages) in the order of Logical data Page Numbers (LPNs) and stored in translation blocks in the flash. The CMT stores the mapping entries (LPN-to-PPN) for those most recently accessed data pages and updates them using the segmented LRU array cache algorithm [28]. The GTD maintains the physical page address information for all the translation pages. One translation page could store 512 mapping entries, if an address is represented in 4 bytes and the page size is 2KB. In this case, the first translation page with stores the mapping information for the first 512 logical pages and so forth, and the location of this translation page will be the first entry in the GTD. Both the CMT and the GTD are stored in the SRAM.
Once a logical request comes, the DFTL will first query the CMT for the mapping information. The request will be directly fulfilled if the mapping is found. Other wise, the DFTL fetches the mapping information from the flash into the CMT by the follow steps: 1) it checks the GTD for the physical location of the corresponding translation page; 2) it reads the translation page for the mapping and adds it into the CMT. A CMT eviction may happen during the above procedure. The evicted item needs to be written back only if it has been changed after loaded. This consists of 3 steps: 1) locate the corresponding translation page by consulting the GTD; 2) read the translation page and write it back to a new physical location with updated information. 3) update the corresponding GTD entry. After the coming logical request is performed, the mapping information may be updated if necessary. Note that it will be always updated in CMT. The update to the translation pages on flash will only happen if a CMT eviction happens.
Page allocation and garbage collection
In DFTL, data pages are written into data blocks whereas translation pages are written into translation blocks. DFTL maintains two blocks called Current Data Block and Current Translation Block for the page allocation. A free block will be chosen as the new Current Data Block or new Current Translation Block from a free block list when pages in either of the two blocks are used up. The garbage collector will choose the block with the least number of active pages as the victim to recycle. If the victim block is a translation block, DFTL copies the active translation pages to the Current Translation Block and update the GTD before erasing the victim block. Otherwise, if the victim is a data block, DFTL relocates the active data pages to the Current Data Block and update the corresponding mapping information in the CMT.
IV Model
In a typical scenario, a user requires secure data storage for sensitive hidden data (which needs to be protected from powerful adversaries), and less sensitive public data (which do not require any special protection mechanisms). The adversary is coercive and can compel the user to hand over encryption keys etc. Under duress, the user may need to reveal keys to public data while denying the existence of the hidden data. An effective PD system should therefore not only hide the contents of the hidden data but also its very existence.
Deployment
PEARL incorporates the PD functionality in the NAND flash FTL. Specifically, PEARL stores multiple logical block volumes on one physical flash device – some of the volumes store hidden data while others store public data. W.l.o.g., for simplicity, we discuss here a design with only two volumes. The data in the public and hidden volumes are encrypted with different encryption keys, and respectively. The keys may be securely derived from user-generated passwords or other more secure mechanisms.
PEARL can be used either in a public-only mode – in which case the user can only access public data – or in a public+hidden mode where the user can access both hidden and public data. To determine the mode of operation, the user provides appropriate passwords/keys at boot time (or when the device is plugged in after a reboot etc). For the public-only mode, the user provides ; to access also hidden data both and are required. Note that under coercion, the user will reveal to the adversary and operate in the public-only mode. As we will see, PEARL ensures that an adversary observing flash state does not gain a non-negligible advantage in detecting the existence of or of any hidden data.
When hidden data is stored on the device, PEARL should be operated in the public+hidden mode since the system running in public-only mode (without the hidden key) may overwrite hidden data (e.g., during garbage collection). As discussed later, hidden data is relocated before an ERASE during garbage collection. Without the hidden key, PEARL cannot re-encrypt and relocate this data to new locations. This is a common assumption for NAND flash PD solutions[41].
Adversary
When defining a threat model, it is important to also consider any hardware-related characteristics that may result in adversarial advantages. The PD adversaries we consider come with the following assumptions:
-
•
Although adversaries can coerce users into giving up encryption keys, they are computationally bounded and “rational” – they stop coercing users if no evidence of hidden data is observed.
-
•
Adversaries are aware of the underlying design of a PD system. In other words, the goal is not to provide security through obscurity. But at the same time, the mere presence of a PD system in the software stack will not serve as evidence that the user is hiding information. Ideally, once plausible deniability systems become efficient enough, they will be simply deployed in the standard OS codebase. Therefore, a flash device with PEARL will not be a red flag to the adversary.
-
•
Adversaries have ”multi-snapshot” capabilities and can access the raw image111The raw image of a devices is not hard to acquire. For example, in many SSDs, this can be easily achieved by opening the covers and directly reading the memory chips with cheap off the shelf readers. of a user’s NAND flash device arbitrary number of times. Note that existing work on flash-based PD systems considers a weak ”single-snapshot” adversary limited to only observing the flash memory once in its lifetime.
-
•
Adversaries can access the physical device only after it is unmounted or powered off [5] (these are commonly denoted as “on-event” adversaries). Thus, the running state of the device and the DRAM contents cannot be captured by the adversary. Indeed, otherwise in the presence of an online adversary capable of monitoring user I/O and device state at runtime, arguably it would be close to impossible to provide strong plausible deniability.
Note that as is the case with all existing PD solutions, PEARL does not protect against denial of service attacks. Specifically, the adversary can overwrite all hidden or public data on disk.
V Hiding Data Using WOM Codes
PEARL hides information by modulating the written public data according to the data to be hidden. As we will show, this is something that WOM codes can be re-purposed for. The end-result of hiding information is a device state that is indistinguishable from the case of a device that was simply writing data multiple times using a WOM code. In this section, we show how it is indeed possible to design such a data encoding scheme by leveraging a special group of write-one-memory (WOM) codes.
V-A Overview
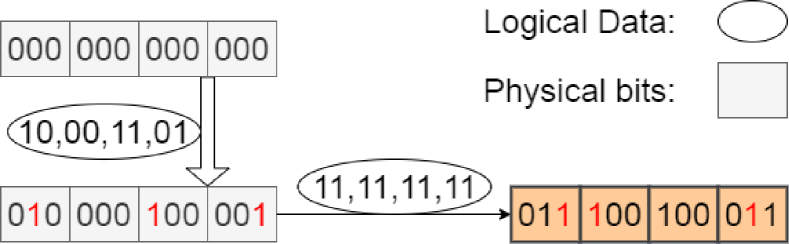
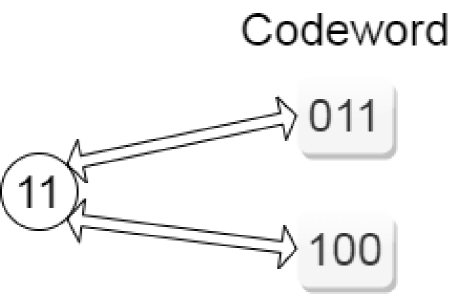
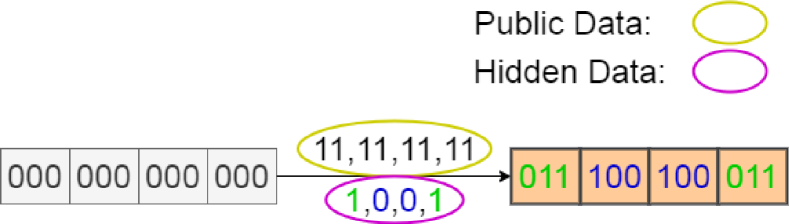
The key idea in PEARL is to store both public data and hidden data in the same physical locations using a special data encoding scheme that renders a sequence of bits encoding public + hidden data bits indistinguishable from a sequence of bits only encoding public data. Before detailing the data encoding scheme used in PEARL, we provide an example to demonstrate how WOM codes can be used to indistinguishably encode hidden data (Figure 3).
WOM codes (details in Section V-B) are special data encoding schemes that allow multiple writes to the same locations of write-once memory by writing to some of the yet-unwritten-to bits (from 0 to 1).
A WOM code (Table I) allows the same physical bits to be written to multiple (e.g., two) times. In Figure 3(a) two consecutive writes of different data ( followed by ) can go forward in the same underlying physical locations. The end physical state is . This is possible because (Figure 3(b)) the WOM code allows data to be represented by either and underlying bit configuration (“codeword”). In the context of flash devices, WOM codes are used to increase the amount of data you can write to a block before it is erased.
Our newly proposed data encoding scheme in PEARL writes public data once but chooses the codeword used based on the bits of the data to hide. This enables it to sureptitiously hide information even in the presence of a powerful multi-snapshot adversary.
For example, as illustrated in Figure 3(c), since the first hidden bit is “1”, “011” is written to the underlying physical cells for the first two public data bits “11”. On the other hand, the second hidden bit is “0”, and in this case “100” is written for the second two public data bits “11”, etc. The resulting final physical state hiding bits is the same () as the physical bits in Figure 3(a) resulting from two innocent writes. An adversary observing this final physical state cannot tell whether it is the result of two innocent sequential public writes as in 3(a) or of an information hiding operation as in 3(c). In other words, it simply cannot distinguish the two cases with any non-negligible advantage and thus determine whether any hidden data exists.
It is clear from the example above that WOM codes have certain desirable properties that could provide opportunities for a data encoding scheme hiding hidden bits in a public cover. However, designing a general purpose data encoding scheme based on WOM codes that enables data hiding and is secure against a powerful adversary is not trivial. Specifically, as we discuss later, (e.g., because of device state biases interfering with indistinguishability and more), not all WOM codes can be used to build suitable data encoding schemes and not all data encoding schemes derived from WOM codes can be re-purposed for data hiding securely. Therefore, we first need identify what types of WOM codes can be re-purposed for our goals and then build a data encoding scheme accordingly.
We start with an introduction of WOM codes in Section V-B. Then we demonstrate the feature of a special group of WOM codes – WOM codes supporting a 1st partition – that can be used to encode hidden bits within public messages in Section V-C. After that, we propose our strategy to convert a WOM code to a hidden data encoding scheme in Section V-D. Finally, we show that not all hidden data encoding scheme based on WOM codes can ensure the deniability of the existence of hidden data, and propose a WOM code that can be indeed re-purposed for PD in the presence of a powerful adversary.
V-B Write-Once Memory Code
Write-once memory (WOM) was first introduced in 1982 by Rivest et al. [44] and models a storage medium consisting of (binary) cells which can transition from a “zero” state to a “one” state only once. WOMs are written to using WOM codes, I/O schemes designed for this invariant. The WOM model was then generalized [11, 10] for storage media cells with more than two possible states. Further, “t-write WOM codes” are WOM codes that can write additional information into the same group of WOM cells multiple () times. The number of bits that can be written on the each write does not need to be the same.
For simplicity and without loss of generality, WOM codes with two states only are used in the rest of the paper. Further, for consistency, initial states of NAND flash cells are considered to be “zero” even if in many chips, empty NAND flash pages physically contains all bits of 1.
It is important to note that physically, NAND flash memory features the WOM invariant. Indeed once a flash page is written, its unwritten cells (only) can accept a second write cycle. Several studies propose WOM codes for lifetime extension by reduction in SSD block erasures [52, 4, 21, 22].
| Data bits | 1st write | 2nd write |
|---|---|---|
| 00 | 000 | 111 |
| 01 | 001 | 110 |
| 10 | 010 | 101 |
| 11 | 100 | 011 |
Table I shows a WOM code example that allows twice the encoding of different configurations of 2 information bits using only 3 physical storage cells/bits. As per the WOM invariant, the 3 physical cells only change from 0 to 1 in both writes (the initial bits are considered to be before any write). For example, if the 2 bit message that needs to be written in the first cycle is , will be physically written to the 3 storage cells. A subsequent 2 bit message will result in a second physical write of . As can be seen, this requires a single change: the first physical cell needs to be set as 1 in the second write (). This elegantly enables in-place updates. Changing into would not have been possible in NAND flash without an expensive ERASE operation which significantly reduces lifetime and increases latencies.
Note that at first glance, it may seem that all the 3 physical cells/bits would change when the 2 bit message remains the same (e.g. ) for both 1st and 2nd write. This is actually not the case. Since both and represent message after the 2nd write, no physical bits need to be set.
Further note that the physical bits written in the second write are context dependent. They relate not only to the message itself but also to the existing data in the written cells. This mandates a read before the second write to perform the encoding correctly. Fortunately, NAND flash reads are much faster than ERASE operations.
V-C WOM code supporting a 1st partition
Notations
“t-write WOM codes” are WOM codes that can write additional information into the same group of WOM cells multiple () times (named “1st write, 2nd write”, … ) before requiring an ERASE. Each write requires a read of the existing physical state context, a proper encoding of the new logical data (“message”) using this context, and finally a physical write of the encoded result. The logical message encoded in the 1st write is called “1st message” and the encoded result is called “1st WOM write codeword’, and so forth. For the sake of simplicity, and w.l.o.g. we consider only 2-write WOM code which has the same message space in both writes in the rest of the paper.
Let – where and – denote the WOM write codewords of a n-bit WOM code. For example, for the WOM code example in Table I, we have .
For any two elements , the relationship is defined by the condition that for all , where is the -th bit of . This is related to the fact that an unset flash bit can be easily set without requiring a page ERASE but not vice-versa. Then, a general definition for a 2-write WOM code can be given as follows [51]:
Definition 1 (2-Write WOM Code).
A 2-write WOM code, denoted as -, is an encoding scheme with message space and codeword space consisting of four algorithms that satisfy the following properties:
-
1.
:
-
2.
: , and for all
-
3.
: , and for all
-
4.
: , and for all
Informally, for the 1st write, any message is associated with a unique WOM write codeword. The 2nd write is a bit more tricky since the 2nd WOM write codeword to be written depends not only on the 2nd message but also on the existing data (1st WOM write codeword) present in that location. Different values may end up being written i.e., may be different from for . As a result, one message could be represented by more than one possible WOM write codeword after the 2nd write. For example, wrt. Table I, the message is always written as in the 1st write, but in the 2nd write it may be represented as either , if the 1st written message was , or otherwise.
may have many different forms. We discovered multiple WOM codes that can represent a message using multiple WOM write codewords in the 2nd write. Our insight then is to use this degree of freedom in the choice of the WOM write codeword in the 2nd write to encode hidden information sureptitiously. For example, two WOM write codeword choices enable the encoding of one hidden bit. Generally, a choice of WOM write codewords allow the encoding of hidden bits. A simple encoding convention would be that using the -th WOM write codeword choice indicates an encoded hidden value of .
In the rest of this paper, for simplicity, and w.l.o.g. we consider WOM codes with two choices only, i.e., which can encode one hidden bit through the encoding of each bit (public) message. These WOM codes have the following properties: (i) each message can be mapped to 2 WOM write codewords in the 2nd write, and (ii) each codeword is corresponding to a few 1st WOM write codewords. We call these WOM codes WOM Codes Supporting A 1st Partition:
Definition 2 (WOM Code Supporting A 1st Partition).
Let denote the set of all 1st WOM write codewords for all possible messages, i.e. . Consider also a partitioning function which on input , outputs two sets and , forming a partition of , namely and .
Then, a - code is said to “support a 1st partition” if:
| (1) |
where and are the 1st and 2nd output of , respectively and and are valid WOM code-specific functions that map input messages to WOM write codewords in .
Note that for a valid 2-write WOM code – which requires – we must have for any and for any .
Specifically, we call a WOM code supporting a 1st partition where for all , a WOM code supporting an equal partition.
Table I illustrates a WOM code supporting a 1st partition, but not an equal partition. Consider . For each message , , and , and are the WOM write codewords in the row corresponding to message where is in the second column and is in the third column. It can be seeen that and for any message . Thus, the WOM code does not support an equal partition.
As we will see later, the ability to support an equal partition enables the design of a plausible deniability mechanism in which the resulting distribution of the written bits does not leak information about the encoded hidden data.
V-D Hidden data encoding scheme
Hidden data encoding
As discussed above, for a WOM code supporting a 1st partition, encoding a “hidden” data bit within a -bit “public” message can be achieved by using the bit to decide on the choice of WOM write codeword to write in the 2nd write.
Then, more generally, the written data is a function of both the public message and the hidden message . Further as we will see, there exists a relationship between the existing data and the resulting encoding.
We call the encoded result the “full write codeword’ and the write of the full write codeword is called a “full write” to distinguish it from a 2nd write of a public-only message. Then, the corresponding simplified encoding function is:
| (2) |
As mentioned earlier, for simplicity, and w.l.o.g. we consider WOM codes with two 2nd WOM write codewords choices only (as in equation 1), i.e., which can encode one single hidden bit with each bit (public) message.
Unfortunately there are no free lunches and, as will be detailed later, the full write codeword can only be written to empty pages with all 0s. In other words, one page cannot be written-to twice anymore. Effectively, the hidden bit is encoded at the cost of the ability of the WOM code to accept additional information before the next ERASE.
Note that one of and are written regardless of the existing data . And, as discussed above, for a valid 2-write WOM code – which requires – we must have and for all possible . This is only possible if the existing data is all 0s, i.e., the encoding works only on empty physical pages, and pages can only be written once before requiring an ERASE.
| Data bits | 1st . write | 2nd write | |
|---|---|---|---|
| Hidden 0 | Hidden 1 | ||
| 00 | 000 | 000 | 111 |
| 01 | 001 | 001 | 110 |
| 10 | 010 | 010 | 101 |
| 11 | 100 | 100 | 011 |
Table II adds the hidden bit encoding cases to the WOM code in Table I. Between ERASEs, 3 flash cells can be written to either: (i) twice with 2-bit public messages or once with a 2-bit public message and a 1-bit hidden message.
The first case corresponds to public-only operation in which the same set of cells can be reused for a 2nd write between ERASEs and the second case corresponds to the case of hidden operation in which hidden messages are to be encoded plausibly deniable.
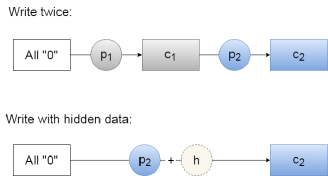
The first case corresponds to a sequence of public writes, e.g., an initial write and subsequent updates to the same location. Starting with an empty page (e.g., of 3 bits for simplicity), a public message can be written into an empty page firstly (as ) in a 1st write (Figure 4). The encoding used is defined by columns 1&2 in Table II. A subsequent public message can be written to the same page (as ) in a 2nd write. Columns 1,3 and 4 in Table II determine the final written state, as a function of 1st WOM write codeword . Note that after the 2nd write the first public message will not be available any more. Only can be decoded from .
In the second hidden operation case, both public () and hidden () messages determine the encoding that gets written () in a full write. is determined by columns 1,3, and 4 of Table II. Once written, both and can be decoded from .
V-E WOM coding & PD
0-1 Distribution Skew
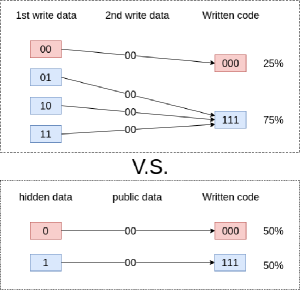
While a step in the right direction, the proposed hidden data encoding results in a bias in the distribution of 1s and 0s in the written data when compared to a public-only operation. This can then be used e.g., by a multi-snapshot adversary to distinguish devices that contain hidden information from devices that do not.
Figure 5 shows a simple example of this bias for the example WOM code in Table II. Consider a 2 bits public message . In public-only operation mode, the message is written in a 2nd write, and the 2nd WOM write codeword will be if the 1st message residing there was , or if 1st message there is either , , or . If the 1st message written is overall uniformly distributed, the ratio between the occurrence of to in the public-only operation storage device should be 1:3.
However, in the case of a hidden operation, the full write codeword ends up being for a hidden bit of , or for a hidden bit of . Thus, for an overall uniformly distributed hidden message, the ratio between the occurrence of to in the storage device will be 1:1.
Given this bias, an adversary can do statistic analysis based on the public data on the storage data and observe a difference between the expected and observed distribution of 0s and 1s.
A counter-argument to be made is that the public operation mode was considering the case of two writes, and in practice numerous pages may end up being written only once. This may be true, however, given the existence and benefits of the WOM encoding in the system, it is reasonable to expect that in many cases, the device converges to a state where most cells have been overwritten at least once. Also, while it is true one can plausibly claim the bias was inherent in the data itself, the security argument is weakened overall.
WOM Code Supporting an Equal Partition
Thus, the question inevitably arises: can we do better? How can we overcome this bias? The answer is WOM codes supporting an equal partition.
To see why that is the case, consider that the bias comes directly from the difference in the probability distribution of 2nd WOM write codeword and full write codeword. Reusing the same group of WOM write codewords in the 2nd write for the hidden data encoding ensures that the 2nd WOM write codewords and full write codewords are indistinguishable by inspecting the individual codes. It is an overall probability distribution that may give the existence of hidden data away.
Note that the probability distribution of 2nd WOM write codeword depends on the number of elements in sets A and B (see equations 1 and 2), while the probability distribution of full write codeword is decided by the distribution of hidden bit . And, since hidden data in a PD system is highly likely to be encrypted, ends up uniformly distributed.
To eliminate the bias, sets A and B need to contain the same number of elements for any arbitrary messages. In other words, the WOM code needs to support an equal partition.
Lemma 1.
The hidden data encoding scheme based on a WOM code supporting an equal partition ensures that an adversary cannot distinguish the 2nd WOM write codeword that encodes public message from the full write codeword that encodes both public message and hidden message .
| Data bits | 1st write | 2nd write | ||
|---|---|---|---|---|
| Hidden 0 | Hidden 1 | |||
| 0 | 000 | 00000 | 11110 | 10011 |
| 1 | 001 | 00001 | 11001 | 10110 |
| 2 | 010 | 00010 | 11010 | 10101 |
| 3 | 011 | 00100 | 11100 | 01111 |
| 4 | 100 | 01000 | 11111 | 01101 |
| 5 | 101 | 10000 | 11101 | 01110 |
| 6 | 110 | 11000 | 11000 | 10111 |
| 7 | 111 | 10100 | 11011 | 10100 |
Table III defines a WOM code supporting an equal partition. For public operation, it allows writing 3 bits of data twice to 5 storage cells. In hidden operation, 1 hidden bit and 3 public bits can be encoded together in 5 storage cells.
One invariant for this code is that for each 2nd WOM write codeword in the “2nd write” column (sub-columns 3 and 4), there exist four 1st WOM write codewords for which , i.e., that can be overwritten to get to . In other words, the size of the sets A or B in this WOM code is 4.
For example, considering and – both of which can be used to represent public message in a 2nd write during public operations – the corresponding set is , composed of the 1st WOM write codewords for messages . Similarly, set is composed of the 1st WOM write codewords for messages . As a result, both and are equally likely to appear in the written device state – for either public and/or hidden operation modes.
Based on the WOM code in Table III, we design PEARL, a plausibly deniable FTL that securely processes the I/O request from the upper layers, manages the unavoidable inherent mappings from logical to physical pages and reclaims pages occupied by the obsolete data. More importantly, PEARL ensures that adversaries cannot detect the existence of hidden data by probing multiple device snapshots.
VI Security Requirements for PEARL
The hidden data encoding scheme presented in Section V ensures that physical pages containing both public and hidden data are indistinguishable from pages containing public data written as 2nd WOM write codewords. However, turning it into a workable PD solution that can protect hidden data from the coercive adversary described in Section IV requires extra work. Specifically, a multi-snapshot adversary can observe not only the state of individual pages, but also state changes across multiple snapshots. Generally speaking, over time, an adversary can learn (1) what kind, and (2) where page state transitions happen. A plausibly deniable FTL needs to ensure that this information does not leak the existence of hidden data.
This is made even more difficult by internal characteristics of NAND flash for which page state transitions are not independent from each other. For example, data updates are performed via an out-place scheme rather than an in-place scheme (updated data is written to a new location rather than where the old data resides). As a result, pages where the up-to-date data is written becomes valid while at the same time the page where the outdated data resided becomes invalid.
To mitigate this, we first explore the page states and the page state transitions in the case of deploying the WOM code. We then introduce key requirements for a secure plausibly deniable FTL. Finally, we provide an efficient solution. The idea is to smartly “cloak” hidden data within plausible public data so that the hidden data induced page state transitions can be plausibly explained as a result of public requests.
Page States
NAND flash contains three types of pages: empty, valid, and invalid. A “valid” page contains active data, whereas an “invalid” page’s data is obsolete and can be erased.
In the case of a 2-write WOM code, NAND flash pages can be categorized at a finer granularity. Firstly, based on their current encoding, pages can be categorized as either “1st write” or “2nd write” pages. 1st write pages contain only public data while 2nd write pages may contain both public data and hidden data. Note that in this case, a page storing both public data and hidden data is still called a 2nd write page although the page is literally written only once.
Secondly, a page can be either valid or invalid depending on the status of the data stored inside. However, since the public data and hidden data in the same page may have different status we need to further distinguish things. We use “up-to-date” and “out-of-date” to indicate data status. Then, since the existence of hidden data should not be exposed to adversaries, a page is denoted as valid as long as the public data there is up-to-date, regardless of whether any hidden data coexists or whether the hidden data is out-of-date. Note that a valid page may contain out-of-date hidden data while an invalid page may contain up-to-date hidden data.
Thus, in summary, a page can be in any of the 5 states: empty, 1st write valid (V1), 1st write invalid (I1), 2nd write valid (V2), and 2nd write invalid (I2). Each physical page transitions between the 5 states directly or indirectly. There may be more than one possible reason for a page to change from one state to another. For example, an empty page may be turned into a V2 page directly because of a full write (defined in Section V), or it can become a V2 page indirectly by first being a V1 page, then an I1 page and finally a V2 page. Thus, the first requirement is shown as Requirement 1.
Requirement 1.
The presence/absence of hidden data is never the only possible reason for a page state transition. Note that a hidden data encoding scheme based on a 2-write WOM code is designed to intrinsically guarantee this.
Figure 6 depicts the page state transition graph for the above 5 states. Transitions are triggered by either the logical requests from the host or the built-in functions of the NAND flash (e.g., garbage collection). Public data can be written to either an I1 page or an empty page, resulting in a V2 page or a V1 page, respectively Hidden data can only be written to an empty page under a cloak of some public data. This is depicted as a full write that transitions a page from state empty to state V2 directly. Garbage collection brings all the pages in a target block back to state empty by an ERASE operation. Before erasing, the up-to-date data in those pages need to be relocated elsewhere, while the state of the page may transition from V1 to I1 or from V2 to I2. Other operations that render data out-of-date include logical data updates and the TRIM operation.
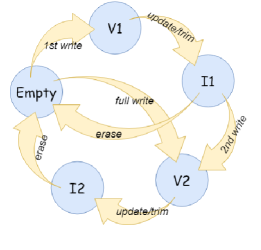
Figure 6 illustrates the fact that a page can transition freely from one state to another independently of the existence of hidden data – all page state transitions can be plausibly explained by public data operations.
Moreover, the plausible public data that can be used as the “cloak” is not unique and in fact has quite a bit of entropy. For example, as Figure 4 depicts, writing hidden data + public data ends up being the same as writing public data + . As the 1st WOM write codeword is completely overwritten by the 2nd WOM write codeword, a relatively large set of public data messages can be plausibly provided as a candidate for . For a WOM code supporting an equal partition and pages contain bits, there are possibilities for .
More specifically, as an example, consider a physical page of 10 physical bits. In PEARL the page can contain 6 bits of public data and 2 bits of hidden data. If the observed physical page data , then and according to Table III. An attacker obtaining a snapshot aiming to determine the value of public data can at most know is that the first 3 bits of are a value in set (the messages corresponding to WOM write codewords in set ) and the last 3 bits of are a value in set (the messages corresponding to WOM write codewords in set ). As a result, has 16 () possible values in total. In reality, a larger page with more physical bits (e.g. bits) results into many possibilities (e.g. ). For further security, this can then be used to select the most semantically plausible values of , e.g., by selecting marching terms from an English dictionary.
Page Operation Priority
The WOM code based hidden data encoding scheme ensures multi-snapshot adversaries cannot tell whether hidden data exists or not by observing state transitions of any single physical page. However, by observing aggregated state transitions of a set of pages over time, it may still be possible for an adversary to detect the existence of hidden data according to where page state transitions happen (which page is written to and which page is erased).
For example, if pages containing up-to-date hidden data have a lower ERASE priority during garbage collection compared to pages containing no hidden data, an adversary could tell whether the hidden data exists through the order in which physical pages get erased. Thus, a second requirement can be concluded as Requirement 2.
Requirement 2.
The priorities assigned to blocks according to which they are erased during garbage collection is not be related to the location, state or existence of hidden data.
Moreover, as illustrated in Figure 4, hidden data in a 2nd write page can be plausibly denied as a sequence of public operations: written to an empty page, and written to an I1 page. Solid reasons should exist to justify why is not written to any other I1 page and is not written to any other empty page etc. This derives the Requirement 3.
Requirement 3.
The presence/absence of hidden data is never the only possible reason for the presence of any public data in a 2nd-write page.
Fulfilling this requirement 3 efficiently is related to how writing priorities for empty pages and I1 pages are defined in an FTL (more details in Section VII).
Note that in order to maximize writing capacity and minimize wear/ERASE cycles, normally I1 pages usually have higher priority to be written to. Otherwise if empty pages are written first, then an I1 page may be erased before the 2nd write happens to it, which is a waste of writing capacity.
VII PEARL Design
PEARL is a FTL that satisfies all the security requirements introduced in Section VI. It is designed based on DFTL (Section III-B). In this section, we firstly describe in detail the data structures used for logical-to-physical address translation and the page allocation mechanism. Based on them, we then introduce how PEARL deals with the public and hidden requests from the host and reclaims the obsoleted pages with garbage collection.
VII-A Address Translation
PEARL manages the logical-to-physical mapping for public data and hidden data separately. Similar to DFTL (Section III-B), two layer page-level maps are used. The public data is managed by a public global translation directory (GTD) plus a few public translation pages, while the hidden data is mapped with a hidden GTD in addition with some hidden translation pages. The hidden GTD is stored in the SRAM together with the public GTD. If no power loss protection is built into the flash device, GTDs may get lost during sudden power loss, but can always be recovered by a full device scan. Furthermore, storing GTD on nonvolatile storage aids recovery from power-failure [46].
Translation pages are stored in the flash. Unlike in the case of DFTL, both translation pages and data pages are stored in the same group of blocks. The public translation pages are encoded as public data, while hidden translation pages are encoded as hidden data.
A cached mapping table (CMT) is used to cache the recently-used mapping information for both public data and hidden data. The corresponding public or hidden translation page will be updated in memory whenever any mapping entry is evicted from the CMT.
VII-B Page Allocation and Garbage Collection
Page Allocation
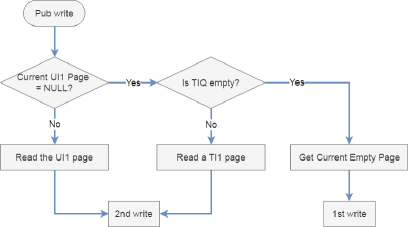
PEARL uses three variables to track candidate pages for writing: a Current Empty Page, a Current UI1 Page, and a TI1 page Queue (TIQ). UI1 pages are I1 pages caused by logical data updates. Whenever the public data in a V1 page gets updated, rather than updating in place, the up-to-date data is written to another page and the V1 page becomes a UI1 page. TI1 pages are I1 pages resulting from TRIM operations that delete data. The deleted data in a TI1 page does not have corresponding up-to-date data in any other pages of the device. We distinguish UI1 from TI1 pages since an adversary can infer when a UI1 page becomes invalid with only one device snapshot (detailed later and in Figure 8). Finally, a free block list (FBL) is used to track empty blocks in the device.
In PEARL UI1 pages have the highest priority to be written to. As a result, since they always get written to first, there ends up being at most one UI1 page in the device, tracked by the Current UI1 Page record. Further, TI1 pages have a higher priority than empty pages to be written to. Overall, public data will be written to an empty page only if the Current UI1 Page is NULL and the TIQ is empty. Figure 7 illustrates the page allocation rule for public data.
In contrast, it should always be the Current Empty Page that is allocated for a hidden data write. This makes it possible for an adversary to infer whether a 2nd write page contains hidden data by inferring whether there exists any I1 page (either UI1 or TI1) when the 2nd write page is written to. Moreover, UI1 pages impose different threats compared to TI1 pages, which can be illustrated with Figure 8 as follow.
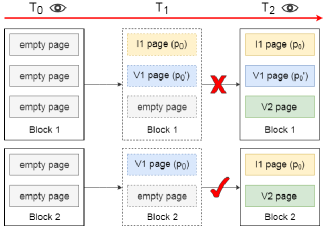
For a UI1 page that becomes invalid before any hidden data is written, an adversary would always know that it is invalid when the 2nd write page is written to. This is straightforward if the adversary can observe the UI1 page before writing the 2nd write page. Besides, the example of block 1 in Figure 8 explains that this is also true even if the adversary can access the device only after the hidden data is written.
The upper half of Figure 8 lists snapshots of block 1 over time. The adversary observe the block at time and . All three pages are empty at time . And they are in state I1, V1 and V2, respectively at time . The I1 page is a UI1 page as it contains the obsoleted data whose corresponding up-to-date data is in the V1 page. Based on the two snapshots, the adversary can infer that: 1) the first page must be a I1 page right after the second page is written to; 2) the third page should be still empty at that time (since pages in one block are written in order). Thus, the adversary can infer (although not directly observe) that there must exist an intermediate state where the there pages are in state I1, V1 and empty, respectively, which is depicted as the snapshot at time . In this case, hidden data becomes the only possible reason for public data to reside in the V2 page rather than the I1 page in time .
On the contrary, an adversary cannot tell whether a TI1 page becomes invalid before or after any hidden data is written as long as she cannot observe the TI1 page before the hidden write happens. This can be demonstrated with the example of block 2 in Figure 8. Similarly, the adversary takes the snapshot at time and . Then she observes the state transition empty I1 in the first page, and the state transition empty V2 in the second page. The only intermediate state she can infer is that the first page was written to be a V1 page at certain time . After that, the adversary has zero knowledge about whether the V1 page is invalidated first or the empty page is written first. Thus, it is completely possible for the second page to be the V2 page at time without any hidden data, as long as the second page is written before the first page becomes invalid.
Thus, to mitigate the possible leaks caused by I1 pages, two tweaks are used regarding the UI1 page and TI1 page: (i) before writing any hidden data, the Current UI1 Page is filled with public data; and (ii) all TI1 pages in the TIQ are written to (with public data either from user requests or from the block with the least number of valid pages) before on-event adversaries are allowed to take a snapshot. These prevent adversaries from detecting the hidden data by analyzing page allocation patterns.
Garbage Collection
PEARL tags the least active block(s) (with the least number of valid pages) as the next victim block(s) for garbage collection. As detailed in Section VI, the status of a page – valid/invalid – is independent of the existence and status of hidden data stored in that page. Thus, the selection of victim blocks does not leak any information to the adversary regarding the presence of hidden data.
Once a victim block is selected, PEARL first checks whether the Current UI1 Page is in the victim block. If yes, the Current UI1 Page is set to NULL. Then all the TI1 pages in the victim block are extracted from the TIQ. These two actions prevent data from being written to a block that will be erased soon. Then, up-to-date public and hidden data in the victim block are relocated to new pages using the same mechanism that is employed during write requests.
Specifically, the hidden data in the victim block (if any) can be encoded and written to empty pages together with certain public data, which comes from either the victim block or a new public write request. As a result, the hidden data that is stored with public data that is subsequently deleted is not lost.
Moreover, as hidden data are re-encrypted (semantically secure, randomized) during relocation, an adversary cannot link a particular hidden data to a public data it is stored with before and after garbage collection. In effect, deleting public data stored in a particular page does not impact the security and consistency of the hidden data within.
VII-C I/O Operations
Common Interface for Public and Hidden Data
As discussed in Section IV, PEARL supports both public and hidden data requests. However, crucially, PEARL does not require different interfaces for accessing public and hidden data. Instead, PEARL separates hidden data requests from public data requests by a simple offset convention. Hidden data requests (received through the unchanged FTL interface) address an offset beyond the physical standard device capacity. This signals to PEARL that these requests are addressed to the hidden volume.
Note that an adversary attempting to access hidden data through this interface would have to provide the correct password at boot-time. Otherwise, the system will be unable to decrypt hidden data. As a result, simply having access to the same interface does not provide any advantage to the adversary in detecting the presence of hidden data.
Preprocessing
Upon receiving I/O requests from upper layers, PEARL divides the incoming requests into page-level requests first, which are then executed individually. To execute these requests, the first step is a logical-to-physical address translation. PEARL first looks up the logical page address in the cached mapping table CMT. If no hit, either the public or the hidden GTD is queried for the location of the corresponding translation page which contains the target physical page mapping entry which can be used to access the page. The mapping is then also cached in the CMT. If this requires a cache eviction, the least recent used entry will be evicted, resulting an update to its corresponding translation page on the device. And if there is any other mapping entries which belong to the same translation page in the CMT, those entries will be written back to the device simultaneously. It is important to note that the (either public or hidden) translation pages are written just like actual (public or hidden) data pages.
Public Write
In the case of a public write, after the address translation, PEARL identifies one page for the public data based on the page allocation algorithm in Figure 7. The public data is written to the page following the WOM code based encoding scheme. If the logical address was originally mapped to a valid V1 page (the write request is an update to existing data), the page now transitions to UI1 status and is set to be the Current UI1 Page. If the logical address was originally mapped to a TI1 page, the page is deleted from the TIQ and then set to be the Current UI1 Page. Finally, the mapping entry is cached in the CMT accordingly.
Hidden Write
Hidden page writes require public data to “cloak” in: first valid page in the least active public data block. This can then be explained as a simple garbage collection related data relocation. Similarly to the other cases, the corresponding public data mapping information is cached in the CMT. The hidden and the public data are then encoded and written to the Current Empty Page and the CMT is updated accordingly. Finally, the Current Empty Page then becomes the next page in the same block, or the first page of a new empty block if the original Current Empty Page was the last page of a block. The new empty block is selected from the FBL.
TRIM
For either a public or a hidden page TRIM request, the deleted data is marked as out-of-date. If the deleted public data was in a V1 page, the page is pushed to the TIQ.
Power Loss
Power-loss recovery is not described in DFTL. For simplicity, we assume the physical device comes with standard enterprise grade power loss protection (PLP) backed by capacitors that power up the device for enough time to guarantee caches and other memory resident data structures can be flushed to disk. PEARL adds to standard PLP the requirement to write our hidden and public GTDs on power loss also. We also note that if PLP is not available, all data structures can be reconstructed by traversing the entire disk.
Encryption
Before encoding, public data and hidden data are first encrypted with different keys using AES-CTR with random IVs. As hidden and public data share physical pages, they can also share the IV in the OOB area of each page.
VIII Security Analysis
The aim of this Section is to show that both the hidden data content and operations are protected from a multi-snapshot on-event adversary. The general idea is that anything that happens between snapshots is a combination of operations. It is then sufficient to show that each such operation does not provide any advantage to a polynomial adversary.
Specifically, we show that any hidden operation leaves the device in a state indistinguishable from a state resulting from a plausible set of public operations. Then, if all operations are sequential, the effect of any combination thereof (whether or not they include hidden operations) can be explained by a plausible set of public operations.
Theorem 1.
A computationally-bounded adversary cannot distinguish a physical page containing both public data and hidden data from a page containing only public data written as 2nd WOM write codewords.
Proof (sketch):Lemma 1 in Section V shows that by construction the encoding scheme prevents an adversary from distinguishing a page containing full write codewords (containing hidden data) from a page containing 2nd WOM write codewords.
Furthermore, hidden data is encrypted using a semantically-secure randomized cipher. Adversaries can certainly interpret all the pages containing 2nd WOM write codewords as hidden data based on the encode scheme, but all she can get will be the encrypted hidden data, indistinguishable from random.
Thus, a physical page containing both public data and hidden data is indistinguishable from a page containing only public data written as 2nd WOM write codewords. ∎
Lemma 2.
For any page state resulting from writing hidden messages (either hidden data or hidden mapping table) to an empty page, there exists at least one sequence of public operations that results in the exact same state.
Proof (sketch):Any hidden message is always written together with some public message (Figure 4) to an empty page, resulting in a page state transition from empty to V2. As shown in Section VI, this page state transition can be plausibly explained as the combination of a sequence of page state transitions (empty V1 I1 V2). Moreover, there exists at least one public operation that can result in each of those page state transitions for the same physical page.
The page state transition empty V1 can be explained by writing some public message . Remember that values are not unique and can be chosen from (Section VI) values. The V1 I1 transition can be plausibly explained as updating or deleting . Finally, recall that was relocated from the block with the least number of valid pages. This transition I1 V2 can be plausibly explained as a garbage collection relocation operation.
The mapping entry for the plausibly appearing public (Figure 4) will not be updated on the device until it is evicted from the CMT. Thus, it is highly possible that this mapping entry change does not need to be flushed out to the device (the mapping entry may be updated again before that), as was already out-of-date when was written.
In summary, the results of writing hidden messages to an empty page can be plausibly explained by a series of public operations. ∎
Theorem 2.
Any page state transition resulting from either a hidden read operation or a hidden trim operation can be plausibly explained by at least one sequence of public operations.
Proof (sketch):As described in Section VII, for either a hidden read or a hidden trim, the only possible state change in the device happens when a mapping entry is evicted from the CMT. In this cases, there are two possibilities. (1) the evicted mapping entry is a hidden entry – in that case a hidden translation page needs to be updated (recall it is treated as a hidden data page) – and according to Lemma 2, the resulting page state transition can be plausibly explained as the result of a sequence of public operations. Or (2) the evicted mapping entry is a public entry – in that case a public translation page needs to be updated – and this can be plausibly explained using public operations only. ∎
Theorem 3.
Any page state transition resulting from a hidden write operation, can also be plausibly explained by at least one sequence of public operations.
Proof (sketch):A hidden write operation writes the hidden data and updates the corresponding mapping entry. The map update happens in the CMT and will be later flushed to the device during a hidden translation page write when a cache eviction happens. As proved in Lemma 2, writing either the hidden data or the hidden translation page can be plausibly explained with several public operations. ∎
Theorem 4.
Any page state transitions resulting from a garbage collection operation can be plausibly explained by at least one sequence of public data operations.
Proof (sketch):This follows by construction. First, note that PEARL select the victim block (the block to be erased) for garbage collection only based on the state of public data in flash devices – the presence/absence of hidden data has no impact on this selection. Moreover, page transitions happen only because up-to-date data in the victim block is relocated to new locations. All data relocations are handled in the same way as new public/hidden data write requests – PEARL employs the I/O operations discussed in Section VII-C to complete these requests. Therefore, by leveraging Theorem 3, we can show that the resulting page state transitions from the hidden write operations performed after a garbage collection can be plausibly explained by a sequence of public operations. ∎
IX Practical Concerns
Crypto Primitive
To ensure PD, both the public and the hidden data encoded with the WOM code must appear to be indistinguishable from cryptographically secure random data. Thus, before encoding, public data and hidden data are first encrypted (semantically secure, randomized) with different keys in PEARL. Considering the special application scenario of disk encryption, crypto primitives used in PEARL implementation must be chosen carefully. For example, when a block cipher mode requiring an initialization vector (IV) is used, each page is usually assigned with a page-specific random IV to enable random access. These IVs must be easily derived from or stored in the storage system. Reusing an IV may result into a catastrophic loss of security. There are a few special purpose block encryption modes that are specifically designed to securely encrypt sectors of a disk, such as the tweakable narrow-block encryption modes (LRW, XEX, and XTS) and the wide-block encryption modes (CMC and EME). The application of these modes of encryption can prevent attacks such as watermarking, malleability, and copy-and-paste, which is critical for PD as a weak encryption system can amplify an adversary’s advantage and enable easy detection of hidden data.
Storage Capacity
The use of WOM codes in PEARL amplifies the size of data because a single logical bit is now represented by multiple bits in storage. Therefore, as expected, the overall logical storage capacity (the total amount of logical data that can be written) of the device reduces. We analyse the extent of this reduction in Section X. However, critically, it is worth noting here that logical storage capacity for public data is not impacted by the amount of hidden data stored in the device. In other words, an adversary cannot detect whether hidden data is being stored with any non-negligible advantage.
Wear on Flash Device
Flash memory has a limited lifetime – measured as the number of program/erase cycles a block can endure before becoming damaged and unusable. Although erasures are the major contributors to cell wear [23], recent studies show that programming also has a substantial impact on flash cell wear. For example, programming MLC cells as SLC [26] or occasionally relieving cells from programming [25] can significantly slow down cell degradation, regardless of the number of erasures. Thus, writing a page twice with the WOM code may increase the page wear. In other words, the number of allowed erasures might decrease.
In PEARL, a page is written-to (programmed) once in the case of both public data and hidden data being stored there. The page appears to be written-to twice when an adversary observes the device. This may allow a new type of side channel attack where the adversary estimates page wear to determine the presence of hidden data – the page wear may end up being slightly decreased than what is expected when the page contains hidden data. A detailed analysis of this physical side-channel and its impact on overall security is the subject of ongoing work.
Attacks on Weak Passwords
The security of all PD systems rely on the confidentiality of the hidden encryption key, which is usually derived from a password. There could be several security issues related to passwords, such as online/offline brute force attacks, social engineering, phishing etc. As a first line of defense, PEARL requires users to choose strong passwords with high entropy [27] thereby presumably making the system more resilient to these attacks.
Adequate Public Cover Traffic for Hidden Data
As in all prior works, PEARL requires public data traffic to hide data. Hidden data is written together with public data – either existing public data relocated during garbage collection or new incoming public data. Garbage collection is triggered only when empty pages are consumed by new public requests. Thus, to enable hidden data writes, sufficient public data traffic is required. In many scenarios this may be a reasonable assumption since in reality the amount of hidden data requiring protection is often less than public data.
X Evaluation
In this section, we firstly analyse storage and I/O overheads in PEARL. We then present a performance evaluation with experimental results.
Storage Overhead
The base (3,5) WOM code used (Table III and Section V-E) in PEARL requires 5 physical bits to store 3 bits of public logical data and 1 bit of hidden logical data. Further, storing metadata (e.g. translation pages) requires a few physical blocks. Overall, this reduces the total amount of logical data that can be stored within the total capacity of the device.
Specifically, the total amount of public data cannot exceed 60% of the total physical device capacity, while the total amount of hidden data cannot exceed 20% of the total device capacity. Thus, around 20% is sacrificed. This can be improved by using a more storage efficient WOM code that supports equal partitions in PEARL. We leave it as future work.
I/O Overhead
Data amplification also contributes to I/O overheads. With the (3,5) WOM code, 5 physical bits encode only 1 hidden bit, which means that 60KB data is accessed from the device for each 12KB of logical hidden data access. Similarly, accessing 12 KB of logical public data requires 20KB of physical data access. This is expected to reduce overall throughput of the system proportionally.
Moreover, as described in Section V, performing a full write or a 2nd write requires reading of some existing public data or the obsolete data in that page. This additional read also contributes to I/O overhead.
Finally, PEARL also requires additional processing time for address translation and data encoding etc., which contributes to I/O overhead as well.
X-A Experimental Results
Setup
PEARL was implemented as a core FTL engine in FlashSim [32], a popular flash based storage system simulation framework. FlashSim is an event-driven simulator (similar to DiskSim[13]) and is widely used to study the performance implications of different FTL schemes [50, 53, 18, 19]. Specifically, the evaluated PEARL uses the data encoding scheme based on the (3,5) WOM code as discussed in Section VII. Besides, as a baseline for comparison, DFTL is also implemented and evaluated under the same device settings. In the experiments below, a 64GB SSD[35] is simulated and the parameters used for this simulation are listed in Table IV. The page read, write and erase time are 130 us, 900 us and 10ms, respectively.
| Read | Write | Erase | (Die, Plane, Block, Page) | Page size |
| 130us | 900us | 10ms | (1, 2, 1437, 768) | 16KB |
Logical Volume Capacity
Although the physical capacity of the SSD simulated is 64GB, the logical capacity for the public volume and the hidden volume are set to 36GB and 12GB respectively. The difference in capacity is due to the use of the (3,5) WOM code, as discussed above. Comparably, the logical volume size when DFTL is used is 54 GB.
Initialization
FlashSim starts by simulating an empty SSD. However, it is well known that the overall performance of an SSD degrades with increasing logical capacity utilization. Thus, for an accurate evaluation, it is important to start with the device at a state where it has been fairly used for storing and accessing data for all volumes. This requires two things. First, the SSD should be “full” – most of the physical pages have been written at least once and contains some data (may be invalid data). Only in this case garbage collection can be triggered. Second, the amount of valid data in each volume should be “equivalent” relative to volume capacity. In this case, the write amplification due to the relocation of valid data will be comparable.
Thus, in the initialization phase for the PEARL evaluation, the SSD was filled with random data coming from the first halves of the public and the hidden volumes respectively until most of the physical pages have been written once and at least one garbage collection has been invoked. When evaluating DFTL, the SSD was filled with random data from the first half of the corresponding logical volume.
| Workload | Avg. Req. | Read | Seq | Avg. Req. Inter- |
| Size (KB) | (%) | (%) | arrival Time (ms) | |
| Financial1 | 3.47 | 23.2 | 2.0 | 8.19 |
| Financial2 | 2.45 | 82.3 | 2.0 | 11.08 |
| Web Search1 | 15.51 | 99.9 | 14.0 | 2.98 |
Performance Metrics
FlashSim reports a total aggregated response time for each request received. This is a combination of the device service time and the effect of queuing delays. Specifically, the response time not only captures the overhead due to the internal processes in an FTL such as address translation and data encoding, but also factors in the time spent by the request in I/O queues etc.
While in certain cases it may be desirable to eliminate scheduling delays etc. from the performance evaluation, this is not possible in the current simulator and would require further kernel instrumentation and more.
Workloads
We used both real-world workloads and synthetic workloads to benchmark PEARL and DFTL. To evaluate performance for real world applications, we used three popular enterprise-scale workload traces (Table V). This includes two different I/O traces (Financial1 and Financial2) for an OLTP application running at a financial institution [29], and an I/O trace from a popular search engine (Web Search1) [30]. These traces were particularly selected since (i) their address spaces fit within the capacity of the SSD being simulated, and (ii) they include enough writes to invoke garbage collections.
Moreover, these traces provide different characteristics which capture numerous real-world usage scenarios. For example, Financial1 is write-dominant while Financial2 and Web Search1 are read-dominant. Further, Web Search1 has more sequential accesses compared to Financial2. Financial1 and Financial2 also have smaller request sizes while Web Search1 requests more data per request on average. The overall parameters for the traces are summarized in Table V.
In addition to the real-world workloads, we also used synthetic workloads to test throughout of the system under conditions of heavy load. As shown in Table V, the average request interval arrival time is usually long in real-world applications. As a result, the available device bandwidth is never fully utilized. In order to test maximum throughput, we ran multiple synthetic workloads where large numbers of requests are submitted to the device at the same time (the request interval arrival time is 0). Specifically, 100000 read or write requests are submitted for either public or hidden data, and each of them requests for a data chunk of 16KB. Similarly, the response time is recorded for each request and we calculate the number of request satisfied during each second (IOPS).
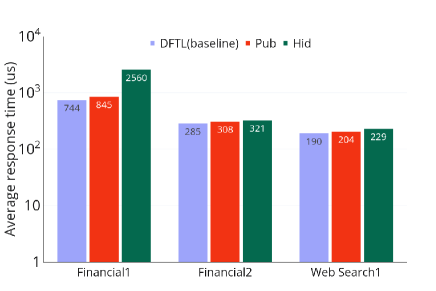
Results for Application Workloads
The three workloads listed in Table V are benchmarked against different FTLs. Figure 9 illustrates average response times for each workload. The y axis is in log scale and the actual values are provided on top of each column for further clarification.
Generally, I/O requests for hidden data consume more time as compared to public data. Comparing with the baseline (DFTL), the overhead for accessing public data ranges from 6% to 13%, while the overhead for accessing hidden data in each workload varies between 13% to 244%. The higher overhead for hidden data access is expected since the amplification of data size for hidden data is 3x the amplification of public data. Thus, a hidden data operation requires more physical page accesses compared to a public operation requesting the same data size.
Further, the average response time increases with increasing percentage of writes in a particular trace. This is more obvious in the case of hidden data accesses. Specifically, for Web Search1, the reported average response time is comparable to the baseline, since more than 99% of the requests are read requests. On the contrary, the average response time when running Financial1 trace is 2-3x higher than the baseline for hidden data, since most of the requests are writes.
Specifically, we can conclude that hidden write requests bring much higher overhead than public write requests. This can be explained with the following reasons. For public data accesses, the overhead for write operations is incurred primarily when the data is written to a 2nd write page. In this case, the old data in the page needs to be read first. A similar overhead is incurred during hidden writes – the public data that will be stored along with the hidden data needs to be read first. However, as hidden data has a larger amplification due to the WOM code compared to public data, the hidden data may be spread across more pages. And each page of hidden data requires a page of public data to be read. As a result, hidden data writes usually require more page operations than public data writes. In addition, a hidden write also requires updating the map entry for the corresponding public data. This may result in additional page accesses. Thus, overall, the overheads for hidden writes are much higher than the overheads for public writes.
Interestingly, the above results indicate that the additional page operations are the main contributors to performance overhead rather than additional data processing (data encoding etc).
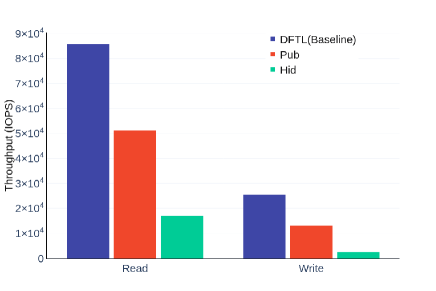
Results for Synthetic Workloads
The baseline (DFTL) read throughput is around IOPS and write throughput is around IOPS. PEARL public throughput is around IOPS for reads and IOPS for writes, while the hidden throughput is IOPS for reads and IOPS for writes. In other words, PEARL throughput is around 60% of the baseline for public data, and 10% – 20% of the baseline for the hidden data.
The performance penalty for public data operations is primarily due to the data amplification resulting from the WOM code: 5 physical bits are used to represent only 3 bits of public data. Meanwhile, additional page reads required during the 2nd write also reduces the write throughput of public data.
Write amplification due to WOM codes also significantly affects the throughput for hidden data operations since 5 physical bits are required for 1 hidden bit. Besides, additional page reads and writes are required for public data that is written together with hidden data and plausibly explains the changes to the device. This explains why the hidden write throughput is around 10% instead of 20% of the baseline.
XI Conclusion
PEARL is the first system that achieves strong plausible deniability for NAND flash devices, secure against realistic multi-snapshot adversaries.
PEARL is based on a new data encoding scheme base on specially designed WOM codes – the first scheme that allows hidden data to surreptitiously coexist in the same physical page as public data. By enabling plausible explanations for all state transitions base on public operations only, PEARL ensures that an on-event multi-snapshot adversary cannot detect the existence of hidden data. PEARL performance is practical and real-world workloads perform comparably with the case of running on a standard device without plausible deniability assurances.
References
- [1] TrueCrypt. "http://truecrypt.sourceforge.net/".
- [2] Ubifs - ubi file-system, 2015. "http://www.linux-mtd.infradead.org/doc/ubifs.html".
- [3] Ross Anderson, Roger Needham, and Adi Shamir. The steganographic file system. In Information Hiding, pages 73–82. Springer, 1998.
- [4] Amit Berman and Yitzhak Birk. Retired-page utilization in write-once memory — a coding perspective. 2013 IEEE International Symposium on Information Theory, pages 1062–1066, 2013.
- [5] Erik-Oliver Blass, Travis Mayberry, Guevara Noubir, and Kaan Onarlioglu. Toward robust hidden volumes using write-only oblivious ram. In Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pages 203–214. ACM, 2014.
- [6] Reporters Without Borders. Internet enemies, 12 March 2012. "http://goo.gl/x6zZ1.".
- [7] Anrin Chakraborti, Chen Chen, and Radu Sion. Datalair: Efficient block storage with plausible deniability against multi-snapshot adversaries. Proceedings on Privacy Enhancing Technologies, 2017(3):179–197, 2017.
- [8] Bing Chang, Fengwei Zhang, Bo Chen, Yingjiu Li, Wen-Tao Zhu, Yangguang Tian, Zhan Wang, and Albert Ching. Mobiceal: Towards secure and practical plausibly deniable encryption on mobile devices. In 2018 48th Annual IEEE/IFIP International Conference on Dependable Systems and Networks (DSN), pages 454–465. IEEE, 2018.
- [9] Chen Chen, Anrin Chakraborti, and Radu Sion. Pd-dm: An efficient locality-preserving block device mapper with plausible deniability. Proceedings on Privacy Enhancing Technologies, 2019(1), 2019.
- [10] A Fiat and A Shamir. Generalized “write-once” memories. IEEE Transactions on Information Theory, 30(3):470–480, 1984.
- [11] Fang-Wei Fu and AJ Han Vinck. On the capacity of generalized write-once memory with state transitions described by an arbitrary directed acyclic graph. IEEE Transactions on Information Theory, 45(1):308–313, 1999.
- [12] Paolo Gasti, Giuseppe Ateniese, and Marina Blanton. Deniable cloud storage: sharing files via public-key deniability. In Proceedings of the 9th annual ACM workshop on Privacy in the electronic society, pages 31–42, 2010.
- [13] Bruce Worthington Greg Ganger and Yale Patt. The disksim simulation environment (v4.0), 2008. "http://www.pdl.cmu.edu/DiskSim/index.shtml".
- [14] Laura M Grupp, Adrian M Caulfield, Joel Coburn, Steven Swanson, Eitan Yaakobi, Paul H Siegel, and Jack K Wolf. Characterizing flash memory: anomalies, observations, and applications. In Microarchitecture, 2009. MICRO-42. 42nd Annual IEEE/ACM International Symposium on, pages 24–33. IEEE, 2009.
- [15] The Guardian. Blackmail fear over lost raf data. 2008.
- [16] Aayush Gupta, Youngjae Kim, and Bhuvan Urgaonkar. DFTL: a flash translation layer employing demand-based selective caching of page-level address mappings, volume 44. ACM, 2009.
- [17] Jin Han, Meng Pan, Debin Gao, and HweeHwa Pang. A multi-user steganographic file system on untrusted shared storage. In Proceedings of the 26th Annual Computer Security Applications Conference, pages 317–326. ACM, 2010.
- [18] Yang Hu, Hong Jiang, Dan Feng, Lei Tian, Hao Luo, and Shuping Zhang. Performance impact and interplay of ssd parallelism through advanced commands, allocation strategy and data granularity. In Proceedings of the international conference on Supercomputing, pages 96–107, 2011.
- [19] H Howie Huang, Shan Li, Alex Szalay, and Andreas Terzis. Performance modeling and analysis of flash-based storage devices. In 2011 IEEE 27th Symposium on Mass Storage Systems and Technologies (MSST), pages 1–11. IEEE, 2011.
- [20] R. P. Weinmann J. Assange and S. Dreyfus. Rubberhose:cryptographically deniable transparent disk encryption system. "http://marutukku.org".
- [21] Adam N Jacobvitz, R Calderbank, and Daniel J Sorin. Writing cosets of a convolutional code to increase the lifetime of flash memory. In 2012 50th Annual Allerton Conference on Communication, Control, and Computing (Allerton), pages 308–318. IEEE, 2012.
- [22] Ashish Jagmohan, Michele Franceschini, and Luis Lastras. Write amplification reduction in nand flash through multi-write coding. In 2010 IEEE 26th Symposium on Mass Storage Systems and Technologies (MSST), pages 1–6. IEEE, 2010.
- [23] Jaeyong Jeong, Sangwook Shane Hahn, Sungjin Lee, and Jihong Kim. Lifetime improvement of nand flash-based storage systems using dynamic program and erase scaling. In 12th USENIX Conference on File and Storage Technologies (FAST 14), pages 61–74, 2014.
- [24] Shijie Jia, Luning Xia, Bo Chen, and Peng Liu. Deftl: Implementing plausibly deniable encryption in flash translation layer. In Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security, pages 2217–2229. ACM, 2017.
- [25] Xavier Jimenez, David Novo, and Paolo Ienne. Wear unleveling: Improving NAND flash lifetime by balancing page endurance. In 12th USENIX Conference on File and Storage Technologies (FAST 14), pages 47–59, Santa Clara, CA, February 2014. USENIX Association.
- [26] Xavier Jimenez, David Novo, and Paolo Ienne. Libra: Software-controlled cell bit-density to balance wear in nand flash. ACM Trans. Embed. Comput. Syst., 14(2), February 2015.
- [27] B. Kaliski. Pkcs 5: Password-based cryptography specification version 2.0, 2000. "https://tools.ietf.org/html/rfc2898".
- [28] Ramakrishna Karedla, J Spencer Love, and Bradley G Wherry. Caching strategies to improve disk system performance. Computer, 27(3):38–46, 1994.
- [29] Bruce McNutt Ken Bates. Umasstracerepository-oltp application i/o. "http://traces.cs.umass.edu/index.php/Storage/Storage".
- [30] Bruce McNutt Ken Bates. Umasstracerepository-search engine i/o. "http://traces.cs.umass.edu/index.php/Storage/Storage".
- [31] Gabriela Kennedy. Encryption policies: Codemakers, codebreakers and rulemakers: Dilemmas in current encryption policies. Computer Law & Security Review, 16(4):240–247, 2000.
- [32] Youngjae Kim, Brendan Tauras, Aayush Gupta, and Bhuvan Urgaonkar. Flashsim: A simulator for nand flash-based solid-state drives. In 2009 First International Conference on Advances in System Simulation, pages 125–131. IEEE, 2009.
- [33] Kingston. Nearly half of organizations have lost sensitive or confidential information on usb drives in just the past two years. 2011.
- [34] Changman Lee, Dongho Sim, Jooyoung Hwang, and Sangyeun Cho. F2fs: A new file system for flash storage. In 13th USENIX Conference on File and Storage Technologies (FAST 15), pages 273–286, 2015.
- [35] Chun-Yi Liu, Jagadish B. Kotra, Myoungsoo Jung, Mahmut T. Kandemir, and Chita R. Das. Soml read: Rethinking the read operation granularity of 3d nand ssds. In Proceedings of the Twenty-Fourth International Conference on Architectural Support for Programming Languages and Operating Systems, ASPLOS ’19, pages 955–969, New York, NY, USA, 2019. ACM.
- [36] Andrew D McDonald and Markus G Kuhn. Stegfs: A steganographic file system for linux. In Information Hiding, pages 463–477. Springer, 1999.
- [37] J. Mull. How a syrian refugee risked his life to bear witness to atrocities, 2012. "shorturl.at/yHJL1".
- [38] BBC News. Uk’s families put on fraud alert. 2007.
- [39] BBC News. Blackmail fear over lost raf data. 2009.
- [40] HweeHwa Pang, Kian-Lee Tan, and Xuan Zhou. Stegfs: A steganographic file system. In Data Engineering, 2003. Proceedings. 19th International Conference on, pages 657–667. IEEE, 2003.
- [41] Timothy Peters, Mark Gondree, and Zachary N. J. Peterson. DEFY: A deniable, encrypted file system for log-structured storage. In 22nd Annual Network and Distributed System Security Symposium, NDSS 2015, San Diego, California, USA, February 8-11, 2014, 2015.
- [42] Denver Post. Password case reframes fifth amendment rights in context of digital world. "http://www.denverpost.com/news/ci_19669803".
- [43] The Register. Youth jailed for not handing over encryption password. 2010.
- [44] Ronald L Rivest and Adi Shamir. How to reuse a “write-once memory”. Information and control, 55(1-3):1–19, 1982.
- [45] Adam Skillen and Mohammad Mannan. On implementing deniable storage encryption for mobile devices. 2013.
- [46] AGYKB Urgaonkar. Dftl: A flash translation layer employing demand-based selective caching of page-level address mappings. 2008.
- [47] WhisperSystems. Github: Whispersystems/whisperyaffs: Wiki, 2012. "https://github.com/WhisperSystems/WhisperYAFFS/wiki".
- [48] Wikipedia. Key disclosure law. "http://en.wikipedia.org/wiki/Key_disclosure_law".
- [49] Computer World. Nasa breach update: Stolen laptop had data on 10,000 users. 2012.
- [50] Zhiyong Xu, Ruixuan Li, and Cheng-Zhong Xu. Cast: A page-level ftl with compact address mapping and parallel data blocks. In 2012 IEEE 31st International Performance Computing and Communications Conference (IPCCC), pages 142–151. IEEE, 2012.
- [51] Eitan Yaakobi, Scott Kayser, Paul H Siegel, Alexander Vardy, and Jack Keil Wolf. Codes for write-once memories. IEEE Transactions on Information Theory, 58(9):5985–5999, 2012.
- [52] Gala Yadgar, Eitan Yaakobi, and Assaf Schuster. Write once, get 50% free: Saving SSD erase costs using WOM codes. In 13th USENIX Conference on File and Storage Technologies (FAST 15), pages 257–271, Santa Clara, CA, 2015. USENIX Association.
- [53] Jian Zhou, Dezhi Han, Jun Wang, Xiaobo Zhou, and Changjun Jiang. A correlation-aware page-level ftl to exploit semantic links in workloads. IEEE Transactions on Parallel and Distributed Systems, 30(4):723–737, 2018.