PEFA: Parameter-Free Adapters for Large-scale Embedding-based Retrieval Models

Wei-Cheng Chang weicheng.cmu@gmail.com AmazonSeattleWashingtonUSA , Jyun-Yu Jiang jyunyu.jiang@gmail.com AmazonPalo AltoCAUSA , Jiong Zhang zhangjiong724@gmail.com AmazonPalo AltoCAUSA , Mutasem Al-Darabsah mutasema@amazon.com AmazonPalo AltoCAUSA , Choon Hui Teo choonhui@amazon.com AmazonPalo AltoCAUSA , Cho-Jui Hsieh chohsieh@cs.ucla.edu UCLALos AngelesCAUSA , Hsiang-Fu Yu rofu.yu@gmail.com AmazonPalo AltoCAUSA and S. V. N. Vishwanathan vishy@amazon.com AmazonPalo AltoCAUSA

(2024)

Abstract.

Embedding-based Retrieval Models (ERMs) have emerged as a promising framework for large-scale text retrieval problems due to powerful large language models. Nevertheless, fine-tuning ERMs to reach state-of-the-art results can be expensive due to the extreme scale of data as well as the complexity of multi-stages pipelines (e.g., pre-training, fine-tuning, distillation). In this work, we propose the PEFA framework, namely ParamEter-Free Adapters, for fast tuning of ERMs without any backward pass in the optimization. At index building stage, PEFA equips the ERM with a non-parametric $k$ -nearest neighbor (kNN) component. At inference stage, PEFA performs a convex combination of two scoring functions, one from the ERM and the other from the kNN. Based on the neighborhood definition, PEFA framework induces two realizations, namely PEFA-XL (i.e., extra large) using double ANN indices and PEFA-XS (i.e., extra small) using a single ANN index. Empirically, PEFA achieves significant improvement on two retrieval applications. For document retrieval, regarding Recall@100 metric, PEFA improves not only pre-trained ERMs on Trivia-QA by an average of 13.2%, but also fine-tuned ERMs on NQ-320K by an average of 5.5%, respectively. For product search, PEFA improves the Recall@100 of the fine-tuned ERMs by an average of 5.3% and 14.5%, for PEFA-XS and PEFA-XL, respectively. Our code is available at https://github.com/amzn/pecos/tree/mainline/examples/pefa-wsdm24.

embedding-based retrieval, bi-encoders, parameter-free adapters, k-nearest neighbor models

^†^†journalyear: 2024^†^†copyright: acmlicensed^†^†conference: Proceedings of the 17th ACM International Conference on Web Search and Data Mining; March 4–8, 2024; Merida, Mexico^†^†booktitle: Proceedings of the 17th ACM International Conference on Web Search and Data Mining (WSDM ’24), March 4–8, 2024, Merida, Mexico^†^†price: 15.00^†^†doi: 10.1145/3616855.3635791^†^†isbn: 979-8-4007-0371-3/24/03^†^†ccs: Computing methodologies Supervised learning^†^†ccs: Computing methodologies Instance-based learning

1. Introduction

Given a user’s query, large-scale text retrieval aims to recall a match set of semantically relevant documents in real-time from an enormous corpus, whose size can be 100 millions or more. Embedding-based retrieval models (ERMs) (Karpukhin et al., 2020; Chang et al., 2020; Xiong et al., 2021), namely bi-encoders (Nigam et al., 2019; Huang et al., 2020), have emerged as the prevalent paradigm for large-scale text retrieval, thanks to recent advances in large language models (LLMs). At the learning stage, ERMs fine-tune parametric Transformer encoders that map queries and documents into a semantic embedding space where relevant (query, document) pairs are close to each other and vice versa. At the inference stage, retrieving relevant documents from the enormous output space can be formulated as the maximum inner product search (MIPS) problem (Yu et al., 2017). With proper indexing data structures, MIPS problem can be efficiently solved by approximate nearest neighbor (ANN) search libraries (e.g., Faiss (Johnson et al., 2019), ScaNN (Guo et al., 2020), HNSWLIB (Malkov and Yashunin, 2018)) in time sub-linear to the size of corpus.

Adapting ERMs to downstream retrieval tasks usually follows the full-parameter fine-tuning paradigm, which requires gradient computations and updates parameters of Transformer encoders. Such full-parameter fine-tuning approach faces challenges in the industrial setup, where learning signals are enormous. In modern e-commerce stores, for example, the number of relevant (query, product) pairs can be billions or more. Full-parameter fine-tuning ERMs on such scale may take thousands of GPU hours due to complicated multi-stage pipeline: pre-training (Chang et al., 2020; Gao and Callan, 2021, 2022), 1st stage fine-tuning with random negatives and BM25 candidates (Karpukhin et al., 2020), 2nd stage fine-tuning with hard-mined negatives (Xiong et al., 2021; Zhan et al., 2021), and 3rd stage fine-tuning with distilled knowledge from expensive cross-attention models (Ren et al., 2021b; Zhang et al., 2022a). Furthermore, these fine-tuning approaches require access to models’ gradient information, which is not accessible for many black box LLMs such as GPT-3 (Brown et al., 2020) and beyond.

In this work, we propose the PEFA framework (i.e., ParamEter-Free Adapters) for fast tuning of black-box ERMs, which doesn’t require any gradient information of the model. The scoring function of PEFA is a convex combination between the ERM and the new non-parametric $k$ -nearest neighbor (kNN) model. The learning of kNN model reduces to constructing ANN index that stores key-value pairs of query embeddings and learning signals. Given a query at inference time, the kNN model seeks close-by training queries in the neighborhood, and aggregates the associated relevant documents as its scoring function. Depending on the definition of neighborhood, we introduce two kNN models under our PEFA framework:

•

PEFA-XS: the neighborhood is defined by the relevant query-document pairs, which is independent to the test-time query.
•

PEFA-XL: the neighborhood is an intersection of the one in PEFA-XS and kNN queries in the training set, which is dependent to the test-time query.

In Summary, we highlight four key contributions below.

•

We propose PEFA, a novel Parameter-free adapters framework for fast tuning ERMs to downstream retrieval tasks.
•

PEFA requires no gradient information of ERMs, hence applicable to black-box ERMs.
•

PEFA is not only applicable to a wide-range of pre-trained ERM, but also effective to fine-tuned ERMs.
•

We demonstrate the effectiveness and scalability of PEFA on two retrieval applications, including document retrieval tasks and industrial-scale product search tasks.

For document retrieval, PEFA not only improves the recall@100 of pre-trained ERMs on Trivia-QA by an average of 13.2%, but also lifts the recall@100 of fine-tuned ERMs on NQ-320K by an average of 5.5%. For NQ-320K dataset, applying PEFA to the fine-tuned $\text{GTR}_{\text{base}}$ (Ni et al., 2022b) reaches new state-of-the-art (SoTA) results, where the Recall@10 of $88.71\%$ outperforms the Recall@10 of $85.20\%$ in the previous SoTA Seq2Seq-based NCI (Wang et al., 2022a), under similar model size for fair comparison. For product search consisting of billion-scale of data, PEFA improves the Recall@100 of the fine-tuned ERMs by an average of 5.3% and 14.5%, for PEFA-XS and PEFA-XL, respectively.

2. Preliminary

2.1. Dense Text Retrieval

Dense text retrieval typically adopts the Embedding-based Retrieval Model (ERM) architecture, also known as bi-encoders (Karpukhin et al., 2020; Xiong et al., 2021; Chang et al., 2020). For simplicity, we use the term passage/document interchangeably in the rest of paper. Given a query $q\in{\mathcal{X}}$ and a passage $p\in{\mathcal{X}}$ , the relevance scoring function $f_{\text{ERM}}(q,p)$ of the ERM is measured by

(1)

f_{\text{ERM}}(q,p;\theta)=\bigl{<}E(q;\theta),E(p;\theta)\bigr{>},

where $E(\cdot;\theta):{\mathcal{X}}\rightarrow{\mathbb{R}}^{d}$ is the encoder parameterized with $\theta$ that maps an input text to a $d$ -dimensional vector space and $\langle\cdot,\cdot\rangle:{\mathbb{R}}^{d}\times{\mathbb{R}}^{d}\rightarrow{\mathbb{R}}$ is the similarity function, including inner product and cosine similarity. Without loss of generality, we use inner product as the scoring function for the rest of paper.

Learning

Suppose the training data is presented as a set of relevant query-passage pairs ${\mathcal{D}}=\{(q_{i},p_{i})\}_{i=1}^{|{\mathcal{D}}|}$ . The encoder parameters $\theta$ are often learned by maximizing the log-likelihood loss function (Karpukhin et al., 2020; Chang et al., 2020) $\max_{\theta}\sum_{(q,p)\in{\mathcal{D}}}\log p_{\theta}(p|q)$ , where the conditional probability is defined by the Softmax function

p_{\theta}(p|q)=\frac{\exp{\big{(}f_{\text{ERM}}(q,p;\theta)\big{)}}}{\sum_{p^{\prime}\in{\mathcal{D}}}\exp{\big{(}f_{\text{ERM}}(q,p^{\prime};\theta)\big{)}}}.

In practice, various negative sampling techniques (Karpukhin et al., 2020; Xiong et al., 2021; Lin et al., 2021; Formal et al., 2022) have been developed to approximate the expensive partition function of the conditional Softmax. We direct interested readers to the comprehensive study (Guo et al., 2022) for more details of learning ERMs.

Inference

Given a query embedding ${\bm{q}}\in{\mathbb{R}}^{d}$ and a corpus of $n$ passage embeddings ${\mathcal{P}}=\{{\bm{p}}_{j}\}_{j=1}^{n}$ where ${\bm{p}}_{j}\in{\mathbb{R}}^{d},j=1,\ldots,n$ , ERMs retrieve $k$ most relevant passages from ${\mathcal{P}}$ in real time, which is a Maximum Inner Product Search (MIPS) problem. Exact inference of MIPS problem requires $O(n)$ time, which is prohibited for large-scale retrieval applications. Thus, practitioners leverage Approximate Nearest Neighbor search (ANN) to approximately solve it in time sub-linear (e.g., ${\mathcal{O}}\big{(}\log(n)\big{)}$ ) to the size of corpus $n$ .

To achieve sub-linear time complexity of ANN search, ANN methods require an additional index building stage to preprocess the corpus ${\mathcal{P}}$ into specific data structures, such as hierarchical graphs (e.g., HNSW (Malkov and Yashunin, 2018), VAMANA (Jayaram Subramanya et al., 2019), etc) and product quantization (e.g., FAISS (Johnson et al., 2019), ScaNN (Guo et al., 2020), etc). Compared to the cost of full-parameter fine-tuning ERMs on GPU machines, the cost of building ANN index is often negligible as the latter takes place on the lower-cost single CPU machine, with much faster computational time.

2.2. Problem Statement

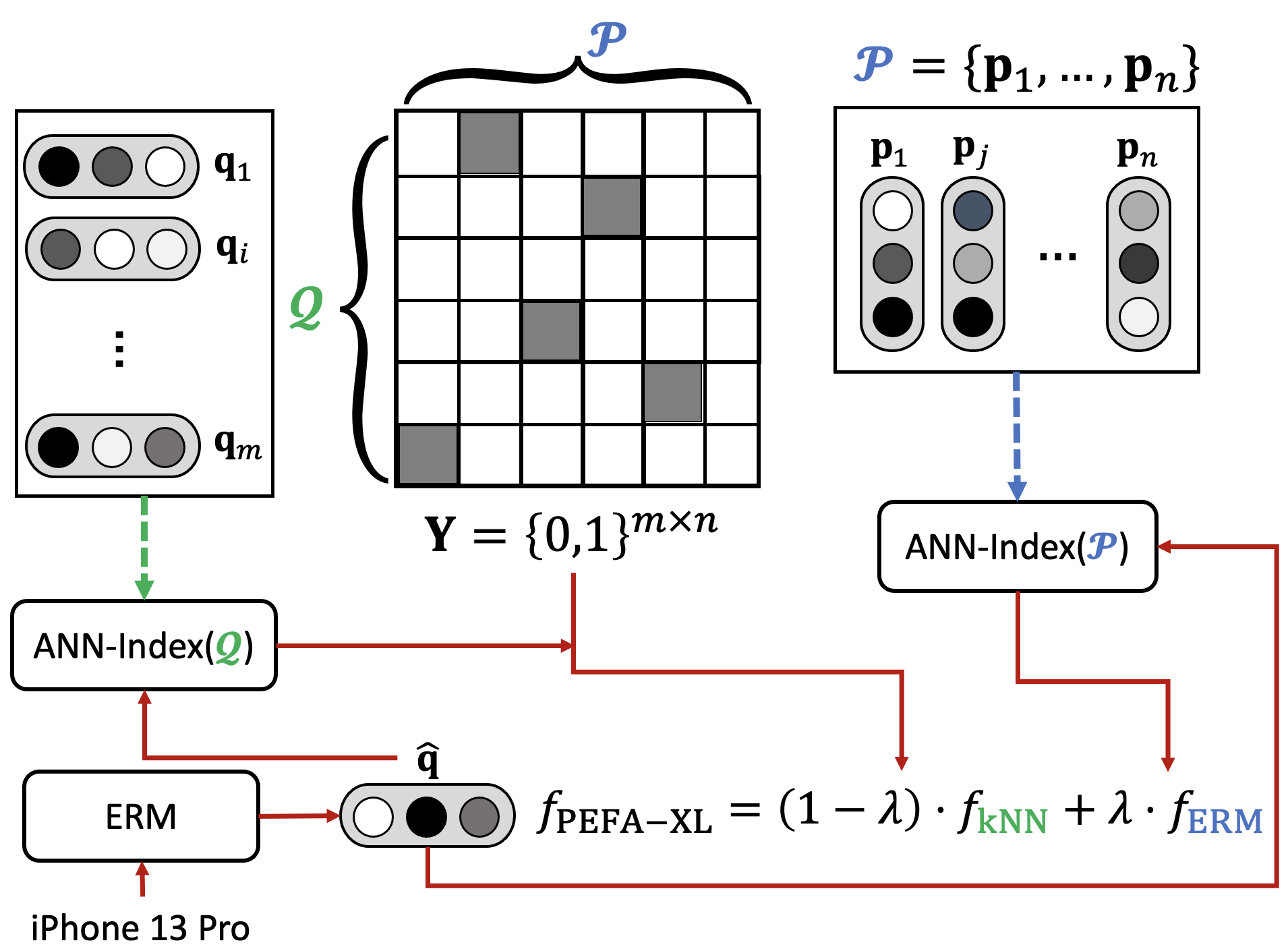
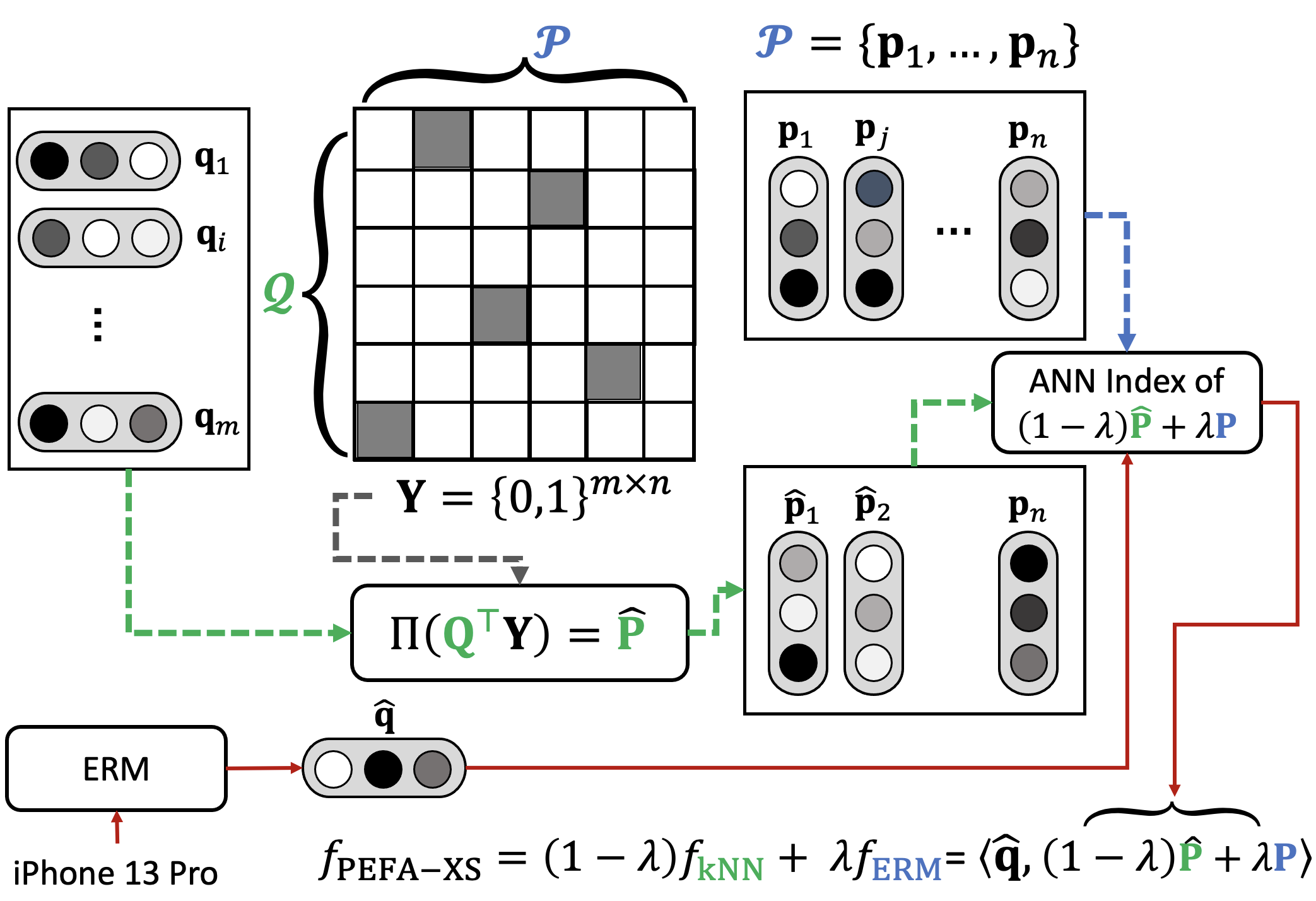
Refer to caption — Figure 1. Illustration of the proposed PEFA-XL method. The green and blue dash line represents computation paths for building ANN index in offline. The red solid line represents computation paths for performing ANN search in online. PEFA-XL requires two ANN indices: one on the passage space ${\mathcal{P}}$ for fast inference of ERM, while the other on the query space ${\mathcal{Q}}$ for fast inference of kNN model.

Notations.

${\mathbf{Y}}\in\{0,1\}^{m\times n}$ is the query-to-passage relevant matrix, namely the supervised training data. The row indices of ${\mathbf{Y}}$ refer to the set of queries ${\mathcal{Q}}$ , and the column indices of ${\mathbf{Y}}$ refer to the set of passages ${\mathcal{P}}$ , respectively. Note that ${\mathcal{P}}$ is also the corpus space used for ANN inference of ERMs. The bold matrices ${\mathbf{P}}\in{\mathbb{R}}^{n\times d}$ and ${\mathbf{Q}}\in{\mathbb{R}}^{m\times d}$ denote the query and passage embeddings of ${\mathcal{P}}$ and ${\mathcal{Q}}$ obtained from the ERM, respectively. We denote ${\mathbf{Y}}_{i,:}\in\{0,1\}^{n}$ as the relevant vector of $i$ th query ${\bm{q}}_{i}$ , representing which set of passages in ${\mathcal{P}}$ are relevant to this query ${\bm{q}}_{i}$ . Similarly, ${\mathbf{Y}}_{:,j}\in\{0,1\}^{m}$ is the relevant vector of $j$ th passage ${\bm{q}}_{j}$ , representing which set of queries in ${\mathcal{Q}}$ are relevant to this passage ${\bm{p}}_{j}$ . Finally, $\hat{{\bm{q}}}\in{\mathbb{R}}^{d}$ is the query embeddings at inference time and $\text{NN}(\hat{{\bm{q}}},{\mathbf{P}};k)$ is the set of $k$ nearest indices in the indexed database ${\mathbf{P}}$ given $\hat{{\bm{q}}}$ .

Problem Setup.

In this work, we propose PEFA, parameter-free adapters for ERMs via equipping it with a non-parametric kNN component. The non-parametric kNN model is learning-free which avoid any optimization step to fine-tune parameters of ERMs. The major computation of PEFA becomes building ANN index storing key-value pairs for serving efficiently at the inference stage. Thus, our PEFA is also applicable to both pre-trained and fine-tuned ERMs, even ones initialized from black-box LLMs. Note that PEFA is orthogonal and complement to most existing literature that aims to obtain better pre-trained or fine-tuned ERMs at the learning stage, including recent studies of the parameter-efficient fine-tuning of ERMs (Jung et al., 2022; Ma et al., 2022; Pal et al., 2023). Finally, for the ease of discussion, we assume embeddings obtained from ERMs are unit-norm (i.e., $\ell_{2}$ normalized), hence the inner product is equivalent to the cosine similarity. The techniques proposed in this paper can be easily extended to non-unit norm cases by replacing the distance metric used in kNN.

3. Proposed Framework

In this section, we propose PEFA, a Parameter-free Adapters framework for fast tuning of ERMs. Given a query embedding $\hat{{\bm{q}}}$ at inference time, our PEFA framework defines the relevant scoring function of a query-passage pair $(\hat{{\bm{q}}},{\bm{p}}_{j})$ as the convex combination between scoring functions of the black-box ERM and a non-parametric kNN model:

(2)

f_{\text{PEFA}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\lambda\cdot f_{\text{ERM}}(\hat{{\bm{q}}},{\bm{p}}_{j})+(1-\lambda)\cdot f_{\text{kNN}}(\hat{{\bm{q}}},{\bm{p}}_{j}),

where $\lambda\in[0,1]$ is the interpolation hyper-parameter to balance the importance between the ERM and the kNN model. Note that the proposed PEFA framework is learning-free. In other words, the underlying parameters $\theta$ of ERM remains unchanged, and Equation 2 is only applied at the inference time.

Next, we present scoring functions of kNN models in a generic form as follows.

(3)

f_{\text{kNN}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\bigl{<}\hat{{\bm{q}}},{\mathbf{Q}}^{\top}{\mathbf{D}}(\hat{{\bm{q}}},{\mathbf{Q}}){\mathbf{Y}}_{:,j}\bigr{>}

where ${\mathbf{D}}(\hat{{\bm{q}}},{\mathbf{Q}})\in{\mathbb{R}}^{n\times n}$ is a normalized diagonal matrix, acting like a gating mechanism that controls which set of training queries the current test query $\hat{{\bm{q}}}$ should pay attention to.

Plugging Equation 3 back to Equation 2, we derive the scoring function of PEFA explicitly

(4)

f_{\text{PEFA}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\lambda\bigl{<}\hat{{\bm{q}}},{\bm{p}}_{j}\bigr{>}+(1-\lambda)\bigl{<}\hat{{\bm{q}}},{\mathbf{Q}}^{\top}{\mathbf{D}}(\hat{{\bm{q}}},{\mathbf{Q}}){\mathbf{Y}}_{:,j}\bigr{>}.

Based on the design of diagonal matrix ${\mathbf{D}}(\hat{{\bm{q}}},{\mathbf{Q}})$ , we present two realizations of kNN models under the PEFA framework, namely PEFA-XL (Section 3.1) and PEFA-XS (Section 3.2). We then discuss their intuitions, time and space complexity, and connections to the related literature. For the rest of the paper, We use HNSW (Malkov and Yashunin, 2018) as the underlying ANN methods in our PEFA framework for complexity analysis and experiment results.

3.1. PEFA-XL

A standard realization of the kNN model is that the test query $\hat{{\bm{q}}}$ only pays attention to top- $k$ most similar training queries in ${\mathcal{Q}}$ . Specifically, ${\mathbf{D}}_{i,i}=1$ if $i\in\text{NN}(\hat{{\bm{q}}},{\mathbf{Q}};k)$ ; otherwise ${\mathbf{D}}_{i,i}=0$ . We can then derive the kNN model of Equation 3 as following:

(5)

f_{\text{kNN}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\bigl{<}\hat{{\bm{q}}},\sum_{i=1}^{n}({\mathbf{D}}_{i,i}{\mathbf{Y}}_{i,j})\cdot{\bm{q}}_{i}\bigr{>}=\sum_{i\in\text{NN}(\hat{{\bm{q}}},{\mathbf{Q}};k)}\bigl{<}\hat{{\bm{q}}},{\bm{q}}_{i}\bigr{>}\cdot{\mathbf{Y}}_{i,j}.

By plugging the query-aware kNN model of Equation 5 into Equation 2, we present the scoring function of PEFA-XL explicitly

(6)

f_{\text{PEFA-XL}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\lambda\bigl{<}\hat{{\bm{q}}},{\bm{p}}_{j}\bigr{>}+(1-\lambda)\sum_{i\in\text{NN}(\hat{{\bm{q}}},{\mathbf{Q}};k)}\bigl{<}\hat{{\bm{q}}},{\bm{q}}_{i}\bigr{>}\cdot{\mathbf{Y}}_{i,j}.

Implementation.

An illustration of PEFA-XL method is presented in Figure 2. Intuitively, the kNN model of PEFA-XL produces its match set by aggregating relevant passages ${\mathbf{Y}}_{i,j}$ of training queries ${\bm{q}}_{i}$ that are in the neighborhood of the test query $\hat{{\bm{q}}}$ . Note that the scoring function of $f_{\text{ERM}}$ in Equation 6 is bounded between $[-1,1]$ as the inner product of two unit-form embeddings are bounded by the range of cosine similarity. On the other hand, the scoring function of $f_{\text{kNN}}$ in Equation 6 needs an additional normalization so that its score is calibrated to $f_{\text{ERM}}$ . In practice, we consider normalizing $f_{\text{kNN}}$ by $k$ , namely $D_{i,i}=1/k$ if $i\in NN(\hat{{\bm{q}}},{\mathbf{Q}};k)$ , so that $f_{\text{kNN}}$ is still upper bounded by $1$ .

Methods	Scoring functions	HNSW index building time	HNSW index size	HNSW inference time
ERM	Equation 1	${\mathcal{O}}\big{(}n\log(n)\big{)}$	${\mathcal{O}}\big{(}nd+\|E_{\mathcal{P}}\|\big{)}$	${\mathcal{O}}\big{(}\log(n)\big{)}$
PEFA-XL	Equation 6	${\mathcal{O}}(n\log(n)+m\log(m))$	${\mathcal{O}}\big{(}nd+\|E_{\mathcal{P}}\|+md+\|E_{\mathcal{Q}}\|+\text{nnz}({\mathbf{Y}})\big{)}$	${\mathcal{O}}\big{(}\log(n)+\log(m)\big{)}$
PEFA-XS	Equation 8	${\mathcal{O}}\big{(}n\log(n)\big{)}$	${\mathcal{O}}\big{(}nd+\|E_{\mathcal{P}}\|\big{)}$	${\mathcal{O}}\big{(}\log(n)\big{)}$

Table 1. Comparing time and space complexity of ERM, PEFA-XS, and PEFA-XL at the inference stage. We use the competitive graph-based ANN algorithm HNSW (Malkov and Yashunin, 2018) as the underlying method for ANN search. The time and space complexity of HNSW is induced from (Wang et al., 2021).

E_{\mathcal{P}}

and

E_{\mathcal{Q}}

represents the edges of HNSW graph for

{\mathcal{P}}

and

{\mathcal{Q}}

, respectively.

Complexity Analysis.

At inference stage, retrieving the match set via PEFA-XL (Equation 6) requires ANN searches on TWO distinct output spaces. Specifically, the ERM requires ANN search on the passage space ${\mathcal{P}}$ of size $n$ , while the kNN model requires ANN search on the query space ${\mathcal{Q}}$ of size $m$ . According to the comprehensive review (Wang et al., 2021), the inference time complexity of HNSW on a data set ${\mathcal{S}}$ is ${\mathcal{O}}\big{(}\log(|{\mathcal{S}}|)\big{)}$ . Thus, the inference time complexity of PEFA-XL becomes ${\mathcal{O}}\big{(}\log(n)+\log(m)\big{)}$ .

Next, we discuss the space complexity of PEFA-XL, which requires to store two HNSW indices as well as the query-to-passage relevant matrix ${\mathbf{Y}}$ . The space complexity of an HNSW index on a data set ${\mathcal{S}}$ is ${\mathcal{O}}\big{(}|{\mathcal{S}}|d+|E_{\mathcal{S}}|\big{)}$ where the former comes from saving the database vectors and the latter comes from saving edges of the HNSW graph. The space complexity of storing ${\mathbf{Y}}$ is ${\mathcal{O}}\big{(}\text{nnz}({\mathbf{Y}})\big{)}$ . Thus, the space complexity of PEFA-XL is ${\mathcal{O}}\big{(}nd+|E_{\mathcal{P}}|+md+|E_{\mathcal{Q}}|+\text{nnz}({\mathbf{Y}})\big{)}$ .

Finally, the time complexity of building HNSW indices for PEFA-XL is ${\mathcal{O}}\big{(}n\log(n)+m\log(m)\big{)}$ because building a HNSW index for a set ${\mathcal{S}}$ takes ${\mathcal{O}}\big{(}|{\mathcal{S}}|\log(|{\mathcal{S}}|)\big{)}$ (Wang et al., 2021). The building time, inference time, and space complexity of PEFA-XL is summarized in Table 1.

Connections to kNN-LM

Using a non-parametric kNN model to improve a parametric neural network has also been studied in the context of $k$ nearest neighbors language modeling (kNN-LM) (Khandelwal et al., 2020; Yogatama et al., 2021; He et al., 2021) and retrieval-augmented LM pre-training (Guu et al., 2020; Lewis et al., 2020; Borgeaud et al., 2022). kNN-LM interpolates the next-token predictive probability by the neural language model and the kNN model. While sharing similar intuitions, PEFA-XL is different from kNN-LM because PEFA-XL requires two ANN searches, one on the passage space ${\mathcal{P}}$ and the other on the query space ${\mathcal{Q}}$ . In contrast, kNN-LM only needs one ANN search on the context space, while inference on the vocab space is exact since the size of vocabulary is small.

3.2. PEFA-XS

In practice, PEFA-XL can be too expensive to deploy due to storing two ANN indices, which double the model storage and inference latency. Thus, we seek an efficient alternative of PEFA-XL that only needs to maintain single ANN index, hence the name PEFA-XS.

Recall that PEFA-XL demands another ANN search because of finding $k$ nearest queries in ${\mathcal{Q}}$ , namely $\text{NN}(\hat{{\bm{q}}},{\mathcal{Q}};k)$ . We can approximate $\text{NN}(\hat{{\bm{q}}},{\mathcal{Q}};k)$ by the set of relevant queries given a target passage ${\bm{p}}_{j}\in{\mathcal{P}}$ . We denote this alternative query set as ${\mathcal{I}}({\bm{p}}_{j},{\mathbf{Y}})=\{i|{\mathbf{Y}}_{ij}>0,i=1,\ldots,n\}$ , which is a function of ${\bm{p}}_{j}$ that is independent to the test query $\hat{{\bm{q}}}$ . In other words, the resulting diagonal matrix ${\mathbf{D}}_{i,i}=1$ if $i\in{\mathcal{I}}({\bm{p}}_{j},{\mathbf{Y}})$ ; other ${\mathbf{D}}_{i,i}=0$ . The approximate kNN model of PEFA-XS becomes

(7)

f_{\text{kNN}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\bigl{<}\hat{{\bm{q}}},\sum_{i\in{\mathcal{I}}({\bm{p}}_{j},{\mathbf{Y}})}{\mathbf{Y}}_{i,j}\cdot{\bm{q}}_{i}\bigr{>}=\bigl{<}\hat{{\bm{q}}},{\mathbf{Q}}^{\top}{\mathbf{Y}}_{:,j}\bigr{>}.

By plugging the query-independent kNN model of Equation 7 back to Equation 2, we present the scoring function of PEFA-XS

f_{\text{PEFA-XS}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\lambda\bigl{<}\hat{{\bm{q}}},{\bm{p}}_{j}\bigr{>}+(1-\lambda)\bigl{<}\hat{{\bm{q}}},{\mathbf{Q}}^{\top}{\mathbf{Y}}_{:,j}\bigr{>}.

Implementation

An illustration of PEFA-XS method is presented in Figure 2. Similar to the implementation design of PEFA-XL, we need to normalize the scoring function of $f_{\text{kNN}}$ in Equation 7 such that its score is upper bounded by $1$ . Thus, we introduce an $\ell_{2}$ normalization operator $\Pi({\bm{x}})=\frac{{\bm{x}}}{\|{\bm{x}}\|}$ that projects an embedding back to the unit-sphere. We can then rewrite the scoring function of PEFA-XS as

(8)

f_{\text{PEFA-XS}}(\hat{{\bm{q}}},{\bm{p}}_{j})=\bigl{<}\hat{{\bm{q}}},\\ \lambda\cdot{\bm{p}}_{j}+(1-\lambda)\cdot\Pi({\mathbf{Q}}^{\top}{\mathbf{Y}}_{:,j})\bigr{>},

where normalization step $\Pi(\cdot)$ can be absorbed in the design of ${\mathbf{D}}$ .

Complexity Analysis

Note that the kNN model of PEFA-XS is independent to the test query $\hat{{\bm{q}}}$ , so the interpolation of two scoring functions can be pre-computed in the embedding space, as derived in Equation 8. This suggests that PEFA-XS only requires a single ANN index, where a set of $n$ interpolated passage embeddings are used. Therefore, the inference of PEFA-XS share the same time and space complexity as ERM alone. Specifically, the time complexity of constructing HNSW index and performing ANN search are ${\mathcal{O}}\big{(}n\log(n)\big{)}$ and ${\mathcal{O}}\big{(}\log(n)\big{)}$ , respectively. The space complexity of storing ANN index is ${\mathcal{O}}(nd+|E_{\mathcal{P}}|)$ . Finally, the time and space complexity of PEFA-XS is summarized in Table 1.

Connections to XMC

Given a passage, aggregating its relevant (as defined by customer behavior signals) query embeddings to be an alternative passage embeddings of itself has also been explored in the extreme multi-label classification (XMC) literature. Specifically, XMC community terms such representation as Postive Instance Feature Aggregation, namely PIFA embeddings (Jain et al., 2019; Chang et al., 2021; Zhang et al., 2021; Yu et al., 2022). However, PIFA embeddings are often an aggregation of sparse tfidf features, and mostly used for unsupervised clustering to partition label space in the XMC literature (Yu et al., 2022). In contrast, PEFA-XS interpolates such alternative passage embeddings with the original passage embeddings, and conduct ANN search on the interpolated ASIN embedding space. As a side note, PIFA embeddings are also closely connected to the simple graph convolution layer in graph neural network (Wu et al., 2019; Chien et al., 2022; Lu et al., 2021), where the input-to-label relevant matrix is viewed as a bipartite graph.

4. Experiments on Document Retrieval

In this section, we empirically verify the effectiveness of PEFA on the document retrieval task. Experiment code is available at https://github.com/amzn/pecos/tree/mainline/examples/pefa-wsdm24.

4.1. Datasets & Evaluation Protocols

Datasets.

We conducted experiments on two public benchmarks for document retrieval, namely the Natural Questions (Kwiatkowski et al., 2019) dataset and the Trivia-QA (Joshi et al., 2017) dataset.

•

Natural Questions (Kwiatkowski et al., 2019): a open-domain question answering dataset which consists of $320k$ query-document pairs, where the documents containing answers are gathered from Wikipedia and the queries are natural questions. The version we use is often referred to as NQ-320K (Bevilacqua et al., 2022; Tay et al., 2022; Wang et al., 2022a).
•

Trivia-QA (Joshi et al., 2017): a reading comprehension dataset which includes $78k$ query-document pairs from the Wikipedia domain. We use the same version as in (Wang et al., 2022a).

The State-of-the-art (SoTA) method, namely NCI (Wang et al., 2022a) consider generated query-document pairs as additional training signals in NQ-320K and Trivia-QA datasets. Following the same setup of NCI (Wang et al., 2022a), we also include those augmented query-document pairs when learning PEFA on NQ-320K and Trivia-QA datasets.

Evaluation Protocols

We measure the performance with recall metrics, which are widely-used in retrieval communities (Karpukhin et al., 2020; Chang et al., 2020; Ni et al., 2022a; Tay et al., 2022; Wang et al., 2022a). Specifically, given a predicted score vector $\hat{{\bm{y}}}\in{\mathbb{R}}^{n}$ and a ground truth label vector ${\bm{y}}\in\{0,1\}^{n}$ , Recall@k is defined as $\text{Recall}@k=\frac{1}{|{\bm{y}}|}\sum_{j\in\text{top}_{k}(\hat{{\bm{y}}})}{\bm{y}}_{j}$ where $\text{top}_{k}(\hat{{\bm{y}}})$ denotes labels with the $k$ largest predicted scores.

4.2. Implementation Details

Comparison Methods.

Our PEFA framework is applicable to any black-box ERMs. We applied PEFA to various competitive ERMs, such as $\text{Sent-BERT}_{\text{distill}}$ (Reimers and Gurevych, 2019), $\text{DPR}_{\text{base}}$ (Karpukhin et al., 2020), $\text{MPNet}_{\text{base}}$ (Song et al., 2020b), $\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a) and $\text{GTR}_{\text{base}}$ (Ni et al., 2022b). We also compare PEFA with recent SoTA Sequence-to-Sequence (Seq2Seq) models, including Differentiable Search Index (DSI) (Tay et al., 2022), Search Engines with Autoregressive LMs (SEAL) (Bevilacqua et al., 2022) and Neural Corpus Indexer (NCI )(Wang et al., 2022a).

Hyper-parameters

PEFA have two hyper-parameters, the interpolation coefficient $\lambda$ in Eq. 2 and the number of nearest neighbors $k$ in Eq. 6 used by PEFA-XL only. We present ablation studies on hyper-parameters in Section 4.4 where $\lambda=\{0.1,0.3,0.5,0.7,0.9\}$ and $k=\{16,32,64\}$ . For $\lambda=1.0$ , PEFA reduce back to its baseline ERM. We consider HNSW for ANN search and set hyper-parameters according to existing work (Nigam et al., 2019; Chang et al., 2021; Magnani et al., 2022). At the index building stage, the maximum edge per node $M=32$ and the size of priority queue for graph construction $efC=500$ . At the online serving stage, the beam search width for graph search $efS=300$ .

4.3. Main Results

NQ-320K

In Table 2, we applied PEFA-XS and PEFA-XL to fine-tuned ERMs: $\text{Sent-BERT}_{\text{distill}}$ (Reimers and Gurevych, 2019), $\text{DPR}_{\text{base}}$ (Karpukhin et al., 2020), $\text{MPNet}_{\text{base}}$ (Song et al., 2020b), $\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a) and $\text{GTR}_{\text{base}}$ (Ni et al., 2022b). These ERMs were full parameter fine-tuned on the NQ-320K dataset. The proposed PEFA framework achieved significant improvement for a wide range of black-box ERMs. The average gain of PEFA-XS over ERMs are $+9.22\%$ and $+5.29\%$ , for Recall@10 and Recall@100, respectively. The average gain of PEFA-XL over ERMs are $+11.33\%$ and $+5.20\%$ for Recall@10 and Recall@100, respectively. For competitive ERMs such as $\text{MPNet}_{\text{base}}$ (Song et al., 2020a) and $\text{GTR}_{\text{base}}$ (Ni et al., 2022b), PEFA further outperform the previous SoTA Seq2Seq method, namely NCI (Wang et al., 2022a). The Recall@10 and Recall@100 of $\text{MPNet}_{\text{base}}$ +PEFA-XL are $88.72\%$ and $94.13\%$ , which is considerably better than the previous SoTA NCI. On the other hand, the original $\text{MPNet}_{\text{base}}$ without PEFA can not outperform the previous SOTA method, NCI.

Methods	Recall@10	Recall@100
BM-25	32.48	50.54
DSI (base) (Tay et al., 2022)	56.60	-
NCI (base) (Wang et al., 2022a)	85.20	92.42
SEAL (large) (Bevilacqua et al., 2022)	81.24	90.93
$\text{Sent-BERT}_{\text{distill}}$ (Reimers and Gurevych, 2019)	67.08	81.40
$+$ PEFA-XS (ours)	80.52	92.22
$+$ PEFA-XL (ours)	85.26	92.53
$\text{DPR}_{\text{base}}$ (Karpukhin et al., 2020)	70.68	85.19
$+$ PEFA-XS (ours)	83.45	92.22
$+$ PEFA-XL (ours)	84.65	92.07
$\text{MPNet}_{\text{base}}$ (Song et al., 2020b)	80.82	92.39
$+$ PEFA-XS (ours)	86.67	94.53
$+$ PEFA-XL (ours)	88.72	95.13
$\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a)	73.63	88.16
$+$ PEFA-XS (ours)	82.52	92.18
$+$ PEFA-XL (ours)	83.69	92.55
$\text{GTR}_{\text{base}}$ (Ni et al., 2022b)	79.74	90.91
$+$ PEFA-XS (ours)	84.90	93.28
$+$ PEFA-XL (ours)	88.71	94.36
Avg. Gain of PEFA-XS over ERM	+9.22	+5.28
Avg. Gain of PEFA-XL over ERM	+11.82	+5.72

Table 2. Our PEFA framework on NQ-320K dataset. Both Seq2Seq models and ERMs are full-parameter fine-tuned. The results of BM-25, DSI (Tay et al., 2022), NCI (Wang et al., 2022a) and SEAL (Bevilacqua et al., 2022) are taken from (Wang et al., 2022a). 1st/2nd place numbers are boldface/underscore, respectively.

Trivia-QA

In Table 3, we applied PEFA-XS and PEFA-XL to pre-trained ERMs. Note that these ERMs were not fine-tuned with any relevant query-document pairs from Trivia-QA. The setup examines the robustness and generalization of our PEFA framework. We observe PEFA-XS and PEFA-XL achieve larger average gain of Recall over the unsupervised ERMs, when comparing Table 3 to Table 2. When the underlying ERM are pre-traiend only (not fine-tuned to the downstream task), PEFA-XS seems to perform slightly better than PEFA-XL in Recall@20, where the former has an average gain of $18.67\%$ while the latter has an average gain of $17.07\%$ .

Methods	Recall@20	Recall@100
BM-25	69.45	80.24
NCI (base) (Wang et al., 2022a)	94.45	96.94
SEAL (large) (Bevilacqua et al., 2022)	81.24	90.93
$\text{Sent-BERT}_{\text{distill}}$ (Reimers and Gurevych, 2019)	51.94	68.50
$+$ PEFA-XS (ours)	86.28	93.33
$+$ PEFA-XL (ours)	83.76	91.83
$\text{DPR}_{\text{base}}$ (Karpukhin et al., 2020)	60.69	73.80
$+$ PEFA-XS (ours)	82.97	91.06
$+$ PEFA-XL (ours)	78.76	89.62
$\text{MPNet}_{\text{base}}$ (Song et al., 2020b)	77.03	87.34
$+$ PEFA-XS (ours)	86.05	92.97
$+$ PEFA-XL (ours)	86.13	92.42
$\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a)	62.74	77.21
$+$ PEFA-XS (ours)	78.39	88.57
$+$ PEFA-XL (ours)	75.13	87.24
$\text{GTR}_{\text{base}}$ (Ni et al., 2022b)	71.75	82.05
$+$ PEFA-XS (ours)	83.81	91.02
$+$ PEFA-XL (ours)	85.30	92.38
Avg. Gain of PEFA-XS over ERM	+18.67	+13.61
Avg. Gain of PEFA-XL over ERM	+17.07	+12.80

Table 3. Our PEFA framework on Trivia-QA dataset. Seq2Seq models are full-parameter fine-tuned while ERMs are unsupervisedly pre-trained. ERMs +PEFA did not fine-tune or update any parameter of the underlying ERMs. 1st/2nd place numbers are boldface/underscore, respectively.

4.4. Ablation Studies

In Table 4, we present ablation studies of two hyper-parameters of our PEFA framework on the NQ-320K dataset. $\lambda$ is the interpolation coefficient that balances $f_{\text{ERM}}$ and $f_{\text{kNN}}$ in Equation 2. When $0.0<\lambda<1.0$ , the Recall@100 of both PEFA-XS and PEFA-XL are consistently higher the ERM alone ( $\lambda=1.0$ ). For PEFA-XS and PEFA-XL, $\lambda=0.5$ and $\lambda=0.1$ mostly yield the largest gain in average, respectively. Crucially, the linear interpolation of PEFA-XS can be pre-computed offline at the HNSW index building stage (see Figure 2) hence did not increase any inference latency overhead compared to the ERMs. For PEFA-XL, besides the hyper-parameter $\lambda$ , it has another hyper-parameter $k$ , controlling the number of nearest neighbors in the kNN model $f_{\text{kNN}}$ . We observed that $k=32$ generally saturate the performance.

ERM	PEFA	Recall@100 of various $\lambda$
ERM	PEFA	0.1	0.3	0.5	0.7	0.9
$\text{DPR}_{\text{base}}$	PEFA-XS	91.48	92.22	91.71	89.87	87.08
	PEFA-XL (k=16)	91.98	90.66	89.72	88.54	87.62
	PEFA-XL (k=32)	92.07	90.50	89.20	88.62	87.46
	PEFA-XL (k=64)	91.93	89.89	88.95	88.39	87.04
$\text{Sentence-T5}_{\text{base}}$	PEFA-XS	91.23	92.16	92.20	91.61	89.72
	PEFA-XL (k=16)	92.53	91.25	90.82	90.69	90.24
	PEFA-XL (k=32)	92.34	91.20	90.96	90.77	90.11
	PEFA-XL (k=64)	92.22	91.26	91.03	90.70	89.90
$\text{GTR}_{\text{base}}$	PEFA-XS	92.11	93.07	93.31	92.85	91.74
	PEFA-XL (k=16)	94.36	93.32	92.81	92.53	91.93
	PEFA-XL (k=32)	94.32	93.23	92.82	92.44	91.79
	PEFA-XL (k=64)	93.93	93.14	92.76	92.29	91.62

Table 4. Ablation study of our PEFA framework on NQ-320K dataset. PEFA-XS has only one hyper-parameter, namely the interpolation coefficient

\lambda

. PEFA-XL has two hyper-parameters:

\lambda

and

k

(number of nearest neighbors). For

\lambda=1.0

, PEFA-XS and PEFA-XL reduce to the same underlying ERM in Table 2.

5. Experiments on Product Search

For large-scale product search system, full-parameter fine-tuning may take thousands of GPU hours. In this section, we conducted experiments on such larger-scale datasets and demonstrated that our PEFA framework is an effective and fast technique that offers sizable improvements to not only a variety of pre-trained ERMs but also the full-parameter fine-tuned ERMs.

5.1. Datasets & Evaluation Protocols

Datasets

We follow similar procedure (Nigam et al., 2019; Chang et al., 2021; Lu et al., 2021; Joshi et al., 2022), to collect datasets from a large e-commerce product search engine. Based on the size of catalog $n=|{\mathcal{P}}|$ , we construct three subsets as follows.

•

ProdSearch-5M: consists of roughly 30 millions of relevant query-product pairs, which covers around 10 millions of queries and 5 millions of products.
•

ProdSearch-15M: consists of roughly 150 millions of relevant query-product pairs, which covers around 40 millions of queries and 15 millions of products.
•

ProdSearch-30M: consists of roughly 500 millions of relevant query-product pairs, which covers around 100 millions of queries and 30 millions of products.

For all proprietary ProdSearch datasets, the data statistics do not reflect the real traffic of the e-commerce system due to privacy concerns. All relevant query-product pairs are random samples from anonymous aggregated search log. We further split those pairs into the training set and the test set by time horizon, where we use first twelve months of search logs as the training set and the last one month of search logs as the evaluation test set.

Methods	ProdSearch-5M		ProdSearch-15M		ProdSearch-30M
Methods	Recall@100	Recall@1000	Recall@100	Recall@1000	Recall@100	Recall@1000
$\text{MPNet}_{\text{base}}$ (Song et al., 2020b)	0.00	0.00	0.00	0.00	0.00	0.00
$+$ PEFA-XS (ours)	11.23	13.14	5.05	11.79	9.67	17.47
$+$ PEFA-XL (ours)	22.83	12.31	23.48	21.56	27.22	18.96
$\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a)	0.44	3.42	1.32	3.44	1.89	5.17
$+$ PEFA-XS (ours)	13.63	17.13	10.39	16.34	13.18	21.28
$+$ PEFA-XL (ours)	23.09	13.43	23.91	23.72	30.10	21.25
$\text{GTR}_{\text{base}}$ (Ni et al., 2022b)	7.85	9.23	6.75	10.33	8.35	9.83
$+$ PEFA-XS (ours)	17.32	19.55	16.83	25.00	18.49	24.38
$+$ PEFA-XL (ours)	27.79	19.23	27.87	28.75	31.71	24.28
$\text{E5}_{\text{base}}$ (Wang et al., 2022b)	9.93	9.75	9.98	12.98	12.01	12.61
$+$ PEFA-XS (ours)	19.23	19.18	17.21	27.78	20.11	26.08
$+$ PEFA-XL (ours)	26.83	17.75	30.48	31.07	31.91	25.49
FT-ERM (Muhamed et al., 2023)	21.32	20.87	21.74	30.04	18.49	24.11
$+$ PEFA-XS (ours)	23.42	22.17	26.34	34.84	23.79	29.61
$+$ PEFA-XL (ours)	29.32	22.87	36.54	37.24	32.99	30.01
Avg. Gain of PEFA-XS	16.97	18.23	15.16	23.15	17.05	23.76
Avg. Gain of PEFA-XL	25.97	17.12	28.46	28.47	30.79	24.00

Table 5. Applying PEFA to pre-trained ERMs (

\text{MPNet}_{\text{base}}

(Song et al., 2020b),

\text{Sentence-T5}_{\text{base}}

(Ni et al., 2022a),

\text{GTR}_{\text{base}}

(Ni et al., 2022b) and

\text{E5}_{\text{base}}

(Wang et al., 2022b)) and the fine-tuned ERMs (FT-ERM (Muhamed et al., 2023)) on three proprietary product search datasets: ProdSearch-5M, ProdSearch-15M and ProdSearch-30M. To avoid disclosing the exact performance of production systems for privacy concerns, all reported numbers are absolute gain of Recall metrics compared to the baseline method

\text{MPNet}_{\text{base}}

. 1st/2nd place numbers are boldface/underscore, respectively.

Evaluation Protocol

To eliminate evaluation bias toward our PEFA framework, all test queries are unseen in the training set. To avoid disclosing the exact performance of production systems, we report absolute gain of Recall@k metrics between the proposed PEFA framework and the baseline ERMs.

We also report the ANN index size (GiB) and the index building time (hours) in offline indexing stage. For online inference, following the ANN benchmark protocol (Aumüller et al., 2020), we consider the single thread setup and report the inference latency (milliseconds/query).

5.2. Main Results

In Table 5, we applied PEFA to pre-trained ERMs (e.g., $\text{MPNet}_{\text{base}}$ (Song et al., 2020b), $\text{Sentence-T5}_{\text{base}}$ (Ni et al., 2022a), $\text{GTR}_{\text{base}}$ (Ni et al., 2022b) and $\text{E5}_{\text{base}}$ (Wang et al., 2022b)) and the fine-tuned ERMs (FT-ERM (Muhamed et al., 2023)). For privacy of the proprietary product search datasets, we only report the absolute gain of Recall metrics compared to the $\text{MPNet}_{\text{base}}$ baseline.

Without PEFA, pre-trained ERMs have much lower Recall metrics compared to FT-ERM, as the latter is carefully pre-trained and fine-tuned. Adding PEFA-XS and PEFA-XL to those pre-trained ERMs significantly lift the Recall to comparable, or even outperform, the fine-tuned FT-ERM. Take the largest dataset ProdSearch-30M as an example. Adding PEFA-XL to $\text{Sentence-T5}_{\text{base}}$ , $\text{GTR}_{\text{base}}$ and $\text{E5}_{\text{base}}$ have a Recall@100 gain of $30.10\%$ , $31.71\%$ and $31.91\%$ , respectively. These recall@100 gain is already outperform the Recall@100 of fine-tuned FT-ERM. On the other hand, PEFA-XS on pre-trained ERMs offer smaller Recall gain compared to PEFA-XL. Only $\text{E5}_{\text{base}}$ $+$ PEFA-XS have a larger Recall@100 gain compared to the fine-tuned FT-ERM.

Similar to the finding of NQ-320K, we also see that PEFA can further improve the performance of fine-tuned ERMs. For example, on the largest dataset ProdSearch-30M, PEFA-XS and PEFA-XL further improve the Recall@100 of the fine-tuned FT-ERM by $5.3\%$ and $14.50\%$ , respectively.

5.3. Indexing and Inference

In Table 6, we discuss the trade-off between the performance and the deployment efficiency for the proposed PEFA framework. Note that PEFA is a parameter-free method without updating model parameters of ERMs, which can be easily implemented in the offline HNSW index building stage. For the largest dataset ProdSearch-30M, the run-time of building HNSW indices for PEFA-XS and PEFA-XL are $1.0$ and $4.7$ hours, respectively. This is much faster than hundred of GPU hours when fine-tuning the FT-ERM on the billion-scale dataset.

Datasets	Methods	Indexing		Serving
Datasets	Methods	disk-size	run-time	Latency
ProdSearch-5M	FT-ERM	13.1	0.3	0.82
	$+$ PEFA-XS	13.1	0.2	0.67
	$+$ PEFA-XL	32.2	0.7	2.15
ProdSearch-15M	FT-ERM	28.6	0.6	0.91
	$+$ PEFA-XS	28.6	0.5	0.94
	$+$ PEFA-XL	100.7	1.9	1.94
ProdSearch-30M	FT-ERM	51.9	0.9	0.77
	$+$ PEFA-XS	51.9	1.0	0.71
	$+$ PEFA-XL	287.7	4.7	1.99

Table 6. For practical deployment consideration, we report the HNSW index size on disk (GiB) and the run-time (hours) of PEFA during offline index building stage. We also report the inference latency (millisecond/query) of the HNSW index for online serving.

Despite larger gain in recall metrics, PEFA-XL comes at the cost of larger HNSW index, longer index building time, and larger inference latency. Specifically, the HNSW index size of PEFA-XL is $3.6$ x larger than the HNSW index of ERM, as PEFA-XL requires two HNSW indices: One HNSW index on the product embeddings ${\mathbf{P}}\in{\mathbb{R}}^{n\times d}$ , while the other HNSW index on the training query embeddings ${\mathbf{Q}}\in{\mathbb{R}}^{m\times d}$ for the kNN modeling. For product search datasets, the number of queries $m$ can be larger than the number of products $n$ . Due to similar reasons, the inference latency of PEFA-XL is $2.4$ x larger than the latency of ERM.

On the other hand, PEFA-XS not only achieves modest gains of recall metrics, but also maintains the same deployment efficiency (e.g., HNSW index size and inference latency) as its baseline ERM. Recall that PEFA-XS maintains only one ANN index because the interpolation of $f_{\text{ERM}}$ and $f_{\text{kNN}}$ is independent to test-time query, which can be pre-computed offline in a single ANN index (see Equation 8 in Section 3.2). From the deployment perspective, PEFA-XS may be a more practical choice as it introduces zero additional overhead to the production system at inference time.

5.4. Effect of Supervised Data Size

The amount of supervised data (i.e., relevant query-product pairs) consumed by PEFA plays a crucial role to the predictive power of PEFA-XS and PEFA-XL, run-time of HNSW index building, and the model size of resulting HNSW indices. Hence, we present such analysis in Figure 3. The amount of supervised data is controlled by the sampling ratio $\{0.05,0.10,0.25,0.50,0.75,0.95\}$ . In particular, we uniformly sample query-product pairs from the relevance matrix ${\mathbf{Y}}\in\{0,1\}^{n\times m}$ in Equation 3.

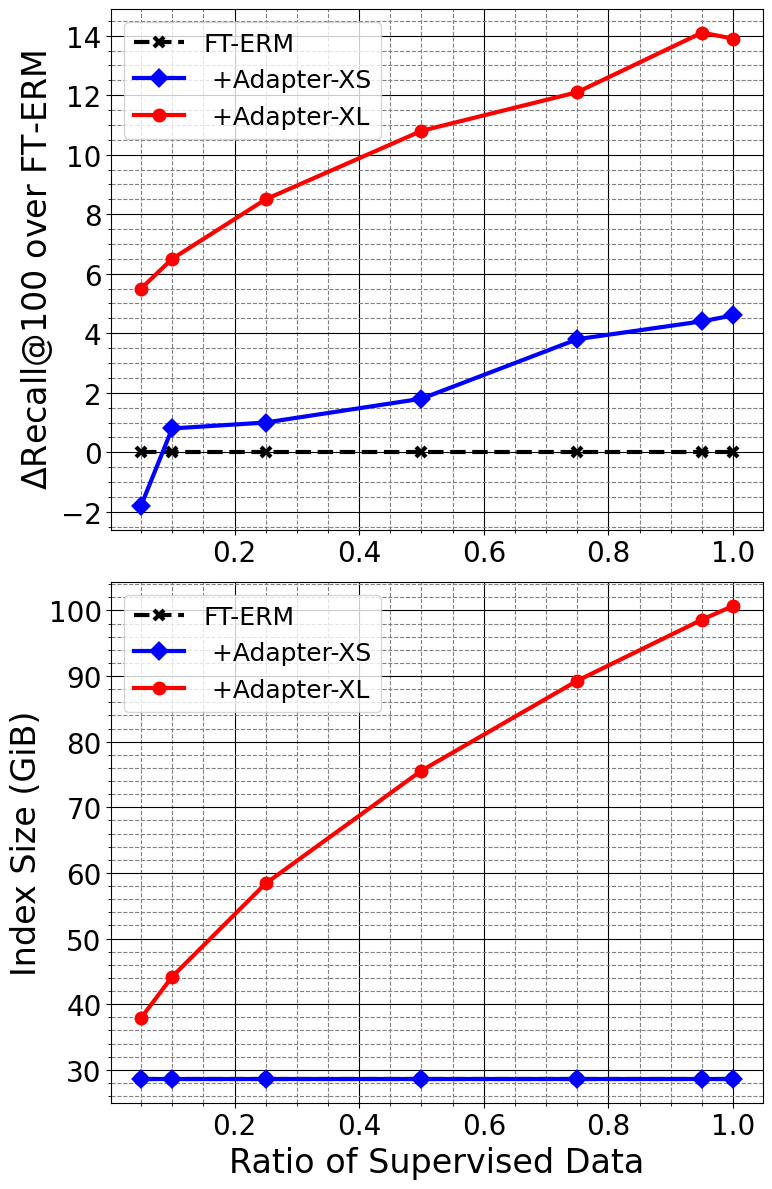
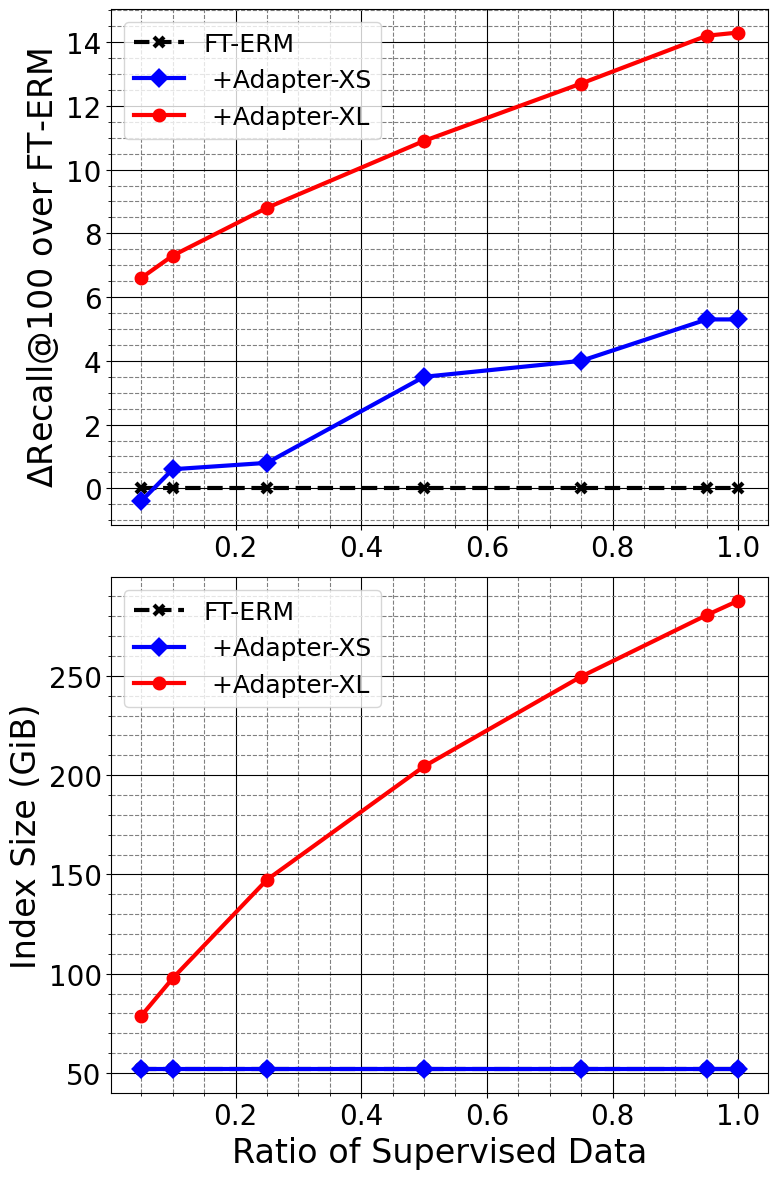
With 10% of the relevant query-product pairs sampled from ${\mathbf{Y}}$ , PEFA-XS reaches the same level of Recall@100 compared to the fine-tuned FT-ERM. With more supervised data, PEFA-XS outperforms FT-ERM eventually. What’s more, the model size of PEFA-XS do not increase as it consumes more supervised data.

For PEFA-XL, interestingly, it can achieve significant improvements in Recall@100 even with just $5\%$ of the supervised data. At $5\%$ of the supervised data usage, the resulting HNSW index is around $1.4$ x times larger than the HNSW index of FT-ERM and PEFA-XS. Also, the inference latency of PEFA-XL seems to be consistently $2$ x larger than the latency of FT-ERM and PEFA-XS across all datasets. Again, it is up to the practitioners to decide the trade-off between the additional performance gain brought by PEFA-XL and the cost of larger index size and inference latency.

6. Related Work

6.1. Dense Text Retrieval

DSSM (Huang et al., 2013) and C-DSSM (Shen et al., 2014) utilize multi-layer perceptron and convolutional neural networks while DPR (Karpukhin et al., 2020) deploys pre-trained neural language models (NLMs) like BERT (Devlin et al., 2019). Some studies attempt to improve ERMs by pre-training and adjusting results. Condenser (Gao and Callan, 2021) pre-trains NLMs with the idea of Funnel-Transformer (Dai et al., 2020) while Co-Condenser (Gao and Callan, 2022) re-ranks its retrieval results with an attentive cross-encoder. DPTDR (Tang et al., 2022) applies prompt-tuning (Liu et al., 2023) to further improve the quality dual encoders for ERMs. However, conventional ERMs could suffer from dealing with tail queries and labels, especially when we have an enormous industry-scale index (Reimers and Gurevych, 2021). Even though some lines of research attempt to address this issue by computing label-centric similarity (Ren et al., 2021a) and multi-view representations (Zhang et al., 2022b), they are infeasible for industrial production due to the requirement of extensive pre-training and additional cross-attentive computations between queries and labels.

Different from existing approaches, our PEFA has no need of pre-training another embedding model, so the enhancement can be achieved within an acceptable short period of only ANN search indexing. Moreover, the kNN model of training queries can further benefit the representation capability of PEFA embedding.

6.2. Inference with Training Instances

Similar to our proposed PEFA framework, some studies also leverage training instances in inference for better performance in various research fields. $k$ nearest neighbors language modeling (kNN-LM) (Khandelwal et al., 2020; Yogatama et al., 2021; He et al., 2021) build a kNN model within the small vocabulary space while PIFA embeddings (Jain et al., 2019; Chang et al., 2021; Zhang et al., 2021; Yu et al., 2022) aggregate sparse representations of training instances for the label space. The derived coresets of training embeddings can be indexed with ANN search to shrink candidate labels and accelerate inference for recommender systems (Jiang et al., 2020) and neural language models (Chen et al., 2019). However, none of the above methods addresses the challenge of large-scale retrieval in an industry scale.

6.3. Parameter-Efficient Tuning of ERMs

To avoid the expensive full-parameter fine-tuning of ERMs for various downstream tasks, there are some preliminary studies on parameter-efficient fine-tuning of ERMs (Jung et al., 2022; Ma et al., 2022; Pal et al., 2023). Nevertheless, as pointed out by (Ma et al., 2022), naively apply existing parameter-efficient fine-tuning methods in the NLP literature, such as Adapter (Houlsby et al., 2019), prefix-tuning (Li and Liang, 2021) and LoRA (Hu et al., 2022), often results in limited success for ERM in the retrieval applications. Furthermore, parameter-efficient fine-tuning approaches still require access to the models’ gradient, which may not be available for the recent powerful large language models (LLMs) such as GPT-3 (Brown et al., 2020). Our proposed PEFA framework is complementary to any pre-trained and fine-tuned ERMs, namely including ERMs derived from parameter-efficient fine-tuning. Notice that our PEFA did not require any gradient information of the underlying ERMs, which can have a broader impact to black-box ERMs where the encoders are initialized from LLMs.

7. Conclusions

In this paper, we propose PEFA, parameter-free adapters for fast tuning of black-box ERMs. PEFA offers flexible choices (i.e., PEFA-XS and PEFA-XL) for practitioners to improve their pre-trained or fine-tuned ERMs efficiently, without any updates to model parameters of ERMs. PEFA-XL brings more significant gain of Recall@k at the cost of doubling the ANN index size and inference latency, while PEFA-XS yields modest gain of Recall@k without any overhead compared to the existing ERM inference pipeline. For document retrieval, PEFA not only improves the recall@100 of pre-trained ERMs on Trivia-QA by an average of 13.2%, but also lifts the recall@100 of fine-tuned ERMs on NQ-320K by an average of 5.5%. For NQ-320K dataset, applying PEFA to $\text{MPNet}_{\text{base}}$ (Song et al., 2020b) and $\text{GTR}_{\text{base}}$ (Ni et al., 2022b) reaches new SoTA results, where the Recall@10 of $88.72\%$ outperforms $85.20\%$ of previous SoTA Seq2Seq-based NCI (Wang et al., 2022a). For product search consisting of billion-scale of data, PEFA improves the Recall@100 of the fine-tuned ERMs by an average of 5.3% and 14.5%, for PEFA-XS and PEFA-XL, respectively.

Ethical Considerations

We discuss ethical implications of our PEFA framework in two perspectives: interpretability and privacy.

Interpretability

Given a query, embedding-based retrieval models (ERMs) retrieve the match set based on similarity search between the query embedding and the corpus of passage embeddings. However, the interpretability and explainability of ERMs is quite limited because we do not know which training examples contribute to or lead to the decisions of the retrieved match-set. Our proposed framework PEFA combines ERMs with a non-parametric kNN component, which enhances the interpretability of ERMs. The kNN component computes similarity scores between the test query and the set of training queries, hence we know which training examples contribute the most to the retrieved match-set.

Privacy

For e-commerce product search, it is crucial to protect customers privacy. Thus, we need to insure the underlying models do not explicitly memorize customers purchase history. When applying PEFA to the product search datasets, we carefully anonymized the search log, hence we never know which customer issues a specific query. Furthermore, we consider yearly-aggregated data of query-product pairs as the training signals in our kNN component. In other words, each query in our training set can not be traced back to its original query session.

References

(1)
Aumüller et al. (2020) Martin Aumüller, Erik Bernhardsson, and Alexander Faithfull. 2020. ANN-Benchmarks: A benchmarking tool for approximate nearest neighbor algorithms. Information Systems 87 (2020), 101374.
Bevilacqua et al. (2022) Michele Bevilacqua, Giuseppe Ottaviano, Patrick Lewis, Scott Yih, Sebastian Riedel, and Fabio Petroni. 2022. Autoregressive search engines: Generating substrings as document identifiers. Advances in Neural Information Processing Systems 35 (2022), 31668–31683.
Borgeaud et al. (2022) Sebastian Borgeaud, Arthur Mensch, Jordan Hoffmann, Trevor Cai, Eliza Rutherford, Katie Millican, George Bm Van Den Driessche, Jean-Baptiste Lespiau, Bogdan Damoc, Aidan Clark, et al. 2022. Improving language models by retrieving from trillions of tokens. In International conference on machine learning. PMLR, 2206–2240.
Brown et al. (2020) Tom Brown, Benjamin Mann, Nick Ryder, Melanie Subbiah, Jared D Kaplan, Prafulla Dhariwal, Arvind Neelakantan, Pranav Shyam, Girish Sastry, Amanda Askell, et al. 2020. Language models are few-shot learners. Advances in neural information processing systems 33 (2020), 1877–1901.
Chang et al. (2021) Wei-Cheng Chang, Daniel Jiang, Hsiang-Fu Yu, Choon-Hui Teo, Jiong Zhang, Kai Zhong, Kedarnath Kolluri, Qie Hu, Nikhil Shandilya, Vyacheslav Ievgrafov, Japinder Singh, and Inderjit S Dhillon. 2021. Extreme Multi-label Learning for Semantic Matching in Product Search. In Proceedings of the 27th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining.
Chang et al. (2020) Wei-Cheng Chang, Felix X. Yu, Yin-Wen Chang, Yiming Yang, and Sanjiv Kumar. 2020. Pre-training Tasks for Embedding-based Large-scale Retrieval. In International Conference on Learning Representations.
Chen et al. (2019) Patrick H Chen, Si Si, Sanjiv Kumar, Yang Li, and Cho-Jui Hsieh. 2019. Learning to Screen for Fast Softmax Inference on Large Vocabulary Neural Networks. In International conference on learning representation (ICLR).
Chien et al. (2022) Eli Chien, Wei-Cheng Chang, Cho-Jui Hsieh, Hsiang-Fu Yu, Jiong Zhang, Olgica Milenkovic, and Inderjit S Dhillon. 2022. Node Feature Extraction by Self-Supervised Multi-scale Neighborhood Prediction. In International Conference on Learning Representations (ICLR).
Dai et al. (2020) Zihang Dai, Guokun Lai, Yiming Yang, and Quoc Le. 2020. Funnel-transformer: Filtering out sequential redundancy for efficient language processing. Advances in neural information processing systems 33 (2020), 4271–4282.
Devlin et al. (2019) Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. 2019. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers). Association for Computational Linguistics, 4171––4186.
Formal et al. (2022) Thibault Formal, Carlos Lassance, Benjamin Piwowarski, and Stéphane Clinchant. 2022. From distillation to hard negative sampling: Making sparse neural ir models more effective. In Proceedings of the 45th International ACM SIGIR Conference on Research and Development in Information Retrieval. 2353–2359.
Gao and Callan (2021) Luyu Gao and Jamie Callan. 2021. Condenser: a Pre-training Architecture for Dense Retrieval. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic, 981–993. https://doi.org/10.18653/v1/2021.emnlp-main.75
Gao and Callan (2022) Luyu Gao and Jamie Callan. 2022. Unsupervised Corpus Aware Language Model Pre-training for Dense Passage Retrieval. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). Association for Computational Linguistics, Dublin, Ireland, 2843–2853. https://doi.org/10.18653/v1/2022.acl-long.203
Guo et al. (2022) Jiafeng Guo, Yinqiong Cai, Yixing Fan, Fei Sun, Ruqing Zhang, and Xueqi Cheng. 2022. Semantic models for the first-stage retrieval: A comprehensive review. ACM Transactions on Information Systems (TOIS) 40, 4 (2022), 1–42.
Guo et al. (2020) Ruiqi Guo, Philip Sun, Erik Lindgren, Quan Geng, David Simcha, Felix Chern, and Sanjiv Kumar. 2020. Accelerating large-scale inference with anisotropic vector quantization. In International Conference on Machine Learning. PMLR, 3887–3896.
Guu et al. (2020) Kelvin Guu, Kenton Lee, Zora Tung, Panupong Pasupat, and Mingwei Chang. 2020. Retrieval augmented language model pre-training. In International Conference on Machine Learning. PMLR, 3929–3938.
He et al. (2021) Junxian He, Graham Neubig, and Taylor Berg-Kirkpatrick. 2021. Efficient Nearest Neighbor Language Models. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic, 5703–5714. https://doi.org/10.18653/v1/2021.emnlp-main.461
Houlsby et al. (2019) Neil Houlsby, Andrei Giurgiu, Stanislaw Jastrzebski, Bruna Morrone, Quentin De Laroussilhe, Andrea Gesmundo, Mona Attariyan, and Sylvain Gelly. 2019. Parameter-efficient transfer learning for NLP. In International Conference on Machine Learning. PMLR, 2790–2799.
Hu et al. (2022) Edward J Hu, yelong shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, and Weizhu Chen. 2022. LoRA: Low-Rank Adaptation of Large Language Models. In International Conference on Learning Representations. https://openreview.net/forum?id=nZeVKeeFYf9
Huang et al. (2020) Jui-Ting Huang, Ashish Sharma, Shuying Sun, Li Xia, David Zhang, Philip Pronin, Janani Padmanabhan, Giuseppe Ottaviano, and Linjun Yang. 2020. Embedding-based retrieval in facebook search. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2553–2561.
Huang et al. (2013) Po-Sen Huang, Xiaodong He, Jianfeng Gao, Li Deng, Alex Acero, and Larry Heck. 2013. Learning deep structured semantic models for web search using clickthrough data. In Proceedings of the 22nd ACM international conference on Information & Knowledge Management. 2333–2338.
Jain et al. (2019) Himanshu Jain, Venkatesh Balasubramanian, Bhanu Chunduri, and Manik Varma. 2019. SLICE: Scalable Linear Extreme Classifiers Trained on 100 Million Labels for Related Searches. In Proceedings of the Twelfth ACM International Conference on Web Search and Data Mining. ACM, 528–536.
Jayaram Subramanya et al. (2019) Suhas Jayaram Subramanya, Fnu Devvrit, Harsha Vardhan Simhadri, Ravishankar Krishnawamy, and Rohan Kadekodi. 2019. DiskANN: Fast accurate billion-point nearest neighbor search on a single node. Advances in Neural Information Processing Systems 32 (2019).
Jiang et al. (2020) Jyun-Yu Jiang, Patrick H Chen, Cho-Jui Hsieh, and Wei Wang. 2020. Clustering and constructing user coresets to accelerate large-scale top-k recommender systems. In Proceedings of The Web Conference 2020. 2177–2187.
Johnson et al. (2019) Jeff Johnson, Matthijs Douze, and Hervé Jégou. 2019. Billion-scale similarity search with GPUs. IEEE Transactions on Big Data 7, 3 (2019), 535–547.
Joshi et al. (2022) Ashutosh Joshi, Shankar Vishwanath, Choon Hui Teo, Rahul Bhagat, Vaclav Petricek, Vishy Vishwanathan, and Jonathan May. 2022. Augmenting Training Data for Massive Semantic Matching Models in Low-Traffic E-commerce Stores. In NAACL-HLT 2022. 160.
Joshi et al. (2017) Mandar Joshi, Eunsol Choi, Daniel Weld, and Luke Zettlemoyer. 2017. TriviaQA: A Large Scale Distantly Supervised Challenge Dataset for Reading Comprehension. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). Association for Computational Linguistics, Vancouver, Canada, 1601–1611. https://doi.org/10.18653/v1/P17-1147
Jung et al. (2022) Euna Jung, Jaekeol Choi, and Wonjong Rhee. 2022. Semi-siamese bi-encoder neural ranking model using lightweight fine-tuning. In Proceedings of the ACM Web Conference 2022. 502–511.
Karpukhin et al. (2020) Vladimir Karpukhin, Barlas Oguz, Sewon Min, Patrick Lewis, Ledell Wu, Sergey Edunov, Danqi Chen, and Wen-tau Yih. 2020. Dense Passage Retrieval for Open-Domain Question Answering. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing (EMNLP). Association for Computational Linguistics, Online, 6769–6781. https://doi.org/10.18653/v1/2020.emnlp-main.550
Khandelwal et al. (2020) Urvashi Khandelwal, Omer Levy, Dan Jurafsky, Luke Zettlemoyer, and Mike Lewis. 2020. Generalization through Memorization: Nearest Neighbor Language Models. In International Conference on Learning Representations. https://openreview.net/forum?id=HklBjCEKvH
Kwiatkowski et al. (2019) Tom Kwiatkowski, Jennimaria Palomaki, Olivia Redfield, Michael Collins, Ankur Parikh, Chris Alberti, Danielle Epstein, Illia Polosukhin, Jacob Devlin, Kenton Lee, et al. 2019. Natural questions: a benchmark for question answering research. Transactions of the Association for Computational Linguistics (TACL) 7 (2019), 453–466.
Lewis et al. (2020) Patrick Lewis, Ethan Perez, Aleksandra Piktus, Fabio Petroni, Vladimir Karpukhin, Naman Goyal, Heinrich Küttler, Mike Lewis, Wen-tau Yih, Tim Rocktäschel, et al. 2020. Retrieval-augmented generation for knowledge-intensive nlp tasks. Advances in Neural Information Processing Systems 33 (2020), 9459–9474.
Li and Liang (2021) Xiang Lisa Li and Percy Liang. 2021. Prefix-Tuning: Optimizing Continuous Prompts for Generation. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 1: Long Papers). Association for Computational Linguistics, Online, 4582–4597. https://doi.org/10.18653/v1/2021.acl-long.353
Lin et al. (2021) Sheng-Chieh Lin, Jheng-Hong Yang, and Jimmy Lin. 2021. In-batch negatives for knowledge distillation with tightly-coupled teachers for dense retrieval. In Proceedings of the 6th Workshop on Representation Learning for NLP (RepL4NLP-2021). 163–173.
Liu et al. (2023) Pengfei Liu, Weizhe Yuan, Jinlan Fu, Zhengbao Jiang, Hiroaki Hayashi, and Graham Neubig. 2023. Pre-train, prompt, and predict: A systematic survey of prompting methods in natural language processing. Comput. Surveys 55, 9 (2023), 1–35.
Lu et al. (2021) Hanqing Lu, Youna Hu, Tong Zhao, Tony Wu, Yiwei Song, and Bing Yin. 2021. Graph-based Multilingual Product Retrieval in E-Commerce Search. In NAACL-HLT (Industry Papers). 146–153. https://doi.org/10.18653/v1/2021.naacl-industry.19
Ma et al. (2022) Xinyu Ma, Jiafeng Guo, Ruqing Zhang, Yixing Fan, and Xueqi Cheng. 2022. Scattered or Connected? An Optimized Parameter-efficient Tuning Approach for Information Retrieval. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management. 1471–1480.
Magnani et al. (2022) Alessandro Magnani, Feng Liu, Suthee Chaidaroon, Sachin Yadav, Praveen Reddy Suram, Ajit Puthenputhussery, Sijie Chen, Min Xie, Anirudh Kashi, Tony Lee, et al. 2022. Semantic Retrieval at Walmart. In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining. 3495–3503.
Malkov and Yashunin (2018) Yu A Malkov and Dmitry A Yashunin. 2018. Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs. IEEE transactions on pattern analysis and machine intelligence 42, 4 (2018), 824–836.
Muhamed et al. (2023) Aashiq Muhamed, Sriram Srinivasan, Choon-Hui Teo, Qingjun Cui, Belinda Zeng, Trishul Chilimbi, and SVN Vishwanathan. 2023. Web-Scale Semantic Product Search with Large Language Models. In Advances in Knowledge Discovery and Data Mining: 27th Pacific-Asia Conference on Knowledge Discovery and Data Mining, PAKDD 2023, Osaka, Japan, May 25–28, 2023, Proceedings, Part III. Springer, 73–85.
Ni et al. (2022a) Jianmo Ni, Gustavo Hernandez Abrego, Noah Constant, Ji Ma, Keith Hall, Daniel Cer, and Yinfei Yang. 2022a. Sentence-T5: Scalable Sentence Encoders from Pre-trained Text-to-Text Models. In Findings of the Association for Computational Linguistics: ACL 2022. Association for Computational Linguistics, Dublin, Ireland, 1864–1874. https://doi.org/10.18653/v1/2022.findings-acl.146
Ni et al. (2022b) Jianmo Ni, Chen Qu, Jing Lu, Zhuyun Dai, Gustavo Hernandez Abrego, Ji Ma, Vincent Zhao, Yi Luan, Keith Hall, Ming-Wei Chang, and Yinfei Yang. 2022b. Large Dual Encoders Are Generalizable Retrievers. In Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Abu Dhabi, United Arab Emirates, 9844–9855. https://aclanthology.org/2022.emnlp-main.669
Nigam et al. (2019) Priyanka Nigam, Yiwei Song, Vijai Mohan, Vihan Lakshman, Weitian Ding, Ankit Shingavi, Choon Hui Teo, Hao Gu, and Bing Yin. 2019. Semantic product search. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2876–2885.
Pal et al. (2023) Vaishali Pal, Carlos Lassance, Hervé Déjean, and Stéphane Clinchant. 2023. Parameter-Efficient Sparse Retrievers and Rerankers Using Adapters. In Advances in Information Retrieval: 45th European Conference on Information Retrieval, ECIR 2023, Dublin, Ireland, April 2–6, 2023, Proceedings, Part II. Springer, 16–31.
Reimers and Gurevych (2019) Nils Reimers and Iryna Gurevych. 2019. Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing (EMNLP).
Reimers and Gurevych (2021) Nils Reimers and Iryna Gurevych. 2021. The Curse of Dense Low-Dimensional Information Retrieval for Large Index Sizes. In Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing (Volume 2: Short Papers). 605–611.
Ren et al. (2021a) Ruiyang Ren, Shangwen Lv, Yingqi Qu, Jing Liu, Wayne Xin Zhao, Qiaoqiao She, Hua Wu, Haifeng Wang, and Ji-Rong Wen. 2021a. PAIR: Leveraging Passage-Centric Similarity Relation for Improving Dense Passage Retrieval. In Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021. 2173–2183.
Ren et al. (2021b) Ruiyang Ren, Yingqi Qu, Jing Liu, Wayne Xin Zhao, QiaoQiao She, Hua Wu, Haifeng Wang, and Ji-Rong Wen. 2021b. RocketQAv2: A Joint Training Method for Dense Passage Retrieval and Passage Re-ranking. In Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Association for Computational Linguistics, Online and Punta Cana, Dominican Republic, 2825–2835. https://doi.org/10.18653/v1/2021.emnlp-main.224
Shen et al. (2014) Yelong Shen, Xiaodong He, Jianfeng Gao, Li Deng, and Grégoire Mesnil. 2014. Learning semantic representations using convolutional neural networks for web search. In Proceedings of the 23rd international conference on world wide web. 373–374.
Song et al. (2020b) Kaitao Song, Xu Tan, Tao Qin, Jianfeng Lu, and Tie-Yan Liu. 2020b. Mpnet: Masked and permuted pre-training for language understanding. Advances in Neural Information Processing Systems 33 (2020), 16857–16867.
Song et al. (2020a) Liuyihan Song, Pan Pan, Kang Zhao, Hao Yang, Yiming Chen, Yingya Zhang, Yinghui Xu, and Rong Jin. 2020a. Large-scale training system for 100-million classification at alibaba. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2909–2930.
Tang et al. (2022) Zhengyang Tang, Benyou Wang, and Ting Yao. 2022. DPTDR: Deep Prompt Tuning for Dense Passage Retrieval. In Proceedings of the 29th International Conference on Computational Linguistics. 1193–1202.
Tay et al. (2022) Yi Tay, Vinh Tran, Mostafa Dehghani, Jianmo Ni, Dara Bahri, Harsh Mehta, Zhen Qin, Kai Hui, Zhe Zhao, Jai Gupta, et al. 2022. Transformer memory as a differentiable search index. Advances in Neural Information Processing Systems 35 (2022), 21831–21843.
Wang et al. (2022b) Liang Wang, Nan Yang, Xiaolong Huang, Binxing Jiao, Linjun Yang, Daxin Jiang, Rangan Majumder, and Furu Wei. 2022b. Text Embeddings by Weakly-Supervised Contrastive Pre-training. arXiv preprint arXiv:2212.03533 (2022).
Wang et al. (2021) Mengzhao Wang, Xiaoliang Xu, Qiang Yue, and Yuxiang Wang. 2021. A comprehensive survey and experimental comparison of graph-based approximate nearest neighbor search. arXiv preprint arXiv:2101.12631 (2021).
Wang et al. (2022a) Yujing Wang, Yingyan Hou, Haonan Wang, Ziming Miao, Shibin Wu, Qi Chen, Yuqing Xia, Chengmin Chi, Guoshuai Zhao, Zheng Liu, et al. 2022a. A neural corpus indexer for document retrieval. Advances in Neural Information Processing Systems 35 (2022), 25600–25614.
Wu et al. (2019) Felix Wu, Amauri Souza, Tianyi Zhang, Christopher Fifty, Tao Yu, and Kilian Weinberger. 2019. Simplifying graph convolutional networks. In International conference on machine learning. PMLR, 6861–6871.
Xiong et al. (2021) Lee Xiong, Chenyan Xiong, Ye Li, Kwok-Fung Tang, Jialin Liu, Paul N. Bennett, Junaid Ahmed, and Arnold Overwijk. 2021. Approximate Nearest Neighbor Negative Contrastive Learning for Dense Text Retrieval. In International Conference on Learning Representations. https://openreview.net/forum?id=zeFrfgyZln
Yogatama et al. (2021) Dani Yogatama, Cyprien de Masson d’Autume, and Lingpeng Kong. 2021. Adaptive semiparametric language models. Transactions of the Association for Computational Linguistics 9 (2021), 362–373.
Yu et al. (2017) Hsiang-Fu Yu, Cho-Jui Hsieh, Qi Lei, and Inderjit S Dhillon. 2017. A greedy approach for budgeted maximum inner product search. In Advances in Neural Information Processing Systems. 5453–5462.
Yu et al. (2022) Hsiang-Fu Yu, Kai Zhong, Jiong Zhang, Wei-Cheng Chang, and Inderjit S Dhillon. 2022. PECOS: Prediction for enormous and correlated output spaces. Journal of Machine Learning Research 23, 98 (2022), 1–32.
Zhan et al. (2021) Jingtao Zhan, Jiaxin Mao, Yiqun Liu, Jiafeng Guo, Min Zhang, and Shaoping Ma. 2021. Optimizing dense retrieval model training with hard negatives. In Proceedings of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval. 1503–1512.
Zhang et al. (2022a) Hang Zhang, Yeyun Gong, Yelong Shen, Jiancheng Lv, Nan Duan, and Weizhu Chen. 2022a. Adversarial Retriever-Ranker for Dense Text Retrieval. In International Conference on Learning Representations. https://openreview.net/forum?id=MR7XubKUFB
Zhang et al. (2021) Jiong Zhang, Wei-Cheng Chang, Hsiang-Fu Yu, and Inderjit S Dhillon. 2021. Fast Multi-Resolution Transformer Fine-tuning for Extreme Multi-label Text Classification. In Advances in Neural Information Processing Systems.
Zhang et al. (2022b) Shunyu Zhang, Yaobo Liang, Ming Gong, Daxin Jiang, and Nan Duan. 2022b. Multi-View Document Representation Learning for Open-Domain Dense Retrieval. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). 5990–6000.